To Calibrate & Validate an Agent-based Simulation Model

An Application of the Combination Framework of BI Solution &

Multi-agent Platform

Thai Minh Truong

1,2

, Frédéric Amblard

, Benoit Gaudou

and Christophe Sibertin Blanc

UMR 5505 CNRS-IRIT, Université Toulouse 1 Capitole, Toulouse, France

CIT, Can Tho University, Can Tho, Vietnam

Keywords: Calibration, Validation, BI Solution, Data Warehouse, Multi-Agent Simulation, Agent-based Model, Brown

Plant Hopper.

Abstract: Integrated environmental modeling approaches, especially the agent-based modeling one, are increasingly

used in large-scale decision support systems. A major consequence of this trend is the manipulation and

generation of huge amount of data in simulations, which must be efficiently managed. Furthermore,

calibration and validation are also challenges for Agent-Based Modelling and Simulation (ABMS)

approaches when the model has to work with integrated systems involving high volumes of input/output

data. In this paper, we propose a calibration and validation approach for an agent-based model, using a

Combination Framework of Business intelligence solution and Multi-agent platform (CFBM). The CFBM is

a logical framework dedicated to the management of the input and output data in simulations, as well as the

corresponding empirical datasets in an integrated way. The calibration and validation of Brown Plant

Hopper Prediction model are presented and used throughout the paper as a case study to illustrate the way

CFBM manages the data used and generated during the life-cycle of simulation and validation.

1 INTRODUCTION

Integrated socio-environmental modeling in general

and multi-agent based simulation approach applied

to socio-environmental systems in particular are

increasingly used as decision-support systems in

order to design, evaluate and plan public policies

linked to the management of natural resources

(Laniak et al., 2013). For example, in the research

about invasions of Brown Plant Hopper (BPH) and

the impact of BPH on rice fields of the Mekong

Delta region (Vietnam), researchers must develop

and integrate several models (e.g. BPH growth

model, light-trap model, BPH migration model).

They must also integrate data from different data

sources and analyze the integrated data at different

scales. Such an integrated simulation system

involving high volume of data raises two problems:

how to manage and analyze outputs of simulation

models considering such a high volume of input?

Although computing power is increasing rapidly,

to determine the accuracy of the simulation outputs

from a large size of inputs with several parameters

and to work on the high computational requirements

in large systems are still the limitations of agent-

based modelling (Crooks and Heppenstall, 2012).

When developing a simulation model, the modelers'

ambition is to achieve a credible model. To obtain a

credible model or to determine the accuracy of the

simulation outputs, calibration and validation are

two necessary processes (Donigian, 2002; Klügl,

2008; Law, 2009). For instance, complex agent-

based models are usually executed with several

parameters and generate a huge amount of data,

which do not have exactly the same structure than

observation data from real system and can be

measured and validated in various conditions. In

such case, calibration and validation are used to

determine which inputs and outputs are appropriate

regarding observation data (Ngo and See, 2012;

Rogers and Tessin, 2004; Said et al., 2002).

Furthermore, calibration and validation are among

the greatest challenges in agent-based modelling

(Crooks et al., 2008; Crooks and Heppenstall, 2012).

Therefore, how to solve the two challenges

(calibration and validation) of agent-based

modelling and simulation when the model deals with

172

Minh Truong T., Amblard F., Gaudou B. and Sibertin Blanc C..

To Calibrate & Validate an Agent-based Simulation Model - An Application of the Combination Framework of BI Solution & Multi-agent Platform .

DOI: 10.5220/0004820401720183

In Proceedings of the 6th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2014), pages 172-183

ISBN: 978-989-758-016-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

integrated systems with a high volume of

input/output data?

In this article, we briefly describe a Combination

Framework of BI solution and Multi-agent platform

(CFBM). CFBM was designed and implemented in

GAMA (Truong et al., 2013) and it can be used to

model and execute agent-based simulation models,

to handle data input/output of the models, and to

conduct data analysis. Subsequently, we expose an

approach for the calibration and validation of multi-

agent models by applying the CFBM, which

proposes a solution to two of the limitations of

agent-based modelling when working in integrated

systems. In addition, a specific measure is presented,

i.e. Jaccard index for ordered data sets, which has

been used to evaluate the accuracy of simulation

outputs.

Hence the major contribution of this article is to

propose an implemented framework (CFBM) to

address two crucial issues in agent-based simulation

that are the calibration and validation of such

models. In order to demonstrate the feasibility and

the interest of the application of such framework, we

apply it to the calibration and validation of a Brown

Plant Hoppe invasion model, which is described

briefly.

In the following sections, we first present the

state of the art of works linking ABMS, BI and

calibration and validation of simulation models

(Section 2). The global architecture of the

Combination Framework of BI solution and Multi-

agent platform is presented in Section 3. In Section

4, we illustrate the calibration and validation

approach for integrated agent-based simulation

models. In Section 5, we apply the approach on an

integrated simulation model, namely the BPH

prediction model, in order to calibrate and validate

the model on the GAMA simulation platform in

order to illustrate the approach. Discussion and

perspectives conclude this article.

2 RELATED WORKS

2.1 Integration of BI Solution into a

Simulation System

Data Warehouse (DW) and analysis tools such as BI

solutions can help users to manage a large amount of

simulation data and to make several data analyses

that support the decision-making processes (Inmon,

2005; Kimball and Ross, 2002). The combination of

simulation tools and DW is on the increase and

being applied in different areas. For example,

although (Madeira et al., 2003; Sosnowski et al.,

2007) are only two applications of OLAP

technologies to a specific problem, these works

demonstrate that a multidimensional database is

suitable to store several hundreds of thousands of

simulation results. Simulation models, DW and

analysis tools with OLAP technologies were also

integrated in decision support systems or forecast

systems (Ehmke et al., 2011; Vasilakis et al., 2008).

In (Mahboubi et al., 2010), Mahboubi et al. also

used data warehouse and OLAP technologies to

store and analyze a huge amount of output data

generated by the coupling of complex simulation

models such as biological, meteorological and so on.

In particular, the authors proposed DW and Online

Analytical Processing tool (OLAP tool) for storing

and analyzing simulation results.

The mentioned state of the art demonstrates

therefore the practical possibility and the usefulness

of the combination of simulation, data warehouse

and OLAP technologies. It also shows the potential

of a general framework that has, as far as we know,

not yet been proposed in the literature.

2.2 Calibration and Validation

What are calibration and validation? The calibration

process is known as a test of a model with known

input and output information. It is used to adjust or

estimate factors for data which are not available. The

validation process is the comparison of model results

with numerical data independently derived from

experiments or observations of the environment.

These two definitions are taken from (Donigian,

2002) who was citing (ASTM, 1984). In the

validation of multi-agent simulation, there are two

kinds of validation: internal validation and external

validation (Amblard et al., 2007). These two

processes are also presented in terms of "face

validation" and "statistical validation" by (Klügl,

2008). Internal validation is used to check the

conformity between specifications and the

implemented model. In the software engineering

field, it is usually called verification and corresponds

to the process which is used to compare the

conceptual model to the computer-generated model.

Internal validation corresponds to building the

model right. External validation is used to check the

similarities between the model and the real

phenomenon. It is also named validation process in

software engineering, so external validation

corresponds to build the right model. In this paper,

we address only the external validation. In the

following, validation then means external validation

ToCalibrate&ValidateanAgent-basedSimulationModel-AnApplicationoftheCombinationFrameworkofBISolution

&Multi-agentPlatform

173

of multi-agent models; and the calibration is the

fine-tuning of the output of simulation model by a

change in the values of parameters. The calibration

involves the validation (especially the similarity

evaluation which is present in both cases) to check

the simulation outputs.

To calibrate and validate a simulation model,

modelers used several different methods: (Donigian,

2002) used the "weight of evidence"; (Ngo and See,

2012; Rogers and Tessin, 2004; Said et al., 2002)

used generic algorithms to optimize the fitness value

of parameters by comparison with the observations

from real systems. In general, these researchers

validate simulation outputs with empirical data and

check fitness conditions by statistic methods such as

Root Mean Squared Error (RMSE) (Ngo and See,

2012; Willmott et al., 1985). Implementing

calibration and validation model in Section 5, we

tune values of parameters in their value domain

(they were specified by expert biologist) by

specifying the different values of all parameters and

execute simulations with all possible cases (full

experimental design in statistical terms). The Jaccard

index (Jaccard, 1908), which can be found in

(Niwattanakul et al., 2013; Rahman et al., 2010;

Sachdeva et al., 2009) is used to estimate the

similarity coefficient between two data sets.

3 COMBINATION FRAMEWORK

OF BUSINESS INTELLIGENCE

SOLUTION AND

MULTI-AGENT PLATFORM

(CFBM)

In this section, we demonstrate the logical

framework to combine BI solution and Multi-agent

platform. This framework has been implemented on

the GAMA simulation platform (Truong et al.,

2013). The CFBM is designed to handle big data

from different data sources and perform analyses on

the integrated data from these sources. It is a

solution to improve the weaknesses of ABMs when

modelling is conducted on an integrated system. In

this framework, we use a BI solution as a database

tool, a multi-agent platform as model design tool and

model execution tool. For the execution analysis

tool, we can either use OLAP analysis tool or use

analysis features of the platform (implemented as an

external plug-in for the platform, e.g. R scripts).

The architecture of the CFBM is illustrated in

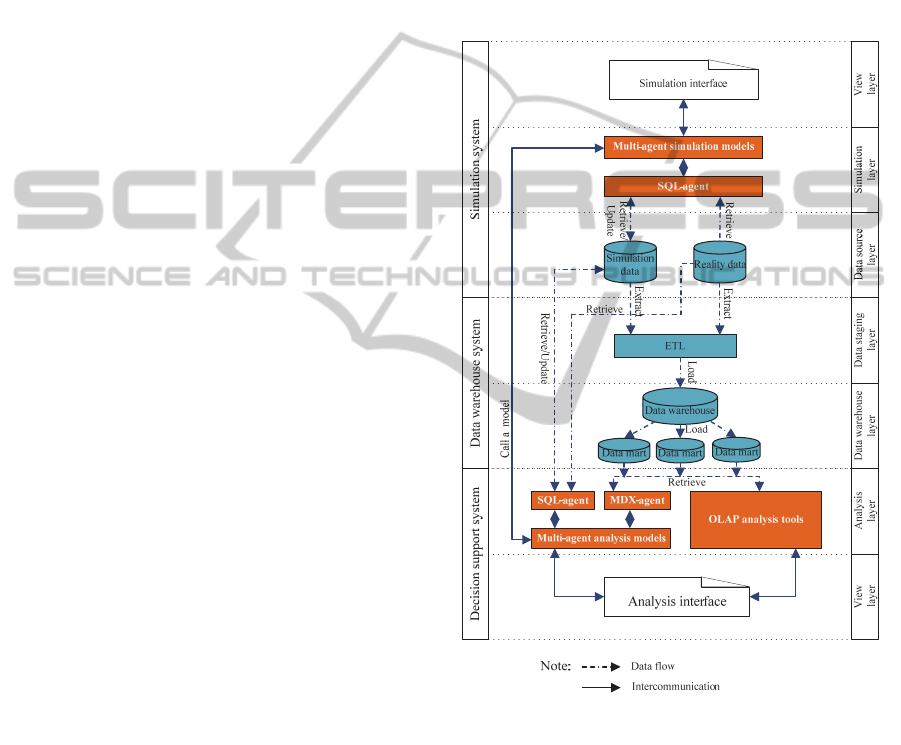
Figure 1. It is formed by three systems and it

supports four tools: model design tool, model

execution tool, execution analysis tool and database

tool.

3.1 Simulation System

The simulation system plays two roles: model design

tool and model execution tool. It is composed of a

multi-agent platform and a relational database. This

system is an Online Transaction Processing (OLTP)

or an operational source system. It is an outside part

of the data warehouse (Kimball and Ross, 2002).

Figure 1: Combination framework of BI solution and

multi-agent platform architecture.

Three layers with five components compose the

simulation system. The simulation interface is the

user environment that helps the modeler to design

and implement his models, execute the models and

visualize results. Multi-agent simulation models

are a set of multi-agent based models. They are used

to simulate the phenomena that the modeler aims at

studying. The SQL-agent plays the role of the

database tool and can access to the relational

database. It is a particular kind of agent that supports

Structured Query Language (SQL) functions to

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

174

retrieve simulation inputs from simulation data or

reality data, to store output simulation data into

simulation data databases and to transform data (in

particular the data type) from simulation model to

relational database, and conversely. Reality data and

Simulation data are relational databases. The reality

database is used to store empirical data gathered

from the target system that are needed for the

simulation and analysis phases. Finally, Simulation

data is used to manage simulation models,

simulation scenarios and the output results of the

simulation models. These two data sources will be

used to feed the second part of the framework,

namely the Data warehouse system

The simulation system helps to implement

models, execute simulations and handle their

input/output data.

3.2 Data Warehouse System

The data warehouse system is conceptualized as a

part of the BI solution. It is an important part to

integrate data from different sources (simulation

data, empirical data and others external data) and is

used as data storage to feed data for decision support

systems.

The data warehouse system is divided into three

parts. ETL (Extract-Transform-Load) is a set of

processes with three responsibilities. First, it extracts

all kind of data (empirical data and simulation data)

from the simulation system. Second, ETL transfers

the extracted data into an appropriate data format.

Finally, it loads the transferred data into a data

warehouse. Data warehouse is used to store

historical data, which are loaded from simulation

system by ETL. Data mart is a subset of data stored

in the data warehouse and it is a data source for

concrete analysis requirements. We can create

several data marts depending on our analysis

requirements. Data mart is a multidimensional

database, which is designed based on

multidimensional approach. It uses star joins, fact

tables and dimension tables to present the data mart

structure data. With a multidimensional structure,

data mart is particularly useful in improving the

performance of analytic processes.

3.3 Decision Support System

In CFBM, the decision support system plays the role

of analysis tool. It is a software environment

supporting analysis, decision-making features and

the visualization of results. In our design, we

propose to use existing OLAP analysis tools, or a

multi-agent platform with analysis features or a

combination of both options. The decision support

system of CFBM is built on four parts. Analysis

interface is a user interface used to handle analysis

models and visualize results. Multi-agent analysis

models are a set of agent-based analysis models.

They are created based on analysis requirements and

handled via analysis interface. MDX-agent is a

bridge between multi-agent analysis models and data

marts. This agent supports MultiDimensional

eXpressions (MDX) functions to query data from a

multidimensional database. OLAP analysis tools

are analysis software packages that support OLAP

operators.

In general, the CFBM is a solution we proposed

to solve the limitations of ABMS in terms of data

management and output analysis with high volume

of data, which have been explained in Section 1.

The key points of the CFBM architecture are that

it contains and adapts the four features of a computer

simulation system (model design, model execution,

execution analysis, and database management). All

these functions are integrated into one multi-agent

platform. The data warehouse manages the related

data. The analysis models and simulation models

can interact with each other. Using the CFBM

architecture, we can build a simulation system not

only suitable for modeling driven approach but also

for data driven approaches. Furthermore, CFBM

brings certain benefits for building simulation

system with complex requirements such as the

integration and analyzes of high volume of data.

4 CALIBRATION & VALIDATION

APPROACH

In this section, we propose an approach to calibrate

and validate an agent-based simulation model. The

approach is an application of CFBM, which we

presented in Section 3. It is useful when we work

with integrated simulation systems, where we need

to control several models with high volume of

input/output data of simulation, observation data

from real system and analysis results. In this part we

detail the practical use of CFBM to calibration and

validation purposes.

4.1 Calibrating an Agent-based Model

In Figure 2, we present an automatic approach with

seven steps for calibrating and validating an agent-

based model. The approach helps modelers to test

their models more systematically in a given

ToCalibrate&ValidateanAgent-basedSimulationModel-AnApplicationoftheCombinationFrameworkofBISolution

&Multi-agentPlatform

175

parameter space, to evaluate (validate) outputs of

each simulation and manage all data in an automatic

manner.

Step 1: Load input Data with Default Parameter

Values. Select a model scenario from the database

then the input data and default parameter values are

loaded from the quartet (model, scenario, input data

set, parameters). This step assures that the correct

input data and default values of parameter are loaded

to simulation model.

Step 2: Execute Simulation Model. The simulation

model is executed with the loaded scenario as input.

In this process, outputs of the simulation are stored

into a database. Because the simulation can be

executed many times (replications) with the same

scenario, to be sure that the system can handle

results, the quartet (model, scenario, replicate,

output) must be stored into the database.

Step 3: Execute Validation Model. The validation

model is used to analyze the variations between

simulation outputs and observations from the real

system. The result of this process is a similarity

coefficient or difference/distance coefficient

between the output data in step 2 and observation

data. The method is used to validate depends on the

properties of data and on the modeler's choice. For

example, we choose Jaccard index method for the

validation of our model in Section 4.

In this step, the validation model loads testing

data set (observations) and corresponding output

data set of the quartet (model, scenario, replicate,

output) to make the comparison between the two

data sets. The result of validation is also stored into

the database with the quartet (model, scenario,

replicate, result of validation).

Step 4: Check Fitness Condition. The result of

validation in Step 3 is compared with a fitness

condition that is defined by the modeler. For

example, the similarity coefficient of Step 3 must be

greater than or equal to 0.90 (see Section 5.2.1).

There are two cases:

 If the fitness is true/yes then do Step 5 (It means

that the input of simulation with the value of the

parameters is accepted).

 If the fitness is false/no then do Step 6 (It means

that the input of simulation with the value of the

parameters is not accepted).

Step 5: Store the Scenario with Fitness

Parameters. Note that the result of each replication

was stored in the quartet (model, scenario, replicate,

result of validation) by step 3. Hence this step only

stores the adaptive scenario and fitness parameter

values in the quartet (model, scenario, replicate,

fitness parameter values).

Step 6: Check Adjustment Condition. The system

checks if there is another instance of parameters in

its population or not. Hence there are two cases:

 If the Adjustment is True/Yes then do Step 7 (It

means that there is another instance of

parameters in its population).

 If the Adjustment is False/No then stopping the

process (It means that there is not any other

instance of parameters in its population).

Step 7: Execute Adjustment Parameters. The

adjustment function concerns the determination of

the new values for parameters. It is used to adjust the

input parameters to improve the output of the model.

The result of this process is the creation of a new

scenario for the simulation model.

This function changes the values of the

parameters to other values in their population and

progresses to step 2.

With the seven-step approach, the calibration

model can execute the simulation model with all

adjusted values of the parameters, manage the whole

input/output data dealt within the processes and

analyze the variant between simulation outputs and

observation data. It helps us to specify appropriate

values of parameters automatically. The calibration

model is an integration of two major models:

simulation model and validation model. It also

handles all data processed by the two models. The

calibration model is a demonstration of the

application of the CFBM, where: BI solution is used

to handle all input/output of the model and empirical

data related with simulating and analyzing while the

analysis model is used to validate the output of the

simulations.

4.2 Validating Simulation Output using

Jaccard Index

There are several methods to measure similarity

between two data sets as mentioned in (Ngo and

See, 2012; Wolda, 1981). Root Mean Squared Error

(RMSE) is usually used to estimate the distance (or

error) between two data sets (simulation outputs and

observations from real system).

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

176

Figure 2: Workflow for the calibration of a model.

In this section, we propose a method to measure

the similarity between two data sets integrating

constraints on the position of elements in the data

sets (ordered data set). In our method, we use

Jaccard index as the similarity coefficient between

two ordered data sets as follow:

Jaccard Index on Ordered Data Sets. Assume that

we have two ordered data sets:

X = {x

, x

, …., x

}

Y = {y

, y

, …., y

}

Definition 1: x

is called match (or similar or equal)

with y

when i = j and value of x

equal value of y

match(x

, y

) = true when i = j and

value(x

) = value(y

) other match(x

, y

) = false

i,j=1..n

(1)

Definition 2: The intersection of X and Y is:

S={s

, s

, …, s

} (2)

where:

 s

= {x

} (or s

= {y

}) when match(x

) = true

 s

= {} = ∅ when match(x

, y

) = false

 i=1..n

Definition 3: The union of X and Y is:

U={u

, u

, …, u

} (3)

where:

 u

= {x

} (or u

= {y

}) when match(x

) = true

 u

= {x

, y

} when match(x

, y

) = false

 i =1..n

Definition 4: The cardinality of an ordered set is

| {} |=0;

| S |=| s

| + | s

| + … + | s

| U |=| u

| + | u

| + … + | u

| = | X |+| Y | - | S |

(4)

Definition 5: Jaccard index of two ordered data sets

is:



,







∩





∪





















(5)

where:

 c: number of matched pairs (xi, yi)

 a: number of x

elements in X and not matched y

in Y

 b: number of y

elements in Y and not matched x

in X

In an easier way, we calculate Jaccard index

between X and Y based on the cardinality of S, X and

Y as equation (6):



,







∩





∪























(6)

where:

 f: cardinality of S.

 d: cardinality of X.

 e: cardinality of Y.

Example 1: Assume that we have the following

data:

 Empirical data set: X={ 1,2,3,4,5}

 Simulation data set: Y={ 3,2,5,6,7}

Jaccard index between X and Y with no constraint on

position of elements:

Intersect(X, Y) = {2, 3, 5}

Union(X, Y) = {1, 2, 3, 4, 5, 6, 7}

J(X, Y) = 3/(2+2+3) = 3/7 = 0.429

However we cannot say x

because we consider

ordered sets. In this case, we apply Jaccard index on

two ordered data sets:

Intersect(X, Y) = { {}, {2}, {}, {}, {} }

Union(X, Y) = { {1,3}, {2}, {3,5}, {4,6}, {5,7} }

(5) => J(X, Y) = 1/(4+4+1) = 1/9 = 0.111 or (6) =>

J(X, Y) = 1/(5+5-1) = 1/9 = 0.111

In Example 1, the similarity coefficient (Jaccard

index) between two data sets with no position

constraint (0.429) is different from the similarity

coefficient between those two data sets with position

constraint (0.111).

ToCalibrate&ValidateanAgent-basedSimulationModel-AnApplicationoftheCombinationFrameworkofBISolution

&Multi-agentPlatform

177

5 CALIBRATION & VALIDATION

OF THE BPH PREDICTION

MODEL

In this section, we demonstrate the calibration and

validation model for an integrated agent-based

simulation model, the BPH prediction model

(Truong et al., 2013). This model is one of the

research results of the DREAM

project, coordinated

between Can Tho University, Vietnam and Institut

de Recherche pour le Développement (IRD), France.

5.1 BPH Prediction Model

BPH Prediction model is used to predict the Brown

Plant Hopper (cricket) density on rice fields in

Mekong Delta, Vietnam. This model contains two

sub-models: BPH Growth Model and BPH

Migration Model. The output is the number of BPHs

in each light-trap distributed in the environment to

catch BPH. Inputs and outputs of the integrated

model are handled via the CFBM in GAMA.

Empirical data such as administrative boundary

(region, river, sea region, land used), light-trap

coordinates, daily trap-densities, rice cultivated

regions, general weather data (wind data), station

weather data (temperature, humidity, etc.), river and

sea regions are used as inputs of the simulation

model and as validation data for the model.

5.1.1 BPH Migration Model

BPH migration model is used to simulate the

invasion of BPHs on the rice fields. The migration

process of BPHs in the studied region is modeled by

a dynamical moving process on cellular automata.

Denoting x(t) as the number of adult BPHs at

time t, the migration model essentially determines

the outcome x

out

(t) at a later time t + 1 from a

specific source cell and the rates of x

out

(t) moving to

all destinations at time (t + 1). Destination cells are

determined by the semi-circle under the wind, while

the radius of the circle is determined by the wind

velocity and the migration time in a day. The local

constraints are also considered by two combinational

indices: attractiveness index and obstruction index (

(Truong et al., 2013).

http://www.ctu.edu.vn/dream/

5.1.2 BPH Growth Model

In the growth model, authors applied a deterministic

model of T variables where T is the life cycle of the

insect. To simplify the implementation process,

these variables will be stored in an array variable V

of length T where an element V[i] marks the number

of insects at age i (i.e. i

day of BPH life cycle). For

each simulation step, all elements of V will be

updated by the following equation:

















∗



∗,1

∈







1



∗



∗,∈







1



∗



∗,∈







1



∗, ∈



(7)

where

  denotes the number of insects at age i,

 



 denotes the ratio of egg number able to

become the nymph,

 



denotes the ratio of nymph number able to

become the adult.

 



denotes the ratio of eggs can be produced by

an adult.

 m denotes the ratio of natural mortality.

 



denotes the egg giving time span.

 



denotes the egg and time span.

 



denotes the nymph time span.

 



denotes the adult time span.

5.2 Calibration & Validation of the

BPH Prediction Model

5.2.1 Parameters for Calibration

From equation (7) in Section 5.1.2, there are several

parameters we can choose for calibration. However,

we only choose T

(adult time span of BPH) and m

(the ratio of natural mortality) as two parameters for

demonstration purpose. BPH has an adult time span

of 8 days in minimum and 12 days in maximum. The

ratio of natural mortality is 0.15 in minimum and

0.35 in maximum. The following populations of the

two parameters are therefore tested:

 T

: [8, 9, 10, 11, 12]

 m=[0.35, 0.25, 0.15]

For the input data of BPH prediction model, we used

the data from 48 light-traps of three typical

provinces in the Mekong Delta region: Soc Trang,

Hau Giang and Bac Lieu from January 1, 2010. With

one input data set, we have 15 scenarios as presented

in Table 1.

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

178

Table 1: The parameters value of scenarios for a complete

experimental design.

Scenario

Parameters

Adult time span (T

)

Ratio of natural

mortality (m)

1 8 0.35

2 9 0.35

3 10 0.35

4 11 0.35

5 12 0.35

6 8 0.25

7 9 0.25

8 10 0.25

9 11 0.25

10 12 0.25

11 8 0.15

12 9 0.15

13 10 0.15

14 11 0.15

15 12 0.15

The Fitness Condition. We try the fitness condition

in two cases:

Case 1: The difference coefficient is equal or less

than 500

if (RMSE<=500.0)

{

saveFitness(MODEL_ID, SCENARIO_ID,

REPLICATE_ID, PARA_VALUES);

}

Case 1: The similarity coefficient is equal or greater than 0.9

if (Jindex>=0.9)

{

saveFitness(MODEL_ID, SCENARIO_ID,

REPLICATE_ID, PARA_VALUES);

}

saveFitness is a user defined function, it writes

the fitness scenario to database.

5.2.2 Simulation Output and Empirical Data

All related operations for validation in the validation

model are shortly introduced in this part. As

mentioned, the output of BPH prediction model is

the BPH density by light-traps and by time. The

empirical data (testing data) is BPH density from 48

light-traps of three typical provinces in the Mekong

Delta region: Soc Trang, Hau Giang and Bac Lieu

from January 1, 2010.

We simulate and predict the infection of the

BPHs on the rice fields of the three provinces in 28

days. The output of the BPH prediction model has

been structured as in Table 2. The structure of

empirical data is presented in Table 3. Each table

has 48 columns and 28 rows. The columns stand for

48 light-traps and the rows for 28 days (prediction

time). In Table 2, s

i,j

is the number of BPH that is

simulated in step i (day i) at light-trap j. In Table 3,

i,j

is the number of BPHs that are caught in day i at

light-trap j on the rice fields of Mekong Delta,

Vietnam. It should be noted that the indices of the

rows and columns starts at 0 for programming

reasons.

Table 2 and Table 3 present two matrixes of

values which have constraints on the position

(location and time) of their elements, hence they are

considered as two ordered data sets.

Table 2: Simulation outputs.

Light-trap

Tr0 Tr1 ... Tr47

day

0 s

0,0

0,1

... s

0,47

1 s

1,0

1,1

... s

1,47

... ... ... ... ...

27 s

27,0

27,1

... s

27,47

Table 3: Empirical data.

Light-trap

Tr0 Tr1 ... Tr47

day

0 e

0,0

0,1

... e

0,47

1 e

1,0

1,1

... e

1,47

... ... ... ... ...

27 e

27,0

27,1

... e

27,47

5.2.3 Validating the Output of the BPH

Prediction Model

The simulation output and testing data have location

constraints (light-trap) and time constraints. Hence,

we use Jaccard index on ordered data sets, which has

been presented in Section 4.2 to estimate the

similarity between the simulation output and the

empirical data. The RMSE method has also been

applied to measure the difference between the two

data sets.

As regard to prediction, we need to predict

different periods of time: from day 0 (initial day) to

6 (1

week), from day 7 to 13 (2

week), from day

14 to 20 (3

week) and from day 21 to 27 (4

week).

Hence for each scenario, we validate the results of

simulation in four cases: 1

week, 2

week, 3

week, 4

week. For each case of validation, we

measure difference coefficient (RMSE) and

similarity coefficient (Jaccard index).

In addition, we also measure RMSE and Jaccard

index of the whole data set (from day 0 to 27 or 4

weeks) for the comparison of the two measures in

each scenario.

5.2.3.1 The Difference Coefficient (RMSE)

The difference coefficient between the two data sets

is calculated based on the equation (8):

ToCalibrate&ValidateanAgent-basedSimulationModel-AnApplicationoftheCombinationFrameworkofBISolution

&Multi-agentPlatform

179





∑∑



,



,













∗

(8)

where:

 m denotes the number of rows of data set

 n denotes the number of columns of data set

 e

i,j

is the empirical data. It denotes the number of

BPHs caught in day i at light-trap j.

 s

i,j

is the simulation output. It denotes the

number of BPHs obtained in step i (day i) at

light-trap j.

The RMSE results of the 15 scenarios are presented

in Table 4.

Table 4: RMSE between simulation output and empirical

data.

Scenario 1

week 2

week 3

week 4

week 4 weeks

483.24 35.53 84.07

1610.25 879.58

474.58 31.73 95.14

1714.17 931.34

57.17 28.34 119.74

1762.46 928.09

53.48 25.71 282.73

1768.57 939.68

51.96 19.16 489.3

1738.06 944.39

484.26 108.54 209.26

1609.61 885.86

472.54 105.35 234.76

1713.14 937.82

56.45 106.86 233.00

1761.98 934.39

54.63 110.65 345.59

1766.14 945.00

84.44 94.69

530.54 1735.76 950.25

488.51

1215.93 2413.06 1863.30 1666.85

473.80

1271.71 2639.58 2322.33 1903.59

83.20

1210.19 2570.50 8826.41 4846.08

139.46

1339.62 2636.22 10508.34 5709.14

15 770.65 1150.98 2588.53 11430.14 6174.68

Based on the difference coefficient condition

(RMSE ≤ 500.0) in Section 5.2.1, we can show that:

the RMSE of the first 14 scenarios fits the

calibration conditions for the 1

week. , this is also

the case for the first 10 scenarios the 2

week and

the first 9 scenarios the 3

week; but none of the 15

scenarios fits the calibration conditions of the 4

week.

5.2.3.2 The Similarity Coefficient (Jaccard

Index)

We apply equation (6) in Section 4.2 to measure the

Jaccard index between the simulation output (Table

2) and empirical data (Table 3). The results are

presented in Table 5.

If we compare the results in Table 5 with the

similarity coefficient condition (Jindex ≥ 0.90) in

Section 5.2.1 then there are not any results fitting the

condition. Certainly, there are no scenarios to be

recognized in the calibration process. This problem

can be explained by the reason that the numbers of

BPHs caught at each light-trap by time has a wide

range of values, from zero to ten thousands. Hence,

to exactly simulate the number of BPHs at each

light-trap over time is impossible or Jaccard index

of two ordered data sets is not suitable to measure

the similarity coefficient between two matrixes of

values where the domain of elements is large. For

this reason, we transformed the number of BPH in

Table 2 and Table 3 to the BPH infection with the

mapping as in Table 6. It means that we change from

the ratio scale to ordinal scale. The scale in Table 6

is proposed by biologists and it was used in (Phan et

al., 2010). The structures of the two transformed

tables are the same as Table 2 and 3, but the value in

each cell ranges from 0 to 4 and its meaning is the

BPH infection level.

Table 5: Jaccard index between simulation output and

empirical data.

Scenario 1

week 2

week 3

week 4

week 4 weeks

1 0.4071 0.3352 0.2826 0.4573 0.3701

2 0.4525 0.3035 0.2672 0.4382 0.3629

3 0.4651 0.2586 0.2936 0.4015 0.3513

4 0.4547 0.2553 0.3085 0.3682 0.3435

5 0.3952 0.2785 0.3387 0.3490 0.3393

6 0.1845 0.1482 0.1894 0.1362 0.1630

7 0.1799 0.1516 0.1923 0.1267 0.1607

8 0.1647 0.1320 0.2001 0.1147 0.1506

9 0.1580 0.1922 0.1910 0.1136 0.1610

10 0.1560 0.1804 0.1894 0.1040 0.1546

11 0.1580 0.1239 0.1831 0.1317 0.1479

12 0.1554 0.1430 0.1920 0.1120 0.1484

13 0.1728 0.1371 0.1944 0.1196 0.1539

14 0.1346 0.1701 0.1633 0.0993 0.1396

15 0.1313 0.1649 0.1602 0.0915 0.1345

Table 6: Transform BPH density to BPH infection.

Number of BPH BPH Infection Meaning

<500 0 Normal

50 − <1500 1 Light infection

1500 − <3000 2 Medium infection

3000 − ≤10000 3 Heavy infection

>10000 4 Hopper burn

We applied the Jaccard index to measure the

similarity of the two transformed tables and its

results are presented in Table 7.

Based on the similarity coefficient condition

(Jindex ≥ 0.9) in Section 5.2.1, we got the same

scenarios, which are fitted with the difference

coefficient conditions in Section 5.2.3.1.

From the validation results, the calibration model

can choose the scenarios with parameters checking

the specified fitness condition in the calibration

model.

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

180

Table 7: Jaccard index on BPH infection data sets.

Scenario 1

week 2

week 3

week 4

week 4 weeks

0.9823 1.0000 0.9941

0.7819 0.9293

0.9823 1.0000 0.9882

0.7534 0.9187

1.0000 1.0000 0.9765

0.7376 0.9147

1.0000 1.0000 0.9535

0.7336 0.9082

1.0000 1.0000 0.9200

0.7376 0.9016

0.9823 0.9862 0.9535

0.7819 0.9169

0.9804 0.9882 0.9292

0.7534 0.9021

1.0000 0.9882 0.9273

0.7323 0.8990

1.0000 0.9862 0.9037

0.7297 0.8922

0.9901 0.9862

0.8736 0.7297 0.8828

0.9765

0.6649 0.6260 0.4197 0.6396

0.9745

0.6622 0.6083 0.3989 0.6265

0.9882

0.6583 0.5975 0.3644 0.6121

0.9765

0.5975 0.6417 0.3419 0.5979

15 0.8329 0.6970 0.6272 0.3257 0.5863

6 DISCUSSION

Applying CFBM to Calibration and Validation.

There have been many studies, which proposed

frameworks aiming at building credible simulation

models (Law, 2009) in general or at validating agent

based simulation models (Klügl, 2008) in particular.

Although those frameworks instructed us the

processes to archive simulation model with the

accuracy of the simulation output, we still need a

concrete approach to solve two challenges of agent-

based models, which we explained in the

introductory section. By applying CFBM, we

developed a calibration and validation approach for

agent-based models that can help not only to handle

the inputs/outputs of agent-based simulation models

but also to calibrate and validate the agent-based

simulation in an automatic manner. In the Section 4,

we did not demonstrate the concrete method to

adjust the parameters of the simulation model such

as "weight of evidence" (Donigian, 2002) or generic

algorithm (Ngo and See, 2012) because of two

reasons: we only propose the general calibration

approach and adjustment method should be

implemented depending on the case study.

Furthermore, our approach only concerns the

management of the input/output data of simulation

model and validation model and the automation of

the calibration process. They are useful when

working on integrated simulation systems with high

amount of data. For instance, we successfully

applied our approach to calibrate and validate the

BPH prediction model with several data sources

such as administrative boundary (region, river, sea

region, land used), light-trap coordinates, daily trap-

densities, rice cultivated regions, general weather

data (wind data), station weather data (temperature,

humidity, etc.), river and sea regions of three

provinces of Mekong Delta region of Vietnam as we

explained in Section 5. It helped us to reduce time

and work force.

Jaccard Index on ordered Data Sets vs. RMSE. In

experiment, we also compared the Jaccard index on

ordered data sets and RMSE by investigating the

variation of RMSE in Table 4 and Jaccard index of

the two BPH infection tables (the results of the

transformation of Table 2 and 3) in Table 7. For

instance, we compared the values of RMSE on the

whole data sets (column 4 weeks in Table 4) with the

values of Jaccard index (column 4 weeks in Table 7)

by using Graphical method as Figure 3. It should be

noticed that the values of RMSE in Figure 3 were

divided by 1000.

Figure 3: RMSE & Jaccard index on whole data sets.

Figure 3 shows that there is an accordance

between RMSE and Jaccard index. For instance, in

scenario 1, as the RMSE get the lowest value of

879.58, the Jaccard index obtains the highest value,

which is 0.9293. In scenario 11, when the RMSE

suddenly increases to 1666.85, the Jaccard index

decreases to 0.6396 as well. In scenario 15, whereas

RMSE gets the highest value 6174.68, the Jaccard

index gets the lowest value, i.e. 0.5863. It proves

that we can use Jaccard index on ordered data for the

transformed data as fitness condition, which has

been presented in Section 5.2.1.

The Combination on the Fitness Condition. In the

calibration of BPH prediction model, we can choose

RMSE or Jaccard index as a fitness condition.

However, it is suggested to use the combination of

both coefficients, for instance:

if ((Jindex>=0.9) & (RMSE<=100))

{

saveFitness(MODEL_ID, SCENARIO_ID,

REPLICATE_ID, PARA_VALUES);

}

0,0000

1,0000

2,0000

3,0000

4,0000

5,0000

6,0000

7,0000

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Value

Scenario

Jindex

RMSE

ToCalibrate&ValidateanAgent-basedSimulationModel-AnApplicationoftheCombinationFrameworkofBISolution

&Multi-agentPlatform

181

The combination of similarity and difference

coefficients helps to have better fitness condition for

choosing the appropriate scenario in calibration.

The Jaccard Index with Aggregation. Assume that

we have two modality matrixes and the domain of

the elements in S and E are [0..k-1], have k values:





,

…

,

…… …



,

…

,







,

…

,

…… …



,

…

,



(9)

The aggregation on the columns on S (or E) has a

matrix:





,

…

,

…… …



,

…

,



(10)

where:

 C denotes aggregation matrix on the columns of

matrix S (or E).

 c

i,j

is the number of elements in row i in S (or E)

having value j.

The aggregation on the rows on S (or E) has a

matrix:





,

…

,

…… …



,

…

,



(11)

where:

 R denotes aggregation matrix on the rows of

matrix S (or E).

 r

i,j

is the number of elements at columns j in S (or

E) having the value i.

Then we can apply the Jaccard index on ordered data

sets to the aggregation matrices (equation 10, 11) of

S and E.

7 CONCLUSIONS

In this paper, we introduced a conceptual

framework, which is adapted to multi-agent models

with high volume of data. CFBM supports experts

not only to model a phenomenon and execute the

models via a multi-agent platform, but also to

manage a set of models with their input and output,

to aggregate and analyze the model output data via

data warehouse and OLAP analysis tools.

The key features of CFBM are that it supplies

four components: (1) model design, (2) model

execution, (3) execution analysis and (4) database

management. These components are coupled and

combined in a simulation system. The distinguished

value of CFBM is that it augments the combination

power of data warehouse, OLAP analysis tools and

of a multi-agent based simulation platform. These

components, when put together, are useful to

develop complex simulation systems with a large

amount of input/output data, which can be a what-if

simulation system, a prediction/forecast system or a

decision support system.

In this article, we proposed an automated

calibration approach; it helps modelers to solve the

limitations of ABMs concerning calibration and

validation of agent-based models with high volume

of data: BI solution is used to manage the high

volume of input/output of the simulation models and

the analysis model is used to validate the accuracy of

simulation outputs on large size of input with

varying parameters. We also proposed a specific

method to measure the similarity coefficient of two

data sets with the constraints on the position of

elements, which is called "Jaccard index on the

ordered data sets". In our opinion, the method can

not only be used as a demonstration of validating for

BPH prediction model but it is also a good approach

to validate the output of other models with

constraints on location and time.

Although our calibration and validation approach

is the automation model with the integration of

coupled models (simulation model and validation

model) we have not succeeded in implementing it in

GAMA. For instance, we execute the BPH

prediction model with all values of the parameters

via batch process. Subsequently, we execute the

validation model to validate the outputs and select

appropriate scenarios based on the fitness condition.

These are still two separate processes but not

integrated in one model as designed in Section 4.

This is the problem that we plan to solve in the

future.

As for further work, on one hand we will

continue to develop and improve features for

specific agents (SQL-agent, OLAP-agent and

Analysis-agent) of the CFBM described in Section 3

to GAMA platform. On the other hand, we will also

apply CFBM on multi-scale in multi-agent

simulation or building what-if system, prediction

system and decision support system.

REFERENCES

Amblard, F., Bommel, P., Rouchier, J., 2007. Assessment

and Validation of Multi-agent Models. In: Phan, D.,

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

182

Amblard, F. (Eds.), Agent-Based Modelling and

Simulation in The Social and Human Sciences. The

Bardwell Press, Oxford, pp. 93–114.

ASTM, 1984. Standard Practice for Evaluating

Environmental Fate Models of Chemicals. American

Society of Testing Materials. Philadelphia.

Crooks, A., Castle, C., Batty, M., 2008. Key challenges in

agent-based modelling for geo-spatial simulation.

Comput. Environ. Urban Syst. 32, 417–430.

Crooks, A. T., Heppenstall, A. J., 2012. Introduction to

Agent-Based Modeling. In: Heppenstall, A.J., Crooks,

A. T., See, L. M., Batty, M. (Eds.), Agent-Based

Models of Geographical Systems. Springer

Netherlands, Dordrecht, pp. 85–105.

Donigian, A. S., 2002. Watershed model calibration and

validation: The HSPF experience. In: Water

Environment Federation. pp. 44–73.

Ehmke, J. F., Grosshans, D., Mattfeld, D. C., Smith, L. D.,

2011. Interactive analysis of discrete-event logistics

systems with support of a data warehouse. Comput.

Ind. 62, 578–586.

Inmon, W. H., 2005. Building the Data Warehouse, 4th ed.

Wiley Publishing Inc.

Jaccard, P., 1908. Nouvelles recherches sur la distribution

florale. Bull Soc. Vaud. Sci. Nat 223–270.

Kimball, R., Ross, M., 2002. The Data Warehouse

Toolkit: The Complete Guide to Dimensional

Modeling, 2nd ed. John Wiley & Sons, Inc.

Klügl, F., 2008. A validation methodology for agent-based

simulations. In: Proceedings of the 2008 ACM

Symposium on Applied Computing. pp. 39–43.

Laniak, G. F., Rizzoli, A. E., Voinov, A., 2013. Thematic

issue on the future of integrated modeling science and

technology. Environ. Model. Softw. 39, 13–23.

Law, A. M., 2009. How to build valid and credible

simulation models. In: Simulation Conference (WSC),

Proceedings of the 2009 Winter. IEEE, pp. 24–33.

Madeira, H., Costa, J. P., Vieira, M., 2003. The OLAP and

data warehousing approaches for analysis and sharing

of results from dependability evaluation experiments.

In: International Conference on Dependable Systems

and Networks. pp. 86–99.

Mahboubi, H., Faure, T., Bimonte, S., Deffuant, G.,

Chanet, J. P., Pinet, F., 2010. A Multidimensional

Model for Data Warehouses of Simulation Results.

Int. J. Agric. Environ. Inf. Syst. 1, 1–19.

Ngo, T. A., See, L., 2012. Calibration and Validation of

Agent-Based Models of Land Cover Change. In:

Heppenstall, A. J., Crooks, A. T., See, L. M., Batty,

M. (Eds.), Agent-Based Models of Geographical

Systems. Springer Netherlands, pp. 181–197.

Niwattanakul, S., Singthongchai, J., Naenudorn, E.,

Wanapu, S., 2013. Using of Jaccard Coefficient for

Keywords Similarity. In: International

MultiConference of Engineers and Computer

Scientists

. pp. 380–384.

Phan, C. H., Huynh, H. X., Drogoul, A., 2010. An agent-

based approach to the simulation of Brown Plant

Hopper (BPH) invasions in the Mekong Delta. In:

Computing and Communication Technologies,

Research, Innovation, and Vision for the Future

(RIVF), 2010 IEEE RIVF International Conference.

IEEE, pp. 1–6.

Rahman, M., Hassan, M. R., Buyya, R., 2010. Jaccard

Index based availability prediction in enterprise grids.

In: Procedia Computer Science. Elsevier, pp. 2707–2716.

Rogers, A., Tessin, P. von, 2004. Multi-objective

calibration for agent-based models.

Sachdeva, V., Freimuth, D., Mueller, C., 2009. Evaluating

the jaccard-tanimoto index on multi-core architectures.

In: Computational Science–ICCS 2009. Springer

Berlin Heidelberg, pp. 944–953.

Said, L. B., Bouron, T., Drogoul, A., 2002. Agent-based

interaction analysis of consumer behavior. In: The

First International Joint Conference on Autonomous

Agents and Multiagent Systems: Part 1. ACM. pp.

184–190.

Sosnowski, J., Zygulski, P., Gawkowski, P., 2007.

Developing Data Warehouse for Simulation

Experiments. In: Rough Sets and Intelligent Systems

Paradigms. Springer Berlin Heidelberg, pp. 543–552.

Truong, T. M., Truong, V. X., Amblard, F., Drogoul, A.,

Benoit, G., Huynh, H. X., Le, M. N., Sibertin-blanc,

C., 2013. An implementation of framework of

Business Intelligence for Agent-based Simulation. In:

The 4th International Symposium on Information and

Communication Technology (SoICT 2013).

Truong, V. X., Huynh, H. X., Le, M. N., Drogoul, A.,

2013. Optimizing an Environmental Surveillance

Network with Gaussian Process − An optimization

approach by agent-based simulation. In: The Sixth

International KES Conference on Agents and Multi-

Agent Systems – Technologies and Applications (KES

AMSTA 2013). IOS Press, pp. 102–111.

Vasilakis, C., El-Darzi, E., Chountas, P., 2008. A decision

support system for measuring and modelling the multi-

phase nature of patient flow in hospitals. In: Intelligent

Techniques and Tools for Novel System Architectures.

Springer Berlin Heidelberg, pp. 201–217.

Willmott, C. J., Ackleson, S. G., Davis, R. E., Feddema, J.

J., Klink, K. M., Legates, D. R., O’Donnell, J., Rowe,

C. M., 1985. Statistics for the evaluation and

comparison of models. J. Geophys. Res. 90, 8995–

9005.

Wolda, H., 1981. Similarity indices, sample size and

diversity. Oecologia 50.3, 296–302.

ToCalibrate&ValidateanAgent-basedSimulationModel-AnApplicationoftheCombinationFrameworkofBISolution

&Multi-agentPlatform

183