
Tracking Assembly Processes and Providing Assistance in Smart
Factories
Sebastian Bader
1
and Mario Aehnelt
2
1
MMIS, University of Rostock, Albert-Einstein-Strasse 22, 18059 Rostock, Germany
2
Fraunhofer IGD, Joachim-Jungius-Strasse 11, 18059 Rostock, Germany
Keywords:
Assembly Tracking, Smart Factory, Assistance, Task Trees, Hidden Markov Models.
Abstract:
Tracking assembly processes is a necessary prerequisite to provide assistance in smart factories. In this paper,
we show how to track the construction of complex components. For this we employ formal task models
as background knowledge and simple sensors like RFIDs. The background knowledge is converted into a
probabilistic model that actually tracks the process. As a result, we are able to provide assistance in smart
factories. We discuss the performance of the approach, as well as potential applications.
1 INTRODUCTION
In manufacturing we face the results of global markets
and competition. Today, enterprises are required to
offer highly customised products in shorter through-
put times with an increasing quality built by insuffi-
ciently qualified personnel. This vicious cycle leads
to growing failure rates and extra costs.
Although, smart factories establish digitalisation
and automation to streamline manufacturing pro-
cesses and quality, there is still the need for manual
manufacturing operations (W
¨
urtz and K
¨
olmel, 2012).
One example is the final assembly of complex prod-
ucts. Here it requires assistance in order to manage
the complexity and heterogeneity of extremely small
lot sizes. In this case, the manufacturing companies
strongly depend on the individual expertise of sin-
gle workers. Additionally they operate with quality
ensuring assistance technologies (Berndt and Sauer,
2012) which aim to reduce manual assembly failures
by guiding the worker step by step through assembly
processes and by evaluating his work quality. How-
ever, overheads for the preparation of required data
and extra costs for assistance technology normally
pay off for greater lot sizes. For smaller ones, we also
need to automate the generation of assistance contents
based on already available engineering data and docu-
ments, like construction plans and comments, photos
collected in previous similar situations.
With our work we specifically address the automa-
tion of assistance models and explanations based on
assembly orders and minimal sensor input, as gen-
erated by RFID systems or infrared light barriers.
We focus on tracking the assembly process to pro-
vide step-by-step work assistance and to detect as-
sembly failures. The underlying goal of our research
is the tracking of assembly tasks using sensors already
present in many companies. This tracking is done to
recognise as many logical errors as possible and to
provide assistance as early as possible. In addition
to the simple sensory inputs, we employ formal task
models to describe the work flow of the construction.
The contribution of the paper is threefold. We
present an integrated formal approach, in which a
probabilistic model is synthesised automatically from
a formal task model. We show how assistance can be
provided using the output of this model. Finally, we
present first results showing the performance of the
system in simulation. After introducing a motivating
example, we discuss some related work. In Sec. 4,
we present our approach on a technical level, Sec. 5
shows how assistance can be provided, and in Sec. 7
results of a first evaluation are shown.
2 A MOTIVATING EXAMPLE
First we discuss a simple example to motivate our re-
search presented below. We assume a smart factory
in which individually customised products are assem-
bled by humans. In particular we assume lot size 1
which means that basically every product is unique
and requires new construction plans and assembly or-
161
Bader S. and Aehnelt M..
Tracking Assembly Processes and Providing Assistance in Smart Factories.
DOI: 10.5220/0004822701610168
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 161-168
ISBN: 978-989-758-015-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

ders. This type of factory can be found for example
in special machinery manufacturing and in a vast ma-
jority of small and medium enterprises.
To streamline production processes most facto-
ries already employ smart systems to track parts and
organise manufacturing and material flows. Manu-
facturing execution systems as well as systems for
production data acquisition collect, analyse and dis-
tribute assembly related information to the shop floor.
There, we find assembly lines and stations in which
the final product is built and installed step-by-step.
Required material and tools are available in storage
boxes close to the workplace. Normally, each part is
RFID-tagged and can be identified and checked-out
using industrial RFID readers. In our example, we
work with smart assembly stations as shown in Figure
1. They are additionally equipped with a computer
screen showing assembly manuals or instructions, and
with storage boxes which can be highlighted in order
to ease the picking of parts, material and components.
Assembly manuals are created with the first proto-
type of a product. Then working instructions are com-
bined with construction model figures and assembly
pictures. When producing in small lot sizes, the man-
ual authoring of working instructions exceeds reason-
able efforts.
Figure 1: Smart assembly work place with assistance dis-
play (DESC leanworkStation).
3 RELATED WORK
Manufacturing research focuses on introducing smart
environments to improve automation and quality of
manufacturing processes based on intelligent mate-
rial flows and build orders. Basic concepts of per-
vasive computing, e.g. context-awareness or situa-
tional behaviour, lead to the design of smart work-
flows (Wieland et al., 2008) within production en-
vironments. They use smart sensor networks and
integrated devices to reach a high degree of self-
organisation and improve the overall efficiency. The
Nexus platform (Cipriani et al., 2011) demonstrated
how context-aware computing integrates with a smart
factory wrt. data models, processes and technologies.
With a continuously growing complexity of man-
ufacturing data we witness new challenges in order to
work efficiently with this data on all operational lev-
els. Emerging assistance technologies address spe-
cific scopes. With a semantic enrichment of data
and manufacturing information systems (Li and Qiao,
2012) propose smarter data logistics which are re-
quired to improve knowledge management assistance.
Here, novel interaction technologies lead to a new
way to assist decision makers and production man-
agers in visually analyzing and steering the manu-
facturing progress and key performance indicators.
(Aehnelt et al., 2013a) and (Aehnelt et al., 2013b)
showed with Plant@Hand a visual analytics platform
which supports production management with multi-
modal and multi-user interaction even embedded in
an smart environment.
Novel approaches, such as the cognitive fac-
tory, additionally combine a high degree of self-
organisation and automation with the individual
strengths and flexibility of the human workforce
(Zaeh et al., 2012). Production orders and processes
are controlled via smart decentralised units steering
the product through a smart shop floor environment.
Although manufacturing efficiency and intelligence
grows, it still requires information assistance which
integrates the manual work into the automated smart
factory.
On the shop floor there has been longterm research
to assist workers with information and tools helping
to understand work tasks and to improve work perfor-
mance and quality. Known assistance solutions show
work related data and documents (e.g. construction
plans, assembly manuals or videos) together with task
descriptions, or analyse work results in order to find
quality issues (Berndt and Sauer, 2012).
However, this assistance requires highly adapted
systems which corporate with the existing technolog-
ical infrastructure of manufacturing enterprises. It
lacks methodologies and technologies which derive
autonomously task models, work related information
and assembly advices from already existing manufac-
turing data.
4 RECOGNISING ASSEMBLY
TASKS
Below we discuss the recognition of assembly tasks
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
162

from a technical point of view. As mentioned above,
task models can be used to represent assembly in-
structions formally. Here, we use them as background
information to synthesise a probabilistic model that is
actually used to track the assembly process.
After introducing task models formally, we show
how to convert them into finite state machines accept-
ing the same language, that is, the same sequences
of atomic actions. The finite state machines are
then converted into Hidden Markov Models (HMMs).
Those models allow to estimate the progress of the
assembly task while receiving a stream of sensory in-
puts. In this section, we mainly follow the work de-
scribed in (Burghardt et al., 2011).
4.1 Formal Task-Models to Capture
Work Flows
The definitions below are adopted version of so called
Concur Task Trees (Paterno and Santoro, 2001). Each
node in such a tree represents a task, and its chil-
dren are corresponding sub-tasks. In addition, to ev-
ery node a temporal operator is attached. It specifies
the order in which the sub-task have to be executed.
Figure 2 shows a simple task model. The overall ob-
ject icaart consists of three parts, namely ic, aa and rt,
which can be constructed in any order (|=|). The sub-
tasks have to be assembled in the given order, e.g., for
ic: i >> c. In this example, two temporal operators are
used: order independence (|=|) and enabling (>>).
Further operations include usually iteration (·
∗
), dis-
abling ([>), and concurrency (|||).
Here, we use those models to capture work flows
occurring in smart factories. The atomic actions in-
clude taking a part from a shelf, measure a certain
item, compose two parts, apply a certain tool, and
other. The different sub-tasks have to be performed
in a given order.
icaart
ic aa rt
|=|
i c
|=|
a a r t
>> >> >>
Figure 2: A task model describing a simple assembly pro-
cess. Atomic tasks are shown in boxes, internal nodes are
represented as ellipses. Children are linked to their parents
using a dashed line and to their siblings using a line labelled
with the temporal order.
Definition 1 (Task Model). Let A be a set of atomic
actions and let O be a set ot temporal operators.
Then, the closure of T = a | (o,t
1
, . . . ,t
n
) with a ∈ A ,
o ∈ O, n > 0 and t
i
∈ T is called the set of task models
over A and O and referred to as T
A,O
.
Usually, internal nodes are used to structure the
model only. But, for our application domain, we at-
tach labels to all internal nodes. Those labels are used
to refer to sub-models and to attach assistance actions
as described below. In Figure 2, the labels are shown
within the nodes.
Without giving a formal definition, we call the set
of all valid sequences of atomic actions, the language
of the task model. For the model from Figure 2 there
are six valid sequences, namely: icaart, icrtaa, aaicrt,
aartic, rticaa, and rtaaic.
4.2 From Task Models to Finite State
Machines
Every task model describes a set of valid sequences
of atomic actions necessary to fulfill the task. Thus,
they represent a language over atomic tasks. Next,
we construct finite state machines which represent the
very same language.
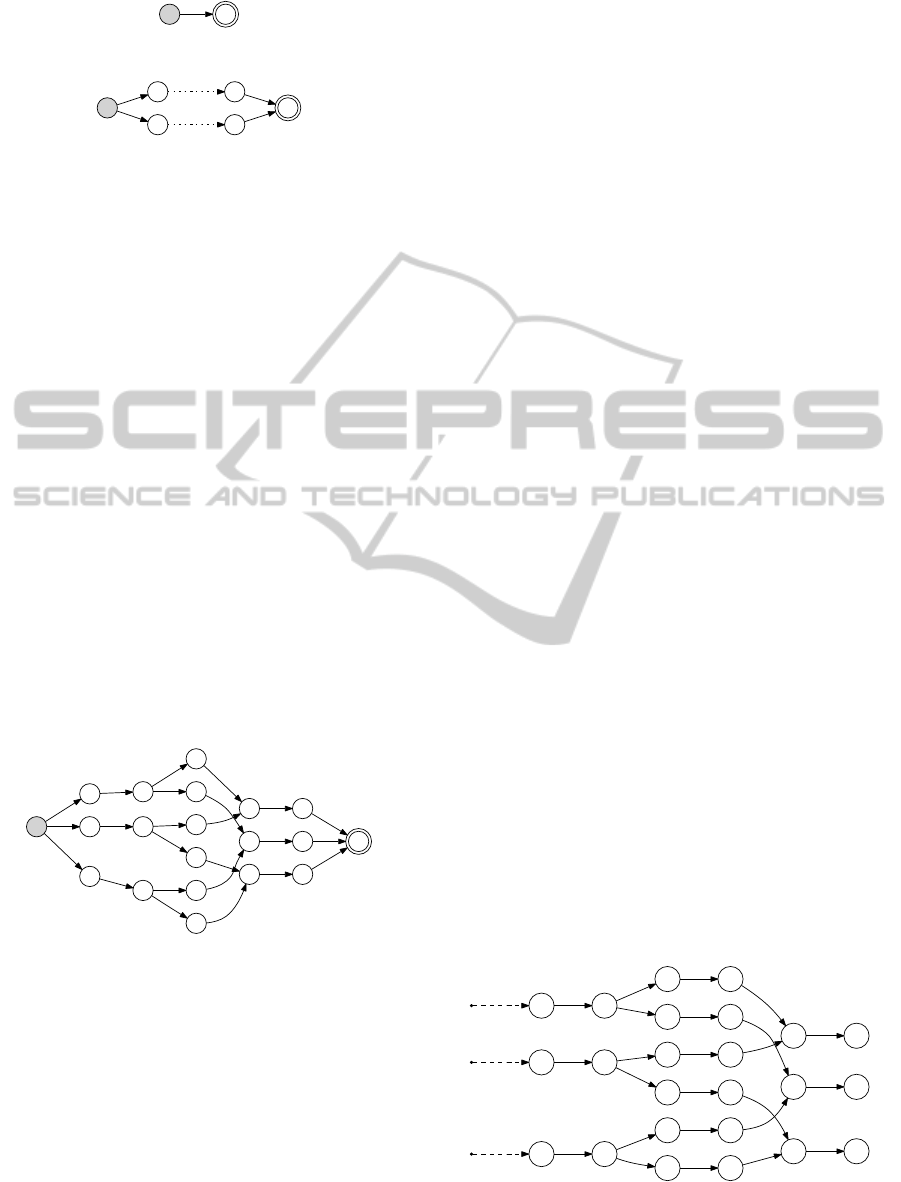
As usual, a finite state machine (FSM) is defined
to be a quintuple (S, s
0
, Σ, δ, F), with S being a set of
states, s
0
∈ S being the initial state, Σ being a set of in-
put symbols, δ : S ×(Σ∪{ε}) → S being a partial tran-
sition function, and F ⊆ S being a set of final states.
A finite state machine for a given task model can
be constructed bottom up, by constructing a FSM for
every atomic task following Definition 2, and then re-
cursively following a conversion procedure depend-
ing on the temporal operator of the task. For the order
independence operator |=|, this procedure is given in
Definition 3. Figure 3 and 4 show FSMs constructed
for an atomic task and an order independent task, re-
spectively.
Definition 2 (FSM Atomic). Let t be a task model for
an atomic action a. Then we define the FSM f for t
as: f := (S, s
0
, Σ, δ, F), with S := {t, t
0
} (with t and t
0
being two new states
1
), s
o
:= t, Σ := {a}, F := {t
0
},
and δ := {(t, a, t
0
)}.
Definition 3 (FSM |=|). Let t be a task model for
order independent sub tasks, i.e., t = (|=|,t
1
, . . . ,t
n
).
Let furthermore f
1
, . . . , f
n
be FSMs constructed for
t
1
, . . . ,t
n
, respectively. Then we define the FSM f for
t as follows:
1
Please note, for a given task t we use t as name for a
state within the HMM. This has been done to prevent the
construction of new names for the states.
TrackingAssemblyProcessesandProvidingAssistanceinSmartFactories
163
0 1
a
Figure 3: A finite state machine for an atomic task.
0
1
ε
3
ε
2
FSM(1)
5
ε
4
FSM(2)
ε
Figure 4: A finite state machine for an order independent
task with two sub-tasks (1 and 2).
f :=(S, s
0
, Σ, δ, F), with S := {t, t
0
} ∪
[
f
i
S( f
i
),
s
o
:=t, Σ :=
[
f
i
Σ( f
i
), F := {t
0
}
δ :={(t, ε, s) | s ∈
[
f
i
s
0
( f
i
)} ∪
[
f
i
δ( f
i
)∪
{(s, ε, t
0
) | s ∈
[
f
i
F( f
i
)}
Similar constructions can be used for every other
temporal operator. After converting a given task
model into a corresponding FSM, this FSM, unfor-
tunately, is (a) highly redundant and (b) contains ep-
silon transitions, i.e., transitions without labels cor-
responding to atomic actions. Both, the redundancy
as well as the ε-transitions can be removed by con-
verting the FSM into a deterministic FSM (without ε-
transitions), and afterwards minimizing the resulting
FSM. For this, we employ standard algorithms as de-
scribed for example in (Hopcroft and Ullman, 1979).
The resulting FSM for the task model from Figure 2
is shown in Figure 5.
19
12
a
0
i
17
r
6
8
a
4 7
r
t
1
3
a
10
r
a
11
t
a
16 5
i c
13
2
i
15
r
c
t
a
14
a
c
18
t
a
9
i
c
Figure 5: A finite state machine encoding the task model
from Figure 2. The initial state is shown with a grey back-
ground (id=19), and the final state shown with double out-
line (id=8).
4.3 From Task Models to Hidden
Markov Models
Hidden Markov Models are a well known technique
for the interpretation of noisy sensor data. For a
general introduction, we refer to (Rabiner, 1989) and
for applications in the context of smart environments
among many other to (Singla and Cook, 2009) and
(Rashidi et al., 2011). Here, we are interested in
the HMM’s ability to compute the most likely se-
quence of probability distribution over states for a
given sequence of observations. Following (Rabiner,
1989), we define a Hidden Markov Model as a quin-
tuple (S, π, T, O, P), with S being a number of states,
π : S → R being an initial probability distribution over
states, i.e.,
∑
s∈S
π(s) = 1, T : S × S → R, being a tran-
sition probability distribution, i.e.,
∑
t∈S
T (s,t) = 1 for
all s ∈ S, O being a set of potential observations, and
P : S × O → R being an observation probability, with
∑
o∈O
P(s, o) = 1 for all s ∈ S.
Based on the FSM introduced above, we construct
a HMM by ‘swapping’ nodes and edges in the graph.
For each pair of state and label attached to an outgoing
edge, a state within the HMM is constructed, i.e., the
states of the HMM coincide with the domain of the
transition function of the FSM.
Definition 4 (HMM for FSM). Let f = (S, s
0
, Σ, δ, F)
be a given FSM, let O
0
be a set of observation sym-
bols, and let O : Σ ×O
0
→ R be a probability distribu-
tion over observations for every input symbol. Then
we define the corresponding HMM as normalised ver-
sion h:
h := (S
0
, π
0
, T
0
, O
0
, P
0
), with S
0
:= dom(δ)
π
0
:= (s, l) 7→
(
1 if s = s
0
0 otherwise
T
0
:= ((s, l), (s
0
, l
0
)) 7→
(
1 if δ(s, l) = s
0
0 otherwise
P
0
:= ((s, l), o) 7→ O(l, o)
The normalised version of the HMM constructed
for the FSM from Figure 5 is shown in Figure 6. The
HMMs constructed in Definition 4 are very restric-
tive in the sense, that only completely valid input se-
quence can be tracked by the HMM. Thus, they are
not yet usable within real settings, because they can-
not handle noise inputs. Therefore, all probability dis-
tributions are softened. Different strategies are dis-
cussed below.
19,a
π=0.33
19,i
π=0.33
19,r
π=0.33
12,a
1.0
0,c
1.0
17,t
1.0
1,a
0.5
1,r
0.5
3,a
1.0
10,t
1.0
4,r
1.0
11,a
1.0
6,a
1.0
13,i
0.5
13,r
0.5
2,c
1.0
15,t
1.0
1.0
16,i
1.0
14,a
1.0
5,c
1.0
18,a
0.5
18,i
0.5
1.0
9,c
1.0
1.0
7,t
1.0
Figure 6: A Hidden Markov Model corresponding to the
task model from Figure 2 and the FSM from Figure 5.
Please note, that no noise has been added yet.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
164

5 PROVIDING ASSISTANCE
Using the approach described above, we are able to
track the progress of the worker. Thus, we can infer
and assist the most likely sub-task currently tackled
by calculating and answering a corresponding infor-
mation demand ID.
Definition 5 (Information Demand). Given a set of
states S corresponding to tasks, a set of individual
workers W and a set of work related, assistive infor-
mation I. The information demand ID : S ×W → P (I)
maps a given state s and worker to a sub-set of the
information I required to understand, prepare and ex-
ecute the task corrsponding to s.
Here, we differentiate between information which
represents procedural knowledge and information
representing declarative knowledge. Both types are
required by the worker for preparing and executing
single assembly tasks. In our case, the procedural
knowledge contains instructions on how to assemble
a component step-by-step, explaining details, orders
and reasons. Declarative knowledge is inherited in
information pieces, which add dimensions, locations,
tools and other facts to the instructions. We use an
XML based annotation language to link tasks to in-
structions:
<ArrayOfInstruction>
<Instruction name="..."
id="...">
<Tasks>...</Tasks>
<Conditions>...</Conditions>
<Description>...</Description>
<Tools>...</Tools>
<Material>...</Material>
<Media>...</Media>
</Instruction>
...
</ArrayOfInstruction>
The application selects the information to be pre-
sented to the worker based on this description and
the probability distribution over sub-tasks (see Fig 7).
This allows to support scenarios in with multiple cor-
rect assembly orders, depending on the worker’s skills
and pre-experiences.
6 TOWARDS GENERATED
ASSISTANCE
A manual formalisation and pre-production of in-
structions is time-consuming and costly. Assistance
applications especially in smart factories can benefit
Figure 7: Plant@Hand assembly assistant application
showing instructions and related information to guide the
assemby process.
from rich data and automation already present today.
Below, we discuss how construction data from earlier
product design and prototype phases can be re-used in
principle.
6.1 Generating Instructions
The worker uses in each assembly task specific com-
ponents, parts, materials as well as tools. For this rea-
son, it requires a workplace re-organisation between
two tasks. We use automatically generate HMMs
(see Sec. 4) based on the construction model with
a detailed bill of materials as well as geometric and
ergonomic conventions. The assistance application
finally generates and shows preparation instructions
(”Take pipe-set MF-L17/8/1 (Z66100000074) ... ”)
and highlights the corresponding storage box from
where the parts can be taken at the workplace. Once a
part or component is picked by the worker, the HMM
is updated and we use the most likely task to gener-
ate matching assembly instructions (”Connect pipe-
set with pump-bleeder.”) from interpreting the con-
struction geometry and domain dependent assembly
procedures (e.g. screwing, welding, bonding). We
then use a visual representation of the model part to
be assembled (see Figure 8) augmented with further
details and generated instructions. Thus, we integrate
declarative and procedural knowledge in a familiar vi-
sual instruction. Knowing only the components to be
assembled is enough information to locate the cor-
responding geometric work view in a 3D construc-
tion model. We finally generate visual hints, annota-
tions and images in order to enhance the construction
model with assembly knowledge. Even if the product
may be individual, a subset of its components may be
used cross-product wide. This makes the re-usage of
information (e.g. assembly pictures) easier in other
situations where the same parts and components have
to be assembled.
TrackingAssemblyProcessesandProvidingAssistanceinSmartFactories
165

Figure 8: Generated visual instruction for assembly of a
chiller component using augmented 3D component model,
text instructions and available media data.
6.2 Generating Explanations
The HMM also helps us to identify assembly failures,
e.g. if a task sequence will not lead to a correctly
assembled component. Then, the assistance appli-
cation shows up any detected issue and tries to give
explanations based on the previous most likely task
(”The pipe-set needs a connection to the cooling cir-
cuit first!”). This creates continuously learning as a
by-product of working. Any time an issue is detected,
the worker can improve his work routine by learning
from automatically generated explanations. Here, it
will make sense to explicitly model specific and re-
curring assembly failures to increase the learning ef-
fect by adding extra training material to false assem-
bly tasks.
7 EVALUATION
Before evaluating the performance of the recognition
below, we introduce a small virtual factory used for
our experiments.
7.1 A Research Factory
To evaluate our approach, we implemented a virtual
factory for the construction of sentences – the Sen-
tenceFactory. As basic building blocks we use char-
acters, that have to be arranged into words and words
are composed into sentences. The system provides
several Web-front-ends: a virtual shelf, an assistance
monitor showing the task model, and a debugging in-
terface showing the probability distribution and inter-
nals of the system.
To keep the implementation simple, only one type
of atomic tasks has been used, namely taking a part
from the shelf. I.e., the atomic action ‘a’ represents
the task of taking part ‘a’ from the shelf. Of course,
in a real factory environment, other atomic tasks are
imaginable. Imagine, for example, a smart meter, able
to measure some value and report this value via wifi.
Then, the measurement itself can be taken as a atomic
task and receiving the measured value as a sensor in-
put.
While processing a stream of sensor inputs, the
probability distribution over sub-tasks is tracked by
the system. Figure 9 shows the evaluation of the
probabilities while processing the input sequence
[i, c, a, a, r, t] using the HMM shown in Figure 6. The
figure shows the probabilities over the non-atomic
sub-tasks, i.e., the sub-models “ic”, “aa”, “rt”. The
probabilities show that all three tasks can easily be
distinguished from each other.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
π i c a a r t
sum over ic
sum over aa
sum over rt
Figure 9: The evolution of the probability distribution while
processing the input sequence [i, c, a, a, r, t] using the HMM
shown in Figure 6.
7.2 Evaluation of Different Errors
As a first experiment, we evaluated our approach by
simulating various kind of sensor errors. Inspired by
the application domain and resulting errors, we con-
centrated on the following types:
1. Missing sensor readings. As most smart storage
systems employ RFID sensors, or infrared light
barriers, it is very likely that taking a part from a
shelf is overlooked by the system.
2. Repeated sensor readings. In particular, while
employing RFID sensors single measurements
might be received multiple times. E.g., taking a
part from the shelf and ‘waiting’ a little too long,
may result in a duplicated RFID event.
The HMM shown in Figure 6 is not yet able to
cope with noisy inputs. To allow for missing read-
ings, we introduce short-cut connections to ‘second
successor’ states within the model. And to allow for
repeated readings, self-transitions are added to every
state, as shown in Figure 10.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
166

19,a
π=0.333
0.238
13,i
0.095
13,r
0.095
12,a
0.571
19,i
π=0.333
0.238
1,a
0.095
1,r
0.095
0,c
0.571
19,r
π=0.333
0.238
18,a
0.095
18,i
0.095
17,t
0.571
6,a
1.000
4,r
0.294
7,t
0.705
0.190
0.238
3,a
0.571
0.238
11,a
0.190
10,t
0.571
0.571
0.238
0.190
0.705
0.294
16,i
0.294
5,c
0.705
0.190
0.238
2,c
0.571
0.190
0.238
15,t
0.571
0.285
0.285
0.238
0.095
0.095
14,a
0.571
0.238
0.190
0.190
0.571
0.238
0.190
0.238
9,c
0.571
0.285
0.285
0.095
0.238
0.095
0.571
0.238
0.190
1.000
0.190
0.571
0.238
1.000
0.190
0.571
0.238
0.571
0.190
0.238
0.095
0.285
0.285
0.095
0.238
Figure 10: The final Hidden Markov Model corresponding
to the task model from Figure 2 and the FSM from Figure 5,
after adding transitions to allow noisy inputs.
We used the log-likelihood of the HMM as a per-
formance measure. The greater the value, the better
is the input sequence recognised by the model. Fig-
ure 11 shows box plots of the log-likelihoods for dif-
ferent types of sequences. For each type, 300 se-
quences have been generated randomly. The figure
shows the median, the lower and upper quartile (as
box), and the whiskers extend to 5% and 95%, respec-
tively. As easily recognisable from the plot, all correct
input sequences are recognised with a log-likelihood
of about −5, the sequences with missing as well as the
repeated inputs are recognised with a slightly worse
value of about −7. In contrast, purely random se-
quences can only be tracked with a value of about
−20. This shows that our approach is indeed able to
track input sequences with the given error character-
istics successfully.
8 CONCLUSIONS AND FUTURE
WORK
The proposed approach enables a new quality of as-
sembly tracking assistance systems in manufacturing.
It supports self-organised as well as pre-planned as-
sembly sequences by tracking work tasks with mini-
−25
−20
−15
−10
−5
0
correct
sequence
missing
inputs
repeated
inputs
random
inputs
type of sequence
log−likelihood
Figure 11: Log-likelihoods for different error types.
mal efforts and generating work instructions and ex-
planations based on a formal task model and exist-
ing engineering data or documents. As mentioned
above, we are aiming at a failure detection and assis-
tance system based on inputs from simple sensors and
background knowledge provided by formal task mod-
els. Both are quasi standard within smart factories, as
most of those factories already employ systems like
RFID to track their parts and provide formal models
like construction plans etc.
Based on the formal description of the workflow,
we synthesise probabilistic models able to track the
assembly process. This model captures the dynam-
ics of the assembly process, by allow the tracking of
every valid sequence of inputs. To accommodate for
likely sensor errors, suitable modification are intro-
duced. The performance of the models is evaluated
through simulated sensor data. Those first results are
promising, as they show the general applicability of
the approach as well as the ability to cope with sensor
noise as appearing within a factory setting.
In the future, we will extend our approach in dif-
ferent dimensions. First of all, a data set will be
recorded within a real factory setting. This will al-
low a better evaluation of the approach. Finally, we
would like to extend the approach towards learning
from observation in the following sense: In many
factories, a lot of knowledge is hidden within single
workers. E.g., an experienced worker simply knows
how to connect certain parts, or will intuitively per-
form necessary steps in an optimal order. This knowl-
edge needs to be extracted.
REFERENCES
Aehnelt, M., Bader, S., Ruscher, G., Kr
¨
uger, F., Urban,
B., and Kirste, T. (2013a). Situation aware interac-
tion with multi-modal business applications in smart
environments. In Hutchison, D., Kanade, T., Kittler,
J., and et al, editors, Human Interface and the Man-
agement of Information. Information and Interaction
TrackingAssemblyProcessesandProvidingAssistanceinSmartFactories
167

for Learning, Culture, Collaboration and Business,
volume 8018 of Lecture Notes in Computer Science,
pages 413–422. Springer, Berlin, Heidelberg.
Aehnelt, M., Schulz, H.-J., and Urban, B. (2013b). To-
wards a contextualized visual analysis of heteroge-
neous manufacturing data. In Proceedings of the 9th
International Symposium on Visual Computing (ISVC
2013).
Berndt, D. and Sauer, S. (2012). Visuelle assistenzsysteme
in der montage verhindern ausf
¨
alle. MM Maschinen-
Markt, (19):46–49.
Burghardt, C., Wurdel, M., Bader, S., Ruscher, G., and
Kirste, T. (2011). Synthesising generative probabilis-
tic models for high-level activity recognition. In Chen,
L., Nugent, C. D., Biswas, J., and Hoey, J., editors,
Activity Recognition in Pervasive Intelligent Environ-
ments, volume 4 of Atlantis Ambient and Pervasive
Intelligence, pages 209–236. Atlantis Press.
Cipriani, N., Wieland, M., Großmann, M., and Nicklas, D.
(2011). Tool support for the design and management
of context models: Selected papers from the 13th east-
european conference on advances in databases and in-
formation systems (adbis 2009). Information Systems,
36(1):99–114.
Hopcroft, J. E. and Ullman, J. D. (1979). Introduction to
Automata Theory, Languages and Computation. Ad-
dison Wesley.
Li, S. and Qiao, L., editors (2012). Ontology-based mod-
eling of manufacturing information and its seman-
tic retrieval: Computer Supported Cooperative Work
in Design (CSCWD), 2012 IEEE 16th International
Conference on.
Paterno, F. and Santoro, C. (2001). The concurtasktrees
notation for task modelling. Technical report.
Rabiner, L. R. (1989). A tutorial on hidden markov models
and selected applications in speech recognition. Pro-
ceedings of the IEEE, 77(2):257–286.
Rashidi, P., Cook, D. J., Holder, L. B., and Schmitter-
Edgecombe, M. (2011). Discovering activities to rec-
ognize and track in a smart environment. IEEE Trans.
Knowl. Data Eng., pages 527–539.
Singla, G. and Cook, D. J. (2009). Interleaved activity
recognition for smart home residents. In Intelligent
Environments’09, pages 145–152.
Wieland, M., Kaczmarczyk, P., and Nicklas, D. (2008).
Context integration for smart workflows: Pervasive
computing and communications, 2008. percom 2008.
sixth annual ieee international conference on: Perva-
sive computing and communications, 2008. percom
2008. sixth annual ieee international conference on
doi - 10.1109/percom.2008.27. Pervasive Computing
and Communications, 2008. PerCom 2008. Sixth An-
nual IEEE International Conference on, pages 239–
242.
W
¨
urtz, G. and K
¨
olmel, B. (2012). Integrated engineering
– a sme-suitable model for business and information
systems engineering (bise) towards the smart factory.
In Camarinha-Matos, L., Xu, L., and Afsarmanesh,
H., editors, Collaborative Networks in the Internet of
Services, volume 380 of IFIP Advances in Informa-
tion and Communication Technology, pages 494–502.
Springer Berlin Heidelberg.
Zaeh, M. F., Ostgathe, M., Geiger, F., and Reinhart, G.
(2012). Adaptive job control in the cognitive factory.
In ElMaraghy, H. A., editor, Enabling Manufacturing
Competitiveness and Economic Sustainability, pages
10–17. Springer Berlin Heidelberg.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
168
