
Fuzzy Cognitive Map Reconstruction
Methodologies and Experiments
Wladyslaw Homenda
1
, Agnieszka Jastrzebska
1
and Witold Pedrycz
2,3
1
Faculty of Mathematics and Information Science
Warsaw University of Technology, ul. Koszykowa 75, 00-662 Warsaw, Poland
2
System Research Institute, Polish Academy of Sciences, ul. Newelska 6, 01-447 Warsaw, Poland
3
Department of Electrical & Computer Engineering
University of Alberta, Edmonton T6R 2G7 AB Canada
Keywords:
Fuzzy Cognitive Maps, Fuzzy Cognitive Map Reconstruction, Fuzzy Cognitive Map Exploration.
Abstract:
The paper is focused on fuzzy cognitive maps - abstract soft computing models, which can be applied to model
complex systems with uncertainty. The authors present two distinct methodologies for fuzzy cognitive map
reconstruction based on gradient learning. Both theoretical and practical issues involved in the process of
a map reconstruction are discussed. Among researched and described aspects are: map sizes, data dimension-
ality, distortions, optimization procedure, etc. Theoretical results are supported by a series of experiments,
that allow to evaluate the quality of the developed approach. The authors compare both procedures and dis-
cuss practical issues, that are entailed in the developed methodology. The goal of this study is to investigate
theoretical and practical problems, that are relevant in the Fuzzy Cognitive Map reconstruction process.
1 INTRODUCTION
Cognitive maps (term fathered by E. Tolman) are
present in sciences since 1940s. The beginnings of the
field are associated with studies on hidden learning
process observed among vertebrate animals. Exper-
iments prove that data units gathered seemingly un-
witting at a previous point of time could be efficiently
processed in order to solve stimuli-triggered problem.
These pieces of information residing in brain ordered
in the cognitive map at the moment of data process-
ing are visualised and associated in order to increase
chances of success.
Associative learning observed among live beings
has become a field of a great interest of artificial in-
telligence, the area of computer science dedicated to
intelligence simulation. Cognitive maps could be ap-
plied in data processing systems, especially in those
dedicated to problem-solving in uncertain and dy-
namic environments. Potential benefits of applying
cognitive maps in data mining are: decreased amount
of calculations required to perform given task, opti-
mized data recollection and enhanced learning pro-
cess, (Papageorgiou and Salmeron, 2013).
Primary, theory of cognitive maps was related
to standard logical notation, the values of the con-
nections could be either +1 or -1. Later research
has proved that incorporating fuzzy logic into cogni-
tive maps could be beneficial as the new data repre-
sentation model could be a better reflection of real-
world relationships. As a result, in Fuzzy Cognitive
Maps the values of the connections are anywhere in-
between -1 and +1. The new information model forms
signed fuzzy digraph, that could be applied in com-
plex systems analysis, (Papakostas et al., 2008), (Pa-
pakostas et al., 2012). Improved modelling capabil-
ities are suitable in systems influenced by the uncer-
tainty factor.
Authors benefit from the research on cognitive
maps, that has been already done and investigate se-
lected practical and theoretical issues of information
processing and mining with the use of cognitive maps,
(Stach et al., 2005), (Stach et al., 2004). This paper
is oriented on Fuzzy Cognitive Maps and customized
framework, which we plan to use to describe eco-
nomic phenomena. Theoretical aspects discussed in
this article are intertwined with practical issues, that
may be solved with the prepared model.
The paper is structured as follows. In Section 2 the
authors discuss two methodologies for Fuzzy Cogni-
tive Map reconstruction. In Section 3 both method-
ologies are applied in a series of experiments. The
aim of the discussion on the selected experiments is
to test the developed procedures, compare their prop-
499
Homenda W., Jastrzebska A. and Pedrycz W..
Fuzzy Cognitive Map Reconstruction - Methodologies and Experiments.
DOI: 10.5220/0004822904990510
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 499-510
ISBN: 978-989-758-015-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

erties and analyze practical aspects of our approach to
FCM reconstruction. Among investigated issues are
data dimensionality, model parameters, and others.
2 METHODOLOGY
2.1 Introductory Remarks
Fuzzy Cognitive Maps are abstract soft computing
models, that are directed graph-alike structures com-
prising of nodes and weights connecting the nodes,
(Kosko, 1986). In practical applications nodes corre-
spond to various phenomena, for example: unemploy-
ment, fuel prices, air pollution, human capital, etc.
Relations between phenomena in a cognitive map are
expressed through weights between nodes. An exam-
ple of a 3-node fuzzy cognitive map is in Figure 1.
Figure 1: Cognitive map n=3.
A map is characterized with a collection nodes
V = {V
1
,V
2
, . . . ,V
n
} and with a weights matrix W ,
which is a nxn matrix. Cognitive map exploration is
performed with activations X. Activations are gath-
ered in a n × N matrix, which each k = 1, . . . , N col-
umn contains nodes activations in the k-th iteration.
Cognitive map computes responses to presented acti-
vations. Responses Y are gathered in a nxN matrix,
alike activations are. In general, responses are com-
puted according to the formula:
Y = f (W ∗ X) (1)
where ∗ is an operation performed on matrices W and
X, which produces a matrix W ∗ X of size nxN, and f
is a mapping applied individually to elements of W ∗
X. Matrix product is an example of such operation
and it is utilized in this study.
Let us denote i-th row, j-th column and an element
in i-th row and j-th column of a matrix A as A
i·
, A
· j
and A
i j
, respectively. In order to compute map’s re-
sponse to k-th activations (response in k-th iteration),
we apply the formula:
Y
·k
= ftras(W · X
·k
) (2)
and, more specifically, i-th node response in k-th iter-
ation is computed by multiplying:
Y
ik
= ftrans(W
i·
· X
·k
) (3)
where f trans is a nonlinear non-decreasing transfor-
mation function. f trans : R → [0, 1]. In this paper we
use sigmoid function chosing the τ parameter equal to
2.5 based on experiments:
f sig(z) =
1
1 +exp(−τz)
, τ > 0 (4)
Computed responses should match actual (ob-
served, measured) status of the corresponding phe-
nomena. We call such actual status a target. With
a given weights matrix, using Formula 3, we calcu-
late nodes’ responses for a given input activation set.
The better the model, the closer are model responses
to the target.
In empirical models based on cognitive maps one
has to take into account certain dose of uncertainty.
No matter at which step we start cognitive map ex-
ploration, there may be a chance of errors of various
nature, for example:
• if weights matrix is constructed based on experts’
knowledge, one may expect diverse, even contra-
dictory, evaluations of relations within the nodes.
Most probably, character of such errors will be
random,
• if for training purposes we use data from measur-
ing devices, there is always a chance of systematic
or random errors (devices and observations (e.g.
meter reading) may be malfunctioning).
These are two common sources of distortions in
a model based on a cognitive map. In this paper we
focus on models with such distortions.
Let us assume that we do not have weights ma-
trix, but activations in consecutive N iterations and
observed (target) status of the corresponding phenom-
ena. We can construct weights matrix W by mini-
mization of the error:
min(error(Y, T GT )) (5)
where Y are map responses and T GT are targets.
2.2 Datasets
We have conducted experiments with the use of two
training (not distorted and distorted) and one testing
datasets. The goal of the procedure for Fuzzy Cogni-
tive Map reconstruction is to build a map, that is the
closest to a perfect map. The perfect map is an ideal
description of a system of interest. Our methodology
attempts at reconstruction of this perfect map, hence
we use the term FCM reconstruction.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
500

For methodological purposes we use three afore-
mentioned datasets. The not distorted training dataset
describes the ideal, perfect map. We use this dataset
for quality assessment purposes - differences between
map response and not distorted training dataset in-
form how the reconstructed model differs from the
ideal one.
The not distorted training dataset is never present
in real data. Modeling real-life phenomena is always
connected with distortions of varied nature. There-
fore, the map reconstruction procedure is based on
distorted training dataset. We investigate two differ-
ent strategies that add distortions to the map. Dis-
torted training dataset derives from not distorted one.
Testing dataset is used for map quality assessment.
Test datasets were half the size of train datasets.
In Section 3 we present dependency between map
size, train dataset size and accuracy.
We have tested two kinds of weights matrices:
• weights matrix with values drawn randomly from
the uniform distribution in the [−1, 1] interval,
values are rounded to 2 decimal points,
• weights matrix with a given share of zeros and
other weights drawn randomly from the uniform
distribution.
First kind of weights matrix does not need to be
explained to greater detail. The second kind repre-
sents a map, in which there is certain share of 0s.
Connections evaluated as 0s inform us that there is
no relationship between given nodes. With a weight
equal to 0 we express also lack of knowledge about
relationship between given phenomena. Such maps
are important from the practical perspective. Hence,
we investigate maps based on weights matrices with
given share of 0’s set to: 90%, 80%, 70% and so on.
Activations are real numbers from the [0, 1] inter-
val drawn randomly from the uniform distribution.
To retain comparability whenever it is possible we
use the same datasets. For example, each experiment
for n = 8 (number of nodes) is based on the same ac-
tivations.
2.3 Experiments’ Methodology
In this section we discuss the methodology of FCM
reconstruction process and methodology of the exper-
iments. The training dataset contains distortions. The
goal of our study on distortions in cognitive maps
training is to prepare a model, which may be ap-
plied to describe real-world phenomena. We present
full course of the experiments, including training and
quality evaluation phase.
The course of the full experiment, including vali-
dation, is the following:
• there is an ideal weights matrix W , that describes
the system perfectly. Given are activations X.
,,Ideal” weights and activations produce ideal tar-
gets (,,ideal” T GT ) based on Formula 1,
• the ideal data gets distorted and the perfect
weights matrix is lost,
• The goal is to reconstruct the map based on:
– activations X,
– distorted target T GT
D
.
• with the use of error minimization procedure
based on gradient weights matrix is reconstructed,
• the quality of the reconstructed map is tested on
training and test datasets.
The procedure described above is a general methodol-
ogy of our approach. The map reconstruction process
in the shape as it is on real data is the following:
• given are activations and distorted targets,
• with the use of gradient learning we reconstruct
the map
• the quality of the model is checked on the testing
dataset.
In the following paragraphs we discuss in greater
detail methodology of our approach. We focus on dis-
tortions and collate model quality with the strength of
distortions. The more susceptible is the procedure to
distortions, the better it performs on real data.
2.3.1 FCM Training with Distortions on the
Weights Level
Figure 2 illustrates FCM training and testing proce-
dure with distortions introduced on the weights level.
In this variant of the proposed procedure map re-
construction is based on:
• activations X,
• targets T GT
W (eights)D(istorted)
distorted through
distortions applied to weights.
Training phase adjusts weights matrix W
0
W
so that:
error
T GT
W D
, f sig(τ,W
0
W
· X)
(6)
is minimized.
The training dataset is distorted on the level of
weights. Distortions are then propagated to targets
T GT
W D
. The training procedure overcomes errors,
that are propagating as a result of a prior distortion.
Training procedure uses conjugate gradients
method. In practical experiments we used a version of
conjugate gradient implemented in R. Gradient-based
optimization minimizes error as in Formula 6. We
tested the procedure against several errors. As a re-
sult of the optimization a new weights matrix W
W f in
FuzzyCognitiveMapReconstruction-MethodologiesandExperiments
501
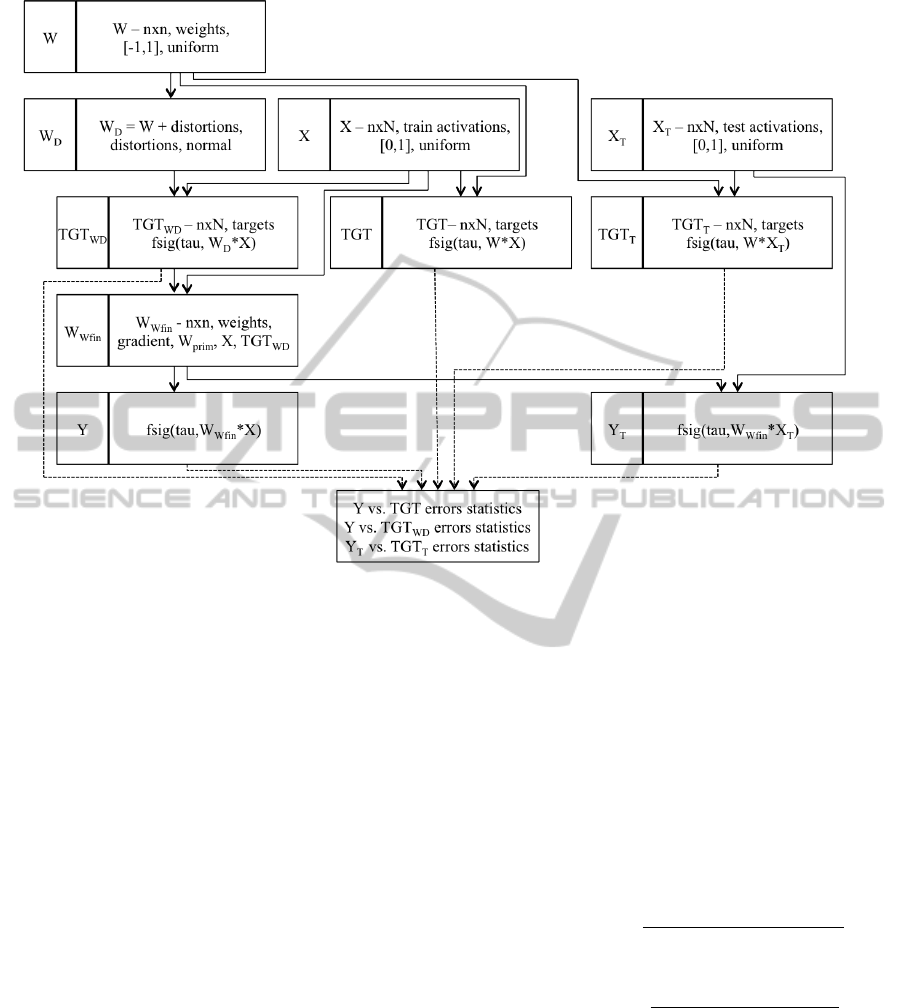
Figure 2: Experiment scheme with distortions introduced on the weights level.
is constructed. Based on activations and W
W f in
model
outputs, denoted as Y , are computed.
In the Figure 2 we have intentionally distinguished
training dataset and test dataset. Model is built on
distorted training dataset and tested on not distorted
training dataset and on the test dataset.
2.3.2 FCM Training with Distortions on the
Target Level
The alternative way to include distortions is to apply
them directly to targets. In this way distortions ap-
pear, but they are not propagated. Detailed experi-
ment scheme is illustrated in Figure 3.
The model training phase is based on conjugate
gradient method and it minimizes error:
error
T GT
T D
, f sig(τ,W
0
T
· X)
(7)
We build the map with the distorted train dataset
and asses its quality based on:
• discrepancies between ,,ideal” target T GT and
model response Y for the training dataset,
• discrepancies between test target T GT
T
and test
model response Y
T
(on the test dataset).
The difference between scheme in Figure 2, when
we distort weights, and scheme in Figure 3, when
we distort target is in the nature of distortion. In the
first case errors are systematically propagated. In the
second case discrepancies occur, but they are not in-
volved in further transformations.
2.3.3 Model Building Phase - Minimization
Criteria
We use conjugate gradient method to reconstruct
weights matrix based on activations and distorted tar-
gets. We have conducted several sets of experiments,
in which we minimize the following errors:
• Mean Squared Error:
MSE(T GT,Y ) =
∑
N
k=1
∑
n
i=1
T GT
ik
−Y
ik
2
N ∗ n
(8)
• Mean Absolute Error:
MAE(T GT,Y ) =
∑
N
k=1
∑
n
i=1
T GT
ik
−Y
ik
N ∗ n
(9)
• Maximum Absolute Error:
MAXA(T GT,Y ) = max
n
|T GT
ik
−Y
ik
:
i = 1, . . . , n, k = 1, . . . , N
o
(10)
In Section 3 we verify the quality of the developed
training procedure based on errors listed above. MSE
and MAE errors average discrepancies between tar-
gets and map responses. MAXA error informs about
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
502
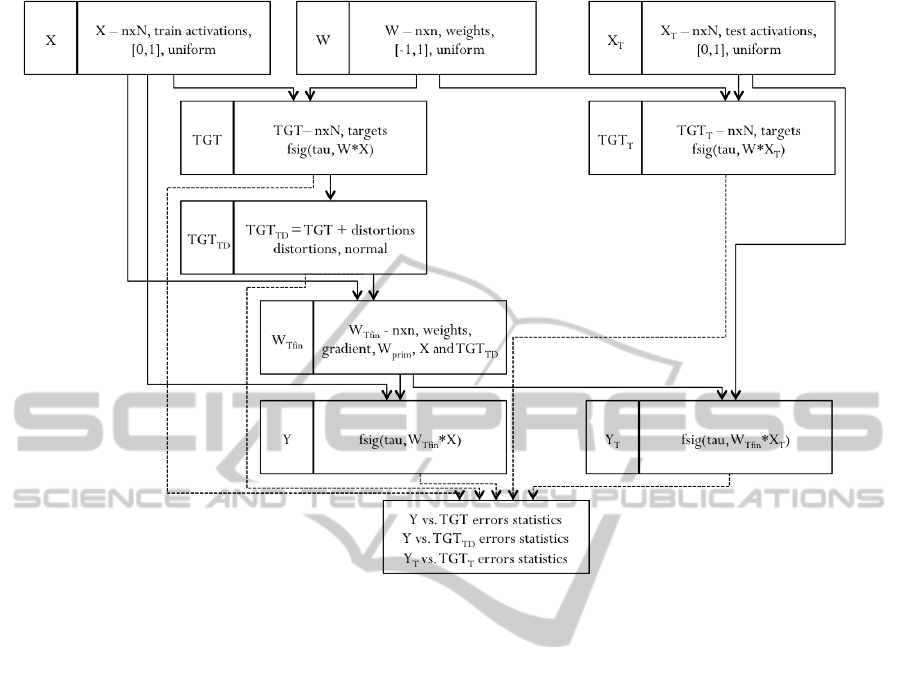
Figure 3: Experiment scheme with distortions introduced on the targets level.
the greatest absolute difference between a single data
point. MSE and MAE allow to infer about models
quality. MAXA plays only informative role.
3 RESULTS
In this section we apply proposed methodology. We
divided this section so that each important aspect of
a FCM reconstruction process is discussed separately.
3.1 Parameters Influence on Errors
In this subsection we investigate relations between
training procedure, data dimensionality and error
rates. We track how the number of nodes and the
number of iterations influence the accuracy. First, we
present FCM reconstruction scheme with distortions
introduced on the target level. Secondly, we discuss
models, that were fitted to data, where distortions ap-
peared on the weights level. Let us recall, that size of
the map (number of nodes) is denoted as n, while the
number of training observations is denoted as N.
We test the quality of the reconstructed map by
comparing map responses, denoted as Y , with targets.
Computed errors: MSE, MAE and MAXA inform
about discrepancies between fitted model to our data.
We test the quality on 3 datasets:
• not distorted train dataset (denoted as train ND),
• distorted train dataset (denoted as train D),
• test dataset.
The first comparison: on not distorted train dataset in-
forms us, how fitted model output differs from ,,ideal”
targets. The second comparison: Y against T GT
W D
or
T GT
T D
informs us how the model adjusts to the data,
that was used to train it. The last comparison uses
test dataset, which is separate and not connected with
train datasets.
Following experiment details are assumed:
• minimized is Mean Squared Error,
• weights matrix is random, the same in each run of
the experiment,
• no more than 100 repetitions of conjugate gradient
algorithm are performed,
• τ = 2.5, distortions on target and weights levels
are random from normal distribution with stan-
dard deviation sd=0.4 and sd=0.8, respectively.
Tests were performed for maps of size 4, 8, 12 and
20. We have investigated how the number of iterations
influences error rates. The number of observations
FuzzyCognitiveMapReconstruction-MethodologiesandExperiments
503
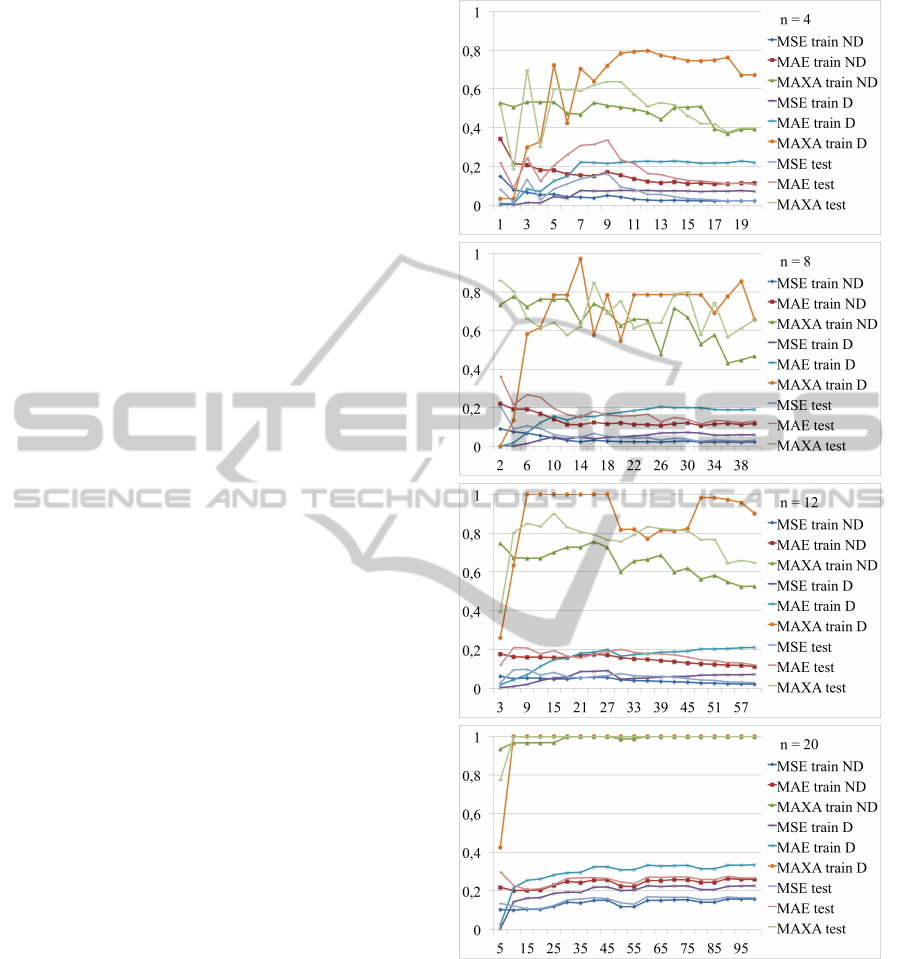
was changing, from 0.25n to 5n. Plots below summa-
rize named errors on training and testing datasets.
3.1.1 Training with Targets Distorted
Plots in Figure 4 show MSE, MAE and MAXA errors
against the size of map training dataset. Plots concern
maps of different sizes (4, 8, 12 and 20), all trained
on distorted targets. MAXA errors do not determine
the overall quality of the model, they play an infor-
mative role. Accuracy of recreated map is confirmed
by MSE and MAE errors, which inform about mean
errors statistics. Plots concern not distorted train, dis-
torted train and test datasets.
One can observe, that with the smallest map we
have the highest instability. MSE and MAE errors sta-
bilize when the number of iterations N is over 3 ∗ n.
For a map of n = 8 nodes MSE and MAE stabilize,
when the number of iterations is over 1.5 ∗ n, for
a map of n = 12 stability is reached when N = n.
The smaller the map, the smaller is the error. Er-
rors, after the stabilization, remain on a steady level
in each case. Adding more observations (greater N)
causes that the error slightly decreases for the train
ND dataset and the test dataset. This is a very attrac-
tive property, map reconstruction procedure is stable
and the model is not overfitted.
Let us closely investigate targets, which were dis-
torted by random values drawn from the normal dis-
tribution with sd=0.4. As a result T GT
T D
contains
significant amount of 0s and 1s, which cannot be pro-
duced as a model response with sigmoid function as in
Formula 4. Due to asymptotic properties of sigmoid
function we cannot expect the map to reach targets
equal to 0 or 1. Nevertheless, it does not mean, that
a map recreated with distorted targets is worse than
a map, that was recreated based on distorted weights.
Side effect of increased map size is duration of
algorithm run. All experiments were performed on
a standard PC. For n=4, n=8, n=12 and n=20 we
needed around 2 seconds, 1 minute, 7 minutes, for
a single map reconstruction, respectively. The in-
crease in computation time with respect to map size
is faster than linear.
3.1.2 Training with Weights Distorted
Similar experiment was conducted for data with dis-
tortion introduced on the weights level. Figure 5 con-
tains error plots for FCMs of various size. The OX
axis informs about the size of the training dataset.
Plots in this case differ from the previous ones.
Fitting procedure in this case was very successful for
smaller maps. It is especially easy to observe for
n = 4, where even MAXA errors are relatively small.
Figure 4: Relation between data dimensionality and errors.
Training with distortions on the target level. Map sizes:
n=4, n=8, n=12 and n=20.
Instability at the beginning, for N = 1, 2, 3 occurred
because of the influence of insufficient data dimen-
sionality. For a map with n = 8 nodes fitting proce-
dure performed also very well. The error on the dis-
torted training dataset was very small. For smaller
maps (n = 4 and n = 8) on the distorted train dataset
MSE and MAE do not reach 0.1.
The situation changes as the size of the map
grows. Training procedure with distortions on the
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
504

Figure 5: Relation between data dimensionality and errors.
Training with distortions on the weights level. Map sizes:
n=4, n=8, n=12 and n=20.
weights level becomes less effective. This map re-
construction procedure is more sensitive to the map
size. Moreover, map reconstruction procedure based
on distorted weights is able to fit the model to the dis-
torted train data relatively well, but on not distorted
dataset and on the test dataset results are worse. It is
especially easy to spot for n = 12.
The larger is the map, the greater is the MSE er-
ror. Smallest error is with respect to the data, that was
Figure 6: Training with distortions introduced on the
weights and targets level: comparison of MSE on not dis-
torted training dataset.
used to train the map, but for the two other datasets
results show clear relation between map size and the
accuracy.
3.1.3 Comparison of the Two Methodologies
Figures 6, 7 and 8 allow to compare the two method-
ologies of map reconstruction. The results of the
two training methods: based on distorted targets and
based on distorted weights are compared for training
and test datasets.
On the distorted training dataset, the one that was
used for map reconstruction, errors are higher for the
methodology based on distorted target. Model built
with distorted weights fits better to the data, that was
used to train it.
Only for the smallest map, model built with dis-
torted weights achieves lower errors. In contrast, for
maps larger than n = 4, models based on distorted tar-
gets are better. MSE errors are even 0.1 lower, than
for the distorted weights method. Method based on
distorted targets does not overfit the map and it per-
forms well on the test and the ,,ideal” datasets.
FuzzyCognitiveMapReconstruction-MethodologiesandExperiments
505
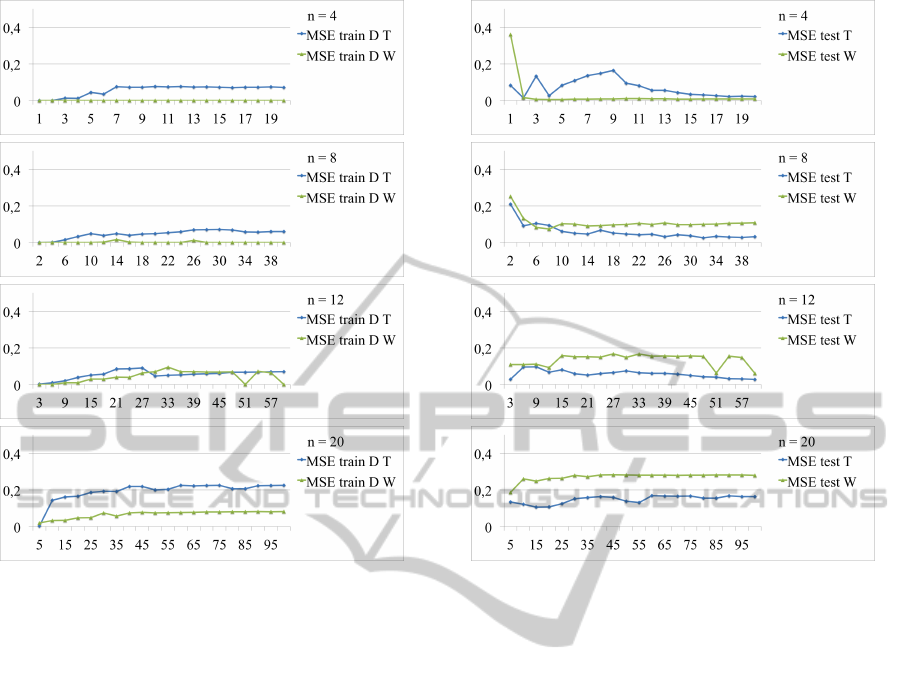
Figure 7: MSE on distorted training dataset. Comparison of
training with distortions on target and weights levels.
3.2 The Influence of Error
Minimization Procedure on Errors
In this section we investigate if the choice of an error
to be minimized influences error rates. In the map
reconstruction procedure we use conjugate gradient
to rebuild the FCM. In the scheme of optimization we
minimize the error between distorted target and map
response. Map response (obtained with new weights)
should be as close to distorted target as possible. In
the experiments we set following parameters:
• n = 8, N = 16,
• weights matrix is random, the same in each run of
the experiment,
• no more than 100 repetitions of conjugate gradient
algorithm are performed,
• τ = 2.5, distortions on target level and on weights
level are random from the normal distribution
with sd=0.4 and sd=0.8, respectively.
We have chose the size of the map and data dimen-
sionality sufficient to comment differences for the two
map reconstruction procedures. Table 1 contains final
errors for various optimization strategies.
If we optimize with MSE, MAE and MAXA re-
sults do not differ significantly, especially for the sec-
Figure 8: Comparison of MSE on test dataset for the two
methodologies.
ond map reconstruction strategy (distorted weights).
Optimization procedure produces similar outputs, tar-
gets are not 0s or 1s.
In the case of training with distortions introduced
on the targets results are less similar, than they were
before. Training with targets, that contain 0s and 1s
makes the results less similar, depending on the kind
of error that we minimize.
3.3 The Influence of the Distortions
Rate on Errors
In this section we investigate how applied scale of dis-
tortion influences the fitness of the reconstructed map.
We analyze this problem separately for the procedure
based on distortion on the weights level and on the
targets level. Firstly, we investigate random errors.
Subsequently, we discuss the influence of systematic
errors. In the experiments in this section we set fol-
lowing experiment details:
• n = 8, N = 16,
• minimized is Mean Squared Error,
• weights matrix is random, the same in each run of
the experiment,
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
506
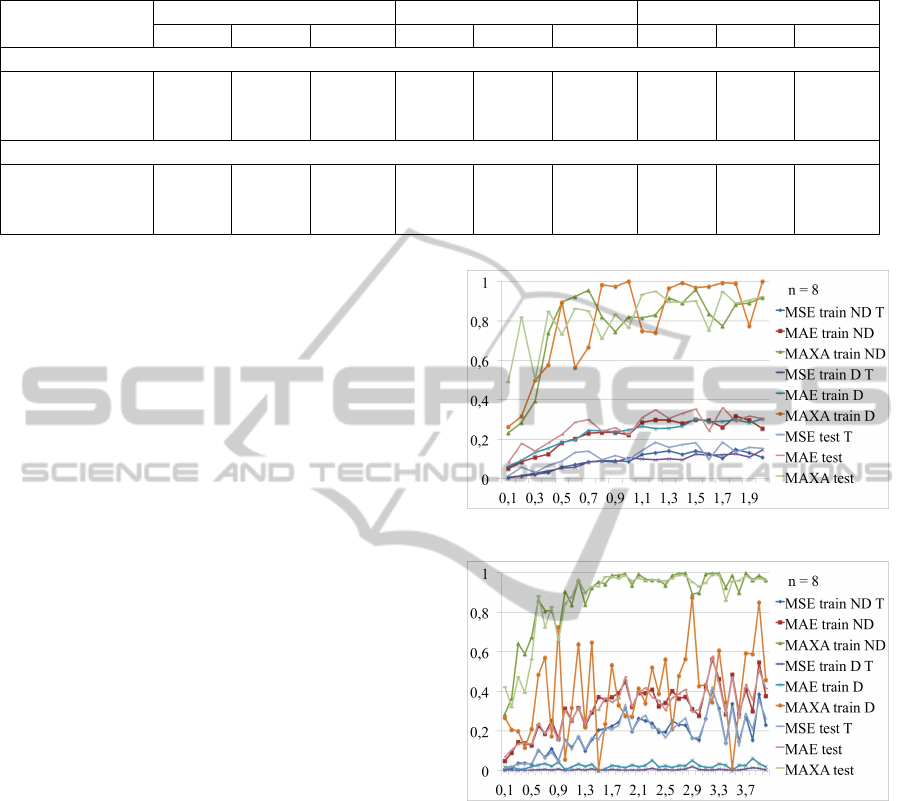
Table 1: Errors on train/test datasets for models based on reconstructed weights with MSE, MAE and MAXA minimization.
minimized error
train ND train D test
MSE MAE MAXA MSE MAE MAXA MSE MAE MAXA
data distorted on targets level
MSE 0.1257 0.2742 0.8087 0.1604 0.3210 0.9559 0.1298 0.2927 0.8588
MAE 0.1740 0.3153 0.8938 0.2039 0.3452 0.9934 0.1851 0.3379 0.8930
MAXA 0.1278 0.2707 0.8652 0.1617 0.3162 0.9767 0.1421 0.2939 0.9257
data distorted on weights level
MSE 0.0368 0.1345 0.5944 0 0.0015 0.044 0.0334 0.1307 0.4156
MAE 0.0369 0.1345 0.6143 0.0002 0.0071 0.0688 0.0354 0.1334 0.4852
MAXA 0.0359 0.1325 0.6034 0.0004 0.0139 0.0656 0.0384 0.1427 0.4816
• no more than 100 repetitions of conjugate gradient
algorithm are performed,
• τ = 2.5.
3.3.1 Distortions Applied on the Target Level
In the case of the first training procedure we apply dis-
tortions directly to targets. We have tested how distor-
tions influence accuracy of the training procedure.
Figure 9 illustrates how the level of distortions in-
fluences errors. Distortions are random from normal
distribution with given standard deviation (distortion
rate sd, on the OX axis) and mean is equal 0.
The larger is the distortion rate, the higher are er-
rors. The constant increasing error rate is visible for
the two train datasets. For the test dataset, the trend
is not strictly increasing, but the tendency is the same
- with the growth of the distortion rate errors become
larger. Nevertheless, errors do not get very large. In
the worst case, for test dataset MAE does not exceed
0.3. MSE for training datasets do not exceed 0.1. This
proves, that the proposed procedure is stable and re-
constructs FCMs well.
3.3.2 Distortions Applied on the Weights Level
Let us compare previous results with fitness of the
procedure based on distorted weights. Figure 10 il-
lustrates how the level of distortions influences errors.
Distortions are random from normal distribution with
given standard deviation (distortion rate sd, on the OX
axis) and mean equal 0.
Distortions rate applied to weights is greater than
before. Targets are from the 0, 1 interval, while
weights are from the [−1, 1] interval. Therefore, on
the OX axis one can observe, that we have conducted
experiments for distortions ranging from 0.1 to 2.0.
In this case the results are less stable. This prop-
erty has been already mentioned. Procedure based
on distorted weights is more sensitive. As a result
lines are not smooth. The tendency of error growth
has been maintained. The higher is the distortions
Figure 9: Errors vs. distortions set on the target level.
Figure 10: Errors vs. distortions set on the weights level.
rate, the larger are errors. Map reconstruction proce-
dure based on distorted weights performs worse than
the procedure based on distorted targets. Errors are
greater. In the worst case, for the MAE error is over
0.45. Please observe, that errors for distorted dataset,
the one which has been used to train the map, is very
small. The model fits to the training data well, but it
does not perform well on other datasets.
3.3.3 Systematic Distortions
Subsequently, we have investigated the influence of
systematic errors on the reconstructed map. Figures
11 and 12 present errors for varying range of system-
atic distortions introduced on the target and weights
levels.
FuzzyCognitiveMapReconstruction-MethodologiesandExperiments
507
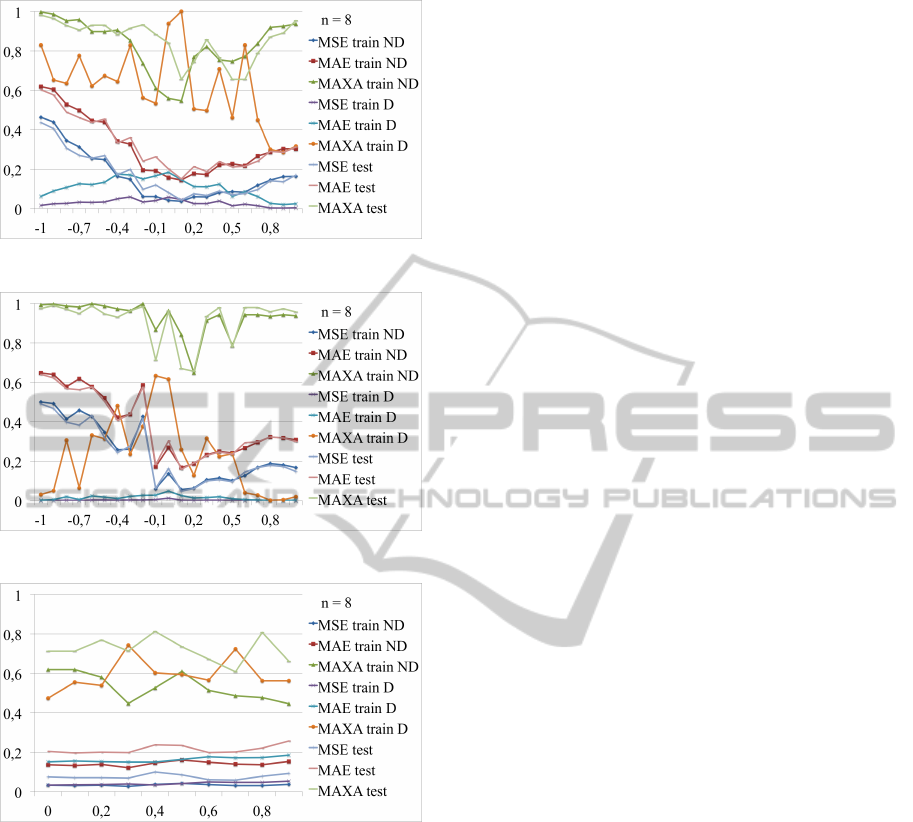
Figure 11: Systematic distortions applied to targets.
Figure 12: Systematic distortions on the weights level.
Figure 13: Errors vs. share of 0s in the weights matrix to be
reconstructed.
In order to include systematic errors, targets and
weights distortions have been drawn from the normal
distribution with standard deviations 0.4 and 0.8, re-
spectively. Mean of the systematic distortions is on
the OX axis. Errors are the lowest in the neighbor-
hood of 0. In both cases we have observed, that errors
were larger for negative mean of distortions.
3.4 The Influence of Weights Matrix
Kind on Errors
Previous experiments were aimed to reconstruct
a map with random weights matrix. In these cases,
matrices were filled with random values from the
[−1, 1] interval. In this section we compare the ef-
fectiveness of the two proposed map reconstruction
procedures for maps that contain certain share of 0s.
The focus on this aspect is driven by practical issues.
In practice, weights matrices, especially large ones,
contain a lot of 0s, that represent lack of relationship
between the nodes or lack of knowledge about such
relations.
In the experiments in this section we have as-
sumed the following:
• n = 8, N = 16,
• minimized is Mean Squared Error,
• no more than 100 repetitions of conjugate gradient
algorithm are performed,
• τ = 2.5, distortions on target and weights lev-
els are random from the normal distribution with
sd=0.4 and sd=0.8, respectively.
We investigate, if the share of 0s in the original
weights matrix influences model fitness and stability.
We have prepared two experiments. First one aims at
map reconstruction without additional assumptions.
This experiment is performed for the training scheme
with distortions on the target level. It is not suitable
for the second training scheme.
The second experiment assumes, that 0s from the
original matrix W are maintained in the final weights
matrix W
f in
. We have tested it with the two training
methodologies.
3.4.1 Distorted Targets. No Assumptions
Regarding the Shape of W
f in
.
We have tested training procedure, which involves
distortions on the target level. Figure 13 illustrates
how the errors change depending on the percentage
of 0s in the original weights matrix.
One can observe that developed procedure is sta-
ble, there are no significant changes in error rates,
as the share of 0s in the original weights matrix in-
creases. Even when the original matrix is all 0s (the
last data point on the plot) map fitness is not bad.
3.4.2 Distorted Targets. Additional Assumptions
Regarding the Shape of W
f in
.
In this experiment we have stated an additional as-
sumption for the reconstructed map. We require that
positions, which were filled with 0s in W remain set to
0 after the optimization. Such experiment is driven by
practical issues. We may know or want to set certain
relation in the reconstructed map to 0.
Figure 14 illustrates how errors change as the
number of 0s in the weights matrix grow.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
508
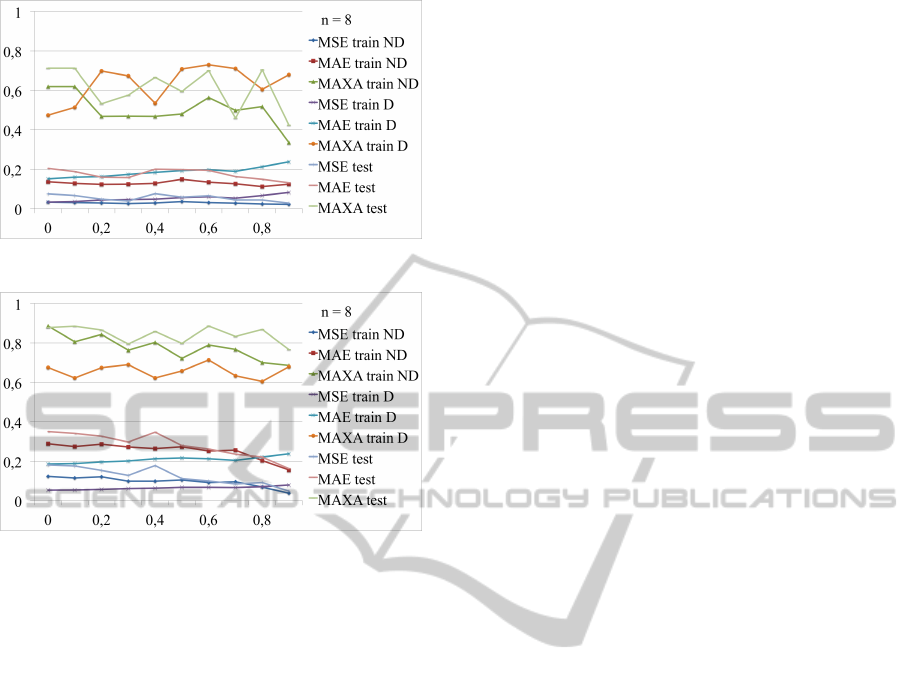
Figure 14: Errors vs. share of 0s in the weights matrix.
Figure 15: Errors vs. share of 0s in the weights matrix.
One may observe, that training procedure is stable
and MSE and MAE errors remain at a fixed rate. An
interesting observation is in the last data point on the
OX, percentage = 90%. For the test and not distorted
datasets the errors there are the smallest, the model is
the closest to the original one.
3.4.3 Distorted Weights. Additional
Assumptions Regarding the Shape of W
f in
.
Similar experiment has been performed for the second
approach to FCM reconstruction.
Figure 15 illustrates how MSE, MAE and MAXA
errors change depending on the share of 0s in the orig-
inal weights matrix W . We have assumed hat in the
final matrix 0s remain unchanged. Similarly as in the
previous case, for the largest share of 0s the model
performs slightly better. Most important conclusion
is that our procedure for both methodologies is resis-
tant to unusual, but important from the practical point
of view matrices.
4 CONCLUSIONS
The authors focus on Fuzzy Cognitive Maps - an im-
portant knowledge representation model. They are
noteworthy tools, able to deal with imprecise, grad-
ual information.
In this paper methodologies for Fuzzy Cognitive
Map reconstruction are proposed. FCM reconstruc-
tion aims at building a map, that fits to the target ob-
servations to the greatest extent. With the map recon-
struction procedure we can rebuild a Fuzzy Cognitive
Map, without any prior knowledge about relations be-
tween maps’ nodes. Our methodology is based on
gradient-based optimization, that minimizes discrep-
ancies between map responses and targets.
The theoretical introduction and discussion on the
developed procedure of FCM reconstruction is sup-
ported by a series of experiments. Presented exper-
iments allow to verify the quality of the developed
approaches in various scenarios. We have discussed
the issues of map size, data dimensionality and dis-
tortion levels. We have investigated properties of the
developed procedure and showed, that it is effective
and stable. Experiments were conducted on three
datasets, addressed are model parameters and final er-
rors.
In future authors plan to research cognitive maps
based on other information representation schemes,
(Pedrycz and Homenda, 2012), (Zadeh, 1997). We
will especially investigate bipolar information repre-
sentation scheme and generalizations of FCMs.
ACKNOWLEDGEMENTS
The research is supported by the National Science
Center, grant No 2011/01/B/ST6/06478, decision no
DEC-2011/01/B/ST6/06478.
Agnieszka Jastrzebska contribution is supported
by the Foundation for Polish Science under Interna-
tional PhD Projects in Intelligent Computing. Project
financed from The European Union within the In-
novative Economy Operational Programme (2007-
2013) and European Regional Development Fund.
REFERENCES
Kosko, B. (1986). Fuzzy cognitive maps. In Int. J. Man
Machine Studies 7.
Papageorgiou, E. I. and Salmeron, J. L. (2013). A review of
fuzzy cognitive maps research during the last decade.
In IEEE Trans on Fuzzy Systems, 21.
Papakostas, G., Koulouriotis, D., and Tourassis, A. P. V.
(2012). Towards hebbian learning of fuzzy cognitive
maps in pattern classification problems. In Expert Sys-
tems with Applications 39.
Papakostas, G. A., Boutalis, Y. S., Koulouriotis, D. E., and
Mertzios, B. G. (2008). Fuzzy cognitive maps for pat-
tern recognition applications. In International Journal
FuzzyCognitiveMapReconstruction-MethodologiesandExperiments
509

of Pattern Recognition and Artificial Intelligence, Vol.
22, No. 8,.
Pedrycz, W. and Homenda, W. (2012). From fuzzy cog-
nitive maps to granular cognitive maps. In Proc. of
ICCCI, LNCS 7653.
Stach, W., Kurgan, L., Pedrycz, W., and Reformat, M.
(2004). Learning fuzzy cognitive maps with required
precision using genetic algorithm approach. In Elec-
tronics Letters, 40.
Stach, W., Kurgan, L., Pedrycz, W., and Reformat, M.
(2005). Genetic learning of fuzzy cognitive maps. In
Fuzzy Sets and Systems, 153.
Zadeh, L. (1997). Towards a theory of fuzzy information
granulation and its centrality in human reasoning and
fuzzy logic. In Fuzzy Sets and Systems, 90.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
510
