
Uneven Distribution of Potential Triplex Sequences in the Human
Genome
In Silico Study using the R/Bioconductor Package Triplex
Matej Lexa
1
, Tom´aˇs Mart´ınek
2
and Marie Br´azdov´a
3
1
Faculty of Informatics, Masaryk University, Botanick´a 68a, 60200 Brno, Czech Republic
2
Faculty of Information Technology, Brno Technical University, Boˇzetˇechova 1/2, 61266 Brno, Czech Republic
3
Biophysical Institute of the Czech Academy of Sciences, Kr´alovopolsk´a 135, 61265 Brno, Czech Republic
Keywords:
Human Genome, DNA Sequence, Non-B-DNA, Triplex, Bioconductor, Repetitive Sequences, Mobile DNA,
Lexicographically Minimal Rotation.
Abstract:
Eukaryotic genomes are rich in sequences capable of forming non-B DNA structures. These structures are
expected to play important roles in natural regulatory processes at levels above those of individual genes,
such as whole genome dynamics or chromatin organization, as well as in processes leading to the loss of
these functions, such as cancer development. Recently, a number of authors have mapped the occurrence of
potential quadruplex sequences in the human genome and found them to be associated with promoters. In
this paper, we set out to map the distribution and characteristics of potential triplex-forming sequences (PTS)
in the human genome sequence. Using the R/Bioconductor package triplex, we found these sequences to be
excluded from exons, while present mostly in a small number of repetitive sequence classes, especially short
sequence tandem repeats (microsatellites), Alu and combined elements, such as SVA. We also introduce a
novel way of classifying potential triplex sequences, using a lexicographically minimal rotation of the most
frequent k-mer to assign class membership automatically. Members of such classes typically have different
propensities to form parallel and antiparallel intramolecular triplexes (H-DNA). We observed an interesting
pattern, where the predicted third strands of antiparallel H-DNA were much less likely to contain a deletion
than their duplex structural counterpart than were their parallel versions.
1 INTRODUCTION
Eukaryotic genomes are rich in sequences capable of
forming non-B DNA structures. Cruciform, slipped,
triplex or quadruplex DNA has been recognized as
a factor in several important biological processes or
functions (Buske et al., 2011) (Bacolla and Wells,
2004). Non-B DNA is often found close to recombi-
nation hotspots and is thought to aid genomic instabil-
ity and evolution (Zhao et al., 2010). The structures it
forms have the ability to modulate replication (Dixon
et al., 2008), transcription (Rich and Zhang, 2008)
or translation (Arora et al., 2008) of DNA/RNA by
mechanisms that may have their origins in times when
nucleic acids dominated all life processes. These
structures are expected to play important roles in nat-
ural regulatory processes at levels above those of in-
dividual genes, such as whole genome dynamics or
chromatin organization (Sarkies et al., 2012) (Maizels
and Gray, 2013), as well as in processes leading to the
loss of these functions, such as cancer development.
For example, a recent study has shown that an
interplay between G4-quadruplexes, FANCJ protein
and DNA replication in cells influences the formation
of euchromatinversus heterochromatinafter the repli-
cation stage (Schwab et al., 2013). Ability to form
H-DNA is often associated with recombinational and
mutational hotspots in the human genome (Akman
et al., 1991).
Recently, a number of authors have mapped the
occurrence of potential quadruplex sequences in the
human genome and other eukaryotic genomes. They
found them to be associated with promoters and cer-
tain classes of repeat elements (Savage et al., 2013)
(Lexa et al., 2013). Possibilities of searching for non-
B DNA (Cer et al., 2011) and specifically triplex/H-
DNA exist as well (Buske et al., 2012) (Hon et al.,
2013). In this paper, we map the distribution and
characteristics of potential triplex-forming sequences
(PTS) in human genomic DNA as detected/predicted
80
Lexa M., Martínek T. and Brázdová M..
Uneven Distribution of Potential Triplex Sequences in the Human Genome - In Silico Study using the R/Bioconductor Package Triplex.
DOI: 10.5220/0004824100800088
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2014), pages 80-88
ISBN: 978-989-758-012-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

using the R/Bioconductor package triplex.
2 SOFTWARE AND METHODS
To analyze the human genome, or other sequence sets,
we employed the R/Bioconductor framework, which
has now matured to the point, where we can use R
to represent biological sequences, search these se-
quences, represent the search results, analyze them
statistically and visualize the results of the searches
and the statistical analysis. All this can be done
with relatively straightforward scripts, using a hand-
ful of well integrated R/Bioconductor software pack-
ages (Lawrence et al., 2013).
2.1 R/Bioconductor Packages used in
this Study
Biostrings. String objects representing biological se-
quences, and matching algorithms (Pages et al.,
2013)
BSgenome. Infrastructure for Biostrings-based
genome data packages (Pages, 2013)
BSgenome.Hsapiens.UCSC.hg19. Homo sapiens
(Human) full genome (UCSC version hg19)
biomaRt. Interface to BioMart databases (e.g. En-
sembl, COSMIC ,Wormbase and Gramene) (Dur-
inck et al., 2009)
triplex. Search and visualize intramolecular triplex-
forming sequences in DNA (Hon et al., 2013)
GenomicRanges. Representation and manipulation
of genomic intervals (Aboyoun et al., 2013)
2.2 General Triplex Detection Pipeline
All types of potential triplexes (parallel and an-
tiparallel) were identified in the human genome
using the Bioconductor triplex package (Hon
et al., 2013). We used the unmasked sequence
from BSGenome.Hsapiens.UCSC.hg19 package
in all analyses. Only potential triplexes with
P value less than or equal 0.05 were consid-
ered for further analysis. A GFF file with all
the identified potential triplexes is available at
http://fi.muni.cz/∼lexa/triplex/hsapiens
pts.gff
2.2.1 Analysis of Coding and Non-coding
Regions
Information about genes was obtained from the En-
sembl database using its Biomart interface. Only
coding genes at chromosomes 1-22, X and Y were
considered (roughly 20k genes) and only their cod-
ing transcripts were selected for analysis (roughly 80k
transcripts). Data about exons of selected transcripts
were downloaded from Ensembl database and used
for identification of promoters, introns, coding re-
gions (CDS), 5’UTR, 3’UTR and intergenic regions.
All this information was stored as individual tracks
(GRanges objects). For the purpose of this study,
promoters were defined as 1000 bp regions upstream
of the coding sequence (flanking the 5’ end). Inter-
genic regions were identified as a complement to cod-
ing transcripts supplemented with promoters. In the
next step we found the overlaps between triplexes and
all prepared tracks. If a given triplex fell into more
than one type of region (e.g. triplex is part of CDS
and intron simultaneously) the triplex was counted in
each overlapping region. Finally, we compared the re-
sults with numbers expected if positioning of poten-
tial triplexes was random. The expected values can be
calculated from the percentage of genome covered by
a certain type of region (see equations 1-5 below).
2.2.2 Analysis of Regions Composed of Repeats
Information about different types of repeating se-
quences was obtained from the UCSC Table Browser,
specifically from the Repeat Masker track (Karolchik
et al., 2004). Data records were organized into 26
classes and 56 families covering both genes (coding
and non-coding) and intergenic regions. At first, we
analysed the number of potential triplexes in regions
with and without repeats in genes and intergenic ar-
eas. As the majority of PTS were located in regions
with repeats, we performed a detailed study of PTS
overlapping individual repeat classes and families. In
this experiment we focused on the number of repeats
(in a given class or family) containing at least one
triplex. The measured values were compared with
numbers expected to be obtained at random.
We were also interested in potential triplexes oc-
curring in close proximity to repeats. Therefore
we extended all repeat regions with flanking areas
(100bps at both ends) and repeated the analysis in-
cluding these expanded areas.
2.2.3 Calculation of Expected Values
Expected values were calculated as the number of
repeats (of given class/family) that would contain at
least one triplex by random choice. This calculation
consists of the following steps:
1. Number of triplexes N
TrRep
that would fall into
a given class or family by random is calculated
using equation 1.
UnevenDistributionofPotentialTriplexSequencesintheHumanGenome-InSilicoStudyusingtheR/Bioconductor
PackageTriplex
81

N
TrRep
=
∑
rep∈ class
len(rep)
len(genome)
(1)
2. For each repeat rep
sel
of a given class/family:
(a) The probability that a randomily selected
triplex is placed ouside of a given repeat is cal-
culated using equation 2.
P
RepComp
=
∑
rep∈ class
len(rep)
− len(rep
sel
)
∑
rep∈ class
len(rep)
(2)
(b) Next, the probability that all triplexes of a given
class/familly are placed outside of a given re-
peat is calculated using equation 3.
P
RepCompAll
= (P
RepComp
)
N
TrRep
(3)
(c) Finaly, the probility that at least one triplex falls
into a given repeat is calculated using equa-
tion 4.
P
Rep
= 1− P
RepCompAll
(4)
3. The overall number of repeats that would contain
at least one triplex by random choice is calculated
as a sum of all probabilities calculated in the pre-
vious step (see equation 5).
N
Rep
=
∑
Rep∈class
P
Rep
(5)
Please note that in equations 1 and 2 we use a sum
for expression of area occupied by repeats. In fact the
real calculation is slightly more complex because the
overlapping repeat regions have to be considered as
well. Concretely, if two repeats of the same class or
family overlap each other then the overlapping part is
counted only once in that sum.
Expected values for repeats supplemented with
flanking areas are calculated analogically.
2.2.4 Analysis of Non-coding Genes
Data about non-coding genes were obtained from
the Ensembl database using the Biomart interface
(roughly 40k genes). All genes were split into 26 cat-
egories based on their biotype (e.g. lincRNA, pseudo-
gene, miRNA, scRNA, etc.) The same type of anal-
ysis, which was performed for repetitive sequences,
was applied for non-coding genes as well.
All types of experiments were applied separately
on a set of parallel, antiparallel and all types of
triplexes (parallel and antiparallel together).
2.3 Classification of Potential Triplex
Sequences
H-DNA often forms in sequences that contain simple
repetitions. The type of triplex that forms (e.g. par-
allel or antiparallel) often depends on the particular
kind of repeat present. We therefore decided to clas-
sify the identified triplexes by the prevailing k-mers
present in their sequences. Although different values
of k will serve the purpose of classification, we se-
lected k = 6 as a value which is not too high since
high values of k would produce a large number of
categories that would be difficult to follow. Because
k = 6 is also the lowest number that can capture well
both, periods of 2 and 3, we chose this value for all
calculations in this study.
The prevailing k-mers for identical classes of se-
quences will sometimes differ, because in a peri-
odic sequence, all rotations of the repeated sequence
monomer will have similar chance of becoming the
most prevalent k-mer. The precise result will depend
on subtle changes in the sequence. For example, for
k = 2, the sequence GCGCGCCGCGC will have 4
CG dinucleotides and 5 GC dinucleotides, we would
therefore label this sequence as ”GC”. A very similar
sequence CGCGCGGCGCG with one C− > G sub-
stitution and one nucleotide moved from the end to
the front has 5 CGs and 4GCs and would therefore be
labeled as ”CG”.
In situations were several rotations of a string may
represent the same feature, we can deterministicaly
choose one of the variants (rotations) to represent
all of them. One way of choosing the representa-
tive string (hexamer) is to choose the one that comes
first in lexicographical order. We therefore propose to
classify and label the sequences with the lexicograph-
ically minimal rotation of the most prevalent k-mer.
This way the DNA sequence gets labeled by the most
prevalent sequence motif, regardless of its exact dis-
tribution. In R, the classification into labelled classes
was achieved by the following R code:
triplex_class <- function(x,k){
s <- as.character(x)
n <- nchar(s)
res <-
names(sort(table(substring(s,1:(n-k+1),k:n))
,decreasing=TRUE)[1])
# the lexicographically minimal rotation
res2 <- paste(res,res,sep="")
sort(substring(res2,1:6,6:11))[1]
}
One can then easily annotate sequences identified
by triplex.search(), and stored in the variable tc, sim-
ply by calling
sort(table(sapply(tc,triplex_class,6))
BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
82

,decreasing=TRUE)
This novel method of annotation will probably
need to be further refined, since in its proposed form
it only works well if the value of k used in the analy-
sis is equal to the intrinsic periodicity of the analysed
sequence. Using hexamers succesfully captures pe-
riods of 1,2,3 and 6 but may give fragmented results
for other periods. We presently solve this by manu-
ally choosing a class name based on an inspection of
the hexamer, such as CTT/GAA (see Table 1).
2.4 Insertions or Deletions in Potential
Triplex Sequences
The output of triplex.alignment() contains the desig-
nation of individual H-DNA strands. They are la-
belled as plus, minus, par+, par−, apar+, apar−
and loop. We used the script count
chars.R to de-
termine the frequency of insertions/deletions (symbol
”-”) or other symbols in the aligned DNA strands. We
expected different tolerance for insertions/deletions
between strands, because the properties of the orig-
inal duplex (strands plus and minus may be quite dif-
ferent from the properties of the third DNA strand
attached via Hoogsteen or reverse Hoogsteen bonds.
The counted insertions were compared to the total
length of each type of strand (regular expression ”.”
for any symbol).
3 RESULTS
A series of calculations were carried out as described
in section 2 to understand the distribution of PTS in
the human genome and determine the properties of
these sequences.
3.1 Distribution of Potential Triplex
Sequences in the Human Genome
To obtain an overall picture of how potential
triplex sequences (PTS) are distributed in the human
genome, we first compared the PTS positions with the
positions of general annotated genome features, such
as protein-coding sequences, promoters, introns and
intergenic regions. There is a clear preference of PTS
to be present in promoters or intergenic regions with
close-to-predicted content in introns and strong avoid-
ance of exons, including 5’- and 3’-UTRs (Figure 1).
Because the intergenic regions in the human
genome are also known to harbor a high number of
repetitive sequences (e.g. 10% Alu (SINE), 15% L1
(LINE), 8% LTR retrotransposons) we calculated the
Potential triplexes in regions
Percentage
0 10 20 30 40 50 60
Intron
Intergenic
Promoter CDS 5'UTR 3'UTR
0 0.5 1 1.5 2 2.5 3
Real
Scaled (20x)
Expected
(a)
Potential triplexes in regions (ratio)
Ratio (Real/Expected)
0.05 0.2 1 2 5 20
20 5 2 1 0.2 0.05
Intron
Intergenic
Promoter CDS 5'UTR 3'UTR
Ratio (Expected/Real)
Real/Expected (>1)
Real/Expected (<1)
(b)
Figure 1: Distribution of potential triplex sequences (PTS)
in genes and intergenic regions. The figure (a) shows the
percentage of all elements in a given region. The four
bars on the right side, namely Promotor, CDS, 5’UTR and
3’UTR, were zoomed in 20× and supplemented with its
own axis. The figure (b) shows the ratio between real and
expected counts. The expected number of triplexes was es-
timated from triplex density and the overall length of se-
quence in a given category.
number of PTS associated with individual repetitive
sequence classes (Figure 2(a)) and families (Figure
2(b)). This analysis shows that only a limited num-
ber of repeat classes and families associate with H-
DNA more frequently than expected from genome av-
erages.
To allow better comparison across families and
classes that would not depend on repeat size and fre-
quency of occurrence, we calculated the ratio between
real and expected counts. In both types of analy-
sis, there is a strong enrichment of PTS sequences in
low complexity sequences and simple repeats (Fig-
ure 2(c)). Such findings are compatible with the
limited number of nucleotide triplets found in sta-
ble H-DNA (Soyfer and Potaman, 1995) (Lexa et al.,
2011) and the general requirement for polypurine and
polypyrimidinetracts in triplexes. We also found SVA
and to a limited extent also SINE and scRNA ele-
ments to have above average PTS association (Figure
2(c)). Of these, specifically SVA and Alu sequences
showed above average association (Figure 2(d)).
We also looked whether there was a difference be-
UnevenDistributionofPotentialTriplexSequencesintheHumanGenome-InSilicoStudyusingtheR/Bioconductor
PackageTriplex
83
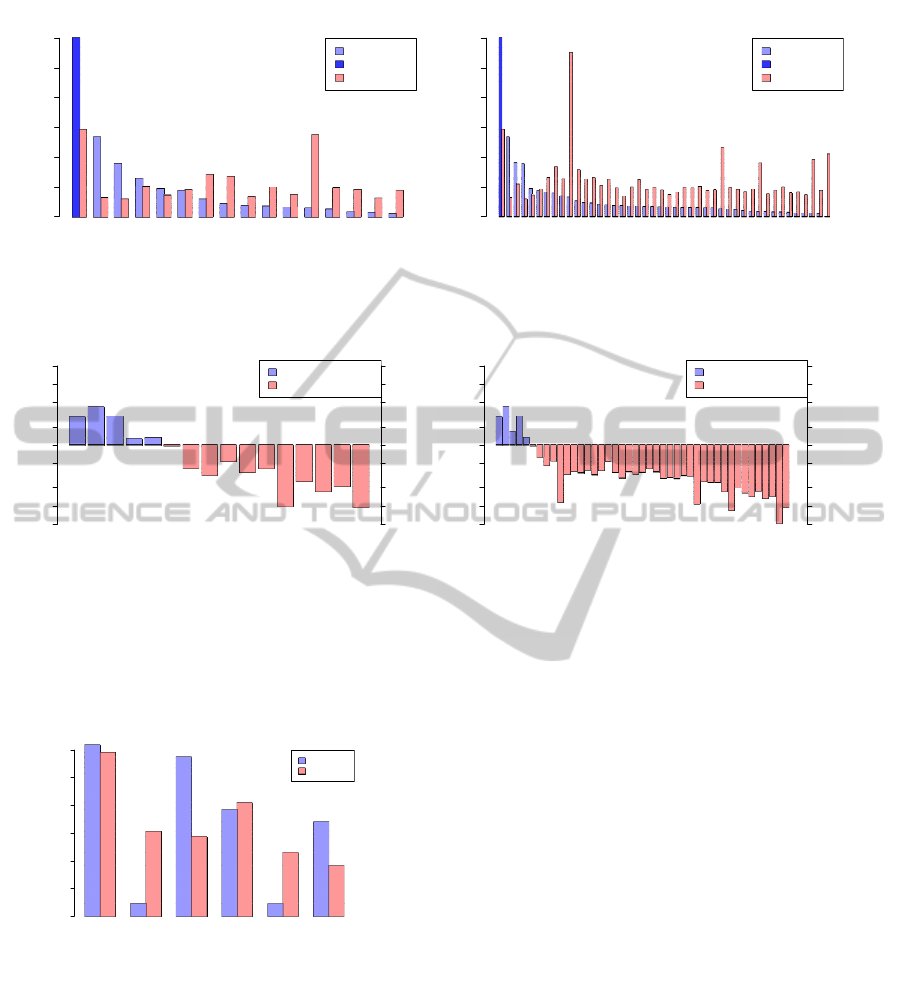
Potential triplexes in repetitive elements (Class)
Percentage
0 5 10 15 20 25 30
SVA
Simple_repeat
Low_complexity
SINE
scRNA
srpRNA
LINE
LTR
snRNA
DNA transposon
rRNA
Satellite
RC
Unknown
tRNA
RNA
Real
Real (> 30 )
Expected
(a) Class
Potential triplexes in repetitive elements (Family)
Percentage
0 5 10 15 20 25 30
SVA
Simple_repeat
Alu
Low_complexity
scRNA
srpRNA
MuDR
L1
ERV
centr
ERV1
TcMar-Tigger
ERVL
PiggyBac
ERVL-MaLR
TcMar-Tc2
snRNA
hAT-Tip100
Merlin
hAT-Charlie
LTR
TcMar-Mariner
rRNA
hAT
Helitron
RTE
L2
TcMar
hAT-Blackjack
ERVK
Gypsy
CR1
MIR
Unknown
Satellite
RTE-BovB
SINE
Dong-R4
DNA transposon
Deu
tRNA
telo
RNA
acro
Real
Real (> 30 )
Expected
(b) Family
Potential triplexes in repetitive elements (Class)
Ratio (Real/Expected)
0.05 0.2 1 2 5 20
20 5 2 1 0.2 0.05
SVA
Simple_repeat
Low_complexity
SINE
scRNA
srpRNA
LINE
LTR
snRNA
DNA transposon
rRNA
Satellite
RC
Unknown
tRNA
RNA
Ratio (Expected/Real)
Real/Expected (>1)
Real/Expected (<1)
(c) Class ratio
Potential triplexes in repetitive elements (Family)
Ratio (Real/Expected)
0.05 0.2 1 2 5 20
20 5 2 1 0.2 0.05
SVA
Simple_repeat
Alu
Low_complexity
scRNA
srpRNA
MuDR
L1
ERV
centr
ERV1
TcMar-Tigger
ERVL
PiggyBac
ERVL-MaLR
TcMar-Tc2
snRNA
hAT-Tip100
Merlin
hAT-Charlie
LTR
TcMar-Mariner
rRNA
hAT
Helitron
RTE
L2
TcMar
hAT-Blackjack
ERVK
Gypsy
CR1
MIR
Unknown
Satellite
RTE-BovB
SINE
Dong-R4
DNA transposon
Deu
tRNA
telo
RNA
acro
Ratio (Expected/Real)
Real/Expected (>1)
Real/Expected (<1)
(d) Family ratio
Figure 2: Association of potential triplex sequences (PTS) with different families of repetitive sequences identified by Re-
peatMasker. The figures (a) and (b) show the percentage of all elements in a given family harboring at least one PTS. The
figures (c) and (d) show ratio between real and expected counts test The expected number of triplexes was estimated from
triplex density and the overall length of sequences of a given family.
Potential triplexes in regions (repetitive/non-repetitive)
Percentage
0 10 20 30 40 50 60
Intergenic
Intergenic non-repeats
Intergenic repeats
Genes
Genes non-repeats
Genes repeats
Real
Expected
Figure 3: Occurrence of repeat and non-repeat-associated
potential triplex sequences (PTS) in different regions of the
human genome. Data shown as percentage of all PTS in the
genome. The expected percentages of triplexes were esti-
mated from average triplex density and the overall length of
sequences of a given genomic region.
tween PTS sequences found in the different regions
of the human genome. While the frequency of PTS in
intergenic regions was slightly higher than in genes,
were they prevailed in introns, they were equally as-
sociated with repeats in both parts, introns and inter-
genic (Figure 3).
3.2 Classification of Potential Triplexes
by Sequence Composition
To classify the detected PTS, we counted all nu-
cleotide hexamers in their sequence and determined
the lexicographically minimal rotation of the preva-
lent hexamer as described in section 2. This anal-
ysis revealed the presence of six main categories of
PTS in the human genome (Table 1). In the order
of prevalence, these were classes labelled by us as
T/A (45.8%), CT/GA (20.6%), CTT/GAA (14.6%),
CCT/GGA (13.1%), C/G (3.6%), CA/GT (1.6%)
and TA/TA (0.5%). The remaining PTS constituted
only 0.3% of detected sequences.
3.3 Tolerance of Different Potential
Triplex Classes and Aligned DNA
Strands for Insertions
We hypothesized that triplex sequences have asym-
metric tolerance for insertions/deletions. Because
the third strand binds to a DNA duplex in its ma-
BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
84

Table 1: Classification of PTSby sequence composition and
the occurrence of different composition classes in the hu-
man genome.
Hexamer Count [%] Class/Composition
TTTTTT 4360 16.6 T/A
AAAAAA 4346 16.5 T/A
AAAAAG
1993 7.6 T/A
CTCTTT 1564 5.9 CT/GA
CTCTCT
1470 5.6 CT/GA
AGAGAG 1444 5.5 CT/GA
CTTTTT
1337 5.1 T/A
CCCCTT 992 3.8 CCT/GGA
AAAAGG 954 3.6 CTT/GAA
AAAGAG
950 3.6 CT/GA
CCCCCT 624 2.4 C/G
AGAGGG
568 2.2 CCT/GGA
AAGGGG 528 2.0 CCT/GGA
CCTCCT
520 2.0 CCT/GGA
CCCTCT 508 1.9 CCT/GGA
CCTTTT
480 1.8 CTT/GAA
CTTCTT 439 1.7 CTT/GAA
CCTTCT
417 1.6 CTT/GAA
AAGAAG 410 1.6 CTT/GAA
AAGAGG
345 1.3 CTT/GAA
AGGAGG 326 1.2 CCT/GGA
AAGGAG
314 1.2 CTT/GAA
AGGGGG 311 1.2 C/G
CCTCTT
285 1.1 CTT/GAA
GTGTGT 225 0.9 CA/GT
ACACAC
187 0.7 CA/GT
ATATAT 144 0.5 TA/TA
AAAGGG 109 0.4 CTT/GAA
CCCTTT
85 0.3 CTT/GAA
OTHER
68 0.3 -
jor grove with lower stringency than seen in Watson-
Crick basepaired duplex, the third strand may be able
to accept insertions, but not deletions when aligned
to the duplex with triplex.alignment(). Although the
ability of H-DNA to accept mismatches, let alone in-
dels, is highly questionable, we still carried out this
calculation, counting the occurrence of the ”-” sym-
bol in different strands and counting the overall length
(Table 2). We found that only 0.75% of positions in
PTS were insertions/deletions in PTS scoring 25 or
more. Moreover, when we compared the occurence
of deletions in the different types of PTS third strand
to the frequencies observed in the duplex at various
score thresholds, we found the percentage to be lower
in parallel strands (0.87-0.97%) and much lower in
antiparallel strands (0.16-0.22%) (Table 3). These
data appear to support our hypothesis of asymmetrical
insertion/deletion distribution among DNA strands in
potential triplexes.
4 DISCUSSION
We have taken a closer look at the output of the
R/Bioconductor triplex search package when ran
against the human genome DNA sequence. In terms
of search results, we were interested to see the differ-
ent categories of human sequences that associate with
potential intramolecular triplexes. The slight over-
representation of PTS in non-coding sequences and
clear absence from coding sequences seen in Figure
1 led us to focus on intergenic DNA, promoters and
introns in more detail (Figure 2(a), 2(b)). H-DNA has
been found in promoters of genes involved in disease
(Bissler, 2007) and cell signalling and communication
(Bacolla et al., 2006).
There is a common theme to the majority of PTS
occurrences we observed in human DNA. Inspection
of Figure 2(b)-2(d) reveals the presence of PTS in or
near Alu, scRNA and simple repeat or low complexity
sequences. Alu sequences are short non-autonomous
retrotransposons (SINE) driven by the L1 LINE el-
ement protein machinery (Dewannieux et al., 2003)
thought to have emerged in primate as duplication de-
scendants of 7SL sc RNA (Kriegs et al., 2007). SVA
repeats, which contained more then twice the num-
ber of PTS than expected by chance are also strongly
associated with PTS. Perhaps not surprisingly, even
SVA elements are evolutionarily related to SINE and
Alu sequences. Their sequence is chimeric and con-
tains two sequences of SINE origin separated by a
variable number tandem repeat (Savage et al., 2013).
According to our study, a large proportion of PTS in
the human genome can therefore be directly attributed
to the proliferation of SINE elements, especially Alu.
Upon first inspection, it becomes clear that most
of the above-mentionedassociations are caused by the
presence of the polyA tail in SINE elements. Because
the poly-A tail is mainly described as a feature cir-
cumventing the problematic polyadenylation in RNA
polymerase III transcripts (Roy-Engel, 2012), there
is a possibility that these sequences do not form any
functionally or evolutionarily meaningful DNA struc-
tures, such as H-DNA. On closer inspection, however,
we notice that the same classes of repeats are also en-
riched for other PTS sequences, raising the possibil-
ity that triplex formation plays a biological role in the
repeat life cycles also at the DNA level. This could
also mean a dual role for the Alu poly-A tail. For
example, (Dewannieux and Heidmann, 2005) men-
tion a 15-50 nucleotide range for increasing effect
of the poly-A tail, a range that also coincides with
cited oligonucleotide lengths for successful H-DNA
formation (Buske et al., 2011). (CT)
n
tandem repeats
have also been implicated in tandem array mainte-
UnevenDistributionofPotentialTriplexSequencesintheHumanGenome-InSilicoStudyusingtheR/Bioconductor
PackageTriplex
85

Table 2: The number of deletions counted in different strands of PTS in the human genome DNA sequence and the total
number of PTS strands examined.
Number of deletions Number of PTS strands of a given type
Score duplex para+ para- anti+ anti- duplex para+ para- anti+ anti-
> 25 7953 3053 2931 202 170 956452 378942 357804 109834 109872
> 35
7443 2934 2834 116 105 853345 365429 345811 70800 71305
> 50 3972 1630 1624 8 10 425395 206228 200898 8985 9284
> 70
1001 442 437 0 0 148244 72251 73930 897 1166
Table 3: The frequency and relative occurrence of deletions in DNA strands of different classes in human PTS.
100*deletions/strand relative to duplex
Score duplex [%] para+ [%] para- [%] anti+ [%] anti- [%] para/duplex anti/duplex
> 25 0.83 0.81 0.82 0.18 0.15 0.98 0.19
> 35
0.87 0.80 0.82 0.16 0.15 0.93 0.17
> 50 0.93 0.79 0.81 0.09 0.11 0.86 0.10
> 70
0.68 0.61 0.59 0.00 0.00 0.88 0.00
nance (Bailey et al., 2013), the mechanism and its de-
pendence on triplex formation is, however, presently
unknown. (Brereton et al., 1993) showed that the A-
rich sequence in a human Alu element can form an
intramolecular triplex in vitro.
Given the presence of PTS in Alu and SVA re-
peats in human, that have evolved as dimers (the for-
mer) and dimer of dimers (the latter) of ancient RNA,
there is a possibility for intramolecular triplexes to aid
the recombination processes leading to chimeric se-
quences. There are indeed many reports of H-DNA
occurrence near recombination hotspots (Napierala
et al., 2004).
Because of the high Alu content of the human
genome, the presence of PTS in Alu elements bi-
ased our estimates of expected PTS association fre-
quency with other elements. Upon subtracting these
from our results, several other classes get into the
”above-expected” occurrence territory, namely the L1
retrotransposon and MuDR DNA transposon as well
as snRNA which often contains a (CT)n dinucleotide
tandem repeat.
We have also noticed a high occurrence of PTS in
the miRNA class of RNAs (data not shown). Kanak
and colleagues (Kanak et al., 2010) recently reported
the discovery of a set of miRNA sequences that could
form triplexes at HIV target sites and suppress its
retroviral activity. An increased presence of PTS se-
quences has recently been reported in the 5’ and 3’-
UTR of plant retroelements, probably analogous to
the reported 3’-UTR HIV regulatory region.
Probably the second most typical location for PTS
in our study were the promoters of genes. The for-
mation of special DNA structures at sequences such
as PTS studied in this paper may create structurally
distinct features providing possibilities for specific
DNA-binding proteins to recognize locations in the
genome for gene regulation or chromatin organiza-
tion. For example, triplex DNA has been found to
be incompatible with nucleosome formation and may
act as a nucleosome barrier (Westin et al., 1995).
They are often found near recombination and muta-
tion hotspots (Napierala et al., 2004)(Akman et al.,
1991). This may be related to the inevitability of
single-stranded DNA stretches at or near the triplexes.
Association of PTS with certain types of repeat ele-
ments could not only suggest a possible function in
the repeat ”life cycle” but also a possible positive se-
lection for repeats with such association, if the pres-
ence of triplexes was required at several locations of
the host genome.
Among the typical hexamers found in triplexes,
we identified a minor group wih prevailing CA/GT
dinucleotide repeats. Although this combination does
not meet the often cited requirement for homopurine
and homopyrimidine tracts in H-DNA, it may ac-
tually form intramolecular triplexes in combination
with other base triplets, as observed by (Gowers and
Fox, 1998). Our extremely low counts (Table 1) seem
to support the notion that if G.T:A and T.A:T triplets
occur in triplexes, they are most likely to be mixed
with other nucleotide combinations.
5 CONCLUSIONS
In this paper we examined the types of sequences
that can be identified in the human genome DNA se-
quence with triplex DNA detection software, namely
the R/Bioconductor package triplex-1.0.10 and its
triplex.search() function. The presented results ex-
amine the usability of the software for genome stud-
BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
86

ies as well as some basic properties of the identi-
fied potential triplex sequences (PTS). We found that
most of the triplex-forming potential of the human
genome is concentrated in simple repeats and flank-
ing regions of repetitive and other genome elements
descending from 7SL RNA, especially Alu and SVA
repeats. We also found potential triplex-forming se-
quences in the miRNA class of RNA genes. Alu ele-
ments are known to contain or flank adenine homonu-
cleotide tracts which replace polyadenylation of its
RNA, but could also carry out a DNA-based function
involving H-DNA formation.
We propose a computational rule to automatically
classify triplex-forming sequences according to the
most prevalent k-mer present in their sequence. For
unambiguity, we include the search for a lexicograph-
ically minimal rotation before assigning the name.
After applying this principle we see that the major-
ity of human PTS fall into four main classes based on
their nucleotide composition (T/A - 45.8%; CT/GA -
20.6%; CTT/GAA - 14.6% and CCT/GGA - 13.1%).
We also characterized the detected PTS based on dele-
tions found in alignments of the third triplex strand
to the DNA duplex, sowing that deletions are present
less frequently in the third strand, especially in an-
tiparallel PTS.
In terms of biological relevance, our studies of
PTS suggest they are positioned non-randomly in the
genome, their sequences fall into a small number of
distinct classes and some of them are associated with
specific types of repeats. Their strand bias for in-
sertions or deletions suggests that these sequences
may indeed form the predicted structures. In future it
would be desireable to single out specific combination
of repeat types and PTS classes, prove the existence
of triplex formation in each case and systematically
search for proteins that could interact with such struc-
tures and provide a more precise clue to their specific
biological function.
ACKNOWLEDGEMENTS
This work was supported by research grants from
the European Social Fund (CZ.1.07/2.3.00/20.0189)
to M.L., 13-36108S (Grant Agency of Science of
CR) to M.B., by IT4Innovations project, reg. no.
CZ.1.05/1.1.00/02.0070 funded by the EU Opera-
tional Programme, by MSMT Grant No.0021630528
and by BUT grant FIT-S-11-1.
REFERENCES
Aboyoun, P., Pages, H., and Lawrence, M. (2013). Genomi-
cranges: Representation and manipulation of genomic
intervals. Technical Report R package version 1.10.7.
Akman, S. A., Lingeman, R. G., Doroshow, J. H., and
Smith, S. S. (1991). Quadruplex dna formation in
a region of the trna gene supf associated with hy-
drogen peroxide mediated mutations. Biochemistry,
30(35):8648–8653.
Arora, A., Dutkiewicz, M., and Scaria, V. (2008). Inhibition
of translation in living eukaryotic cells by an rna g-
quadruplex motif. RNA, 14:1290–1296.
Bacolla, A. and Wells, R. (2004). Non-b dna conformations,
genomic rearrangements, and human disease. Journal
of Biological Chemistry, 279:47411–47414.
Bacolla, A., Wojciechowska, M., Kosmider, B., Larson,
J. E., and Wells, R. D. (2006). The involvement of
non-b dna structures in gross chromosomal rearrange-
ments. DNA Repair, 5:1161–1170.
Bailey, A. D., Pavelitz, T., and Weiner, A. M. (2013).
The microsatellite sequence (ct)n.(ga)n promotes sta-
ble chromosomal integration of large tandem arrays of
functional human u2 small nuclear rna genes. Molec-
ular and Cellular Biology, 18(4):2262–2271.
Bissler, J. J. (2007). Triplex dna and human disease. Fron-
tiers in Bioscience, 12:4536–4546.
Brereton, H., Firgaira, F., and Turner, D. (1993). Origins
of polymorphism at a polypurine hypervariable locus.
Nucleic Acids Research, 21(11):2563–2569.
Buske, F. A., Bauer, D. C., Mattick, J. S., and Bailey, T. L.
(2012). Triplexator: detecting nucleic acid triple he-
lices in genomic and transcriptomic. Genome Re-
search, 22(7):1372–1381.
Buske, F. A., Mattick, J. S., and Bailey, T. L. (2011). Po-
tential in vivo roles of nucleic acid triple-helices. RNA
Biology, 8(3):427–439.
Cer, R. Z., Bruce, K. H., Mudunuri, U. S., Yi, M., Vol-
fovsky, N., Luke, B. T., Bacolla, A., Collins, J. R.,
and Stephens, R. M. (2011). Non-b db: a database
of predicted non-b dna-forming motifs in mammalian
genomes. Nucleic Acids Research, 39(Database
issue):D383–D391.
Dewannieux, M., Esnault, C., and Heidmann, T. (2003).
Line-mediated retrotransposition of marked alu se-
quences. Nature Genetics, 35:41–48.
Dewannieux, M. and Heidmann, T. (2005). Role of
poly(a) tail length in alu retrotransposition. Genomics,
86(3):378–381.
Dixon, B., Lu, L., Chu, A., and Bissler, J. (2008). Recq
and recg helicases have distinct roles in maintaining
the stability of polypurine.polypyrimidine sequences.
Mutation Research, 643:20–28.
Durinck, S., Spellman, P., Birney, E., and Huber, W. (2009).
Mapping identifiers for the integration of genomic
datasets with the r/bioconductor package biomart. Na-
ture Protocols, 4:1184–1191.
Gowers, D. and Fox, K. (1998). Triple helix formation at
(at)n adjacent to an oligopurine tract. Nucleic Acids
Research, 26(16):3626–3633.
UnevenDistributionofPotentialTriplexSequencesintheHumanGenome-InSilicoStudyusingtheR/Bioconductor
PackageTriplex
87

Hon, J., Martinek, T., Rajdl, K., and Lexa, M. (2013).
Triplex: an r/bioconductor package for identifica-
tion and visualization of potential intramolecular
triplex patterns in dna sequences. Bioinformatics,
29(15):1900–1901.
Kanak, M., Alseiari, M., Balasubramanian, P., Addanki,
K., Aggarwal, M., Noorali, S., Kalsum, A., Ma-
halingam, K., Pace, G., Panasik, N., and Bagasra, O.
(2010). Triplex-forming micrornas form stable com-
plexes with hiv-1 provirus and inhibit its replication.
Applied Immunohistochemistry and Molecular Mor-
phology, 18(6):532–545.
Karolchik, D., Hinrichs, A. S., Furey, T. S., Roskin, K. M.,
Sugnet, C. W., Haussler, D., and Kent, W. J. (2004).
Ucsc table browser data retrieval tool. Nucleic Acids
Research, 32(Database issue):D493–D496.
Kriegs, J. O., Churakov, G., Jurka, J., Brosius, J., and
Schmitz, J. (2007). Evolutionary history of 7sl rna-
derived sines in supraprimates. Trends in Genetics,
23(4):158–161.
Lawrence, M., Huber, W., Pags, H., Aboyoun, P., Carl-
son, M., Gentleman, R., Morgan, M. T., and Carey,
V. J. (2013). Software for computing and annotat-
ing genomic ranges. PLoS Computational Biology,
9(8):e1003118.
Lexa, M., Kejnovsky, E., Steflova, P., Konvalinova, H., Vor-
lickova, M., and Vyskot, B. (2013). Quadruplex-
forming sequences occupy discrete regions inside
plant ltr retrotransposons. Nucleic Acids Research,
page 10.1093/nar/gkt893 (ePub).
Lexa, M., Martinek, T., Burgetova, I., Kopecek, D., and
Brazdova, M. (2011). A dynamic programming algo-
rithm for identification of triplex-forming sequences.
Bioinformatics, 27(18):2510–2517.
Maizels, N. and Gray, L. (2013). The g4 genome. PLoS
Genetics, 9(4):e1003468.
Napierala, M., Dere, R., Vetcher, A. A., and Wells, R. D.
(2004). Dna replication repair and recombination:
Structure-dependent recombination hotspot activity of
gaattc sequences from intron 1 of the friedreich’s
ataxia gene. The Journal of Biological Chemistry,
279:6444–6454.
Pages, H. (2013). Bsgenome: Infrastructure for biostrings-
based genome data packages. Technical Report R
package version 1.26.1.
Pages, H., Aboyoun, P., Gentleman, R., and DebRoy, S.
(2013). Biostrings: String objects representing bio-
logical sequences, and matching algorithms. Techni-
cal Report R package version 2.26.3.
Rich, A. and Zhang, S. (2008). Timeline: Z-dna: the long
road to biological function. Nature Reviews Genetics,
4:566–572.
Roy-Engel, A. M. (2012). A tale of an a-tail. the lifeline of
a sine. Mobile Genetic Elements, 2(6):282–286.
Sarkies, P., Murat, P., Phillips, L., Patel, K., Balasubra-
manian, S., and Sale, J. (2012). Fancj coordinates
two pathways that maintain epigenetic stability at g-
quadruplex dna. Nucleic Acids Research, 40(4):1485–
1498.
Savage, A. L., Bubb, V. J., Breen, G., and Quinn, J. P.
(2013). Characterisation of the potential function of
sva retrotransposons to modulate gene expression pat-
terns. BMC Evolutionary Biology, 13(101).
Schwab, R. A., Nieminuszczy, J., Shin-ya, K., and
Niedzwiedz, W. (2013). Fancj lets chromatin stay
true. Journal of Cell Biology, 201:33–48.
Soyfer, V. and Potaman, V. (1995). Triple-helical nucleic
acids. Springer-Verlag, Heidelberg.
Westin, L., Blomquist, P., and Milligan, J. F. e. a. (1995).
Triple helix dna alters nucleosomal histone-dna in-
teractions and acts as a nucleosome barrier. Nucleic
Acids Reserch, 23:2184–2191.
Zhao, J., Bacolla, A., Wang, G., and Vasquez, K. (2010).
Non-b dna structure-induced genetic instability and
evolution. Cellular and Molecular Life Sciences,
67(1):43–62.
BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
88
