
Complete Distributed Search Algorithm for Cyclic Factor Graphs
Toshihiro Matsui and Hiroshi Matsuo
Department of Computer Science and Engineering, Nagoya Institute of Technology,
Gokiso-cho Showa-ku Nagoya Aichi 466-8555, Japan
Keywords:
Max-Sum, Factor-graph, Pseudo-tree, Distributed Constraint Optimization, Multi-agent, Cooperation.
Abstract:
Distributed Constraint Optimization Problems (DCOPs) have been studied as fundamental problems in multi-
agent systems. The Max-Sum algorithm has been proposed as a solution method for DCOPs. The algorithm
is based on factor graphs that consist of two types of nodes for variables and functions. While the Max-Sum
is an exact method for acyclic factor-graphs, in the case that the factor graph contains cycles, it is an inexact
method that may not converge. In this study, we propose a method that decomposes the cycles based on cross-
edged pseudo-trees on factor-graphs. We also present a basic scheme of distributed search algorithms that
generalizes complete search algorithms on the constraint graphs and Max-Sum algorithm.
1 INTRODUCTION
Distributed Constraint Optimization Problems
(DCOPs) (Farinelli et al., 2008; Mailler and Lesser,
2004; Modi et al., 2005; Petcu and Faltings, 2005b;
Zhang et al., 2005) have been studied as fundamental
problems in multi-agent systems. The DCOP is
a constraint optimization problem that consists of
variables and constraint/objective functions that
are distributed among the agents. Multi-agent
cooperation problems including distributed resource
scheduling, sensor networks and smart grids are
represented as DCOPs (Maheswaran et al., 2004;
Miller et al., 2012; Zhang et al., 2005).
The Max-Sum algorithm (Farinelli et al., 2008) is
a solution method for DCOPs. The algorithm is based
on factor graphs that consist of two types of nodes
for variables and functions, while traditional methods
are based on constraint graphs. The computation of
the Max-Sum basically resembles DPOP (Petcu and
Faltings, 2005b), which is a dynamic programming
based on the pseudo-tree of the constraint graph.
When Max-Sum is applied to acyclic factor
graphs, each agent performs as a root node of the
tree, and hence the agent computes a global objective
function for its variable. Namely, each agent individ-
ually (but cooperatively) computes a global objective
function for its variable. This nature is considerable
in an autonomy of agents since every agents observe
the whole system. It also enables agents to determine
the optimal assignments of their variables without ex-
plicit top-down controls of similar methods (Modi
et al., 2005; Petcu and Faltings, 2005b). Therefore,
how to employ the techniques of standard complete
DCOP algorithms on the framework of factor graph
and Max-Sum is an important issue as a basic study.
However, in acase where the factor graph contains cy-
cles, the Max-Sum is an inexact method that may not
converge, since computation on different paths can-
not be separated. For the cyclic factor-graphs, several
approaches have been proposed. In bounded Max-
Sum (Rogers et al., 2011), a graph is approximated
to a minimum (maximum) spanning tree using pre-
processing that eliminates the cycles. Then the Max-
Sum is applied to the spanning tree as an exact so-
lution method. In Max-sum AD (Zivan and Peled,
2012), directed acyclic graphs (DAGs) are employed
to reduce incorrect computation. In this method, the
computation of the Max-Sum is limited in the same
direction of the edges of the DAGs. The directions of
the edges are alternatively inverted after the computa-
tion of Max-Sum.
We present a basic scheme of complete search al-
gorithms that resembles Max-Sum. Since complete
solution methods (Modi et al., 2005; Petcu and Falt-
ings, 2005b) based on pseudo-trees have been devel-
oped for constraint graphs, similar approaches can
be applied into factor-graphs. In this study, we pro-
pose a method that decomposes the cycles based on
a cross-edged pseudo-tree (Atlas and Decker, 2007)
on factor-graphs. With the proposed method, a mod-
ified acyclic graph that resembles the original factor-
graph is generated. Moreover, we also present a ba-
sic scheme of distributed search algorithms that gen-
184
Matsui T. and Matsuo H..
Complete Distributed Search Algorithm for Cyclic Factor Graphs.
DOI: 10.5220/0004824301840192
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 184-192
ISBN: 978-989-758-016-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

eralizes complete search algorithms on the constraint
graphs (Modi et al., 2005) and Max-Sum algorithm.
While the complete search method is generally ineffi-
cient in complex problems with many cycles, our cur-
rent interest is the generalization of complete search
methods on pseudo-trees (Modi et al., 2005) and
Max-Sum algorithm.
As shown above, we apply the method based on
pseudo-trees to decompose cycles in factor-graphs.
In most studies, pseudo-trees including cross-edged
pseudo-trees (Atlas and Decker, 2007) are applied
to constraint graphs. While the pseudo-trees on
factor-graphs resemble the cases on traditional con-
straint networks, there are several important differ-
ences. First, in the case of factor graphs, there is
the same separator in both directions on edges of the
pseudo-tree. Here, the separator is a set of variables
which are shared by two different components of a
graph. Therefore, separators are simply computed by
a single bottom-up computation on a pseudo-tree. In
contrast, in the case of constraint graphs, there are
different separators in different directions on edges.
Second, since functions are still separated as single
nodes in the decomposed tree, it inherently avoids
double counting of a function in any path of aggre-
gation of evaluation values. Those properties easily
enable the decomposition of cycles. In addition, af-
ter the transformation, each agent node simply has its
original variable/function. As a result, only neighbor-
hood nodes and separators are modified. A different
type of method based on junction trees (Vinyals et al.,
2011) has been proposed to transform the graphs of
problems. The main purpose of this method is the
manipulation to replace variables and functions into
different agents.
Our current contribution is that we present a vari-
ation of Max-Sum algorithms that is a complete so-
lution method based on pseudo-trees on cyclic factor
graphs. Basic effects and overheads of this type of
complete algorithms are almost clear since those re-
semble the cases of algorithms based on constraint
networks and pseudo-trees. While the algorithm is
complete, its computational cost, memory use and/or
message size exponentially grow with the size of sep-
arators, also known as the induced width. On the
other hand, there are several issues on search algo-
rithms based on Max-Sum since all nodes perform
as root nodes and their computation is partially inte-
grated. Therefore, as the first study, we evaluate the
possibilities of pruning instead of relatively obvious
comparisons with other Max-Sum algorithms. Since
sophisticated pruning methods need more works for
the case of multiple root nodes, here the proposed
method cannot be easily compared with the state-
of-art of efficient search methods with a single root
node (Yeoh et al., 2008). From another point of view,
the proposed generalization will be a base of new ap-
proximate algorithms where agents have their own
controls as root nodes.
The rest of the paper is organized as follows. In
Section 2, we give background for the study. Then,
in Section 3, we propose the method to decompose
cycles in factor-graphs. Next, we introduce a scheme
for distributed search on the decomposed graphs in
Section 4. The proposed methods are experimentally
evaluated in Section 5. We conclude our study in Sec-
tion 6.
2 PRELIMINARY
2.1 DCOPs
A distributed constraint optimization problem
(DCOP) is defined as follows. A DCOP is defined
by (A, X,D,F), where A is a set of agents, X is a set
of variables, D is a set of domains of variables, and
F is a set of objective functions. A variable x
n
∈ X
takes values from its domain defined by the discrete
finite set D
n
∈ D. A function f
m
∈ F is an objective
function defining valuations of a constraint among
several variables. Here, f
m
represents utility (or cost)
values that are maximized (or minimized).
X
m
⊂ X defines a set of variables that are included
in the scope of f
m
. F
n
⊂ F similarly defines a set of
functions that include x
n
in its scope. f
m
is formally
defined as f
m
(d
i
,·· · ,d
k
) : D
i
× · ·· × D
k
→ N
0
, where
{x
i
,·· · ,x
k
} = X
m
. f
m
(d
i
,·· · ,d
k
) is also simply de-
noted by f
m
(x
i
,·· · ,x
k
) or f
m
(X
m
).
The aggregation F(X) of all the ob-
jective functions is defined as follows:
F(X) =
∑
m s.t. f
m
∈F,X
m
⊆X
f
m
(X
m
). The goal is
to find a globally optimal assignment that maximizes
(or minimizes) the value of F(X).
The variables and functions are distributed among
the agents in A. Each agent locally knows the set of
variables and the set of functions in the initial state.
A distributed optimization algorithm is performed to
compute the globally optimal solution.
2.2 Factor Graph
The factor graph is a representation of DCOPs. The
factor graph consists of variable nodes, function
nodes and edges. An edge represents a relationship
between a variable and function. Figure 1 shows a tra-
ditional constraint network and factor graphs. In the
constraint network (a), nodes represent variables and
CompleteDistributedSearchAlgorithmforCyclicFactorGraphs
185
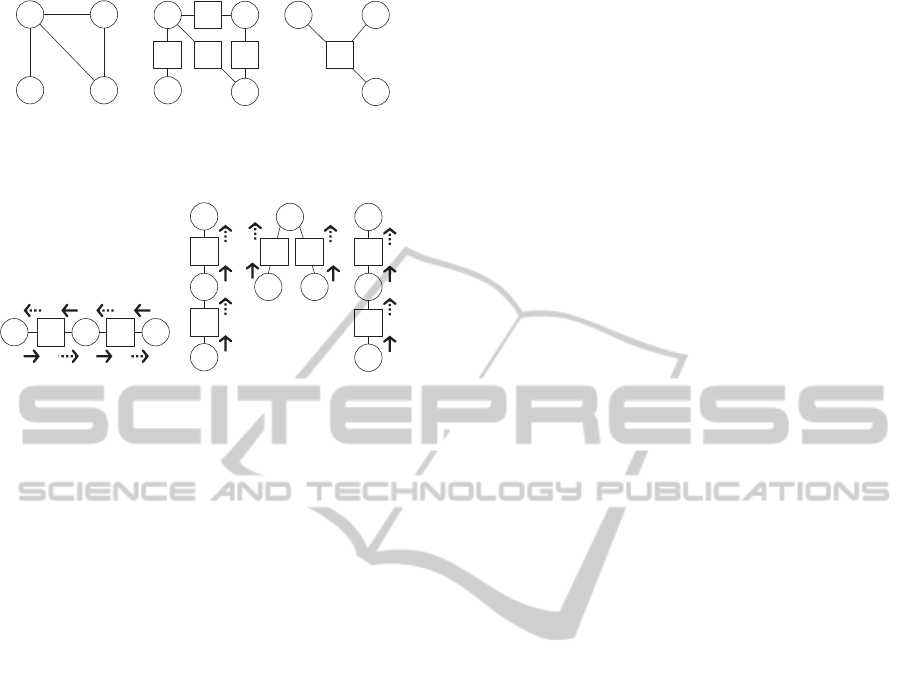
x
0
x
1
x
2
x
3
(a) constraint network
(b) factor graph
x
0
x
1
x
2
x
3
f
0
f
3
f
1
f
2
(c) factor graph of
ternary function
x
0
x
1
x
2
f
0
f
0
f
3
f
1
f
2
Figure 1: Factor graph.
(a) integrated representation
x
0
x
1
x
2
f
0
f
1
x
0
x
1
x
2
f
0
f
1
x
2
x
1
x
0
f
1
f
0
x
0
x
1
x
2
f
0
f
1
(b) separated representation
Figure 2: Symmetric computation on factor graph.
edges represent binary functions. The factor graph (b)
represents the same problem. As shown in the case of
a ternary function (c), the factor graph directly repre-
sents n-ary functions. Each agent has at least a func-
tion node or a variable node. In the following, we
simply use a model in which a node corresponds to
an agent. The Max-Sum algorithm is based on the
factor graph.
2.3 Max-Sum Algorithm
The Max-Sum algorithm is a solution method for
DCOPs. The computation of the method is performed
on a factor graph. Each node of the factor graph corre-
sponds to an agent that is also called a variable node or
function node. Each node communicates with neigh-
borhood nodes using messages, and computes glob-
ally optimal solutions.
The information of a message is an evaluation
function for a variable. The function is represented
as a table of evaluation values for the variable’s val-
ues. A node computes a table for each variable that
corresponds to each neighborhood node. The table
is then sent to the corresponding neighborhood node.
Therefore, a node knows evaluation functions for all
neighborhood nodes. The evaluation function that is
sent from variable node x
n
to function node f
m
is de-
noted by q
x
n
→ f
m
(x
n
). Similarly, r
f
m
→x
n
(x
n
) denotes
the evaluation function sent from function node f
m
to
variable node x
n
. An evaluation function q
x
n
→ f
m
(x
n
)
that is sent from variable node x
n
to function node f
m
is represented as follows.
q
x
n
→ f
m
(x
n
) = 0 +
∑
m
′
s.t. f
m
′
∈F
n
\{ f
m
}
r
f
m
′
→x
n
(x
n
) (1)
Here, F
n
denotes the set of neighborhood function
nodes of variable node x
n
. An evaluation function
r
f
m
→x
n
(x
n
) that is sent from function node f
m
to vari-
able node x
n
is represented as follows.
r
f
m
→x
n
(x
n
) = max
X
m
\{x
n
}
f
m
(X
m
)+
∑
n
′
s.t. x
n
′
∈X
m
\{x
n
}
q
x
n
′
→ f
m
(x
n
′
)
!
(2)
Here, X
m
denotes the set of neighborhood variable
nodes of function node f
m
. max
X
m
\{x
n
}
denotes
the maximization for all assignments of variables in
X
m
\ {x
n
}. A variable node x
n
computes a marginal
function that is an evaluation function of x
n
. The
marginal function z
n
(x
n
) is represented as z
n
(x
n
) =
∑
m s.t. f
m
∈F
n
r
f
m
→x
n
(x
n
). z
n
(x
n
) corresponds to global
objective values for variable x
n
. The value of x
n
that
maximizes z
n
(x
n
) is therefore the globally optimal as-
signment. Each variable node chooses such assign-
ment as the optimal solution.
2.4 Issues on Max-Sum
If the factor-graph is acyclic, the computation of Max-
Sum on the tree is considered a set of bottom-up com-
putations that are simultaneously performed for dif-
ferent root nodes. The root node of each compu-
tation is a variable node. In each computation, dy-
namic programming is performed from leaf nodes to
the root node. The computation shown in Figure 2(a)
can be decomposed into the computations shown in
Figure 2(b). There are three trees rooted at variable
nodes. While all variable nodes individually com-
pute the global optimal objective value, several nodes
share common computation and communication.
This characteristic is interesting because each
variable node has authority to determine its optimal
assignment based on its knowledge of the global ob-
jective value. However, there are multiple optimal
solutions, and some tie-break methods are necessary
to avoid inconsistent decisions among multiple root
nodes. A simple method for the tie-break adds small
weight values for each value of variables.
In the case of cyclic factor-graphs, the computa-
tion of Max-Sum is incorrect. As shown in the In-
troduction, several studies address this issue (Rogers
et al., 2011; Zivan and Peled, 2012). On the other
hand, there are opportunities to construct exact solu-
tion methods based on a tree that is equivalent to the
original factor graph. In the next section, we present
a method to decompose the cycles into a tree.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
186

3 DECOMPOSITION OF CYCLES
3.1 Representations for Decomposition
In the Max-Sum algorithm, each variable/function
node corresponds to an agent. To represent a network
of the agents, we explicitly introduce another type of
node, agent nodes. Here, we call the graph based on
agent nodes the agent-graph. An initial agent-graph
directly corresponds to the original factor-graph. On
the agent-graph, cycles in the original factor-graph are
decomposed. We denote the components of the agent
graph as follows. a
i
: an agent node. X
i
: set of variable
nodes that belong to a
i
. F
i
: set of function nodes that
belong to a
i
. Nbr
i
: set of neighborhood nodes of a
i
.
In agent a
i
of the variable node, X
i
contains one vari-
able while F
i
is an empty set. Similarly, in agent a
i
of
the function node, F
i
contains one function and X
i
is
an empty set. Nbr
i
is defined as a set of agent nodes
that have variables or functionsrelating to variables or
functions of a
i
. Formally, Nbr
i
= {a
j
|∃x
n
∈ X
i
,∃ f
m
∈
F
j
,x
n
∈ X
m
} ∪ {a
j
|∃ f
m
∈ F
i
,∃x
n
∈ X
j
,x
n
∈ X
m
}.
In the transformation of the graph, we employ a
spanning tree on the agent-graph. Based on the span-
ning tree, agent nodes in Nbr
i
are categorized as fol-
lows. a
prnt
i
: parent node. Chld
i
: child nodes. Ancst
i
:
ancestor nodes. Dscnd
i
: descendant nodes.
3.2 Transformation of Graph
To eliminate cycles, graph decomposition methods
based on spanning trees (pseudo-trees) are applied. A
well-known pseudo-tree is based on depth-first search
trees on graphs. With a depth-first search tree, edges
in the original graph are categorized into tree-edges,
which are edges of the spanning tree, and other back-
edges. Such a pseudo-tree is preferable since it does
not contain cross-edges between any two nodes in dif-
ferent subtrees. However, the depth of the tree is rela-
tively large. Another problem is that the condition of
an exact pseudo-tree limits the types of spanning tree.
On the other hand, when there are edges between
different subtrees, the edges are decomposed using
the technique of cross-edged pseudo-tree (Atlas and
Decker, 2007). In this case, a copy of variables relat-
ing to a cross-edge is added. With the copy of the
variable, several edges including the edge between
different subtrees are modified to meet the condition
of the pseudo-tree. In previous studies, decomposi-
tions of cycles were mainly discussed on constraint
graphs. Here, we apply the cross-edged pseudo-tree
on factor-graphs.
As a decomposition of the cycles, each edge of the
spanning tree separates the graph into two parts. Both
1 generate an agent-graph and a spanning tree
2 in a pre-processing.
3 wait for processing of all child nodes a
j
in Chld
i
.
4 if a
i
corresponds variable node x
n
in the factor graph
{
5 let Nbr
n
i
denote
6 {a
j
| f
m
∈ F
j
∧ f
m
∈ F
n
∧ a
j
/∈ (Ancst
i
∪ Dscnd
i
)}.
7 if Nbr
n
i
is not empty {
8 a
k
← the lowest node in Ancst
i
∩ (∩
a
j
∈Nbr
n
i
Ancst
j
).
9 add x
n
to X
k
. store F
n
to a
k
.
10 store each ( f
m
,a
j
) s.t. f
m
∈ F
j
∧ f
m
∈ F
n
to a
k
.
11 store end point (x
n
,a
i
) of equal constraint edge for
x
n
12 to a
k
.
13 for each ( f
m
,a
j
) s.t. f
m
∈ F
j
∧ f
m
∈ F
n
{
14 remove (x
n
,a
i
) from a
j
. store (x
n
,a
k
) to a
j
.
15 if a
j
/∈ (Ancst
i
∪ Dscnd
i
) {
16 remove a
i
from Nbr
j
. remove a
j
from Nbr
i
. } }
17 remove x
n
from X
i
. remove F
n
from a
i
.
18 erase each ( f
m
,a
j
) s.t. f
m
∈ F
j
∧ f
m
∈ F
n
∧
19 ¬(∃n
′
,n
′
6= n, f
m
/∈ F
n
′
) from a
i
.
20 store end point (x
n
,a
k
) of equal constraint edge for
x
n
21 to a
i
. } }
22 for each a
j
s.t. a
j
∈ Nbr
i
∧ a
j
∈ Ancst
i
\ {a
prnt
i
} {
23 remove a
j
from Nbr
i
. remove a
i
from Nbr
j
. }
25 Sep
i,prnt
i
←
/
0. SepTrm
i,prnt
i
←
/
0.
26 for each child node a
j
in Chld
i
{
27 Sep
i, j
← Sep
j,i
. Sep
i,prnt
i
← Sep
i,prnt
i
∪ Sep
j,i
.
28 SepTrm
i,prnt
i
← SepTrm
i,prnt
i
∪ SepTrm
j,i
. }
29 for each (x
n
′
,a
i
) in SepTrm
i,prnt
i
{
30 remove (x
n
′
,a
i
) from SepTrm
i,prnt
i
.
31 remove x
n
′
from Sep
i,prnt
i
. }
32 if the copy of x
n
have been stored to a
k
{
33 add (x
n
,a
k
) to SepTrm
i,prnt
i
. add x
n
to Sep
i,prnt
i
. }
34 for each (x
n
′
,a
j
) s.t. x
n
′
∈ X
i
∧ f
m
∈ X
n
′
∧ f
m
∈ F
j
∧
35 a
j
∈ Ancst
i
∧ (a
j
is the highest node for the same x
n
′
)
{
36 add (x
n
′
,a
j
) to SepTrm
i,prnt
i
. add x
n
′
to Sep
i,prnt
i
. }
37 for each (x
n
′
,a
j
) s.t. f
m
∈ F
i
∧ x
n
′
∈ F
m
∧ x
n
′
∈ X
j
∧
38 a
j
∈ Ancst
i
∧ (a
j
is the highest node for the same x
n
′
)
{
39 add (x
n
′
,a
j
) to SepTrm
i,prnt
i
. add x
n
′
to Sep
i,prnt
i
. }
41 prepare a
i
to manage each Sep
i, j
and
42 a variable/function in the original factor graph.
Figure 3: Procedure of transformation (agent node a
i
).
parts are related to a set of variables called separa-
tor. The separator is considered as an interface that is
commonly used in those parts. Here, let Sep
i, j
denote
the separators between agent-node i and j.
The procedure to transform a graph is shown be-
low. The pseudo code and an example of transforma-
tion are shown in Figure 3 and 4, respectively.
1) generate an agent-graph based on the original
factor-graph (lines 1-2). The graph in Figure 4(a) is
an agent graph that corresponds to the original factor
graph. Here, nodes are arranged based on a spanning
tree rooted at node a
0
that corresponds to x
0
.
CompleteDistributedSearchAlgorithmforCyclicFactorGraphs
187

x
0
f
0
x
1
x
2
x
3
f
1
f
2
(a) original network
tree edge
back edge
cross edge
a
0
a
1
a
2
a
3
a
4
a
5
a
6
x
0
f
0
x
3
x
1
x
2
x
3
f
1
f
2
=
(b) decomposition of cross-edge
a
0
a
1
a
2
a
3
a
4
a
5
a
6
equal
constraint
x
0
f
0
x
3
x
1
x
2
x
3
f
1
f
2
{x
0
}
{x
3
}
{x
0
,x
1
,x
3
}
{x
0
,x
1
,x
3
}
{x
2
,x
3
}
{x
2
,x
3
}
(c) elimination of back edge in agent-network
a
0
a
1
a
2
a
3
a
4
a
5
a
6
separators
x
0
f
0
x
1
x
2
f
1
f
2
x
3
{x
0
}
{x
3
}
{x
0
,x
1
,x
3
} {x
2
,x
3
}
(d) result
{x
0
,x
1
,x
3
} {x
2
,x
3
}
a
0
a
1
a
2
a
3
a
4
a
5
a
6
Figure 4: Transformation.
2) in a bottom-up manner, execute computation of
agent node a
i
as follows (lines 3-39).
3) if a
i
has a variable x
n
∈ X
i
that is an end point
of each cross-edge, compute set Nbr
n
i
of agent nodes
that have another end point of each cross-edge (lines
4-6). Then, generate a copy of x
n
into the lowest com-
mon ancestor node of nodes in Nbr
n
i
(line 8). Elim-
inate the cross-edges from both agent-graph and the
corresponding factor-graph (lines 14-19). Instead of
the cross-edges, add edges between the copy of the
variable and related function nodes (lines 9, 10 and
14). In addition, add a special edge that represents
equal constraint between the copy and original vari-
able x
n
(lines 11 and 20). In Figure 4(a), since edge
(x
3
, f
2
) connects the two nodes in different subtrees,
this edge is decomposed. Here Nbr
n
6
for agent node
a
6
and variable x
3
contains a
5
. In Figure 4(b), a copy
of variable x
3
is placed in a
1
corresponding to f
0
,
which is the lowest common ancestor node of orig-
inal nodes x
3
and f
2
. Now, edge (x
3
, f
2
) and ( f
1
,x
3
)
is connected to the copy of x
3
by storing information
of corresponding variables/functions into a
1
, a
4
and
a
5
. In addition, a special edge that represents equal
constraint between the copy and the original variable
x
3
(i.e. between a
1
and a
6
) is inserted.
4) eliminate back-edges in the agent-network by
removing corresponding information of neighbor-
hood nodes (lines 22 and 23). In Figure 4(c), a back-
edge between agents a
0
and a
4
is eliminated. Note
that this does not affect the computation of separa-
tors. Neighborhoodsin the agent-networkare referred
in solution methods.
5) compute separators Sep
i, j
for each neighbor-
hood node a
j
of a
i
. Also, information of variables
Sep
i,prnt
i
and SepTrm
i,prnt
i
are computed for i’s par-
ent node prnt
i
(lines 25-). SepTrm
i,prnt
i
stores infor-
mation of the highest agent node for each variable.
Namely, (x
j
,a
k
) ∈ SepTrm
i,prnt
i
represents that agent
nodes higher than a
k
do not relate with variable x
j
.
Therefore, such x
j
is removed from the separator at
agent node a
k
(lines 29-31). For child node a
j
, Sep
i, j
is the same as Sep
j,i
(line 27). Additionally, Sep
i,prnt
i
and SepTrm
i,prnt
i
are aggregated for child nodes (line
27 and 28). For the parent, the separator is based
on separators of child nodes (line 27) and nodes that
have functions/variables neighboring the functions/-
variables in a
i
(lines 32-39). This computation is per-
formed in a bottom up manner after the elimination
of cross-edges and back-edges in the agent-network.
Figure 4(c) shows the separators.
6) prepare each agent node so that it manages
its original function/variable and separators (lines 41-
42). After the generation of separators, each node
is modified to have the original variable or function.
Figure 4(d) shows the result of the transformation.
In the pseudo code, we assumed that each node
can access variables of neighborhood agent nodes for
the sake of simplicity. In actual computation, the
communication is performed using messages. In ad-
dition, a lock-and-commit protocol is necessary for
mutual execution between nodes in different sub-
trees. The resulting agent-graph resembles the orig-
inal graph, except for cross-edges and separators. An
important point is that a separator is common in both
directions on an edge of spanning trees. Therefore,
each node can simultaneously perform as a root node
of this tree, similar to the Max-Sum in the case of
trees.
3.2.1 Generalization of Max-Sum
With the separators, computation of Max-Sum is gen-
eralized to agent-nodesas follows. Here, X
m,n
denotes
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
188

assignments for variables in separator Sep
m,n
.
q
a
n
→a
m
(X
n,m
) = max
X
′
\X
n,m
0+
∑
m
′
s.t. a
m
′
∈Nbr
n
\{a
m
}
r
a
m
′
→a
n
(X
n,m
′
)
!
(3)
where all X
n,m
′
are compatible with X
n,m
, X
′
=
S
m
′
s.t. a
m
′
∈Nbr
n
X
n,m
′
.
r
a
m
→a
n
(X
m,n
) = max
X
′′
\X
m,n
f
m
(X
m
)+
∑
n
′
s.t. a
n
′
∈Nbr
m
\{a
n
}
q
a
n
′
→a
m
(X
m,n
′
)
!
(4)
where X
m
and all X
m,n
′
are compatible with X
m,n
, X
′′
=
S
n
′
s.t. a
n
′
∈Nbr
m
X
n,m
′
.
z
n
(x
n
) = max
X
′
\{x
n
}
∑
m s.t. a
m
∈Nbr
n
r
a
m
→a
n
(X
n,m
)
!
(5)
where all X
n,m
are compatible with x
n
, X
′
=
S
m
′
s.t. a
m
′
∈Nbr
n
X
n,m
′
.
As a result of the decomposition of cycles, there is
a well-known issue of the induced width on the graph.
Namely, when there are many cycles in the graph, the
decomposition of the cycles needs a large size of sep-
arators. Such separators exponentially increase the
number of combinations of assignments. While there
are opportunities for efficient/approximate methods
for this issue, in this study, we focus on the base-line
scheme to decompose cycles in the factor graphs.
4 DISTRIBUTED SEARCH
4.1 Basic Idea
When factor-graphs are trees, the Max-Sum algorithm
is exactly a dynamic programming method. For each
message, evaluation values for all values of a variable
are simultaneously computed and sent. In this com-
putation, only bottom up messages are employed as
shown in Figure 2(b). The size of a message depends
on the size of the corresponding separator. When we
decompose cycles into separators, the size of a mes-
sage is exponential in the size of the separator.
To reduce the size of each message, tree search
can be introduced into the scheme of Max-Sum.
In this computation, with top-down messages, each
agent node requests evaluation values for each as-
signment of a separator between a neighboring agent
node. The neighboring node then returns the evalu-
ation value for the assignment. If appropriate search
strategies and pruning methods are available, there are
opportunities to reduce the search processing. On the
other hand, in the search processing, evaluation val-
ues for assignments that have not been expanded are
necessary. Since such an unknown evaluation value
is represented with its lower and upper bound values,
those boundaries are introduced to the Max-Sum.
We propose a scheme that simultaneously per-
forms solution methods based on tree search and dy-
namic programming for trees rooted at each agent
node. This scheme generalizes complete search meth-
ods on pseudo-trees and the Max-Sum algorithm on
trees. While the original Max-Sum is defined for
maximizing problems, in the following, we prefer
minimizing problems since it is easy to employ prun-
ing based on the lower limit cost value 0. Namely,
maximization operators in equations (3), (4) and (5)
are replaced by minimization operators. While the
pruning can be applied to maximization problems, it
needs additional computation to estimate the upper
limit of objective values. Max-Sum for minimization
problems have been addressed in (Zivan and Peled,
2012).
To resolve symmetric solutions, in agent-node of
variable x
n
, we add a weight value p
n
(x
n
) to evalua-
tion values. p
n
(x
n
) represents the preference of value
x
n
. The values of p
n
(x
n
) must be sufficiently smaller
than the values of original functions. Moreover, sum-
mations of the weight values must be different values
for all assignments. Here, we use hierarchical values
that are implemented additional digits. The summa-
tions in equations (3) and (5) are modified to include
p
n
(x
n
).
4.2 Boundary of Cost Values
As shown above, in the processing of tree search,
boundaries of evaluation values are necessary to eval-
uate unknown assignments and to detect termination.
Here, we introduce lower limit value 0 and upper limit
value ∞ of cost values. Since unknown assignments
are evaluated using a pair of lower and upper limit
values, cost values are generally represented by lower
and upper bound values. When both boundaries take
the same value, it is the true value.
For evaluation value q
a
n
→a
m
, its lower bound
value q
⊥
a
n
→a
m
is defined as follows. q
⊥
a
n
→a
m
(X
m,n
) =
q
a
n
→a
m
(X
m,n
) if q
a
n
→a
m
(X
m,n
) has been received. Oth-
erwise q
⊥
a
n
→a
m
(X
m,n
) = 0. In the case of upper bound
value q
⊤
a
n
→a
m
, ∞ is used as the default value. Sim-
ilarly, r
⊥
a
m
→a
n
and r
⊤
a
m
→a
n
are defined for r
a
m
→a
n
.
z
⊥
n
(x
n
) and z
⊤
n
(x
n
) are also defined for z
n
(x
n
). Bound-
aries of q
a
n
→a
m
and r
a
m
→a
n
immediately take the same
value in the end nodes of trees. In other nodes,
both boundary values are separately aggregated in
each direction. Therefore, the boundaries take dif-
CompleteDistributedSearchAlgorithmforCyclicFactorGraphs
189

ferent values until the true cost value is aggregated.
The boundaries basically resemble those shown in
ADOPTs (Modi et al., 2005).
4.3 Distributed Search Algorithm
In the tree search processing, each agent node re-
quests evaluation values for each assignment of a sep-
arator for a neighboring agent node. For each request,
a message that contains the assignment is sent. On
the other hand, the neighborhood node then returns
the evaluation value for the assignment using a mes-
sage that contains the assignment and the related cost
value.
In the agent node a
n
of variable x
n
, when lower
and upper bounds of r
a
m
→a
n
(s) take the same value,
no more search for a
m
and s is necessary. Namely,
if r
⊥
a
m
→a
n
(s) = r
⊤
a
m
→a
n
(s), then a
n
searches for other
assignments of Sep
n,m
. Similarly, if q
⊥
a
n
→a
m
(s) =
q
⊤
a
n
→a
m
(s), then a
m
terminates search for a
n
and s.
Each agent node can simultaneously send different
assignments for different neighborhood agent nodes.
That absorbs differences in multiple search process-
ing. In the agent node a
n
of variable x
n
, when
lower and upper bounds of marginal function z
⊤
(x
n
)
take the same value, agent a
n
can decide the op-
timal assignment of x
n
. If z
⊥
n
(x
n
) = z
⊤
n
(x
n
), then
argmin
x
n
z
⊤
n
(x
n
) is the optimal assignment.
The pseudo code of the distributed search in agent
node a
n
of variable x
n
is shown in Figures 5. After
initialization, each agent node requires cost values for
assignments of separators sending CONTEXT mes-
sages to neighborhoodnodes. On the other hand, each
agent node sends cost values for the received assign-
ment using COST messages. Here, node a
n
stores
the received assignments into s
m
. Those assignments
are called current context. While most of the process-
ing in agent node a
m
of function f
m
is similar to that
shown in Figure 5, only agent nodes a
n
of variables
x
n
compute the optimal assignments x
∗
n
.
In the processing of lines 21-22 in Figure 5, ap-
propriate search strategies are employed to choose as-
signment s. In the case of the best-first strategy, s of
minimum r
⊥
a
m
→a
n
(s) or q
⊥
a
n
→a
m
(s) is preferred. For the
depth-first strategy, an assignment whose boundaries
are still open is selected based on an ordering.
4.4 Correctness and Complexity
The proposed method transforms cyclic factor-graphs
into equivalent acyclic graphs. In addition, the search
method can be considered as a simplified version of
ADOPT (Modi et al., 2005) that is a complete algo-
rithm on pseudo-trees while we applied it to factor-
1 Main{
2 Initialize.
3 until forever {
4 until receive loop is broken { receive messages. }
5 Maintenance. } }
6 Initialize{
7 for all a
m
∈ Nbr
n
{ s
m
← ε.
8 for all s ∈
∏
x
i
∈Sep
n,m
D
i
{
9 r
⊥
a
m
→a
n
(s) ← 0. r
⊤
a
m
→a
n
(s) ← ∞. } }
10 Maintenance. }
11 Receive(CONTEXT, s) from a
m
{ s
m
← s. }
12 Receive(COST, s, r
′⊥
a
m
→a
n
(s), r
′⊤
a
m
→a
n
(s)) from a
m
{
13 r
⊥
a
m
→a
n
(s) ← r
′⊥
a
m
→a
n
(s). r
⊤
a
m
→a
n
(s) ← r
′⊤
a
m
→a
n
(s). }
14 Maintenance{
15 for all s ∈
∏
x
i
∈Sep
n,m
,a
m
∈Nbr
n
D
i
{
16 update z
⊥
n
(s) and z
⊤
n
(s). }
17 x
∗
n
← d s.t. (x
n
,d) ∈ argmin
s
z
⊤
n
(s).
18 for all a
m
∈ Nbr
n
{
19 if s
m
6= ε {
20 send (COST, s
m
, q
⊥
a
n
→a
m
(s
m
), q
⊤
a
n
→a
m
(s
m
)) to a
m
.
}
21 choose s s.t. r
⊥
a
m
→a
n
(s) 6= r
⊤
a
m
→a
n
(s)
22 based on a search strategy.
23 send (CONTEXT, s) to a
m
. }
Figure 5: Distributed search (agent node a
n
of variable x
n
).
graphs. The proposed method is therefore complete
and sound.
Since the proposed method expands an assign-
ment for each separator at the same time, in
the worst case, its number of iterations depends
on (
∏
Sep
n,m
∏
x
j
∈Sep
n,m
D
j
) × (
∏
Sep
m,n
∏
x
k
∈Sep
m,n
D
k
).
Here Sep
n,m
and Sep
m,n
are separators (corresponding
to Equations (3) and (4)) on the longest path of the
pseudo-tree. While the size of messages is linear in
the number of variables in the corresponding separa-
tor, in the worst case, the space complexity for stores
of received cost values is still exponential in the num-
ber of variables in the corresponding separator. There
are opportunities to reduce the size of the stores of
cost values using additional methods that decompose
the separator into iterative search.
5 EVALUATION
The proposed method was experimentally evaluated.
There are a number of studies addressing solution
methods based on search and dynamic programming
with efficient methods on constraint graphs. It is ob-
vious that the performances of the proposed method
basically follow the results of previous works. We
therefore focused on the characteristics of distributed
search processes rooted at different nodes on the same
decomposed factor graphs.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
190
We employed factor graphs that consist of vari-
ables and ternary functions. The size of domain of
each variable is three. Cost values take 0 or 1 based
on (maximum) constraint satisfaction problems. For
all functions, a ratio of inconsistent pairs of values
was set. As spanning trees, we employed breadth-first
search trees. The results were averaged for twenty
instances. In the search processing, the following
search strategies were applied. bst: best first. dpt:
depth first. mix: half of agent nodes are bst and oth-
ers are dpt. In addition, we applied a pruning based
on global upper bound cost values (gub). For the pro-
cessing, each agent propagate its best global upper
bound using CONTEXT messages. When the lower
bound cost value of an assignment exceeds the gub,
the search for the assignment is pruned even if its
boundaries are still open.
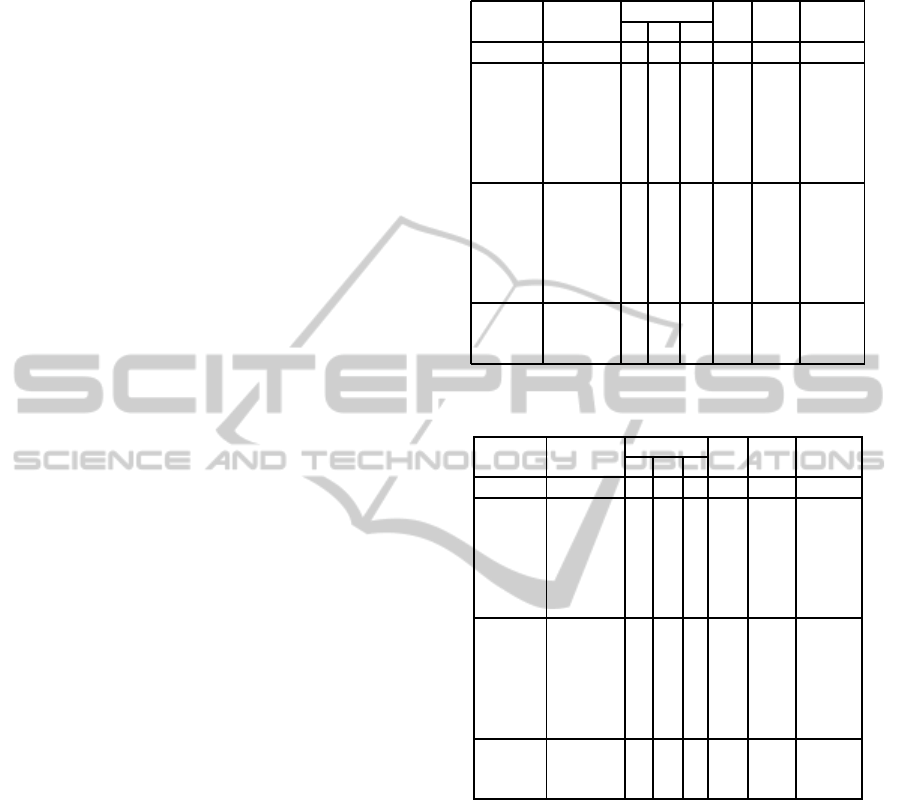
Table 1 shows the results in the case of cyclic
graphs. The result shows that the iteration of bst
varies widely in comparison to that of dpt. While mix
employs bst and dpt, it takes more iterations on the av-
erage. It reveals that there were a mismatch between
different strategies. We also evaluated the number of
assignment whose boundaries did not converge. The
ratio of assignments with the open boundaries is rel-
atively large in the case of sparsely constrained prob-
lems. Namely, there were effects of pruning. Addi-
tionally, gub increased the ratio of open assignments.
It can be considered that several agents help other
agents through the gub. Table 2 shows the case that
factor graphs are trees. Compared with these results,
we can see that the effect of pruning is relatively large
in the case of cyclic graphs.
6 CONCLUSIONS
We proposed a method that decomposes the cycles
in factor-graphs based on a cross-edged pseudo-tree.
The proposed method generates a modified acyclic
graph that resembles the original factor-graph. In ad-
dition, we presented a scheme of distributed search
algorithm that generalizes complete search algorithms
on the constraint graphs and Max-Sum algorithm.
Detailed analysis of the distributed search on the
modified graphs, and a more sophisticated solution
method based on the proposed scheme will be in-
cluded in future works. To improve the proposed
method, there are several directions of the research.
An approach applies efficient pruning methods in ex-
isting search methods for DCOPs (Yeoh et al., 2008).
In this case, the property that all agents simultane-
ously perform as root nodes and intermediate/leaf
nodes have to be considered to manage multiple prun-
Table 1: Cyclic graph.
(21 variables, 13 3-ary functions, (max) CSP)
inconsistent alg. iteration #open #closed rate of
pairs min max ave asgn. asgn. open asgn.
0 all 11 17 14 2089 166 92.64%
2014/01/03 bst 105 2188 1000 168 2086 7.47%
bst-gub 105 2188 1000 491 1764 21.77%
dpt 138 2165 986 18 2237 0.79%
dpt-gub 112 2111 943 267 1987 11.86%
mix 138 2557 1150 25 2230 1.12%
mix-gub 112 2557 1071 337 1917 14.96%
2014/02/03 bst 95 2293 1007 160 2095 7.11%
bst-gub 95 2293 1007 478 1777 21.20%
dpt 146 2157 995 6 2248 0.29%
dpt-gub 122 2151 968 166 2089 7.35%
mix 134 2659 1238 20 2235 0.88%
mix-gub 122 2609 1178 213 2042 9.46%
1 bst/bst-gub 164 2526 1190 3 2252 0.13%
dpt/dpt-gub 148 2175 1006 0.5 2254 0.02%
mix/mix-gub 176 2582 1289 3 2252 0.14%
Table 2: Tree.
(31 variables, 15 3-ary functions, (max) CSP).
inconsistent alg. iteration #open #closed rate of
pairs min max ave asgn. asgn. open asgn.
0 all 15 17 16 42 228 15.67%
2014/01/03 bst 33 57 45 3 267 0.94%
bst-gub 33 57 45 13 257 4.78%
dpt 33 49 42 6 264 2.26%
dpt-gub 33 49 42 10 260 3.54%
mix 39 57 46 5 265 1.81%
mix-gub 39 57 46 11 259 4.04%
2014/02/03 bst 35 51 42 2 268 0.78%
bst-gub 35 51 42 35 235 12.87%
dpt 35 49 42 3 268 0.93%
dpt-gub 35 49 42 13 257 4.65%
mix 39 53 47 2 268 0.72%
mix-gub 39 53 46 20 250 7.46%
1 bst/bst-gub 44 62 51 0 270 0
dpt/dpt-gub 39 45 42 0 270 0
mix/mix-gub 43 59 51 0 270 0
ing processes. Another approach simply employs in-
ference methods instead of search. This approach will
be technically easier than search methods. In the case,
several approximation (Rogers et al., 2011; Petcu and
Faltings, 2005a) and filtering methods reduce compu-
tation and the number of messages will be applied. In
addition, there are opportunities to partially integrate
search and inference methods.
ACKNOWLEDGEMENTS
This work was supported in part by KAKENHI, a
Grant-in-Aid for Scientific Research (C), 25330257
and the Artificial Intelligence Research Promotion
Foundation.
CompleteDistributedSearchAlgorithmforCyclicFactorGraphs
191

REFERENCES
Atlas, J. and Decker, K. (2007). A complete distributed con-
straint optimization method for non-traditional pseu-
dotree arrangements. In AAMAS07, pages 111:1–
111:8.
Farinelli, A., Rogers, A., Petcu, A., and Jennings, N. R.
(2008). Decentralised coordination of low-power em-
bedded devices using the max-sum algorithm. In AA-
MAS08, pages 639–646.
Maheswaran, R. T., Tambe, M., Bowring, E., Pearce, J. P.,
and Varakantham, P. (2004). Taking DCOP to the Real
World: Efficient Complete Solutions for Distributed
Multi-Event Scheduling. In AAMAS04, pages 310–
317.
Mailler, R. and Lesser, V. (2004). Solving distributed con-
straint optimization problems using cooperative medi-
ation. In AAMAS04, pages 438–445.
Miller, S., Ramchurn, S. D., and Rogers, A. (2012). Opti-
mal decentralised dispatch of embedded generation in
the smart grid. In AAMAS12, volume 1, pages 281–
288.
Modi, P. J., Shen, W., Tambe, M., and Yokoo, M. (2005).
Adopt: Asynchronous distributed constraint optimiza-
tion with quality guarantees. Artificial Intelligence,
161(1-2):149–180.
Petcu, A. and Faltings, B. (2005a). A-DPOP: Approxima-
tions in distributed optimization. In CP05 - workshop
on Distributed and Speculative Constraint Process-
ing, DSCP.
Petcu, A. and Faltings, B. (2005b). A scalable method for
multiagent constraint optimization. In IJCAI05, pages
266–271.
Rogers, A., Farinelli, A., Stranders, R., and Jennings, N. R.
(2011). Bounded approximate decentralised coordi-
nation via the Max-Sum algorithm. Artificial Intelli-
gence, 175(2):730–759.
Vinyals, M., Rodriguez-Aguilar, J. A., and Cerquides, J.
(2011). Constructing a unifying theory of dynamic
programming dcop algorithms via the generalized dis-
tributive law. Autonomous Agents and Multi-Agent
Systems, 22(3):439–464.
Yeoh, W., Felner, A., and Koenig, S. (2008). BnB-ADOPT:
an asynchronous branch-and-bound DCOP algorithm.
In AAMAS08, pages 591–598.
Zhang, W., Wang, G., Xing, Z., and Wittenburg, L. (2005).
Distributed stochastic search and distributed breakout:
properties, comparison and applications to constraint
optimization problems in sensor networks. Artificial
Intelligence, 161(1-2):55–87.
Zivan, R. and Peled, H. (2012). Max/min-sum distributed
constraint optimization through value propagation on
an alternating DAG. In AAMAS12, volume 1, pages
265–272.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
192
