
Dirichlet-tree Distribution Enhanced Random Forests for Head Pose
Estimation
Yuanyuan Liu
1,2,3
, Jingying Chen
1,2
, Leyuan Liu
1,2
, Yujiao Gong
1
and Nan Luo
1
1
National Engineering Research Center for e-Learning, Central China Normal University, Wuhan, China
2
Collaborative & Innovative Center for Educational Technology (CICET), Wuhan, China
3
Huazhong University of Science and Technology Wenhua College, Wuhan, China
Keywords:
Dirichlet-tree Distribution Enhanced Random Forests, Head Pose Estimation, Gaussion Mixture Model,
Positive Patch Extraction.
Abstract:
Head pose estimation is important in human-machine interfaces. However, illumination variation, occlusion
and low image resolution make the estimation task difficult. Hence, a Dirichlet-tree distribution enhanced
Random Forests approach (D-RF) is proposed in this paper to estimate head pose efficiently and robustly under
various conditions. First, Gabor features of the facial positive patches are extracted to eliminate the influence
of occlusion and noise. Then, the D-RF is proposed to estimate the head pose in a coarse-to-fine way. In order
to improve the discrimination capability of the approach, an adaptive Gaussian mixture model is introduced
in the tree distribution. The proposed method has been evaluated with different data sets spanning from −90
◦
to 90
◦
in vertical and horizontal directions under various conditions.The experimental results demonstrate the
approach’s robustness and efficiency.
1 INTRODUCTION
Head pose estimation is important in many human
machine interfaces such as (Chen and Chen, 2011;
McFarlane, 2002). Head orientation is related to a
persons direction of attention, it can present useful
information about what the person is paying atten-
tion to. Different methods have been developed for
two types of image data, i.e., 2D images or depth
data. Methods on depth data can provide high accu-
racy, however they require special hardware (e.g. ex-
pensive depth sensor) and need more computations.
In this study, we focus on 2D images. Lots of work
have been done on head pose estimation for 2D im-
ages, some are based on local facial features (Shotton
and Fitzgibbon, 2011; Sun and Kohli, 2012; McFar-
lane, 2002), while others are based on the globe image
(Dantone and Gall, 2012; Gourier and Hall, 2004; Li
and Wang, 2010). However, illumination variation,
occlusion and low image resolution make the estima-
tion task difficult. Hence, a Dirichlet-tree distribution
enhanced Random Forests approach (D-RF) is pro-
posed in this paper to estimate head pose efficiently
and robustly under various conditions.
Random Forest (RF) (Breiman, 2001) is a popu-
lar method in computer vision given their capability
to handle large training datasets, high generalization
power and speed, and easy implementation. Some
works showed the power of random forest in map-
ping image features to votes in a generalized Hough
space (Gall and Lempitsky, 2009) or to real-valued
functions (Sun and Kohli, 2012). Recently, multiclass
RF has been proposed in (Huang and Ding, 2010) for
real-time head pose recognition from 2D video data
and 3D range images (Fanelli and Gall, 2011; Fanelli
and Weise, 2011; Shotton and Fitzgibbon, 2011). Fur-
thermore, Gall et al. (McFarlane, 2002) improved
the classification rate by modifying the optimization
scheme at each node of the trees. Matthias et al.
(Dantone and Gall, 2012) proposed a conditional ran-
dom forest to estimate head pose under various con-
ditions only in the horizontal direction. The accu-
racy rate reaches 72.3% with five yaw angle classes.
In order to improve the accuracy and efficiency, a
Dirichlet-tree distribution algorithm is introduced into
random forest framework to estimate head pose.
The Dirichlet-tree distribution was proposed by
Dennis (Minka, 1999). It is the distribution over
leaf probabilities that results from the prior on branch
probabilities. Minka proved the high accuracy and
efficency of the distribution. Some researchers used
a Dirichlet-tree distribution in multi-objects track-
87
Liu Y., Chen J., Liu L., Gong Y. and Luo N..
Dirichlet-tree Distribution Enhanced Random Forests for Head Pose Estimation.
DOI: 10.5220/0004825000870095
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 87-95
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
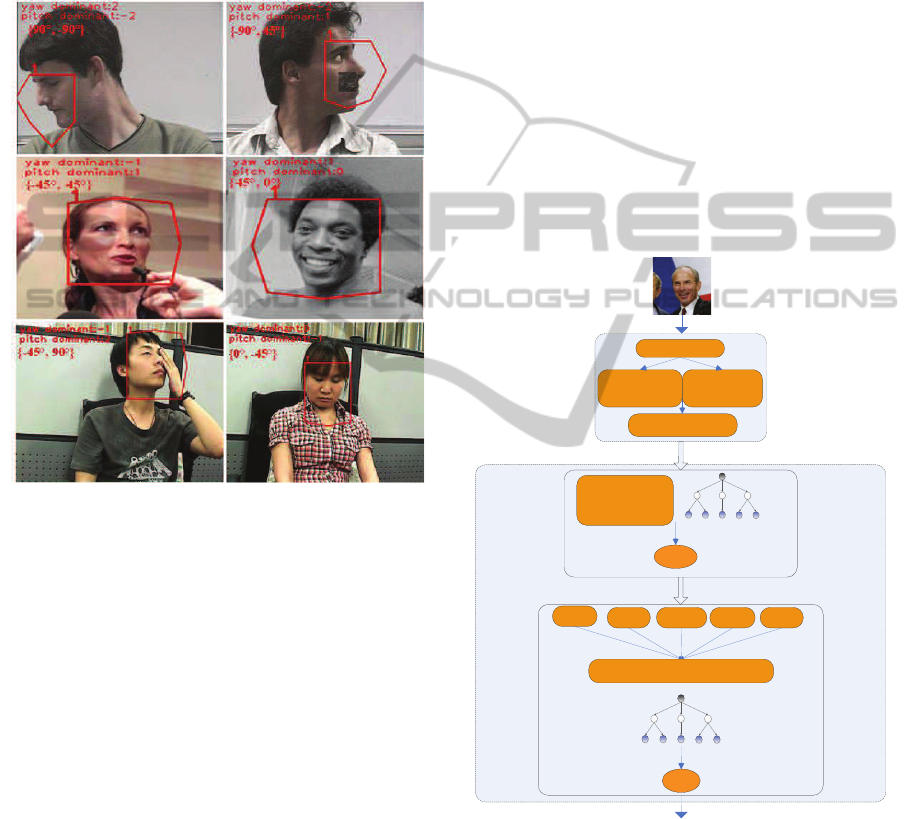
ing (Yan and Han, 2011) and affective computing
(Figueiredo and Jain, 2002). In this work, the D-RF is
proposed to estimate head poses in vertical and hori-
zontal directions under various conditions (occlusion,
different expression, low image resolution and vari-
ous, illuminations) as shown in Figure 1, where the
estimation results are given in the upper left corner in
the images.
Figure 1: Examples of head pose estimation in the horizon-
tal and vertical direction under various conditions.
The main contributions of this paper are as fol-
lows. First, in order to eliminate the influence of
occlusion and noise, histogram distributions of fa-
cial squares and Gabor features based PCA are ex-
tracted for positive and negative patch classification,
where PCA is used to reduce Gabor feature dimen-
sions. Then, a D-RF approach is proposed to estimate
head poses in a coarse-to-fine way. Meanwhile, an
adaptive Gaussian mixture model is introduced in the
classification frameworkto improvethe accuracy. De-
tails are discussed in the following sections.
The rest of the paper is organized as follows: Sec-
tions 2 details about Dirichlet-tree distribution en-
hanced random forests for multiclass head pose esti-
mation; Section 3 presents the experiment results and
discussions; Section 4 gives the conclusions.
2 D-RF FOR HEAD POSE
ESTIMATION
The flowchart of the proposed approach is given in
Figure 2. In the first stage, facial patches are ex-
tracted and classified. In the second stage, a Dirichlet-
tree distribution is introduced into the random forests
frameworkto estimate head pose in the horizontal and
vertical directions. The proposed D-RF consists of
four layers. D-L1 and D-L2 are two layers in the hor-
izontal direction, D-L1 represents the coarse classifi-
cation while D-L2 is the refined classification. D-L3
and D-L4 are two layers in the vertical direction. D-
L3 represents the vertical coarse classification based
on the refined classification in the horizontal direc-
tion, while D-L4 the represents final refined classifi-
cation in the vertical and horizontal directions. De-
tails are given in the following.
D-L1
The first stage:
Positive patch
extraction
Horizontal
estimation
Face detection
PCA features
subspace
from Gabor
Input image
Positive facial patches
Vote
Vote
Final estimated angles
{yaw°,pitch°}
Estimated yaw angles
angle1
angle2 angle3 angle4 angle5
Gussian mixture
model
Positive patch
classification
1 0 -1
2 1 0 -1 -2
Dirichlet-tree
enhanced
Random forests
Gussian
mixture model
Vertical
estimation
Dirichlet-tree enhanced
Random forests
Gussian
mixture model
Histogram
distribution
The second
stage :
Head pose
estimation in
the horizontal
and vertical
directions
D-L1
D-L3
D-L2
D-L4
1 0 -1
2 1 0 -1 -2
Figure 2: The flowchart of the proposed approach.
2.1 Facial Patch Extraction and
Classification
The extracted facial area using Jones&Viola detector
(Jones and Viola, 2003) usually includes some noise
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
88
for head pose estimation, such as hair, neck and occlu-
sion. In order to eliminate noise, the facial area is seg-
mented into foreground and background areas. The
foreground areas include positive patches and nega-
tive patches, where the positive patches are contribute
to estimate head pose while the negative pathces in-
cluding occlusion or noise may introduce errors for
the task. In the work, we segment background areas
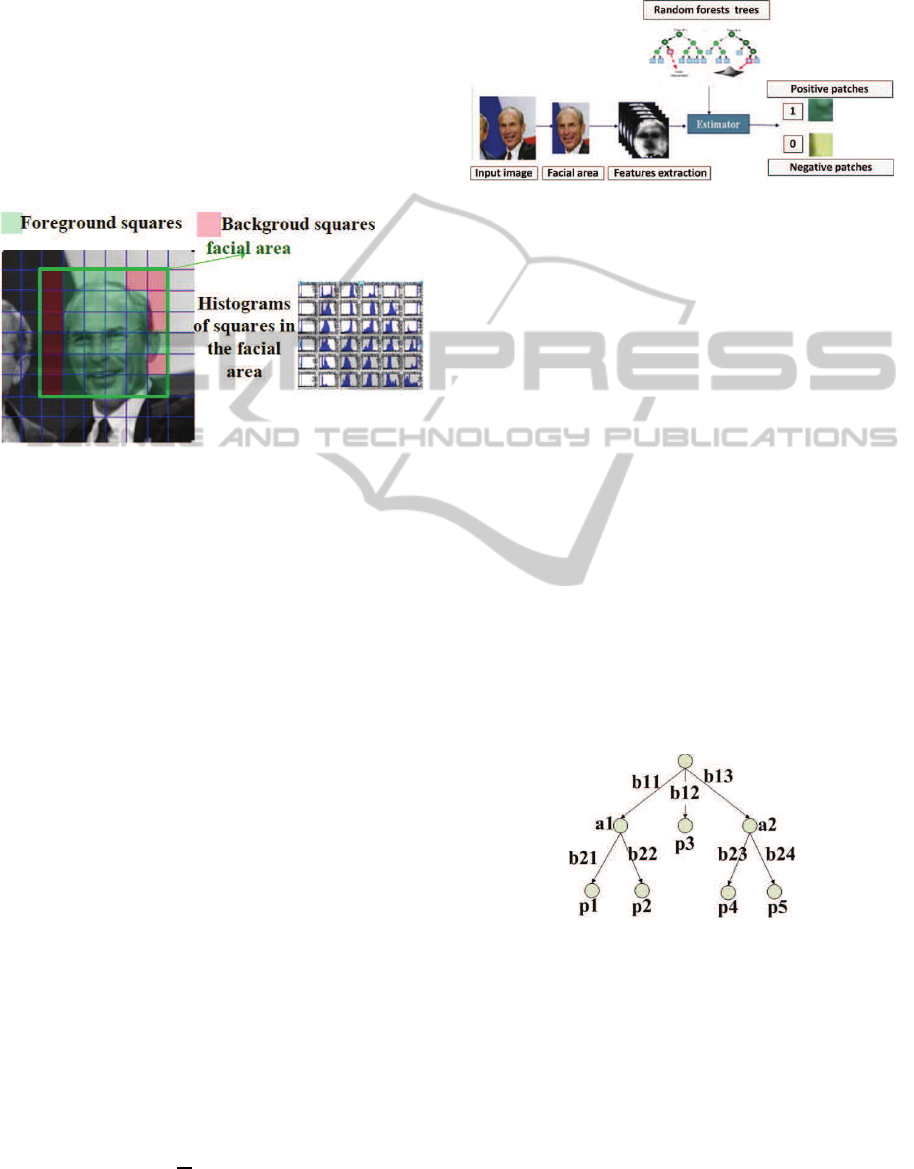
based on histogram distributions firstly(see Figure 3).
The process of positive facial patch extraction is given
in Figure 4.
(a) (b)
Figure 3: Foreground and background squares.
Step 1. Segment Background Squares: The de-
tected facial area is divided into 6*6 non-overlapping
squares as shown in Figure 3(a), histogram distribu-
tions of the squares are computed as shown in Figure
3(b). We utilize the uniformity of histogram distri-
butions of the squares to segment most of the back-
ground areas.
Step 2. Classify the Positive and Negative
Patches: 200 patches are randomly extracted from
the rest of patches with background removed, which
includes positive and negative facial patches. The
positive and negative patches are classified using RF
(Fanelli and Gall, 2011; Breiman, 2001; Dantone and
Gall, 2012). In order to model the random tree, the
train set of positive facial patches are labelled as 1 and
the negative facial patches are labelled as 0. A tree T
grows based on Gabor features and gray histograms
distribution of the labelled patches. The training and
testing similar to the RF (Fanelli and Gall, 2011;
Breiman, 2001; Dantone and Gall, 2012). When all
test patches P arrive at leaves of trees in the forest,
we use the probability p(c = k|l
t
(P)) stored at the leaf
to judge whether the test patch belongs to a class k
, where k = 1 represents the positive patches while
k = 0 represents the negative patches. The probability
of the forest is obtained by averaging over all trees’
leaves:
p(c
i
|P) =
1
T
∑
t
p(c = k|l
t
(P)) (1)
where l
t
is the corresponding leaf for the tree T
t
. The
algorithm diagram is shown in Figure 4.
Figure 4: Positive patches extraction and classification.
2.2 Head Pose Estimation using D-RF
Methods using RF to estimate head pose in the hor-
izontal direction are presented in (Dantone and Gall,
2012; Murphy-Chutorian and Trivedi, 2009) . Actu-
ally, head pose in the vertical direction is also use-
ful to indicate a person’s attention. Hence, D-RF is
proposed in this work to estimate head pose in both
horizontal and vertical directions under various con-
ditions.
2.2.1 D-RF
The Dirichlet-tree is the distribution over leaf proba-
bilities [p
1
...p
i
] that results from this prior node prob-
abilities [a
1
...a
k
] on branch probabilities b
ji
(Minka,
1999), where i is the number of a leaf , k is the num-
ber of a prior node, j is the layer of a branch as shown
in Figure 5. Because of this distribution’s high ac-
curacy and efficiency (Minka, 1999), it is introduced
into the random forests framework to estimate head
pose in a coarse-to-fine way in the paper.
Figure 5: A general Dirichlet-tree distribution.
From the Dirichlet-tree distribution (see Figure 5),
it is noted that each child layer in the forest is related
to his parent. Hence, the D-RF only computes the
probability of a tree in the child layer instead of all
trees’ probabilities in the forest. While the original
random forest estimates the head pose using leaves’
probabilities of all training trees to vote in the hori-
zontal and vertical directions. Therefore, D-RF can
provide high accuracy and efficiency. The training
and testing of the D-RF are given below.
Dirichlet-treeDistributionEnhancedRandomForestsforHeadPoseEstimation
89

Training. Each tree T in the forest T = {T
t
}
is built and selected randomly from a different set of
the training images. From each image, we extract a
set of facial patches P
i
= {I
i
, C
i
}. Where I
i
represents
the appearance and C
i
represents the set of annotation
angles of different head poses in the Dirichlet-tree.
In our case, the patch appearance I
i
is defined
by multiple channels I = (I
1
i
, I
2
i
, I
3
i
). I
1
i
contains the
gray values of the raw facial patch with dimension as
31*31. I
2
i
represents the Gabor features based PCA of
positive facial patches with dimensions as 35*12. I
3
i
is the histogram distributions of the patches. The set
of C
n
i
= (c
1
i
, (c
2
i
|c
1
i
), (c
3
i
|c
2
i
, c
1
i
), (c
4
i
|c
3
i
, c
2
i
, c
1
i
)) con-
tains the annotated discrete angles in different layers
of the Dirichlet-tree, where c
1
i
are 3 yaw rotation an-
gles in the first layer of the Dirichlet-tree distribution
, c
2
i
|c
1
i
are 5 yaw angles refined from c
1
i
in the second
layer, c
3
i
|c
2
i
, c
1
i
are 15 pitch angles under condition of
each yaw angle c
2
i
in the third layer, c
4
i
|c
3
i
, c
2
i
, c
1
i
are 25
refined angles based on the above annotated angles at
leaves of the Dirichlet-tree in the fourth layer.
We define a patch comparison feature as our bi-
nary tests φ, similar to (Fanelli and Gall, 2011;
Breiman, 2001; Dantone and Gall, 2012):
φ = |R
1
|
−1
∑
j∈R
1
I
f
( j) − |R
2
|
−1
∑
j∈R
2
I
f
( j) > τ (2)
where R
1
and R
2
are two random rectangles within
the positive facial patches, I
f
(j) is the feature channel
f ∈ { 1, 2...} and τ is a threshold.
The training of a sub-forest in the D-RF is given
below:
1. Divide the set of patches P into two subset P
L
and P
R
for each φ.
P
L
= {P|ϕ < τ}, P
R
= {P|ϕ > τ} (3)
where φ is the patch comparison feature (Eq.(2)) and
τ is a threshold that has been predefined.
2. Select the splitting candidate φ which maxi-
mizes the evaluation function Information Gain(IG).
IG = argmax
φ
(H(P|a
j
)−(ω
L
H(P
L
|a
j
)+ω
R
H(P
R
|a
j
)))
(4)
where ω
L
, ω
R
are the ratio between the number of
samples in set P
L
(arriving to left subset using the bi-
nary tests), set P
R
(arriving to right subset using the
binary tests) and set P (total node samples). H(P|a
j
)
is the defined class uncertainty measure and the en-
tropy of the continuous patch labels,
H(P|a
j
) = −
N
∑
i=1
∑
i
p(c
i
|a
j
, P
n
)
|P|
log(
∑
i
p(c
i
|a
j
, P
n
)
|P|
)
(5)
where p(c
i
|a
j
, P
n
) indicates the probability that the
patch P
n
belongs to the head pose class c
i
in the sub-
fores a
j
of the j-th layer in the D-RF.
3. Create a leaf l when IG is below a predefined
threshold or when a maximum depth is reached. Oth-
erwise continue recursivelyfor the two subsets P
L
and
P
R
at the first step.
Testing. We initially run a positive facial patch
extraction algorithm (Sec.2.1) to find the position and
the size of the positive patch. Each positive facial
patch is then fed to the trees in the D-RF. At each
node of a tree, the patches are evaluated according to
the stored binary test and passed either to the right
or left child until a leaf node is reached. By passing
all the positive patches down all the trees in the D-
RF for head pose estimation, each positive patch P
n
ends in a set of leaves L of the different sub-forest of
D-RF instead of ending all leaves of the random for-
est. In each leaf l, there are classification probabilities
of head pose and the distributions of the continuous
head pose parameter by a multivariate Gaussian as in
(Breiman, 2001; Dantone and Gall, 2012):
p(c
m
i
|l
a
j
= N(c
m
i
|a
j
;
c
m
i
|a
j
,
∑
a
j
) (6)
where c
m
i
|a
j
and
∑
a
j
are the mean and covariancema-
trix of the head pose classification probabilities of the
sub-forest a
j
of the j-th layer in the D-RF.
When the patch reaches to the leaves of the sub-
forest, the next sub-forest from D-RF should be
loaded based on the prior class decision C(P).
The class decision function of the sub-forest is de-
fined as
C(P) = arg max
a
j
∈C
n
i
p(c
i
|a
j
, p) (7)
where p(c
i
|a
j
, p) is the estimation probability of D-
RF in condition of sub-forest a
j
of the j-th layer and
is computed by an adaptive Gaussion mixture model
described in the following. The final head pose is
then obtained by performing adaptive Gaussian mix-
ture model for voting.
2.2.2 Adaptive Gaussian Mixture Model for
Voting
Because the D-RF is a distribution of multi-layer ran-
dom forests, so an adaptive Gaussian mixture model
is introduced into classify final head pose probability
in this study. We can improve the Eq.(6) as
p(c
i
|a
j
, l
ji
) = N(c
i
|a
j
;
c
i
|a
j
,
∑
l
ji
),
c
i
|a
j
= {δ
ji
(k) · c
j
i
(k)}, k = 1, 2, 3, 4
c
i
∈ {−90
◦
, −45
◦
, 0
◦
, 45
◦
, 90
◦
}
(8)
where j is the sub-forest number in the layer of the D-
RF, i is the child node of the sub-forest j, k is the layer
number in the D-RF, c
i
|a
j
and
∑
l
ji
are the mean and
covariancematrix of theii-th head pose class under the
j-th layer in the D-RF.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
90

When presenting with a test image, the adaptive
Gaussian mixture model can adaptively select T
t
trees
from D-RF based on the estimated probability p(α|P)
in different layer nodes of the D-RF. Similarly, the
probability p(α|P) can be learned by a RF on the prior
training set α. To this end,
p(c
i
|α, P) =
1
T
t
∑
j
k
j
∑
t=1
p(c
i
|l
t,a
j
(P)) (9)
where l
t
, a
j
is the corresponding leaf for patch P of
the tree in D-RF. The discrete values k
j
are computed
such that Σ
j
k
j
= T
t
and
k
j
≈ T
t
·
Z
α∈a
j
P(α|P)da (10)
2.2.3 Head Pose Estimation in the Horizontal
and Vertical Direction
In order to obtain head pose estimation in the horizon-
tal and vertical directions under various conditions,
D-RF is trained as described in Sec.2.2.1. Since it is
difficult to obtain continuous ground truth head pose
data from 2D images, we annotate rotation angles as
”1, 0, 1” and ”2, -1, 0, 1, 2” in two layers. ”1, 0,
1” represent yaw rotation angles as ”90
◦
, 0
◦
, 90
◦
” and
”2, -1, 0, 1, 2” represent refined yaw rotation angles
as ”90
◦
, −45
◦
, 0
◦
, 45
◦
, 90
◦
”. We store the multivari-
ate adaptive Gaussian distribution in the leaf as define
in Eq.(8). The Dirichlet-tree distribution (Figure 5) is
introduced to RF as D-RF (see Figure 6 and 7). Fig-
ure 6 shows the framework of head pose estimation
using D-RF in the horizontal direction, where a is the
estimation result in the horizontal direction, and D-L1
and D-L2 are two layers in the horizontal direction in
D-RF. Then, five yaw angles can be estimated in the
second layer in the D-RF.
Figure 6: Head pose estimation in the horizontal direction.
After the yaw angles have been classified, pitch
angles are estimated under the condition of the classi-
fied yaw angles a. Figure 7 shows the framework of
estimation using D-RF in the vertical direction, and
D-L3 and D-4 are two layers in the vertical direc-
tion in D-RF. And the angle annotation in the verti-
cal direction are similar to horizontal rotation angles.
When the patches are sent down through all vertical
layers in D-RF, sub-trees are selected from sub-forests
in D-L3 and D-L4 layers of the D-RF using Eq.(10)
and Eq.(8). Finally, we can estimate 25 discrete yaw
and pitch angles that are stored at leaves of the D-RF,
i.e. {90
◦
, 90
◦
}, {90
◦
, 45
◦
}...{0
◦
, 0
◦
}...{−90
◦
, −90
◦
}.
Figure 7: Head pose estimation in the vertical direction.
3 EXPERIMENTS
The proposed approach have been tested with Point-
ing’04 head pose database (Gourier and Hall, 2004),
LFW database (Huang and Ramesh, 2007) and the
database of our laboratory (see Figure 8). The Point-
ing’04 database consists of 2940 images with dif-
ferent poses and expressions. The LFW database
consists of 5749 individual facial images. The im-
ages have been collected ’in the wild’ and vary in
poses, lighting conditions, resolutions, races, occlu-
sions, and make-up. Our laboratory database has
been collected using 20 different persons with dif-
ferent poses, expressions and occlusions, and the ref-
erence angles have been annotated using the method
similar to LFW (Huang and Ramesh, 2007).
For evaluation, we divided the datasets into a
training set and a testing set. The training set con-
sists of 2100 images from Pointing’04 database. The
testing set includes the rest of 840 images from Point-
ing’04 database, 1500 images from LFW database
and 200 images from our lab database.
3.1 Training
For training the trees in the Pointing’04 database, we
fixed some parameters on the basis of empirical obser-
vations, e.g., the trees have a maximum depth of 15
and at each node we randomly generate 2000 split-
ting candidates and 25 thresholds. Each tree grows
based on a randomly selected subset of 186 images.
Sub-trees in different layers of the Dirichlet-tree have
been trained independently.
Dirichlet-treeDistributionEnhancedRandomForestsforHeadPoseEstimation
91
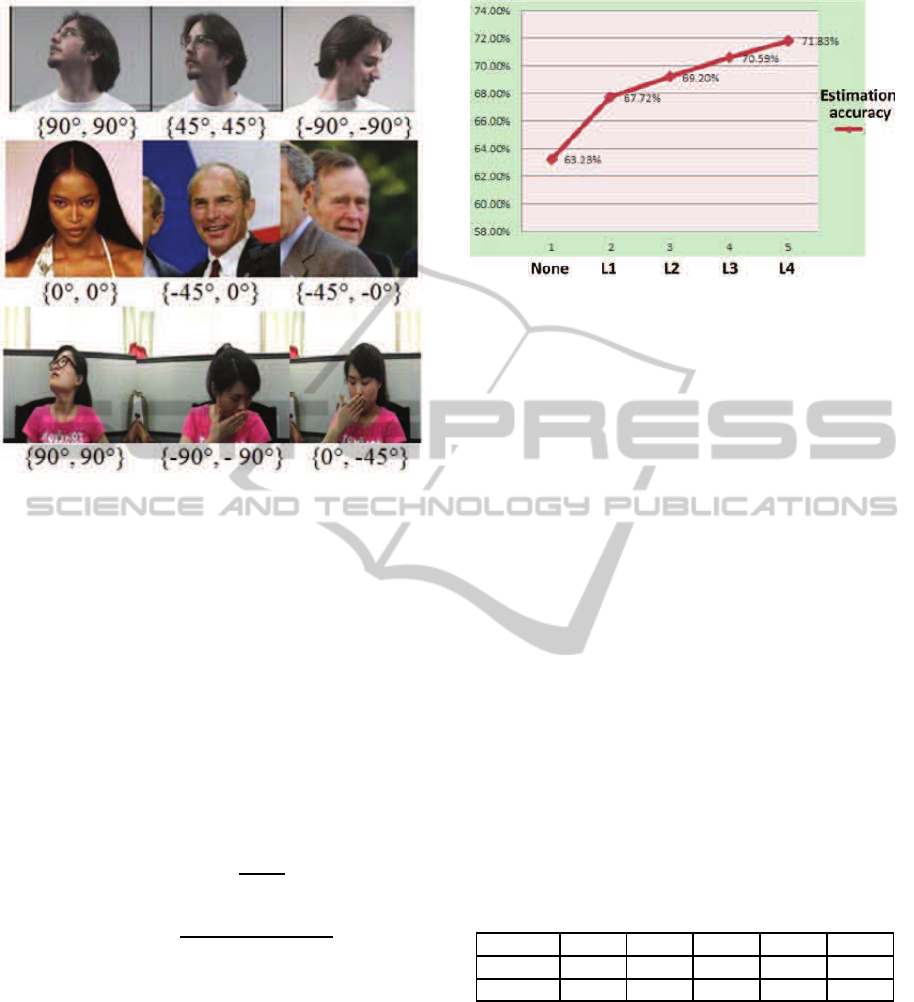
Figure 8: Examples of images from the databases, Point-
ing’04 database (the first row), LFW database (the second
row), and our lab database (the third row).
3.2 Testing
In order to evaluate the proposed approach, estima-
tion accuracy is defined in Eq.(11), where Num is the
number of correct estimation samples in the testing
set and Total is the number of testing images. Let
Y
0
, Y
1
, Y
2
, Y
3
, Y
4
be the estimation accuracies of 5 yaw
angles and P
0
, P
1
, P
2
... be the estimation accuracies
of the pitch angles under the correspondent yaw an-
gle. Q(P
i
|Y
i
) denotes the final estimation accuracy in
leaves of the last layer, which is defined as:
Accuracy =
Num
Total
(11)
Q(P
i
|Y
i
) =
< P
i
,Y
i
> ·P
i
∑
n
j=1
< P
j
,Y
i
> ·P
j
(12)
D-RF consist of four layers, layer 1(D-L1), layer
2(D-L2), layer 3(D-L3), layer 4(D-L4). Figure 9
shows final estimation accuracies using different lay-
ers of D-RF for 25 head pose classes estimation.
None represents the average accuracy of 25 head pose
classes using the original random forest. While L1 to
L4 represent the accuracies of 25 head pose classes
using 1 to 4 layers of the D-RF. L1 and L2 repre-
sent the estimated average accuracies of 25 head pose
classes using only one layer (i.e.D-L1) and two lay-
ers( i.e. D-L1 and D-L2) in D-RF, respectively. L3
and L4 represent the estimated average accuracies of
Figure 9: Accuracy comparison in different layers of the
D-RF.
25 head pose classes using three layers (i.e. D-L1, D-
L2 and D-L3) and four layers (i.e. D-L1,D-L2, D-L3
and D-L4) in D-RF, respectively. As shown in Figure
9, the final accuracy of original random forest (RF)
reaches to 63.23%, and the proposed approach im-
proves the accuracy with the introduction of the dif-
ferent layers of the Dirichlet-tree. The optimal esti-
mation accuracy is 71.83% using 4 layers of the D-
RF.
3.2.1 Comparison between the D-RF and RF
In order to compare the proposed D-RF with the RF,
the same features are used in the comparison experi-
ments.
1) Head pose estimation in the horizontal direc-
tion: The estimation results for different yaw rotation
angles are presented in Table 1. The first row (RF) is
the estimation accuracy using RF and the second row
(D-RF) is the estimation accuracy using D-RF. The
average accuracy of the D-RF and RF are 83.52% and
78.40% respectively. D-RF provides higher average
accuracy than RF in the horizontal direction.
Table 1: The Yaw estimation accuracies (%) comparison.
90
◦
45
◦
0
◦
−45
◦
−90
◦
RF% 80.59 76.79 78.66 75.62 80.29
D-RF% 82.63 83.87 82.2 83.25 84.14
2) Head pose estimation in vertical and horizon-
tal directions under various conditions: The experi-
ments results are shown in Table 2, where columns
D-RF and RF describe the accuracies obtained using
the proposed D-RF and RF respectively.
As shown in Table2, the average accuracy of the
D-RF and RF are 71.83% and 62.23% respectively.
D-RF provides higher average accuracy than RF in
the horizontal and vertical directions.
3) Computation time: The experiments have been
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
92
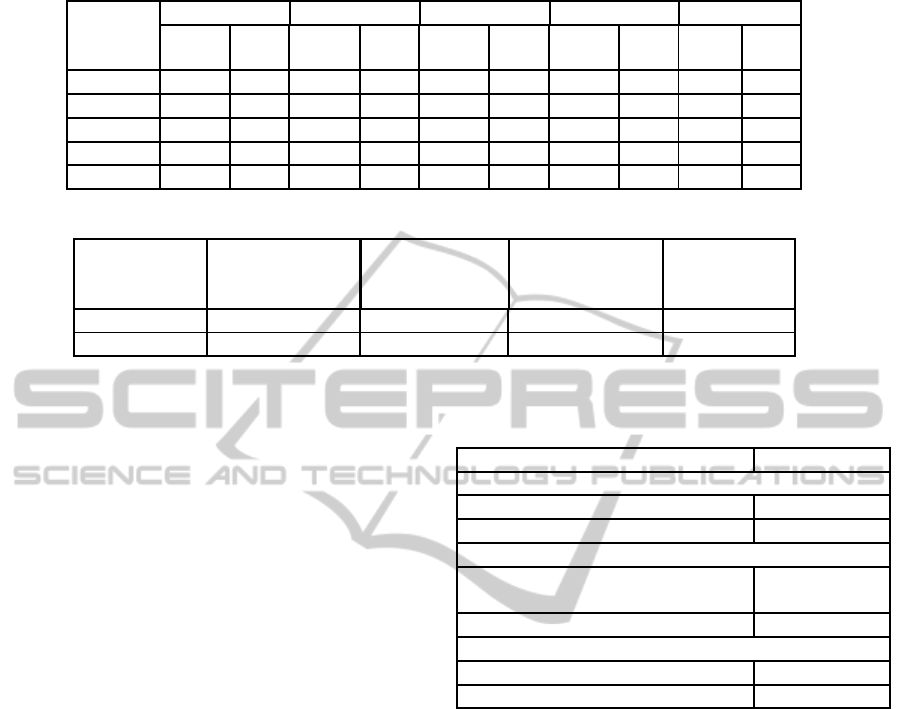
Table 2: The final estimation accuracies (%) using D-RF and RF.
H
H
H
H
H
Pitch
Yaw
90
◦
45
◦
0
◦
−45
◦
−90
◦
D-RF RF D-RF RF D-RF RF D-RF RF DRF RF
(%) (%) (%) (%) (%) (%) (%) (%) (%) (%)
90
◦
72.1 61 69.7 62.5 72.3 71.6 68.3 55.6 70.6 65.9
45
◦
73 52.3 72.6 73.1 73.2 69.4 71.9 43.9 71.5 66.2
0
◦
79.3 75.2 75.9 64.1 78.7 70.6 74 69.8 80 75.7
−45
◦
72.4 66 70.5 72.8 70.1 73.2 68.8 50.7 67.9 49.4
−90
◦
67.2 58.8 70.3 60.3 70.7 67 69.4 45.2 65.3 60.4
Table 3: Computing time in D-RF and in RF.
Time Positive patches Yaw estimation Pitch estimation Total running
¯u(s) extraction Time
/algorithm
Our approach 0.206914 0.430245 0.352829 0.98995
RF — 0.696799 0.671794 1.36859
conducted on a PC with Intel(R)Core(TM) i5-2400
CPU@ 3.10GHz. The computation time of D-RF and
RF is given in Table 3. From the table, one can see
that the D-RF is faster than the RF.
3.2.2 Results with Different Composition
Methods
Experiment results using different composition meth-
ods are given in Table 4. The training and testing are
based on the proposed D-RF. First, Table 4 describes
whether the proposed positive patch extraction bene-
fits the head pose estimation or not. The results show
that positive patches extraction can increase the esti-
mation accuracy by 3.31%. Then it gives the results
using different image features, one is the feature com-
bination of Gabor features, gray values and Histogram
distributions of facial patches and the other is only
gray values of raw image patches. Finally, it shows
different estimation results with different voting mod-
els, i.e. adaptive Gaussian mixture model and fixture
Gaussian model. From this table, one can see that
the composition method of positive patches extrac-
tion, features combination and the adaptive Gaussian
mixture model can give optimal estimation accuracy.
3.2.3 Results of the Occluded Face Images
We randomly add black blocks on the images from
the databases. Some example results on the occluded
test images using the proposed approach are shown
in Figure 10, where the estimation results are given
in the upper left corner in the images. Comparison
results of the same occluded test images using the D-
RF and RF respectively are shown in Figure 11. From
this figure, one can see that the D-RF performs better
Table 4: Comparison of estimation accuracies of different
methods.
Different Methods Accuracy (%)
1.Using Positive patches extraction or not
Positive areas extracting 71.83
Non Positive areas extracting 67.14
2.Using different features
Features combination
71.83
(Gabor+Gray+Histogram)
Image pixels gray 68.37
3.Using different voting models
Adaptive Gaussian mixture model 71.83
Fixed Gaussian model 53
than the RF, the D-RF classifies the poses correctly
while the RF fails to do it.
4 CONCLUSIONS
In this paper, we propose a robust and efficient ap-
proach for head pose estimation in the vertical and
horizontal directions under various conditions. First,
in order to eliminate the influence of occlusion and
noise, Gabor features and gray histogram distribu-
tions of facial areas are extracted for positive and neg-
ative patch classification. Then, a Dirichlet-tree dis-
tribution enhanced random forests approach is pro-
posed to estimate head poses in a coarse-to-fine way.
Meanwhile, an adaptive Gaussian mixture model is
introduced in the classification framework to improve
the accuracy. Experiment results show that the pos-
itive feature patch extraction benefits the head pose
estimation and the D-RF performs more accurate and
Dirichlet-treeDistributionEnhancedRandomForestsforHeadPoseEstimation
93

Figure 10: Example results of the occluded test images us-
ing D-RF.
Figure 11: Results of the same occluded test images using
the D-RF and RF respectively, where the estimation results
are given in the upper left corner in the images.
efficient than the RF . In future work, more experi-
ments will be conducted to evaluate the methods per-
formance under different noise. Also, this method
could be used to estimate the head pose in a wide
scene, e.g. the attention of students in a classroom.
ACKNOWLEDGEMENTS
This research was supported by the National Key
Technology Research and Development Program
(No.2013BAH72B01) and MCM20121061, the Nat-
ural Science Foundation of Hubei Province (No.
2011CDB159), Research Funds of CCNU from the
Colleges Basic Research and Operation of MOE
(Grant No.: CCNU13B001), Wuhan Chenguang
Project (2013070104010019), Central China Normal
University Research Start-up funding (Grant No.:
120005030223) , the Scientific Research Foundation
for the Returned Overseas Chinese Scholars (Grant
No.: (2013) 693), Hubei province natural science
foundationNo. 2013CFB209),NewCentury Excellent
Talents in University (NCET-11-0654),and Young
foundationof Huazhong university of science and tec-
knology, WenHua colloge(J0200540102).
REFERENCES
Breiman, L. (2001). Random forests. In Machine Learning.
Chen, J. and Chen, D. (2011). A feature-based detection
and tracking system for gaze and smiling behaviours.
In International Journal of Computer Systems Science
Engineering. 3: 207214.
Dantone, M. and Gall, J. (2012). Real time facial feature de-
tection using conditional regression forests. In CVPR.
Fanelli, G. and Gall, J. (2011). Real time head pose estima-
tion with random regression forests. In CVPR.
Fanelli, G. and Weise, T. (2011). Real time head pose esti-
mation from consumer depth cameras. In DAGM.
Figueiredo, M. and Jain, A. (2002). Unsupervised learn-
ing of finite mixture models. In IEEE Transaction on
Pattern Analysis and Machine Intelligence.
Gall, J. and Lempitsky, V. (2009). Class-specic hough
forests for object detection. In CVPR.
Gourier, N. and Hall, D. (2004). Estimating face orienta-
tion from robust detection of salient facial features in
pointing 2004. In ICPR international Workshop on
Visual Observation of Deictic Gestures.
Huang, C. and Ding, X. (2010). Head pose estimation
based on random forests for multiclass classification.
In ICPR.
Huang, G. and Ramesh, T. (2007). Learned-miller. labeled
faces in the wild:a database for studying face recogni-
tion in unconstrained environments. In Technical re-
port, University of Massachusetts.
Li, Y. and Wang, S. (2010). Person-independent head pose
estimation based on random forest regression. In
ICIP.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
94

McFarlane, D. (2002). Comparison of four primary meth-
ods for coordinating the interruption of people in
human-computer interaction. In Human-Computer In-
teraction.
Minka, T. (1999). The dirichlet-tree distribution. In
http://research.microsoft.com/minka/papers/dirichlet/
minkadirtree.pdf.
Murphy-Chutorian, E. and Trivedi, M. (2009). Head pose
estimation in computer vision: A survey. In Transac-
tions on Pattern Analysis and Machine Intelligence.
Shotton, J. and Fitzgibbon, A. (2011). Real-time human
pose recognition in parts from single depth images. In
CVPR.
Sun, M. and Kohli, P. (2012). Conditional regression forests
for human pose estimation. In CVPR.
Yan, X. and Han, C. (2011). Mutiple target tracking by
probability hypothesis density based on dirichlet dis-
tribution. In Journal of XiAn JiaoTong University.
Dirichlet-treeDistributionEnhancedRandomForestsforHeadPoseEstimation
95
