
Gradual Improvement of Image Descriptor Quality
Heydar Maboudi Afkham, Carl Henrik Ek and Stefan Carlsson
Computer Vision and Active Preception Lab., KTH, Stockholm, Sweden
Keywords:
Image Summarization, Image Classification.
Abstract:
In this paper, we propose a framework for gradually improving the quality of an already existing image de-
scriptor. The descriptor used in this paper (Afkham et al., 2013) uses the response of a series of discriminative
components for summarizing each image. As we will show, this descriptor has an ideal form in which all cat-
egories become linearly separable. While, reaching this form is not feasible, we will argue how by replacing a
small fraction of these components, it is possible to obtain a descriptor which is, on average, closer to this ideal
form. To do so, we initially identify which components do not contribute to the quality of the descriptor and
replace them with more robust components. Here, a joint feature selection method is used to find improved
components. As our experiments show, this change directly reflects in the capability of the resulting descriptor
in discriminating between different categories.
1 INTRODUCTION
The performance of every computer vision method
highly depends on techniques used for extracting
features and summarizing them. The role of these
techniques is to convert a given region on the im-
age into statistics that are deemed to be meaningful
and are usable by different methods (Lowe, 2004;
Dalal and Triggs, 2005; Viola and Jones, 2001; Winn
et al., 2005) and the outcome is usually referred as
the descriptor. In the task of image classification,
many studies have focused on improving the qual-
ity of the descriptor by building more sophisticated
bag-of-words (BOW) models (Lazebnik et al., 2006;
Zhang and Chen, 2009; Morioka and Satoh, 2010;
Savarese et al., 2006). These improvements are usu-
ally measured with respect to a base descriptor and
are achieved by discarding the original descriptor and
proposing new ways of collecting statistics from the
images. In the recent literature, many different strate-
gies for collecting such statistics have been proposed.
Among these strategies one can mention the use of
spatial pyramid kernels (Lazebnik et al., 2006) which
exploits the bias of the dataset or collecting differ-
ent joint statistics (Zhang and Chen, 2009; Morioka
and Satoh, 2010; Savarese et al., 2006; Csurka and
Perronnin, 2011) which encodes the relation between
features pairs on the image.
While employing more sophisticated descriptors
will increase the training and testing complexity, no
improvement in the accuracy can be guaranteed, since
it is not clear if they respond to the data in hand.
It should be mentioned that usually such descriptors
are used, when experiments using simpler descrip-
tors have failed to meet the required learning accu-
racy. In this paper, we investigate the idea of improv-
ing the quality of a descriptor by replacing the non-
informative components. This way it is possible to
obtain a higher quality descriptor while keeping the
complexity low. The method introduced in this pa-
per, uses a systematic manner which keeps what is
discriminative in the original descriptor and focuses
on improving the parts that fail to discriminate be-
tween the different categories. As we will demon-
strate, by updating a small fraction of the components,
with more sophisticated measurements, it is possible
to obtain a descriptor with significantly higher quality,
while taking the computational advantage of the fact
that most statistics are calculated using simple mea-
surements.
This paper uses the qualitative vocabulary based
descriptor (QVBD), introduced in (Afkham et al.,
2013), as the base descriptor. The statistics collected
by this descriptor are max pooled responses of a series
local classifiers rather than the frequency of the local
features. This framework has shown to be efficient
when applied to both 2D and 3D datasets (Afkham
et al., 2013; Madry et al., 2013). Each element of this
descriptor corresponds to the response coming from a
classifier which measures a certain property of the im-
age (Explained in §2). Here, we ask the question: “Is
it possible to improve the quality of QVBD descrip-
233
Maboudi Afkham H., Henrik Ek C. and Carlsson S..
Gradual Improvement of Image Descriptor Quality.
DOI: 10.5220/0004826402330238
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 233-238
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

tor by replacing some of these classifiers?” and if so
“Which classifiers should be replaced?”. To answer
these questions, we organize this paper as following
: The QVBD framework is summarized in §2 and in
§3, we argue how this descriptor has an optimal form
in which all categories are linearly separable. In sec-
tion §4, we show how using joint feature selection it is
possible to obtain more accurate local classifiers and
in section §5, we experimentally evaluate our frame-
work. Finally, §6 concludes the paper.
2 BASE DESCRIPTOR
As mentioned, this work uses the QVBD (Afkham
et al., 2013) as the base descriptor. For a dataset con-
taining N categories and a given visual vocabulary
D, the QVBD framework trains N × |D| classifiers,
to measure the properties of local features. To train
the classifier corresponding to category n and word
w ∈ D , the local features assigned to the word w are
collected from all the training images and labeled ac-
cordingly (Positive if they belong to category n and
negative otherwise). Let {(x
i
, l
n
i
)}
M
i=1
be the set of
these local features, with l
n
i
∈ {1, −1} being the bi-
nary labeling according to category n. The linear clas-
sifier f
n
w
is trained over these features and is defined
as
f
n
w
= argmin
f
{
1
M
∑
x
i
|x
T
i
f − l
n
i
|
2
+ λ| f |
2
}. (1)
The role of f
n
w
is to measure the quality of the local
features assigned to the word w with respect to cate-
gory n. To that end, it is possible to construct a de-
scriptor D ∈ R
N×|D|
for each image, where each ele-
ment of this descriptor is associated with a classifier
f
n
w
and its value is determined by max-pooling over
response of this classifier over the local features as-
signed to the word w in this image. More formally
this descriptor is defined as
D[n, w] = M (I, n, w), (2)
where,
M (I, n, w) = max
{
P( f
w
n
(x)) : x ∈ I, l(x) = w
}
. (3)
Here l(x) is the index of the visual word that the fea-
ture x is assigned to and P(·) is the logistic function.
This summarization can be seen as a feature selection
technique, where the features with highest likelihood
are used for describing the image.
3 IDEAL DESCRIPTOR
The descriptor defined in the previous section has
an ideal form in which all categories become lin-
early separable. To discuss this form, lets assume
that we are facing a simplified problem with N cat-
egories and a vocabulary containing only one word
(|D| = 1). Having this setting, if we assume that the
classifiers f
n
are ideal (which means for an image I
belonging to the category n, M (I, n) = 1 and ∀m 6= n
: M (I, m) = 0) then it can be easily verified that the
descriptor D can perfectly separate the categories us-
ing linear classifiers. While training such classifiers
is not possible, knowing about this theoretical form
gives us a direction for improving already available
descriptors.
Now, lets assume that the classifiers f
n
are not
ideal (∀I, n : M (I, n) ∈ [0, 1]). For category n, we wish
to replace f
n
with a classifier f
n
0
such that the result-
ing descriptor becomes, on average closer to the ideal
descriptor. It should be mentioned that the closer we
get to the ideal descriptor the more linearly separa-
ble the object categories will become. To achieve this
goal, the f
n
0
should be constructed with the property
that for the positive samples P,
1
|P|
∑
I∈P
M (I, n) <
1
|P|
∑
I∈P
M
0
(I, n) < 1 (4)
and for the negative samples N,
0 <
1
|N|
∑
I∈N
M
0
(I, n) <
1
|N|
∑
I∈N
M (I, n). (5)
Here, M
0
(I, n) is defined as Eq. 3 but uses f
n
0
in-
stead of f
n
when evaluating the local feature with re-
spect to category n. Unfortunately finding the clas-
sifier f
n
0
that satisfies these inequalities is hard and
requires that this problem to be viewed as a complex
latent variable model (Kumar et al., 2010; Yang et al.,
2012). It can be argued that this problem can be ap-
proximated by simply picking a classifier f
n
0
which
has a lower empirical loss than the original f
n
.
So far, we have shown that it is theoretically pos-
sible to replace one of the classifiers within the clas-
sifier pool and result in a closer descriptor to the ideal
descriptor. Going to the large problem with N cate-
gories and arbitrary vocabulary size. We wish to se-
lect only a few classifiers and replace them with more
accurate classifiers. The local classifiers f
n
w
can be
scored based on their empirical loss, calculated on the
training or the validation set, given by
L
emp
( f
n
w
) =
1
N
∑
x
L(x, ¯y
C
; f
n
w
). (6)
The value of the empirical loss is a heuristic measure-
ment for evaluating the behaviour of the local classi-
fiers. The classifiers with less miss-classification tend
to have a lower empirical, compared to the ones with
high miss-classification. Classifiers with high empir-
ical loss tend to make more noisy decisions on the
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
234

data which makes the resulting descriptor D less accu-
rate. For a binary classifier f
n
w
, the value of L
emp
( f
n
w
)
is low if one of the following conditions is met: (a)
The word w has very distinctive properties for class n
which is resulting in a strong classifier, (b) The word
w is only frequent on the positive data or (c) it is only
frequent on the negative data. The main remaining
type of words are the ones that are frequent on both
positive and negative regions but the feature is not
distinctive enough for construction of a strong clas-
sifier. To improve the quality of the local classifiers
not much can be done for the ones with low empirical
loss, since they are either discriminate the categories
properly or we lack sufficient data for training.
We have shown that it is possible to improve the
quality of a given descriptor by replacing the high-
loss classifiers. The question that remains the be an-
swered is, “How can we obtain the replacement clas-
sifiers?”. A fair answer to this question is that find-
ing these classifiers is task dependant and can be very
challenging. In the next section, we will focus on an
example of a joint feature selection model that can be
used for replacing the high-loss classifiers. Studies
such as (Afkham et al., 2012) have shown that use of
similar schemes for building joint feature classifiers,
can result in classifiers that have significantly higher
average perception than the single feature classifiers.
In this paper we employ latent svm (Felzenszwalb
et al., 2010) for building the joint feature classifiers.
4 JOINT FEATURES
As mentioned, a property of features assigned to a
word, w with high empirical loss is that they are fre-
quent on both positive and negative regions and are
not discriminative. Since every instance of w in the
positive set, has the property that it has appeared on
the same object category, it can be coupled with more
distinctive features of that object category to build a
richer joint feature and use that in the summarization
D (Eq. 3). In this work we will treat the joint features
as constellation models.
Let’s assume that {(x
i
, ¯y
n
i
)}
M
i=1
are the features as-
signed to w, which has a high empirical loss with
respect to category n. The aim is to find a se-
ries of local features ¯x
1
i
, . . . , ¯x
p
i
in the neighbour-
hood of each x
i
such that the concatenated vec-
tors {([x
i
, ¯x
1
i
, . . . , ¯x
p
i
], ¯y
n
i
)}
M
i=1
become linearly separa-
ble according to the binary labeling. To formulate this
selection let
F
x
i
= {[x
i
, ¯x
1
i
, . . . , ¯x
p
i
] : ¯x
j
i
∈ N
δ
(x
i
)}, (7)
be the set of all possible joint features centered at x
i
where M features are chosen from its spatial neigh-
borhood with size δ. In this work the features in the
neighbouring of x
i
are partitioned into four quadrants
and each of the four support features is selected from
a different quadrant.
Given a decision boundary β it is possible to select
a joint feature within F
x
i
as the feature which best rep-
resents the decision boundary and is given by
Φ(F
x
i
, β) = arg max
φ∈F
x
i
{φ
T
β}. (8)
Using this definition each decision boundary imposes
a different feature selection and changes the original
classification problem into {(Φ(F
x
i
, β), ¯y
n
i
)}
M
i=1
. With
this change the feature selection problem is reduced
to finding the decision boundary β such that its cor-
responding joint features are linearly separable with
respect the binary labeling. This formulation is a part-
based model and which can be solved using the latent
svm model (Felzenszwalb et al., 2010). Fig. 2 and
Fig. 3 show the outcome of this training and how this
feature selection can discriminate between different
object categories.
5 EXPERIMENTS AND RESULTS
In this section, we wish to experimentally demon-
strate how replacing a small fraction of the classifiers
of the base descriptor with more sophisticated classi-
fiers, will effect the over all quality of the descriptor.
As the proof of concept, we have conducted the ex-
periments on the MSRCv2 dataset (Winn et al., 2005).
Although this dataset is relatively small compared to
other datasets, it is considered as a challenging and
difficult dataset. Further, due to the small number
of images in this dataset high-dimensional summa-
rizations easily over-fit to the training set and loose
their performance. To conclude the experiments, we
compare the performance of our method with already
published methods that are based on similar local fea-
tures. This means that works such as (Schroff et al.,
2008) that use the color information for describing
images are not considered as a relevant benchmark.
Although color is a very strong information cue on
this dataset, it is not captured by the SIFT features
(Lowe, 2004).
In this work we have followed the experimental
setup used in (Zhang and Chen, 2009; Morioka and
Satoh, 2010; Afkham et al., 2013). In this setup, nine
out of fifteen classes are chosen ({cow, airplanes,
faces, cars, bikes, books, signs, sheep, chairs}) with
each class containing 30 images. The focus of these
experiments is to summarize the whole image into one
GradualImprovementofImageDescriptorQuality
235
0 500 1000 1500 2000 2500
0.6
0.65
0.7
0.75
0.8
0.85
Measuring the effect of composite features
Vocabulary Size
Accuracy
α = 0.0
α = 0.05
α = 0.10
α = 0.15
α = 0.20
0 200 400 600 800 1000 1200 1400 1600 1800 2000
0.72
0.74
0.76
0.78
0.8
0.82
0.84
0.86
0.88
0.9
Vocabulary Size
Accuracy
Comparision between larger patches and Constellation Features
α = 0.0 , patch = 16x16
α = 0.0 , patch = 32x32
α = 0.0 , patch = 64x64
α = 0.20 , patch = 16x16
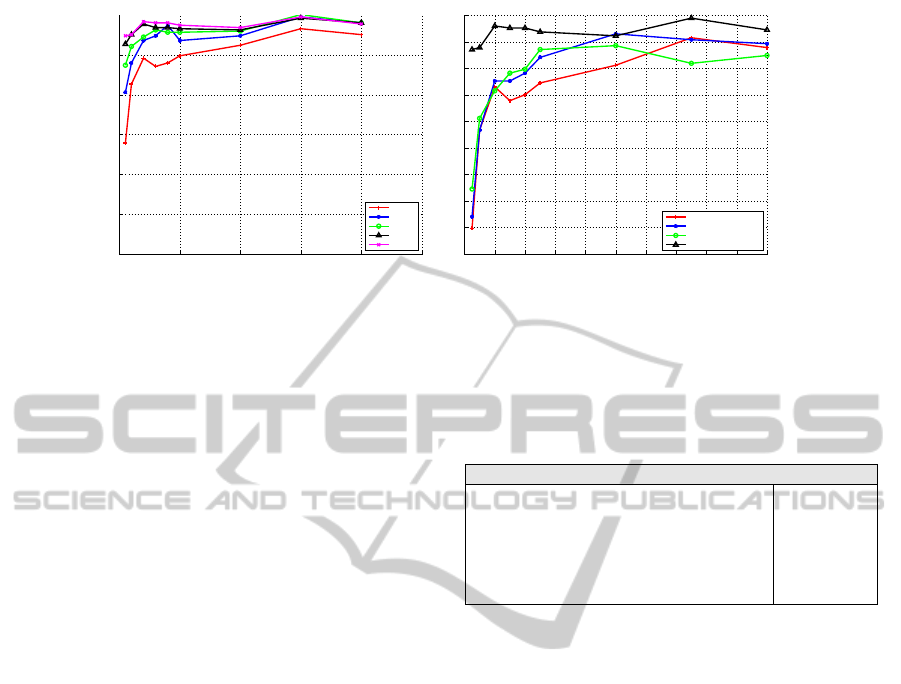
Figure 1: (Right) This plot shows how gradually replacing the local classifiers with joint classifiers in the summarization D
improves the over all performance of the descriptor in all vocabulary sizes. Here α represent the fraction of the classifiers
that are replaced. (Left) To show the effect of discriminative feature selection this figure compares the performance of D with
α = 0.2 with vocabularies built with spatially larger SIFT features.
vector and predict the category labeling of the im-
ages based on this vector. For each experiment, the
images of each category were randomly divided into
15 training and 15 testing images and no background
was removed from the images. The random sampling
of training and testing images were repeated 5 times
to eliminate the train and test partitioning effects. In
all experiments SIFT features (Vedaldi and Fulkerson,
2008; Lowe, 2004) were densely sampled at every 5
pixels from multiple image scales with scale step 1.3.
Visual vocabularies with different sizes {50, 100, 200,
300, 400, 500, 1000, 1500, 2000} were computed
over the SIFT features obtained from the training sub-
set using a standard k-means algorithm. In all experi-
ments we use the LibLinear (Fan et al., 2008) package
to train the linear classifiers over the D descriptors.
To efficiently search for joint features, we rely on
a predefined search structure. This structure can be
seen as the feature architecture, as it defines how joint
features are constructed. While there are many dif-
ferent ways to define this architecture, we focus on
a simple constellation model with four support fea-
tures. As discussed in §4 to facilitate the search, the
spatial neighboring of a feature x
i
was partitioned into
four quadrants and one support feature was selected
from each quadrant. The size of each single feature
is 16 × 16 pixels and the neighbourhood size of the
constellation δ, is chosen to be 60 pixels.
Fig. 1(Left) shows how gradually replacing the
local classifiers with joint classifiers effects the over-
all quality of the descriptor. In this experiment, α is
the fraction of the local classifier that are replaced by
joint feature classifiers. For all vocabularies, we grad-
ually increase the value of α from 0.0 to 0.20. To
do so, we initially sort the classifiers of each class
based on the discussions in §3 and replace the ones
with highest empirical loss. As it can be seen in Fig.
Table 1: Comparison between the classification rates ob-
tained by the proposed method and the previously published
methods on MSRCv2 dataset.
Method Acc %
2
nd
order spatial (Zhang and Chen, 2009) 78.3 ± 2.6%
10
th
order spatial (Zhang and Chen, 2009) 80.4 ± 2.5%
QPC (Morioka and Satoh, 2010) 81.8 ± 3.4%
LPC (Morioka and Satoh, 2010) 83.9 ± 2.9%
D -(α = 0.00) (Afkham et al., 2013) 88.3 ± 3.6%
D -(α = 0.10) 90.0 ± 3.2%
1(Left), only with 5% of the classifiers replaced, we
observe a boost in the quality of the descriptor regard-
less of the size of vocabulary. Here, this improvement
is not obtained by completely changing the method
but by keeping what was considered to be informa-
tive and replacing the parts that didn’t contribute to
the quality. It should also be noticed that that as we
increase the percentage of the joint classifiers in the
classifier pool, the discriminative power of the de-
scriptor increases. This is specially interesting be-
cause the performance of the different vocabularies
becomes more similar with increase of α. This be-
haviour can be motivated using the discussions of §3.
Since with introduction of joint classifiers the descrip-
tor gets closer to the ideal descriptor, the images tend
to get closer to perfect linear separability, independent
of the size of the vocabulary. Figure 1(Right), shows
that this effect is not achieved by simply building the
based descriptor on larger patches. Finally, the per-
formance of this method compared with previously
published methods is presented in table 1.
6 CONCLUSIONS
In this paper, we have discussed a framework that
enables us to improve the quality of a descriptor by
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
236

Cow Feature Face Feature Car Feature Bike Feature
Figure 2: (Best viewed in digital format) The feature selection is optimized for each object class separately and the score
represents how good the located features fit the model. In this figure a word w (green patch) is selected which was a candidate
for joint feature selection in all object classes. Each column visualises the feature selection (white patches) done for a
different object class. Based on the score of the feature selection it can be seen how sensitive the method is to the features
that exist on the object class.
Figure 3: (Best viewed in digital format) This figure shows how the feature selection is consistent across each object class.
In this figure the same word as Fig. 2 is selected on different instances of each object class and it can be seen there is a
large consistency in feature selection done for each class. It should be mentioned consistency in feature selection does not
necessarily imply that the root should also lay in a globally similar context. Since a visual word can appear on many different
global structures, it is the role of the optimizer to select support features that are discriminative and is shared between these
global structures.
keeping the components (local classifiers) of the de-
scriptor that are informative and replacing the ones
that are deemed to be less informative. To achieve
this we have argued that the QVBD has an optimal
form and by replacing these components the descrip-
tor get closer to this form. As our experiments show,
replacing a small fraction of these classifiers can have
a significant effect on the over all quality of the de-
scriptor. As we have discussed, finding proper re-
placement classifiers is both challenging and task de-
GradualImprovementofImageDescriptorQuality
237

pendent and study of finding such classifiers on larger
datasets is left to future studies. Meanwhile, due to
the arguments in §3, a similar behaviour is expected
on any dataset if the replacement classifier is correctly
trained.
ACKNOWLEDGEMENTS
This work was supported by The Swedish Foundation
for Strategic Research in the project Wearable Visual
Information Systems”.
REFERENCES
Afkham, H. M., Carlsson, S., and Sullivan, J. (2012). Im-
proving Feature Level Likelihoods using Cloud Fea-
tures. In ICPRAM (2), pages 431–437.
Afkham, H. M., Ek, C. H., and Carlsson, S. (2013). Qual-
itative Vocabulary Based Descriptor. In International
Conference on Pattern Recognition Applications and
Methods, pages 1–6.
Csurka, G. and Perronnin, F. (2011). Fisher Vectors: Be-
yond Bag-of-Visual-Words Image Representations. In
Richard, P. and Braz, J., editors, Computer Vision,
Imaging and Computer Graphics. Theory and Appli-
cations, pages 28–42. Springer Berlin Heidelberg.
Dalal, N. and Triggs, B. (2005). Histograms of Oriented
Gradients for Human Detection. In CVPR (1), pages
886–893.
Fan, R.-E., Chang, K.-W., Hsieh, C.-J., Wang, X.-R., and
Lin, C.-J. (2008). LIBLINEAR: A Library for Large
Linear Classification. Journal of Machine Learning
Research, 9:1871–1874.
Felzenszwalb, P. F., Girshick, R. B., McAllester, D., and
Ramanan, D. (2010). Object Detection with Dis-
criminatively Trained Part-Based Models. PAMI,
32(9):1627–1645.
Kumar, M. P., Packer, B., and Koller, D. (2010). Self-Paced
Learning for Latent Variable Models. In Lafferty, J.,
Williams, C. K. I., Shawe-Taylor, J., Zemel, R. S., and
Culotta, A., editors, Advances in Neural Information
Processing Systems 23, pages 1189–1197.
Lazebnik, S., Schmid, C., and Ponce, J. (2006). Beyond
Bags of Features: Spatial Pyramid Matching for Rec-
ognizing Natural Scene Categories. In CVPR, pages
2169–2178.
Lowe, D. G. (2004). Distinctive Image Features from Scale-
Invariant Keypoints. International Journal of Com-
puter Vision, 60(2):91–110.
Madry, M., Afkham, H. M., Ek, C. H., Carlsson, S., and
Kragic, D. (2013). Extracting Essential Local Ob-
ject Characteristics for 3D Object Categorization. In
IEEE International Conference on Intelligent Robots
and Systems (IROS).
Morioka, N. and Satoh, S. (2010). Building Compact Local
Pairwise Codebook with Joint Feature Space Cluster-
ing. In ECCV (1), pages 692–705.
Savarese, S., Winn, J., and Criminisi, A. (2006). Discrimi-
native Object Class Models of Appearance and Shape
by Correlatons. In CVPR.
Schroff, F., Criminisi, A., and Zisserman, A. (2008). Object
Class Segmentation using Random Forests. In Pro-
ceedings of the British Machine Vision Conference,
pages 54.1–54.10. BMVA Press.
Vedaldi, A. and Fulkerson, B. (2008). VLFeat: An Open
and Portable Library of Computer Vision Algorithms.
Technical report.
Viola, P. and Jones, M. (2001). Robust real-time face detec-
tion. In Computer Vision, 2001. ICCV 2001. Proceed-
ings. Eighth IEEE International Conference on, page
747.
Winn, J., Criminisi, A., and Minka, T. (2005). Object Cate-
gorization by Learned Universal Visual Dictionary. In
ICCV.
Yang, W., Wang, Y., Vahdat, A., and Mori, G. (2012). Ker-
nel Latent SVM for Visual Recognition. In Bartlett,
P., Pereira, F. C. N., Burges, C. J. C., Bottou, L., and
Weinberger, K. Q., editors, Advances in Neural Infor-
mation Processing Systems 25, pages 818–826.
Zhang, Y. and Chen, T. (2009). Efficient Kernels for identi-
fying unbounded-order spatial features. In CVPR.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
238
