
Robust Object Tracking using Log-Gabor Filters and Color
Histogram
Oumaima Sliti, Chekib Gmati, Fouzi Benzarti and Hamid Amiri
Tunis El Manar University, National Engineering School of Tunis, Tunis, Tunisia
Keywords: Object Tracking, Mean Shift, Log-Gabor Filter, Enhancement, Feature Encoding.
Abstract: The performance of the tracking algorithm relies heavily on the target structural information accuracy. In
this paper, we propose a robust object tracking method based on the log-Gabor texture and color histogram.
Our hypothesis is that by adding log-Gabor filter to color features, and then embedded it in the mean shift
framework, tracking performances will notably enhance. Compared with several methods of state-of-the-art
mean shift trackers, our approach extracts the target information efficiently. Experimental results on various
challenging videos show that the proposed method improves the tracking with fewer mean shift iterations.
1 INTRODUCTION
During the last two decades, real-time object
tracking exists as a critical task in computer vision
applications (Yilmaz, 2006). To overcome issues
like non-rigid target structures, clutters and changing
appearance patterns of the target, several algorithms
have been established. The mean shift tracking
algorithm has been quite popular lately by dint of its
robustness and simplicity.
The target form is represented often as the color
histogram, but it is inclined to fail especially when
the target and its background have similar
appearance. Therefore, the background-weighted
histogram (BWH) has been proposed to decrease
background intrusion in target representation
(Comaniciu, 2003). Yet, after demonstrating that the
BWH -based mean shift tracker and the conventional
mean shift tracking method (Comaniciu, 2002) are
equivalent, Ning et Zhang (Ning, 2012) proposed the
corrected background-weighted histogram (CBWH).
However, applying only color histograms in the
mean shift algorithm has some deficiency (Yang,
2005). First, for the loss of the spatial information of
the target, and second, for the confusion between the
target and its background. Therefore, edge features
(Haritaoglu, 2001) and Local Binary Pattern (LBP)
texture (Ning, 2009) has been associated to the color
histogram for a better target representation. Among
these feature, the joint color-LBP texture histogram
proposed by Ning (Ning, 2009), reaches the better
tracking performance of the target. Indeed, the
texture patterns, which offer the spatial structure of
the target, are successful features to recognize and
represent objects (Sonka, 2007). For three decades,
the exploitation of features based on Gabor filters
has been privileged, for their properties in image
processing such as invariance to illumination and
scale (Fischer, 2007) and (Kong, 2009).
In this paper, a robust mean shift tracker is
proposed. We chose a bank of log-Gabor filter to
model the target texture and then combined it with
color to form an effective target representation.
Compared with several state-of-art variants of mean
shift tracker, this algorithm proves to be efficient in
exploiting the target structural information and thus
it reaches higher tracking performance with fewer
mean shift iterations.
Section 2 briefly describes the mean shift
algorithm. Section 3 discusses the theoretical
background of the features used in this framework.
Yet, experimental results are presented and
discussed in section 4. Finally, section 5 concludes
the paper.
2 CONVENTIONAL MEAN SHIFT
ALGORITHM
2.1 Target Representation
In the mean shift algorithm, the target model is
687
Sliti O., Gmati C., Benzarti F. and Amiri H..
Robust Object Tracking using Log-Gabor Filters and Color Histogram.
DOI: 10.5220/0004829306870694
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 687-694
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

usually represented by its PDF (Comaniciu, 2003).
Target Model: In the beginning, let us define the
target model representation:
The pixel locations of the target model, centred at 0
are denoted by
∗
…
. We consider the function
∶
→
1…
which associates to each pixel
location
∗
its indicator
∗
in the histogram bin.
The target model is computed as:
..
∑
‖
∗
‖
∗
(1)
Note that
is the probabilities of feature1..
in the target model, present the Kronecker delta
function,
is the number of feature spaces, and
is an isotropic kernel, which attribute smaller
weights to pixels distant from the centre. The
kernel
has a monotonic and convex decreasing
profile, and it is presented as a function :
0,∞
→
and
‖
‖
(Comaniciu, 2003).
By imposing
∑
1
1
, the normalization constant
is defined as:
1
∑
‖
∗
‖
⁄
(2)
Target Candidates: First, let us consider
…
as the pixel locations of the target
candidate which is centered on the location in the
current frame. The target candidate model
corresponding to the candidate region is computed
by
̂
̂
..
̂
∑
(3)
The scale of the target candidate (i.e., the number of
pixels) is determined by the constant which plays
the same role as the bandwidth (radius) in the case
of kernel density estimation.
Similar to the target model, and by imposing the
condition
∑
1
1
, we obtain the normalization
constant
1
∑
(4)
The correspondence between the two normalized
histograms of the target model and the candidate
model ̂
is calculated by a metric based on the
Bhattacharyya coefficient:
̂
,
∑
̂
(5)
From where, the distance between ̂
and is
calculated by:
̂
,
1
̂
,
(6)
2.2 Mean shift tracking
Beginning by
location in the previous frame, the
iterative process is initialized. To minimize the
distance (6) between ̂
and we should
maximize the Bhattacharyya coefficient. Taylor
expansion is used around̂
, from where the
linear approximation of the Bhattacharyya
coefficient (5) is calculated by:
̂
,
∑
̂
∑
(7)
Where
∑
∗
(8)
The first term in (7) is independent of y, thus, in
order to minimize the distance in (6), the second
term in (7) would be maximized. The estimated
target moves, in the iterative process, from to a
new position
, is computed by:
∑
∑
(9)
’
, we suppose that the derivative of
exists for all
0,∞
(Comaniciu, 2003).
Choosing the kernel with the Epanechnikov
profile, (9) would be reduced to:
∑
∑
(10)
Using (10), the mean shift locates, in the new frame,
the most analogous region to the object.
3 PROPOSED METHOD
3.1 Log-Gabor Filter
For texture analysis, Gabor filters (Fischer, 2007)
are often used for its efficiency of acquiring
simultaneous localization of frequency and spatial
information. However, the maximum bandwidth
captured by those filters is approximately one
octave. Whenever the bandwidth is larger, the DC
component is directly obtained from the Gabor
spectrum. This could be overcome by using the log-
Gabor function proposed by Field (Field, 1987)
which has two important characteristics to note.
First, by definition, log-Gabor function has no DC
component, which improves the contrast between
the target and its background. Second, the transfer
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
688

function of the log-Gabor filter allows us to obtain
large spectral information. Besides, log-Gabor
function’s bandwidth could vary from one to three
octaves. Thus, the features used become more
informative, effective and reliable (Zhitao, 2002).
Those proprieties preserve true texture structures of
the target. In this paper we adopted the new design
of log-Gabor wavelets proposed in (Fischer, 2007).
Log-Gabor filter have a Gaussian transfer function,
viewed on the logarithmic frequency scale. It can be
divided in polar coordinate system, into two
components:
1-the radial filter which the frequency response
is obtained by:
⁄
∙
(11)
2-the angular filter’s frequency response is defined
as:
∙
(12)
By multiplying these two components, the overall
log-Gabor transfer function is obtained:
,
∙
(13)
where,, are the log-polar coordinates,
and
present respectively the center frequency and the
orientation angle of the filter,
is the scale
bandwidth and
represents the angular bandwidth.
Often, a problem appears in the first scales, because
Eq. (11) would have significant amplitude
beyond the Nyquist frequency2
).
Indeed, cut off sharply the filter response beyond the
Nyquist frequency, distorts the filter form in the
spatial domain (which could cause the appearance of
side lobes or ringing). That’s why, high frequencies
are not covered in many implementations, and a part
of the spectrum is frequently discarded, e.g. in (Ro,
2001). In order to overcome this problem, Nestares
and al. included a non-oriented high-pass filter
(Nestares, 1998). Thus, to prevent the loss of
information of the target, we adopted the Gaussian
high-pass oriented filters proposed by Fischer, which
have a smooth shape without extra side lobes
(Fischer, 2007).
3.2 Target Representation with Joint
Color-log-Gabor Texture
Histogram
The object and its background texture are frequently
different, from where came the idea to joint log-
Gabor texture to color feature for tracking.
To construct the filter bank, we used four
different scales to insure the variation of radial
frequency and six orientations. In the feature
extraction process, every frame in the video (i.e. in
the space domain) would be transformed to the
frequency domain by applying the Discrete Fourier
transform (DFT) (Moisan, 2011). Thus, each pixel
represents a particular frequency contained in the
real domain image. To extract local frequency
information, the image is convolved with banks of
quadrature pairs of log-Gabor wavelets, and we
reaches the best empirical results by using value of
=
= 0.65. While in the frequency domain, we
can multiply the image with the filter. Then, the
multiplied image is converted back to the space
domain, by applying the inverse discrete Fourier
transform.
Employing discrete Fourier transform (DFT),
regular or inverse, offers an output of complex
numbers, which is not a problem for the
convolutions described above. But, the mean shift
tracker is not designed to work with complex
numbers, so it is a problem when using the filtered
images for tracking, thus, the idea proposed in this
section is to use a feature encoding (Sanderson,
2000) and (Daugman, 2002).
Figure 1: The process of phase quadrant demodulation.
Implementation (Feature Encoding): First, the 2D
image (frame) is broken up into its number of rows.
Each row (i.e. a 1D signal), would be convolved
with 1D Gabor wavelets. Actually, the angular
direction is taken instead of the radial one,
corresponding to the columns of the 2D image, as
the maximum independence occurs in the angular
direction. According to the technique of the phase-
quadrant demodulation, each phase of the output of
the filtering process will be coded on two bits. The
output of phase quantization is a grey code, so that
when going from one quadrant to another, only 1 bit
changes, this will limit the errors if the phase is
calculated to the boundary between adjacent
quadrants. The feature encoding process is presented
in Figure 1. Finally, the encoding process generates
a bitwise template containing a number of bits of
information. The number of bits in the texture
RobustObjectTrackingusingLog-GaborFiltersandColorHistogram
689

template will be:
2
.
Afterwards, we use the generated bitwise template
with the RGB channels to jointly describe the target
model using (1), then embed it into the mean shift
tracking framework. In order to acquire the texture
and color distribution of the target region
,
we use
(1) where888. The first three
dimensions (i.e. 8 ×8 ×8) illustrate the quantized
bins of color channels, and the fourth dimension (i.e.
T) is the bin of the log-Gabor texture patterns in the
generated template. As well, the target candidate
model ̂ is calculated by (3).
4 EXPERIMENTAL RESULTS
AND DISCUSSION
In this section, representative and extensive
experiments are performed to testify and illustrate
the proposed joint log-Gabor texture-color model
based mean shift tracking algorithm.
It will be compared with several state-of-art
variants of mean shift tracker, we denote by M1 the
background-weighted histogram (BWH) method,
M2 the corrected background-weighted histogram
(CBWH) method, M3 the joint color and LBP
texture method and by M4 our proposed method.
In this paper, we just present some experimental
results of different challenging public video
sequences. The color of the target and its
surrounding area could have the same color, the
objects being tracked could change in shape and size
due to the camera motion. These four algorithms are
implemented in MATLAB R2013a interface and run
on a PC with Intel® Core™2 Duo 2.1GHz CPU and
2 GB RAM, and tested on complexes sequences.
The first experiment is on a video sequence of
shoe_attack (Figure 2) with 115 frames of spatial
resolution 360×480. In this video, we will track a
region of size 42×28, and compare the target
locating accuracies by the four target representations
M1, M2, M3 and M4. Since no motion model has
been affected, and despite the alter of decrease and
increase of image intensity due to the camera’s
flashes (frame 52), the tracker adapted greatly to the
non-stationary character of the head’s movements
which alternates abruptly with its fast reaction. The
joint log-Gabor texture with the color feature proves
to be robust to partial occlusion (frame 80), clutter,
(a)
(b)
(c)
(d)
Figure 3: Tracking results of shoe_attaque sequence by the target representation models (a) M1, (b) M2, (c) M3 and (d) M4.
Frame 52, 80, 90, 94 and 115 are displayed.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
690

Frame 29_M3
Frame 29_M4
distractors (frame 90), and camera motion (frame
115). In fact, the log-Gabor feature is actually
responsive not only to the target itself, but also to the
texture of the background. Consequently, the target
is localized by tracking the non-background part of
the filtered frames which have a positive impact on
tracking performance.
To demonstrate the robustness of our approach,
Figure 3 presents the surface computed by the
Bhattacharyya coefficient for the 81× 81 pixels
rectangle marked in Figure 3, frame 29.
The target model has been compared with the target
candidates of the first frame obtained by sweeping in
frame 29 the rectangular region inside the bigger
one. The iteration numbers of mean shift tracking
with M1, M2, M3 and M4, in the frame number 29
are 6, 4, 4 and 2 respectively. While most of the
tracking approaches based on only color
(Comaniciu, 2003) and (Ning, 2012) and LBP
texture (Ning, 2009), must proceed an exhaustive
search in the rectangle to find the maximum of
similarity, our proposed algorithm converged in
lower number of iterations because it suppresses the
backgrounds feature.
Figure 3: The similarity surface (values of the
Bhattacharyya coefficient) of the two methods
corresponding to the rectangle marked in frame 29_ (M3
and M4) in the shoe_attack sequence. The red triangles in
the similarity surface represents the initial point, the blue
triangle represent the final position. We can see that M4
converges much faster than M3.
The second experiment is on a video sequence of a
sprint with 173 frames of spatial resolution
360×480. In this movie, we will track a region of
size 82×33, describing the sprinter with heavy
occlusions and whose dress color is the same as its
background. So, the methods based only on color
histogram M1 and M2 drift away and fail to track
the target. To save space, Figure.3 presents only
tracking results of the M3 and M4. During the
sequence, the target form is often fuzzy, nevertheless
the methods M3 and M4 based on texture joint color
histogram can still locate the target. For this video
we had a partial occlusion due to background color,
thus, we used a bank of different log-Gabor filters
constructed with six different scales and eight
different orientations. It can be experimentally
observed that the proposed approach can still locate
the target when heavy occlusion appears starting
with frame 156.
(a)
(b)
Figure 4: Tracking results of sprint sequence by the target
representation models (a) M3 and (b) M4. Frame 116, 156
and 171 are displayed.
The second experiment is on a racing sequence
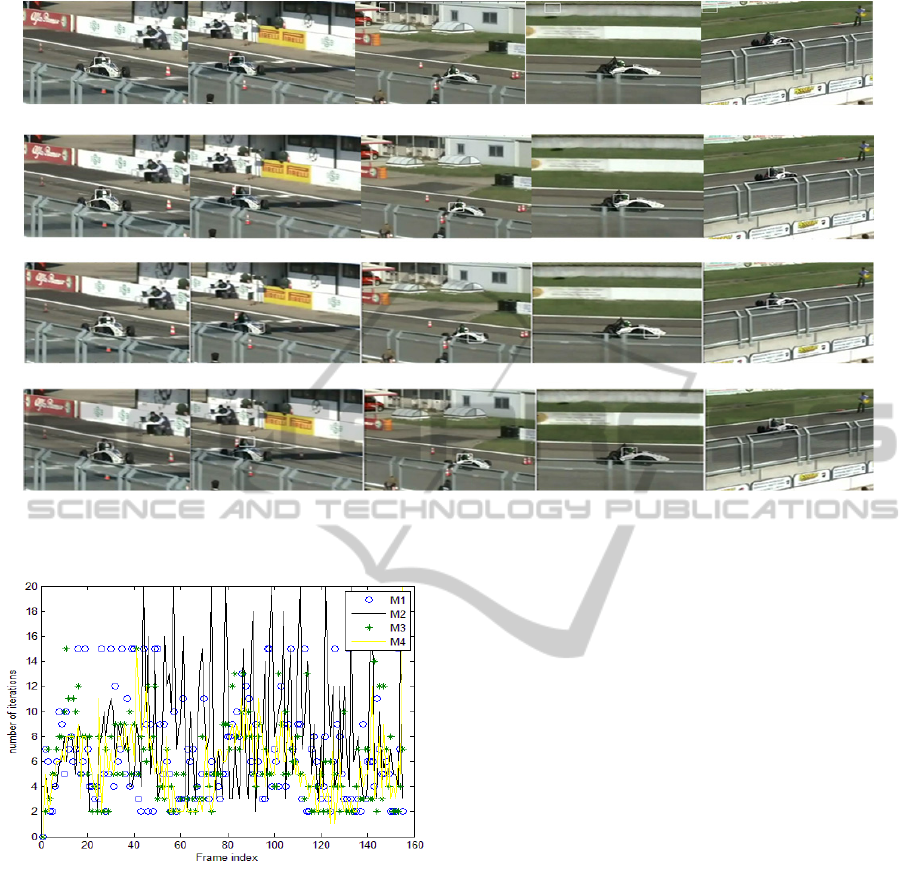
(Figure 5) of about 155 frames, the driver’s head
was used as target model of size 30 ×40. The tracker
was tested for the intense blurring (frame 17) caused
by a shadow, scale changes due to the camera
motion (frames 49 and 81), and the dramatic
changes in appearance (frame130). However, neither
M1 nor M3 can locate the target object while both
M2 and M4 can still track the target accurately. The
forth row of Table 1 gives the total numbers of
iterations of the four methods, and it indicates that
the proposed approach has the fewer number of
iterations then M2, which prove that M4 performs
better than the other trackers. The number of mean
shift iterations necessary for each frame with the
four methods is shown in Figure 6.
The peaks correspond to occlusion and the fast
move of the driver’s head caused by the high speed
of the racing care. The M1 have few number of
iteration, M3 need a tough search especially when
no model has been affected to his head, but, our
proposed algorithm succeeds to locate the target
with less iteration. In addition, the intense blurring
present in last frames due to the camera motion,
RobustObjectTrackingusingLog-GaborFiltersandColorHistogram
691
(a)
(b)
(c)
(d)
Figure 5: Tracking results of racing sequence by the target representation models (a) M1, (b) M2, (c) M3 and (d) M4. Frame
9, 17, 49, 81 and 130 are displayed.
Figure 6: The number of mean shift iterations function of
the frame index for the racing sequence.
does not influence the tracker performance for M4
(frame between 100 and 155) unless it failed to
locate the target for M1and M3, while M2 locate the
target but with an exhaustive search showed in the
last and largest peak. In all these cases, M4 prove to
be robust to the relative large movement between
two consecutive frames which puts more of a burden
on the mean shift procedure. In the tennis_table
sequence of 300 frames, we will track the player’s
movements which alternate between slow and fast
action and compare the target locating accuracies by
the four target representations.
In this video the tracking is made more challenging
by the quality of the sequence due to the camera
motion and image compression artefacts. As shown
in figure 7, in this scene the target appearance is
slightly similar to its background. Figures 7(a)–7(b)–
7(c) and 7(b) present the mean shift tracking results
by the four target representation. Because the initial
target region contains much of the background, the
accuracy of the target location of mean shift tracking
with M3 loses the object after frame 10 due to the
change of the background caused by the camera
motion. To save space, we show the experimental
results only for first 43 frames. However, our
proposed model M4 and the two methods based on
color histogram M1 and M2, extract the main target
features while suppressing the background features
so that the target location is much more robust than
that by M3 model. For each frame of this sequence,
the minimum value of the distance of Bhattacharya
(7), i.e., the distance between the target model and
the target candidate, is shown in Figure 8.
The compression noise, and the fast movement
of the player elevates the residual distance value
from 0 (perfect match) to an about 0.35. Significant
deviations from this value correspond to occlusions
generated by the background where other persons
exist and the player’s moves (large changes in the
representation). For example, the distance 0.5 peak
corresponds to the partial occlusion in frame 278.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
692

(a)
(b)
(c)
(d)
Figure 7: Tracking results of Tennis_table sequence by the target representation models (a) M1, (b) M2, (c) M3 and (d) M4
Frame 3, 14, 24, and 43 are displayed.
Figure 8: The minimum value of Bhattachayya distance
function of the frame index for the Tennis_table sequence.
The mean distance of Bhattacharyya is 0.2894 per frame.
At the end of the sequence, the person being tracked
gets out of the scene, which produces a complete
occlusion. Our proposed method proves to be robust
not only because it succeed to localize the target, but
also it tracks the key feature points of candidate
region with less number of iterations (refer to Table
1), though it needs additional computation to
calculate the log-Gabor banc of filter. In our
approach we used four scales and six orientations,
Table 1: The number of mean shift iterations by the two
methods.
Video
sequence
Frames
Target
Represen-
tations
Mean shift iteration
Total
number
Average
number
Shoe_attack
115
M1
M2
M3
M4
402
438
386
427
3.49
3.8
3,35
3,71
Sprint
173
M3
M4
1039
869
9,03
7,55
Racing
155
M1
M2
M3
M4
838
1278
1034
919
5,4
8,24
6,67
5,92
Tennis_table
44
M1
*
M2
M3
M4
195
183
202
181
4,43
4,15
4,59
4,11
* Since the target is lost after frame 44 for M1, we only use the
first 44 frame in the calculation for M1.
RobustObjectTrackingusingLog-GaborFiltersandColorHistogram
693

but, in complexes scenes, sometimes we increase
these numbers in order to make sure that the feature
contains accurate information about the object.
Thus, we adjust the log-Gabor filter parameters
ourselves to find the best settings that different log-
Gabor filters makes us think about speeding up the
program, so, we aim to implement it in C/C++
which guaranty a significant speedup, making real
time processing possible.
5 CONCLUSION
In this paper we presented a new filter based
approach for video tracking of arbitrary objects.
Log-Gabor feature is a powerful tool to measure the
spatial structure of local image texture which has
been modelled by a bank of log-Gabor wavelets. In
order to improve the robustness of target
representation and reduce the computational cost, we
proposed a joint color and log-Gabor texture based
mean shift tracking algorithm. Our proposed method
use only one target representation and localize the
new object and background appearances in every
frame. The system deals with different objects and
settings and is robust to perspective transformations,
rotations, heavy occlusion and lightening conditions.
REFERENCES
Comaniciu D., and Meer P., Mean shift: a robust approach
toward feature space analysis, IEEE Trans. Patt. Anal.
Mach. Intell. 24(5) (2002) 603–619.
Comaniciu D., Ramesh V., and Meer P., Kernel-based
object tracking, IEEE Trans. Patt. Anal. Mach. Intell.
25(5) (2003) 564–575.
Daugman J., How iris recognition works. Proceedings of
2002 International Conference on Image Processing,
Vol. 1, 2002.
Field D. J., “Relations between the statistics of natural
images and the response properties of cortical cells”
Vol.4 No.12J.Opt.Soc.Am.A, December 1987.
Fischer S., Sroubek F., Perrinet L., Redondo R., and
Cristobal G., “Self invertible 2d log-Gabor wavelets”
Int. J. Comput. Vision, vol. 75, no. 2, pp. 231–246.
2007.
Haritaoglu I., and Flickner M., Detection and tracking of
shopping groups in stores, Proc. IEEE Conf. Computer
Vision and Pattern Recognition, Kauai, Hawaii, 2001,
pp. 431–438.
Kong A., “An analysis of Gabor detection,” in Image
Analysis and Recognition, ser. Lecture Notes in
Computer Science, Kamel M., and Campilho A., Eds.
Springer Berlin / Heidelberg, 2009, vol. 5627, pp. 64–
72.
Moisan L., Periodic plus Smooth Image Decomposition, J.
Math. Imaging Vision , vol. 39:2, pp. 161-179, 2011
Nestares O., Tabernero A., Navarro R., and Portilla
J.,"Efficient spatial-domain implementation of a
multiscale image representation based on Gabor
functions", J. Electron. Imaging. 7(1), 166-173 (Jan
01, 1998).
Ning J., Zhang L., Zhang D., and Wu C., “Robust object
tracking using joint color-texture histogram’
International Journal of Pattern Recognition and
Artificial Intelligence Vol. 23, No. 7 (2009) 1245–
1263.
Ning J., Zhang L., Zhang D., and Wu C., ‘’Robust Mean
Shift Tracking with Corrected Background-Weighted
Histogram’’ IET Comput. Vis., 2012, Vol. 6, Iss. 1,
pp. 62 – 69
Ro Y.M., Kim M., Kang H.K., Manjunath B.S., and Kim
J., 2001. MPEG-7 homogeneous texture descriptor.
ETRI Journal, 23(2):41–51.
Sanderson S., Erbetta J., Authentication for secure
environments based on iris scanning technology. IEE
Colloquium on Visual Biometrics, 2000.
Sonka M., Hlavac V., and Boyle R., Image Processing,
Analysis and Computer Vision, 3rd ed. (Thomson,
2007).
Yang C., Ramani D., and Davis L., Efficient mean-shift
tracking via a new similiarity measure, Proc. IEEE
Conf. Computer Vision and Pattern Recognition I
(2005) 176–183.
Yilmaz A., Javed O., and Shah M., Object tracking: A
survey, ACM Comput. Surv. 38(4) (2006).
Zhitao X., Chengming Y. M. G., and Qiang L., “Research
on log gabor wavelet and its application in image edge
detection,” Sixth International Conference on Signal
Processing, 2002.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
694
