
Overlapping Clustering with Outliers Detection
Amira Rezgui
1
, Chiheb-Eddine ben N’Cir
1
and Nadia Essoussi
2
1
LARODEC, ISG Tunis, University of Tunis, Bardo, Tunis, Tunisia
2
LARODEC, FSEG Nabeul, University of Carthage, Nabeul, Tunisia
Keywords:
Overlapping Clustering, Non Disjoint Groups, Parametrized R-OKM, Outliers Detection.
Abstract:
Detecting overlapping groups is an important challenge in clustering offering relevant solutions for many
applications domains. Recently, Parametrized R-OKM method was defined as an extension of OKM to control
overlapping boundaries between clusters. However, the performance of both, OKM and Parametrized R-OKM
is considerably reduced when data contain outliers. The presence of outliers affects the resulting clusters and
yields to clusters which do not fit the true structure of data. In order to improve the existing methods, we
propose a robust method able to detect relevant overlapping clusters with outliers identification. Experiments
performed on artificial and real multi-labeled data sets showed the effectiveness of the proposed method to
produce relevant non disjoint groups.
1 INTRODUCTION
Data mining aims at modeling relationships and dis-
covering hidden patterns in large databases. Clus-
tering is an important task in data mining. It aims
to find groups from unlabeled data by organizing a
given set of data into coherent clusters, such that
all data within the same cluster are similar to each
other, while data from different clusters are dissimi-
lar. However, this definition of clustering could be a
crucial issue in many applications of clustering where
data need to be assigned to more than one cluster. For
example, in social network analysis, community ex-
traction algorithms should be able to detect overlap-
ping clusters because an actor can belong to multiple
communities (Wang et al., 2010). In video classifi-
cation, overlapping clustering is a necessary require-
ment while video can potentially have multiple genres
(Yang et al., 2007). In emotion detection, overlapping
clustering methods should be able to detect several
emotions for a specific piece of music (Trohidis et al.,
2008). In biology, many genes are multi-functional
and need to be assigned to multiple overlapping clus-
ters (Battle et al., 2005) (Eran et al., 2003). In infor-
mation retrieval and text mining, documents can dis-
cuss several themes (Sahami et al., 1996).
The possibility that an observation belongs to
more than one cluster is usually ignored. How-
ever, some researchers have focused on this prob-
lem known as ”overlapping clustering”. Recently, a
new clustering method referred to as Parametrized R-
OKM (Ben N’Cir et al., 2013), generalizes k-means
approach to detect non disjoint clusters. This method
extends OKM (Cleuziou, 2008) to control the sizes of
overlaps and offers for users the possibility to regu-
larize the overlaps. Although the ability of OKM and
Parametrized R-OKM to produce non-disjoint clus-
ters, their performance could be considerably reduced
in presence of outliers. Known that these methods are
based on centroids as representatives of each cluster,
the noisy observations lead to produce clusters which
do not fit the true structure of data.
In order to deal with this issue, we propose a
robust method referred to Robust Parametrized R-
OKM, taking into account the presence of outliers.
When performing the learning of data, the proposed
method identifies on each step observations which
will be classified as outliers to improve the quality of
obtained non-disjoint groups.
The remainder of this paper is organized as fol-
lows: Section 2 presents related works on overlapping
clustering. Then, Section 3 describes the motivation
of this work by presenting the importance of detect-
ing outliers. Section 4 describes the proposed Ro-
bust Parametrized R-OKM while Section 5 describes
experiments performed on artificial and real overlap-
ping data sets to check the effectiveness of the pro-
posed method. Finally Section 6 gives conclusions
and some future improvements of this work.
279
Rezgui A., Ben N’Cir C. and Essoussi N..
Overlapping Clustering with Outliers Detection.
DOI: 10.5220/0004830002790286
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 279-286
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 OVERLAPPING CLUSTERING
Many methods were proposed to solve the issue
of overlapping clustering. Two classes of methods
have been led: Heuristic and Theoretical. Heuristic
methods are based on proposing new clustering
processes based on intuitive learning for example
CBC (Pantel and Dekang, 2002), POBOC (Cleuziou
et al., 2004) or the extension of results of well
known methods (Bezdek, 1981) (Krishnapuram and
Keller, 1993) (Dempster et al., 1977) to have non
disjoint clusters. These heuristic methods can lead
to non disjoint partitioning, but good results are not
ensured because they are not based on theoretical
model to introduce overlaps. However, this issue
is solved for theoretical methods where overlaps
are introduced in their optimized criteria. Example
of these Methods are OKM (Cleuziou, 2008) and
Parametrized R-OKM (Ben N’Cir et al., 2013).
• Parametrized R-OKM
In order to detect overlapping clusters with control of
overlaps, Parametrized R-OKM method generalizes
OKM and allows the user to parameterize the size of
the overlaps according to his expectations. Given a
data set X with N data and a number K of expected
clusters, the aim of Parametrized R-OKM is to find
the binary assignment matrix Π(N × K) and the clus-
ter representativesC = {C
1
,...,C
K
} such that the fol-
lowing objective criterion is minimized:
J(Π,C) =
∑
x
i
∈X
|Π
i
|
α
d(x
i
,im
Π,C
(x
i
))
2
, (1)
with im
Π,C
(x
i
) is the combination of clusters’ repre-
sentatives which represents the gravity center of clus-
ters prototypes to which observation x
i
belongs and is
defined by:
im
Π,C
(x
i
) =
∑
π
k
∈Π
i
C
k
|Π
i
|
, (2)
where π
k
the set of objects which belongs to the
k
th
cluster, C
k
the prototype of cluster π
k
, |Π
i
|
α
the
weight assigned to observation x
i
, Π
i
the set of clus-
ters to which x
i
belongs to, |Π
i
| its cardinality and
α a positive parameter to control the size of the over-
laps. The parameter α is considered as a penalty term:
the penalization is more important when α → +∞ and
then overlaps are reduced. However the penalization
is reduced when α → 0 and the method produces large
overlaps. Particularly when α = 0 Parametrized R-
OKM coincides with OKM.
The objective function of Parametrized R-OKM
J(Π,C) is minimized by alternating two independent
steps:
1. Assignment of observationsto one or several clus-
ters: This step orders the clusters from the nearest
cluster to farthest one then assigns the observation
to several clusters while the objective function is
minimized.
2. Update of clusters’ representatives: This step up-
date the clusters’ representatives after each as-
signment step. By using the lagrange multipliers
method, by differentiating with respect to C
k
and
setting derivative to zero, optimal clusters’ rep-
resentatives C
∗
k
to made the objective function of
Parametrized R-OK minimized are defined by:
C
∗
k
=
∑
x
i
∈π
k
1
|Π
i
|
2−α
C
k
i
∑
x
i
∈π
k
1
|Π
i
|
2−α
, (3)
where C
k
i
= |Π
i
|.x
i
− (|Π
i
| − 1).im
Π,C(x
i
)
.
3 PROBLEM DESCRIPTION
In real life applications of overlapping clustering, data
are usually complex and contain outliers. Outliers,
also referred to as noise, are observations which are
grossly different from the remaining set of data. In-
tuitively, an outlier can be defined by an observation
that deviates so much from other observations.
The presence of outliers in data affects the clus-
tering algorithm by biasing the structure of obtained
clusters as the case of Parametrized R-OKM. Figure
1 shows patterns obtained with parametrized R-OKM
in two artificial data sets: the first example is free of
outliers while the second contains a noisy observa-
tion. The application of Parametrized R-OKM with 2
clusters using Euclidean distance in the first data set
leads to non disjoint clusters. However, in the sec-
ond data set the application of Parametrized R-OKM
results in two disjoint groups where the outlier itself
forms one cluster and all remaining observations are
grouped in the other cluster..
4 ROBUST PARAMETRIZED
R-OKM
In order to make robust the identification of over-
lapping clusters in presence of outliers, we propose
a new method denoted by Robust Parametrized
R-OKM. This proposed method takes into account
that data may contain noise. Therefore, it can detect
more relevant clusters by giving the possibility to
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
280
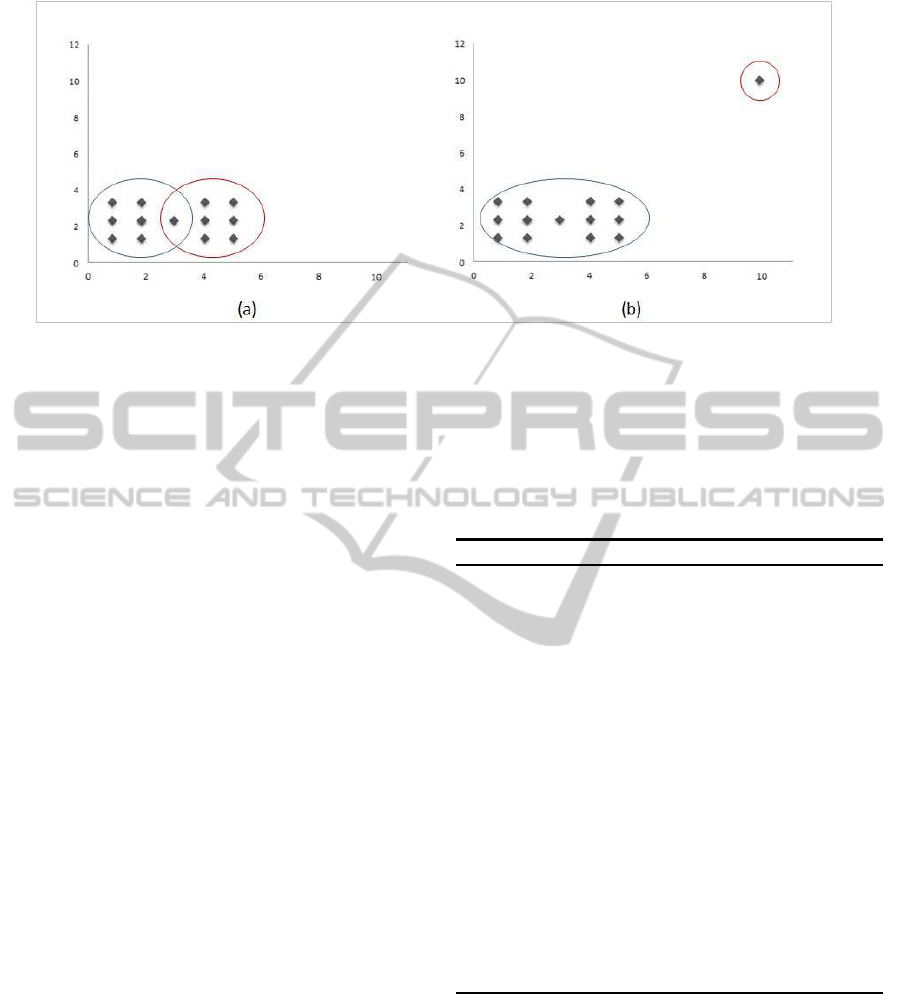
Figure 1: Clusters obtained using Parametrized R-OKM ( K=2) in a two dimensional artificial data sets: (a) tow non disjoint
clusters obtained in a data set free of outliers and (b) two disjoint clusters obtained in a data set containing a noisy observation.
user to control the size of overlaps: Based on the
Noise Clustering approach (Dav`e, 1991), we propose
to add a new fictive cluster in which outliers will be
assigned to. All the observations whose distances
from the set of prototypes exceed a fixed threshold
are considered as outliers and assigned to the fictive
cluster.
4.1 Objective Function of Robust
Parametrized R-OKM
The Objective function of Robust Parametrized R-
OKM aims to model the local error on each obser-
vation x
i
defined by the squared Euclidean distance
between x
i
and its representative denoted as image
im(x). Given a data set X with N data over R
P
and
a number K
′
= K + 1 of expected clusters, the aim of
Robust Parametrized R-OKM is to find the binary as-
signment matrix Π(N × K
′
) and the cluster represen-
tatives C = {C
1
,. ..,C
K
} ∪C
‡
such that the following
objective function is minimized:
J(Π,C,δ) =
∑
x
i
∈X,x
i
/∈C
‡
|Π
i
|
α
d(x
i
,im
Π,C
(x
i
))
2
+
∑
x
i
∈C
‡
|Π
i
|
α
δ
2
, (4)
where |Π
i
|
α
the weight of observation x
i
, |Π
i
| the
number of clusters to which x
i
belongs to, α a pos-
itive parameter used to control the size of overlaps,
im
Π,C
(x
i
) the image of observation x
i
, C
‡
the noise
cluster and δ
2
the distance between the cluster noise
and each observation denoted by noise distance.
4.2 Algorithm Resolution and
Optimization
The main algorithm of the Robust Parametrized R-
OKM is described by Algorithm 1.
Algorithm 1: Robust Parametrized R-OKM.
Require: X :a set of input data.
K : a number of clusters.
ε : a minimum improvement in the objective function.
t
max
:a maximum number of iterations.
δ
2
: the distance noise
Ensure: Π: assignment of observations over K clusters.
1: Initialize representatives of clusters C
0
randomly over X
2: Initialize the distance noise δ
2
3: Initialize clusters memberships Π
0
i
using
Robust.Multi.ASSIGN(x
i
,C
0
)
4: Compute the objective function J(J(Π
0
,C
0
,δ) ).
5: while J
Π
t−1
,C
t−1
,δ
− J(Π
t
,C
t
,δ) > ε and t < t
max
do
6: Set t = t + 1
7: Update clusters’ representatives C
t
8: Update distance noise δ
2
9: Compute new assignments Π
t
using
Robust.Multi.ASSIGN(x
i
,C
t
,Π
t
)
10: Compute objective function J(Π
t
,C
t
,δ)
11: end while
12: return Π
t
the final cluster memberships matrix.
The optimization of the objective function is realized
by iterating 3 steps:
1. computation of cluster representatives ;
2. computation of distance noise δ
2
;
3. multi-assignment (Π) of observations.
The above steps are iterated until a stopping criterion
is reached. The stopping rule of Robust Parametrized
R-OKM algorithm is characterized by two criteria:
the maximum number of iterations or the minimum
OverlappingClusteringwithOutliersDetection
281

improvement of the objective function between two
iterations.
We present in the next, a detailed description
of the optimisation steps of Robust Parametrized R-
OKM.
4.3 Computation of Cluster
Representatives
Given a cluster π
h
and a set of K clusters’ represen-
tatives {C
k
}
K
h=1
\ {C
h
} the problem of finding C
∗
k
that
minimize the objective function J(Π,C, γ) can be ex-
pressed as a convex optimization problem which is
solved using the lagrange multipliers method. By dif-
ferentiating J(Π,C, γ) with respect to C
k
and setting
derivative to zero, optimal clusters’ representative C
∗
k
which minimize the objective function are computed
as the following:
C
∗
k
=
∑
x
i
∈π
k
,π
k
6=C
‡
1
|Π
i
|
2−α
C
k
i
∑
x
i
∈π
k
1
|Π
i
|
2−α
, (5)
where C
k
i
is defined by :
C
k
i
= |Π
i
|.x
i
− (|Π
i
| − 1).im
Π,C(x
i
)
(6)
The computation of the new clusters’ prototypes en-
sures that the objective function is decreased after
each update of clusters’ prototypes.
4.4 Multi-assignment
Based on the assignment heuristic used for
Parametrized R-OKM, we derive a new heuris-
tic taking into account the possibility that an
observation be assigned to the noise cluster. It
looks for the nearest cluster of observation x
i
. If the
distance between this observation and the nearest
cluster exceeds the distance noise, this observation
is identified as outlier. Conversely, it scrolls through
the list of centers from the nearest to the farthest,
and assigns the observation x
i
to the nearest cluster.
The new assignment is kept only if it is better than
the old one. This assignment heuristic is detailed in
Algorithm 2.
4.5 Computation of Distance Noise
In order to determine the noise distance, we assume
that this distance depend on the variation of obser-
vations with respect to clusters prototypes which is
defined by:
Algorithm 2: Robust.Multi.ASSIGN.
Require: x
i
:Vector in R
d
.
{C
1
,. ..,C
K
} : K clusters’ representatives.
Π
old
i
: Old assignment of observation x
i
.
γ : Parameter to control outliers.
Ensure: Π
i
: New assignment for x
i
.
1: Search C
∗
the nearest cluster where C
∗
=
argmin
C
k
∑
k∈Π
i
|Π
i
|
α
kx
i
−C
k
k
2
2: Compute the distance between the observation and the
nearest cluster
3: if |Π
i
|
α
kx
i
−C
∗
k
2
≥ δ
2
then
4: x
i
is an outlier Π
i
= {C
‡
}
5: Return Π
i
6: else
7: Initialize Π
i
= {C
∗
} the nearest cluster where C
∗
=
argmin
C
k
ω
i
|Π
i
|
α
kx
i
−C
k
k
2
8: Looking for the next nearest cluster C
∗
which is not in-
cluded in Π
i
9: Compute im
Π
′
,c
(x
i
) with assignments Π
′
i
= Π
i
∪ {C
∗
}
10: if |Π
′
i
|
α
kx
i
− im
Π
′
,C
(x
i
)k
2
< |Π
i
|
α
kx
i
− im
Π,C
(x
i
)k
2
then
11: Π
i
← Π
′
i
and go to step 9
12: else
13: compute im
old
(xi) with assignment Π
old
i
14: if |Π
i
|
α
kx
i
− im
Π,C
(x
i
)k
2
≤ |Π
i
|
α
old
kx
i
− im
Π,C
(x
i
)k
2
then
15: Return Π
i
16: else
17: Return Π
old
i
18: end if
19: end if
20: end if
δ
2
= γ
N
∑
i=1
K
∑
k=1
d
2
ik
N × K
, (7)
where γ is the value of the parameter used to obtain δ
from the average of distances. A proper selection of
the parameter γ will control the classification result
and the proportion of observations that are considered
as outliers. The specification of the parameter γ is
fixed by the user.
According to this definition, the noise distance
depends generally on the non-weighted distances
of all feature vectors to all prototype vectors. Thus
this distance is not fixed but it is modified in each
iteration of the algorithm after the update of clusters’
representatives.
5 EXPERIMENTS AND RESULTS
To check the effectiveness of Robust Parametrized R-
OKM to produce suitable overlapping clusters within
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
282

Figure 2: Experiments on artificial data set: (a) the artificial data set, (b)two clusters obtained using Parametrized R-OKM
with α = 1 and (c)two clusters obtained using Robut Parametrized R-OKM with α = 1 and γ = 0.5.
noisy data, we perform experiments on artificial and
real overlapping data sets using a standard desktop
computer. Running times of each method are not re-
ported while all the methods need less than one 1 sec-
ond to return results.
5.1 Experiments on Artificial Data Sets
The examples included in Figure 2(b) and Figure
2(c) show the ability of Robust Parametrized R-OKM
method lead to clusters which fit the true structures in
data.
To check the effectiveness of Robust Parametrized
R-OKM, , we generate an artificial data set over two
dimensions as described in Figure 2(a). This data set
is characterized by two apparent groups in data and
some observations which have different characteris-
tics than the remaining data. We report obtained par-
titioning using Parametrized R-OKM with α = 1 and
Robut Parametrized R-OKM with α = 1 and γ = 0.5
as described in Figure 2(b) and Figure 2(c). These
figures show that Parametrized R-OKM leads to clus-
ters with large overlaps and does not identify the two
apparent groups. This problem is solved when using
the proposed Robust Parametrized R-OKM.
To illustrate sensitivity of Robust Parametrized R-
OKM to the parameter γ, we report obtained clusters
with different values of γ using a fixed value of α as
shwon in Figure 3. These results provethat the perfor-
mance of Robust Parametrized R-OKM depends on a
suitable configuration of the parameter γ. This corre-
lation can be explained by the fact that the parame-
ter γ is used to control the number of outlier points.
In fact, the parameter γ controls the distance between
each observation and the prototype of cluster in which
the outliers are assigned to. This distance depends on
this parameter. As well as γ is small and near to 0 the
distance noise becomes more smaller leading to large
detection of outliers.
5.2 Experiments on Real Data Set
In order to evaluate the performance of Robust
Parametrized R-OKM, results are compared through
external validation measures which are Precision, Re-
call, F-measure and Rand Index. The reported scores
are averages and standard deviations obtained over
ten runs.
Let X = {X
1
,. ..,X
N
} be the set of observations, C =
{c
1
,. ..,c
K
} a partition of X into K classes, R =
{r
1
,..., r
k
1
} a partition of X into K
1
clusters specified
by the clustering algorithm.
Given the notations:
• ”TP” designs the number of pairs of observations
in X that share at least one class in C and share at
least one cluster in R.
• ”TN” the number of pairs of observations in X
that do not share any class in C and do not share
any cluster in R;
• ”FN” designs the number of pairs of observations
in X that share at least one class in C and do not
share any cluster in R;
• ”FP” designs the number of pairs of observations
in X that do not share any class in C and share at
least one cluster in R
the validation measures are computed as follows:
Precision =
TP
TP+ FP
.
Recall =
TP
TP+ FN
.
F − measure =
(2× Recall× Precision)
(Recall + Precision)
.
Rand Index =
TP+ TN
TP+ FN + FP+ TN
.
Experiments are performed in three domains where
data need to be assigned to more than one cluster. The
statistic of the used data sets are described in Table 1.
OverlappingClusteringwithOutliersDetection
283

Figure 3: Sensitivity of Robust Parametrized R-OKM method to the parameter γ.
Table 2: Comparison of Robust Parametrized R-OKM with existing overlapping clustering methods on Benchmark data sets.
Data sets Methods Precision Recall F-measure Rand Index
EachMovie fuzzy c-means (θ = 0.33) 0.610 ± 0.001 0.734 ± 0.001 0.666 ± 0.001 0.696 ± 0.001
OKM 0.465± 0.020 0.921±0.055 0.618± 0.001 0.532± 0.032
Robust Parametrized R-OKM(γ = 0.8) 0.627± 0.010 0.857± 0.020 0.724 ± 0.02 0.621± 0.03
Parametrized R-OKM(α = 0.1) 0.474± 0.016 0.900± 0.042 0.621± 0.024 0.547± 0.024
Robust Parametrized R-OKM(γ = 1.0) 0.680± 0.024 0.727± 0.084 0.699± 0.024 0.640 ± 0.025
Emotion fuzzy c-means (θ= 0.1667) 0.493 ± 0.003 0.357 ± 0.001 0.414 ± 0.002 0.524 ± 0.002
OKM (α = 0) 0.483± 0.000 0.647± 0.029 0.553± 0.011 0.508± 0.001
Robust Parametrized R-OKM(γ = 10) 0.657±0.004 0.512± 0.017 0.578 ±0.012 0.517± 0.003
Parametrized R-OKM(α = 5.0) 0.506± 0.002 0.213± 0.007 0.300± 0.008 0.531 ± 0.000
Robust Parametrized R-OKM(γ = 0.1) 0.698± 0.000 0.222± 0.021 0.337± 0.024 0.440± 0.004
Scene FCM(θ = 0.1667) 0.324± 0.004 0.482± 0.022 0.388± 0.005 0.706± 0.008
OKM 0.233± 0.006 0.928± 0.013 0.372± 0.008 0.397± 0.019
Parametrized R-OKM(α = 2.0) 0.451± 0.000 0.417± 0.001 0.433± 0.001 0.789 ± 0.000
Robust Parametrized R-OKM(γ = 0.8) 0.488± 0.030 0.652± 0.119 0.548± 0.023 0.632± 0.019
Table 1: Data sets description.
Data set Observation Dimension Labels Overlap
EachMovie 75 3 3 1.14
Music 593 72 6 1.86
Scene 2407 6 1.07 1.86
Table 2 and Table 3 report average scores and standard
deviations of Precision, recall, F-measure.
In Eachmovie, Emotion and Scene data sets, re-
sults obtained with Robust Parametrized R-OKM out-
perform results obtained with FCM and Parametrized
R-OKM. For example, in Eachmovie data set the
F-measure obtained with Robust Parametrized R-
OKM (0.724) outperform the F-measure obtained
with OKM (0.618) and the F-measure obtained with
FCM(0.666). The improvement of F-measure with
proposed methods is induced by the improvement of
classification precision compared to OKM and FCM
methods.
In Emotion and Scene data set, the improvement
of the F-measure obtained with the proposed method
compared to the F-measure obtained with Robust
Parametrized R-OKM is induced by the improvement
of classification precision. For example, in Emo-
tion data set, the average of Precision using Robust
Parametrized R-OKM with α = 5 and γ = 0.1 is equal
to 0.506 while the average of Precision when using
Parametrized R-OKM with α = 5 is equal to 0.698.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
284

Table 3: Sensitivity of proposed methods to the parameter γ on Benchmark data sets.
Data sets Methods Precision Recall F-measure Rand Index
EachMovie Robust Parametrized-OKM(α = 0,γ = 1) 0.632± 0.02 0.886± 0.05 0.737±0.03 0.635± 0.04
Robust Parametrized-OKM(α = 0,γ = 0.8) 0.627± 0.01 0.857± 0.02 0.724± 0.02 0.621± 0.03
Robust Parametrized-OKM(α = 0,γ = 0.7) 0.623± 0.01 0.868± 0.04 0.725± 0.01 0.619± 0.02
Robust Parametrized R-OKM(α = 1,γ = 1) 0.691± 0.05 0.635± 0.03 0.659±0.03 0.619± 0.05
Robust Parametrized R-OKM(α = 1,γ = 0.7) 0.691±0.06 0.621± 0.06 0.652± 0.04 0.611± 0.06
Robust Parametrized R-OKM(α = 1,γ = 0.5) 0.661± 0.03 0.605± 0.07 0.631± 0.05 0.583± 0.04
Robust Parametrized R-OKM(α = 1.5,γ = 1) 0.719±0.10 0.632± 0.05 0.668±0.05 0.631± 0.06
Robust Parametrized R-OKM(α = 1.5,γ = 0.7) 0.711± 0.09 0.611± 0.05 0.653± 0.01 0.617± 0.18
Robust Parametrized R-OKM(α = 1.5,γ = 0.5) 0.663± 0.03 0.603± 0.07 0.630± 0.05 0.583± 0.04
Emotion Robust Parametrized-OKM(α = 0,γ = 0.3) 0.659± 0.005 0.519± 0.038 0.580± 0.022 0.521± 0.007
Robust Parametrized-OKM(α = 0,γ = 0.4) 0.657± 0.005 0.491± 0.013 0.562± 0.006 0.510± 0.000
Robust Parametrized-OKM(α = 0,γ = 0.8) 0.654± 0.003 0.492± 0.039 0.561± 0.024 0.507± 0.009
Robust Parametrized-OKM(α = 0,γ = 5.0) 0.661± 0.006 0.487± 0.02 0.560± 0.011 0.510± 0.002
Robust Parametrized R-OKM(α = 5,γ = 0,1) 0.698± 0.000 0.222± 0.021 0.337± 0.024 0.440± 0.004
Robust Parametrized R-OKM(α = 5,γ = 0,5) 0.677± 0.00 0.203± 0.00 0.313± 0.00 0.428± 0.000
Robust Parametrized R-OKM(α = 5,γ = 0.7) 0.679± 0.002 0.207± 0.00 0.318± 0.00 0.429± 0.00
Robust Parametrized R-OKM(α = 5,γ = 1.0) 0.672± 0.000 0.200± 0.004 0.308± 0.004 0.424± 0.001
Robust Parametrized R-OKM(α = 0.1,γ = 0,1) 0.700± 0.002 0.285± 0.006 0.405± 0.006 0.462± 0.003
Robust Parametrized R-OKM(α = 0.1,γ = 0.3) 0.681± 0.001 0.244± 0.015 0.388± 0.011 0.454± 0.004
Robust Parametrized R-OKM(α = 0.1,γ = 0.5) 0.676± 0.002 0.262± 0.034 0.377± 0.036 0.447± 0.011
Robust Parametrized R-OKM(α = 0.1,γ = 1.0) 0.676± 0.001 0.256± 0.037 0.370± 0.039 0.445± 0.013
Scene Robust Parametrized-OKM(α = 2.0,γ = 0.2) 0.514± 0.055 0.960± 0.000 0.672± 0.040 0.509± 0.051
Robust Parametrized-OKM(α = 2.0,γ = 0.5) 0.480± 0.050 0.557± 0.048 0.511± 0.009 0.578± 0.025
Robust Parametrized-OKM(α = 2.0,γ = 0.8) 0.488± 0.030 0.652± 0.119 0.548± 0.023 0.632± 0.019
Robust Parametrized-OKM(α = 2.0,γ = 5.0) 0.514± 0.000 0.682± 0.005 0.586± 0.001 0.688± 0.000
Robust Parametrized R-OKM(α = 0.8,γ = 0.2) 0.514± 0.053 0.960± 0.000 0.668± 0.045 0.509± 0.051
Robust Parametrized R-OKM(α = 0.8,γ = 0.5) 0.492± 0.041 0.585± 0.064 0.529± 0.002 0.593± 0.013
Robust Parametrized R-OKM(α = 0.8,γ = 1.0) 0.471± 0.020 0.672± 0.110 0.548± 0.023 0.631± 0.018
Robust Parametrized R-OKM(α = 0.8,γ = 5.0) 0.514± 0.000 0.726± 0.039 0.586± 0.002 0.688± 0.000
Robust Parametrized R-OKM(α = 0.4,γ = 0.2) 0.514± 0.053 0.960± 0.000 0.668± 0.045 0.509± 0.051
Robust Parametrized R-OKM(α = 0.4,γ = 0.8) 0.473± 0.018 0.639± 0.135 0.536± 0.038 0.623± 0.009
Robust Parametrized R-OKM(α = 0.4,γ = 1.0) 0.525± 0.002 0.672± 0.003 0.590± 0.003 0.686± 0.000
Robust Parametrized R-OKM(α = 0.4,γ = 5.0) 0.516± 0.002 0.684± 0.008 0.588± 0.004 0.689± 0.001
Table 3 evaluates the sensitivity of proposed
method to the parameter γ respectively on Emotion,
EachMovie and Scene data sets. Using EachMovie
and Scene data sets, F-measure and Rand Index de-
crease when γ decrease. However F-measure and
Rand Index decrease when γ increase using Emotion
data set.
6 CONCLUSIONS
Overlapping clustering is a necessary requirement for
many applications of clustering where data need to
be assigned to more than one cluster. Existing over-
lapping clustering methods can produce non disjoint
clusters, but its is not well adapted for clustering noisy
data. The performance of these methods are reduced
when data contain noisy observations. The proposed
method, Robust Parametrized R-OKM solves this is-
sue and identifies more relevant clusters which fit the
true structures in data. Experiments performed in arti-
ficial and real data sets showed the robustness of pro-
posed method when data contain noise.
As future work, we plan to confirm preliminary
obtained results on other real overlapping data sets.
Instead, one could add an auto adjusted value of γ to
automatically control the outliers boundaries in real
life applications of overlapping clustering.
REFERENCES
Battle, A., Segal, E., and Koller, D. (2005). Probabilis-
tic discovery of overlapping cellular processes and
their regulation. Journal of computational biology
: a journal of computational molecular cell biology,
12(7):909–927.
Ben N’Cir, C., Cleuziou, G., and Essoussi, N. (2013). Iden-
tification of non-disjoint clusters with small and pa-
rameterizable overlaps. In Computer Applications
Technology (ICCAT), 2013 International Conference
on, pages 1–6.
Bezdek, J. C. (1981). Pattern recognition with fuzzy objec-
tive function algoritms. Plenum Press, 4(2):67–76.
OverlappingClusteringwithOutliersDetection
285

Cleuziou, G. (2008). An extended version of the k-means
method for overlapping clustering. In International
Conference on Pattern Recognition ICPR, pages 1–4,
Florida, USA. IEEE.
Cleuziou, G., Martin, L., Vrain, C., and Vrain, C. (2004).
Poboc: an overlapping clustering algorithm. applica-
tion to rule-based classification and textual data. In
Proceedings of the 16th European Conference on Ar-
tificial Intelligence (ECAI-04), pages 440–444.
Dav`e, R. N. (1991). Characterization and detection of
noise in clustering. Pattern Recognition Letters,
12(11):657–664.
Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).
Maximum likelihood from incomplete data via the em
algorithm. Journal of the royal statistical society, se-
ries B, 39(1):1–38.
Eran, S., Alexis, B., and Daphne, K. (2003). Decompos-
ing gene expression into cellular processes. In Pacific
Symposium on Biocomputing’03, pages 89–100.
Krishnapuram, R. and Keller, J. M. (1993). A possibilistic
approach to clustering. Trans. Fuz Sys., 1(2):98–110.
Pantel, P. and Dekang, L. (2002). Discovering word senses
from text. In Proceedings of ACM SIGKDD Con-
ference on Knowledge Discovery and Data Mining,
pages 613–619.
Sahami, M., Hearst, M. A., and Saund, E. (1996). Apply-
ing the multiple cause mixture model to text catego-
rization. In Saitta, L., editor, Machine Learning, Pro-
ceedings of the Thirteenth International Conference
(ICML ’96), pages 435–443.
Trohidis, K., Tsoumakas, G., Kalliris, G., and Vlahavas,
I. P. (2008). Multi-label classification of music into
emotions. In Bello, J. P., Chew, E., and Turnbull, D.,
editors, ISMIR, pages 325–330.
Wang, X., Tang, L., Gao, H., and Liu, H. (2010). Discov-
ering overlapping groups in social media. In Proceed-
ings of the 2010 IEEE International Conference on
Data Mining, ICDM ’10, pages 569–578, Washing-
ton, DC, USA. IEEE Computer Society.
Yang, J., Yan, R., and Hauptmann, A. G. (2007). Cross-
domain video concept detection using adaptive svms.
In Proceedings of the 15th international conference
on Multimedia, MULTIMEDIA ’07, pages 188–197,
New York, NY, USA.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
286
