
Removing Motion Blur using Natural Image Statistics
Johannes Herwig, Timm Linder and Josef Pauli
Intelligent Systems Group, University of Duisburg-Essen, Bismarckstr. 90, 47057 Duisburg, Germany
Keywords:
Deconvolution, Bayesian Inference, Sparse Gradient Priors, Two-color Model, Parameter Learning.
Abstract:
We tackle deconvolution of motion blur in hand-held consumer photography with a Bayesian framework com-
bining sparse gradient and color priors for regularization. We develop a closed-form optimization utilizing
iterated re-weighted least squares (IRLS) with a Gaussian approximation of the regularization priors. The
model parameters of the priors can be learned from a set of natural images which resemble common image
statistics. We throughly evaluate and discuss the effect of different regularization factors and make sugges-
tions for reasonable values. Both gradient and color priors are current state-of-the-art. In natural images the
magnitude of gradients resembles a kurtotic hyper-Laplacian distribution, and the two-color model exploits
the observation that locally any color is a linear approximation between some primary and secondary col-
ors. Our contribution is integrating both priors into a single optimization framework and providing a more
detailed derivation of their optimization functions. Our re-implementation reveals different model parameters
than previously published, and the effectiveness of the color priors alone are explicitly examined. Finally, we
propose a context-adaptive parameterization of the regularization factors in order to avoid over-smoothing the
deconvolution result within highly textured areas.
1 INTRODUCTION
Removing motion blur due to camera shake is a spe-
cial branch of the ill-posed deconvolution problem.
Its specific challenges are the relatively large blur ker-
nels and image noise which usually is stronger here,
because camera shake is often caused by longer expo-
sure times during low-light photography where sensor
noise is inherently amplified due to higher analog gain
and shot noise. Another characteristic property is that
the blur kernels are not isotropic as with out-of-focus
blur, but instead these point spread functions (PSFs)
model the path of motion that a handheld camera un-
dertakes during the exposure time of the photograph,
and therefore the PSFs have a ridge-like and sparse
appearance (Liu et al., 2008).
We here tackle the problem of non-blind decon-
volution where the motion blur kernel (or PSF) is ex-
actly known a priori. In the real world, the gyroscope
of a mobile phone camera might give a good estimate
of the blur kernel. It is however not straightforward
to synchronize the gyroscope with start and end time
of the exposure. If motion information is not avail-
able at all, then we talk about blind deconvolution
where the blur kernel needs to be estimated solely
with the help of the blurred image at hand (Shi et al.,
2013; Dong et al., 2012a). Since this is rather difficult
there are also some image fusion approaches, known
as semi-blind deconvolution (Yuan et al., 2007; Ito
et al., 2013; Wang et al., 2012). Thereby, multi-
ple differently blurred or otherwise multimodal im-
ages are taken from the same scene with the same or
different sensor which helps further constraining the
blur kernel (Yuan et al., 2007; Ito et al., 2013; Wang
et al., 2012). Our approach assumes a globally con-
stant blur kernel (Schmidt et al., 2013), but in gen-
eral image blur is space-varying (Sorel and Sroubek,
2012; Ji and Wang, 2012; Whyte et al., 2012; Gupta
et al., 2010) because objects at different distances in
the scene are blurred differently. Also, there are nat-
ural design constraints on the camera optics, so that
an image is usually sharper in the center compared to
its border. Additionally, there could be moving ob-
jects in the scene which overlay the movement of a
hand-held camera (Cho et al., 2012). However, usu-
ally only static scenes are considered when there is
only one image available.
1.1 Regularization
Most non-blind deconvolution approaches apply a
regularization term to the gradients of the image, by
125
Herwig J., Linder T. and Pauli J..
Removing Motion Blur using Natural Image Statistics.
DOI: 10.5220/0004830201250136
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 125-136
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

−0.2−0.1 0 0.1 0.2
0
5
10
15
p(d
i
)
d
i
0 0.1 0.2 0.3 0.4 0.5
−5
0
5
ln p(|d
i
|)
|d
i
|
(a) Ground truth images
−0.2−0.1 0 0.1 0.2
0
5
10
15
p(d
i
)
d
i
0 0.1 0.2 0.3 0.4 0.5
−5
0
5
ln p(|d
i
|)
|d
i
|
(b) Blur added – typical camera shake blur
−0.2−0.1 0 0.1 0.2
0
5
10
15
p(d
i
)
d
i
0 0.1 0.2 0.3 0.4 0.5
−5
0
5
ln p(|d
i
|)
|d
i
|
(c) Blur added – linear motion in y direction
−0.2−0.1 0 0.1 0.2
0
5
10
15
p(d
i
)
d
i
0 0.1 0.2 0.3 0.4 0.5
−5
0
5
ln p(|d
i
|)
|d
i
|
(d) Noise added (no blur!) – σ = 5%
Figure 1: Histograms of x-derivatives and x-derivative magnitudes. Colors correspond to Fig. 4.
penalizing steep gradients that could be indicative of
noise. Regularization based upon the `
2
norm (Gaus-
sian prior) and the `
1
norm (Laplacian prior, total
variation (Chan and Shen, 2005)) tend to oversmooth
the deconvolution results. The so-called sparse pri-
ors (Levin and Weiss, 2007; Levin et al., 2007b;
Li et al., 2013) more adequately capture the ob-
served hyper-Laplacian gradient distributions (Srivas-
tava et al., 2003; Huang, 2000). Here, the color
model-based regularization (Joshi et al., 2009) mo-
tivated by (Cecchi et al., 2010) imposes a two-color
model upon locally smooth regions. Thereby, we
concurrently make use of global and local sparseness
(Dong et al., 2012b) alike by using gradient and color
priors, respectively.
1.2 Sparse Gradient Prior
Most ’real’ images resemble a common gradient dis-
tribution (Levin and Weiss, 2007; Levin et al., 2007b;
Simoncelli, 1997). Under for example the `
1
-norm,
the gradient magnitude for a pixel i is calculated by
k(∇I)
i
k
1
=
n
∑
k=1
|d
k,i
|, (1)
where d
k,i
represents the k-th partial derivative,
~
d
k
,
evaluated at pixel i of image I. Such a directional
derivative
~
d
k
:= vec(I ∗ G
k
) can be determined by
convolving the image I with derivative filter kernels
G
k
, like
1 −1
and
1 −1
>
and the second-
order derivatives
∂I
∂x
2
,
∂I
∂y
2
,
∂I
∂xy
.
In Fig. 1, we examine the gradient distributions of
the images from Fig. 4 and compare them with un-
wanted deconvolution results. These histogram plots
show that only the ground truth photographs exhibit
the kurtotic hyper-Laplacian shape, but blurry and
noisy images show totally different statistics. How-
ever, if the blur is linear and orthogonal to the direc-
tion of the derivative, then edges stay mostly intact –
but still the kurtotic tail is lowered (compare Fig. 1(a)
and 1(c)). Similarly to our analysis (Lin et al., 2011)
shows gradient distributions of examplarily patches of
motion blurred vs. sharp textures.
Instead of using gradients as a sparse prior, one
could use any kind of filtering result that provides a
sparse representation of the image. We also tried the
learned filters approach within the Fields-of-Experts
(FoE) framework. Thereby we modified the MAT-
LAB code of (Weiss and Freeman, 2007) so that we
obtained a kurtotic curve model. Then we learned two
different sets of 5 and 25 filters of 15 × 15 pixels. As
opposed to (Schmidt et al., 2011) we did not find an
increase in performance, but our results were compa-
rable to the sparse gradient prior.
1.3 Two-color Model
As in (Joshi et al., 2009), for each pixel ~c
i
of a latent
image estimate I, we define a pixel neighborhood –
e. g. using a square 5 × 5 window – and determine
the primary and secondary colors within this neigh-
borhood. Thereby, an initial two-color model is ob-
tained by k-means clustering (with k = 2). While k-
means provides a good heuristic for finding an ini-
tial two-color model, the drawback is that one color
sample can always only be assigned to exactly one
cluster, and therefore noise is not appropriately han-
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
126
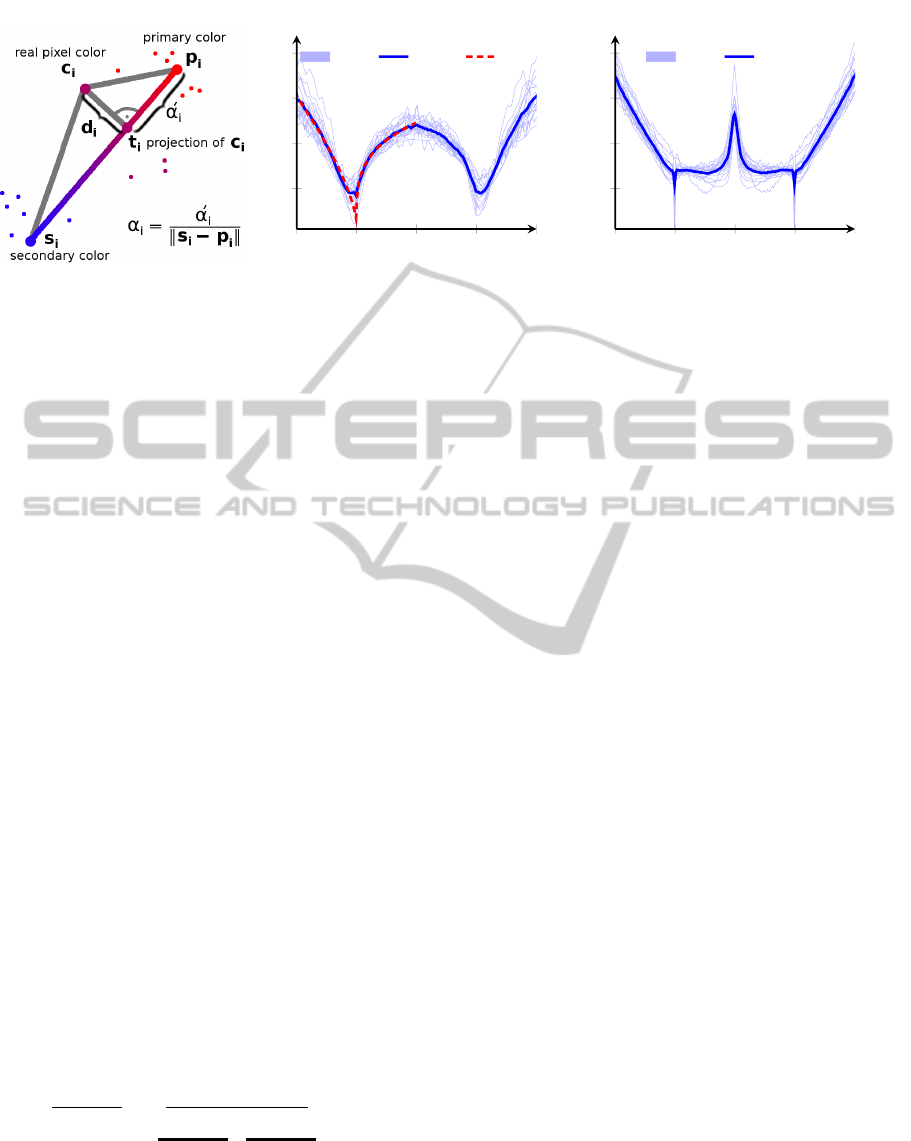
(a) Two-color model by Joshi
−0.5 0 0.5 1 1.5
0
1
2
3
− ln p(α)
α
data mean fit
(b) α distribution after EM clustering
−0.5 0 0.5 1 1.5
0
1
2
3
− ln p(α)
α
data mean
(c) α distribution after k-means
Figure 2: The two-color model, and the accompanying alpha distributions learned from real images.
dled. A fuzzy expectation-maximization (EM) algo-
rithm based upon the method described in (Joshi et al.,
2009) therefore refines the color clusters. Finally, the
primary color ~p
i
is assigned to the cluster whose cen-
ter lies closest to the color of the center pixel ~c
i
defin-
ing the neighborhood. The secondary color
~
s
i
is as-
signed to the other cluster. The two-color model as
depicted in Fig. 2(a) now works upon the assump-
tion that the color ~c
i
can be represented by a linear
interpolation between its associated primary and sec-
ondary colors ~p
i
∈ R
3
and
~
s
i
∈ R
3
, where α
i
∈ R is the
interpolation or mixing parameter (Joshi et al., 2009,
see eq. 7):
~c
i
u
~
t
i
:= α
i
~
s
i
+ (1 − α
i
)~p
i
. (2)
In contrast to (Joshi et al., 2009), ~p
i
and
~
s
i
have been
swapped with regard to α
i
, such that α
i
is minimal at
~p
i
instead of
~
s
i
, because this will simplify our IRLS
optimization later on.
2 THE COLOR PRIOR
The so-called alpha prior introduced by (Joshi et al.,
2009) penalizes α
i
values which would put the esti-
mated color ~c
i
far away from either the primary or
secondary color. The penalty is based upon the ob-
served α
i
distribution in natural images. The value of
α
i
for a pixel ~c
i
, given ~p
i
and
~
s
i
, is calculated using
(Joshi et al., 2009, eq. 10):
α
i
=
α
0
i
k
~
s
i
− ~p
i
k
=
(
~
s
i
− ~p
i
)
(
~
s
i
− ~p
i
)
>
(
~
s
i
− ~p
i
)
| {z }
=:
~
`
i
∈R
3
>
(~c
i
− ~p
i
).
(3)
Typical distributions of α values determined from
natural images using either the refined EM or bare k-
means color clustering are shown in Fig. 2(b) and
2(c). As in Fig. 2(b), these negative log-likelihoods
can be fit with a piecewise hyper-Laplacian prior term
of the form
b|α
i
|
a
= b |
~
`
i
>
~c
i
−
~
`
i
>
~p
i
|
a
. (4)
We calculated the two-color model from about
400 images of the Berkeley image segmentation
database. For a custom set of fit parameters, the
constructed color models were exported into Matlab
and approximate probability densities have been esti-
mated for each image using a Parzen window method.
Then, a non-linear least-squares fit was performed us-
ing Matlab’s fminsearch() method for the piece-
wise hyper-Laplacian function described above. In
(Joshi et al., 2009) a 2 pieces fit is proposed, but we
found that it is not sufficiently accurate for approach-
ing the statistics of the relatively noise-free ground
truth images. The resulting parameters for our 3
pieces fit are:
a = 0.7153, b = 0.8066 for α
i
< −0.5;
a = 0.6448, b = 4.5318 for − 0.5 ≤ α
i
< 0;
a = 0.2298, b = 2.7372 for 0 ≤ α
i
.
2.1 Optimization Techniques
For weighted least squares (WLS) (Faraway, 2002,
p. 62), a weighting matrix W ∈ R
s×s
is introduced.
The WLS objective function therefore is
s
∑
k
s
∑
l
r
k
W
k,l
r
l
= k~y − T~xk
2
W
= (~y − T~x)
>
W (~y − T~x),
(5)
where k · k
W
is the Mahalanobis distance when W =
Σ
−1
. In order to minimize this function, we need to
determine the gradient and set it equal to zero. The
WLS derivative
RemovingMotionBlurusingNaturalImageStatistics
127

∂
∂~x
k~y − T~xk
2
W
= −2T
>
W~y + 2T
>
W T~x (6)
yields the system of the so-called normal equations of
WLS (Gentle, 2007, p. 338)
(T
>
W T )
| {z }
A
~x − T
>
W~y
| {z }
~
δ
=
~
0 (7)
which represents a linear equation system of the form
A~x −
~
δ =
~
0. Here, A = T
>
W T is too large to be in-
verted in-place, and hence we use the CG (Conjugate
Gradient) method.
The M-estimator (Meer, 2004, p. 47) applies a ro-
bust penalty or loss function ρ to the error residuals
r
i
. For ρ(r
i
) := |r
i
|
p
, p 6= 2, the optimization becomes
non-linear. However, the iteratively re-weighted least
squares (IRLS) method (Scales et al., 1988; Scales
and Gersztenkorn, 1988) approximates the solution
by turning the problem into a series of WLS sub-
problems. A faster version of this algorithm for the
problem at hand is discussed in (Krishnan and Fergus,
2009). In each IRLS iteration, a new set of weights is
learned from the previous solution. For the first it-
eration, all weights can be initialized with a constant
value. The weights w
i
of the diagonal WLS weighting
matrix W are ([1]: (Meer, 2004, p. 48); [2]: (Scales
et al., 1988, p. 332)):
w
(τ+1)
i
= w(r
(τ)
i
)
[1]
=
1
r
(τ)
i
dρ(r
(τ)
i
)
dr
(τ)
i
[2]
= p|r
(τ)
i
|
p−2
. (8)
2.2 Minimizing the Alpha Prior
As already shown in Fig. 2(b), the α
i
distribution is
bimodal since both α
i
= 0 and α
i
= 1 are minima and
the distribution is symmetric at α
i
= 0.5. However,
since we want to bias the observed color ~c
i
to the pri-
mary color ~p
i
at α
i
= 0, only the unimodal prior (rep-
resented by the red, dashed line) is used. The weights
of the alpha prior in IRLS step (τ + 1) that follow by
applying eqn. 8 to eqn. 4 are:
w
(τ+1)
i
= a · b · |α
(τ)
i
|
a−2
.
Note that the constant coefficient a is missing in
this term given by (Joshi et al., 2009, eqn. 13).
With these weights, the WLS can be performed
with the RGB components of the latent image I ∈
R
m×n
as the parameter vector ~x :=
~c
1
>
, . . . ,~c
s
>
>
=
(I
R,1
,I
G,1
,I
B,1
, . . . , I
R,s
,I
G,s
,I
B,s
)
>
∈ R
3s
of eqn. 5 with
s = mn the total amount of image pixels. Following
the definition of α
i
(eqn. 3) and splitting α
i
into a vari-
able and a constant part, the WLS coefficient matrix
T is block diagonal:
T :=
−
~
`
1
>
0
.
.
.
0 −
~
`
s
>
∈ R
s×3s
.
The constant part ~y of the WLS objective function is
then a vector
~y :=
−
~
`
1
>
~p
1
, . . . , −
~
`
s
>
~p
s
>
∈ R
s
.
Due to the block-diagonal form of T , the WLS
normal equations can be evaluated for the alpha prior
individually per pixel. Inserting the above definitions
and expanding eqn. 6 leads to the gradient in block
matrix form
∂
∂~x
λ
α
k~y − T~xk
2
W
=
2λ
α
R
1
~c
1
.
.
.
R
s
~c
s
| {z }
A~x
−2λ
α
R
1
~p
1
.
.
.
R
s
~p
s
| {z }
~
δ
∈ R
3s
(9)
with R
i
:= w
(τ)
i
·
~
`
i
~
`
i
>
∈ R
3×3
where the 3 × 3 ma-
trix R
i
is called the re-weighting term by (Joshi et al.,
2009, eqn. 13), and contains the weights w
(τ)
i
learned
from the previous IRLS iteration’s deconvolution re-
sult. The outer product
~
`
i
~
`
i
>
appears because of the
matrix products T
>
· ... · T and T
>
· ... ·~y in the term
2T
>
W T~x − 2T
>
W~y. λ
α
is a regularization factor of
the alpha prior.
2.3 Penalty on the Distance d
Besides the prior on α
i
values, another penalty term
is introduced by (Joshi et al., 2009) that minimizes
the squared distance d
2
i
(Fig. 2(a)). In contrast to the
α
i
prior, this penalty term is not based upon any ob-
served probability distribution in real images. Instead,
the d
i
is simply minimized (Joshi et al., 2009, eqn. 8).
Given ~p
i
and
~
s
i
, then o
d
(~c
i
) := λ
d
· d
2
i
= λ
d
k~c
i
−
~
t
i
(~c
i
)k
2
= λ
d
k~c
i
− [α
i
(~c
i
) · (
~
s
i
− ~p
i
) +~p
i
]k
2
whereby
the regularization factor λ
d
specifies the strength of
this penalty term. In the above objective function,
~c
i
∈ R
3
represents the color of a single pixel i of the
latent image I, and is thus a variable. α
i
and hence
~
t
i
are functions of ~c
i
(see eqn. 3). This is different from
the alpha prior, where the calculated α
i
was fixed dur-
ing the CG optimization because the weights for the
hyper-Laplacian alpha prior only get updated between
IRLS iterations. ~p
i
and
~
s
i
, on the other hand, can be
regarded as constants until a new color model is built.
The d penalty term is optimized by least-squares
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
128

and its gradient is
∂
∂~c
i
o
d
(~c
i
) = λ
d
~c
i
−
~
t
i
(~c
i
)
>
~c
i
−
~
t
i
(~c
i
)
= 2λ
d
id
3
−
∂
∂~c
i
~
t
i
(~c
i
)
>
~c
i
−
~
t
i
(~c
i
)
with id
3
being a 3 × 3 identity matrix. Further differ-
entiation leads to
∂
∂~c
i
α
i
(~c
i
) =
∂
∂~c
i
~
`
i
>
(~c
i
− ~p
i
) =
~
`
i
,
∂
∂~c
i
~
t
i
(~c
i
) =
∂
∂~c
i
α
i
(~c
i
)(
~
s
i
− ~p
i
) =
~
`
i
(
~
s
i
− ~p
i
)
>
,
such that
∂
∂~c
i
o
d
(~c
i
) = 2λ
d
h
id
3
+
~
`
i
(~p
i
−
~
s
i
)
>
i
~c
i
−
~
t
i
(~c
i
)
.
As α
i
(~c
i
) contains both a part that is dependent on
~c
i
and one that is constant (namely
~
l
i
), the gradient
is split up for the CG method. The RGB blocks for
the pixels i = 1, . . . , s of the vectors (A~x)
3i−2,..., 3i
and
(
~
δ)
3i−2,..., 3i
∈ R
3s
are:
2λ
d
h
id
3
+
~
`
i
(~p
i
−
~
s
i
)
>
ih
~c
i
+
~
`
i
>
~c
i
(~p
i
−
~
s
i
)
i
∈ R
3
,
2λ
d
h
id
3
+
~
`
i
(~p
i
−
~
s
i
)
>
ih
~p
i
+
~
`
i
>
~p
i
(~p
i
−
~
s
i
)
i
∈ R
3
.
(10)
3 SPARSE & COLOR PRIORS
For a closed-form expression of the linear system
A~x −
~
δ =
~
0, the gradients of the sparse prior, the data
likelihood, the color prior α (eqn. 9) and the penalty
term on d (eqn. 10) are summed up. Since the data
likelihood and the sparse prior work on intensity im-
ages, the individual color channels ∈ R
s
are extracted
from the RGB vector ~x ∈ R
3s
and the blurry image
~
b ∈ R
3s
, and then combined again after the gradients
of the penalty terms are applied as shown in Fig. 3.
Thereby, the binary operator ext : {R,G,B} ×
R
3s
→ R
s
extracts the color channel specified by
the first argument from an image ~v ∈ R
3s
into a
vector ~u ∈ R
s
. The unary operator join · merges a
set {(R,~u
R
),(G,~u
G
),(B,~u
B
)} of 3 separate channels
back into an RGB image ~v.
The data likelihood term and the sparse prior are
applied to the three color channels ∈ R
s
of the current
estimate ~x ∈ R
3s
and the blurry input image
~
b ∈ R
3s
individually, where s is the total number of image pix-
els. The weights in the matrices W
k
, R
i
, as well as the
primary and secondary colors of the two-color model,
are recalculated after each IRLS iteration. In the first
iteration, λ
α
and λ
d
are set to 0 and hence only the
sparse prior is active then.
3.1 Regularization Parameters
First, we want to find a suitable range of parameter
values with which reasonable deconvolution results
can be achieved. Therefore, the blurred, noisy ver-
sions of the ground truth images from Fig. 4 have
been deconvolved, using their accompanying PSFs as
shown. For the sparse prior a hyper-Laplacian expo-
nent of γ = 0.5 was used together with the default
first- and second-order derivative filters (5 filters in
total). The exponent γ = 0.5 was chosen because of
γ ∈ [0.5, 0.8] for the gradient distribution of most nat-
ural images (Huang, 2000, pp. 19–24). The influence
λ
∇,k
of the second-order derivatives was set to a con-
stant
1
4
, as done by (Levin et al., 2007a).
We used PSNR (peak signal-to-noise ratio)
and MSSIM (multi-scale structural similarity index)
(Wang et al., 2003) for evaluating the goodness of the
deconvolution results. Thereby, MSSIM takes into ac-
count interdependencies of local pixel neighborhoods
which otherwise get averaged out by the more tra-
ditional but established PSNR method. High-quality
digital images have PSNRs between 30db and 50db,
whereas 20db to 30db are still regarded as acceptable.
With PSNR we have a contex-independent measure
for sole signal quality, and MSSIM gives us the sim-
ilarity between a ground truth and estimated texture
without severely punishing correlated errors. There
are metrics available that quantize the degree of image
blur directly, but since these are more or less based
on the same kurtotic model of the distribution of gra-
dients (Yun-Fang, 2010; Liu et al., 2008) where our
optimization model for natural images is built upon,
we did not consider these further. Frequency-based
methods to blur detection (Marichal et al., 1999) can
only quantify the global blur of an image but do not
cope with space-varying blur which is introduced by
our non-linear and context-dependent regularization
approach, and hence were not considered.
The diagrams in Fig. 5 show the mean MSSIM
and PSNR (thick line) for various noise levels, aver-
aged over the entire set of images and as a function of
the regularization parameter λ
∇
. The thin lines repre-
sent the maximum and minimum MSSIM and PSNR
values of all 8 images, and the error bars denote the
sample standard deviations. On average and also sub-
jectively, best results were obtained for λ
∇
between
0.5 and 2.5 depending on the noise level.
The paper by (Joshi et al., 2009) suggests a re-
duced regularization factor, λ
∇
, in the initialization
phase of the sparse prior in order to preserve de-
tails. Then, λ
∇
can be increased, once the penalty
terms based upon the two-color model become ac-
tive. However, their proposed values are inconsis-
RemovingMotionBlurusingNaturalImageStatistics
129

A~x = join
j,
C
>
K
Σ
−1
C
K
| {z }
Data likelihood
+λ
∇
∑
k
λ
∇,k
C
>
G
k
W
k
C
G
k
|
{z }
Sparse prior
· ext( j,~x)
j ∈ {R, G,B}
+ 2λ
α
R
1
~c
1
.
.
.
R
s
~c
s
| {z }
Alpha prior
+2λ
d
h
id
3
+
~
`
1
(~p
1
−
~
s
1
)
>
ih
~c
1
+
~
`
1
>
~c
1
(~p
1
−
~
s
1
)
i
.
.
.
h
id
3
+
~
`
s
(~p
s
−
~
s
s
)
>
ih
~c
s
+
~
`
s
>
~c
s
(~p
s
−
~
s
s
)
i
| {z }
d penalty term
∈ R
3s
~
δ = join
j, C
>
K
Σ
−1
· ext( j,
~
b)
| {z }
Data likelihood
j ∈ {R, G,B}
+ 2λ
α
R
1
~p
1
.
.
.
R
s
~p
s
| {z }
Alpha prior
+2λ
d
h
id
3
+
~
`
1
(~p
1
−
~
s
1
)
>
ih
~p
1
+
~
`
1
>
~p
1
(~p
1
−
~
s
1
)
i
.
.
.
h
id
3
+
~
`
s
(~p
s
−
~
s
s
)
>
ih
~p
s
+
~
`
s
>
~p
s
(~p
s
−
~
s
s
)
i
| {z }
d penalty term
∈ R
3s
Figure 3: Combining the color and sparse priors within the IRLS optimization framework.
tent: λ
∇
= 0.25 followed by λ
∇
= 0.5 is mentioned
at one occasion, λ
∇
= 1 at another. This approach
can be problematic if the initial λ
∇
is chosen too low
(e.g. λ
∇
= 0.8). Details are preserved, but also arti-
facts within near-to homogeneous regions are intro-
duced as can be deduced from Fig. 5. Here, the
thin curves denoting the absolute minima of MSSIM
values are significantly worse than their overall mean
substracted by their standard deviation (whereas this
gap is not observable for the maximum value curves;
this observation is only true up until λ
∇
= 1.0). On
the other hand, a high regularization factor such as
λ
∇
= 3.0 over-smoothes the image. We therefore sug-
gest a nearly constant regularization factor for the gra-
dient prior. E.g., for a noise standard deviation of
σ = 2.5%, λ
∇
might initially be set to 1.5 and then be
increased to 2. Note that λ
∇
= 2 is slightly above the
optimal value discovered for this noise level in Fig. 5;
experience shows, though, that rather smooth images
require a slightly higher λ
∇
.
4 EVALUATION
First, we discuss the effects of the color prior and then
we show some qualitative results.
4.1 Understanding the Color Prior
In order to better understand the practical implications
of the two-color model, we show some segmentation
into primary and secondary colors in Fig. 6. The
original image is decomposed by EM clustering of
a 5 × 5 pixel neighborhood into a layer of primary
colors (Fig. 6(b)) and secondary colors (Fig. 6(c)).
The two-color model applies only at pixels where the
color difference between both layers is large enough.
Fig. 6(a) shows in black where the two-color model
does apply, and in white where the priors derived from
this model cannot be utilized. In these cases, a dif-
ferent kind of prior, e. g. a gradient prior, must be
used. (Joshi et al., 2009) suggest to generally com-
bine both a sparse gradient prior and the two-color
model (where applicable) with a reduced regulariza-
tion factor for the former.
The histograms of the negative log-likelihoods in
Fig. 7 illustrate the effect of the alpha prior penalty
term on the distribution of alpha values. Both ex-
ample images have been initially deconvolved with a
sparse prior (λ
∇
= 2, γ = 0.5) before enabling the two-
color model (λ
α
= 5 for the first image, and λ
α
= 100
for the second which amplifies the effect for illustra-
tion purposes; λ
d
= 0). The red line shows the dis-
tribution after the initial sparse prior deconvolution.
The blue and green lines show the distribution after
1, respective 2, further IRLS iterations with the now
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
130

(a) (b) (c) (d) (e) (f) (g) (h)
Figure 4: Ground truth pictures and their accompanying blur kernels. Image sizes are approx. 800 × 600 pixels and blur
kernels are 27 × 27, 49 × 29, 31 × 31, 39 × 39, 27 × 27, 29 × 29, 51 × 45, 95 × 95, respectively.
(a) Noise standard deviation σ = 1%
(b) Noise standard deviation σ = 2.5%
(c) Noise standard deviation σ = 5%
Figure 5: Average MSSIM and PSNR values for the evaluation image set with its paired blur kernels of Fig. 4 at three different
noise levels σ as a function of the regularization parameter λ
∇
.
RemovingMotionBlurusingNaturalImageStatistics
131

(a) Two-color mask
(b) Primary colors (c) Secondary colors
Figure 6: Exemplary two-color model for the ground truth
image of Fig. 4(c). The two-color mask shows where the
color prior can be applied.
active alpha prior, while retaining sparse prior regu-
larization. The grey line, in comparison, illustrates
how the final distribution would have looked like if
the alpha prior was never activated. Note how the
shown distributions have a shape similar to the ones
from Fig. 2(c), which is because the k-means only
algorithm without EM refinement was used here to
construct the color model. In comparison with the
prior on distances d
i
, the alpha prior is more effective.
Both penalty terms require surprisingly large regular-
ization factors, especially compared to the parameters
mentioned by (Joshi et al., 2009).
In Fig. 10, we show the effects of different
amounts of regularization by λ
α
. The color noise
in the right Fig. 10(c) might indicate too few it-
erations with the sparse prior before the first color
model was built by EM clustering. Hence, this result
with stronger regularization is not necessarily worse:
Some edges, e. g. at the perimeter of the blue parking
meter sign, or the white graffiti at the building wall
in the background, appear more clearly defined with
larger λ
α
. If λ
α
becomes too large, the edges become
jagged and the image more and more resembles the
primary color layer. Strongly structured images with
lots of edges seem to profit more from the prior on
alpha values. Unlike the sparse prior, there is no rec-
ommendation for the choice of λ
α
. Hence, some ex-
perimentation is required for each individual image.
4.2 Qualitative Evaluation
We show exemplarily qualitative results in Fig. 8 and
Fig. 9, whereby the second example is an image of
much less texture than the first image, and also it has
much more noise added. Therefore the quality met-
rics show better values for the second example. An-
other reason for that can be found in the different blur
kernels which are shown in Fig. 4. The second exam-
ple is convolved with a PSF that has a weaker ridge
along its motion path with only two achnor points,
whereas the first example has a PSF with a stronger
ridge that is equally thick along its whole motion path.
Therefore, the first PSF mixes more pixels and it is
more ill-posed to deconvolve. On the other hand, the
second PSF mixes two locally aggregated clusters of
pixels (due to its two main anchor points) which are
seperated relatively far from each other. It can be seen
in both cases that the Gaussian prior performs bet-
ter than Richardson-Lucy, although it does not even
conform with the real kurtotic model of the gradi-
ent distribution. The Gaussian prior was only justi-
fied because it is inexpensive to compute. But still its
smoothing capabilities successfully reduce noise and
hence outperform Richardson-Lucy. As expected, the
Laplacian prior performs a little better but at the cost
of much higher computation time. The sparse prior is
in most cases an enhancement over the Laplacian, and
as shown, even sub-optimal parameters tend to give
good results. The color prior again adds more com-
putational costs, but only minor improvements can
be visually recognized, like some sharper edges and
slightly reduced color noise, in the results of Fig. 8.
The quantitative metrics are even a little worse when
the color prior is enabled. The border effects in the de-
convolution results are common artifacts which (Zhou
et al., 2014) claims to reduce.
5 CONTEXT-ADAPTIVE PRIOR
Our experiments with the sparse priors suggest that
these tend to oversmooth the result image if the cho-
sen regularization factor λ
∇
is too large, and on the
other hand produce a noisy result image if λ
∇
is too
small. We therefore suggest a variable regularization
that can adapt to local image structure. This would
allow the user to have more control over the trade-
off between regularization blur and noise, by choos-
ing a stronger regularization in locally smooth image
regions where blur does not cause so much trouble,
and a weaker regularization in highly structured areas
(at the cost of introducing noise at these locations).
We experimentally study manual adaptation with user
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
132

Initial 1 iteration 2 iterations Sparse only result
−0.5
0
0.5
1
1.5
0
2
−ln p(α)
α
(a) Fig. 4(g), λ
α
= 5
−0.5
0
0.5
1
1.5
0
2
−ln p(α)
α
(b) Fig. 4(d), λ
α
= 100
−1
−0.5
0
0.5
1
0
5
10
−ln p(d)
d
(c) Fig. 4(g), λ
d
= 5
−1
−0.5
0
0.5
1
0
5
10
−ln p(d)
d
(d) Fig. 4(d), λ
d
= 100
Figure 7: Effects of the alpha and distance penalty terms on images of Fig. 4(g) and Fig. 4(d).
(a) Ground truth image (b) Synthetically blurred image (c) Richardson-Lucy
MSSIM 0.455, PSNR 18.37 dB
(d) Gaussian prior: γ = 2, λ
∇
= 8
MSSIM 0.560, PSNR 20.43 dB
(e) Laplacian prior: γ = 1, λ
∇
= 2
MSSIM 0.605, PSNR 20.88 dB
(f) Sparse prior: γ = 0.5, λ
∇
= 1
MSSIM 0.618, PSNR 20.87 dB
(g) Sparse prior: γ = 0.5, λ
∇
= 2
MSSIM 0.585, PSNR 20.49 dB
(h) Color prior
γ = 0.5, λ
∇
= 2, λ
α
= 5, λ
d
= 5
MSSIM 0.602, PSNR 20.79 dB
(i) Cropped details, 4× enlarged
Figure 8: Deconvolution of the image of Fig. 4(c) with ground truth kernel and noise level σ = 5%.
RemovingMotionBlurusingNaturalImageStatistics
133

(a) Ground truth image (b) Synthetically blurred image (c) Richardson-Lucy
MSSIM 0.548, PSNR 18.62 dB
(d) Gaussian prior: γ = 2, λ
∇
= 9
MSSIM 0.599, PSNR 21.27 dB
(e) Laplacian prior: γ = 1, λ
∇
= 3
MSSIM 0.674, PSNR 23.48 dB
(f) Sparse prior: γ = 0.5, λ
∇
= 1.5
MSSIM 0.688, PSNR 23.72 dB
(g) Sparse prior: γ = 0.8, λ
∇
= 2.0
MSSIM 0.683, PSNR 23.70 dB
(h) Color prior
γ = 0.5, λ
∇
= 2, λ
α
= 1, λ
d
= 1
MSSIM 0.666, PSNR 22.59 dB
(i) Cropped details, 4× enlarged
Figure 9: Deconvolution of the image of Fig. 4(h) with ground truth kernel and noise level σ = 1%.
(a) λ
α
= 0.1 MSSIM 0.682, PSNR 22.15 dB (b) λ
α
= 2 MSSIM 0.685, PSNR 22.19 dB (c) λ
α
= 100 MSSIM 0.674, PSNR 21.86 dB
Figure 10: Deconvolution of the image of Fig. 4(c) with fixed σ = 2.5%, λ
∇
= 2, λ
d
= 0 but varying λ
α
.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
134

(a) Sketch (b) Edge map
(c) Constant (d) Adaptive
(e) Ground truth (f) Blurry, σ = 2.5%
Figure 11: Locally varying vs. constant regularization of
the sparse prior, besides ground truth and blurry images.
intervention. The idea is to provide the user with ei-
ther the blurry image or, if the blur is too strong to be
able to recognize regions of salient structure, a rough
estimate of the deblurred image from the first IRLS
iteration. The user can then paint over the edges and
other structured areas of the image to indicate weaker
regularization, as illustrated in Fig. 11(a). The lines
painted by the user can then be blurred slightly using
a Gaussian filter to make the change in regularization
less abrupt. The resulting image is then inverted and a
threshold is introduced so that the sketched areas also
experience a certain minimum amount of regulariza-
tion (e. g. at least 25% regularization in comparison to
areas where the user has indicated no important struc-
ture). This leads to an edge map like the one shown
in Fig. 11(b). The intensities resulting from this edge
map are then added as additional weights (multipliers)
λ
∇,k,i
to the penalty terms ρ
∇
(d
k,i
). The results shown
in Fig. 11 are encouraging. Recently, (Cui et al.,
2014) proposed a similar regularization approach as
an extension to Richardson-Lucy which is reported to
successfully reduce ringing artifacts.
6 CONCLUSIONS
On the basis of the work by (Levin et al., 2007b)
and their hyper-Laplacian penalty term, an extensi-
ble software framework for deconvolution using the
IRLS method has been developed. Because regular
photographs contain more than just intensity infor-
mation, a further regularization approach based upon
the two-color model proposed by (Joshi et al., 2009)
has been re-implemented and integrated into our op-
timization framework. In the evaluation part, we pro-
posed suitable regularization parameters for the pre-
sented penalty terms. Although enabling the addi-
tional color prior results in slightly sharper edges for
some images (e.g. Fig. 8), its huge computational
cost may not justify its general usage. Just using
the sparse gradient prior even with the faulty Gaus-
sian optimization model significantly performs better
than Richardson-Lucy. With the additional computa-
tional cost when optimizing with a hyper-Laplacian
exponent that better models the kurtotic shape of
the sparse gradient distribution in an image, the de-
convolution results take another significant leap for-
ward. Finally, our experimental work showed that fur-
ther context-adaptive regularization of gradient priors
seems promising in avoiding over-smoothing. The
presented deconvolution approach is robust in terms
of image noise but performs poorly in case the blur
kernel is not perfectly estimated (Zhong et al., 2013).
REFERENCES
Cecchi, G. A., Rao, A. R., Xiao, Y., and Kaplan, E. (2010).
Statistics of natural scenes and cortical color process-
ing. Journal of Vision, 10(11):1–13.
Chan, T. and Shen, J. (2005). Image Processing And Anal-
ysis: Variational, Pde, Wavelet, And Stochastic Meth-
ods. Siam.
Cho, S., Wang, J., and Lee, S. (2012). Video deblurring for
hand-held cameras using patch-based synthesis. ACM
Trans. on Graphics, 31(4):64:1–64:9.
Cui, G., Feng, H., Xu, Z., Li, Q., and Chen, Y. (2014). A
modified Richardson–Lucy algorithm for a single im-
age with adaptive reference maps. Optics & Laser
Technology, 58:100–109.
Dong, W., Feng, H., Xu, Z., and Li, Q. (2012a). Blind image
deconvolution using the fields of experts prior. Optics
Communications, 285:5051–5061.
Dong, W., Shi, G., Li, X., Zhang, L., and Wu, X. (2012b).
Image reconstruction with locally adaptive sparsity
and nonlocal robust regularization. Image Communi-
cation, 27:1109–1122.
Faraway, J. J. (2002). Practical regression and
ANOVA using R. Online. http://cran.r-project.org/
doc/contrib/Faraway-PRA.pdf.
RemovingMotionBlurusingNaturalImageStatistics
135

Gentle, J. (2007). Matrix algebra: theory, computations,
and applications in statistics. Springer texts in statis-
tics. Springer, New York, NY.
Gupta, A., Joshi, N., Zitnick, L., Cohen, M., and Curless, B.
(2010). Single image deblurring using motion density
functions. In ECCV ’10: Proc. of the 10th Europ.
Conf. on Comp. Vision.
Huang, J. (2000). Statistics of natural images and models.
PhD thesis, Brown Univ., Providence.
Ito, A., Sankaranarayanan, A. C., Veeraraghavan, A., and
Baraniuk, R. G. (2013). Blurburst: Removing blur due
to camera shake using multiple images. ACM Trans.
Graph. Submitted.
Ji, H. and Wang, K. (2012). A two-stage approach to blind
spatially-varying motion deblurring. In IEEE Conf.
on Comp. Vision and Pattern Recogn. (CVPR), pages
73–80. IEEE Comp. Soc.
Joshi, N., Zitnick, C., Szeliski, R., and Kriegman, D.
(2009). Image deblurring and denoising using color
priors. In IEEE Conf. on Comp. Vision and Pattern
Recognition (CVPR), pages 1550–1557. IEEE Comp.
Soc.
Krishnan, D. and Fergus, R. (2009). Fast image deconvo-
lution using hyper-laplacian priors. In Neural Inform.
Proc. Sys.
Levin, A., Fergus, R., Durand, F., and Freeman, W. T.
(2007a). Deconvolution using natural image priors.
Technical report, MIT.
Levin, A., Fergus, R., Durand, F., and Freeman, W. T.
(2007b). Image and depth from a conventional camera
with a coded aperture. ACM Trans. Graph., 26.
Levin, A. and Weiss, Y. (2007). User assisted separation
of reflections from a single image using a sparsity
prior. IEEE Trans. Pattern Anal. and Mach. Intell.,
29(9):1647–1654.
Li, X., Pan, J., Lin, Y., and Su, Z. (2013). Fast blind deblur-
ring via normalized sparsity prior. Journal of Inform.
& Comp. Sc., 10(16):5083–5091.
Lin, H. T., Tai, Y.-W., and Brown, M. S. (2011). Motion reg-
ularization for matting motion blurred objects. IEEE
Trans. Pattern Anal. and Mach. Intell., 33(11):2329–
2336.
Liu, R., Li, Z., and Jia, J. (2008). Image partial blur de-
tection and classification. In IEEE Conf. on Comp.
Vision and Pattern Recognition (CVPR), pages 1–8.
IEEE Comp. Soc.
Marichal, X., Ma, W.-Y., and Zhang, H.-J. (1999). Blur
determination in the compressed domain using DCT
information. In Intern. Conf. on Image Proc. (ICIP),
pages 386–390.
Meer, P. (2004). Robust techniques for computer vision.
In Medioni, G. and Kang, S. B., editors, Emerging
Topics in Computer Vision, chapter 4. Prentice Hall
PTR, Upper Saddle River, NJ.
Scales, J. A. and Gersztenkorn, A. (1988). Robust methods
in inverse theory. Inverse Problems, 4(4):1071.
Scales, J. A., Gersztenkorn, A., and Treitel, S. (1988). Fast
l
p
solution of large, sparse, linear systems: Applica-
tion to seismic travel time tomography. Journal of
Computational Physics, 75:314–333.
Schmidt, U., Rother, C., Nowozin, S., Jancsary, J., and
Roth, S. (2013). Discriminative non-blind deblurring.
In IEEE Conf. on Comp. Vision and Pattern Recogni-
tion (CVPR), pages 604–611. IEEE Comp. Soc.
Schmidt, U., Schelten, K., and Roth, S. (2011). Bayesian
deblurring with integrated noise estimation. In
IEEE Conf. on Comp. Vision and Pattern Recognition
(CVPR), pages 2625–2632. IEEE Comp. Soc.
Shi, M.-z., Xu, T.-f., Feng, L., Liang, J., and Zhang, K.
(2013). Single image deblurring using novel image
prior constraints. Optik - International Journal for
Light and Electron Optics, 124(20):4429–4434.
Simoncelli, E. (1997). Statistical models for images: Com-
pression, restoration and synthesis. In In 31st Asilo-
mar Conf on Signals, Systems and Computers, pages
673–678. IEEE Comp. Soc.
Sorel, M. and Sroubek, F. (2012). Restoration in the pres-
ence of unknown spatially varying blur. In Gunturk,
B. and Li, X., editors, Image Restoration: Fundamen-
tals and Advances, pages 63–88. CRC Press.
Srivastava, A., Lee, A. B., Simoncelli, E. P., and c. Zhu, S.
(2003). On advances in statistical modeling of natural
images. Journal of Math. Imaging and Vision, 18:17–
33.
Wang, S., Hou, T., Border, J., Qin, H., and Miller, R.
(2012). High-quality image deblurring with panchro-
matic pixels. ACM Trans. Graph., 31(5).
Wang, Z., Simoncelli, E. P., and Bovik, A. C. (2003). Multi-
scale structural similarity for image quality assess-
ment. In Proc. of the 37th IEEE Asilomar Conf. on
Signals, Systems and Computers.
Weiss, Y. and Freeman, W. (2007). What makes a good
model of natural images? In IEEE Conf. on Comp.
Vision and Pattern Recognition (CVPR), pages 1–8.
IEEE Comp. Soc.
Whyte, O., Sivic, J., Zisserman, A., and Ponce, J. (2012).
Non-uniform deblurring for shaken images. Intern.
Journal of Comp. Vision, 98(2):168–186.
Yuan, L., Sun, J., Quan, L., and Shum, H.-Y. (2007).
Blurred/non-blurred image alignment using sparse-
ness prior. In Proc. of the 11th Intern. Conf. on Comp.
Vision (ICCV), pages 1–8.
Yun-Fang, Z. (2010). Blur detection for surveillance video
based on heavy-tailed distribution. In Asia Pacific
Conf. on Postgrad. Research in Microelectronics and
Electronics, pages 101–105.
Zhong, L., Cho, S., Metaxas, D., Paris, S., and Wang, J.
(2013). Handling noise in single image deblurring us-
ing directional filters. In IEEE Conf. on Comp. Vision
and Pattern Recogn. (CVPR), pages 612–619. IEEE
Comp. Soc.
Zhou, X., Zhou, F., Bai, X., and Xue, B. (2014). A bound-
ary condition based deconvolution framework for im-
age deblurring. Journal of Computational and Applied
Mathematics, 261:14–19.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
136
