Integrated Supply Chain Network Design for Packaged Gases

Tejinder Pal Singh

, Nicoleta Neagu

, Michele Quattrone

and Philippe Briet

Air Liquide, 12800 W. Little York Rd., Houston, 77041, U.S.A.

Air Liquide, 1 chemin de la Porte des Loges, Les Loges-en-Josas, F-78350, France

Air Liquide, 75 Quai d'Orsay, Paris, F-75321, France

Keywords: Network Design, Optimization, Location-Routing, Packaged Gases, Inventory Management, Decomposition

Approach, Heuristics, Mixed Integer Linear Programming Model.

Abstract: Network design of the supply chain is an important and strategic aspect of logistics management. In this

paper, we address the network design problem specific to packaged gases (e.g., cylinder) supply chain. We

propose an integrated framework that allows for the determination of the optimal facility locations, the

filling plant production capacities, the inventory at plants and hubs, and the number of packages to be routed

in primary and secondary transportation. We formulate the problem as a mixed integer program and then

develop a decomposition approach to solve it. We illustrate the proposed framework with numerical

examples from real-life packaged gases supply chain. The results show that the decomposition approach is

effective in solving a broad range of problem sizes. We also benchmark the results from the decomposition

approach by solving the complete packaged gases network design model for smaller test cases.

1 INTRODUCTION

Supply chain networks are essential within the world

wide economic activities. They are fundamental to

stay competitive in today’s markets through efficient

delivery of products (e.g., energy, food,

pharmaceutics, and clothing). The optimal supply

chain network design is the basis for its efficiency.

Moreover, the network design is a complex topic as

it needs to take into account and integrate many

aspects of real life problems.

In this paper we consider the packaged gases

supply chain with its specific characteristics.

Network configuration in packaged gases (also

referred as cylinder distribution) is a strategic

decision that impacts the tactical delivery planning

and daily scheduling and transportation operations.

A typical cylinder supply chain network consists of

filling plants, hubs/distribution centres, and

customers. Filling plants supply cylinders to hubs

which distribute them to customers. It is also

possible for filling plants to directly supply the

customers. Filling plants and hubs manage cylinder

stocks in order to enable the supply chain to

maintain an adequate service level. The agility of the

supply chain and the operational efficiency are

constrained by the structure of the network

determining the flow of material.

Optimizing the network design problem for

cylinder distribution consists of determining the

locations for filling plants/hubs, the production tools

to be installed at the plants, the primary and the

secondary flows, as well as the inventory at plants

and customer locations. The framework based on a

mixed-integer linear programming (MILP) model is

developed to capture a real-life packaged gases

business model. The mathematical model contains

constraints on network structure, primary

transportation, i.e., flow of cylinders among

different supplier locations, secondary

transportation, i.e., flow of cylinders from supplier

locations to customers, stock management and assets

management. The proposed framework has been

developed by leveraging the best practices and

knowledge of logistics experts within packaged

gases supply chain. Therefore, the framework can be

used to determine a new cylinder supply

chain/logistics network for a new market or to study

the impact of change in different elements of the

supply chain, e.g., when new customer accounts are

opened or old accounts are closed, change in

customer demand, impact of new filling centres/hubs

and assets like filling tools and manpower. We show

the efficiency of the proposed framework for real-

371

Singh T., Neagu N., Quattrone M. and Briet P..

Integrated Supply Chain Network Design for Packaged Gases.

DOI: 10.5220/0004830703710381

In Proceedings of the 3rd International Conference on Operations Research and Enterprise Systems (ICORES-2014), pages 371-381

ISBN: 978-989-758-017-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

life test cases provided by the packaged gases supply

chain managers.

The paper is organized as follows. Section 2

outline the state of the art related to integrated

supply chain decision models. In Section 3, we

provide the problem description and in Section 4 we

represent the mathematical model with the objective

function and the business constraints. In Section 5,

we discuss the solution approaches used to solve the

integrated model. Section 6 presents the obtained

results and Section 7 concludes the paper with

possible future research directions.

2 LITERATURE REVIEW

The network design problem in packaged gases

consists of three main sub-problems:

 Facility location: It involves the improvement of

the existing network and the determination of the

best configuration.

 Inventory management: It consists of

determining the best inventory levels at

hubs/plants.

 Routing: Optimization of flows determining the

optimal flows of goods through the network.

The network design problems are complex as they

involve strategic decisions which influence tactical

and operational decisions (Crainic and Laporte,

1997). The strategic decisions are mainly related to

facility locations, their capacities and what products

need to be produced at each plant, etc. The tactical

decisions are related to inventory management and

manpower, and depend on the strategic decisions

whereas operational decisions like routing are

directly related to tactical and strategic decisions

made earlier. In other words, it means that if facility

location decisions are sub-optimal, even if

production, inventory and distribution plans are fully

optimized, the supply chain may still be operating

inefficiently. Therefore, for determining the best

network configuration, all the costs at the three

levels need to be taken into account to optimize the

system-wide production, inventory and distribution

costs. One of the challenges in the network

configuration is that customer demands and cost

parameters may change over time and it is very hard

to change the facility location decisions once a

supply chain network is configured. Thus, it is

critical to design a supply chain network that is

optimal and is not sensitive to changes in the

operational parameters. The integrated network

design problem has been usually solved by

considering the integration of two sub-problems

while approximating the third one. We provide

following few approaches in the literature for

solving the integrated network design problem.

The facility location problem integrated with

routing is proved to be NP-complete by Krarup and

Pruzan (1983). The objective function and the

constraints of the models they propose are linear.

The reader is referred to the reviews provided by

Klose and Drexl (2005) and ReVelle and Eislet

(2005). The facility location problem and its variants

have been widely researched on theoretical models

but the problem is rarely approached from a supply

chain management and real-life perspective (Melo et

al., 2009).

Most of the papers in the literature study the

integration of two of the above three important

decisions: location-routing models (LR), inventory-

routing models, and location-inventory (LI) models.

For reviews on location-routing models, readers can

refer to Balakrishnan et al. (1987) and Min et al.

(1998). In LR models, both the location problem and

the vehicle routing problem (VRP) are typically NP-

hard, which makes the integrated model even more

complex. In this paper, the VRP problem is solved

by approximating the routes based on either a

heuristic approach or historical data. The resulting

routing costs are then fed as an input to the location

model. For inventory-routing models, please refer to

Kleywegt et al. (2002) and Adelman (2003). LI

models also study the location, inventory and

distribution coordination issues by either ignoring

the inventory costs or approximating the non-linear

costs with linear functions. In this paper, inventory

costs are considered but assumed to be linear similar

to some papers that consider inventory costs. Refer

to the papers Daskin (1999), Shen (2000), and

Erlebacher (2000) for a better understanding of LI

models.

The case that motivated this research deals with

the network design for packaged gases distribution.

The problem addressed in the current paper

combines some elements of LR and LI models to

determine an optimal network design by minimizing

the sum of the production costs, the transportation

costs and the inventory costs. Our mathematical

model can be classified as a deterministic single-

period MILP model with multiple products applied

to a three-level network. The main contribution of

our work is that it integrates supply chain network

design decisions without fixing the fillings plant

locations with inventory and resource allocation

decisions required at the plants. We also consider the

transportation costs for the entire supply chain

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

372

including the transhipment costs among different

facilities by deciding the replenishment frequency.

3 PROBLEM DESCRIPTION

We address the network design problem specific to

packaged gases supply chain occurring in real-life.

The problem consists of determining the number and

the location of the production plants and the

distribution centres, the allocation of customer

demands to distribution centres, and the allocation of

distribution centres to production plants. The main

goal is to identify the optimal configuration for

producing and delivering packaged gas products to

customers at the lowest cost while satisfying the

network constraints.

More specifically, this network design problem

aims in helping the decision making on locations for

building plants, the production tools to be installed

at the filling plants, the primary and the secondary

flows, as well as the inventory at plants and hubs. A

diagram of the packaged gases distribution network

is shown in the Figure 1. The nodes of the network

are classified in four categories: filling plants, hubs,

agent distributors, and end users (or reseller). Each

location has a certain inventory capacity to satisfy

customer demand. Customers manage their own

inventories by placing orders at the right time.

Therefore, in the current problem we consider the

inventory decisions only at filling plants and hub

locations.

Figure 1: Diagram of the Distribution Network.

The arrows in Figure 1 represent the transport of

packaged gases which is classified as:

 Primary transport which occurs between filling

plants and hub locations.

 Secondary transport which represents the

transport between hub/filling plants and

client/agent/reseller locations.

 Tertiary transport which happens between

agent/reseller and client locations.

This paper will not handle the whole distribution

network but rather will focus on the primary and

secondary transport. Agents/distributors, resellers

and end users will all be called customers without

distinction in the rest of the paper. Since tertiary

flows happen between customers of different types,

they are not considered in this problem. The word

“plant” by itself is referring to both hubs and filling

plants. In this paper we also assume that the vendor

who supplies cylinders to the customers owns the

whole packaged gases supply chain network.

Therefore, we do not consider any ordering costs

between different plants. We do consider the

transportation cost of transhipments among different

plants which is a function of replenishment periods

for the primary flows.

The main goals of the proposed methodology are

related to the location decisions of plants,

production, and to the hubs/filling plants transport

and inventory. The primary goals of the network

design problem for packaged gases are as follows,

see also Figure 2:

 Determine the number and the locations of the

hubs and the filling plants.

 Determine the production of different products at

the filling plants.

 Determine the primary and the secondary

transportation cylinder flows, i.e. the customer-

plant allocation decisions.

 Determine the inventory levels at plants

consisting of working stock & the safety stocks

at the plants.

These four issues are fundamental in the structure of

a supply chain. Nevertheless, these issues are

interrelated by the cylinders flows and it is clear that

it would be a source of improvement to treat them

all at the same time. A general description of all the

key aspects of the problem as well as the hypotheses

assumed at this stage is presented in the following

sub-sections.

3.1 Multi-products Network

We assume that different products may be

considered while designing the distribution network.

This means that different products are filled at a

plant, and transported to others plants and

customers. Therefore, each product has to be

IntegratedSupplyChainNetworkDesignforPackagedGases

373

Figure 2: Network design problem.

characterized depending on its package, its

composition and the filling tools that are compatible

with it.

3.2 Plant Locations and Filling Tools

The network design problem considers as input a set

of potential locations already identified. A hub or a

filling plant may be built on a location if selected by

the optimizer. The total amount of cylinders

distributed to the customers are filled on the filling

plants and delivered from the hubs (or the plants).

The maximum numbers of plants in the network is a

function of the number of the potential locations

provided in the input.

A product is defined as a cylinder of a given size

filled with different gases in various percentages.

The products are filled with gases using filling tools.

Several different tools may be used at a filling plant;

each of them allows filling a given set of products

and has its own production capacity and cost.

3.3 Cylinder Flows

Two categories of cylinder flows are considered in

this problem: primary and secondary. These two

categories find their differences on two levels:

 Primary flows are an internal choice of

optimization of the distribution without direct

income. They usually go from one vendor site to

another and require handling during the round

trip: a tractor pulls a trailer of full products from

site A to site B, leaves the trailer on site B and

takes back a trailer of empty products from site B

to site A.

 Secondary flows are a direct source of income

for the vendor as customers have to pay for the

delivered cylinders. A secondary round trip is

usually composed with several drops on different

customers’ sites where full products have to be

unloaded before empty products are loaded on

the trailer.

The transport cost is usually composed of a fixed

cost and a variable cost. The fixed cost consists of

truck costs, driver costs, and extra fees and the

variable cost is dependent on the distance and the

duration of the round trips. However, we model the

cost of a round trip with an average variable cost per

driver distance taking every cost into consideration.

The handling cost of the cylinders on plants is

taken into consideration independently. In this

paper, we are approximating the routing costs to

serve each customer and therefore, do not consider

the routing decisions in the model.

3.4 Primary Transport Cost

The primary transport cost is quite straightforward to

estimate. As primary trips are defined as full trailer

load deliveries in the model, the cost of primary

round trips between two identified plants can be

known before solving the network design.

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

374

3.5 Secondary Transport Cost

Contrary to the primary transport, secondary

transport cost is difficult to estimate precisely. In the

network design model, we do not consider day-to-

day demand data which implies that it is impossible

to build actual secondary round trips. In the model,

each customer has a global demand over a year and

it is not possible to know which customers will order

on the same day. Also, secondary unit transport

costs are provided as an input to the problem and

therefore, the actual costs can not be calculated until

the plant-customer allocation decisions are made.

Therefore, we determine the cost to deliver a unit

cylinder to a customer from each potential location

by modelling the average round trips during which

the customer will be delivered. The round trip does

not consist of a single delivery but multiple

deliveries and this makes the secondary transport

cost approximation realistic. For a given customer,

an average round trip starting from a given plant is

modelled by:

 The driven route split in one dispersion ring

which represents the zone where the delivered

customers are located and an approach distance

to go from the plant to the dispersion ring.

 The average number of customers visited during

such a round trip.

 The average number of cylinders delivered

during such a round trip.

The radius of the dispersion ring (see Figure 3) is set

for every customer to a value determined

experimentally from real round trips or from round

trips generated from a heuristic approach used

during the pre-processing of data. The heuristic

approach used is not discussed in this paper. The

dispersion ring has its centre on the customer under

consideration. The approach distance is the shortest

distance from the plant to the dispersion ring.

Another value found experimentally determines the

percentage of customers included in the same

dispersion ring which can be delivered in the same

round trip. This coefficient aims at correcting the

fact that one dispersion ring could withhold several

round trips. The secondary round trips have to

respect the following constraints:

 The average number of cylinders delivered

during the round trip can not exceed the capacity

of the trailer used.

 The duration of the round trip can not overcome

the maximum driver work time. The round trip

duration is mainly a function of the number of

customers visited during the trip.

Figure 3: Secondary round trip model.

3.6 Trucks

Only two standard trucks are considered in the

problem. One truck type is dedicated to primary

transport and the other one to the secondary

transport. Each type of truck is characterized by its

capacity, speed and cost per distance travelled. We

assume no limit on the number of trucks of each

type that are available for distribution in the model.

3.7 Inventory Management

It is important for the cost evaluation of a plant to

determine the investment cost necessary for the

stocks on its site. The required stock at a plant is

composed of:

 Replenishment stock which includes the products

filled on the plant everyday and the products

delivered from other plants at each primary round

trip.

 Delivery stock which represents all the products

which are being delivered to customers and other

plants every day. When calculating the size of this

stock, we assume that the same number of products

is delivered every day for this plant.

The stocks take into consideration the variation of

demands over a year through a variance of the

cylinder flows. The variance of the flows is

supposed to be directly proportional to the average

volume delivered per day.

4 MATHEMATICAL MODEL

To solve the integrated network design problem we

propose a mixed integer programming model. In this

section we present the main parameters, decision

variables and the corresponding mathematical

model. We consider the design of a three-tiered

supply chain consisting of filling plants, hubs, and

customers as described in Section 3. Each customer

IntegratedSupplyChainNetworkDesignforPackagedGases

375

has deterministic demand. The proposed model

provides the needed decisions on how many filling

plants and hubs to locate, where to locate them

among the list of potential locations, how often to

replenish the products at the hubs from the filling

plants, what level of working and safety stocks to

maintain at the plants, so as to minimize the total

system costs consisting of total location,

transportation and inventory costs. In other words,

the objective is to find the optimal trade-off between

transportation costs and all the other costs, mainly

the location costs. Inventory costs are a function of

the replenishment periods and the demand allocation

to the plants.

To simplify the mathematical model, we define

two units of measure. We define Equivalent

Cylinder (EqCyl) as the unit of area occupied by a

50-litre water capacity compressed gas cylinder for

transportation on a truck. As the model deals with

more than one product, and a truck is allowed to

transport many products together, to quantify the

capacity of the trucks and also to define the demands

of different customers, EqCyl would be used. We

also introduce a measure of time called Work Unit

(WU). A WU is a unit of time to a physical activity

for which time is the main factor to represent work

e.g. filling and handling of cylinders. All parameters

and variables that denote time are expressed in terms

of WU.

Inputs & Parameters

I: Set of customers

J: Set of potential locations

P: Set of products

T: Set of filling tools

R: Set of replenishment periods between plants

: Fixed cost (yearly) of locating a filling plant at

location j, for each j  J

: Fixed cost (yearly) of locating a hub at

location j, for each j  J

: Fixed inventory holding cost per EqCyl per

year at location j, for each j  J



: Fixed cost of a full time employee per year



: Primary handling productivity at any plant

(WU/year/employee)



: Secondary handling productivity at any plant

(WU/year/employee)



: Work time (in WU) needed to handle one

package of product p at a plant for primary

transport, for each p  P



: Work time (in WU) needed to handle one

package of product p at a plant for secondary

transport, for each p  P

: Work time (in WU) necessary to fill one

package of product p using tool t, for each p  P

and t  T

: Area (in EqCyl) occupied by one package of

product p, for each p  P

: Filling productivity (WU/employee/year) of a

filling tool t, for each t  T

: Fixed cost of using a tool t per year, for each

tool t  T

: Maximum time (in WU) available to fill

packages with tool t per year, for each tool t  T

: Binary parameter, 1 if a filling tool t can fill a

package of product p, for each p  P and t  T, 0

otherwise



: Average number of packages consumed

(yearly) at customer i for product p, for each i 

I and p  P



: Variance of demand (yearly) for product p,

for each p  P



: Constant representing number of working

days per year (e.g. 250)



: Truck capacity for primary transportation

: Average cost per distance travelled during

primary transport for a replenishment period r,

for each r  R



: Average cost per EqCyl from location j to

serve customer i, for each j  J and i  I

M: Maximum number of tools at any filling plant

Decision Variables

: Binary variable, 1 if a filling plant is build on

location j, for each j  J, 0 otherwise

: Binary variable, 1 if a hub is build on location

j, for each j  J, 0 otherwise

: Total number of employees working on

location j, for each j  J

jpt

: Number of packages of product p filled per

year at location j by tool t, for each j  J, p  P,

and t  T, a discrete variable



: Number of filling tools of type t required at

the location j, for each j  J, and t  T, a discrete

variable

jkr

: Binary variable, 1 if primary trips are used

between locations j & k after replenish period r

such that j  k, for each j  J, k  J and r  R, 0

otherwise

jkpr

: Number of EqCyl of product p delivered

from location j to location k during primary trips

undergone every replenish period r such that j 

k, for each j  J, k  J, p  P, and r  R



: Binary variable, 1 if customer i can be

delivered products from location j , for each j 

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

376

J, i  I, 0 otherwise



jip

: Number of EqCyl of product p delivered

from location j to customer i during secondary

trips, for each j  J, i  I, p  P



: Stock at location j of packages of product p,

for each j  J, p  P

The objective function is composed of five main

parts as shown below:

 Fixed costs of hubs and filling plants.

 Fixed costs of filling tools.

 Manpower cost dedicated to filling and handling

packages.

 Total inventory cost.

 Transport cost, excluding the handling cost at the

filling plants and hubs.

Location costs are strategic costs that are incurred

when configuring the network. The first two terms in

the objective function ensure that fixed costs for

either a hub or a filling plant are applied to each

selected location. Filling tool costs, manpower costs,

and inventory costs are the costs associated with the

tactical decisions whereas transport costs are the

operational costs. The mathematical formulation of

the objective function is given below in equation (1).

Minimize

∑







































∑



























∑























∑















∑

















(1)

The business constraints which are related to the

network structure and flow, primary and secondary

transport, and inventory management are given

below, (2) – (11):









,∀



∈



(2)







∑



























∑∑







































∑













,∀



∈















(3)

∑



























jkr

∀



∈



,∈



,∈



(4)

∑









 0, ∀



∈



(5)

∑









 1, ∀



∈



,∈



(6)

∑















∑













, ∀



∈



,∈

(7)

∑















, ∀



∈



(8)

∑





















∑









∀∈,∈

(9)

∑





















, ∀



∈



,∈

(10)







∑







1





























∑











max 1,















∑



















∑









,

∀



∈



,

∈

(11)

5 SOLUTION APPROACH

The mathematical formulation of network design is a

MILP problem. As the traditional facility location

problem is NP-complete (Krarup and Pruzan, 1983),

we simplify the model by approximating the routing

costs. Moreover, in this paper we are dealing with a

real-life large-scale problem occurring in packaged

gases supply chain. Therefore, we analysed various

solving techniques: from near-optimal methods up to

approximate ones. The near-optimal approach can be

used for small problem instances whereas

approximate methods can be applied in the context

of large-scale problems. Moreover, we can compare

the near-optimal solutions to the approximate ones

to benchmark the approximate solutions. In this

paper, we provide details about the approximate

approaches in order to achieve a reasonable

computation time.

5.1 Mono-product Approximation

As the number of products occurring in the

packaged gases network design problem implies

high complexity, the first approximate approach

considered consists of grouping the multi-products

into a single product which we call a mono-product

problem. To that aim, each product is treated

relatively to its volume of equivalent cylinder

(EqCyl) and its type is ignored. Converting multiple

product constraints into single product constraints

may cause solution infeasibility; the constraints are

modified carefully to minimize the likelihood of

such infeasibility. As the modified model becomes a

single-product model, variables are no longer

depending on the number of products available. For

IntegratedSupplyChainNetworkDesignforPackagedGases

377

example, consider the variable x

jpt

representing the

number of packages of product p filled per year at

location j by tool t, for each j  J, p  P, and t  T.

In the mono-product approximation, x

jpt

is changed

to x

defining the number of EqCyl of the single

product filled per year by tool t at location j.

Similarly, constraints (3), (4), (7), (9), (10), and (11)

are modified along with the objective function to

represent a single product network design problem.

The resulting problem is also a MILP problem

but we do not show the modified model in this

paper. The network design problem becomes a

unique flow problem and thus, it is easier to solve.

We compare the results of this approach with the

results obtained by solving the complete model in

Section 6. It is shown that this approach gives good

solutions especially for placing the hubs’ locations

and satisfactory results for secondary transport

decisions. As this approach does not treat different

types of products, the number of filling tools

installed at the filling plants is underestimated

compared to the optimal solutions. This approach

can be used when the problem size is very large and

the main interest is to find the network configuration

i.e. location of hubs and allocation of customers to

hubs whereas resource/inventory optimization can

be done separately. Figure 4 shows the physical

representation of the mono-product approach.

Figure 4: Scheme of Mono-product Approximation.

5.2 Two-steps Decomposition

In order to reduce the computation time, a typical

approach for large-scale problems is based on

problem decomposition. We consider a two-step

decomposition approach to generate an approximate

solution. In the first step of the decomposition

approach, the hubs’ locations and the hub-customer

allocation decisions are determined by solving the

mono-product flow problem with minimization of

the secondary transportation costs and the hub costs.

Secondary transportation cost is more a function

of number of cylinders transported between hubs

and customers and independent of different

products. Therefore it is a safe approximation to

determine hubs through optimization of mono-

product flow problem. In the second-step, the

residual problem is solved based on the multi-

product model. The second step optimization

determines if the hub built on a given location is a

filling plant or not and decides the tools associated

with this given filling plant by minimizing the

production and the primary transportation costs

(tools, sourcing, manpower). Moreover, it optimizes

the inventory management by defining the frequency

of trips between plants and the flow quantities for

the primary transportation. Figure 5 shows the two-

step decomposition decisions graphically.

Figure 5: Two-step decomposition decisions.

The size of the residual problem in the second

step can be further reduced by grouping the products

into families of products. The product families are

created by selecting the products among the most

requested customer’s products. Thus, the whole set

of products is aggregated into families of products.

A family essentially is a set of products that can be

produced by the same tools. This further reduces the

problem size and helps to obtain good results in a

reasonable time compared to the complete problem.

The grouping does not change the model as it is

done in the input data. The second-step model is also

an MILP problem and is still hard to be solved to

optimality for large-scale network problems. One of

the reasons of the complexity to solve the second-

step model optimally is that a significant number of

binary variables still remain to be optimized for

primary transportation.

The MILP mathematical models in our testing

are solved on a 2.66 GHz, 16 GB RAM server using

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

378

CPLEX

. By tuning the CPLEX parameters, the

performance of the CPLEX has been improved on

the test cases used. The upper limit on the number of

cutting plane passes CPLEX performs when solving

the root node of a MILP model is set to 1. The

number of rows in the problem with cuts added is set

to 30 times the original number of rows. Relaxation

Induced Neighbourhood Search (RINS) heuristic

explores the neighbourhood of the current

incumbent solution to try to find a new, improved

incumbent after every 70 nodes are visited. It is also

important to manage the memory problems that

occur on a server when solving a large-scale

problem. Therefore, the number of stored solutions

kept in the solution pool on the server is set to 10. If

the node file parameter in CPLEX is set to 0, when

the tree memory limit is reached, optimization is

terminated. By setting the node file parameter to 3,

the node files are transferred to disk in compressed

form and CPLEX actively manages which nodes

remain in memory for processing. An optimality gap

has been used for test cases as it is hard to solve the

test cases for full optimization. The optimality gap

represents the maximum ratio between the optimal

solution of the MILP program and its Linear

Programming (LP) relaxation. In other words,

optimality gap represents how far the current

solution is from its lower bound.

6 NUMERICAL RESULTS

In this section our objective is to assess the

performance of the solution approaches considered

in this paper. The proposed solution approaches

have been applied to 3 real-life test cases

(summarized in Table 1) characterizing the network

design problems occurring within the packaged

gases distribution networks in different geographical

zones. The problem size of a test case is determined

mainly by the number of customers, potential

locations, types of tools available, and the number of

products to be distributed. The given test cases are

very different in terms of problem structure and size.

This provides a good opportunity to test the

approaches for different problem settings and

evaluate their scalability.

Table 1: Real-life network design test cases.

Test

Case

Customers

Potential

Locations

Tools Products

1 520 4 3 5

2 1,964 14 6 4

3 12,036 26 3 43

Each test case in Table 1 has been solved by

different approaches providing near-optimal and

approximate solutions. It has been observed for the

small test cases (e.g. containing up to 2000

customers), a near-optimal solution can be reached

in a reasonable computation time (e.g. 60 min for

test case 2). For test cases 1 and 2, the facility

location decisions i.e. the number and the set of

locations to be opened as filling plants/hubs from the

mono-product and the two-steps approaches are

exactly the same as from the near-optimal solution.

This shows that both the approximate approaches are

successful in determining optimal strategic

decisions. In the test results, mono-product approach

underestimates the total network cost which is

expected due to the simplification of the model.

Therefore, we do not consider mono-approach for

tactical and operational decisions as it solves an

approximate model. For test case 1, two-steps

approach provides the same network cost as from

the near-optimal method with the same optimality

gap.

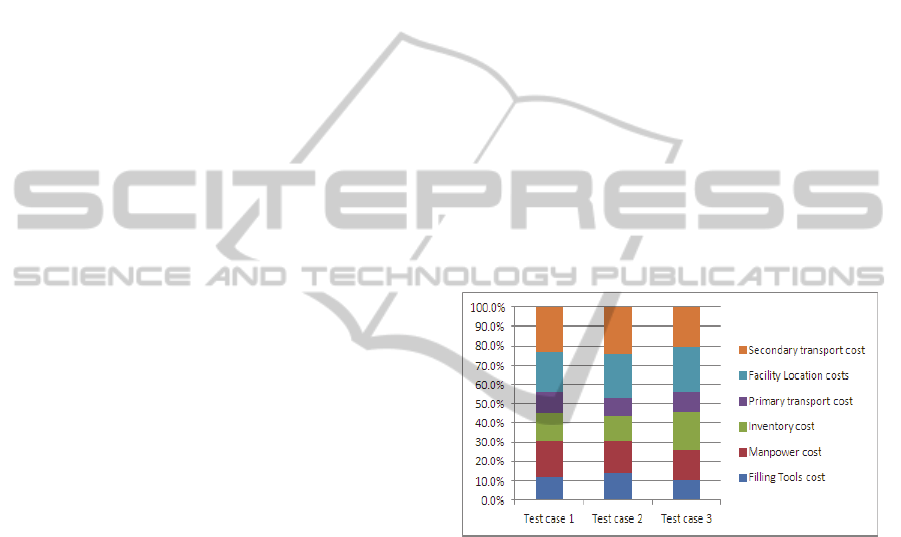
Figure 6: Network Design Costs for 3 test cases.

For test case 2, the two-steps approach provides

a solution with 1.19% higher network cost than the

near-optimal solution. For test case 3, the near-

optimal solution was not generated as we could not

solve the complete problem within an acceptable

optimality gap. For real-life network design, we

believe that the computation time in a few hours is

acceptable due to the fact that the opportunities to

setup a new supply chain network or completing

overhauling an existing one are not very frequent.

The computation time for test cases 1 and 2 with the

two-steps is relatively small but test case 3 takes

more than 15 hours to obtain a solution within the

optimality gap of 0.43%. It is also possible to

achieve a solution in few hours by increasing the

optimality gap to 5% as shown in the Table 2. For

test case 3, the benchmarking of two-steps

decomposition solution is done by comparing the

IntegratedSupplyChainNetworkDesignforPackagedGases

379

Table 2: Performance Test Results.

Test Case Gap (%) Solution Approach

Solver

Time (min)

Total cost

(Є)

# Filling Plants # Hubs

0.5

Mono-product 2 561,891 2 3

Two-steps 6 782,070 2 3

Near-optimal 4 782,070 2 3

0.5

Mono-product 11 2,147,515 6 11

Two-steps 593 2,276,267 6 12

Near-optimal 63 2,303,703 6 12

0.5 Mono-product 121 19,289,480 11 18

5.0 Two-steps 332 24,125,572 11 18

0.43 Two-steps 948 23,160,386 11 18

facility location decisions with a manual solution

based on the network designer’s experience. The gap

analysis with the manual solution shows that the

two-steps solution for test case 3 provides a solution

with total network cost which is 6.4% less than the

manual solution.

Figure 6 shows the different cost components as

percentages of the total network design cost for test

case 3 with optimality gap of 0.43%. Figure 6 shows

that the facility location costs and the secondary

transportation costs are the highest cost components

of the total network cost and therefore, have more

influence on the network design decisions. Since the

network design model studied in this paper is

deterministic, we also perform sensitivity analysis to

check the impact of different parameters on the

facility location and other network decisions. The

parameters which are more likely to change over

time are demand, unit transportation cost, and

manpower cost.

Figure 7: Demand sensitivity analysis.

Figure 7 shows the location decisions of

scenarios obtained by changing the demand at each

customer equally for test case 2 which is solved with

near-optimal approach. The results show that the

facility location decisions i.e. the number and the set

of opened facilities do not change even with more

than 5% increase or decrease in demand at each

customer location. The main reason for such

stability is that we increased the product demand

equally for all the customers to perform sensitivity

analysis. In reality, the demand of different

customers does not homogenously increase or

decrease over time. Also, the impact of demand

change on inventory and transportation costs (both

primary and secondary) is more compared to the

other costs. When facility location decisions don’t

change with modified demand, the change in

inventory and transportation costs is nearly linear

with demand change. Table 3 provides similar

sensitivity analysis results for unit transportation

cost and manpower cost for test case 2. Manpower is

mainly a function of demand and therefore, does not

influence facility location decisions significantly as

evident from the results. For test case 2, manpower

costs have to increase or decrease at least 20% to

make a change in the facility location decisions.

Since the primary and the secondary transportation

costs represent a significant portion of network

design costs, the facility location decisions are

sensitive to the unit transportation cost. An increase

in the unit transportation cost causes more hubs to

open along with filling plants which is expected to

minimize the secondary transportation costs.

Table 3: Cost sensitivity analysis.

Unit Transportation Cost Manpower Cost

% Change Filling plants Hubs Filling plants Hubs

-20.0% 4 10 7 13

-15.0% 4 11 6 12

-10.0% 5 11 6 12

-5.0% 6 12 6 12

0.0% 6 12 6 12

5.0% 6 13 6 12

10.0% 7 14 6 12

15.0% 7 14 6 12

20.0% 7 14 5 11

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

380

7 CONCLUSIONS

In practice supply chain network configuration

typically involves optimizing strategic decisions

without considering their impact on all the tactical

delivery planning and daily scheduling decisions. In

this paper we optimize not only strategic decisions

but also consider all tactical and operational

decisions in the mathematical model for the network

configuration. We specifically consider the

integrated network design problem dedicated to the

packaged gases distribution. The main goals for

solving the integrated network design problem

include determining the locations of the hubs and the

filling plants, the production capacity of the filling

plants, the primary and the secondary cylinders

flows and the inventory of both the filling plants and

the hubs. To solve it, we propose a mathematical

model which combines both the location-routing and

the location-inventory integrated models and

approximates the routing cost used in both the

integrated models. In order to solve real large-scale

problems, we propose approximate decomposition

based approach. We applied near-optimal and

approximate approaches on 3 real-life test cases

from packaged gases cylinder distribution. The

obtained solutions are within an acceptable

optimality gap from the optimal solutions. The

results indicate that mono-approach and two-steps

approaches are capable to generate good facility

location solutions in a reasonable time and are

comparable to near-optimal solutions on smaller test

cases. The difference between mono-product and

two-steps is that two-steps method provides a better

estimate of tactical and operational costs. For large-

scale test cases, it is hard to obtain near-optimal

solutions whereas two-steps approximation can

generate good solutions in an acceptable time.

Therefore, near-optimal approach is suitable for

smaller test cases and approximation approaches for

large-scale test cases.

In the future, further studies on improvements

relative to the computation time to solve the

complete model without using decomposition

approach can be envisioned. Also, further research

can be done to benchmark the approximate

approaches considered in this paper for large-scale

test cases. Even though we performed sensitivity

analysis for few input parameters, future work can

be focussed on developing and solving a robust

model for packaged gases network design.

REFERENCES

Adelman, D., 2003. A price-directed approach to

stochastic inventory/routing, Working Paper,

University of Chicago.

Balakrishnan, A., Ward, J. E., Wong, R. T., 1987.

Integrated facility location and vehicle routing models:

recent work and future prospects, American Journal of

Math. and Management Sciences, 7, 35-61.

Crainic, T. G., Laporte, G., 1997. Planning models for

freight transportation. European Journal of

Operations Research, 97, 409-438.

Daskin, M. S. and Owen, S. H., 1999. Location models in

transportation, in Handbook of Transportation Science

(Eds R. Hall), 311-360.

Erlebacher, S.J., Meller, R. D., 2000. The interaction of

location and inventory in designing distribution

systems. IIE Transactions, 32, 155-166.

Kleywegt, A., Nori, V. S., Savelsbergh, M. W. P., 2002.

The stochastic inventory routing problem with direct

deliveries. Transportation Science, 36, 94-118.

Klose, A., Drexl, A., 2005. Facility location models for

distribution system design. European Journal of

Operational Research, 162, 4–29.

Krarup, j., Pruzan, P. M., 1983. The simple plant location

problem-survey and synthesis. European Journal of

Operational Research, 2, 36-81.

Melo, M., Nickel, S., Saldanha-da-Gama, F., 2009.

Facility location and supply chain management – a

review. European Journal of Operations Research,

196 (2), 401–412.

ReVelle, C., Eiselt, H., 2005. Location analysis: a

Synthesis and survey. European Journal of

Operational Research, 165, 1–19.

Shen, Z. M., 2000. Approximation Algorithms for Various

Supply Chain Problems, PhD Thesis. Dept. of Ind.

Eng. and Mgmt. Sciences, Northwestern University.

IntegratedSupplyChainNetworkDesignforPackagedGases

381