
Building Surgical Team with High Affinities
A Bicriteria Mixed-integer Programming Approach
Christine Di Martinelly
1
and Nadine Meskens
2
1
IESEG School of Management, (LEM-CNRS and HEMO), 3 rue de la Digue, 59000 Lille, France
2
Catholic University of Louvain (UCL), Louvain School of Management, Campus Mons,
Chaussée de Binche, 151, 7000 Mons, Belgium
Keywords: Health Care Management, Operating Theatre, OR in Health, Multiobjective Mixed Integer Program.
Abstract: Assuming a task-based approach to model the demand for the nurses in the operating rooms, the paper
proposes a bicriteria mixed-integer approach to build surgical teams with high affinities while minimizing
the nurses’ waiting time. The suggested model builds nurse rosters considering their availabilities, legal
constraints and affinities with the operating surgeons. The model is solved using an -constraint approach
and is tested on instances of a Belgian hospital. From the experiments, it appeared that the 2 objectives
considered are conflicting. Relaxing the criterion of the affinities has an impact on the waiting time.
In the document, the terms used to designate persons
are taken in a generic sense and refer to males and
females without distinction.
1 INTRODUCTION
The operating rooms are one of the cornerstones of
hospital activity. It represents one of the highest
budget expenses. Managing the operating rooms is a
complex task that deals with human and material
management: on one side, there is the planning and
scheduling of the surgical interventions while
minimizing the operating costs of the operating
rooms and managing the specific materials; on the
other side, there is the planning and rostering of
human resources considering legal and personal
constraints and preferences of the various staff
members (surgeons, anaesthesiologists, nurses)
while satisfying the patients. Also, the managed
resources are in limited supply.
The objective of this research paper is to help the
operating room manager to put together surgical
teams to improve the planning and scheduling.
Traditional approaches developed to plan and
schedule the surgical interventions are made of 2
steps. The time horizon considered is usually one
week. First, the surgical interventions are planned
taking into account the availabilities of rooms and
surgeons. A surgical intervention is assigned to a
day and a room. Then, the surgical interventions are
scheduled daily under the constraints on the
availabilities of personnel and materials.
Numerous papers studied the complexity of
planning and scheduling the operating rooms
(Cardoen et al., 2010). The various problems studied
differentiate on basis of the constraints, decision
variables, objectives and solution methods. The
composition of the surgical team has been of little
interest so far in operations management.
Yet, an increasing number of studies (Mazzocco
et al., 2009); (Weaver et al., 2010); (Kurmann et al.,
2012) demonstrated that cooperation, coordination
and communication between the members of a
surgical team have a positive impact on the patient
surgical outcome. To the best of our knowledge,
only Meskens et al., (2012) took into account the
affinities of the surgical team while scheduling the
surgeries. While considering the affinities of the
personnel, no author considered the nurses’ working
conditions (maximum number of work per week,
days-off, breaks,…).
Those elements are usually considered in the
literature of ‘nurse rostering’ or ‘nurse scheduling’.
Burke et al., (2004) and, more recently, Van den
Bergh et al., (2013) provided detailed reviews on the
subject. It is worth noting that none of the papers
mentioned considered the specific case of the
operating rooms.
Indeed, in most of the hospital departments, the
417
Di Martinelly C. and Meskens N..
Building Surgical Team with High Affinities - A Bicriteria Mixed-integer Programming Approach.
DOI: 10.5220/0004831804170424
In Proceedings of the 3rd International Conference on Operations Research and Enterprise Systems (ICORES-2014), pages 417-424
ISBN: 978-989-758-017-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

demand for nurses is modeled based on shift. The
number of staff required is determined to meet a
service measure such as for instance a ratio
nurse/patient (Ernst et al., 2004). In the operating
rooms, on the contrary, the demand for staff is based
on a list of tasks. Each task is a surgical intervention
characterized by a starting time and duration, to be
scheduled and performed.
The objectives considered when building the
nursing roster are usually the minimization of the
salary costs and the maximization of the nurses’
preferences. The nurses’ preferences are measured in
terms of requests to work at specific time periods
(shifts, day-offs, etc.) (Jaumard et al., 1998); (Bard
and Purnomo, 2005). However, the models were not
taking into account preferences in terms of co-
workers or affinities between the surgical team
members.
The objective of this paper is to form surgical
teams (surgeon, nurses) with a high affinity degree
while taking into account the availaibilities of nurses
and the legal constraints on working conditions
(days-off, breaks,…). We also want to minimize the
waiting time of nurses in the operating rooms so that
we minimize idle time and limit overtime payments.
We face a multiobjective problem with two
criteria : to minimize the waiting time of nurses and
to maximize the affinities of the surgical teams.
A lexicographic optimization was considered to
solve this problem in Di Martinelly and Meskens
(2013). It means that an order of importance was set
between the objectives: the first objective is
optimized; then the second one is optimized under
the constraint that the first one stays optimal. There
are 2 main limitations to this approach: the decision
maker has to determine which objective is the most
important to him and none of the solutions generated
is a compromise between the objectives; the solution
is optimal regarding one of the objectives. For
instance, the operating room manager (the decision
maker) will have to settle for a nurse schedule that is
either optimum for the waiting time or optimum for
the affinities of the surgical teams; he won’t be
provided with a compromise schedule that would
probably best suit him.
The approach considered in this paper is
different. There is no order of importance between
the objectives and both objectives are optimized. We
build the set of Pareto optimal solutions (or part of
it). The main advantage of this method is the
possibility to provide the operating room manager
with the set of compromise solutions (meaning the
non-dominated solutions in the Pareto sense). The
manager can thus choose among them the solution
he prefers and estimates the trade-offs between the
possible solutions.
The originality of the research is the integration
of personnel affinities in the rostering while keeping
the personnel costs under control. The problem is
modeled as a multiobjective mixed-integer program.
It is solved using an ε-constraint approach. The
approach is then tested on real data of a Belgian
hospital. The rest of the paper is organized as
follows: in section 2, we present the context of the
paper. In section 3, we propose a mixed-integer
program to build the surgical teams and nurse
rosters. The model is then tested on real data and the
results are discussed in section 4. We finish with
conclusion and future work.
2 THE GENERAL FRAMEWORK
The objective of the framework is to provide the
decision maker with a tool to obtain a surgical
schedule that both satisfy human and managerial
constraints. It uses a holistic view of the problem.
The first part consisted in a model developed by
Di Martinelly et al., (2011). It considered the
planning and scheduling of surgical interventions
over 5 days. Each surgical intervention is done by a
surgeon, which has availabilities over the week. It
requires a number of resources (rooms,
anesthesiologists, nurses) to be available. At every
time period, the suggested planning must satisfy the
constraints on the number of nurses available. The
results of this model indicate the starting time of
each surgical intervention in a specific room, on a
specific day.
The detailed surgical schedule over the week is
the workload pattern used to build the nurse rosters
and the surgical teams while taking into account the
working rules.
The remainder of this paper focuses on the
second part of the framework: a multiobjective
mixed-integer program that establishes surgical
teams maximizing the affinities between the nurses
and the surgeons while making the schedule efficient
for nurses. We then suggest a solving multiobjective
approach based on the -constraint method.
3 METHODOLOGY
3.1 Problem Description
Each surgical intervention requires a number of
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
418

nurses (
), which are present during the entire
surgical time (
). A surgical intervention is done by
one specific surgeon. Each operating surgeon has a
degree of preferences to work with each nurse.
The affinity between surgeons and nurses is
expressed through an affinity matrix. Based on the
preferences expressed by a surgeon to work with a
nurse, a score that varies between 0 and 9 is
assigned; a score of 0 represents a total
incompatibility while a 9 is a strong preference.
A pretreatment is realized: based on the affinity
matrix and knowing that a surgery is assigned to one
surgeon, we can deduce the degree of affinity
between the surgery k and the nurse i (
).
The availability of nurse i is defined in a matrix
for each day and time period
. If
1, it
means that a nurse can be assigned to a surgical
intervention; 0 otherwise. The nurses’ availabilities
are checked for the whole surgical intervention time.
Nurses can start working at different time periods
(
), with
min
∀,∀. Each nurse i can
work up to a certain number of periods per day d
(
) and per week (
). The values are based on the
working contract and work regulations. This
modeling technique enables us to take into account
nurses’ requirement (half-day working, 35 hours or
40 hours, etc.).
We determine which nurse i is assigned to the
surgical intervention k (
). A nurse is assumed to
attend the whole assigned surgery k.
As aforementioned, the surgical planning is a
data of our problem and is done for a 5-day period.
It is obtained by solving the model proposed by Di
Martinelly et al. (2011) as mentioned in point 2. The
surgical planning is done assuming a number of
nurses available and paid and it may require a
certain amount of overtime work.
The objective of the present model is, based on
this demand for nurses, to obtain the best allocation
of nurses to the surgeries.
The quality of the nurse roster is evaluated either
by the total waiting time of nurses or by the
affinities of the surgical team (
∑
∗
).
3.2 Mathematical Model
Sets
set of operating days , 1,..,
set of time periods per day , 1,..,
set of surgical interventions over the period ,
1,..,
set of nurses , 1,..,
Parameters
:degree of affinity between the surgeon
(related to surgery ) and the nurse
:availability of nurse in period on day
{0,1}
:time period at which nurse starts working
on day
:number of nurses required to perform
surgical intervention
:starting time of surgical intervention in
period on day {0,1}
:duration of surgical intervention in time
periods
:available working time in time periods for
nurse on day
:available working time in time periods for
nurse over the horizon
Variables
:abinary variable that represents the
assignment of nurse to surgical intervention
:thetime period at which nurse finishes her
surgical interventions for day
:the waiting time in periods of nurse over
day
Model
∗
∗
(1)
∗
(2)
s.t.
∀,∀,∀
(3)
∀
(4)
∗
∀
(5)
∗
∗
∀,∀
(6)
∗
∗
∀,∀,∀
(7)
BuildingSurgicalTeamwithHighAffinities-ABicriteriaMixed-integerProgrammingApproach
419

,
0,∀,∀
(8)
∈
0,1
, ∀,∀
(9)
Objective (1) is intended to give the nurses a
schedule that minimizes the total waiting times.
Objective (2) maximizes the affinities between the
surgeons leading the intervention and the nurses.
Equations (3) ensure that a nurse will be assigned
to a surgical intervention only if he is available; it
also ensures that a nurse can only attend a surgical
intervention at a time. Equations (4) ensure that
there is the required number of nurses to perform the
surgery. Equations (5) ensure that a nurse doesn’t
work more than the authorized time over the week.
Equally, equations (6) ensure that the daily working
time of a nurse is respected.
Equations (7) determine when the last surgical
intervention of a nurse finishes each day (Makespan
of a nurse i activity on day d). Equations (8) define
the variables as positive. Finally, equations (9)
define the assignment of a nurse to a surgery as a
binary variable.
3.3 ε-Constraint based Approach
The multiobjective mixed-integer linear program
described in point 3.2 provides each week the nurse
rosters. Our objective is not to provide the decision-
maker with all the non-dominated solutions but with
a set of them. In a formal way x
*
is a non-dominated
solution if and only if, in the case of a maximization
of all objective functions, there is not any x X
(where X is the feasible set of variables that satisfies
the constraints) such that f
i
(x
*
) f
j
(x) for all i, and
f
j
(x
*
) < f
j
(x) for at least one j (Hwang et al., 1979).
The most widely used technique to solve a
multiobjective linear problem is the weighting
method. However, this technique has some
disadvantages, which make it difficult to apply in
our problem: the scaling of the objective function,
the choice of the weights, and the number of runs
needed to generate several alternative solutions
(Mavrotas, 2009).
As a result, we used the second more popular
approach, the ε-constraint method (Haimes et al.,
1971, Chankong and Haimes, 1983). This method
has in addition the advantage of being independent
of the decision space (Ehrgott and Ruzika, 2008).
In case of 2 objective functions, the ideal and
nadir points can easily be determined (Ehrgott,
2005). Those points are used to build the payoff
table without weakly efficient points.
Algorithm to find the ideal and nadir points.
1. Solve the single objective problems
and
. Denote the
optimal objective values by w
and a
2. Solve
with the additional
constraint
3. Solve
with the additional
constraint
4. Denote the optimal objective values
obtained in steps 2 and 3 by
and
, respectively
5. The nadir point is
,
and the
ideal point is
,
)
The payoff table, based on the nadir and ideal points,
is expressed in table 1. The ideal point
,
)
corresponds in our case to a non-existent point.
Table 1: Payoff table.
Any value outside the ranges determined by the
nadir and ideal points will be discarded. The ranges
are then explored starting from the values obtained
from the ideal point until we reach the nadir point.
We run in parallel two ε-constraint methods and
we start building the Pareto set at the extreme points.
The first ε-constraint method maximizes the
affinities with the additional constraint (the ε-
constraint) on the waiting time (
). The first value
obtained is one of the extreme points, (
,
|
).
The second ε-constraint method minimizes the
total waiting time with the additional constraint on
the affinities (
). The other extreme point obtained
is (
|
,
). The ε-constraints are relaxed at each
iteration. We iterate as long as the values obtained
are better than the nadir point.
Algorithm for the ε-constraint method.
1. Set
to
and the number of
iterations
to 1
2. Set
to
and the number of
iterations
to 1
3. Set the Pareto optimal set to ∅
4. While (
|
) and (
|
)do
Solve
with the additional
constraint
; the solution is
|
Set
∗1.05
and
1
Solve
with the additional
constraint
; the solution is
|
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
420

Set
∗0.95
and
1
Add the points (
,
|
)and
(
|
,
)to
End.
4 RESULTS AND DISCUSSION
4.1 Test Instances
We tested our model on a data set obtained from a
Belgian hospital. The surgical interventions take
place between 8 AM and 6 PM at the latest. Each
hour is divided in quarter (for a total of 40 quarters a
day). There are 8 instances in the set (8 weeks).
Each week, the number of surgeries varies between
49 and 90, the number of operating surgeons
between 22 and 38 and there are 7 operating rooms.
The model described by Di Martinelly et al.,
(2011) was run on those data to get the detailed
planning and scheduling of the surgical interventions
(day and time of the surgical interventions). It was
run with the restriction that there were 12 nurses
available at every time period of every day. A pool
of 14 nurses is available; some of them are working
the entire day, others are working only in the
mornings or only in the afternoons.
The affinity matrix is built by asking each
surgeon to assess his affinity with each nurse using a
scale between 0 and 9 (9 being the highest affinity)
and is built for the entire period.
4.2 Results and Discussion
The model was developed and solved using FICO
Xpress-Optimizer. It was tested on a computer with
2.2 GHz CPU and 8 GB of RAM.
Table 2 displays the payoff table for each
instance.
From this table, we can note that both objectives
are conflicting: minimizing the waiting time
generates surgical teams with affinities lower by
14% on average; while maximizing the affinities
creates teams that have to wait up-to 50 times more!
The points (47; 821) and (338; 1091) correspond
to the maximization of the affinities under the
constraint on the waiting time and the minimization
of the waiting time under the constraint on the
affinities, respectively.
Each of those points represents the weekly roster
for all nurses obtained by using as input the planning
and scheduling of surgical interventions of week 5,
taking into account the nurses’ availabilities (day-
offs), maximum working time per day and per week
(full time/part time) and the operating surgeons’
affinities with the nurses.
Table 2: Payoff table of the test instances.
week w
I
w
N
a
I
a
N
1 0 263 653 592
2 40 257 1152 1021
3 4 208 1093 1007
4 50 295 794 600
5 47 338 1091 821
6 71 378 899 840
7 75 376 776 707
8 64 357 976 745
Figures 1 and 2 display illustrations of the rosters
obtained for a particular day of week 5, either
minimizing the waiting time with a constraint on the
affinities (Figure 1) or maximizing the affinities with
a constraint on the waiting time (Figure 2). The
horizontal axis represents the hours (expressed in
quarter; 1 is 8 AM while 40 is 6 PM); the vertical
axis represents the nurse’s ID. The roster of a
particular nurse is represented on several lines. Each
line corresponds to a surgical intervention. For
instance, on figure 1, nurse no. 1 is assigned to 3
surgical interventions; nurse no. 14, which starts
working in the afternoon (data of the problem), is
assigned to 2 surgical interventions.
We can note several differences between the two
figures: the nurses are different (nurses 3, 8 and 13
are working in the second schedule, not in the first
one), they are not working at the same time periods
(and thus the surgical teams are different), and the
number of nurses who are working is different. On
figure 1, it can be noted that only 10 nurses are
required to do the surgical planning; on figure 2, 13
of them are needed. It can be considered that the
assignment of figure 1 gives additional flexibility.
Indeed, if an emergency occurs or one of the nurses
calls in sick, one of the 4 remaining nurses can be
used. On figure 2, some nurses have rather long
waiting times between the surgical interventions. For
instance, nurse no. 10 has to wait 18 quarters
between jobs. The objective pursued was to
maximize affinities with a constraint on the total
waiting time, which may results in differences for
the nurses.
Figures 1 and 2 are the extreme solutions of the
Pareto set. The other compromise rosters are built by
BuildingSurgicalTeamwithHighAffinities-ABicriteriaMixed-integerProgrammingApproach
421

degrading the optimal value obtained on each
objective function and by using it as a constraint to
optimize the other objective function.
Figure 1: Tuesday roster for week 5 obtained by
minimizing the waiting time under the constraint on the
affinities.
Figure 2: Tuesday roster for week 5 obtained by
maximizing the affinities under the constraint on the
waiting time.
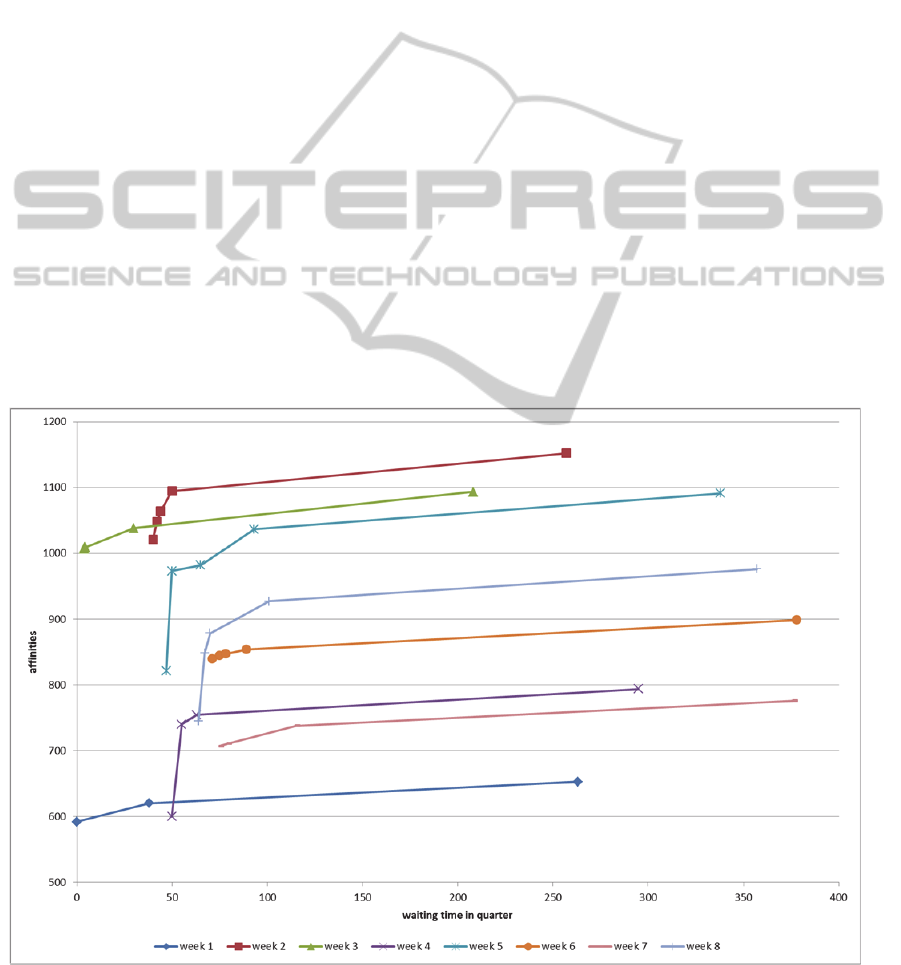
Figure 3 displays the Pareto frontier built for
each instance by degrading the values by 5%.
Starting from the extreme points of the Pareto
curves, the waiting time criterion is degraded by 5%.
The affinity level is increased by 8.5% on average.
By degrading the affinity level by 5%, the waiting
time of nurses is improved by an average of 380%.
However, there are differences between the
instances. It seems that the differences are more
related to the characteristics of the planning rather
than to the surgical loads (average number of nurses
per surgery, total operating time for nurses or
number of surgery over the week).
The relation between the two objectives is not
linear; degrading the affinities has a more impact on
the waiting time than the impact of the degradation
of the waiting time on the affinities.
5 CONCLUSIONS
The approach used in this paper considered a task-
based approach to model the demand for nurses in
the operating room. The present paper focused on
the building of surgical teams (surgeon, nurses) with
a high affinity degree while taking into account
availaibilities of nurses and the legal constraints on
working conditions (days-off, maximum working
time per week,…). The waiting time of nurses is also
minimized in order to limit idle time and overtime
payments.
The problem was modeled as a multiobjective
mixed-integer problem and solved using an -
constraint approach. This approach was chosen
because it allows the generation of non-dominated
nurse rosters. The decision maker can choose the
one he prefers and estimates the trade-offs between
alternative solutions.
The model was tested on real data from a
hospital. From those experiments, we could
conclude that the objectives are conflicting and that
degrading the affinities has a more impact on the
waiting time than the impact of the degradation of
the waiting time on the affinities.
From the analysis of the results, it appears that
there is an imbalance in the waiting time of the
nurses. A third objective could be added to minimize
the maximum waiting time of the nurses.
Currently, the authors are working on an
extension of the model that takes into account break
time periods for nurses.
Future work deals with assessing how those
conclusions are robust to variations in the work
availabilities of nurses and to the affinity matrix.
Affinities between the nurses could easily be
integrated. The affinity matrix could also be adapted
to take into account the nurses specialty.
REFERENCES
Bard, J. F. & Purnomo, H. W. 2005. Preference
Scheduling For Nurses Using Column Generation.
European Journal Of Operational Research, 164, 510-
534.
Burke, E., De Causmaecker, P., Berghe, G. & Van
Landeghem, H. 2004. The State Of The Art Of Nurse
Rostering. Journal Of Scheduling, 7, 441-499.
Cardoen, B., Demeulemeester, E. & Beliën, J. 2010.
Operating Room Planning And Scheduling: A
Literature Review. European Journal Of Operational
Research, 201, 921-932.
Chankong, V. & Haimes, Y. Y. 1983. Multiobjective
Decision Making: Theory And Methodology, North-
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
422
Holland.
Di Martinelly, C., Baptiste, P. & Maknoon, Y. 2011.
Evaluation De L’impact De L’intégration De La
Conception D’horaires Infirmiers Sur La
Programmation Opératoire 9e Congrès International
De Génie Industriel. Saint-Sauveur, Canada.
Di Martinelly, C. & Meskens, N. Surgical Team Rostering
Taking Into Account Affinities. International
Symposium On Operational Research And
Applications, 08-10 May 2013 2013 Marrakesh,
Morroco.
Ehrgott, M. 2005. Multicriteria Optimization, Springer.
Ehrgott, M. & Ruzika, S. 2008. Improved Ε-Constraint
Method For Multiobjective Programming. Journal Of
Optimization Theory And Applications, 138, 375-396.
Ernst, A. T., Jiang, H., Krishnamoorthy, M. & Sier, D.
2004. Staff Scheduling And Rostering: A Review Of
Applications, Methods And Models. European
Journal Of Operational Research, 153, 3-27.
Haimes, Y. Y., Lasdon, L. S. & Wismer, D. A. 1971. On
A Bicriterion Formulation Of The Problems Of
Integrated System Identification And System
Optimization. Ieee Transactions On Systems, Man,
And Cybernetics, 1, 296-297.
Hwang, C. L., Masud, A. S. M. & Paidy, S. R. 1979.
Multiple Objective Decision Making, Methods And
Applications: A State-Of-The-Art Survey, Springer-
Verlag Berlin.
Jaumard, B., Semet, F. & Vovor, T. 1998. A Generalized
Linear Programming Model For Nurse Scheduling.
European Journal Of Operational Research, 107, 1-
18.
Kurmann, A., Tschan, F., Semmer, N. K., Seelandt, J.,
Candinas, D. & Beldi, G. 2012. Human Factors In The
Operating Room – The Surgeon's View. Trends In
Anaesthesia And Critical Care, 2, 224-227.
Mavrotas, G. 2009. Effective Implementation Of The Ε-
Constraint Method In Multi-Objective Mathematical
Programming Problems. Applied Mathematics And
Computation, 213, 455-465.
Mazzocco, K., Petitti, D. B., Fong, K. T., Bonacum, D.,
Brookey, J., Graham, S., Lasky, R. E., Sexton, J. B. &
Thomas, E. J. 2009. Surgical Team Behaviors And
Patient Outcomes. The American Journal Of Surgery,
197, 678-685.
Meskens, N., Duvivier, D. & Hanset, A. 2012. Multi-
Objective Operating Room Scheduling Considering
Desiderata Of The Surgical Team. Decision Support
Systems.
Van Den Bergh, J., Beliën, J., De Bruecker, P.,
Demeulemeester, E. & De Boeck, L. 2013. Personnel
Scheduling: A Literature Review. European Journal
Of Operational Research, 226, 367-385.
Weaver, S. J., Rosen, M. A., Diazgranados, D., Lazzara,
E. H., Lyons, R., Salas, E., Knych, S. A., Mckeever,
M., Adler, L. & Barker, M. 2010. Does Teamwork
Improve Performance In The Operating Room? A
Multilevel Evaluation. Joint Commission Journal On
Quality And Patient Safety, 36, 133-142.
Figure 3: Efficiency frontier built for the different weeks tested.
BuildingSurgicalTeamwithHighAffinities-ABicriteriaMixed-integerProgrammingApproach
423

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
424
