Using Clustering Method to Solve Two Echelon Multi-Products

Location-Routing Problem with Pickup and Delivery

Younes Rahmani, Ammar Oulamara and Wahiba Ramdane Cherif

LORIA Laboratory, Lorraine University, Nancy, France

Keywords: Transportation, Optimization, Location-Routing Algorithms, Pickup and Delivery, Clustering Heuristic,

Multi Products.

Abstract: In this paper, we consider the Location Routing Problem in two-echelon network with Multi-Products, and

Pickup and Delivery (LRP-MPPD-2E). The objective of LRP-MPP-2E is to minimize simultaneously the

location and routing costs, considering many realistic non-tackled constraints in the literature. The first

echelon deals with simultaneously selection of processing centers from a set of potential sites and the

construction of the primary tours such that each primary tour starts from the main depot, visits the selected

processing centers and returns to the main depot. The second echelon aims at assigning customers to the

selected processing centers and defining the secondary tours. Each secondary tour, starts at a processing

center, visits a set of customers, through one or several processing centers, and then returns to the first

processing center. We develop a Hybrid Clustering Algorithm (HCA) with the objective of constructing

Global-Clusters such that each Global-Cluster represents the set of clients associated to one feasible

secondary tour, then Cplex Solver calculates the feasible tour within Global-Cluster. The HCA is compared

with a Nearest Neighbour heuristic (NNH), which actually is the only available method for this problem,

and with a Clustering-NNH in which Cplex solver is used to improve each secondary route obtained by

NNH. Computational experiments are conducted to evaluate the performances of proposed approaches.

1 INTRODUCTION

By the emergence of complex logistic networks, the

enterprises need more flexible and efficient decision

methods to manage the involved flows. The location

routing problem (LRP) and its variants are the

models of the literature that addressing issues related

to these complex logistic networks. The LRP allows

combining the strategic decisions related to the

selection of potential sites with the tactical and

operational decisions related to the assignment of

customers to the selected potential sites and the

construction of routes in order to serve all customers

demands. The objective of the LRP is to minimize

the total cost including routing costs, vehicle fixed

costs, and potential site operating costs. Many

authors showed that ignoring routing in the location

problem might lead to sub-optimal solution (Prins et

al., 2006a).

A wide variety of application fields are

concerned by LRP and its variants, which explain a

growing number of LRP studies considered in the

literature. Some review of LRP models, approaches

and applications could be found in many studies

(Min et al., 1998); (Nagy and Salhi, 2007);

(Duhamel et al., 2010); (Derbel et al., 2012);

(Borges et al., 2013). Exact approaches such as

mixed integer linear programming, brach and-bound

are proposed (Laporte and Nobert, 1988); (Labbe et

al., 2004); (Contardo et al., 2013); (Saraiva de

Camargo et al., 2013); (Hashemi and Seifi, 2013).

For large instances of LRP problems heuristic and

meta-heuristic approaches are developed in the

literature, such as: nearest neighbour method

(Rahmani et al., 2013b), simulated annealing, (Wu et

al., 2002); (Yu et al., 2010); (Doulabi and Seifi,

2013); (Albareda-Sambola et al., 2005); (Mousavi

and Tavakkoli-Moghaddam, 2013); (Ghaffari-Nasab

et al., 2013); (Fazel et al., 2013), memetic

algorithms (Prins et al., 2006b), greedy randomized

adaptive search procedure (Prins et al., 2012);

(Duhamel et al., 2009), variable neighborhood

search algorithms, (Melechovsky and Prins, 2005);

(Schwengerer et al., 2012); (Jarboui et al., 2013),

and ant colony optimisation (Ting et al., 2013).

According to (Mehrjerdi and Nadizadeh, 2013),

425

Rahmani Y., Oulamara A. and Ramdane Cherif W..

Using Clustering Method to Solve Two Echelon Multi-Products Location-Routing Problem with Pickup and Delivery.

DOI: 10.5220/0004832804250433

In Proceedings of the 3rd International Conference on Operations Research and Enterprise Systems (ICORES-2014), pages 425-433

ISBN: 978-989-758-017-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Example of LRP-MPPD-2E with 5 processing centers and 6 clients. The primary vehicle’s capacity is 12 and the

secondary vehicle capacity is equal to 6. The forth-processing center is not even opened. Three primary trips are

represented. It should be mentioned that customer 5 asks for both c-products (p1 and p2). Each of these demands is satisfied

with a separate secondary vehicle, p1 by route 4 and p2 by route 6.

heuristic algorithms applied to LRP in literature

could be divided into sequential, iterative,

hierarchical and clustering methods. In sequential

methods, first the total sum of distances from the

potential sites to all customers is minimised. A set of

potential sites is selected then the vehicle routing

problem (VRP) is solved. In iterative methods, the

routing and the location problems are solved

iteratively. In hierarchical heuristics, the location of

the potential sites is solved as the principal problem

then the routing is considered as the secondary

problem. The clustering methods, proceed by

partitioning the customers into clusters, one cluster

per potential site or one per vehicle route then solve

the routing problem for each cluster and find the best

location of potential sites.

The potential of cluster analysis to solve the LRP

problems has been recognized by several authors

(Bruns and Klose, 1995); (Barreto et al., 2007).

However, few studies have considered the

clustering approaches for the LRP, such as:

(Özdamar and Demir, 2012); (Barreto et al., 2007);

(Mehrjerdi and Nadizadeh, 2013); (Guerrero and

Prodhon, 2013). To the best of our knowledge, the

clustering methods have never been applied to the

LRP in a two-echelon network. Our contribution, in

this paper, is to develop a clustering approach to a

general and complex LRP in a two-echelon network

that was proposed in (Rahmani et al., 2013a).

The rest of this paper is organized as follows.

Section 2 presents the considered LRP problem and

its specific constraints. Section 3 explains briefly the

nearest neighbour method that was already applied

to the studied problem. Section 4 gives the details of

the proposed clustering approach. Experimentation

and concluding remarks are discussed in the section

5 and section 6, respectively.

2 PROBLEM DESCRIPTION

A new complex LRP, named LRP-MPPD-2E (2

Echelon Multi-products Location-Routing problem

with Pickup and Delivery) has been defined

(Rahmani et al., 2013a). The proposed model was

inspired by a real problem encountered in the

context of the distribution of shoes (Carrera et al.,

2010). The goal is to locate processing centers

(intermediate stores, relays, logistic platforms) to

optimize the distribution of different kinds of shoes

from a central platform to final stores. The proposed

model combines two families of realistic constraints

that have not been considered simultaneously in

LRP literature: multi-products constraint and pickup

and delivery constraints.

In LRP-MPPD-2E, two levels are considered: at

the first level, tours are constructed from a main

depot to a set of active processing centers that must

be selected, and at the second level, a set of vehicles

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

426

visit customers from the selected processing centers.

We denote primary and secondary tour the tours

constructed at the first and the second level,

respectively. The LRP-MPPD-2E is an extension of

the LRP-2E (for recent studies on LRP-2E, see

(Nguyen et et al., 2012), (Boccia et al., 2010). A

concise formulation and heuristic approaches based

on neighbourhood strategy was proposed in

(Rahmani et al., 2013a).

The LRP-MPPD-2E is modelled as an undirected

and valuated graph G = (N, A, l). N refers to the set

of nodes, where 



∪



, in which 



and 



represent the sets of the potential processing centers

nodes (considered as depots in the case of LRP), and

the customers, respectively. Node 0 is considered

as a depot. A is the set of edges and l refers to a

function that associate a positive cost (time) to each

arc (typically travel time). At depot there is a set V1

of homogeneous fleet of (primary) vehicles. Each

primary vehicle has a limited capacity CV1 and a

fixed cost FV1. Another set V2 of homogeneous

fleet of (secondary) vehicles is available at the

processing center’s sites. Each secondary vehicle has

a limited capacity CV2 and a fixed cost FV2 (we

consider the general case when CV1 is different

from CV2). Each potential processing center has an

opening cost.

Each client asks for one or several type of

products denoted c-products, known in advance and

could be satisfied. In each processing center, pickup

and delivery operations are performed. Primary

products, denoted h-products, are delivered from

main depot to active processing centers. Each active

processing center can receive only one type of h-

products. The h-products are transformed into final

products, denoted c-products. Each processing

center should provide exactly one secondary c-

product.

We consider two types of vehicles as explained

above. The primary vehicles should pick up the h-

products from the main depot and deliver them to

the active processing centers, which have been

opened, such as each processing center is visited

only once in each primary tour. When once

satisfying the demand of processing centers, the

secondary vehicles can pickup c-products, which are

available in the processing centers, and continue

their trips in a way that each customer and

processing center is visited at most once by each

secondary trip. The secondary trips start from an

active processing center, which will represent the

departure node, serve several customers, can visit

one or several processing centers and must end up at

the departure node. We assume that products have

the same size, the splitting demand of customers for

a given c-product is not allowed, and that each

processing center can provide exactly one type of c-

product.

The goal of LRP-MPPD-2E is to determine the

location of active processing centers, the assignment

of customers to the opened processing centers and

the construction of the corresponding primary and

secondary tours with a minimum total cost. The total

cost includes the opening cost of processing centers,

the exploitation cost of vehicles and the sum of

edges costs traversed by vehicles. An illustrative

example of the two-echelon model is given in

Figure. 1.

3 NEAREST NEIGHBOUR

HEURISTIC (NNH)

In this section, we explain briefly the neighbour

nearest heuristic, named NNH, proposed in

(Rahmani et al., 2013a), which is actually the only

proposed method for LRP-MPPD-2E.

For the primary routes a constructive approach,

based on two steps is used. In the first step, a

processing center is selected according to some

criteria in order to initialize the route. Then the

nearest neighbour strategy is used in the second step

to complete the tours. Both steps are repeated until

all activated processing centers could satisfy the

customer demands. To construct the secondary

routes all inactive processing centers are ignored,

then an open processing center is selected according

to some criteria. To compute the current route a

nearest neighbour strategy is used. This process is

repeated until all customer requests are satisfied. A

neighbour candidate (active processing center or

client) is inserted in the tour if all constraints are

satisfied, otherwise a second neighbour candidate

will be checked, until neither processing center nor

client can be inserted in the tour. In that case a new

secondary tour is started. This process is repeated

until all demands of customers are satisfied.

4 HYBRID CLUSTERING

ALGORITHM (HCA)

In this section, a Hybrid Clustering Algorithm -

HCA is proposed for the LRP-MPPD-2E.

The hybrid-clustering algorithm - HCA, is a non-

trivial extension of a greedy clustering method

proposed by (Mehrjerdi and Nadizadeh, 2013) for a

UsingClusteringMethodtoSolveTwoEchelonMulti-ProductsLocation-RoutingProblemwithPickupandDelivery

427

Figure 2: HCA for the LRP-MPPD-2E.

classical LRP with a fuzzy demands. The proposed

HCA algorithm proceeds in five steps (see Figure.

2). In the first step, customers are clustered using an

algorithm based on nearest neighbour, such that each

cluster should involve only clients that request the

same product (Figure. 2a). In the second step, the

gravity center of each cluster is calculated. This

allows to select a set of potential processing centers

(Figure. 2b). In the third step, clusters are merged as

well as possible in order to create the Global-

Clusters (GC) in which only one vehicle will be

exploited. That means each Global-Cluster

represents one feasible secondary tour (Hamiltonian

tour). This merging step considers the distance

between the gravity centers of the clusters as well as

the route time limit, (Figure. 2c). In order to ensure

the feasibility of the solution in each Global-Cluster,

the merged clusters should not have any common

client, because the exploited vehicle for each

Global-Cluster must visit only once each customer

and each processing center. The clusters are

allocated to the opened processing center(s) in the

forth step, considering the distance between the

processing centers and the gravity center of the

clusters as well as the capacity of the processing

centers (Figure. 2d). Finally, in the fifth step, Cplex

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

428

solver is used to find a feasible secondary tour in

each Global-Cluster (Figure. 2e). Details of the

HCA’s steps are given bellow.

4.1 Clustering the Customers

The goal of the first step of the HCA is the

clustering of the customers. The customers are

separated into different groups considering their

intra distance, the sum of their customer’s demands,

the vehicle capacity, the time route limit, and an

estimation of the route travel time given in formula

(1) in which





_ and 



_ present the number of

clients and processing centers, respectively in cluster

cl.

_ is the maximum distance between two

clients in cluster cl. The maximum distance between

the processing centers and the clients in cluster cl is

denoted by

_.

  



  



  

2









(1)

The T value associated to a cluster cl, is an

overestimation of a route starting from a processing

center, visiting all the customers assigned to the

cluster cl, and ending at the starting processing

center.

More precisely, for each c-product p, a set of

non-clustered customers (NCCp) is initialised by all

customers j such as Q

>0, where Q

indicates the

quantity of the product p asked by the customer j. At

first, a customer is selected randomly from a set

NCCp, then the nearest customer to the last selected

customer of the current cluster is chosen from

NCCp. Therefore the clusters are formed for a

single. The nearest customer is selected as follow:

when a new customer j for product p is selected, (j is

the closest customer regarding the distance to the

current customer in the cluster cl), before its

assignment to cl, we verify two conditions in order

to limit the size of each cluster. Firstly, the sum of

the amounts requested by the assigned clients to the

cluster cl should not exceed the secondary vehicle

capacity CV2. The second constraint equation (1),

with 



_ =1) checks that the estimated travel time

in a cluster cl doesn’t exceed the time route limit. If

these two conditions are fulfilled, the new customer

is assigned to the current cluster. Otherwise, the

algorithm searches for a new customer closer to the

last added member of the cluster in NCCp. The

algorithm creates a new cluster if there is no

customer to be assigned to the current cluster. The

algorithm stops when there is no unassigned

customer. Figure (3.a) illustrates the cluster’s

selection algorithm.

4.2 Processing Center (PC) Selection

In the second step of the HCA, the method of

(Mehrjerdi and Nadizadeh, 2013) for establishing

the processing centers is used. This method is based

on a gravity center criterion as illustrated by

Equation (2), in which (X

(cl)

) is the coordinates

of the gravity center of the cluster cl and (x

) is the

coordinates of customer i, where n

is the number of

customers assigned to cluster cl.

(cl)

)=

∑









∑











(2)

For each processing center, we calculate the sum of

the distances between this potential site and all the

gravity centers.

The potential sites are re-indexed in non-

decreasing order according to their Euclidean

distance to the gravity center of the clusters. If the

current opened top-ranked potential site is not able

to fulfil all the remaining customers’ demands, the

next potential site of the sorted list is selected to be

open. This procedure is repeated until all the clusters

are covered. Therefore, each selected processing

center will be assigned to one or more cluster and

each cluster is covered by one or more processing

centers.

4.3 Merging the Clusters into

Global-Cluster

In this step, the clusters are merged in order to create

a set of Global-Clusters (GC) in which represents

one feasible secondary route. Since the assigned

vehicle to each Global-Cluster must visit customers

and processing centers only once, then the merged

clusters should not have any common client.

At first, a cluster cl will be selected randomly,

and then a sorted list of the not merged clusters cl' is

constructed according to the distance between the

gravity centers of cl and cl'. The first cluster in the

list is added into the current Global-Cluster (GC) if

the value of T Calculated by equation (1), with

_cl equal to the number of merged clusters in GC

did not exceed the time route limit (Figure. 2c). This

procedure is repeated until that no cluster can be

added to the current Global-Cluster. In that case,

either the process stops because all the clusters are

merged or the process is restarted to search for a

new Global-Cluster.

UsingClusteringMethodtoSolveTwoEchelonMulti-ProductsLocation-RoutingProblemwithPickupandDelivery

429

Figure 3: Clustering Customers step of the HCA

Algorithm.

4.4 Assigning Clusters to Processing

Center(S)

In the forth step of the HCA, the clusters are

respectively allocated to the processing center that

were ranked and opened in the processing center

selection step. Each processing center serves as

many clusters as possible according to its capacity.

Note that we can’t allocate two clusters cl

, cl

to the

same processing center when they were merged in

the same GC. Because a vehicle cannot visit a

processing center twice in a given route. In order to

allocate the clusters to the processing center, the

Euclidian distance between the gravity center of

each cluster and the opened processing center is

calculated. Then the unassigned clusters are ranked

in an ascending order based upon the distance of

their gravity centers to the processing center. The

top-ranked cluster cl

will be allocated to the top-

ranked processing center pr: 1) if the processing

center pr has enough capacity to cover the total

demands of the cluster cl

, and 2) if this processing

center pr is not already affected to a cluster cl

, such

as cl

and cl

belong to the same Global-Cluster. The

allocation process to the processing center pr is

finished when there is not enough capacity to

allocate a new cluster. In that case, the allocation

procedure is repeated for the next top-ranked

processing center until all clusters are allocated.

4.5 Routing Problem

In the fifth and last phase of the HCA, the routing

problem is solved for each Global-Cluster (GC) with

the relevant processing centers and assigned clients.

Actually, each Global-Cluster is served by exactly

one vehicle and the vehicle is not allowed to visit

any node two times. Cplex solver is used to create

one secondary route per one Global-Cluster. The

routing between the selected processing centers for

the first level (primary tours) is obtained by a

vehicle routing nearest neighbour heuristic.

5 COMPUTATIONAL

EXPERIMENTS

In this section, we review the performance of the

HCA, Iterative HCA (IHCA) and Clustering-NNH

method in comparison with NNH (Rahmani et al.,

2013a, briefly presented in section 3). In Iterative

HCA, the HCA algorithm is executed 10 times with

a new client, chosen randomly, to initialize the

clustering step. In Clustering–NNH, firstly NNH is

applied in order to create the routes, and then each

secondary route is considered as a Global-Cluster

and a Cplex solver is used for each Global-Cluster to

improve the secondary routes. We note that the

routing in primary level is kept like in NNH.

Since our problem is not considered in the

literature, we have adapted a known LRP-2E

instance from (Prodhon et al., 2012) to our problem

(Rahmani et al., 2013a). These instances are grouped

in four subsets with the following features: number

of customers nϵ{20,50,100,200}, uniform

distribution demands in interval [11,20], number of

satellites-depots mϵ{5,10}, with their opening

costs, β={1,2,3} is manner of customers distribution,

for instance, β = 1 means a uniform distribution of

customers.

In order to adapt these instances to our problem,

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

430

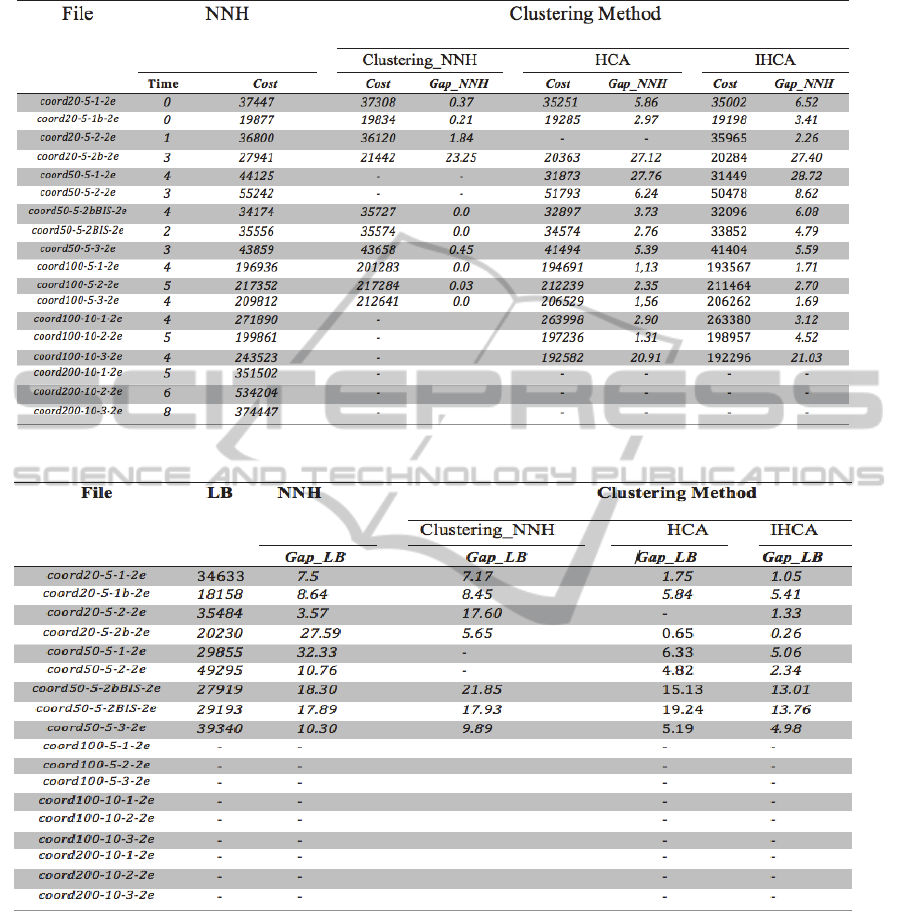
Table 1: Improvement of the Clustering Method against NNH.

Table 2: Evaluation of the Clustering Method against Cplex Lower Bound.

we have considered the following hypotheses:

 Each satellite-depot corresponds to a processing

center in our problem.

 We consider 3-district products: one h-product

{p0} and two others c-products {p1, p2}.

 Each client asks for products, p1 or p2 or both

products with equal probability.

 The capacity CV1 must be greater than the

quantity of all h-product demands.

We added the h-product demand for each processing

center, such as the demand of each h-product is

equal to 1/5 of c-product availability in this

processing center.

The proposed heuristic was coded in C++ and we

evaluated its performance on a PC with Intel (R)

Core (TM) Solo CPU 1.40 GHz, 2GB of RAM. The

routing steps of HCA use a Cplex solver version

14.0. Cplex Solver is unable to find any optimal

solution. However, a feasible solution is obtained

when we limit the computation time to one hour.

Table 2 shows the improvement result details of

proposed heuristics.

In Table1, the first column indicates the problem

UsingClusteringMethodtoSolveTwoEchelonMulti-ProductsLocation-RoutingProblemwithPickupandDelivery

431

name “coord n − m – β -2E”. In columns 2 and 3,

the best result of the neighbour nearest heuristic

(NNH) is reported. The results of Clustering-NNH

are gathered in columns 4 and 5, the results of HCA

are represented in columns 6 and 7, and the results

of IHCA are represented in columns 8 and 9.

Column “Time” and “Cost” present the computation

time (in seconds) of NNH and the obtained value of

the total cost, respectively. The percentage of

“Gap_NNH” indicates the improvement of the

Clustering methods in comparison with NNH

solution. It is calculated as (NNH Cost -

Clustering_NNH) / NNH Cost for column 5, (NNH

Cost - HCA Cost) / NNH Cost for column 7, and

(NNH Cost – IHCA Cost) /NNH Cost for column 9.

In Table 2, a comparison with the lower bound

LB provided by Cplex is given. This LB is obtained

by solving a mixed linear formulation of LRP-MPP-

2E (Rahmani et al., 2013a). The value of LB is given

in column 2. Columns 3, 4, 5, and 6 present the gap

between the lower bound (LB), and heuristic

solution. It is calculated as (Cost - LB) / Cost.

Results in table 1 show that HCA outperforms

NNH and the Clustering_NNH for n < 200 except

for the third instance. For n >= 200, it is not

possible to evaluate the performance of HCA,

because Cplex cannot generate any solution after 1

hour processing time (see Table 2). The maximum

and minimum gap (improvement) between the HCA

solution and the NNH solution are 27.76% and

1.13%, respectively. Furthermore, The HCA

methods outperforms the Clustering_NNH, since

HCA is able to solve 14 instances while

Clustering_NNH only solves 10 instances

Clustering_NNH doesn’t succeed to improve all

results of NNH (only 6 instances are outperformed).

The average improvement of HCA in comparison

with NNH is 7,99 %, against 2,61% of improvement

is obtained by the clustering-NNH. Note that we

limited the computation time of HCA to one hour;

however we noticed that the solution is obtained on

average after only 10 minutes.

The results of HCA are enhanced by IHCA from

7,98% to 8,99%. Results also show that IHCA is

able to resolve some instances when HCA don’t

succeed to find any solution (instance 3).

6 CONCLUSIONS

Some studies from the literature on routing problems

confirm the interest of the clustering technique for

the location routing problem but only a few papers

deal with the application of the clustering techniques

for a classical location routing problems. In this

paper, we have developed a Hybrid Clustering

Algorithm (HCA) for a more complex location

routing problem, considering many realistic non-

tackled constraints in the literature. The studied

problem, named LRP-MPPD-2E, has been proposed

recently in (Rahmani et al., 2013a). The authors

proposed a Nearest Neighbour Heuristic (NNH) to

solve the problem. Computational results show that

the HCA outperforms the result of NNH. In

addition, HCA works better than another clustering

technique, in which the secondary tours of NNH are

used to form the Global-Clusters. Iterative HCA,

which is a randomised version of HCA, outperforms

all the methods.

In further researches, we aim to improve HCA

with metaheuristic techniques and an iterative

process. For example, to improve the computation

time of HCA, we can use a metaheuristic approach

instead of Cplex to solve the routing problems. The

primary tours can easily be improved by more

sophisticated heuristic like the one that is used in

this paper. It would be also interesting to develop

more efficient lower bound. Another perspective is

to generalize the LRP-MPPD-2E to deal with some

other realistic constraints such as splitting of demand

and the possibility to provide several types of c-

products per processing center.

REFERENCES

Albareda-Sambola, M., Diaz, J.A., Fernandez, E., 2005.,

A compact model and tight bounds for a combined

location-routing problem. Computers & Operations

Research 32,407–428.

Barreto, S., Ferreira, C., Paixao, J., Sousa Santos, B.,

2007., Using clustering analysis in a capacitated

location-routing problem. European Journal of

Operational Research 179 (2007) 968–977.

Boccia, M., Crainic, T. G., Sforza, A., Sterle, C., 2010.

Experimental Algorithms. Springer.

Bruns, A., Klose, A., 1995. An iterative heuristic for

location- routing problems based on clustering. In:

Proceedings of the Second International Workshop on

Distribution Logistics, The Netherlands, pp. 1–6.

Carrera, S., Portmann, M.C., Ramdane Cherif, W.,

2010. Scheduling problems for logistic platforms with

fixed staircase component arrivals and various

deliveries hypotheses. Actes parus dans la série

Lecture Notes in Management Science, Proceedings of

the 2th International Conference on Applied

Operational Research - ICAOR, Turku, Finlande,

pages 517–528.

Contardo, C., Cordeau, J. F., Gendron, B. 2013. A

computational comparison of flow formulations for

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

432

the capacitated location-routing problem. Original

Research Article, Discrete Optimization, In Press,

Corrected Proof, Available online 8 August 2013.

Derbel, H., Jarboui, B., Hanafi, S., Chabchoub, H., 2012.

Genetic algorithm with iterated local search for

solving a location routing problem. Original Research

Article, Expert Systems with Applications, Volume 39,

Issue 3, Pages 2865-2871.

Duhamel, C., Lacomme, P., Prins, C., Prodhon, C., 2009.

A GRASP ELS approach for the capacitated location-

routing problem. Computers & Operations

Research.doi:10.1016/j.cor.2009.07.004.

Fazel Zarandi, M. H., Hemmati, A., Davari, S., Turksen,

B., 2013. Capacitated location-routing problem with

time windows. under uncertainty. Original Research

Article, Knowledge-Based Systems, Volume 37, Pages

480-489.

Ghaffari-Nasab, N., Ghazanfar Ahari, S., Ghazanfari, M.,

2013. A hybrid simulated annealing based heuristic

for solving the location-routing problem with fuzzy

demands. Original Research Article Scientia Iranica,

Volume 20, Issue 3, June 2013, Pages 919-930.

Guerrero, W. J., Prodhon, C., 2013. Capacitated

hierarchical clustering heuristic for multi depot

location-routing problems.1 International Journal of

Logistics Research and Applications: A Leading

Journal of Supply Chain Management

Hashemi Doulabi, S. H., Seifi, A., 2013. Lower and upper

bounds for location-arc routing problems with vehicle

capacity constraints. Original Research Article,

European Journal of Operational Research, Volume

224, Issue 1, Pages 189-208.

Jarboui, B., Derbel, H., Hanafi, S., Mladenović, N., 2013.

Variable neighborhood search for location routing.

Original Research Article, Computers & Operations

Research, Volume 40, Issue 1, Pages 47-57

Labbe, M., Rodríguez-Martin, I., Salazar-González, J. J.,

2004. A branch-and-cut algorithm for the plant-cycle

location problem. Journal of the Operational Research

Society 55 (5), 513–520.

Laporte, G., Nobert, Y., 1988. Solving a family of multi-

depot vehicle routing and location-routing problems.

Transportation Science 22 (3), 161–172.

Melechovsky, J., Prins, C., 2005. A metaheuristic to solve

a location routing problem with non-linear costs.

Journal of Heuristics 11, 375–391.

Min, H., Jayaraman, V., Srivastava, R, 1998. Combined

location-routing problems: A synthesis and future

research directions. European Journal of Operational

Research 108(1), 1–15.

Mousavi, M., Tavakkoli-Moghadam, R., 2013. A hybrid

simulated annealing algorithm for location and routing

scheduling problems with cross-docking in the supply

chain. Original Research Article, Journal of

Manufacturing Systems, Volume 32, Issue 2, Pages

335-347.

Nagy, G., Salhi, S., 2007. Location-routing: Issues,

models and methods. European Journal of

Operational Research 177 (2), 649–672.

Nguyen, V.-P., Prins, C., Prodhon, C., 2012. Solving the

Two-Echelon Location Routing Problem by a hybrid

GRASPxPath Relinking complemented by a learning

process. European Journal of Operational Research,

216, pp. 113-126.

Özdamar, L., Demir, O., 2012. A hierarchical clustering

and routing procedure for large scale disaster relief

logistics planning. Original Research Article.

Transportation Research Part E: Logistics and

Transportation Review, Volume 48, Issue 3,Pages

591-602.

Prins, C., Prodhon, C., Wolfler Calvo, R., 2006a. Solving

the capacitated location-routing problem by a GRASP

complemented by a learning process and a path

relinking. 4OR 4,221–238.

Prins, C., Prodhon, C., Wolfler-Calvo, R., 2006b. A

memetic algorithm with population management for

the capacitated location-routing problem.

EvoCOP2006, 183-194.

Rahmani, Y., Oulamara, A., Ramdane Cherif, W., 2013a.

MultiProducts LocationRouting problem with Pickp

and Delivery: Two-Echelon model. 11th IFAC

Workshop on Intelligent Manufacturing (IMS 2013),

pages 22-24 May, São Paulo, Brazil, pages 124-129,

2013.ISBN: 978-3-902823-33-5.

Rahmani, Y., Oulamara, A., Ramdane Cherif, W., 2013b.

Multi-products Location-Routing problem with Pickup

and Delivery, ICALT IEEE, 29-31 May, Sousse,

Tunisie, pages 115,122.

Rui Borges Lopesa, b., Carlos Ferreiraa, b., Beatriz Sousa

Santos and Sergio Barreto, 2013. A taxonomical

analysis, current methods and objectives on location-

routing problems.

Saraiva de Camargo, R., Miranda, G., Løkketangen, A.,

2013. A new formulation and an exact approach for

the many-to-many hub location-routing problem.

Original Research Article, Applied Mathematical

Modelling, Volume 37, Issues 12–13, 1 July 2013,

Pages 7465-7480.

Schwengerer, M., Pirkwieser, S., and Raidl. G. R.,2012. A

variable neighborhood search approach for the two-

echelon location-routing problem. In J.-K. Hao and M.

Middendorf, editors, Evolutionary Computation in

Combinatorial Optimisation - EvoCOP 2012, volume

7245 of LNCS, pages 13-24. Springer, Heidelberg.

Ting, C. J., Chen, C. H., 2013. A multiple ant colony

optimization algorithm for the capacitated location

routing problem, Original Research Article.

International Journal of Production Economics,

Volume 141, Issue 1, Pages 34-44.

Wu, T. H., Low, C., Bai, J. W., 2002. Heuristic solutions

to multi-depot location-routing problems. Computers

& Operations Research 29 (10), 1393–1415.

Yu, V. F., Lin, S. W., Lee, W., Ting, C. J., 2010. A

Simulated Annealing Heuristic for the Capacitated

Location Routing Problme. Computers and Industrial

Engineering 58 (2), 288–299.

Zare Mehrjerdi, Y., Nadizadeh, A., 2013. Using greedy

clustering method to solve capacitated location-routing

problem with fuzzy demands. European Journal of

Operational Research.

UsingClusteringMethodtoSolveTwoEchelonMulti-ProductsLocation-RoutingProblemwithPickupandDelivery

433