Using MACBETH with the Choquet Integral Fundamentals to Model

Interdependencies between Elementary Concerns in the Context of

Risk Management

Diana F. Lopes

, Carlos A. Bana e Costa

, Mónica D. Oliveira

and Alec Morton

CEG-IST, Centre for Management Studies of Instituto Superior Técnico, Universidade de Lisboa,

Avenida Rovisco Pais, 1049-001 Lisbon, Portugal

Management Science Department, University of Strathclyde, 16 Richmond Street, Glasgow G1 1XQ, Scotland, U.K.

Keywords: Interactions, Value Interactions, Choquet Integral, MACBETH, Risk Evaluation.

Abstract: Effective risk management typically requires the evaluation of multiple consequences of different sources of

risk, and multicriteria value models have been used for that purpose. The value of mitigating a risk impact is

often considered by risk managers as dependent on the levels of other impacts, therefore there is a need for

procedures to identify and model these interactions within a value measurement framework. The Choquet

Integral (CI) has been used for this purpose, and several studies in the performance measurement literature

have combined the 2-additive CI operator with the MACBETH approach to model interdependencies in real

contexts. In this paper, we propose an alternative procedure to model interdependencies and determine the

CI parameters from one single MACBETH global matrix. The procedure is illustrated with the construction

of a descriptor of impacts to evaluate the risk impacts at ALSTOM Power. The paper further explains the

questioning protocol to apply the proposed procedure, as well as how decision-makers can interpret the CI

parameters.

1 INTRODUCTION

Risk management relates to all sources of risk that

can affect an organization in terms of its goals and

vision (Aven, 2008) (p. 6). Typically, risks are

characterized in terms of their probability of

occurrence and impact (or consequences) (Williams,

1996) and depending on the context, the risk impact

can be evaluated on a single concern or on multiple

concerns – also described in the literature as

dimensions or attributes (Aven, 2008) (p. 42). For

example in a project management context, the

concerns may be timely delivery, incurred costs

within the budget envelope, and conformance to

specifications of the project. Multicriteria value

models can assist in evaluating those impacts

(Linkov et al., 2006). Value models demand for the

structuring of concerns in a value tree, with key

concerns (or criteria) being independent axes for the

evaluation of impacts. Very often, key concerns are

a cluster of interdependent elementary concerns

(EC) (Bana e Costa et al., 1999) (having also been

described as interacting criteria (Clivillé et al.,

2007); (Grabisch et al., 2010)), and therefore

modelling should identify and account for possible

value interdependencies between EC. This is a major

challenge in Multiple Criteria Decision Analysis

(MCDA) literature (Grabisch et al., 2010), and

several studies have explored the use of Choquet

integral (CI) operators in modelling

interdependencies. In particular, many of them use

an extension of MACBETH (Measuring

Attractiveness by a Categorical Based Evaluation

Technique) (Bana e Costa et al., 2012) with CI

operators (Berrah et al., 2007); (Clivillé et al., 2007;

Brosig, 2012); (Merad et al., 2013). Nonetheless,

these applications entail methodological problems.

With the aim of creating a tool to be easily used

for decision aid in the context of multicriteria value

measurement and to overcome pitfalls from previous

studies, this paper exploits an alternative procedure

to use MACBETH with the CI, through the use of a

MACBETH global matrix. The use of the proposed

procedure is illustrated with a case of evaluation of

interdependent risk impacts at ALSTOM Power.

This paper is organized in four sections. Section

2 presents a literature review. Section 3 proposes the

116

Lopes D., Bana e Costa C., Oliveira M. and Morton A..

Using MACBETH with the Choquet Integral Fundamentals to Model Interdependencies between Elementary Concerns in the Context of Risk

Management.

DOI: 10.5220/0004833701160126

In Proceedings of the 3rd International Conference on Operations Research and Enterprise Systems (ICORES-2014), pages 116-126

ISBN: 978-989-758-017-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

MACBETH global matrix with the CI to model

interdependencies, being applied to the context of

modelling interdependencies at ASTOM Power.

Section 4 presents concluding remarks and describes

ongoing research.

2 LITERATURE REVIEW

This section starts by clarifying key concepts and the

nomenclature in use in this paper. It then reviews

previous studies that have modelled

interdependencies, emphasizing those that have used

CI operators and MACBETH.

2.1 Nomenclature

Previous studies modelling interdependencies used a

diverse terminology. We start by clarifying the

nomenclature adopted in the remaining of this paper.

Departing from the value-focused thinking

framework of Keeney (1992), we adopt “the

approach of structuring concerns” of Bana e Costa et

al. (2005), which makes clear the difference between

concerns, key concerns (KC) and elementary

concerns. A concern (also called “point of view” by

Bana e Costa et al. (1999) and “objective” by

Keeney (1992) is any aspect within a specific

decision context seen as relevant at the eyes of at

least one actor for the analysis (Bana e Costa et al.,

2005). Stated objectives, points of view, active

characteristics of the options and possible

consequences of potential options are all concerns

(Bana e Costa et al., 1998). Key concerns are the

“ends objectives [concerns]” (Keeney, 1992) that

emerge progressively from the structuring phase,

and need to respect necessary preferential

independence conditions (Bana e Costa et al., 2005),

so that they can be isolated from the other KC. Each

of them must be measurable and operational by

assigning a natural, proxy or indirect, or a

constructed descriptor of impacts (i.e., ordered set of

plausible impact levels (Bana e Costa et al., 2002;

Bana e Costa et al., 2005)). Very often, a KC is

defined by a cluster of several interrelated

elementary concerns which are usually seen as

means to achieve ends (Bana e Costa et al., 1999). It

is on the level of the EC that value dependencies (to

be modelled with the CI) occur.

Since there is no agreement in literature

regarding the meaning of concept of interaction or

judgmental dependencies, it is useful to clarify this

concept. There are two main types of preferential

independence conditions: (1) ordinal independence

and (2) cardinal independence. The first one is

verified when options or alternatives can be ranked

with respect to one KC independent of their impact

in other aspects; the second one is verified, when,

additionally, the difference in attractiveness between

the options can be measured with respect to one KC

independently of their impact in other aspects (Bana

e Costa et al., 2005). For instance, consider the

following two concerns “peak noise level during the

night” and “noise level during the whole day” (Bana

e Costa et al., 2005). Whichever the average noise

during the day, low peaks during the night are

always preferred to high peaks - this is an example

of ordinal independence. However, if the difference

of attractiveness between two night peak levels

depends of the average noise level during the whole

day, cardinal dependence occurs (Bana e Costa et

al., 2005). In this sense, interactions are related to

preferential dependence, and these can be expressed

in different ways (Bana e Costa et al., 2005), for

instance by antagonism (in which the combined

impacts are valued less than the sum of the values of

impacts) and by synergism (with the combined

impact valuing more than the sum).

Marichal (2000) suggests the existence of three

types of interactions: (1) correlation, (2)

complementarity/substitutiveness and (3)

preferential dependence. In the scope of our study

we suggest that correlations should not be

considered because they refer to environmental

(physical or statistical) and not judgmental relations

between concerns (von Winterfeldt et al., 1986).

E.g., the costs and safety of a road infrastructure are

statically correlated, in the sense that higher safety

usually requires higher investments, but they can be

taken as two (judgmentally independent) key

concerns, because the DM is able to rank levels from

one KC and can judge the difference in

attractiveness between any two impact levels from

one KC without knowing their impact on the other

KC. Hence, in contrast to what it is stated in other

studies such as Shah et al. (2013) and Marichal

(2000), correlations can be ignored unless they are

redundant (Bana e Costa et al., 2005). On the other

hand, we believe that substitutiveness and

complementarity are types of preferential

dependence, more precisely extreme situations of

antagonism and synergism, respectively. For

example, substitutiveness corresponds to a situation

when the combined impact is valued less than the

sum of individual impacts, being the value of the

individual impacts close to the value of the

combined impact (Grabisch et al., 2004). Hence,

there is no need to distinguish between preferential

UsingMACBETHwiththeChoquetIntegralFundamentalstoModelInterdependenciesbetweenElementaryConcernsin

theContextofRiskManagement

117

or value dependence and substitutiveness/

complementarity.

2.2 MACBETH Basics

MACBETH is a multicriteria decision analysis

approach that requires only non-numerical

judgments about differences in attractiveness

between options to help the decision maker (DM)

measure the relative attractiveness or value of

options (Bana e Costa et al., 2012). Within a

multicriteria value measurement framework,

MACBETH has been most commonly used to build

value functions and weight criteria in additive

models. For building value functions, the

MACBETH questioning protocol consists in asking

the DM to qualitatively judge the difference in

attractiveness between impact levels, two at a time,

based on seven semantic categories: “is there no

difference, or is the difference very weak, weak,

moderate, strong, very strong, or extreme?” (Bana e

Costa et al., 2012). During this questioning protocol,

a matrix with the categorical judgments of the DM is

populated. Each time a qualitative judgment is

introduced in the matrix, the M-MACBETH DSS

verifies its consistency and offers suggestions to

solve eventual inconsistencies (Bana e Costa et al.,

2008). After the consistency verification, the

software derives, by mathematical programming, an

interval numerical scale which has to be analysed

and validated by the DM (Bana e Costa et al., 2012).

A slightly different procedure than the one just

described has been used for weighting EC with CI

and MACBETH. Previous studies have shown that

MACBETH provides a simple and transparent

approach in modelling complex multidimensional

problems, and hence its wide applicability in MCDA

(examples are (Bana e Costa et al., 1999); (Bana e

Costa et al., 2002); (Carnero, 2006); (Bana e Costa

et al., 2008); (Barin et al., 2012)).

As described above, in its most common use,

MACBETH applications use an additive value

model by taking “difference independence” as a

modelling hypothesis (Bana e Costa et al., 2012). As

mentioned in Edwards et al. (1994) (p. 315)

“violations of conditional monotonicity, usually easy

to detect judgmentally, mean that additive models

should not be used”, and interdependent EC should

be combined/aggregated to form a KC (Bana e Costa

et al., 2005).

2.3 Modelling Interdependent EC

For cases of interdependent EC, there has been an

increase in studies using procedures with operators

of CI family that belong to the non-additive measure

family. These CI operators are represented by a

mathematical expression that aggregates impact

values of multiple interdependent EC into a single

global score (Mayag et al., 2011).

Several studies have applied these CI operators

in many evaluation contexts such as to: (i) evaluate

supplier’s performance (Clivillé et al., 2006);

(Berrah et al., 2007); (Feyziog

lu et al., 2010),

employees’ performance (Gürbüz, 2010) and action

plans in an organization in industrial contexts

(Clivillé et al., 2007); (Merad et al., 2013); (ii)

assess academic performance of faculty members in

the education sector (Cardin et al., 2013); (iii)

evaluate classical swine fever control strategies in

the animal health literature (Brosig, 2012), (iv)

evaluate a new waste incinerator plant location in

the environment context (Bottero et al., 2013); and

(iv) more recently, in the risk management context,

to build a value- and risk-based performance

measurement and management system (Vernadat et

al., 2013).

Some of these studies lack information about the

questioning protocol applied and do not explain how

to convert impacts into value or how to determine

the CI parameters (Feyziog

lu et al., 2010). Other

studies convert quantitative impacts into values

linearly and therefore presuppose that a unit of

impact has always the same value, which is a strong

assumption (in other words, problems on the

interpretation of commensurate scales - see section

3.1) (Bottero et al., 2013); (Cardin et al., 2013).

Other studies weight EC based only on the notion of

importance (Labreuche et al., 2005); (Brosig, 2012)

with no reference to impact ranges – in fact, this has

been described as the most common critical mistake

in decision analysis (Keeney, 1992). Some studies

require a direct elicitation of numerical information

about the overall value of each option from the DM

(Grabisch et al., 2000); (Grabisch et al., 2008);

(Merad et al., 2013), there being many practical and

theoretical issues regarding this type of elicitation,

as discussed by Morton et al., (2009). Several

studies make use of local judgments, instead of

global judgments, to model interdependencies

between EC – examples are (Clivillé et al., 2006);

(Clivillé et al., 2007); (Gürbüz, 2010); (Merad et al.,

2013); (Vernadat et al., 2013), with most of these

studies using the CI with MACBETH. By local

judgment we mean a judgment involving one EC

alone; by global judgment we mean a judgment

involving the interrelated EC all together.

Nonetheless, the use of local judgments is

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

118

incoherent because under the presence of

interdependencies between several EC, one cannot

assess local judgments in an EC without considering

the levels of impact in the remaining EC. To

illustrate this problem, we recall the study by

Clivillé et al. (2007) that evaluates four actions to

improve the profit margins of a company using CI

with MACBETH. One KC concern of this study is

“service rate”, composed by three EC: “average

delay”, “order receive time” and “accuracy

shipments”. Regarding local judgments for the

“average delay” EC, the DM evaluated as “extreme”

(“6”, see the highlighted judgment in Fig. 1(a)) the

difference in attractiveness between an action “TI”

and a “neutral” action (N). However, if there exist

interdependencies between EC, that judgment may

change with the impacts in the remaining EC and

therefore these should be fixed before the

questioning (a further explanation on this is provided

in sections 2.4 and 3.3). In addition to the previous

problem, some studies such as Clivillé et al. (2006),

Clivillé et al. (2007) and Gürbüz (2010) make use of

two types of matrices – a first matrix with local

judgments (see Fig. 1(a)) and a second with global

judgments (see Fig. 1(b)) – that can be problematic.

Even if the local judgments, present in the first

matrix, were asked to the DM in the form of global

judgments, the use of two matrices could entail

incoherence and inconsistency problems. To expose

these problems, we recall once again the study by

Clivillé et al. (2007). If the “good” and “neutral”

actions present in Fig. 1(a) were taken as being

“neutral” in the remaining EC, i.e. globally

comparing the difference in attractiveness between

two actions (G

) and (N

), the same global

judgment is also present in Fig. 1(b) – see the

highlighted judgment (“weak”). However, that

judgment is inconsistent with the highlighted

judgment in Fig. 1(a). In fact, the difference in

attractiveness between an action “TI” (which is less

attractive than a “good” action in terms of “average

delay”) and a “neutral” action (N) is “extreme”,

which implies that the difference in attractiveness

between a “good” and a “neutral” action needs to be

“extreme”, being inconsistent with the previous

“weak” judgment. Taking into account the limitation

associated to the use of separated matrices, this

paper exploits the use of global judgments within

one single MACBETH global matrix. In addition, it

is worthwhile to note that some studies such as

Clivillé et al., (2006), Clivillé et al., (2007) and

Vernadat et al., (2013) apply MACBETH to build

value functions based just on the set of local

judgments between consecutive ordered levels given

by the DM (diagonal of the MACBETH matrix Fig.

1(a)). However, according to Bana e Costa et al.,

(2008), “it is recommended to ask for some

additional judgments to perform a number of

consistency checks”. If MACBETH is only applied

to the diagonal of the matrix, the procedure does not

make use of all the potential of the MACBETH

method and DSS. Thus, no consistency checks are

made and the MACBETH judgments are used to

solve an equation system by attributing a single

number to each semantic category (with ‘very

weak’=1, ‘weak’=2,..., and ‘extreme’=6) – see Fig. 1

– which is an arbitrary assumption. Therefore, it

seems also important to overcome these issues, as

other numerical values or ranges can be attributed to

each semantic category, and consistency checks are

also a key feature for a procedure to be used in real

decision aid settings.

This study exploits the use of MACBETH with

the CI to model interdependencies and overcoming

the limitations pointed above, using a single

MACBETH matrix with global judgments and all

the features of the MACBETH method and DSS.

The aim is to propose a tool that can easily be used

for decision support, as it will be described in

section 3.

2.4 Choquet Integral Operators

This section introduces basic concepts regarding CI

operators, and a brief explanation of the meaning of

CI parameters. The operators of the CI family,

introduced by Choquet (1953), belong to the non-

additive measures family and are being applied to

model interdependencies between EC. Since we are

dealing with interdependencies, the basic idea

behind these operators consists in questioning the

DM about their preferences on a set of “binary

options” to determine the value of the CI parameters

– Shapley and interaction parameters, which we

describe below. As suggested by the name, these

binary options must perform with superior and

inferior reference levels on each EC. Depending on

the context, best and worst, or good and neutral

references, or other superior and inferior references

can be used (for instance, the good corresponds to an

undoubtedly attractive level and neutral to a level

which is neither attractive nor repulsive (Mayag et

al., 2011) at the eyes of the DM; and the best

corresponds to the most attractive level and the

worst to the most repulsive level (Grabisch et al.,

2004)).

Using the best and worst references, options

which are best and/or worst on all the m EC are used

UsingMACBETHwiththeChoquetIntegralFundamentalstoModelInterdependenciesbetweenElementaryConcernsin

theContextofRiskManagement

119

Figure 1: (a) Local judgments used to build the value function on the EC “average delay” and (b) the matrix that compares

interdependent EC (global judgments). Note that HR, CI, QE and TI are abbreviations of the actions that are being

evaluated, 'human resources', 'continuous improvement', 'quality and environment' and 'technical investment', respectively

(Clivillé et al., 2007).

in the CI – for instance (B

...W

), is a binary

option which is in the best (B) level on EC 1 and 2

and in the worst (W) level on the remainder EC, in a

context of m EC.

To better understand the reason why we should

ask the DM about their preferences on the set of

binary options, consider a case with three EC and

two swings: (i) a swing from an option (W

)

to an option (B

) and (ii) another swing from

) to (B

). These swings just differ on

the level of EC 2 - worst and best in the first and

second swings, respectively. In the context of

independent EC, both swings are equally valued, and

there is no need to take into account of the different

baselines. Under the presence of value

interdependencies, these swings are differently

judged and one needs to consider all the swings with

different baselines.

To apply these operators, the monotonicity

condition is required. E.g., consider the following

sets of elementary concerns S, T and M, and their

corresponding complement sets S

, T

and M

; if S 

T  M, the option which is at the best level in all the

EC present in T and at the worst level in the EC

present in T

) dominates the option

) which is in the best level in all the EC from

S and in the worst level in the EC from S

, because

the former is at least as attractive as the latter, then:

)W,B(V)W,B(VMTS

SAg

TAg



(1)

This condition illustrates that the EC cannot be

modelled as ordinally dependent. After having

information from the DM regarding the numerical

values of the binary options, the CI is applied,

making use of the following formula – eq. system

(2), the general formulation of CI operators.

























)x(v....)x(v)x(v

0)x(v

)})]B...BB({(V

))x(v)x(v[()u(V

u)m()m(u)2()2(u)1()1(

u)0()0(

)m()1i()i(Ag

u)1i()1i(u)i()i(Ag

(2)

Where V

represents the aggregated value (global

score) of an option u, v

(i)

corresponds to the i-th

overall value of the option u in ascending order

thatis related to a specific EC and baseline (for

instance, all worst or all best) in the other EC, x

(i)u

represents the impact level of the option u in the EC

i and V

({B

(i)

}) the aggregated value of an option

which is in the best level in the EC i and in the worst

level in the other EC. Note that this mathematical

formulation is coherent with the impact values (V

and v

(i)

) on an unipolar scale i.e. the impact values

are in the [0,1] range (Grabisch, 2005).

The exponential complexity of the general

formula of the CI has shown to be prohibitive in

many applications (Grabisch, 2005; Grabisch et al.,

2010), as 2

–2 variables need to be determined,

corresponding to the aggregated value of all the

binary options (2

) excluding the known aggregated

values of the options which are worst all over and

best all over, that for convention, value 0 and 1,

respectively (Grabisch et al., 2010). To overcome

this issue, particular CI operators have been

proposed, such as the k-additive ones, highly spread

in decision analysis literature. K-additivity fixes the

degree of interaction between EC: 1-additivity does

not allow interaction between EC (corresponding to

an additive model); 2- additivity allows interaction

up to 2 EC, etc. Note that a k-additive operator, that

allows interaction up to k EC, requires the definition

















parameters, which makes, in practice,

(N,G,G) (G,N,G) (G,G,N) (N,N,G) (N,G,N) (G,N,N) (N,N,N)

(N,G,G)

Null Moderate (3)

(G,N,G)

Null Extreme (6)

(G,G,N)

Null Null (0)

(N,N,G)

Null Weak (2)

(N,G,N)

Null V. Weak (1)

(G,N,N)

Null Weak (2)

(N,N,N)

Null

(a) (b)

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

120

the 2-additivity the best compromise between

complexity and richness of the model (Grabisch et

al., 2010). In the 2-additivity case the mathematical

formulation is given by a linear part, identical to the

additive model, modified by effects coming from the

interaction represented by the second parcel (see the

first equation of the eq. system (3)). Grabisch (1997)

explains how to obtain the eq. system (3) from (2).























jujiui

}j,i{

ijiuii

|)x(v)x(v|I

)x(vs)u(V

(3)

where v

corresponds to the overall value of the

option u on the EC i considering a specific baseline

(for instance, all worst or all best) in the other EC; s

corresponds to the Shapley parameter of the EC i

(see section 3.3); I

the interaction parameter

between the EC i and j.

The Shapley and the interactions parameters are

key concepts for the understanding and analysis of

interdependencies between EC. As remarked in

Grabisch (1997) (p. 171), the Shapley value “can be

interpreted as a kind of average value of the

contribution of element i [EC i in our study] alone in

all coalitions [considering different baselines in the

other EC]”. With regard to the interaction parameter

between 2 EC for instance, it “can be interpreted as a

kind of average value of the added value given by

putting i and j together, all coalitions being

considered” (Grabisch, 1997) (p. 171), i.e. an

average of the added value given by putting together

the 2 EC together, being all the baselines considered.

The interaction parameters I

range in the interval [-

1,1] with: (a) I

> 0 for a synergistic behaviour

between EC i and j, (b) I

< 0 for an antagonistic

behaviour between EC i and j, and (c) I

= 0 when

there is no interaction between EC i and j. In the

next section, the mathematical formulations – see

Eqs. (4) and (7) - of these CI parameters are

represented and examples are used to illustrate these

definitions to DM.

3 METHODOLOGICAL

FRAMEWORK

Departing from a real case study in risk

management, this section explains how the use of a

global MACBETH matrix with the CI can be

applicable to properly model interdependencies

between EC. Special emphasis is also given to the

protocol of questioning and to providing an intuitive

interpretation of the parameters of the CI that can be

explained to a DM.

3.1 Structuring the Evaluation

Problem

A key business area of ALSTOM Power is to

construct and commission power plants. When

building power plants, ALSTOM needs to prioritize

risks that can threaten the construction projects. In a

real case study (Figueiredo et al., 2009) developed

with a group of ALSTOM risk managers (the DM),

one KC identified was” Health and Safety” which

refers to injuries resulting from incidents that occur

inside site barriers, and takes into account two

interdependent EC: (a) number of injuries and (b)

severity of the injury.

For applying the CI, in each EC a descriptor of

impacts and two reference levels within the

descriptor need to be defined. The use of reference

levels in every EC ensures commensurateness

between EC (Grabisch et al., 2004).

“Commensurateness means that one shall be able to

compare any element of one point of view [EC in

our study] with any element of any other point of

view” (Grabisch et al., 2004) (p. 565), by

considering a baseline defined by those reference

levels since we are in the presence of

interdependencies. As described in section 2.4,

depending on the evaluation context, the reference

levels can be defined as best and worst (Labreuche

et al., 2003) or as good (G) and neutral (N) (Mayag

et al., 2011) levels or as other superior and inferior

references. It is important to note that in addition to

the two reference levels – which in the ALSTOM

example, are the “best” and the “worst” levels –

other impact levels can be defined. This is the case

of descriptors in tables 1 and 2.

Table 1: Descriptor of impacts for the EC 1 “Number of

injuries”.

Levels of impact Description

B= Best 0

I 3

W = Worst 10

Since we are dealing with interdependencies and

global preference modelling, the next step is to

define all the combinations of different impact levels

across EC, from tables 1 and 2), being then pairwise

compared in a global MACBETH matrix (see the

next section). In our example, 12 combinations of

UsingMACBETHwiththeChoquetIntegralFundamentalstoModelInterdependenciesbetweenElementaryConcernsin

theContextofRiskManagement

121

impacts are considered (from crossing impact levels

of tables 1 and 2, leading to table 3). Note in table 3

that if there are no injuries, the impact level of the

EC 2 is irrelevant, and so all levels in the

constructed descriptor which have no injuries as a

component are evaluated as being indifferent.

Table 2: Descriptor of impacts for the EC 2 “Severity of

the injury”.

Levels of impact Description

B = Best First aid incident (FAI)

M Medical treatment incident (MTI)

L Loss time incident (LTI)

W = Worst Fatality (Fatal.)

Table 3: Constructed descriptor of impacts for the KC

“Health and Safety” (B and W stand for Best and Worst,

respectively; and the indices refer to the EC 1 and EC 2).

Levels of impact Description

; B

No injury

3 FAI

10 FAI

3 MTI

10 MTI

3 LTI

10 LTI

3 fatalities

W1W

10 fatalities

3.2 Value Measurement with

MACBETH

Many studies, such as Berrah et al., (2007) and

Clivillé et al. (2007), use MACBETH in a first step

to build, what these authors name “elementary

expressions” (value functions) in each EC by using

local judgments (as shown in Fig. 1(a)); and in a

second step to construct a matrix to compare pairs of

EC (a matrix requiring global judgments - as shown

in Fig. 1(b)). As described in detail in section 2.3,

only a simplified version of MACBETH is used in

these studies, and the judgments used in building

‘value functions’ cannot be local judgments; and if

they are global judgments, they coincide with some

of the judgments used in the second step of ‘building

weights’ (see Fig. 1(b)), which demand for

consistency checks when filling the matrices. The

use of a single MACBETH matrix of global

judgments can avoid these judgmental

inconsistencies. Also, using such a matrix allows for

accounting for DM’s differences of opinion or

hesitation that are relevant in real decision contexts.

Accordingly, we propose using one global

MACBETH matrix with all the judgments

comparing all the levels of the constructed descriptor

from Table 3. The rationale behind the use of a

global matrix is as follows:



under the presence of interdependencies, all the

judgments required to evaluate impact levels are

global;



the use of a single global matrix allows for

depicting cases of inconsistencies between

judgments, as well as allows for a clear and

simple protocol of questioning DM; also cases of

differences of opinion or hesitation can populate

the matrix;



and the numerical scales generated by applying

the MACBETH approach to the global matrix

can be used not only with the CI, but also to test

whether other non-additive models are

appropriate (we do not pursue this research line

in this study).

Thus, we propose using a single global matrix, such

as the one depicted in Fig. 2(a) (making use of all

the levels of impact of Table 3). MACBETH is then

used with the DM to quantify the relative

attractiveness of the impact levels through a

qualitative pairwise comparison questioning mode

similar to the one described in section 2.2. For

instance, reading Fig. 2(a), the DM judged as

“moderate” the difference of attractiveness between

“no injury” and “3 FAI”. It should be emphasized

that this is a global judgment for it involves the

impact levels in the two EC, according to the

constructed descriptors described in Table 3.

Fig. 2 presents relevant information from the

single global MACBETH matrix in the M-

MACBETH DSS: Fig. 2(a) presents the matrix of

judgments filled with the DM. Note that

disagreement or hesitation between two or more

semantic categories when making judgments is

allowed – e.g. ‘mod-strg’, ‘strg-vstrg’ and ‘vstrg-

'extr’ in Fig. 2(a), corresponding to ‘moderate or

strong’, ‘strong or very strong’ and ‘very strong or

extreme’, respectively. As this matrix is consistent,

M-MACBETH DSS proposes a numerical scale that

can be adjusted until an interval scale validated by

the DM is achieved (Fig. 2(b)). Note that in Fig. 2(c)

the semantic categories are quantified by more than

one single number.

Judgments in Fig. 2(a) show an example of

judgmental dependencies between the two EC. For

instance, the DM judged the difference in

attractiveness between no FAI (B

) and 10 FAI

) to be ‘moderate or strong’; and the

difference between no fatality (B

) and 10

fatalities (W

) as ‘extreme’– see the highlighted

judgments in Fig. 2(a). These judgments indicate

that the EC “number of injuries” is cardinally value

dependent with the EC “severity of the injury”; and

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

122

other judgments also suggest that the EC “severity

of the injury” is cardinally value dependent with the

EC “number of injuries”.

Once determined the value scores of all the

combinations (see Fig. 2(b)), the next step consists

in calculating and intuitively interpreting the CI

parameters.

3.3 Interpretation of the CI Parameters

The Shapley parameters can be interpreted as an

average value of the contribution of EC i

considering different baselines in the other EC (all

worst, all best, all the combinations with worst and

best levels). Its mathematical representation is given

by eq. system (4). In the context of independency,

the Shapley parameters act like ‘weights’ in the

additive model (Grabisch et al., 2010), in the sense

that the contribution of an EC i is the same,

independently of the chosen baseline to the

remainder EC.

























KAgiKAg

i\NK

)]B(V)BB(V[

|!K|)!1|K|m(

(4)

To better explain this parameter to a DM,

consider the EC “number of injuries” of our case

study. The Shapley parameter for this EC is given by

an average of the value of two swings, e.g.,

averaging the value from improving from 10

fatalities (W

) to no fatality (B

) with the

value from improving from 10 FAI (W

) to no

FAI (B

), the two cases depicted in Fig. 3. Note

that both swings depict the case from going to the

worst to the best level in the first EC, and when

different levels of the second EC are fixed. This

means that with interdependent EC the same swing

needs to be evaluated together with different

baselines. Using the rescaled value scores (from Fig.

2(b)) in eq. system (4), the Shapley parameter for

“number of injuries” is:











































)]BW(V)BB(V[

)]WW(V)WB(V[

21Ag21Ag21Ag21Ag1

(5)

The same logic is applied to calculate the Shapley

parameter for the EC “severity of the injury”. I.e.,

averaging the value of two swings: going from 10

fatalities (W

) to 10 FAI (W

) and going from

no fatality (B

) to no FAI (B

Mathematically, this parameter is given by:











































)]WB(V)BB(V[

)]WW(V)BW(V[

21Ag21Ag21Ag21Ag2

(6)

Regarding the interaction parameter, I

, it can be

interpreted as an average of the added value given

Figure 2: (a) Global MACBETH matrix of judgments, (b) numerical scales (left: basic MACBETH scale; right: MACBETH

scale rescaled), (c) values or ranges of numerical values for the seven MACBETH semantic categories.

(a) (b)

(c)

UsingMACBETHwiththeChoquetIntegralFundamentalstoModelInterdependenciesbetweenElementaryConcernsin

theContextofRiskManagement

123

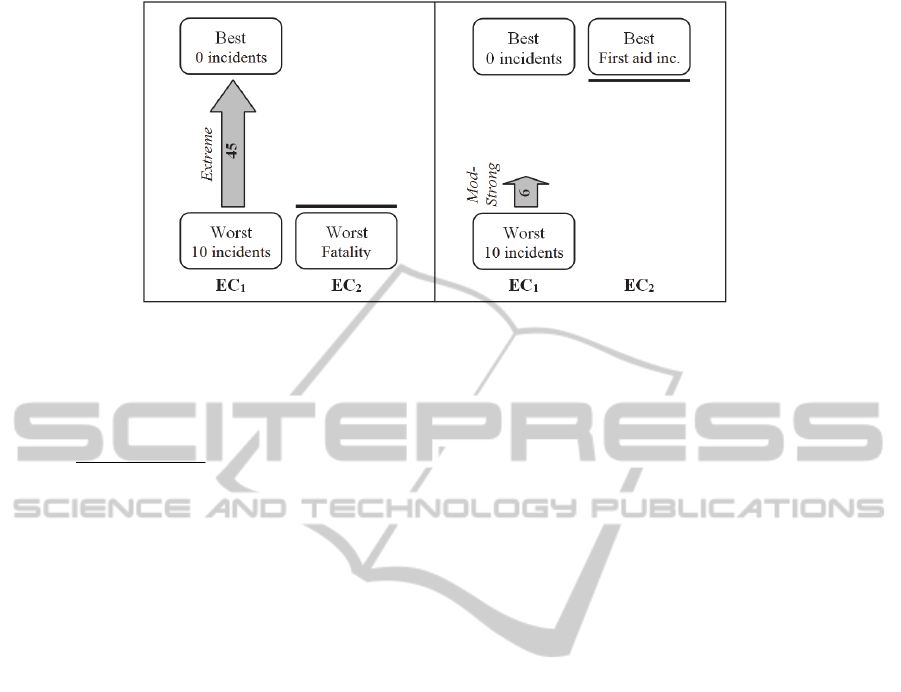
Figure 3: Illustrative image to help the understanding of Shapley parameter of the EC 1 “number of injuries”.

by putting all the EC in a set A together (Grabisch,

1997), when all the baselines are considered.

Mathematically, it is expressed by (7).



















A,NA

),BB(V)1(

)!1|A|n(

|!K||)!A||K|n(

)A(I

LKAg

|L||A|

A\NK

(7)

In case of interdependencies, the combined effect of

having two best levels is more or less than the sum

of individual effects (Bana e Costa et al., 2005).

Thus, there is a parameter to correct this situation,

that is, an interaction parameter named I

(in the

domain [-1,1] with positive values standing for a

synergistic behaviour between EC i and j, negative

values for an antagonistic behaviour between EC i

and j, and null values for no interaction between EC

i and j), as computed in eq. (8).

AgAg

AgAgAgAg

)2W1W(V)2B1W(V

)2W1W(V)2W1B(V)2W1W(V)2B1B(V







(8)

Rewriting eq. (8) and using the rescaled value scores

presented in Fig. 2(b), the I

parameter assumes the

value of -39/45. This value is negative, being in line

with expectations since there is an antagonism

between the two EC. I.e., according to the DM,

independently of the EC, a single best level has

almost the same attractiveness as two best levels,

since there is a very low difference in value between

the referred options - see Fig. 2(b). Said in another

way, no injury of any type of incident or any number

of FAI has almost the same attractiveness as no FAI.

4 CONCLUSIONS

There is scope for developing tools to assist the

modelling of interdependent EC for decision aid.

This paper has identified some problems (such as the

use of local judgments to model interdependencies)

and challenges from using CI operators, proposing a

simple procedure to use the CI operators with

MACBETH. We have shown how a single

MACBETH matrix can be populated with global

(qualitative) judgments, by applying the MACBETH

protocol of questioning and method, and how it can

be coupled with CI operators. This approach allows

for: (i) detecting inconsistent judgments and

modelling cases of differences in opinion or

hesitation; (ii) including more judgments than the

ones required in some of the previous studies

(promoting more robust results), if that is found

appropriate in the decision context; and (iii) using

the M-MACBETH DSS to assist the whole process

with the DM (for instance, detecting inconsistencies

and including judgments of hesitation or of

differences in opinion). This study has illustrated

how one single MACBETH matrix can be the

starting point to test the compatibility of judgments

with the 2-additive CI formulation; and attempted to

provide a more intuitive explanation on the values of

the Shapley and interaction parameters.

Many aspects related to the use of a global

MACBETH matrix require further research. First,

the proposed approach needs to be applied to real

cases (and we are doing so in the health and safety

context). Second, it is relevant to analyse how the

global matrix can assist in cases in which there are

infeasible combinations between impact levels of

different EC, such as with the EC of the reputation

case developed in Bana e Costa et al., (1999). In

fact, some combinations of impact levels across EC

can be infeasible, leading for instance that levels

such as (W

), (W

) and (W

) cannot

be observed in the decision context, and therefore it

is not possible to build “elementary expressions”

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

124

using the same baseline. Third, it is worth exploring

the compatibility of the global MACBETH matrix

with the general formulation of the CI operators for

more than two EC and with other mathematical

formulations, such as with the multilinear one.

Finally, it seems pertinent to exploit the CI

mathematical formulation to model non-monotonic

decision problems which involve not only cardinally

but also ordinally interdependent EC.

ACKNOWLEDGEMENTS

This work was funded by National Funds from the

Portuguese Public Budget through FCT –

Fundação

para a Ciência e a Tecnologia,

within the project

PTDC/EGE-GES/119230/2010.

REFERENCES

Aven, T., 2008. Risk analysis: assessing uncertainties

beyond expected values and probabilities, Wiley.

Bana e Costa C. A., Ensslin L. and Costa A.P., 1998.

Structuring the process of choosing rice varieties at the

south of Brazil. Multi-Criteria Evaluation in Land-Use

Management, Beinat E., Nijkamp P.(eds.), Kluwer

Academic Publishers, Environment & Management. 9:

33-45.

Bana e Costa, C. A. and Beinat, E., 2005. Model-

structuring in public decision-aiding. Working Paper

LSE OR 05.79 – London School of Economics.

Bana e Costa, C. A., Carnero, M. C. and Oliveira, M. D.,

2012. A multi-criteria model for auditing a Predictive

Maintenance Programme. European Journal of

Operational Research 217: 381–393.

Bana e Costa, C. A., Corrêa, E. C., de Corte, J.-M. and

Vansnick, J.-C., 2002. Facilitating bid evaluation in

public call for tenders: a socio-technical approach. The

Internation Journal of Management Science 30: 227-

242.

Bana e Costa, C. A., de Corte, J.-M. and Vansnick, J.-C.,

2012. MACBETH. International Journal of

Information Technology & Decision Making 11(2):

359-387.

Bana e Costa, C. A., Ensslin, L., Corrêa, E. C. and

Vansnick, J.-C., 1999. Decision Support Systems in

action: Integrated application in a multicriteria

decision aid process. European Journal of Operational

Research 113: 315-335.

Bana e Costa, C. A., Lourenço, J. C., Chagas, M. P. and

Bana e Costa, J. C., 2008. Development of reusable

bid evaluation models for the Portuguese Electric

Transmission Company. Decision Analysis 5(1): 22-

42.

Barin, A., Canha, L. N., Abaide, A. R., Orling, R. B. and

Martins, L. F. G., 2012. Selection of renewable energy

technologies in landfills: The M-MACBETH decision

support. Fuelling the Future: Advances in Science and

Technologies for Energy Generation, Transmission

and Storage. A. Mendez-Vilas, Universal-Publishers:

98-102.

Berrah, L. and Clivillé, V., 2007. Towards an aggregation

performance measurement system model in a supply

chain context. Computers in Industry 58: 709-719.

Bottero, M., Ferretti, V. and Mondini, G., 2013. A

Choquet integral-based approach for assessing the

sustainability of a new waste incinerator. International

Journal of Multicriteria Decision Making 3(2/3): 157.

Brosig, J., 2012. Multi-criteria evaluation of classical

swine fever control strategies using Choquet integral

(chapter three). Alternative Classical Swine Fever

control strategies - a simulation study. Agricultural

and Food Sciences. Christian-Albrechts, University of

Kiel. PhD thesis.

Cardin, M., Corazza, M., Funari, S. and Giove, S., 2013.

Building a global performance indicator to evaluate

academic activity using fuzzy measures. Neural Nets

and Surroundings. Apolloni B., Bassis S., Esposito A.

and Morabito F. C., Springer Berlin Heidelberg. 19:

217-225.

Carnero, M. C., 2006. Predictive maintenance programme

audit with MACBETH. Safety and Reliability for

Managing Risk. C. G. Soares and E. Zio, Taylor &

Francis Ltd. 1: 109-115.

Choquet, G., 1953. Theory of capacities. Annales de

l’Institut Fourier 5: 131-295.

Clivillé, V., Berrah, L. and Mauris, G., 2007. Quantitative

expression and aggregation of performance

measurements based on the MACBETH multi-criteria

method. International Journal of Production

Economics 105: 171-189.

Clivillé, V., Mauris, G. and Berrah, L., 2006. A quantified

industrial performance measurement system based on

a Choquet fuzzy integral. IEEE International

Conference on Fuzzy Systems, Vancouver, BC,

Canada.

Edwards, W. and Barron, F.H., 1994. SMARTS and

SMARTER: Improved simple methods for

multiattribute utility measurement. Organizational

Behavior and Human Decision Processes 60: 306-325.

Feyziog

lu, O. and Büyüközkan, G., 2010. Evaluation of

Green Suppliers Considering Decision Criteria

Dependencies. Multiple Criteria Decision Making for

Sustainable Energy and Transportation Systems.

Ehrgott M., Naujoks B, Stewart T.J. and W. J.,

Springer Berlin Heidelberg. 634: 145-154.

Figueiredo, M. S. M. and Oliveira, M. D., 2009.

Prioritizing risks based on multicriteria decision aid

methodology: Development of methods applied to

ALSTOM power. IEEE International Conference on

Industrial Engineering and Engineering Management,

Hong Kong.

Grabisch, M., 1997. k-order additive discrete fuzzy

measures and their representation. Fuzzy Sets and

Systems 92: 167-189.

Grabisch, M., 2005. Une approach constructive de la

UsingMACBETHwiththeChoquetIntegralFundamentalstoModelInterdependenciesbetweenElementaryConcernsin

theContextofRiskManagement

125

décision multicritère. Traitment du Signal 22(4): 321-

337.

Grabisch, M. and Labreuche, C., 2004. Fuzzy measures

and integrals in MCDA. Multiple Criteria Decision

Analysis: State of the Art Surveys. Figueira J., Greco

S. and Ehrgott M., Kluwer Academic Publishers: 563-

608.

Grabisch, M. and Labreuche, C., 2010. A decade of

application of the Choquet integral and Sugeno

integrals in multicriteria decision-aid. Annals of

Operations Reasearch 175(1): 247-290.

Grabisch M., Kojadinovic I. and Meyer P., 2008. A review

of methods for capacity identification in Choquet

integral based multi-attribute utility theory

applications of the Kappalab R package. European

Journal of Operational Research 186: 766-785.

Grabisch M. and Roubens M., 2000. Application of the

Choquet integral in multicriteria decision making.

Fuzzy Measures and Integrals - Theory and

Applications. Grabisch M., Murofushi T. and Sugeno

M., Physica Verlag: 348-374.

Gürbüz, T., 2010. Multiple criteria human performance

evaluation using Choquet integral. International

Journal of Computational Intelligence Systems 3(3):

290-300.

Keeney, R. L., 1992. Value-Focused Thinking: a path to

creative decision making. Cambridge, Harvard

University Press.

Labreuche, C. and Grabisch, M., 2003. The Choquet

integral for the aggregation of interval scales in

multicriteria decision making. Fuzzy Sets and Systems

137: 11–26.

Labreuche C. and Le Huéde F., 2005. Myriad: a tool suite

for MCDA. International Conference of the Euro

Society for Fuzzy Logic and Technology (EUSFLAT),

Barcelona, Spain.

Linkov, I., Satterstrom, F. K., Kiker, G., Batchelor, C.,

Bridges, T. and E., F., 2006. From comparative risk

assessment to multi-criteria decision analysis and

adaptive management: Recent developments and

applications. Environment International 32: 1072–

1093.

Marichal, J.-L., 2000. An axiomatic approach of the

discrete Choquet integral as a tool to aggregate

interacting criteria. IEEE Transactions on Fuzzy

Systems 8(6): 800-807.

Mayag, B., Grabisch, M. and Labreuche, C., 2011. A

characterization of the 2-additive Choquet integral

through cardinal information. Fuzzy Sets and Systems

184: 84-105.

Merad, M., Dechy, N., Serir, L., Grabisch, M. and Marcel,

F., 2013. Using a multi-criteria decision aid

methodology to implement sustainable development

principles within an organization. European Journal of

Operational Research 224: 603–613.

Morton, A. and Fasolo, B., 2009. Behavioural decision

theory for multi-criteria decision analysis: a guided

tour. Journal of the Operational Research Society 60:

268-275.

Shah, L. A., Etienne, A., Siadat, A. and Vernadat, F. B.,

2013. Value-risk graph: a decision-making tool for

supply chain and industrial system engineering. 6th

IFAC International Conference on Management and

Control of Production and Logistics. September 11-

13, Fortaleza, Ceará, Brazil.

Vernadat, F., Shah, L., Etienne, A. and Siadat, A., 2013.

VR-PMS: a new approach for performance

measurement and management of industrial systems.

International Journal of Production Research: 1-19.

von Winterfeldt D. and Edwards W., 1986. Decision

analysis and behavioral research. Cambridge,

Cambridge University Press.

Williams, T. M., 1996. The two-dimensionality of project

risk. International Journal of Project Management

14(3): 185-186.

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

126