
Computational Study for Workforce Scheduling and Routing Problems
J. Arturo Castillo-Salazar, Dario Landa-Silva and Rong Qu
Automated Scheduling, Optimisation and Planning (ASAP) Research Group, School of Computer Science,
Jubilee Campus, The University of Nottingham, Wollaton Road, NG8 1BB, Nottingham, U.K.
Keywords:
Workforce Scheduling and Routing, Mathematical Programming, Benchmark Datasets and Results.
Abstract:
We present a computational study on 112 instances of the Workforce Scheduling and Routing Problem
(WSRP). This problem has applications in many service provider industries where employees visit customers
to perform activities. Given their similarity, we adapt a mathematical programming model from the literature
on vehicle routing problem with time windows (VRPTW) to conduct this computational study on the WSRP.
We generate a set of WSRP instances from a well-known VRPTW data set. This work has three objectives.
First, to investigate feasibility and optimality on a range of medium size WSRP instances with different dis-
tribution of visiting locations and including teaming and connected activities constraints. Second, to compare
the generated WSRP instances to their counterpart VRPTW instances with respect to their difficulty. Third, to
determine the computation time required by a mathematical programming solver to find feasible solutions for
the generated WSRP instances. It is observed that although the solver can achieve feasible solutions for some
instances, the current solver capabilities are still limited. Another observation is the WSRP instances present
an increased degree of difficulty because of the additional constraints. The key contribution of this paper is to
present some test instances and corresponding benchmark study for the WSRP.
1 INTRODUCTION
A lot of research has been dedicated to the Vehicle
Routing Problem with Time Windows (VRPTW).
Research literature on workforce scheduling is also
abundant. For these problems, benchmark instances
and results have been published, which can be used
to assess the performance of new proposed solu-
tion methods. This is not the case for the com-
bined problem of Workforce Scheduling and Rou-
ting. To the best of our knowledge, there are no
benchmark datasets that have been studied to the same
extent as VRPTW and workforce scheduling inde-
pendently. Our long term goal is to develop po-
werful algorithms to tackle WSRP. This study re-
presents our first step towards achieving that goal.
Here, we take some well-known VRPTW instances
(Solomon, 1987) and include additional data to trans-
form them into WSRP instances. We then conduct
computational experiments to assess the difficulty of
these generated WSRP instances compared against
the original VRPTW ones. We use a modern ma-
thematical programming solver in our experiments al-
lowing us to obtain an updated perspective of the ca-
pability of such solution method to tackle the WSRP
and establishing a base-line to compare future work.
We use the term Workforce Scheduling and Rou-
ting Problem (WSRP) in reference to problems where
employees travel across different locations to perform
their work. WSRPs combine characteristics of the
general employee scheduling problem (Glover and
McMillan, 1986) and vehicle routing problem with
time windows (VRPTW) (Solomon, 1987) to des-
cribe the work of mobile employees in an organisa-
tion. Some service provider-industries require em-
ployees to visit customers at their premises to per-
form specific activities. Examples of such service
industries include healthcare, security, communica-
tions, domestic cleaning, etc. Customers are located
at different addresses and require service within a
time window or other timing requirement. In most
cases, travelling time is considered part of emplo-
yees’ working time. As a result, reductions in travel
time could mean more time to perform additional cus-
tomers visits. Scheduling employees to meet these
time windows on visits whilst reducing travel time is
a difficult process for medium to large size scenarios.
WSRP’s size is often given by the number of emplo-
yees and the number of activities.
Although at first, WSRP could be seen as iden-
tical to VRPTW, there are important differences. In
VRPTW scenarios, the number of vehicles is usually
434
Arturo Castillo-Salazar J., Landa-Silva D. and Qu R..
Computational Study for Workforce Scheduling and Routing Problems.
DOI: 10.5220/0004833904340444
In Proceedings of the 3rd International Conference on Operations Research and Enterprise Systems (ICORES-2014), pages 434-444
ISBN: 978-989-758-017-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

not fixed (minimising the number of vehicles is often
the goal) and vehicles types are often the same. Ne-
vertheless, research on scenarios with heterogeneous
fleet of vehicles (Dondo and Cerd
´
a, 2007) and where
the number of vehicles is limited (Chuin Lau et al.,
2003) has also been reported. In WSRP scenarios, the
number of employees is usually known in advance.
An objective is often to balance the workload instead
of reducing the number of workers. Workforce is he-
terogeneous since every employee is different consi-
dering their individual skills, training, attitudes, etc.
Castillo-Salazar et al. (2012) describe WSRP’s
main characteristics. Time window refers to the pe-
riod by which the service should start. Start and end
location indicate if employees start/end their work at
home, central building, etc. Service time refers to ac-
tivities’ duration at customer premises. Skills reflect
the potential diversity of abilities in the workforce.
Transportation mode specifies if it is possible to use
more than one medium of transportation between the
visiting locations, i.e. walking, car, public transport,
etc. Connected activities handle all time dependant
relations between two or more activities, for example
synchronisation and precedence. Teaming considers
activities needing a team of employees. Clustering,
refers to forming groups of visits based on geographi-
cal location usually to reduce the size of the problem.
Given the similarity between WSRP and VRPTW,
researchers have successfully utilized VRPTW mod-
els and solution techniques to obtain feasible solu-
tions for WSRP-like scenarios. For example, home
healthcare (Cheng and Rich, 1998; An et al., 2012;
Nickel et al., 2012), patrolling of security officers
(Misir et al., 2011; Chuin Lau and Gunawan, 2012),
engineers/technicians on field (G
¨
unther and Nis-
sen, 2012). These previous works cover: time win-
dows, start/end location, skills, service time and trans-
portation mode. Other characteristics such as con-
nected activities, teaming and clustering have been
researched to a lesser extent in the WSRP literature.
There are some exceptions, for example, connected
activities have been considered by Rasmussen et al.
(2012), while teaming has been considered in Li et al.
(2005) and Dohn et al. (2009).
Connected activities and Teaming are important
features of WSRP because they allow the modelling
of scenarios with linked activities. Depending on the
service sector, this could be for example, conducting
a 2nd visit within a day to administer an additional
medication dose to the patient, or bringing two spe-
cialist technicians at the same time to install and cal-
ibrate equipment, etc. These constraints already exist
in the VRPTW literature (Toth and Vigo, 1987; Tail-
lard et al., 1996; Bredstr
¨
om and R
¨
onnqvist, 2008).
Bredstr
¨
om and R
¨
onnqvist (2008) apply their ma-
thematical model of VRPTW with temporal pre-
cedence and synchronisation constraints to tackle
home healthcare and forest operations, which are ex-
amples of WSRP scenarios. In their experiments, the
majority of instances have 20 visits only and all visits
are uniformly distributed in a square area, hence with
no apparent clusters of visits. As part of our study
we adapt 112 VRPTW instances, 56 of them contain
25 visits and the remaining 56 contain 50 visits. Ad-
ditionally, clusters of visits are present in half of the
instances. This brings us closer to having problem
instances reflecting real-world WSRP scenarios.
Our study has three objectives. The first objective
is to use Bredstr
¨
om and R
¨
onnqvist (2008) VRPTW
model to tackle medium size WSRP instances (in-
cluding 20 or more visits). The second objective is to
assess the difficulty of the adapted problem instances
as a result of adding connected activities and team-
ing constraints. We aim to test by experimentation
whether WSRP is a more difficult problem to solve
than traditional VRPTW for a mathematical program-
ming solver. The third objective is to establish the
computational time that a mathematical solver needs
to find feasible solutions, if such solutions exist, for
our adapted data set. Regarding the third objec-
tive, most research papers report computation time
within minutes when solving small instances. Using a
solver to obtain optimal solutions in medium to large
instances has been reported to take up to 64 hours (Li
et al., 2005). Commonly, real-world WSRP scenarios
have a planning time horizon of one day, and the prob-
lem can be solved at the beginning of the working day
or at the end of the previous one. In such scenarios,
waiting many hours to obtain a solution is not prac-
tical. Therefore, our experiments consider three dif-
ferent computation time settings for the mathematical
solver: 15 min, 60 min and 240 min.
The remaining of the paper has 4 sections. Section
2 explains Bredstr
¨
om and R
¨
onnqvist (2008) model,
and the adaptations performed for tackling WSRP.
Section 3 describes the data set used and how it is
generated from the original widely known Solomon
(1987) instances. Section 4 describes our experiments
and results, divided in 3 sub-sections, each of them
focusing in one of the three objectives stated above.
Finally, section 5 provides our conclusions.
2 INTEGER LINEAR MODEL
The integer linear programming model used for the
present computational study is the one by Bredstr
¨
om
and R
¨
onnqvist (2008). The model was chosen be-
ComputationalStudyforWorkforceSchedulingandRoutingProblems
435

cause it considers synchronisation and precedence
constraints. Both constraints are necessary to model
situations in which more than one employee need to
arrive at a location at the same time or when activi-
ties depend on the finishing/starting time of other ac-
tivities. There are other models in the literature that
contain these constraints, for example the one by Ko-
rsah et al. (2010). But the Korsah et al. model uses
more variables to capture the waiting time of vehi-
cles. Another model including synchronisation and
precedence constraints is the one by Rasmussen et al.
(2012) , which also uses more variables to record if
an activity is performed or not by an employee. We
aim to schedule all activities, otherwise we consider
the scenario as infeasible. Such infeasible scenarios
occur due to limited number of workers, and the avail-
ability or lack of skills. The extra variables in the
models by Korsah et al. and Rasmussen et al. re-
quire much more memory when tackled by the solver.
Since the features modelled with those extra variables
are not required in our study we opt for the Bredstr
¨
om
and R
¨
onnqvist model.
In the WSRP the number of employees is limited.
The set N is all clients locations. Then, o,d repre-
sent the same location (start and end) but two differ-
ent nodes are required for modelling purposes. A is
a set containing all clients locations N plus o,d. K
is the set of all employees. Time windows are given
with the values a
i
for the earliest start time and b
i
for
the latest start time of visit i. All visits have a set du-
ration given by D
i
. Travel time between visits i and j
is a predefined value T
i j
. Variables t
ik
contain the time
when visit i starts, performed by employee k, all times
are given in minutes after the start of the time horizon.
Finally, each employee has a time window represent-
ing their working time. Terms a
k
i
and b
k
i
represent the
start and the end of the working time for employee k
respectively. The term E
i j
includes the travelling time
from visit i to visit j plus the duration of visit at node
i (E
i j
= T
i j
+ D
i
).
The objective function (1) has two elements: the
cost for assigning a preferred visit to an employee c
ik
and the travel time of all employees when performing
their visits. In the original model by Bredstr
¨
om and
R
¨
onnqvist there is a third element to balance distance
and time. Such element is not used here because dis-
tance and travel time between visits or locations are
equal in the Solomon instances. We set the weights in
the objective function (1) to the same value α
p
= α
T
.
All visits need to be performed (2). All employees
must start and return to the initial location after the
last visit o, d (3). Constraint (4) preserves employees’
flow conservation. Every visit time window must be
satisfied (5, 6 and 7). All visits need to be performed
during the employees starting and ending times (8).
When two or more visits require starting at the same
time, a synchronisation constraint (9) is necessary for
every pair of visits. Other type of temporal dependen-
cies are covered by constraint (10). The binary deci-
sion variables x
i jk
are set to 1 if employee k travels
from i to j and are set to 0 otherwise (11). Apart from
the objective function, another change made to the
model is in the scheduling variables t
ik
. In the orig-
inal model the scheduling variables are positive real
numbers. Here, the scheduling variables are enforced
to be positive integers (12). Such change makes the
problem harder to solve but provides an exact time
for the activities without introducing rounding errors
for seconds and milliseconds. In our data sets, all em-
ployees have the same starting and ending time which
matches the time horizon of every instance.
min α
p
∑
k∈K
∑
(i, j)∈A
c
ik
x
i jk
+ α
T
∑
k∈K
∑
(i, j)∈A
T
i j
x
i jk
(1)
s.t.
∑
k∈K
∑
j:(i, j)∈A
x
i jk
= 1 ∀ i ∈ N, (2)
∑
j:(o, j)∈A
x
o jk
=
∑
j:( j,d)∈A
x
jdk
= 1 ∀ k ∈ K, (3)
∑
j:(i, j)∈A
x
i jk
−
∑
j:( j,i)∈A
x
jik
= 0 ∀ i ∈ N, ∀ k ∈ K, (4)
t
ik
+ E
i j
x
i jk
≤ t
jk
+ b
i
− b
i
x
i jk
∀k ∈ K,∀i, j ∈ A, (5)
a
i
∑
j:(i, j)∈A
x
i jk
≤ t
ik
∀ k ∈ K, ∀ i ∈ N, (6)
t
ik
≤ b
i
∑
j:(i, j)∈A
x
i jk
∀ k ∈ K, ∀ i ∈ N, (7)
a
k
i
≤ t
ik
≤ b
k
i
∀ k ∈ K, ∀ i ∈o,d, (8)
∑
k∈K
t
ik
=
∑
k∈K
t
jk
∀ i, j ∈ P
sync
, (9)
∑
k∈K
t
ik
+ p
i j
≤
∑
k∈K
t
jk
∀ i, j ∈ P
prec
, (10)
x
i jk
∈ {0,1} ∀ k ∈ K, ∀ i, j ∈ A, (11)
t
ik
∈ Z
+
∀ k ∈ K, ∀ i ∈ N. (12)
(13)
3 WSRP PROBLEM INSTANCES
3.1 Description of Solomon’s Instances
Solomon (1987) data set for the VRPTW has been
used broadly in the literature. There are 56 instances
grouped according to two criteria: varying the plan-
ning horizon and visits-location. Combining these
criteria forms 6 groups: R100, R200, C100, C200,
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
436

(a) Clustered - C (b) Random - R (c) Mixed - RC
Figure 1: Three different types of location arrangement of visits in the Solomon’s data set (Solomon, 1987). Original
instances with 100 visits each. The depot is identified with a black cross.
RC100, RC200. Groups R100 and RC100 have short
planning horizon (230 and 240 minutes) and groups
RC200, R200, C100 and C200 have longer planning
horizons of more than 900 minutes. Considering the
location of visits which vehicles have to complete,
there are three different types: clusters (C), random
(R) and mixed (RC). Figure 1 shows the layout of
the instances according to their location of visits. In
sub-figure 1(a) (C group) ten clusters can be appre-
ciated. A random layout of visit locations is present
in sub-figure 1(b) (R group). Finally, a mixed sce-
nario is shown in sub-figure 1(c) with five clusters
and some random visits (RC group). All instances
in each type of visit-location group (C, R and RC)
have the same distribution of visits. In total, there are
17 clustered, 23 random and 16 mixed instances. All
clustered instances (C) have a visit duration of 90 min
while random and mixed instances (R and RC) have a
visit duration of 10 min.
3.2 Generating WSRP Instances
We took a data set with 56 instances having 100 vis-
its each. For this study we use versions of each in-
stance with 25 and 50 visits since preliminary exper-
iments with all 100 visits resulted in the solver run-
ning out of memory. We took the first 25 and 50 visits
in the order in which they appear in the original 100
visit file since as suggested by Solomon, doing this
provides a good distribution of visits. In total, 112
instances were generated, 56 instances with 25 vis-
its and 56 instances with 50 visits. Moreover, the 112
instances were adapted to include enough information
to be representative of WSRP scenarios. First, in the
VRPTW there is no limit in the number of vehicles
to complete all visits. In contrast, in WSRP the num-
ber of employees is known in advance, perhaps with
the exception of casual employees who are called “on
demand” if needed. Even though, casual employees
can be added for a day or two when necessary, it is
often preferred no to use them, and try to complete
all visits with the staff available. As a result, we de-
fined a set of workers for every instance by setting
the ratio of employees to visits to 1/5. This value was
decided following our conversations with a home care
provider, and it also matches the assumption by Bred-
str
¨
om and R
¨
onnqvist (2008). The home care provider
told us that their average visit duration is currently
50 min. At present, the provider gives a maximum
of 30 min for the carer to move from one location to
another and carers must start and end their working
day at the provider’s main site. Current shift length
is 8 hours with a break of 1 hour, or two breaks of
30 min each. Taking this into account, we determine
the mean visits per employee per day x by solving the
simple equation 50x + 30(x + 1) + 60 = 480, where
x + 1 is the number of trips in a route including the
last trip returning to the provider’s main site. It is as-
sumed that the breaks are taken near a visit. The result
is x = 4.875 rounded to 5. In other words, instances
with 25 activities have a workforce of 5 employees
and instances with 50 visits have a workforce of 10
employees. In some instances we further reduced the
workforce by one employee emulating an absent em-
ployee. The capacity of each vehicle in VRPTW can
refer to the number of hours every employee is al-
lowed to work under his/her contractual agreement.
In this study, we it is assumed that employees are
available to work throughout the time horizon.
Teaming is included in the adapted instances by
making a percentage of visits to require more than one
employee to be performed. As suggested by Bred-
str
¨
om and R
¨
onnqvist (2008, p. 11), we set 10% of
the visits in each instance to requiring two employees
for the whole duration of the visit. Employees’ pref-
erences are not included in the original Solomon data
set but required to compute the objective function (1).
For this, we randomly assigned a preference (high,
medium, low and not-preferred) value for each em-
ployee in regards to each visit.
ComputationalStudyforWorkforceSchedulingandRoutingProblems
437

Finally, the last addition to the data set is con-
nected activities. There are 5 types of connected ac-
tivities, as defined by Rasmussen et al. (2012): syn-
chronisation, overlapping, minimum difference, max-
imum difference and min-max difference. Each type
relates two visits. Synchronisation when both activi-
ties start at the same time. Overlapping, for a period
of time both activities are being performed simulta-
neosly. Minimum difference restricts the start of the
second activity after a minimum time has passed from
the staring of the first one. Maximum time difference
limits the start of the second activity from immedi-
ately up to a defined value. Finally, min-max differ-
ence is a combination of the previous two, with a spe-
cific time window (minimum and maximum starting
time) for the second activity in relation to the com-
mencing of the first one. The procedure to add con-
nected activities constraints is as follows. Every visit
has a 25% probability of having a connected activity
constraint with the activity that immediately follows
in the original Solomon’s instance. Rasmussen et al.
(2012) used three different percentages 10%, 20% and
30%. The visits order remain the same. If there is
a connected activity constraint, then we must choose
between one of the 5 different types. In real scenar-
ios the two first types (synchronisation and overlap-
ping) occur more often than the last three. Hence,
we assigned the following probabilities to each type:
35% to each synchronisation and overlapping; 10%
to each of maximum, minimum and min-max differ-
ence. When using the previously described procedure
to create connected activities constraints, sometimes
the added constraints make the instance infeasible,
e.g. an overlapping constraint for two activities that
given their duration and time windows can definitely
not overlap. In such cases the constraint is discarded
and another one tried.
Changing the Solomon dataset with the adap-
tations described above, could make the problem
instances to become easier to solve than the origi-
nal ones. The experiments in subsection 4.3 aim to
test this possibility by solving the WSRP model with
and without the teaming and connected activities con-
straints. In the following, we refer to the 112 gener-
ated problem instances as WSRP instances.
3.3 Other Instances in the Literature
There are other problem instances used in published
papers relating to problems that can be seen as WSRP.
Examples include the Akjiratikarl et al. (2007) data
set which is based on a council in Wales scheduling
care workers across the region The home health care
data set by Bertels and Fahle (2006) is a generated
one and it consists of 120 test scenarios containing
between 20 and 50 nurses and up to 200 jobs. Such
data set does not include any jobs requiring more than
one worker (nurse) and there is no presence of con-
nected activities. The manpower allocation problem
(Li et al., 2005) contains job-teaming constraints but
the number of instances (25) is limited for our study
and the number of jobs in each instance is on average
300, which the solver cannot handle. Moreover, there
is no set number of workers available since the objec-
tive is to find a minimum workforce size. There is also
the data set by Cheng and Rich (1998) which is con-
sidered too small, with 4 nurses and 10 jobs. Finally,
the most complete data set which includes both team-
ing and connected activities constraints is the one by
Rasmussen et al. (2012) . In that data set, the majority
of instances are understaffed which leaves some activ-
ities not performed. The IP Model used here does not
consider such possibiliy so it would result in having
infeasible instances.
4 EXPERIMENTS AND RESULTS
4.1 Description of Experiments
Three sets of experimental results are described in the
following subsections. The first set relates to the ob-
jective of tackling WSRP with the IP model by report-
ing on gap achieved. The second set addresses the
second objective of studying whether or not the ad-
ditional connected activities and teaming constraints
makes the WSRP easier or more difficult to solve.
Finally, the third set is associated to the first set to
analyse how much time is necessary to find a feasible
solution for the adapted instances. Additionally, the
third set of experiments also provides an insight into
the type of method used by the solver when finding
feasible solutions, either through branching-cutting or
with heuristics. All the experiments are performed
using Gurobi version 5.5 and CPLEX 12.5. The re-
sults produced by the two solvers do not differ much.
Nevertheless, using our computational setting, Gurobi
finds better results for more instances. Therefore, we
report the Gurobi results only. No parameter tuning
was performed on either of the solvers apart from set-
ting a time limit. Our goal does not include to com-
pare both solvers. A x64-based computer with a pro-
cessor Intel Core 2 Duo (3.16 GHz) and 4 gigabytes
of RAM was used in the experiments.
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
438

(a) Cl00 with all constraints and 15 min time limit. (b) C200 with all constraints and 15 min time limit.
(c) R200 with all constraints and 15 min time limit. (d) RC200 with all constraints and 15 min time limit.
Figure 2: Results of experiments with time limit of 15 min showing gap reduction for feasible instances found (26 in total).
4.2 Feasibility and Optimality
All 112 WSRP instances are tackled using the model
described in section 2. We initially set the compu-
tational time to 15 minutes. For every instance, we
record the time at which the first feasible solution is
found, if such solution exits. Also, for instances with
at least one feasible solution, we report on the gap re-
duction when the computation time limit is reached.
If at any time the gap is 0, i.e. an optimal solu-
tion is found, that time is also recorded. Instances
are grouped by the distribution of visits (clustered,
random or mixed) and the size of the planning hori-
zon. Knowing for which instances feasible solutions
are achieved provides an insight into the clustering
component of the visits since around a third of the
instances have clustered visits e.g. C100 and C200.
In this first set of experiments, at least one feasible
solution is achieved for 26 out of the 112 instances.
From those 26 instances, the optimal solution (gap
0.0%) is found for 7 of them. Figure 2 shows the
gap reduction achieved within 15 minutes for the 26
instances. The figure shows one graph for each of the
4 groups (C100, C200, R200, RC200) with feasible
solutions found. For the remaining 86 instances, in-
feasibility was reported by the solver for 7 instances.
In the remaining 79 instances, Gurobi times out after
15 minutes with no additional information. No fea-
sible solution is achieved within 15 minutes for any
instance within the R100 and RC100 groups. Even-
thoug all instances involve the same number of activ-
ities, groups R100 and RC100 seem harder to solve
because they have a shorter planning horizon (230 and
240 minutes) when compared to the other four groups
where the planning horizon is 900 minutes or more.
The duration of the planning horizon also dictates em-
ployees’ available working time, resulting in less ca-
pacity of working hours in such scenarios. Addition-
ally, the random distribution of visits in these two (R)
groups (see Figure 1) does not exploit the cluster fea-
ture that other scenarios present. Once an employee
enters a cluster region it is very likely that he/she re-
mains there for other visits rather than travelling to a
different cluster location, saving time overall. Gurobi
finds only 4 feasible solutions for instances in group
R200 with randomly spread visits. All the 7 optimal
solutions that were found (see Table 1) are in the clus-
tered groups (C) and the majority in group C100. This
group has the second largest planning horizon of all
instances (1236 minutes) giving more working time
overall. All infeasible instances are shown in Table 2,
almost all of them corresponding to group R100.
4.3 Effect of Teaming and Connected
Activities Constraints
In these experiments we remove the constraints for
teaming and connected activities from the 112 WSRP
instances. Therefore, all visits require one employee
only and every activity is independent of the others.
The other attributes, planning time horizon length,
activities duration, activities time windows, etc. re-
main unchanged. We also allow 15 minutes of com-
putational time for each instance. As in the previous
ComputationalStudyforWorkforceSchedulingandRoutingProblems
439

Table 3: Number of feasible solutions found in every group. Values in parentheses indicate the number of instances per group.
Teaming and Connected Activities (TC) Time Limit C100(18) C200(16) R100(24) R200(22) RC100(16) RC200(16) Total(112)
1 with TC constraints 15 min 10 8 0 4 0 4 26
2 without TC constraints 15 min 13 13 3 12 8 10 59
Table 1: Instances where Gurobi finds optimal solutions,
showing two times: first feasible solution and optimal.
Instance Feasible Optimal Instance Feasible Optimal
C101 25 5 0.62 0.62 C105 25 5 2.0 3.86
C105 50 10 168.0 522.08 C106 25 5 0.67 0.67
C107 25 5 2.0 2.78 C201 25 5 1.0 1.63
C201 50 10 43.0 44.99
Table 2: Infeasible instances and time required to prove in-
feasibility.
Instance Time Instance Time
R101 25 5 1.53 R101 50 10 20.05
R102 50 10 82.75 R103 50 10 104.99
R104 50 10 296.3 R105 25 5 4.78
RC102 50 10 188.63
experiments, we record the number of instances for
which at least a feasible solution is achieved and the
corresponding rate of improvement (gap reduction).
Our aim is to find out if more feasible solutions are
found compared to the results from the previous ex-
periments (subsection 4.2). If that is the case, it could
suggest that teaming and connected activities make
the problem harder to solve. Constraints for teaming
and connected activities are considered together be-
cause a teaming constraint is modelled as a connected
activity constraint of the synchronisation type. If a
visit x requires a team of m workers, then m−1 virtual
visits are created with the same requirements as the
original visit x. Afterwards, a synchronisation con-
straint is created between each possible pair of vis-
its. Such procedure guarantees that all employees re-
quired to perform visit x arrive at the same time, ef-
fectively forming a team.
Table 3 shows the number of instances in each
group for which at least one feasible solution was
achieved within 15 minutes computation time. The
first row summarises the results from the first set of
experiments in the previous subsection. The second
row summarises the results when teaming and con-
nected activities constraints are relaxed. After com-
paring both rows it is clear that removing these con-
straints allows the solver to find feasible solutions for
more instances. If we compare only the instances
where a known feasible solution is known (from pre-
vious subsection 4.2), results in Table 4 show that
significantly better gaps are achieved (approximately
10% overall) when the teaming and connected activ-
ities constraints are relaxed. Table 4 shows that the
version of the problem instance without these con-
straints achieves a better gap than its complete coun-
terpart. As it can be noticed, for the majority of
instances the result is = or >, with the exception of
one instance (C106 50 10) but the difference is very
small (0.04%). Additionally, for 59 of the instances a
feasible solution is achieved when both teaming and
connected activities constraints are relaxed This is in
contrast to the only 26 instances for which a feasible
solution was found when both types of constrains are
present.
In all groups of instances, removing the teaming
and connected activities constraints produces an im-
provement in the number of instances achieving feasi-
bility. Groups R100 and RC100 for which no feasible
solution was found before, now have 3 and 8 instances
with feasible solutions respectively. But overall, these
groups still remain as the two groups with the least
number of feasible solutions reported. Such result
confirm that even when the teaming and connected
activities constraints are relaxed, a group of clustered
visits is easier to solve than a random distribution of
visiting locations. In general, our results for this sec-
ond set of experiments suggest that the adaptations
made to the Solomon instances to generate WSRP
problem instances, make the problem harder for a cur-
rent solver to tackle. Figure 3 shows the gap reduction
for the instances achieving feasibility within 15 min-
utes (900 seconds) without teaming and connected ac-
tivities constraints, grouped by location and planning
horizon. In the next set of experiments, we extend the
computation time given to the solver in order to in-
vestigate the rate of improvement in the gaps and find
more feasible solutions.
4.4 Extending Computational Time
In this set of experiments we increase the computa-
tion time from 15 to 60 minutes and then up to 240
minutes. Our objective is to further investigate feasi-
bility and optimality in the WSRP instances with ex-
tended computation time available for the mathemati-
cal programming solver. In the results of the first set
of experiments (section 4.2) Gurobi timed out in 79
instances without finding feasible solutions for any
of them. In this third set of experiments, those 79
instances, without conclusive results before, are tack-
led once more using 60 minutes and 240 minutes of
computation time. A computation time beyond 240
minutes is not practical for a problem with a planning
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
440

(a) Cl00 without TC constraints. (b) C200 without TC constraints.
(c) Rl00 without TC constraints. (d) R200 without TC constraints.
(e) RCl00 without TC constraints. (f) RC200 without TC constraints.
Figure 3: Gap reduction of feasible solutions for instances without Teaming and Connected activities (TC) constraints.
Table 4: Feasible solutions with final gap achieved after
15 min computation time. The second (w/TC) and third
(wo/TC) columns show gap results with and without the
teaming and connected activities constraints respectively.
Instance w/TC wo/TC Instance w/TC wo/TC
C101 25 5 0 = 0 C101 50 10 0.07 > 0
C102 25 5 22.1 > 12.4 C105 25 5 0 = 0
C105 50 10 0.04 > 0 C106 25 5 0 = 0
C106 50 10 0.03 < 0.34 C107 25 5 0 = 0
C107 50 10 2.9 > 0 C108 25 5 20.4 > 4.55
C201 25 5 0 = 0 C201 50 10 0 = 0
C202 25 5 26.1 > 1.63 C203 25 5 49.7 > 25.4
C205 25 5 21.8 > 1.82 C206 25 5 27.2 > 1.56
C207 25 5 40.6 > 11.9 C208 25 5 50.5 > 16.5
R201 25 5 5.77 > 4.56 R202 25 5 33.3 > 16.3
R205 25 5 16.3 > 6.52 R209 25 5 53.2 > 14
RC201 25 5 9.29 > 0.84 RC202 25 5 32.9 > 31.5
RC205 25 5 21.2 > 19.6 RC206 25 5 58.8 > 44.9
Mean w/TC: 18.93 Mean wo/TC: 8.24
horizon of 1 day in the majority of WSRP scenarios.
Increasing the computational time to 60 minutes
for the 79 instances produced feasible solutions for 3
Table 5: Instances for which feasible solutions were found
within the time limit of 60 minutes. The time in seconds
at which Gurobi found the first feasible solution is shown,
together with the initial gap and final gap values.
Instance 1st feasible Initial Final
R201 50 10 2594 18.6% 12.3%
R210 25 5 2099 42.6% 31.7%
RC106 25 5 1915 40.9% 39.1%
of those instances, none of them achieving optimal-
ity. The remaining 76 instances again timed out with
no further information. Details of these additional re-
sults is shown in Table 5. It should be noted that the
computation time for finding the first feasible solu-
tion for the 3 instances is more than 30 minutes (1800
seconds). The difference between the initial gap and
the final gap values is less than 11%. Figure 4 shows
the gap reduction achieved over the given computa-
tion time.
We then increased the computation time from 60
to 240 minutes, aiming to find out the practical lim-
its (assuming that more than 4 hours of computation
ComputationalStudyforWorkforceSchedulingandRoutingProblems
441
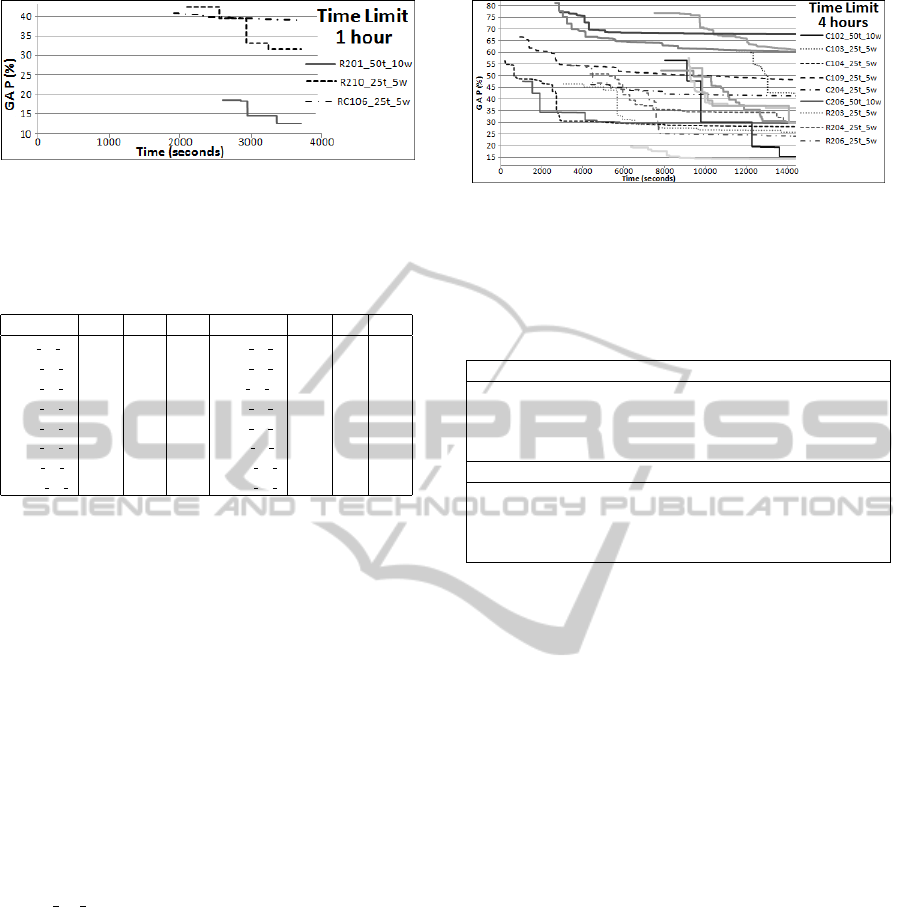
Figure 4: Gap reduction of instances for which feasible so-
lutions are achieved within the time limit of 60 minutes.
Table 6: Feasible solutions and initial/final gap achieved
after 240 min computation time (first solution time shown
in seconds). For all these instances no feasible solution was
found in the previous experiments with 15 and 60 minutes.
Instance Time Initial Final Instance Time Initial Final
C102 50 10 8008 56.5% 15.32% C103 25 5 11501 61.4%42.44%
C104 25 5 174(*) 56.7% 28.1% C109 25 5 919(*) 66.7%48.13%
C204 25 5 4401 46.2% 41.19% C206 50 10 1041(*)47.7%29.55%
R203 25 5 3057(*) 46.6% 25.75% R204 25 5 4378 50.8%30.30%
R206 25 5 3384(*) 55.8% 23.85% R208 25 5 7825 52.1% 30.1%
R211 25 5 9172 57.5% 35.95%RC101 50 10 6348 19.4%14.27%
RC201 50 10 9320 53.20% 29.6% RC203 25 5 7500 76.9%61.14%
RC204 25 5 2869(*) 77.1% 67.66% RC207 25 5 2642(*)81.2%60.08%
time is not practical) of a current solver when tackling
difficult WSRP instances. Feasible solutions were
found for 16 instances. Table 6 provides informa-
tion about these results. Rows marked with an (*)
indicate instances for which feasible solutions were
found before 3600 seconds (60 min), but for which
no feasible solution had been reported in the previous
experiments (with 15 and 60 minutes). This could be
explained by the search strategy used by Gurobi, as
the frequency of using heuristics and how deep it goes
into the branching tree might depend on the computa-
tion time available. Figure 5 complements Table 6 as
a visual representation of the gap reduction over the
240 minutes for the instances that achieve feasible so-
lutions. A reduction of 15% in gap when compared to
the initial solution is achieved for all instances except
RC101 50 10. As noted before, for some instances
a first feasible solution is found before 60 minutes,
rows marked with (*) in Table 6, which shows that
analysing the first hour of computation results in a
four-hour experiment is not equivalent to restricting
the computation time to only one hour with Gurobi.
4.5 Methods used by Gurobi
Gurobi provides information regarding the current
gap achieved while performing the optimisation. In
our experiments, we set up the solver to report the gap
reduction every 15 seconds. When a gap reduction is
achieved, the method used is reported by the solver.
The objective in this set of experiments is to identify
which method is used by Gurobi when finding bet-
Figure 5: Gap reduction of instances for which feasible so-
lutions are achieved within the time limit of 240 minutes.
Table 7: Summary of methods used by Gurobi during the
optimisation process. Columns H/B report the number of
gap reductions within a group of instances that are achieved
with Heuristics (H) or Branching (B). Within every group
the number of instances with feasible solutions is reported.
Time(#) C100 H/B C200 H/B R100 H/B
15m(112) 10 26/16 8 27/11 0 0/0
*15m(112) 13 50/12 13 71/19 3 10/5
60m(79) 0 -/- 0 -/- 0 -/-
240m(112) 14 95/23 10 83/23 0 0/0
Time(#) R200 H/B RC100 H/B RC200 H/B
15m(112) 4 25/10 0 0/0 4 57/14
*15m(112) 12 75/21 8 48/25 10 99/20
60m(79) 2 8/1 1 3/2 0 -/-
240m(112) 11 196/27 2 11/1 8 126/15
ter solutions for each instance. For every new feasi-
ble solution Gurobi reports whether the solution was
found by branching or by heuristics (Inc., 2013). If
most of the time new feasible solutions are found this
is achieved by heuristics, it would justify developing
our own. In all previous experiments, without exemp-
tion, Gurobi found more gap improvements when us-
ing heuristics. It is expected that MIP heuristics find
more feasible solutions than the branching process for
the VRPTW. The adaptations to the data set and mod-
ification of the VRPTW model to tackle WSRP have
similar results. In fact, the number of times a heuris-
tic within Gurobi finds a better solution is in general
larger for instances that include the additional con-
straints in the WSRP instances.
Table 7 summarises the number of times a gap
reduction was achieved for every group of instances
in all experiments. The table has four rows but split
in two parts vertically, each part has three groups of
instances. Note that the second row in each part,
marked with (*), refers to all instances without the
teaming and connected activities constraints. The
third row in each part shows the 79 instances that
timed out after 15 minutes in the first set of experi-
ments but then executed for up to 60 minutes. The
number in parentheses after the time limit is the num-
ber of instances used in that set of experiments. In
all groups there are more gap reductions achieved by
heuristics than by branching (H/B values).
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
442

Table 8: Results summary for all experiments. Gurobi did
not find a feasible solution for 60 instances.
Set FeasibleInfeasible
Not
Set FeasibleInfeasible
Not
found found
C100 14 0 4 C200 10 0 6
R100 0 6 18 R200 11 0 11
RC100 2 1 13 RC200 8 0 8
Totals Feasible 45 Infeasible 7 Not found 60
5 CONCLUSIONS
In this study we applied a vehicle routing problem
with time windows (VRPTW) model that incorpo-
rates temporal precedence and synchronisation con-
straints to tackle the workforce scheduling and rou-
ting problem (WSRP). We extended 112 well-known
VRPTW instances to generate a set of 112 difficult
WSRP instances. Using a current powerful opti-
misation solver, only some of the generated WSRP
instances were tackled with some success. For 60
instances, the solver could not even find a feasible so-
lution (see Table 8). This suggests that alternative so-
lution methods should be considered besides existing
mathematical programming solvers.
This computational study provides solid evidence
than the WSRP problem instances are more challeng-
ing than the VRPTW ones from which they were gen-
erated. Our experiments provide an insight into what
makes this problem more difficult and also provides
an updated perspective on the practical applicability
of existing optimisation solvers to tackle scenarios in-
volving the scheduling and routing of workforce. The
generated WSRP instances are more difficult to solve
due to the additional teaming and connected activities
constraints (similar results are reported by Rasmussen
et al. (2012) ). Additionally, we found that WSRP
instances with clustered visiting locations tend to be
easier to solve according to the gap reduction rate re-
ported by the solver in our experiments.
Finally, we established that the computational
time for a mathematical solver to find good feasible
solutions for the generated WSRP problem instances
needs to be more than 1 hour. Considering only the
45 instances for which feasible solutions were found,
for 29 of them feasible solutions were found within
an hour. For the reminder 16, feasible solutions were
found within 1 to 4 hours. Nevertheless, for 90%
of the instances, feasible solutions were found within
2 hours and 5 minutes. Adding two more hours of
computational time achieved only 10% more feasi-
ble solutions. We consider this not to be practical,
hence suggest a maximum computation time of 2
hours when solving WSRP instances with planning
time horizon of one day.
REFERENCES
Akjiratikarl, C., Yenradee, P., and Drake, P. R. (2007).
Pso-based algorithm for home care worker schedul-
ing in the uk. Computers & Industrial Engineering,
53(4):559–583.
An, Y.-J., Kim, Y.-D., Jeong, B., and Kim, S.-D. (2012).
Scheduling healthcare services in a home healthcare
system. Journal of the Operational Research Society,
63:1589–1599.
Bertels, S. and Fahle, T. (2006). A hybrid setup for a hybrid
scenario: combining heuristics for the home health
care problem. Computers & Operations Research,
33(10):2866–2890.
Bredstr
¨
om, D. and R
¨
onnqvist, M. (2008). Combined
vehicle routing and scheduling with temporal pre-
cedence and synchronization constraints. European
Journal of Operational Research, 191(1):19–31.
Castillo-Salazar, J. A., Landa-Silva, D., and Qu, R. (2012).
A survey on workforce scheduling and routing prob-
lems. In Proceedings of the 9th International Con-
ference on the Practice and Theory of Automated
Timetabling, pages 283–302.
Cheng, E. and Rich, J. L. (1998). A home health care rou-
ting and scheduling problem. Technical Report TR98-
04, Rice University, Texas.
Chuin Lau, H. and Gunawan, A. (2012). The patrol schedul-
ing problem. In Proceedings of the 9th International
Conference on the Practice and Theory of Automated
Timetabling, pages 175–192.
Chuin Lau, H., Sim, M., and Meng Teo, K. (2003). Vehicle
routing problem with time windows and a limited
number of vehicles. European Journal of Operational
Research, 148:559–569.
Dohn, A., Kolind, E., and Clausen, J. (2009). The man-
power allocation problem with time windows and job-
teaming constraints: A branch-and-price approach.
Computers & Operations Research, 36(4):1145–
1157.
Dondo, R. and Cerd
´
a, J. (2007). A cluster-based opti-
mization approach for the multi-depot heterogeneous
fleet vehicle routing problem with time windows. Eu-
ropean Journal of Operational Research, 176:1478–
1507.
Glover, F. and McMillan, C. (1986). The general employee
scheduling problem. an integration of ms and ai. Com-
puters & Operations Research, 13(5):563–573.
G
¨
unther, M. and Nissen, V. (2012). Application of parti-
cle swarm optimization to the british telecom work-
force scheduling problem. In Proceedings of the 9th
International Conference on the Practice and Theory
of Automated Timetabling, pages 242–256.
Inc., G. O. (2013). Gurobi Optimizer, Reference Manual
version 5.5. Gurobi Optimization Inc.
Korsah, G. A., Stentz, A., Dias, M. B., and Aslam, I.
(2010). Optimal vehicle routing and scheduling with
precedence constraints and location choice. In IEEE
International Conference on Robotics and Automation
Workshop on Intelligent Autonomous Systems.
ComputationalStudyforWorkforceSchedulingandRoutingProblems
443

Li, Y., Lim, A., and Rodrigues, B. (2005). Manpower
allocation with time windows and job-teaming con-
straints. Naval Research Logistics, 52(4):302–311.
Misir, M., Smet, P., Verbeeck, K., and Vanden Bergue, G.
(2011). Security personnel routing and rostering: a
hyper-heuristic approach. In Proceedings of the 3rd
International Conference on Applied Operational Re-
search, pages 193–206.
Nickel, S., Schr
¨
oder, M., and Steeg, J. (2012). Mid–term
abd short–term planning support for home health care
services. European Journal of Operational Research,
219:574–587.
Rasmussen, M. S., Justesen, T., Dohn, A., and Larsen, J.
(2012). The home care crew scheduling problem:
Preference-based visit clustering and temporal depen-
dencies. European Journal of Operational Research,
219(3):598–610.
Solomon, M. M. (1987). Algorithms for the vehicle rou-
ting and scheduling problems with time windows con-
straints. Operations Research, 35(2):254–265.
Taillard, E. D., Laporte, G., and Gendreau, M. (1996).
Vehicle routeing with multiple use of vehicles. Jour-
nal of the Operational Research Society, 47:1065–
1070.
Toth, P. and Vigo, D. (1987). The vehicle routing problem,
volume 9. Society for Industrial and Applied Mathe-
matics.
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
444
