
Expression, Pose, and Illumination Invariant Face Recognition using
Lower Order Pseudo Zernike Moments
Madeena Sultana
1
, Marina Gavrilova
1
and Svetlana Yanushkevich
2
1
Department of Computer Science, University of Calgary, 2500 University Drive NW, Calgary, AB, T2N 1N 4, Canada
2
Department of Electrical and Computer Engineering, Schulich School of Engineering, University of Calgary, 2500
University Drive NW, Calgary, Alberta, T2N 1N 4, Canada
Keywords: Face Recognition, Pseudo Zernike Moment (PZM), k-Nearest Neighbors (k-NN), Discrete Wavelet
Transform (DWT), Face Normalization.
Abstract: Face recognition is an extremely challenging task with the presence of expression, orientation, and lightning
variation. This paper presents a novel expression and pose invariant feature descriptor by combining
Daubechies discrete wavelets transform and lower order pseudo Zernike moments. A novel normalization
method is also proposed to obtain illumination invariance. The proposed method can recognize face images
regardless of facial orientation, expression, and illumination variation using small number of features. An
extensive experimental investigation is conducted using a large variation of facial orientation, expression,
and illumination to evaluate the performance of the proposed method. Experimental results confirm that the
proposed approach obtains high recognition accuracy and computational efficiency under different pose,
expression, and illumination conditions.
1 INTRODUCTION
Face recognition remains an actively researched
domain due to constantly increasing demands on
performance in a wide range of applications.
Following two decades of research, current face
recognition systems have reached a certain state of
of maturity. However, this success is limited to some
controlled settings. It has been noted that
performance of many benchmark face recognition
methods deteriorates significantly in uncontrolled,
real world environment (Herman et al., 2009,
Sultana and Gavrilova, 2013). The main constraints
of current face recognition systems are varying
Illumination, viewing directions, poses, head tilts,
and facial expressions. Due to the aforementioned
natural constraints, intra-class variation of face
images might be very large while interclass
difference becomes quite small – consequently
making the face recognition systems performance
deteriorate. Thus, at present time, an efficient face
recognition system should have the following
properties (Wang et al., 2013, Bairagi et al., 2012):
1) High recognition accuracy.
2) Pose and facial expression invariance.
3) Insensitiveness to lightning variation.
4) Low computation time.
Most of the existing face recognition methods
are inclined to accomplish one or two of the above
properties by controlling or disregarding the other
conditions. For example, Demirel and Anbarjafari
(Demirel and Anbarjafari, 2008) proposed a pose
invariant face recognition method using grey level
histograms disregarding lightning variation. An
expression invariant face recognition method with
computational efficiency is proposed by Bairagi et
al. (Bairagi et al., 2012), but does not consider
lightning variation. In 2013, Wang et al. (Wang et
al., 2013) resolved the illumination problem without
considering the varying facial expression and pose.
Therefore, a face recognition system combining
accuracy, computational efficiency, and robustness
to pose, expression, and illumination is still a
challenge.
In the proposed method, we combined
Daubechies Discrete Wavelet Transform (DWT)
(Shen and Strang, 1998) with lower order Pseudo
Zernike Moments (PZMs) (The and Chin, 1988) as
feature vector. It is evident from the previous
research works that discrete wavelet transform is
insensitive to facial expression and small occlusions
(Foon et al., 2004). Haddadnia et al. (Haddadnia et
216
Sultana M., Gavrilova M. and Yanushkevich S..
Expression, Pose, and Illumination Invariant Face Recognition using Lower Order Pseudo Zernike Moments.
DOI: 10.5220/0004842602160221
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 216-221
ISBN: 978-989-758-003-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

al., 2003) has identified that PZMs can be used as
rotation, scale, and translation invariant facial
features. Moreover, an optimum choice of orders of
PZMs can effectively reduce feature dimensions
leading to high-speed processing without
deteriorating the recognition accuracy. In our
approach, we combined lower order pseudo Zernike
moments, discrete wavelet transform, and k-NN
classifier to develop an expression and pose
invariant as well as computationally efficient face
recognition system. A novel normalization method is
proposed and utilized in preprocessing stage to
eliminate extensive lightning variations.
Therefore, the major contributions of this
research work is twofold: 1. Presenting a novel
expression and pose invariant face descriptor by
fusing optimal features of PZM and DWT; 2.
Integrating a novel face normalization method to
achieve illumination invariance.
2 RELEVANT WORK
For more than two decades, moment invariants are
considered as an important global shape feature for
many pattern recognition applications. Authors of
(Foon et al., 2004) confirmed that a small set of
orthogonal moments such as Zernike moments and
PZMs can efficiently represent images by their
discriminative and non-redundant features.
However, moment based face recognition system is
still an undermined research area. In this section, a
discussion of some of the previous works on
orthogonal moment based face recognition is
presented.
PZMs were first utilized for face recognition by
Haddadnia et al. (Haddadnia et al., 2003). In their
study, it is shown that PZM performs better than
Zernike and Legendre moments. A comparatively
recent study (Nabatchian et al., 2008) also
demonstrates that PZM performs the best among
other commonly used moment invariants for face
recognition. In 2004, Pang et al. (Pang et al., 2006)
gained 36.23% reduction in computation time by
combining Symmlet orthonormal wavelet filter of
order 5 and PZM. However, this study lacks
investigation of optimum order of PZM and
experimentation is conducted using only one
database, where expression and pose invariant
features were not studied as well. Behbahani and
Bastani (Behbahani and Bastani, 2011) used PZM
with probabilistic neural network classifier for face
recognition. A very recent study (Farokhi et al.,
2013) has confirmed that ZM can also be used for
noise and rotation insensitive infrared face
recognition. Although from the above discussion it
is apparent that ZM and PZMs are producing very
promising result for face recognition, most of the
previous works lack the following studies:
1) Majority the experiments are conducted using
only one trivial database (e.g. AT&T).
2) Performance evaluation of the methods under
pose, expression, and illumination changes
remained unconsidered.
Along with presenting a novel PZM based face
recognition method these issues are also addressed
in experimentation section of this paper.
3 PROPOSED METHOD
The proposed face recognition system has three
stages: image normalization, features extraction by
DWT and PZM, and classification of faces by k-NN.
The novelty of the proposed method lies in a new
normalization method, and in fusing DWT and PZM
with optimal parameters for recognition of face
images under unconstraint environment. Each of the
stages is described in the following sub-sections.
3.1 Normalization
In this section, a novel face normalization method is
proposed that eliminates the variation in illumination
and shadowing while preserving enough details to be
used for the recognition purpose. The novelty of this
method lies in improving a well-known
normalization method Weber-face (Wang et al.,
2011) by applying bi-lateral filter (Paris et al., 2007)
and integrating gamma correction (Tan and Triggs,
2007) for detail enhancement. We refer this
normalization method as Improved Weber-face.In
the proposed normalization method, gamma is
applied at first to enhance details of the darker
regions and compress highlights of the brighter
regions. It reduces the intra-class variability due to
extensive illumination change. Next, illumination
invariant face is generated using Weber-face and bi-
lateral filter since gamma correction cannot remove
the influence of the overall intensity gradients.
Weber-face normalization is proposed by Wang et
al. in 2011 which outperformed a number of state-
of-the-art normalization methods. In this method, at
first Gaussian filter smoothens the image then
Weber’s local descriptor is used to generate a ratio
image called Weber-face. Gaussian filter blurs the
edges since it averages the pixel values using the
Expression,Pose,andIlluminationInvariantFaceRecognitionusingLowerOrderPseudoZernikeMoments
217

same kernel everywhere in the image. Whereas,
bilateral filter uses different size of kernels
depending on the content of the image which
consequently preserves edges better than Gaussian
filter (Paris et al., 2007). To improve the smoothing
and edge preserving feature of Weber-face method,
we replaced the Gaussian filter by bilateral filter. As
a result, the proposed method will normalize face
images with less intra-class variability while
preserving more interclass details. This stage can be
considered as image pre-processing where face
images will be normalized if required. The
normalization method is as follows:
Step 1: Apply gamma correction on the input image
I for detail enhancement. Gamma correction of a
grayscale image I is as follows (Gamma correction):
,
0.018
,
5.5
,
(1)
,
0.018
′
,
1.099,
.
0.099, (2)
where I(x,y) and I'(x,y) are the pixels at (x,y)
coordinate of the grayscale and gamma corrected
grayscale images, respectively. The gamma
correction of a color image is as follows:
,, 0.018
5.5,
5.5,
5.5 (3)
,, 0.018
1.099
.
0.099,
1.099
.
0.099,and
′ 1.099
.
0.099, (4)
where R', G', B' are the gamma corrected red (R),
green (G), and blue (B) channels of the color image.
The gamma corrected color image then converted to
grayscale image (Y) using the following equation:
0.299
0.587
0.114′ (5)
Step 2: Smoothen the input image Y while
preserving the interclass details (e.g. edges) using
bilateral filter B(σ
s
, σ
r
)
∗
,
, (6)
Where * is the convolution operator and B(σ
s
, σ
r
) is
the kernel function of bilateral filter with space
parameter σ
s
and range parameter σ
r
.
Step 3: Finally, generate the improved Weber-face
(W) from Y΄ by applying Weber local descriptor
(Wang et al., 2011):
arctan∝
∑∑
,
∆,∆
,
∈∈
,
where A={-1,0,1}. (7)
3.2 Feature Extraction
This section presents a novel feature descriptor by
combining Daubechies DWT and lower order
pseudo Zernike moments to obtain expression and
pose invariance. We used DWT for the following
three reasons (Foon et al., 2004, Pang et al., 2006):
Low frequency subband is expression and small
occlusion invariant.
Lower resolution image facilitates fast
computation and low storage.
Decomposition to low frequency subband
smoothens image thus reduces noise.
Two-dimensional (2D) DWT decomposes an
input image into four sub-bands, one low frequency
component (LL) and three detail components (LH,
HL, HH). From experimentation we found that
expression features are mostly eliminated at the 3
rd
level of decomposition, yet it preserves enough
details to represent facial features of the individual.
Therefore, we decomposed all face images up to 3
rd
level and considered the LL subband as DWT face
feature. All the images are resized to 128×128 pixels
as part of pre-processing. Thus, size of the final low
frequency component image (LL) after 3
rd
level of
decomposition is 16×16. Pseudo Zernike moment
invariants are then computed from LL subband to
represent the feature vector of the face image.
The orthogonal property of PZMs can uniquely
represent an image regardless of geometric rotation
and also reduces information redundancy (Teh et al.,
1988). The kernel of PZM is a set of orthogonal
moments inside a unit circle and is defined in polar
coordinates (Behbahani and Bastani, 2011). The two
dimensional PZM of order n and repetition m of an
image in polar coordinate f(r, θ) are defined as (The
et al., 1988, Behbahani and Bastani, 2011):
,
,
, (8)
where
,
,
√
1
and
,
,,∈
11
,
R
nm
(r) is the radial polynomial and is defined as
follows:
∑
1
!
!
|
|
!||!
||
(9)
PZMs of different orders are non-redundant
which can act as discriminative features for face
recognition. In addition, the rotation invariant
property of PZM will facilitate pose invariance.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
218
3.3 Classification
Finally, the query image is classified by matching its
feature vector to that of database images. The feature
vectors of the database images are obtained from
feature database. The k-NN classifier (Cover and
Hart, 1967) is chosen since it performs better than
PNN and LDA for lower dimension of Zernike
moments (Nabatchian et al., 2008). Moreover, k-NN
is simple and has a wide range of applications. K-
NN classifier classifies objects based on the closest
training samples in the feature space. The closest k
neighbors are determined by applying a distance
function. In the proposed method, we considered
Euclidean distance and k=1.
From existing works we know that higher order
PZMs have better discriminative features but they
are more noise sensitive and computationally
expensive. Conversely, the lower order PZMs have
less feature dimension, ease of computation, better
noise tolerance but less discriminative features.
Therefore, it is very important to optimally combine
the PZM features to achieve the best performance in
terms of both recognition rate and computation time.
The following section describes feature set
optimization process to obtain the best result from
the proposed system.
4 FEATURE OPTIMIZATION
We optimized the order of the PZM, and the order
and type of DWT to obtain the best performance.
Also, we investigated how the performance of the
proposed system vary for different values of k of k-
NN classifier with different distance functions. This
process can be considered as selection of best
feature set and all experimentations are done only
once on AT&T database (AT&T Lab). The obtained
feature set can be applied to any database and there
is no need to fine tune the feature set again for any
application of this method.
It is obvious that higher order PZM has greater
number of features which consequently increase the
computation time. On the other hand, lower order
PZM has ease of computation due to their small
number of features but individually does not possess
enough discriminating information for pattern
recognition. Therefore, 1
st
to 12
th
order moments are
combined and experimented to find the optimum
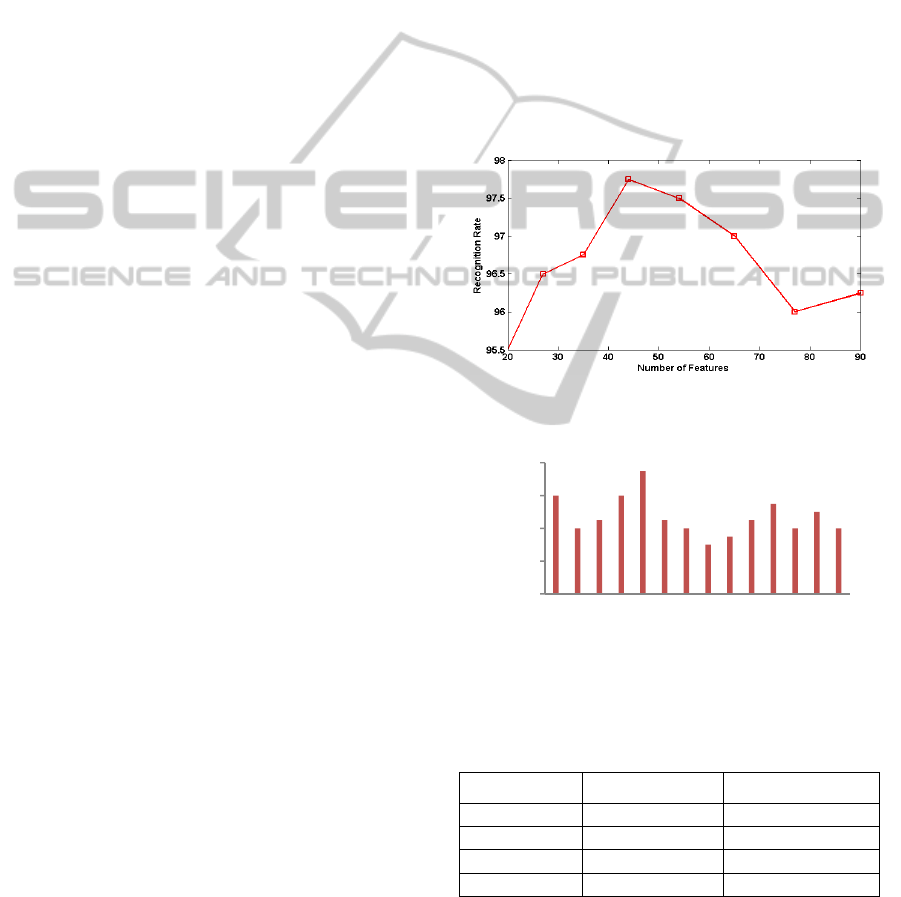
combination which produces the best result. Fig. 1
illustrates the number of features of PZM at different
orders and corresponding recognition accuracy. The
best result is achieved for 44 features which is the
combination of 1
st
to 8
th
order PZMs. A performance
drop is also observed for the combination of higher
order PZM features in Fig. 1. This is probably
because higher order PZM features are more
sensitive to noise and contain information which
reduces the inter-class variation of face images.
Next, a choice of the best wavelet basis among Haar,
Daubechies, and Symmlet filters of different orders
is obtained. From Fig. 2 one can see that Daubechies
filter of order 6 (db6) has the best recognition rate
with 1
st
to 8
th
order PZM features.
Finally, the performance of Euclidean, cosine,
Manhattan distance and correlation with k=1 and 3
of k-NN classifier is investigated and the best result
is obtained for Euclidean distance with k=1. Table 1
summarizes the results of this experimentation.
Figure 1: Variation of recognition rate for different
number of PZM features
Figure 2: Recognition rate of various wavelets filters
Table 1: Classification accuracy of various distance
methods for k=1, 3 on AT&T database.
Distance Accuracy (k=1) Accuracy (k=3)
Euclidean 97.75 91.25
Cosine 96.75 89.75
Manhattan 96.5 90
Correlation 95.5 85
5 EXPERIMENTAL RESULTS
Performance of the proposed method is evaluated on
94
95
96
97
98
Haar
db3
db4
db5
db6
db7
db8
Sym4
Sym5
Sym6
Sym7
Sym8
Sym9
Sym10
RecognitionRate(%)
DiscreteWaveletFilter
Expression,Pose,andIlluminationInvariantFaceRecognitionusingLowerOrderPseudoZernikeMoments
219

the following four standard face image databases:
AT&T (AT&T Lab): It contains 400 greyscale
images of size 92×112 pixels. There are 10 different
images for each of the 40 distinct subjects. Images
were taken at different times, illumination, facial
expressions, side movements, and facial details.
AR (Martinez and Kak, 2001): It contains color
images of 70 males and 56 females. Each subject
has 26 different images in two sessions. Each
session has 13 different images per subjects in
different conditions expression (natural, smile,
anger, screaming), illumination (left light on, right
light on, both lights on), and occluded conditions.
Yale (Yale database): It contains total 165 images
of 15 subjects. Images were taken in different facial
expressions: happy, normal, sad, sleepy, surprised,
wink and lightning conditions with/without glasses.
Sheffield (Sheffield database): It contains facial
images of mixed race/gender/appearance of 20
individuals. Each individual is shown in a range of
poses from profile to frontal views.
The above four databases contain face images
with large variations in expression, pose, and
illumination. During experimentation we created
three databases by randomly picking images from
these four databases to evaluate the performance our
system in different conditions in varying conditions:
DB1: We created this database by randomly
picking 40 subjects from AT&T, AR, and
Sheffield database. Therefore, this database
comprises of images with large variation of
pose and expression with little or no
illumination change.
DB2: This database is created by randomly
picking 40 images from Yale and AR database.
Therefore, it contains facial images with large
variation of illumination conditions with little or
no expression change.
DB3: This database contains all images from
DB1 and DB2.
Fig. 3 shows some sample images from DB1 and
DB2.
Figure 3: Sample face images from DB1 (row 1) and DB2
(row 2).
Fig. 4. shows 10 fold cross validation results of
well-known Principle Component Analysis (PCA)
and the proposed method on DB1, DB2, and DB3.
From Fig. 4 one can see that the proposed method
consistently maintains highest recognition rate
regardless of expression, pose, and illumination
changes. We compared the performance of the
proposed normalization method and Weber-face
normalization method. For this experimentation, the
proposed feature descriptor is combined with
Weber-face and improved Weber-face methods,
respectively.
The performance comparison of the Weber-face
and proposed improved Weber-face method on DB2
and DB3 is shown in Fig. 5. Fig. 5 shows that the
proposed improved weber-face method has better
recognition rate under varying illumination
conditions than Weber-face method. The
computational efficiency of the proposed method is
evaluated as well. The extraction time of 44 features
and the classification time of the proposed method
are computed on AT&T database. The result is
compared to solely PZM based method using the
same experimental setup.
Figure 4: Recognition rate of PCA and the proposed
method on different databases.
Figure 5: Recognition rate of Weber-face and Improved
Weber-face method on DB2 and DB3.
Table 2 shows that proposed integrated DWT
and PZM based feature extraction obtains 12.57
times reduction in computation time over solely
PZM based feature extraction. Therefore, it has been
demonstrated that the use of low dimensional
subband image and small number of features makes
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
220

our system computationally very efficient. All
experiments are carried out on MATLAB R2013a,
Windows 7 OS, Intel Core i3 2310M processor with
4GB RAM.
Table 2: Computation time (in seconds) on AT&T
database.
Method
Feature
extraction time
of 400 images (s)
Classification time
per fold (s)
Overall
time (s)
PZM
227.21
0.016
227.226
Proposed
Method
18.07 18.086
6 CONCLUSIONS
Recognizing faces in varying illumination, pose, and
expression condition with computational efficiency
is the most difficult problem of today’s face
recognition systems. An efficient face recognition
system should be able to cope with all of these
problems. In this paper, a novel lower order PZM
based method is presented which can efficiently
recognize faces regardless of illumination, pose, and
expression change. Due to optimal choice of features
the method obtains much better recognition rate with
less computation time. Extensive experimentation
confirms the high recognition rate, computational
efficiency, and robustness of the proposed method
under varying conditions. We believe that the
proposed method has a very good potential to cope
with the real challenges of current face recognition
systems. Future works include analyzing the
performance of the proposed method for other
biometric recognition applications such as
recognition of ear, palmprint etc.
ACKNOWLEDGEMENTS
Authors would like to thank NSERC and URGC
Seed grant for partial support of this project.
REFERENCES
AT&T Lab. Cambridge; www.cl.cam.ac.uk/research/dtg/
attarchive/facedatabase.html, Accessed on 8 Oct., 2013.
Bairagi, B. K., Chatterjee, A., Das, S. C., Tudu, B., 2012.
Expressions invariant face recognition using SURF
and Gabor features, 3rd Int. Conf. on Emerging
Applications of Information Tech. (EAIT), 170-173.
Behbahani, E. F., Bastani, A., 2011. Human face
recognition by pseudo Zernike moment and
probabilistic neural network, Int. J. of Engineering
Science and Tech., 3(7), 5466-5469.
Cover, T., Hart, P., 1967. Nearest neighbor pattern
classification. IEEE Trans. Inf. Theory, 13(1), 21-27.
Demirel, H., Anbarjafari, G., 2008. High performance
pose invariant face recognition, VISAPP, 282-285.
Farokhi, S., Shamsuddin, S. M., Flusser, J., Sheikh, U. U.,
Khansari, M., Jafari-Khouzani, K., 2013. Rotation and
noise invariant near-infrared face recognition by
means of Zernike moments and spectral regression
discriminant analysis. Journal of Electronic
Imaging, 22(1), 013030-013030.
Foon, N. H., Pang, Y. H., Jin, A. T. B., Ling, D. N. C.,
2004. An efficient method for human face recognition
using wavelet transform and Zernike moments, Int.
Conf. on Computer Graphics, Imaging and
Visualization (CGIV), 65-69.
Gamma correction; http://software.intel.com/sites/
products/documentation/hpc/ipp/ippi/ippi_ch6/ch6_ga
mma_correction.html# ch6_gamma_correction,
Accessed on 8 Oct., 2013.
Haddadnia, J., Ahmadi, M., Faez, K., 2003. An efficient
feature extraction method with pseudo-Zernike
moment in RBF neural network-based human face
recognition system, EURASIP journal on applied
signal processing, 890-901.
Herman, J., Rani, S., Devaraj, D., 2009. Face recognition
using generalized pseudo Zernike moment, Annual
IEEE India Conference, 1-4.
Martinez, A.M., Kak, A.C., 2001. PCA versus LDA, IEEE
TPAMI, 23(2), 228-233.
Nabatchian, A., Abdel-Raheem, E., Ahmadi, M., 2008.
Human face recognition using different moment
invariants: A comparative study, Congress on Image
and Signal Processing CISP’08, 3, 661-666.
Pang, Y. H., Teoh, A. B., Ngo, D. C., 2006. A
discriminant pseudo Zernike moments in face
recognition, J. of Research and Practice in
Information Technology, 38(2), 197.
Paris, S., Kornprobst, P., Tumblin, J., Durand, F., 2007. A
gentle introduction to bilateral filtering and its
applications, ACM SIGGRAPH 2007 courses, 1.
Sultana, M., Gavrilova, M., 2013. A Content Based
Feature Combination Method for Face Recognition,
CORES, 197-206.
Sheffield database; http://www.sheffield.ac.uk/eee/
research/iel/research/face, Accessed on 8 Oct., 2013.
Shen, J., Strang, G., 1998. Asymptotics of daubechies
filters, scaling functions, and wavelets, Applied and
Computational Harmonic Analysis, 5
(3), 312-331.
Tan, X., Triggs, B., 2007. Preprocessing and feature sets
for robust face recognition, CVPR, 7, 1-8.
Teh, C. H., Chin, R. T., 1988. On image analysis by the
methods of moments, IEEE TPAMI, 10(4), 496-513.
Wang, B., Li, W., Yang, W., Liao, Q., 2011. Illumination
normalization based on Weber's law with application
to face recognition. Signal Proc. Lett., 18(8), 462-465.
Wang, H., Ye, M., Yang, S., 2013. Shadow compensation
and illumination normalization of face
image, Machine Vision and Applications, 1-11.
Yale database; http://cvc.yale.edu/projects/yalefaces/
yalefaces.html, Accessed on 8 Oct., 2013.
Expression,Pose,andIlluminationInvariantFaceRecognitionusingLowerOrderPseudoZernikeMoments
221
