Combining Learning-to-Rank with Clustering

Efstathios Lempesis and Christos Makris

Department of Computer Engineering and Informatics, University of Patras, Patras, Greece

Keywords: Ranking, Learning-to-Rank, Clustering, Relational Ranking, Web Information Filtering and Retrieval,

Searching and Browsing, Text Mining.

Abstract: This paper aims to combine learning-to-rank methods with an existing clustering underlying the entities to

be ranked. In recent years, learning-to-rank has attracted the interest of many researchers and a large

number of algorithmic approaches and methods have been published. Existing learning-to-rank methods

have as goal to automatically construct a ranking model from training data. Usually, all these methods don't

take into consideration the data's structure. Although there is a novel task named “Relational Ranking”

which tries to make allowances for the inter-relationship between documents, it has restrictions and it is

difficult to be applied in a lot of real applications. To address this problem, we create a per query clustering

using state of the art algorithms from our training data. Then, we experimentally verify the effect of

clustering on them.

1 INTRODUCTION

Nowadays, due to the evolution of the web it is

common knowledge that it is difficult to find the

desired information, so it is important to have search

engines intelligent enough to meet our demands. As

the user issues queries, we deem the ranking

problem for information retrieval as the demand to

order the stored set of documents by relevance to

these queries. Ranking appears in many information

retrieval problems, such as web search retrieval,

collaborative filtering, entity ranking, sentiment

analysis and text summarization. There are two

types of ranking problems: ranking creation and

ranking aggregation (Li, 2011). Ranking creation

exploits the content of the document (as it appears as

a set of features) in order to create a ranked list of

documents, while ranking aggregation fuses multiple

ranking lists, in order to create a unified ranked list.

The ranking module is responsible for matching

between queries and indexed documents. A well-

defined ranking module processes incoming queries

and provides a matching score between them and the

stored documents. Due to the fast development of

the web and the flood of information, it is also as

important as ever to have efficient and effective

rankers that can rank this glut of information

according to the users' queries.

In recent years (Liu, 2011; Li, 2011) it has

become possible to embrace machine learning

technologies in order to build effective rankers,

exploiting the large number of available training

data. This embracement initiated a new research area

called learning to rank, that combines traditional

rankers with machine learning techniques; this area

has become one of the most active in the area of web

information retrieval.

Learning to rank or machine-learned ranking

(MLR) automatically constructs ranking models

from training data in terms of a loss function; it can

be phrased in different types of supervised or semi-

supervised machine learning problems. The ranking

model has as purpose to produce a proper ranked list

in new queries by exploiting the training data lists of

items with each list providing some partial order

between its items. To grant this order either

numerical scores, ordinal scores or binary judgments

(degree of relevance) are provided. Its methods can

be categorized as: the pointwise approach, the

pairwise approach, and the listwise approach (Liu,

2011). These approaches differ according to the loss

functions they employ. Regarding the pointwise

approach, which can be considered as a

classification or regression problem by learning the

rank values of the documents, the input space

consists of a feature vector for each discrete

document and the output space consists of the

relevance grades. The input space of the pairwise

approach, which treats the pair of documents as

independent quantities and learns a classification or

286

Lempesis E. and Makris C..

Combining Learning-to-Rank with Clustering.

DOI: 10.5220/0004846802860294

In Proceedings of the 10th International Conference on Web Information Systems and Technologies (WEBIST-2014), pages 286-294

ISBN: 978-989-758-024-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

regression model to correctly order these pairs,

consists of feature vectors of pairs of documents and

the output space consists of the pairwise preference

{+1,−1} between each pair of documents. The input

space of the listwise approach consists of a corpus of

documents related to a single query and considers

them as a training example. Its output space contains

the ranked list of the documents. The main problem

with the pointwise and pairwise approaches is that

their loss functions are associated with particular

documents while most evaluation metrics of

information retrieval compute the ranking quality for

individual queries and not for documents. The goal

of the listwise approach is to maximize the

evaluation metrics such as NDCG and MAP.

A lot of the real ranking procedures actually

think of the relationship between the documents, but

all of the proposed learning-to-rank algorithms,

which belong to any of the above approaches, do not

take this into account. We could imagine this

connection as the relationships between the clusters,

the parent-child hierarchy etc.

Similar to the toy example in Kurland's PhD

thesis (Kurland, 2006), let q = {computer, printer}

be a query, and consider the documents:

d1 = computer, company, employ, salary

d2 = computer, investment, employer, company

d3 = taxes, printer, salary, company, employer

d4 = computer, printer, disk, tape, hardware

d5 = disk, tape, hardware, laptop

d6 = disk, tape, floppy, cd rom, hardware

Both the documents and the query are

represented using a vector space representation

(Baeza-Yates and Ribeiro-Neto, 2011) and the

weight for each term in a vector is its frequency

within the corresponding document (or query). If we

rank the documents regarding q, we may get the

following ranking:

Ranked list = d4, d1, d2, d3, d5, d6 (d4 is the top

retrieved document. )

However, since it is more rational to suppose

that the fundamental topic of the query is “computer

hardware” rather than “business”, we would like to

have d5 and d6 ranked as high as possible in the list.

Clustering the documents using the scheme, where

each document belongs to exactly one cluster, into

two clusters, could result in the following clusters: A

= {d1, d2, d3}, B = {d4, d5, d6}. If we took this

clustering into account and applied the cluster

hypothesis then d5 and d6 would be ranked higher

than d1, d2 and d3. That is the desirable outcome,

since d5 and d6, though not containing any of the

terms that occur in q are more close to the query's

topic(computer hardware), than d1, d2 and d3,

which contain one query term, but do not seem to

discuss the query topic.

As another sign of the significance of clustering

in (Zeng et al., 2004) it has been mentioned that

existing search engines such as Google

(www.google.com), Yahoo (http://search.yahoo.

com/) and Bing (www.bing.com) often return a long

list of search results, ranked by their relevancies to

the given query. As a consequence, Web users must

sequentially seek the list and examine the titles and

snippets to discern their desired results.

Undoubtedly, this is a time consuming procedure

when multiple sub-topics of the given query are

mingled together. They propose that a possible

solution to this problem is to (online) cluster search

results into different groups, and to enable users to

recognize their required group.

Carrot2 (http://search.carrot2.org/stable/search)

is a real illustration of this approach.

The aim of present work is to investigate whether

it is possible or not to integrate into the learning-to-

rank algorithm's procedure, without user

intervention, the information that we gain by

clustering following the well known cluster

hypothesis of the information retrieval area

(Kurland, 2006; Gan, Ma and Wu, 2007; van

Rijsbegen 1984) and examine the results of this

venture. Hence, after the off-line building of the

clusters and during the algorithm's function we

provide to each document the bonus that

corresponds to its cluster. Through this procedure

we build on the assumption that a document, which

belongs to one cluster, will be near the other

documents of its cluster at the ranked list. In a

narrow sense, we estimate that the documents, which

belong to the best cluster, will be at the top of the

ranked list and as a consequence we will have better

ranked lists and better measure metrics.

Before concluding the introduction we describe

some basic notions:

The BM25 weighting scheme (Robertson et al.,

2004) is a ranking function used by search engines

to rank matching documents according to their

relevance to a given search query.

Mean Average Precision (MAP) (Baeza-Yates

and Ribeiro-Neto, 2011) for a set of queries q

, ...q

is the mean of the average precision scores for each

query.

DCG (Baeza-Yates and Ribeiro-Neto, 2011)

measures the usefulness, or gain, of a document

based on its position in the result list. The gain is

accumulated from the top to the bottom of the result

list with each result’s gain being discounted at lower

CombiningLearning-to-RankwithClustering

287

positions.

Precision (Baeza-Yates and Ribeiro-Neto, 2011)

is defined as the fraction of the retrieved documents

that are relevant. These values are typically

evaluated at a given cut-off rank, considering only

the topmost results; in this case it is called precision

at k or P@k.

Finally, the paper is organized as follows. The

algorithms under examination are presented in

Section 2. In Section 3, we present our ideas and

how we implemented them, while in Section 4 we

present the clusters' creation and our key findings. In

Section 5 we conclude our results and discuss open

problems and future work.

2 ALGORITHMS UNDER

EXAMINATION

The learning-to-rank algorithm, that we enhnces in

order to perform the experiments are AdaRank (Xu

and Li, 2007), RankBoost (Freund, Iyer, Schapire,

Singer, 2003) and RankNet (Burges, Shaked,

Renshaw, Lazier, Deeds, Hamilton and Hullender,

2005).

RankBoost is a pairwise learning-to-rank

algorithm and like all the boosting algorithms it

operates in rounds. On each round, RankBoost calls

the weak learner with a view to producing a weak

ranking. Also, RankBoost holds a distribution,

which is selected to accentuate different parts of the

training data, which is passed on each round to the

weak learner. If a pair of instances is assigned with a

high weight, it indicates a great importance that the

weak learner orders that pair correctly. The final

ranking is a weighted sum of the weak rankings.

AdaRank is a listwise learning-to-rank algorithm

and similarly like all the boosting algorithms it

operates in rounds. AdaRank uses a training set as

input and takes the performance measure function

and the number of iterations as parameters.

AdaRank runs rounds and at each round, it retains a

distribution of weights over the queries in the

training data, it creates a weak ranker. Initially,

AdaRank defines equal weights to the queries and

then at each round it increases the weights of those

queries that are not ranked properly. As a result, the

learning at the next round concentrates on the

generation of a weak ranker that is able to work on

the ranking of those ‘hard’ queries. Finally, it

outputs a ranking model by linearly combining the

weak rankers. The AdaRank's characteristic attribute

is that for the computation of the distribution of the

weights over the queries it uses the evaluation of the

documents' labels of the ranked list and not the

documents' values directly.

RankNet is a pairwise learning-to-rank algorithm

where the loss function, as it is obvious, is defined

on a pair of documents, but the hypothesis is defined

with the use of a scoring function. The target

probability is defined based on the ground truth

labels of the given two documents related to a

training query. Thereafter, the difference between

the scores of these two documents given by the

scoring function is used to construct the modelled

probability and the cross entropy between the target

probability and the modelled probability is used as

the loss function. A neural network is used as the

model and gradient descent as the optimization

algorithm to learn the scoring function.

3 OUR APPROACH

Intuitively, the basic insight behind our idea is

centered around the hypothesis that the quality of

ranking, which is the result of the learning-to-rank

process, can be improved if we take into account the

auxiliary information provided by the multi-way

inter-relationship between all the documents.

A novel task named “Relational Ranking” (Liu,

2011) for learning-to-rank, apart from the properties

of each individual document in the ranking

procedure, also makes allowances for the inter-

relationship between the documents. The kind of this

connection determines the targeted application; for

example measures of disjointedness (overlap

minimization) are applied to search result

diversification, while measures of content similarity

for topic extraction/distillation. Generally, the

ranked lists are generated by sorting the documents

according to their scores output by the learned

model. However, it is common sense that in some

practical cases we should allow for the relationships

between the documents, and it is not adequate to

define the scoring function exclusively on discrete

documents. The existing works on relational ranking

do not only use a matrix or a graph, which must be

predefined by experts, to model the relationship, but

also are based on pairwise relationship. The pairwise

relationship, either similarity, dissimilarity, or

preference, is very restrictive and so it is very

difficult to use relational ranking in a lot of real

applications. For example (Liu, 2011), all the

webpages in the same website have a inter-

relationship. It is more rational to use a hypergraph

to model such inter-relationships.

We try to cope with the above restrictions and to

WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies

288

create a non-predefined structure that illustrates the

multi-way inter-relationship between all the

documents. This paper has as purpose to present

how we can incorporate in an existing learning-to-

rank algorithm’s function the clustering’s structure

so as to gain better ranked lists.

The objective of the clustering (Kurland, 2006;

Gan, Ma and Wu, 2007) is to separate an

unstructured corpus of documents into clusters. We

want the documents to be as similar to each other in

the same cluster and as dissimilar to documents from

other clusters as possible. The cluster hypothesis

(Kurland, 2013; van Rijsbergen, 1979) states the

fundamental assumption we make when using

clustering in information retrieval, namely that

documents in the same cluster behave similarly with

respect to relevance to information needs. So, if

there is a document from a cluster that is relevant to

a query, then it is likely that other documents from

the same cluster are also relevant. Many researchers

(Raiber and Kurland, 2012; Hearst and Pedersen,

1996) have depicted that the cluster hypothesis holds

on the Web and since clustering has gained great

attention, much research (McKeown et al., 2002;

Liu, Bruce, 2004) has been done on what are its

benefits. So, it states that the users should expect to

see similar documents close to each other in a

ranked list. Of course, one could argue that cluster

hypothesis is valid only if the similarity measure

used for the clustering is similar to the content based

algorithm used for the query. However it is rational

to assume that the provided clustering gathers

documents according to their information content.

Hence, since information retrieval aims at satisfying

information needs, clustering could be useful for the

information seeker. Thus, our intention is to make

the most of the benefits of the clustering and those

of learning-to-rank in order to improve the efficacy

in the ranked lists.

The learning-to-rank algorithms are iterative.

This attribute helps our approach to gather each

document near its cluster's documents at the ranked

list gradually during the algorithm's iterations. Our

approach is to create a per query clustering and to

give to each document, during algorithm’s iterations,

a bonus proportional to the cluster in which it

belongs to. So, we estimate that with the passage of

iterations similar documents will appear together,

since we promote similar documents with similar

bonus, and particularly the documents, which belong

to the cluster that has the centroid with the best

BM25 (Manning, Raghavan, Schutze, 2008) value,

will be at the top of the ranked list as they are the

documents that get the greatest bonus. With this

process, we regard that there should be a uniform

classification where the documents will be displayed

in descending order according to their labels.

With the above-mentioned, we expect that we

will take better evaluations according with the

performance measures such as MAP, NDCG@k and

P@k (Baeza-Yates and Ribeiro-Neto, 2011).

Our conviction that through the above process

we will take better retrieval metrics is based on the

assumption that the cluster, which has the centroid

with the best BM25 value, will contain the

documents that have the best label and consequently

are the most relevant. So, through the iterations this

cluster will be appeared at the top of the ranked list

and as a consequence the documents with the best

label, will appear at the top of the ranked list

respectively. Therefore, we will get better

performance measures. Here is an example of

ranked lists, where the numbers 4, 3, 2, 1, 0 are the

documents' labels and the number 4 indicates the

best relevance and the number 0 indicates the

irrelevance, which illustrates graphically our goal.

We should also mention that each of the number

(0,1,2,3,4) indicates a distinguished cluster and each

document belongs to the cluster of its label:

default our conviction

1st result: 4 4

2nd result: 3 4

3rd result: 4 3

4th result: 1 3

5th result: 2 2

6th result: 3 2

7th result: 2 2

8th result: 1 1

9th result: 2 1

10th result: 0 0

As default we consider a ranked list that has been

generated by a learned model based on the single

documents. The above example depicts how we

want to muster each cluster's documents together

and promote the best clusters with the best relevance

labels at the top of the ranked list. It is obvious that

according to our conviction we get better

performance metrics.

A main framework for a learning-to-rank

algorithm, which operates according to our

approach, would be the following:

CombiningLearning-to-RankwithClustering

289

Figure 1: Learning-to-Rank algorithm’s framework using

our approach.

Observing the above framework we notice that

the innovative idea, which stands out from the

common learning-to-rank algorithms, is the clusters'

creation and the bonus insertion as the algorithms'

function is intact.

For all of our experiments, we chose that the

given bonus should contain the BM25 value. We

made this choice, because the BM25 value has been

used quite widely and quite successfully across a

wide range of experiments and it has been shown to

be the best of the known probabilistic weighting

schemes. Furthermore, it is evident that the BM25

value can completely depict the degree of correlation

between the cluster and the query.

As bonus for AdaRank-CC algorithm we use the

product (b/s)*f(x) where b is the BM25 value of the

cluster's centroid in which the document belongs to,

s is the sum of the bm25 values of the clusters'

centroids that correspond to the specific query and

f(x) is the document's value from the algorithm.

We decided to divide the BM25 value with the s

value so as to give to each document a normalized

bonus in relation to the other clusters' BM25 values.

So, before the algorithm starts we create the

clustering and at the end of each iteration, after the

algorithm's function is complete, we update the

value of each document as following



















 / ∗





(1)

As bonus for the RankBoost-CC algorithm we

have experimented with many values, following the

same reasoning as before, but none of these

improved the efficiency of RankBoost algorithm.

So, we did not get an indicative type of bonus.

However, the most successful formula was (b/s)*f(x)

where b is the BM25 value of the cluster's centroid

in which the document belongs to, s is the sum of

the bm25 values of the clusters' centroids that

correspond to the specific query and f(x) is the

document's value from the algorithm. The values are

the same as in AdaRank-CC algorithm, but without

having the desired results.

In the following we present the AdaRank-CC

and RankBoost-CC algorithms which follow the

same philosophy.

AdaRank-CC/RankBoost-CC Algorithm:

Clustering:clusters' creation

Initialization:AdaRank's/RankBoost's

initialization

For

 AdaRank's/RankBoost's function

 For each document

◦ Find the cluster in which document

belongs to and get its BM25 value

◦ Update the value of the document

using the above BM25 value

 End for

End for

Output:AdaRank-CC's/RankBoost-CC's

output

As bonus for the RankNet-CC algorithm we use

(b/10

)*f

value

(x) where b is the BM25 value of the

cluster's centroid in which the document belongs to

and f

value

(x) is a document's feature value from the

algorithm. At this algorithm, we use the documents'

vectors updating their feature values at each iteration

instead of the documents' values as we did before.

We decided to divide the BM25 value with the

number 10000, because through the experiments we

got the best results.

So, before the algorithm starts we create the

clustering and at the end of each iteration, after the

algorithm's function is complete, we update the

elements of the documents' vectors as follows:























/10





∗







(2)

The RankNet-CC algorithm follows the

AdaRank-CC's and RankBoost-CC's philosophy,

but, instead of updating the documents' value, it

updates each element of the documents' feature

vector.

So in contrast to the AdaRank-CC and

RankBoost-CC algorithms, the RankNet-CC

algorithm, based on the theory that better feature

vectors provide better results, tries to update the

documents' feature vectors at each iteration,

promoting the documents that belong to the clusters

with the best BM25 value. With the above-

mentioned, at each iteration we provide better

feature values at the documents' vectors, which

belong to the best clusters, targeting the neural

network to provide better values to these documents.

WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies

290

4 EXPERIMENTAL

EVALUATION

We conducted experiments to investigate the

performance of our implementations using the two

Microsoft Learning to Rank Datasets

(http://research.microsoft.com/en-us/projects/mslr/).

Also, for our experiments we used the RankLib

(http://people.cs.umass.edu/~vdang/ranklib.html)

library, which contains eight popular learning-to-

rank algorithms and many retrieval metrics.

These two datasets are machine learning data and

they consist of feature vectors exported from query-

url pairs in company with relevance judgment labels.

The queries and urls are represented by IDs. Also,

each query-url pair is represented by a 136-

dimensional vector, in which every dimension

provide some information. In order to create our

clustering, we have chosen 24 specific features,

which we consider as more informative, so as to

create a better clustering. We have selected the

features 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60,

65, 70, 75, 80, 85, 90, 95, 110, 130, 133, 134, 136

that correspond to the whole document's covered

query term number, covered query term ratio, stream

length, IDF(Inverse document frequency), sum of

term frequency, min of term frequency, max of term

frequency, variance of term frequency, sum of

stream length normalized term frequency, min of

stream length normalized term frequency, max of

stream length normalized term frequency, mean of

stream length normalized term frequency, variance

of stream length normalized term frequency, sum of

tf*idf, min of tf*idf, max of tf*idf, mean of tf*idf,

variance of tf*idf, BM25, PageRank, QualityScore2,

Query-url click count and url dwell time

respectively.

The purpose of our experiments was to depict the

usefulness of exploiting cluster information in

Learning-to-Rank. We have created a per query

clustering using the algorithm k-means++, which is

a variant of the k-means algorithm (Gan, Ma and

Wu, 2007) for choosing the initial values (or

"seeds") for the implementation of the algorithm. In

the assignment step of the k-means++ algorithm,

each document was assigned to the cluster whose

mean was the “nearest” to it according to the

squared Euclidean distance. We chose euclidean

measure and the specific set of features so that

documents in the same cluster can have similar

characteristics concerning the various anticipated

information needs. We should also note that every

dataset has a variable number of documents that

correspond to a specific query. Hence, we have

queries that have for example 5 results and others

that have 40 results. For this reason, we have queries

that have from 2 to 5 clusters, depending on the

number of their documents.

As we will see, in the presentation of the

experiments, though our approach aims at evaluation

effectiveness it also comes as an extra bonus an

improvement in efficiency.

4.1 Experiments with MSLR-WEB10K

In this experiment, we made use of the MSLR-

WEB10K data to test the performance of AdaRank,

AdaRank-CC, RankNet and RankNet-CC. The

MSLR-WEB10K consists of 10,000 queries and is

partitioned into 5 folders.

The following table shows the difference in the

value of metrics, based on the average of the five

folders, between AdaRank and AdaRank-CC.

Table 1: Comparison between AdaRank and AdaRank-

CC.

AdaRank AdaRank-CC

NDCG@3 0,36562 0,36758

NDCG@5 0,31002 0,34954

NDCG@10 0,34352 0,39596

P@3 0,69476 0,69438

P@5 0,66332 0,66174

P@10 0,59406 0,62542

MAP 0,57236 0,57622

The following table shows the difference in

iterations, based on the average of the five folders,

between AdaRank and AdaRank-CC.

Table 2: Comparison between AdaRank and AdaRank-

CC.

AdaRank AdaRank-CC

NDCG@3 54,4 39,8

NDCG@5 119,2 59,4

NDCG@10 95 35

P@3 10,6 8,6

P@5 7,8 7,6

P@10 122,2 43,8

MAP 163 62

The following table shows the difference in the

value of metrics, based on the average of the five

folders, between RankNet and RankNet-CC.

4.2 Experiments with MSLR-WEB30K

In this experiment, we made use of the MSLR-

WEB30K data to test the performance of AdaRank,

AdaRank-CC, RankNet and RankNet-CC. The

CombiningLearning-to-RankwithClustering

291

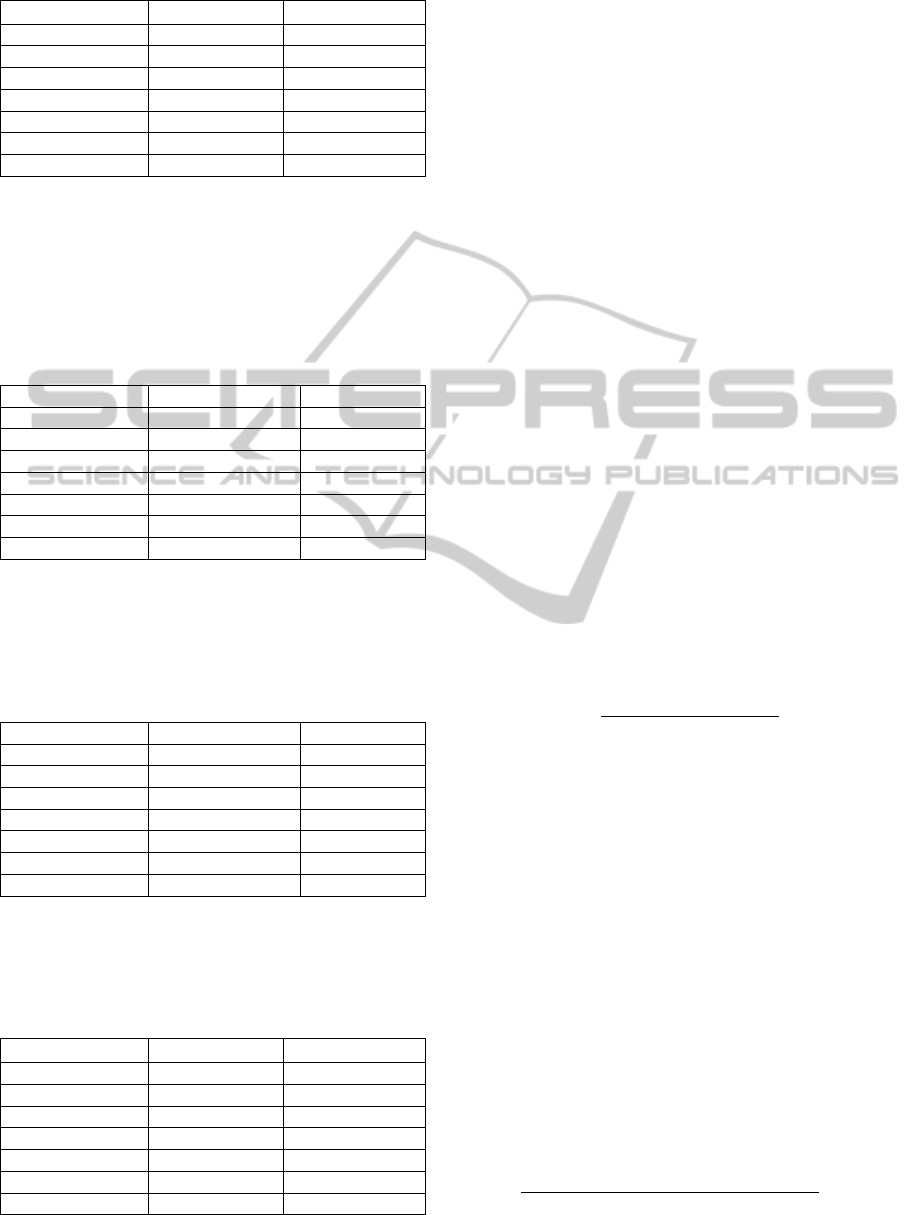
Table 3: Comparison between RankNet and RankNet -CC.

RankNet RankNet -CC

NDCG@3 0,1573 0,1531

NDCG@5 0,1683 0,1665

NDCG@10 0,2002 0,2038

P@3 0,4716 0,4711

P@5 0,4480 0,4410

P@10 0,4431 0,4415

MAP 0,4421 0,4446

MSLR-WEB30K consists of 30,000 queries and is

partitioned into 5 folders.

The following table shows the difference in the

value of metrics, based on the average of the five

folders, between AdaRank and AdaRank-CC.

Table 4: Comparison between AdaRank and AdaRank-

CC.

AdaRank AdaRank-CC

NDCG@3 0,38562 0,34059

NDCG@5 0,30028 0,33694

NDCG@10 0,34796 0,39516

P@3 0,69632 0,69736

P@5 0,66686 0,66588

P@10 0,60698 0,63182

MAP 0,57822 0,58574

The following table shows the difference in

iterations, based on the average of the five folders,

between AdaRank and AdaRank-CC.

Table 5: Comparison between AdaRank and AdaRank-

CC.

AdaRank AdaRank-CC

NDCG@3 39,2 64,8

NDCG@5 110,2 62,6

NDCG@10 84,8 31

P@3 9,1 8

P@5 18,8 6,8

P@10 86,6 46,6

MAP 169 51,8

The following table shows the difference in the

value of metrics, based on the average of the five

folders, between RankNet and RankNet-CC.

Table 6: Comparison between RankNet and RankNet -CC.

RankNet RankNet -CC

NDCG@3 0,1558 0,1593

NDCG@5 0,1686 0,1690

NDCG@10 0,2019 0,2043

P@3 0,4706 0,4718

P@5 0,4475 0,4433

P@10 0,4422 0,4410

MAP 0,4435 0,4467

4.3 Inference from the Experiments

Regarding the AdaRank-CC, which is an algorithm

that doesn't use directly the documents' values with

the additional bonus in its function, is that exploiting

the clustering and the bonus to each document

during the iterations, we can get better results

considering the NDCG@k, MAP and P@k metrics

simultaneously in fewer iterations. More precisely,

observing the graphs we understand that for

NDCG@3 and P@3 we have approximately the

same results between the default AdaRank and

AdaRank-CC. But, for NDCG@5, P@5 and

especially for NDCG@10, P@10 and MAP we

observe that the AdaRank-CC provides better

results. This observation confirms our conviction

that through the bonus during the iterations we will

direct the documents of the best clusters at the top of

the ranked list and this also shows that we gather the

documents with the best labels at the top 10

positions and as result we have better evaluation.

Hence, we conclude that our approach to

combine learning-to-rank with an existing clustering

can be integrated with positive results in fewer

iterations at an algorithm such as the AdaRank

which is positively affected by the additional bonus

that are given to the documents. We infer this

algorithm's improvement to the additional bonus

observing the calculation of distribution at each

iteration. The distribution's calculation is the

following (Li, 2011):







exp



,





∑

exp



,









(3)

where E(π,y) is the evaluation conducted at the list

level, t is the number of iteration, π is the ranked list

of documents, y is the list of documents' labels and i

is the number of query.

So, the distribution's calculation is based on the

evaluation of the documents' labels and not on the

documents' values, given by the scoring function of

the algorithm, in which we put the additional bonus.

In contrast to the above conclusions, regarding

the Rank-Boost-CC, for which the documents'

values have an important role in algorithm's

distribution determination, we don't get better

evaluation. More precisely, we can understand the

effect of the documents' value, observing how the

distribution is calculated. At each iteration the

distribution is calculated using this formula (Liu,

2011):









,















,



exp

























(4)

WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies

292

where Z

is a normalization factor, t is the number of

iteration, x is a document, a

is a parameter and h(x)

is the document's value.

So, the distribution's calculation is based on the

documents' values which contain the additional

bonus. It is clear that, in contrast to the AdaRank as

it uses the documents' labels evaluation, the

documents' value plays a significant role to the

distribution's value. Since, we don't get better result

using the additional bonus for this kind of

distribution calculation, we can deduce that the

additional bonus adversely affects these algorithms

such as RankBoost as it adversely distorts the

calculation of the distribution.

Regarding the RankNet-CC, for which at the end

of each iteration we update the elements of the

documents' vectors in order to create better vectors

and as consequence better results, from the results

we can observe that the metrics between RankNet

and RankNet-CC are approximately equal and so we

can not infer reliable conclusions. Slightly better

results in favour of RankNet-CC we can observe for

the metrics NDCG@10 and P@10 and this remark

agrees with the observation that we made for the

AdaRank-CC concerning the above two metrics.

5 CONCLUSIONS

In this paper we have proposed new versions of the

AdaRank, RankBoost and RankNet learning to rank

algorithms, referred to as AdaRank-CC, RankBoost-

CC and RankNet-CC respectively. In contrast to

existing methods, AdaRank-CC, RankBoost-CC and

RankNet-CC take into consideration the multi-way

inter-relationship between all documents, since we

have separated the unstructured set of documents

into clusters using the k-Means++ algorithm.

Our basic finding in this work is that algorithms

such as AdaRank-CC, for which the additional

bonus doesn't affect the computation of the

distribution of weights over the queries, can indeed

improve both effectiveness and efficiency, as we can

get better overall quality according to the well

known evaluation metrics (NDCG, MAP, various

levels of precision) and simultaneously decrease the

number of iterations. As future work, it could be

interesting to further investigate how we can get the

similar results to those of the AdaRank-CC and the

other algorithms that use directly the documents'

values with the additional bonus in their function

and consequently they are affected by them.

ACKNOWLEDGEMENTS

This research has been co-financed by the European

Union (European Social Fund – ESF) and Greek

national funds through the Operational Program

"Education and Lifelong Learning" of the National

Strategic Reference Framework (NSRF) - Research

Funding Program: Thales. Investing in knowledge

society through the European Social Fund.

REFERENCES

Baeza-Yates R., and Ribeiro-Neto B., (2011) Modern

Information Retrieval: the concepts and technology

behind search. Addison Wesley, Essex.

Burges C., Shaked T., Renshaw E., Lazier A., Deeds M.,

Hamilton N. and Hullender G., (2005) Learning to

Rank using Gradient Descent, ICML 2005: 89-96.

Freund Y., Iyer R., Schapire R. E, Singer Y., An

Efficient Boosting Algorithm for Combining

Preferences. In Journal of Machine Learning Research

4 (2003), 933-969.

Gan G., Ma C. and Wu J. (2007). Data Clustering: Theory,

Algorithms, and Applications.

DOI=http://dx.doi.org/10.1137/1.9780898718348.

Hearst A. M., Pedersen J. O., Reexamining the Cluster

Hypothesis: Scatter/Gather on Retrieval Results, In

Proceedings of ACM SIGIR '96, August, 1996, Zurich.

Kurland O., Inter-Document similarities, language models,

and ad-hoc information retrieval. Ph.D. Thesis (2006).

Kurland O., The Cluster Hypothesis in Information

Retrieval, SIGIR 2013 tutorial (2013).

http://iew3.technion.ac.il/~kurland/clustHypothesisTutoria

l.pdf.

Li H., Learning to Rank for Information Retrieval and

Natural Language Processing. (2011) Morgan &

Claypool.

Liu T. Y., Learning to Rank for Information Retrieval.

(2011) Springer.

Liu, X, and W. Bruce C. 2004. Cluster-based retrieval

using language models. In Proc. SIGIR, pp. 186-193.

ACM Press. DOI: doi.acm.org/10.1145/

1008992.1009026.

Manning C. D., Raghavan P., Schutze H., (2008)

Introduction to Information Retrieval, Cambridge

University Press, pp. 232-234.

McKeown et al. (2002), Tracking and Summarizing News

on a Daily Basis with Columbia’s Newsblaster, In

Proc. Human Language Technology Conference.

Raiber F., Kurland O. (2012), Exploring the Cluster

Hypothesis, and Cluster-Based Retrieval, over the

Web, ACM CIKM: 2507-2510.

Robertson, S., Zaragoza, H., Taylor, M. (2004) Simple

BM25 extension to multiple weighted fields.. In

CIKM 2004: Proceedings of the thirteenth ACM

International Conference on Information and

Knowledge Management, pages 42-49.

CombiningLearning-to-RankwithClustering

293

van Rijsbergen, C. J.: Information Retrieval, 2nd edn.,

Butterworths (1979).

Xu J. and Li H., (2007) AdaRank: A Boosting Algorithm

for Information Retrieval, SIGIR 2007: 391-398.

Zeng H.-J., He Q.-C., Chen Z., Ma W.-Y., Ma J. (2004),

Learning to Cluster Web Search Results. SIGIR 2004:

210-21.

WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies

294