Sampling based Bundle Adjustment using Feature Matches
between Ground-view and Aerial Images
Hideyuki Kume, Tomokazu Sato and Naokazu Yokoya
Nara Institute of Science and Technology, 8916-5 Takayama, Ikoma, Nara, Japan
Keywords:
Structure-from-Motion, Bundle Adjustment, Aerial Image, RANSAC.
Abstract:
This paper proposes a new pipeline of Structure-from-Motion that uses feature matches between ground-
view and aerial images for removing accumulative errors. In order to find good matches from unreliable
matches, we newly propose RANSAC based outlier elimination methods in both feature matching and bundle
adjustment stages. To this end, in the feature matching stage, the consistency of orientation and scale extracted
from images by a feature descriptor is checked. In the bundle adjustment stage, we focus on the consistency
between estimated geometry and matches. In experiments, we quantitatively evaluate performances of the
proposed feature matching and bundle adjustment.
1 INTRODUCTION
Structure-from-Motion (SfM) is one of key technolo-
gies developed in computer vision field, and SfM
has been used to achieve great works such as ‘build-
ing Rome in a day’ (Agarwal et al., 2009) and
‘PTAM’ (Klein and Murray, 2007). In SfM, one es-
sential problem is accumulation of estimation errors
for a long image sequence. Although many kinds
of methods that reduce accumulative errors are pro-
posed, SfM methods essentially cannot be free from
accumulative errors unless some external references
(e.g., like GPS, aerial images, and feature landmarks)
are given.
The techniques that remove accumulative errors
in the bundle adjustment (BA) stage of SfM using
some external references are called as extended bun-
dle adjustment (extended-BA), and earlier researches
of extended-BA mainly focused on the combination
of GPS and SfM (Lhuillier, 2012). In this paper, we
employ the framework of extended-BA to the SfM
problem that uses an aerial image as an external ref-
erence. In order to successfully use an aerial image
as a reference of SfM, successful matching between
aerial image and ground-view image is very impor-
tant. To find good matches from unreliable matches,
in addition to the use of GPS and gyroscope sensors
embedded in most of recent smartphones, we newly
use two methods: (1) RANSAC (Fischler and Bolles,
1981) based outlier elimination in the feature match-
ing stage by focusing on consistency of orientation
and scale extracted from images by feature descriptor
like SIFT (Lowe, 2004) and (2) RANSAC based out-
lier elimination in the BA stage using consistency of
estimated geometry and matches.
2 RELATED WORK
In order to reduce accumulative errors in SfM, loop
closing techniques (Williams et al., 2009) are some-
times employed with the BA. Although these tech-
niques can reduce accumulativeerrors, it is essentially
difficult for the techniques that rely on only images to
remove accumulative errors for a long sequence with-
out the loop.
In order to reduce accumulative errors in gen-
eral movement of camera, several kinds of external
references such as GPS (Lhuillier, 2012) and road
maps (Brubaker et al., 2013) are used with SfM.
Lhuillier (Lhuillier, 2012) proposed extended-BA us-
ing GPS that minimizes the energy function defined
as the sum of reprojection errors and a penalty term
of GPS. This method can globally optimize camera
parameters and reduce accumulative errors by updat-
ing parameters so as to minimize the energy func-
tion. However, the accuracy of this method is directly
affected by errors of GPS positioning, which easily
grow to the 10m level in urban areas. Brubaker et
al. (Brubaker et al., 2013) proposed the method that
uses community developed road maps. Although this
692
Kume H., Sato T. and Yokoya N..
Sampling based Bundle Adjustment using Feature Matches between Ground-view and Aerial Images.
DOI: 10.5220/0004850306920698
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 692-698
ISBN: 978-989-758-009-3
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

method can reduce accumulative errors by matching
trajectory from SfM to road maps, there are ambigui-
ties for some scenes such as straight roads or Manhat-
tan worlds.
On the other hand, in order to estimate abso-
lute camera positions and postures, some methods
estimate camera parameters directly from references
without SfM (Pink et al., 2009; Noda et al., 2010).
Pink et al. (Pink et al., 2009) used aerial images as
references and estimated camera parameters based on
feature matching between input images and aerial im-
ages. However, it is not easy to find good matches
for all the images of a long video sequence especially
for the scenes where unique landmarks cannot be ob-
served. Although Mills (Mills, 2013) proposed a ro-
bust feature matching procedure that compares orien-
tation and scale of each matches with dominant ori-
entation and scale identified by histogram analysis,
it cannot work well when there exist a huge num-
ber of outliers. Noda et al. (Noda et al., 2010) re-
laxed the problem by generating mosaic images of
the ground from multiple images for feature match-
ing. However, accumulative errors are not considered
in this work. Unlike previous works, we estimate
relative camera poses for all the frames using SfM,
and we remove accumulative errors by selecting cor-
rect matches between aerial image and ground-view
image from candidates by employing a multi-stage
RANSAC scheme.
3 FEATURE MATCHING
BETWEEN GROUND-VIEW
AND AERIAL IMAGES
In this section, we propose a robust method to obtain
feature matches between ground-view and aerial im-
ages. As shown in Figure 1, the method is composed
of (1) ground-view image rectification by Homogra-
phy, (2) feature matching, and (3) RANSAC. Here,
in order to achieve robust matching, we propose new
criteria for RANSAC with consistency check of ori-
entation and scale from a feature descriptor. It should
be noted that matching for all the input frames are not
necessary in our pipeline. Even if we can find only
several candidates of matched frames, they can be ef-
fectively used as references in the BA stage.
3.1 Image Rectification by Homography
Before calculating feature matches using a feature de-
tector and a descriptor, as shown in Figure 1, we rec-
tify ground-view images so that texture patterns are
similar to those of the aerial image. In most cases,
aerial images are taken very far away from the ground
and thus they are assumed to be captured by an ortho-
graphic camera whose optical axis is directed to grav-
ity direction. In order to rectify ground-view images,
we also assume that the ground-view images contain
the ground plane whose normal vector is directed to
gravity direction. Then, we compute Homography
matrix using the gravity direction in camera coordi-
nate system which can be estimated from the vanish-
ing points of parallel lines or a gyroscope.
3.2 Feature Matching
Feature matches between rectified ground-view im-
ages and the aerial image are calculated. Here, we
use GPS data corresponding to the ground-view im-
ages to limit searching area in the aerial image. More
concretely, we select the region whose center is GPS
position and its size is l × l. In the experiment de-
scribed later, l is set to 50 [m]. Feature matches are
then calculated by a feature detector and a descriptor.
We employ SIFT (Lowe, 2004) in the experiment be-
cause of its robustness for changes in scale, rotation
and illumination.
3.3 RANSAC with Orientation and
Scale Check
As shown in Figure 1, tentative matches often include
many outliers. In order to remove outliers, we use
RANSAC with consistency check of orientation and
scale parameters.
For matches between rectified ground-view im-
ages and the aerial image, we can use the similarity
transform which is composed of scale s, rotation θ
and translation τ
τ
τ. In RANSAC procedure, we ran-
domly sample two matches (minimum number to es-
timate similarity transform) to compute the similarity
transform (s, θ,τ
τ
τ). Here we count the number of in-
liers which satisfy
|a
a
a
k
− (sR(θ)g
g
g
k
+ τ
τ
τ)| < d
th
, (1)
where a
a
a
k
and g
g
g
k
are the 2D positions of the k-th match
in the aerial image and the rectified ground-view im-
age, respectively. R(θ) is the 2D rotation matrix with
rotation angle θ and d
th
is a threshold. After repeating
random sampling process, the sampled matches with
the largest number of inliers are selected.
The problem here is that the distance-based crite-
rion above cannot successfully find correct matches
when there exist a huge number of outliers. In or-
der to achieve more robust matching, we modify the
criterion of RANSAC by checking the consistency of
SamplingbasedBundleAdjustmentusingFeatureMatchesbetweenGround-viewandAerialImages
693

Ground-view image
Aerial image
(1) Homography
(2) Feature matching
(3) RANSAC with
orientation and scale check
Figure 1: Flow of feature matching.
orientation and scale from a feature descriptor. Con-
cretely, we count the number of inliers which simul-
taneously satisfy Equation (1) and the following two
conditions.
max

s
gk
· s
s
ak
,
s
ak
s
gk
· s

< s
th
, (2)
aad(θ
gk
+ θ, θ
ak
) < θ
th
, (3)
where (s
ak
, s
gk
) and (θ
ak
, θ
gk
) are the scale and orien-
tation of feature points for the k-th match on the aerial
image and the rectified ground-view image, respec-
tively. The function ‘aad’ returns the absolute angle
difference in the domain [0
◦
, 180.0
◦
]. s
th
and θ
th
are
thresholds for scale and angle, respectively.
4 SAMPLING BASED BUNDLE
ADJUSTMENT
Even by the modified RANSAC proposed in previous
section, it is not possible to remove all the incorrect
matches in principle because there may exist repeti-
tive and similar patterns, e.g., road signs in real envi-
ronments. In order to overcome this difficulty, we also
employ RANSAC for the BA stage by focusing on
consistency between feature matches and estimated
camera poses from images.
4.1 Definition of Energy Function
In order to consider the matches between ground-
view and aerial images, here, an energy function is
defined and minimized. The energy function E is
defined by using reprojection errors for ground-view
(perspective) images Φ and the aerial (orthographic)
image Ψ as follows:
E({R
R
R
i
,t
t
t
i
}
I
i=1
, {p
p
p
j
}
J
j=1
) =
Φ({R
R
R
i
,t
t
t
i
}
I
i=1
, {p
p
p
j
}
J
j=1
) + ωΨ({p
p
p
j
}
J
j=1
), (4)
where R
R
R
i
and t
t
t
i
represent rotation and translation from
world coordinate system to camera coordinate system
for the i-th frame, respectively. p
p
p
j
is a 3D position
of the j-th feature point. I and J are the number of
frames and feature points, respectively, and ω is a
weight that balances Φ and Ψ. Since the energy func-
tion is non-linearly minimized in BA, good initial val-
ues of parameters are required to avoid local minima.
Before minimizing the energy function, we fit the pa-
rameters estimated by SfM to the positions from GPS
by 3D similarity transform. In the following, the en-
ergy associated with reprojection errors Φ and Ψ are
detailed.
4.1.1 Reprojection Errors for Ground-view
Images
The commonly used reprojection errors employ the
pinhole camera model which cannot deal with projec-
tions from behind the camera. Projections from be-
hind the camera often occur in BA with references due
to dynamic movement of camera parameters by refer-
ences. Here, instead of common squared distance er-
rors on image plane, we employ the reprojection error
by using angle of rays as follows:
Φ({R
R
R
i
,t
t
t
i
}
I
i=1
, {p
p
p
j
}
J
j=1
) =
1
∑
I
i=1
|P
P
P
i
|
I
∑
i=1
∑
j∈P
P
P
i
Φ
ij
, (5)
Φ
ij
= ∠

x
ij
f
i

,

X
ij
Z
ij

2
+ ∠

y
ij
f
i

,

Y
ij
Z
ij

2
,
(6)
(X
ij
,Y
ij
, Z
ij
)
T
= R
R
R
i
p
p
p
j
+ t
t
t
i
, (7)
where P
P
P
i
is a set of feature points detected in the i-
th frame. Function ∠ returns an angle between two
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
694

vectors, (x
ij
, y
ij
)
T
is a detected 2D position of the j-
th feature points in the i-th frame, and f
i
is the focal
length of the i-th camera.
Here, we split the angular reprojection error
into xz component and yz component because Jaco-
bian matrix of E required by non-liner least squares
method such as Levenberg-Marquardt method be-
comes simple. Especially, the first term of Φ
ij
does
not depend on the y component of t
t
t
i
and the sec-
ond term does not depend on the x component of t
t
t
i
in this definition. We have experimentally confirmed
that this splitting largely affects the performance of
convergence.
4.1.2 Reprojection Errors for Aerial Image
The reprojection errors for the aerial (orthographic)
image are defined as follows:
Ψ({p
p
p
j
}
J
j=1
) =
1
∑
i∈M
M
M
|A
A
A
i
|
∑
i∈M
M
M
∑
j∈A
A
A
i


a
a
a
j
− pr
xy
(p
p
p
j
)


2
,
(8)
where M
M
M is a set of frames in which feature matches
between ground-view and aerial images are obtained.
A
A
A
i
is a set of feature points which are matched to the
aerial image in the i-th frame. a
a
a
j
is the 2D position
of the j-th feature point in the aerial image. pr
xy
is a
function that projects a 3D point onto xy plane (aerial
image coordinate system).
4.2 RANSAC for Bundle Adjustment
RANSAC scheme is introduced in BA by using the
consistency between feature matches and estimated
camera poses from images. First, we randomly sam-
ple n frames from the candidates of matched frames
and do BA using feature matches included in sampled
frames, i.e., using a set of selected frames M
M
M
′
instead
of M
M
M in Equation (8). Then we count the number of
inlier frames which satisfy the following two condi-
tions.
average
j∈A
A
A
i
(α
ij
) < α
th
, (9)
∠

R
R
R
T
i
(0, 0, 1)
T
, o
o
o
i

< β
th
, (10)
where α
ij
is an angular reprojection error of the j-th
feature point on aerial image coordinate system. o
o
o
i
is the direction of optical axis in world coordinate
system calculated from Homography and similarity
transform estimated in the feature matching stage. α
th
and β
th
are thresholds. Here, α
ij
is computed as fol-
lows:
α
ij
= ∠

a
a
a
j
− pr
xy
(R
R
R
T
i
t
t
t
i
), pr
xy

R
R
R
T
i
(x
ij
, y
ij
, f
i
)
T

.
(11)
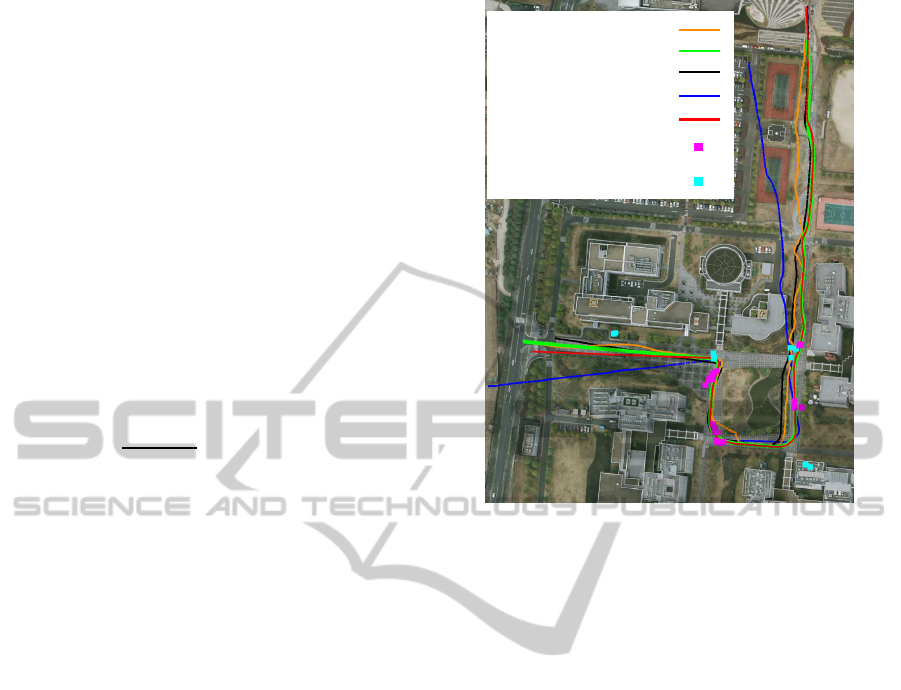
GPS on iPhone
RTK-GPS (Ground truth)
Correctly matched feature point
on aerial image
Incorrectly matched feature point
on aerial image
BA with references without RANSAC
BA without references
BA with references and RANSAC
Figure 2: Experimental environment and results.
After repeating the random sampling process at
given times, sampled frames with the largest number
of inlier frames are selected. Finally, camera poses
are refined by redoing BA using feature matches with
selected inlier frames as references.
5 EXPERIMENTS
In order to validate the effectiveness of the proposed
method, we quantitatively evaluated performances of
sampling based BA as well as the feature matching
process.
5.1 Experimental Setup
We used iPhone 5 (Apple) as a sensor unit includ-
ing a camera, GPS and gyroscope. The camera cap-
tured video images (640× 480 pixels, 2471 frames,
494 seconds). GPS and gyroscope measured position
at 1 Hz and gravity direction for every frame, respec-
tively. We also used RTK-GPS (Topcon GR-3, 1 Hz,
accuracy of horizontal positioning is 0.03 [m]) to ob-
tain the ground truth positions. Positions from GPS
data were assigned temporally to the nearest frame.
As the external reference, we downloaded the aerial
image covering the area used in this experiment from
Google Maps [maps.google.com] whose coordinate
system is associated with the metric scale, i.e., 19.2
[pixel] = 1 [m]. Figure 2 shows an aerial image and
GPS positions.
SamplingbasedBundleAdjustmentusingFeatureMatchesbetweenGround-viewandAerialImages
695

Angle [ ] Scale
325.56
0.06
Angle [ ] Scale
334.02
0.85
332.84
0.91
330.88
0.84
352.56
0.43
156.73
1.06
Similarity transform
SIFT keypoints
(a) Without orientation and scale check
Angle [ ] Scale
158.71
1.19
Angle [ ] Scale
159.92
1.11
154.96
0.89
154.24
1.25
148.45
1.12
Similarity transform
SIFT keypoints
(b) With scale check, with/without orientation check
Angle [ ] Scale
66.47
0.07
Angle [ ] Scale
164.35
0.86
334.38
0.82
334.94
0.78
329.40
0.68
171.96
0.46
Similarity transform
SIFT keypoints
(c) Without orientation and scale check
Angle [ ] Scale
336.34
0.96
Angle [ ] Scale
342.27
0.90
338.34
0.90
339.67
0.73
341.82
0.77
333.08
0.77
Similarity transform
SIFT keypoints
(d) With orientation check, with/without scale check
Figure 3: Selected inliers for example images. Solid and dashed lines are correct and incorrect matches, respectively. Relative
angle and scale of matched feature points are shown in bottom right table with corresponding lines’ colors. Green points are
ground truths of camera positions. RANSAC with/without orientation check for (b) and scale check for (d) gave the same
results.
Angle [ ] Scale
3.87
0.89
Angle [ ] Scale
343.16
1.63
19.02
0.80
12.64
1.22
13.32
0.93
Similarity transform
SIFT keypoints
Angle [ ] Scale
169.41
1.07
Angle [ ] Scale
169.48
0.99
168.87
1.15
163.06
1.17
170.35
1.04
Similarity transform
SIFT keypoints
Figure 4: Examples of incorrect matches by RANSAC with orientation and scale check. The interpretations of symbols are
the same as Figure 3.
In order to obtain initial values for BA, we em-
ployed VisualSFM (Wu, 2011) as a state-of-the-art
implementation of SfM. For non-linear minimization,
we used ceres-solver (Agarwal et al., 2013).
5.2 Result of Feature Matching
In this experiment, we evaluate the effectiveness
of proposed feature matching process including
RANSAC with scale and orientation check described
in Section 3. Here, we have compared four types of
RANSAC by enabling and disabling scale and orien-
tation check. In order to countthe number of correctly
matched frames, we first selected frames which have
four or more inlier matches after RANSAC. From
these frames, we manually counted frames whose
matches are correct. Here, we set d
th
= 2 [pixel],
s
th
= 2 and θ
th
= 40 [
◦
].
Table 1 shows rates of frames in which all the se-
lected matches are correct. From this table, we can
confirm that the rates are significantly improved by
scale and orientation check. Figure 3 shows effects of
scale and orientation check for sampled two images.
In both cases, RANSAC without scale and orientation
check could not select correct matches and proposed
RANSAC with scale and orientation check could se-
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
696

lect correct matches. However, as shown in Figure
4, incorrect matches still remain even if we use both
scale and orientation check.
5.3 Result of Bundle Adjustment
In this experiment, we evaluate the effectiveness of
BA with RANSAC described in Section 4. In this
stage, the frames with GPS data were sampled (650
of 2471 frames) and used in order to reduce com-
putational time. As external references, we used
frames and feature matches selected with orientation
and scale check described in previous section. Here,
we set ω = 10
−5
, α
th
= 10.0 [
◦
], β
th
= 150.0 [
◦
], and
n = 2.
We first evaluate the proposed RANSAC in terms
of capability to select frames whose matches are cor-
rect. Here, as shown in Table 1, 10 of 14 frames
have correct matches. We tested all the pairs of 14
frames as samples of RANSAC, and the number of
inlier frames that are selected in each trial is checked.
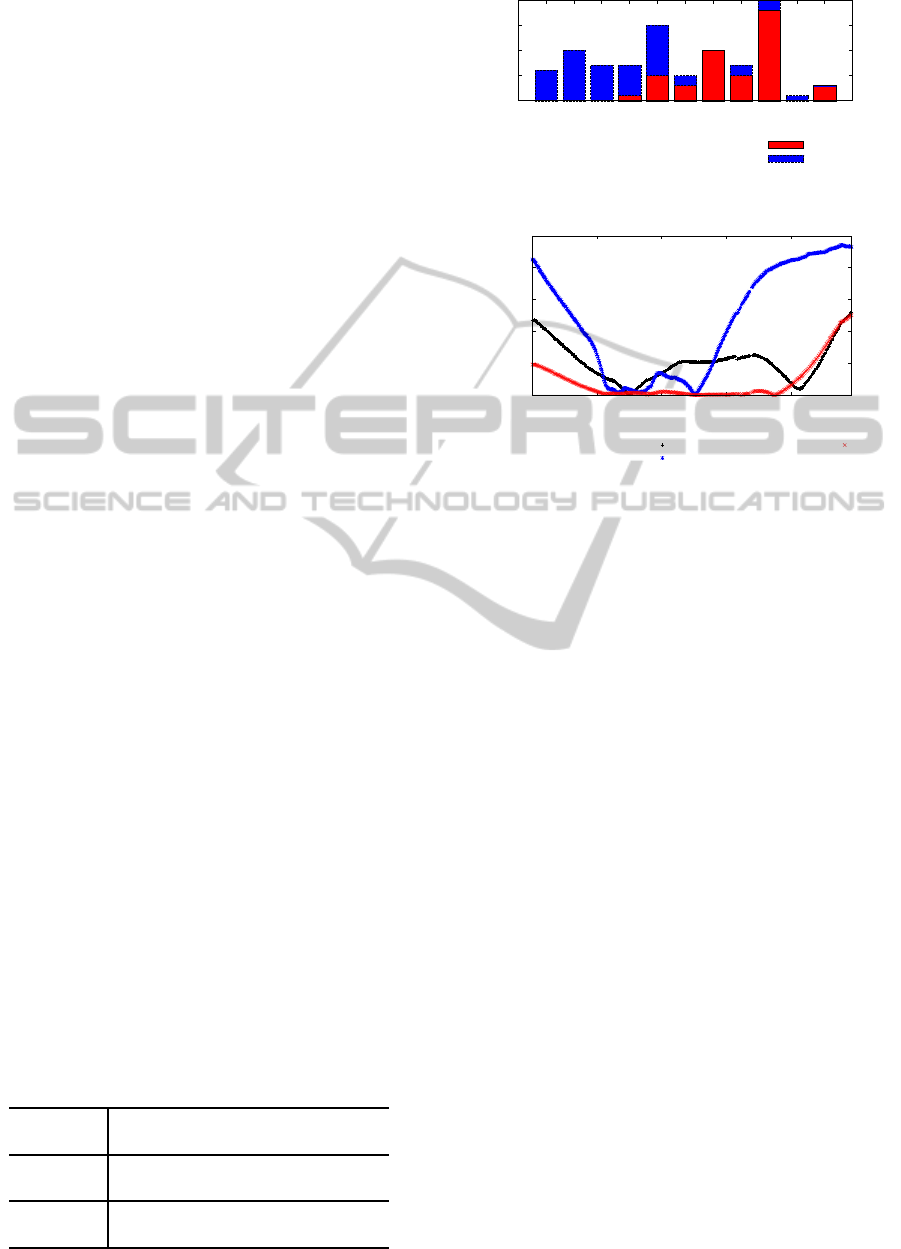
Figure 5 shows the number of trials and inlier frames
derived by each trial. From this figure, we can see that
the sampled frames without incorrect matches tend to
increase the number of inlier frames. We also con-
firmed that the trials which derive the largest num-
ber of inlier frames successfully selected all of collect
matches.
Next, we evaluate the accuracy of the proposed
method by comparing the following methods.
• BA without references (Wu, 2011),
• BA with references without RANSAC which uses
all the matches obtained by feature matching pro-
cess,
• BA with references and RANSAC.
Since the BA without reference cannot estimate the
metric scale, we fitted the camera positions estimated
by SfM to the ground truths by similarity transform.
Figures 2 and 6 show the estimated camera positions
and horizontal position errors for each frame, respec-
tively. From these results, it is confirmed that es-
timated camera positions by BA without references
Table 1: Rates of frames in which all the selected matches
are correct. Number of frames in which all the selected
matches are correct / number of frames which have four or
more inlier matches are shown in bracket.
w/ orientation w/o orientation
check check
w/ scale 0.714 0.103
check (10 / 14) (9 / 87)
w/o scale 0.134 0.005
check (9 / 67) (2 / 380)
0
5
10
15
20
0
1 2
3
4
5 6 7 8 9 10
Number of trials
Number of inlier frames
Sampled frames without incorrect matches
Sampled frames with incorrect matches
Figure 5: Number of trials and inlier frames derived by each
trial.
0
10
20
30
40
50
0 500 1000 1500 2000
Horizontal position error [m]
Frame number
BA w/o references
BA w/ references w/o RANSAC
BA w/ references and RANSAC
Figure 6: Horizontal position error in each frame.
are affected by accumulative errors. The BA with-
out RANSAC is affected by incorrect matches. The
proposed BA with RANSAC can reduce the accumu-
lative errors. It should be noted that, in the end of the
sequence, the accumulative errors are still remained
because there are no available matches.
6 CONCLUSIONS
In this paper, we have proposed a method to remove
accumulative errors of SfM by using aerial images as
external references that already exist for many places
in the world. To this end, we have proposed SfM
method that uses feature matches between ground-
view and aerial images. In order to find correct
matches from unreliable matches, we have introduced
the new RANSAC schemes to both feature matching
and bundle adjustment stages. In experiments, we
have confirmed that the proposed method is effective
for estimating camera poses of real video sequence
taken in an outdoor environment. In the future, we
will test the effectiveness of the proposed method in
various environments including roadways.
ACKNOWLEDGEMENTS
This research was partially supported by JSPS Grant-
in-Aid for Scientific Research No. 23240024 and
“Ambient Intelligence” project granted from MEXT.
SamplingbasedBundleAdjustmentusingFeatureMatchesbetweenGround-viewandAerialImages
697

REFERENCES
Agarwal, S., Mierle, K., and Others (2013). Ceres solver.
https://code.google.com/p/ceres-solver.
Agarwal, S., Snavely, N., Simon, I., Seitz, S. M., and
Szeliski, R. (2009). Building Rome in a day. In Proc.
Int. Conf. on Computer Vision, pages 72–79.
Brubaker, M. A., Geiger, A., and Urtasun, R. (2013).
Lost! leveraging the crowd for probabilistic visual
self-localization. In Proc. IEEE Conf. on Computer
Vision and Pattern Recognition, pages 3057–3064.
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: a paradigm for model fitting with appli-
cations to image analysis and automated cartography.
Communications of the ACM, 24(6):381–395.
Klein, G. and Murray, D. (2007). Parallel tracking and map-
ping for small AR workspaces. In Proc. Int. Symp. on
Mixed and Augmented Reality, pages 225–234.
Lhuillier, M. (2012). Incremental fusion of structure-from-
motion and GPS using constrained bundle adjust-
ments. IEEE Trans. on Pattern Analysis and Machine
Intelligence, 34(12):2489–2495.
Lowe, D. G. (2004). Distinctive image features from
scale-invariant keypoints. Int. J. Computer Vision,
60(2):91–110.
Mills, S. (2013). Relative orientation and scale for improved
feature matching. In Proc. IEEE Int. Conf. on Image
Processing, pages 3484–3488.
Noda, M., Takahashi, T., Deguchi, D., Ide, I., Murase,
H., Kojima, Y., and Naito, T. (2010). Vehicle ego-
localization by matching in-vehicle camera images to
an aerial image. In Proc. ACCV2010 Workshop on
Computer Vision in Vehicle Technology: From Earth
to Mars, pages 1–10.
Pink, O., Moosmann, F., and Bachmann, A. (2009). Vi-
sual features for vehicle localization and ego-motion
estimation. In Proc. IEEE Intelligent Vehicles Sympo-
sium, pages 254–260.
Williams, B., Cummins, M., Neira, J., Newman, P., Reid, I.,
and Tard´os, J. (2009). A comparison of loop closing
techniques in monocular SLAM. Robotics and Au-
tonomous Systems, 57(12):1188 – 1197.
Wu, C. (2011). VisualSFM: A visual structure from motion
system. http://ccwu.me/vsfm/.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
698