Weighted SIFT Feature Learning with Hamming Distance

for Face Recognition

Guoyu Lu

, Yingjie Hu

and Chandra Kambhamettu

University of Delaware, Newark, U.S.A.

eBay Research, San Jose, U.S.A.

Keywords:

Face Recognition, SIFT Feature, Hamming Descriptor, Feature Transformation, Dimensional Reduction,

Feature Weighting.

Abstract:

Scale-invariant feature transform (SIFT) feature has been successfully utilized for face recognition for its

tolerance to the changes of image scaling, rotation and distortion. However, a big concern on the use of

original SIFT feature for face recognition is SIFT feature’s high dimensionality which leads to slow image

matching. Meanwhile, large memory capacity is required to store high dimensional SIFT features. Aiming to

ﬁnd an efﬁcient approach to solve these issues, we propose a new integrated method for face recognition in this

paper. The new method consists of two novel functional modules in which a projection function transforms

the original SIFT features into a low dimensional Hamming feature space while each bit of the Hamming

descriptor is ranked based on their discrimination power. Furthermore, a weighting function assigns different

weights to the correctly matched features based on their matching times. Our proposed face recognition

method has been applied on two benchmark facial image datasets: ORL and Yale datasets. The experimental

results have shown that the new method is able to produce good image recognition rate with much improved

computational speed.

1 INTRODUCTION

The basic task of face recognition is to identify the

query face image in the given images or videos, e.g.,

to compare a query face image with an image having

the already conﬁrmed identiﬁcation. Scale-invariant

feature transform (SIFT) (D.Lowe, 2004) is an algo-

rithm used in computer vision for translating images

into a set of features (SIFT features), each of which

is invariant to scaling and rotation, robust to distor-

tion and partially change in illumination. Owing to

the invariant characteristic, SIFT has been widely ap-

plied to the areas of object recognition, motion track-

ing, robot localization, to name but a few. How-

ever, some concerns have been raised about the efﬁ-

ciency of SIFT feature even though it has the capabil-

ity of outperforming most conventional local feature

techniques for face recognition. One of the main is-

sues of using SIFT feature is the high dimensionality

of the feature which introduces heavy computational

cost for image matching. Pertaining to a real world

face recognition problem, usually a large number of

images are depicted by SIFT features in the train-

ing data, each being represented in a 128-dimensional

space. Such circumstance can signiﬁcantly decrease

the image matching speed for face recognition. There

have been some attempts to use different approaches

to speed up the matching process, such as implement-

ing SIFT feature by multi-core systems (Zhang et al.,

2008) and building multi-scale local image structures

for face recognition (Geng and Jiang, 2011).

Inspired by LDAHash method (Strecha et al.,

2012), this paper proposes a new projection function

that reduces the curse of dimensionality and further

transforms the low dimensional feature space into a

Hamming space to reduce memory consumption and

improve matching speed. Meanwhile, we have de-

veloped a new method based on Hamming descrip-

tors utilizing the transitive closure of the descriptors

(Strecha et al., 2010) to improve image matching ac-

curacy. Unlike the method in which separated sub-

regions are represented by local binary pattern (LBP)

(Ahonen et al., 2006), our new Hamming descriptors

retain the scale invariant characteristic of SIFT and

allows the learning from the interesting points in the

training images. Thereafter, an improved grid-based

method (Bicego et al., 2006) uses the learned Ham-

ming descriptors to test the query image pertaining to

Lu G., Hu Y. and Kambhamettu C..

Weighted SIFT Feature Learning with Hamming Distance for Face Recognition.

DOI: 10.5220/0004859806910699

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 691-699

ISBN: 978-989-758-004-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

a face recognition task.

SIFT feature is generally agreed to be capable

of producing satisfactory performance on afﬁne and

scaling transformations (Kri

zaj et al., 2010; Soyel and

Demirel, 2011). However, it lacks of the capability on

handling strong illumination changes and large rota-

tions, both of which may exist in face images, which

may produce a risk of relatively high false positive

matching rate in recognition. In the new proposed

method for face recognition, we use Random Sample

Consensus (RANSAC) (Fischler and Bolles, 1981)

to identify the correctly matched descriptors in the

learning period and then apply a weighting model to

assign higher weights to those more commonly cor-

rectly matched descriptors through an online recogni-

tion process. Thus the matching points retaining high

true positive rate will play a more essential role in the

matching process.

The remainder of the paper is organized as fol-

lows. Section 2 presents a review of the related work

in which SIFT feature has been used for face recogni-

tion. Section 3 proposes our new method that projects

SIFT descriptors into a lower dimension Hamming

space. Section 4 describes a new weighting method

for improving matching accuracy. Section 5 presents

the experimental results and the ﬁndings, followed by

the conclusion of this paper in section 6.

2 RELATED WORK

During the last two decades, signiﬁcant progress has

been made in face recognition with the development

of a variety of methods. Classical statistical algo-

rithms have been widely used for face recognition

problems and have performed well under some cir-

cumstances. Eigenfaces (Turk and Pentland, 1991)

and Fisherfaces (Belhumeur et al., 1997; Jiang, 2011)

are two classical face recognition methods that em-

ploy principal component analysis (PCA) and lin-

ear discriminant analysis (LDA), respectively. Eigen-

faces and Fisherfaces based methods handle face im-

ages as a global feature, which is sensitive to face ex-

pression and head rotation. Thus, the performance

from Eigenfaces and Fisherfaces based methods is not

promising when face images have certain changes or

distortions.

To mitigate the various issue raised by global fea-

ture method in face recognition applications, local

features have been deployed for their invariant char-

acteristics on face scaling, rotation and other changes.

Recent research attempts to use local feature for face

recognition. SIFT feature is a method that is invari-

ant to image scale and rotation, which offers a ro-

bust matching technique to achieve high face recog-

nition rate with only a small set of features trans-

lated from face images. It has been incorporated into

a variety of computational models and systems for

image recognition problems, including face recogni-

tion. One representative work can be found in (Bicego

et al., 2006). They applied SIFT features to a grid-

based method for image matching in which the aver-

age minimum pair distance was used as the match-

ing criterion. Their approach not only decreased the

false positive rate (FPR) of the image matching, but

also reduced the computational complexity. To pro-

duce high recognition rate, SIFT feature was em-

ployed for describing local marks (Fernandez and Vi-

cente, 2008; Rosenberger and Brun, 2008) and was

combined with a clustering-based method (Luo et al.,

2007). In the clustering-based method, face images

are usually clustered into 5 regions: two eyes, nose,

and mouth corners. Although the recognition accu-

racy rate can be slightly improved compared with the

method in (Bicego et al., 2006), extra computational

time for clustering is required.

Recently, more sophisticated face recognition

methods using SIFT feature have been developed and

applied to real world applications. Geng and Jiang

(Geng and Jiang, 2011) introduced a method that

created a framework trained by multi-scale descrip-

tors on the smooth parts of face. To reduce the fea-

ture quantization error, SIFT feature has been incor-

porated with a kernel based model for face recog-

nition, such as Sparse Representation Spatial Pyra-

mid Matching (KSRSPM) method (Gao et al., 2010).

Also, SIFT feature has been studied for solving 3D

face recognition problems and reported to able to pro-

duce high recognition accuracy (Mian et al., 2008).

Our method utilizes the grid-based approach for

local feature matching with the adjustment of mak-

ing the method more robust on face rotation. For lo-

cal feature matching, we reduce the dimensionality

of the original SIFT feature by our learned projection

matrix. Furthermore, the learned low dimensional lo-

cal feature is mapped to Hamming space. Each bit of

the learned Hamming descriptor is weighted by our

ranking method to reduce the ambiguity in matching

the descriptors. We also give the weight for each de-

scriptor to highlight the most discriminant descriptor,

which improves the face recognition accuracy.

Grid-based methods offers an effective and scal-

able approach for building high performance system

to solve face recognition problems (Bicego et al.,

2006; Luo et al., 2007; Majumdar and Ward, 2009).

The basic idea behind grid-based methods is to di-

vide a face image into several subregions to reduce

image matching time and false positive rate. Com-

(a) Face images are di-

vided into 4 ∗ 4 grids,

where the left eyes and

left mouth corners are not

in the same corresponding

grid

(b) Face images are di-

vided into 2 ∗2 grids. The

eyes and mouth corners ba-

sically locate in the same

grids, e.g., the left eyes and

left mouth corners are in

the same grid, respectively.

Figure 1: An example of face images divided into different

number of sub regions.

pared with cluster-based image matching methods,

grid-based methods are able to produce high recog-

nition rate, but with much less computational time.

Such characteristic makes this approach an appropri-

ate method for handling large face image databases.

A grid-based method needs to specify an appropri-

ate number of subregions to divide face images. For

example, to improve the computing speed, 4 ∗4 grids

(16 subregions) are speciﬁed in (Majumdar and Ward,

2009) for facial image matching. However, too many

subregions may decrease rotation invariance and in-

crease the matching error rate within the correspond-

ing subregions. Figure 1 gives a simple example to

demonstrate the difference of face image division us-

ing different number of subregions for face image di-

vision. As shown in Figure 1(a), 4 ∗4 grids are used

to divide face images. The same components of a per-

son’s face images are not in the same corresponding

grids, e.g. the left eyes in Figure 1(a) are not in the

same gird (grid(2,1)). Using 2 ∗ 2 grids in Figure

1(b), the same components (the left eyes) in the two

face images are in the same grid (grid(1,1)). There

is no signiﬁcant difference between using 2 ∗2 grids

and 4 ∗4 grids in terms of matching speed, as the

features are unequally extracted from subregions (i.e.

most features are extracted from certain key parts in a

face, such as eyes and mouth corners). Figure 2 gives

an example of extracting features from two facial im-

ages using a grid-based method. Due to the efﬁciency

in fast matching computing and rotation invariance,

we choose 2 ∗2 grids for dividing the symmetric parts

of face images in our proposed method.

Figure 2: The features extracted from two images. Most

features are extracted from the key parts of faces, such as

eyes, eyebrows, nose and mouth.

3 DESCRIPTOR LEARNING

3.1 Real-value Descriptor Learning

LDAHash (Strecha et al., 2012) is an approach that

projects the original high dimensional local features

into lower dimensional binary feature space. The ap-

proach generates compact binary vectors transformed

from original real-value vectors and preserves the

properties of the original vectors extracted from fa-

cial images. Using binary descriptors, LDAHash re-

quires much less memory storage than real-value de-

scriptors and leads to faster similarity computation for

image retrieval. Additionally, LDAHash enlarges the

distribution distance between positive and negative

pairs by a projection function, where negative pairs

are randomly selected. Nevertheless, in real world im-

age recognition problems, the similarity between pos-

itive and random negative descriptor pairs can be very

small. Thus, one of the main challenges in face recog-

nition research is how to use the local matching fea-

tures (e.g. SIFT features) to distinguish the positive

descriptors from negative descriptors. In many cases,

there are some features (descriptors) that are very

close to the query features (descriptors). Such fea-

tures are deﬁned as nearest neighbor negative descrip-

tors (Philbin et al., 2010), if they are not explained by

the RANSAC transformation. The matching features

are considered to be the positive descriptors pairs if

they satisfy the RANSAC transformation. Figure 3

gives an example that demonstrates the difference be-

tween the positive descriptors and the nearest neigh-

bor negative descriptors for facial image matching.

(a) The initial

matching out-

come obtained

by a Grid-based

matching method.

(b) The positive

descriptor pairs

are ﬁtted in the

RANSAC trans-

formation for

image matching.

est neighbor

negative descrip-

tors created by

SIFT algorithm

which are not

satisﬁed with

the RANSAC

transformation.

Figure 3: An example of positive and the nearest neighbor

negative descriptors for face recognition.

Differences of covariance (DIF) was used in LDA-

Hash for distinguishing positive and negative descrip-

tors to controll their weights (Strecha et al., 2010).

The performance obtained by DIF is heavily depen-

dent on the appropriate choice of the relevant param-

eters used for assigning weights, while other settings

may result in the failure of eigen-decomposition for

real-value scope. Such issue poses a big challenge to

LDAHash based face recognition methods.

To deal with the issues of reducing feature di-

mensionality and ﬁnding the appropriate parameters

for LDAHash method, we propose a new projecting

function that takes into account the nearest neighbor

negative pairs for similarity matching. This new de-

veloped projecting function is used for reducing the

curse of feature’s dimensionality and separating pos-

itive, nearest neighbor negative and random negative

pairs as well. Although most mismatching is caused

by the nearest neighbor negative pairs, random nega-

tive pairs should not be neglected as they may crowd

into the group of the nearest neighbor negative pairs

after the projection.

A loss function is used in the proposed projection

function to reduce the mismatching between positive

and negative descriptor pairs:

L =αM ·{P ·(X

) ·P

|P}

−βM ·{P ·(X

) ·P

|NN}

−γM ·{P ·(X

) ·P

|RN}

(1)

where:

X,Y

are two descriptors’ matrices;

P, NN and RN represent the positive pairs, near-

est neighbor negative pairs and random negative

pairs, respectively;

α,β,γ are the three weight variables for positive,

nearest neighbor negative and random negative

pairs, respectively;

T represents transformation matrix;

M is a function for calculating the average dis-

tance;

P is a projection function.

In our experiment, the three groups of descriptor

pairs (P, NN, RN) initially have the equal weights, i.e.

α, β and γ have the same initial value.

Here, we substitute M{X

|·} with a covariance

matrix denoted by

∑

, and rewrite Eq.1 as:

L =αM(P

∑

) −βM(P

∑

)

−γM(P

∑

)

(2)

Then, we can have the following equations

derived from Eq.2:

L =αM(P

∑

)

−{βM(P

∑

) + γM (P

∑

)}

(3)

L =αM(P

∑

)

−M{P (β

∑

+ γ

∑

}

(4)

L = αM(P

∑

) −M (P

∑

) (5)

where,

∑

= β

∑

+ γ

∑

(6)

The coordinates are transformed by pre-

multiplying

∑

(−1/2)

and

∑

(−T /2)

, so that

the second term of Eq. 6 turns into a constant that the

loss function

L does not need to take into account.

L ∝ M{P

∑

(−1/2)

∑

(−T /2)

}

= M{P

∑

(−1)

}

(7)

Eigen-decomposition can be used here for cal-

culating the loss function, since

∑

(−1)

and

∑

(−1)

are symmetric positive semi-deﬁnite ma-

trices. The projection function minimizes the loss

function and yields the k smallest eigenvectors of

∑

(−1)

. The weights are given to the three classes

of descriptor pairs (α, β and γ) for optimizing the pro-

jection function.

The main difference between our proposed

method and DIF method in LDAHash is that the

choice of parameters does not create a non symmetric

positive semi-deﬁnite matrix, i.e. our proposed pro-

jection is able to produce more reliable results for di-

mension reduction. With our new projection function,

the values of α, β and γ are not critical to the perfor-

mance of the given image matching task, while the ra-

tio of β and γ plays an important role in the projection

function. Using the new projection function, the sce-

nario of setting the extreme values of β or γ will be the

same as ignoring random negative or nearest neighbor

negative pairs. Under such scenario, the projected de-

scriptors will still be better classiﬁed than those in the

original feature space. The results of the three classes

of descriptor pairs before and after the projection are

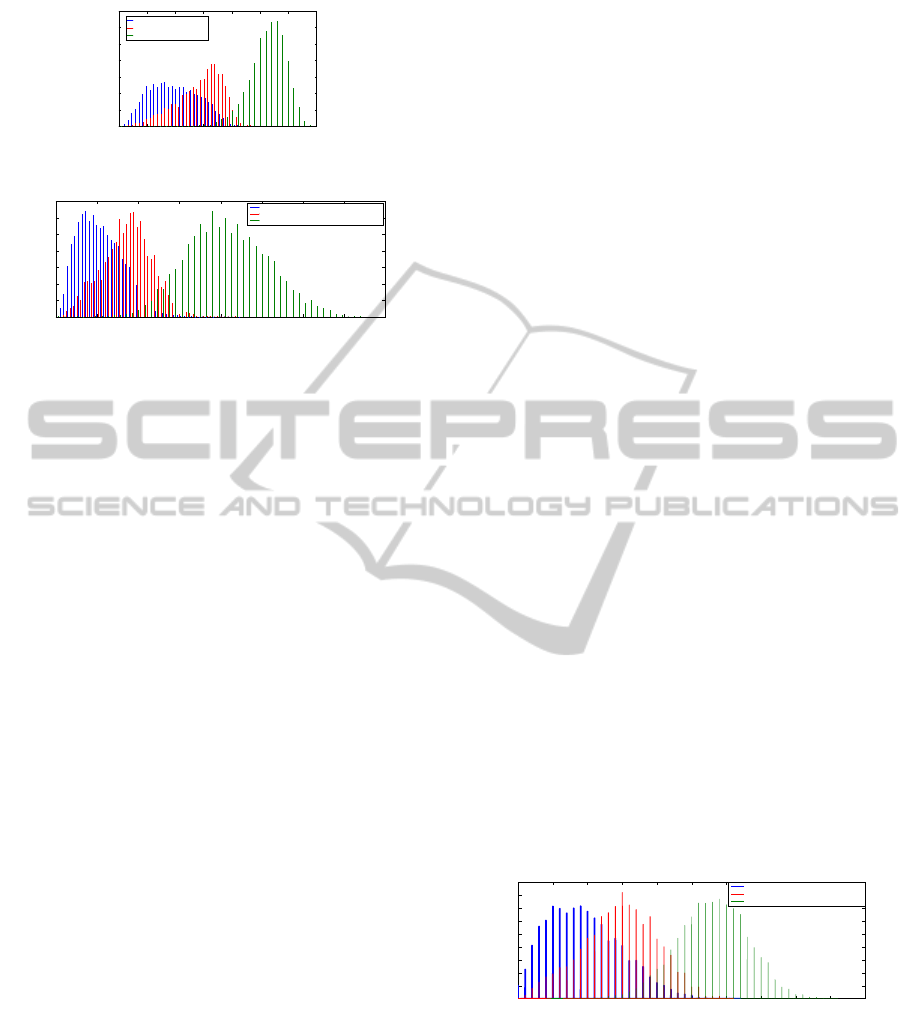
plotted in Figure 4. The descriptor pairs are projected

into a 64-dimensional space.

As shown in Figure 4, the distribution of positive

descriptor pairs becomes much more compact after

the projection than before the projection, compared

to the nearest neighbor negative and random negative

pairs. Also, random negative descriptor pairs are dis-

tributed in a more sparse manner. More importantly,

the distribution distance between positive descriptors

and the nearest neighbor negative descriptors is en-

larged, which is the same for positive descriptors and

random negative descriptors. Meanwhile, the over-

lapping area between positive pairs and the nearest

neighbor negative pairs is shrunken. Such phenom-

ena suggest that the improved performance of image

matching can be certainly guaranteed using the pro-

jected real-value features in a low-dimensional space.

0 100 200 300 400 500 600 700

0.02

0.04

0.06

0.08

0.1

0.12

0.14

Pair distance

Percentage

Original descriptor pair distance

Positive pair distance

Nearest neighbor negative pair distance

Random negative pair distance

(a) The original pair distance be-

fore the projection.

0 500 1000 1500 2000 2500 3000 3500 4000

0.01

0.02

0.03

0.04

0.05

0.06

0.07

Pair distance

Percentage

Pair distance after projecting into 64−D space

Positive pair distance

Nearest neighbor negative pair distance

Random negative pair distance

(b) The new pair distance after the projection.

Figure 4: Descriptor pairs’ distance histogram before and

after they are projected into a new space, where X-axis is the

distance of the descriptor pairs while Y-axis represents the

percentage. (Blue, red and green are separately represent-

ing positive, nearest neighbor negative and random negative

descriptor pairs.)

3.2 Hamming Descriptor Projection

To reduce the computational cost, our proposed new

method further projects the new low dimensional de-

scriptors into a Hamming space. As discussed in

the previous sections, the computation using Ham-

ming vectors is much faster than that using real-value

vectors. Moreover, the memory required for storing

descriptors can be signiﬁcantly reduced if real-value

descriptors are transformed into a Hamming space.

Hereby, the projection from a real-value space to a

Hamming space is formulated as:

y = I

(x −θ) (8)

where x is the projected real-value descriptors, y

is the descriptors in a Hamming space and θ is a

threshold to be learned to ensure that the projected

Hamming descriptors best represent the original real-

value descriptors’ property; I

denotes a sign indica-

tor function.

In our proposed projection function, we introduce

a set of nearest neighbor negative descriptors to opti-

mize a threshold θ and give the weights to different

false matching rates based on three categories of de-

scriptors calculated by LDAHash method. The basic

idea here used for optimizing θ is to either minimize

the false matching rate or maximize the true match-

ing rate. In this study, we choose minimizing the false

matching rate to optimize θ. The false negative (FN)

rate can be computed using the following equation:

FN(θ) =Pr{min(x

) < θ ≤ max(x

)|P}

=Pr{(min(x

< θ)|P}+ 1

−Pr{(max(x

) < θ)|P}

=cd f {min(x

)|P}−cd f {max(x

)|P}

(9)

cd f is the cumulative distribution function. The

false positive rate is divided into two parts: one is

used for describing the nearest neighbor negative de-

scriptors and is denoted by FPN; the other part is

for random negative descriptors and is denoted by

FPR. FPN and FPR can be computed by the follow-

ing Eq.10 and Eq. 11:

FPN(θ) =Pr{min(x

) ≥ θ

∪max(x

) < θ)|NN}

=1 −cd f (min(x

)|NN)

+ cd f (max(x

)|NN)

(10)

FPR(θ) =Pr{min(x

) ≥ θ

∪max(x

) < θ)|RN}

=1 −cd f (min(x

)|RN)

+ cd f (max(x

)|RN)

(11)

The overall false matching rate is given by:

F(θ) = α

FN + β

FPN + γ

FPR (12)

, β

and γ

are the weights given to the different

false rates. The higher the α

, the lower the false neg-

ative rate is. cd f is a cumulative distribution function

that creates the distribution corresponding to every θ

to be tested. In our experiment, α

, β

and γ

are ini-

tialized to be 1 and θ is accurate to one decimal place.

The distance between three classes of descriptor pairs

is shown in Figure 5.

0 5 10 15 20 25 30 35 40 45 50

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

Hamming descriptor pair distance

Percentage

Pair distance after projecting into 64−D Hamming space

Positive pair distance

Nearest neighbor negative pair distance

Random negative pair distance

Figure 5: The descriptor pair distance after projecting into a

Hamming space. (Blue, red and green are separately repre-

senting positive, nearest neighbor negative and random neg-

ative descriptor pairs.)

From Figure 5, we can see that the descriptors in

a low-dimensional Hamming space performs more or

less the same as the transformed SIFT descriptors in a

64-dimensional (64-D) space. The binary descriptor

preserves the properties of 64-D descriptors and per-

forms much better than using 128-D SIFT features.

3.3 Bit Ranking in Hamming Space

Hamming descriptor is advantageous for its efﬁcient

storage and easy computation. However, as Hamming

descriptors have only two value options for each di-

mension and the length of the descriptor is limited,

there usually exist multiple descriptors sharing the

same Hamming distance to the query descriptor. In

dealing with this problem, we rank each bit of the

Hamming descriptor and give different weights for

the dimensions, which will help to reduce the ambi-

guity in matching the descriptors.

Ideally, in Hamming space, if two descriptors

are coming from the same point(positive descriptors),

they should share the same value in the corresponding

dimension. However, in practice, there will be several

bits differ for the two descriptors from the same pos-

itive descriptor pair. The value of each dimension of

the descriptor is distributed differently. This results in

the difference of the discrimination power among all

the descriptors’ dimensions. For example, two Ham-

ming descriptors H1 and H2 have the same distance

to the query descriptor Hq. H1 differs from Hq in

the ith bit, while H2 differs from Hq in the jth bit. If

ith dimension has more discrimination power than the

jth dimension, we consider the distance between H1

and Hq is larger than the distance between H2 and

Hq. We learn the discrimination power by complying

with the idea of decreasing the positive descriptors’

distance and increasing the negative descriptors’ dis-

tance.

As descriptors will loose information after hash-

ing, we use the real-value projected descriptors to

learn the ranking. If the descriptors’ value of the

same point is quite similar and very distant to the de-

scriptors’ value of other points, the hashing results

of this point’s descriptors have strong conﬁdence to

be correct. On the other side, if the same points’

descriptors’ value is not distinguishable from other

points, the Hamming descriptor of this dimension is

less credible than other dimensions with high correct-

ness conﬁdence. For the ith dimension, we calculate

the weight as the following equation:

∑

)∈N

√

−y

)

Nbn

∑

)∈P

√

−x

)

Nbp

(13)

Where Nbn and Nbp are representing negative and

positive descriptor pairs number. For all the nega-

tive descriptor pairs (e.g.(y

) ∈N), we calculate the

sum of all the descriptor pairs’ Euclidean distance and

further divide the sum by the negative descriptor pairs

number. The same for positive descriptors. The di-

vision result will be the weight for this dimension.

However, the complexity of computing the distance of

positive and negative descriptor pairs is O(n

), which

consumes a large amount of time. As an alternative,

we use the positive descriptor pairs’ standard devia-

tion to substitute the Euclidean distance, as Eq.14.

N−1

∑

−µ)

∑

N p

NDes

∑

NDes

−µ

des

)

N p

(14)

In Eq.14, N is the number of all the descriptors

and µ is the mean of all the descriptors’ ith dimen-

sion value. For the positive standard deviation part,

N p is the number of different points. Ndes repre-

sents the descriptor number of the current point. µ

des

is the ith dimension’s mean value of the descriptors

from the same point. Both Eq.13 and Eq. 14 can

describe the distribution of the descriptor’s value be-

fore hashing. The larger negative descriptor value dis-

tance and the smaller positive descriptor value dis-

tance, the more conﬁdence we have for this dimen-

sion. As a result, we will give a higher weight to this

dimension. As Eq.14 uses standard deviation to sub-

stitute the Euclidean distance of each descriptor pair,

the time complexity is O(n), which is much smaller

than the method used in Eq. 13.

4 FEATURE WEIGHTING

A weighting function with a RANSAC model is used

for identifying the true positive matching between the

descriptors in two images. Generally, the correctly

matched points during the training stage are more

likely to contribute better performance for the testing

data. Therefore, different weights are assigned to the

different points, based on their matching performance

obtained in the training stage.

Initially, we give all the points the weight of 1.

The weights of the points will increase by 1, if the

descriptors extracted from the points satisfying the

RANSAC transformation during the image matching.

Figure 6 gives such an example.

Figure 6: The points that ﬁt RANSAC transformation in

three images. The green point in the middle image matches

the corresponding points in the left and right images, while

the red point in the middle image only matches the corre-

sponding points in the left image.

In Figure 6, the weight of the green point in

the middle image will be increased to 3, since it is

matched to the corresponding points in the left and

right images. The red point in the middle image

only matches the corresponding point in left image,

so that its weight will be increased to 2. The larger

the weight, the more important the features for face

recognition. Our main goal here is to highlight the

true positive matching points. RANSAC may mis-

takenly identify the correct matching points as false

matching points, when there are some rotation and il-

lumination changes in the matching images. For this

reason, we do not give any penalty to the false positive

matching points, and the matched point (true posi-

tive matching point) should be weighted n times more

than an unmatched (false positive) point. Here n rep-

resents the number of matching between query and

training images. For example, let us consider a test

using the same images from Figure 6. The feature

highlighted in green (with weight ’3’) have the more

importance than the feature in red (with the weight

’1’) in terms of improving face recognition rate.

(a) The face image matching result obtained by using the

original 128-D SIFT features. It consists of 16 true positive

matching (including 3 RANSAC misjudges) and 11 false

positive matching (excluding RANSAC misjudges). The

true positive matching rate is 59.2%.

(b) The face image matching result obtained by using the

64-D projected real-value features. It consists of 20 true

positive matching (including 6 RANSAC misjudges) and 12

false positive matching (excluding RANSAC misjudges).

The true positive matching rate is 62.5%.

the 64-D projected Hamming descriptors. It consists of 13

true positive matching (including 2 RANSAC misjudges)

and 6 false positive matching (excluding RANSAC mis-

judges). The true positive matching rate is 68.4%.

Figure 7: The comparison of the face image matching per-

formance obtained using three feature techniques.

The whole learning process is complex but can be

performed ofﬂine. During the ofﬂine learning step, all

the image features can be projected into a Hamming

space and stored into a binary ﬁle, which requires

much smaller memory capacity. After the recognition

methods have been trained through an ofﬂine step, the

online face recognition process for testing will be per-

formed much faster using Hamming descriptors.

5 EXPERIMENT AND

DISCUSSION

5.1 Dataset

Two benchmark face image datasets (ORL and Yale

dataset) are used in this study for evaluating our pro-

posed for face recognition. The ﬁrst dataset is ORL

dataset (Samaria and Harter, 1994) that contains the

subjects (face images) collected by AT&T Laborato-

ries and Cambridge University Engineering Depart-

ment. The dataset consists of ten different individ-

uals, each having 40 distinct subjects. The images

were taken at different time moments with different

lighting conditions. Thus, the face images in the

dataset were with the variation affected by different

factors, such as facial expressions (e.g. open/closed

eyes, smiling/not smiling) or facial details (with

glasses/without glasses). The second dataset is the

Yale face database (Belhumeur et al., 1997) that con-

tains 165 grayscale images in GIF format collected

from 15 individual participants. Each individual has

11 images under different viewing conditions with

various facial expression or conﬁguration, such as

the illumination (left or right light), with or without

glasses, and the emotions (happy, sad, surprised, etc).

Both of ORL and Yale datasets are publicly available.

5.2 Experiment Results

To evaluate the performance of our new proposed

method for face recognition, we present a compara-

tive experiment using the new learned 64-D projected

Hamming descriptors, the projected 64-D real-value

descriptors and the original 128-D SIFT features. Fig-

ure 7 illustrates the comparison of matching results.

The experimental result shows that the matching

accuracy from the new learned Hamming descriptors

is better than that from the original SIFT features.

More importantly, Hamming descriptors reduces the

false positive rate compared with using the original

SIFT features.

Additionally, to test the robustness of our new de-

veloped method, we further applied it on the stan-

dard ORL face database (head rotation) and Yale face

database (illumination change). We use half images

for training and the rest for testing. Compared to

classical PCA (Turk and Pentland, 1991), LDA (Bel-

humeur et al., 1997), conventional SIFT method (Ma-

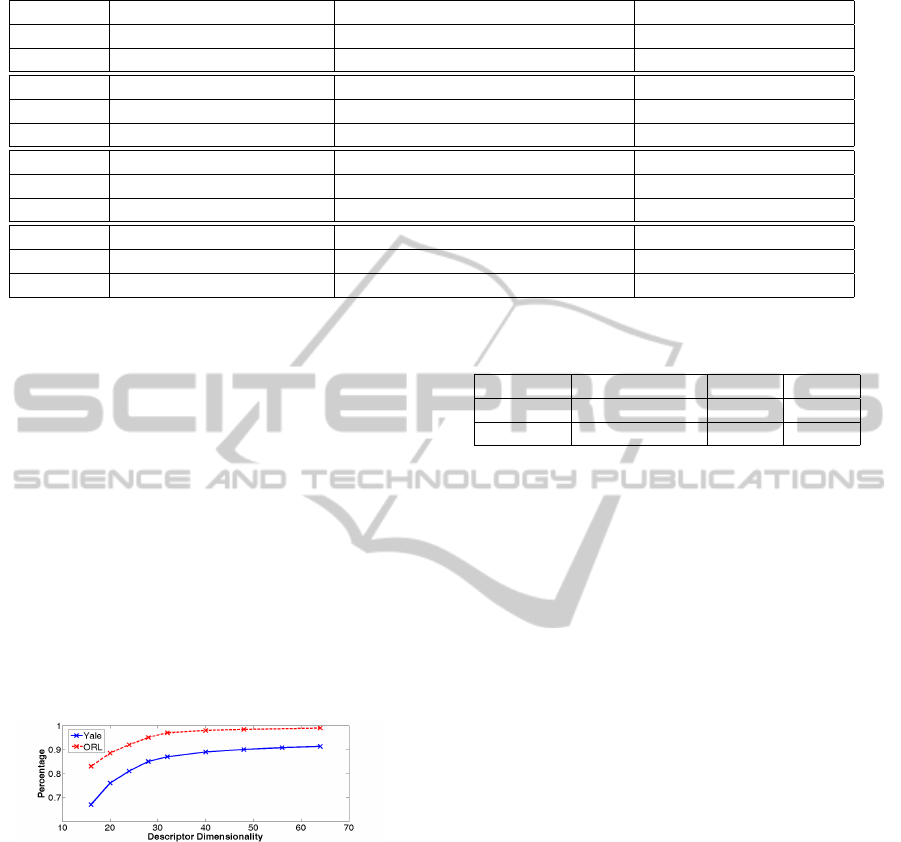
Table 1: Testing accuracy of ORL and Yale data using different face recognition methods.

Database PS-64 HS-64 HS-32

Yale 92.9% 91.8% 87.3%

ORL 99.1% 99.1% 97.3%

Database HS-16 PCA LDA

Yale 67.8% 67.8% 82.4%

ORL 83.3% 88.6% 91.2%

DataBase SIFT Method (Wright and Hua, 2009) Method (Lu et al., 2010)

Yale 85.8% 91.4% 89.1%

ORL 95.8% 96.5% 94.8%

DataBase Method (Liu et al., 2012) Method (Yang and Kecman, 2010) -

Yale 83.4% - -

ORL 98.9% 98.4% -

jumdar and Ward, 2009) and some state-of-art meth-

ods ((Wright and Hua, 2009; Lu et al., 2010; Liu

et al., 2012; Yang and Kecman, 2010)), Table 1 sum-

marizes the experimental results for face recognition.

We denote the projected 64-D real-value descriptors

as PS-64 and the 64-D Hamming descriptors as HS-

64, and summarize the testing accuracy in Table 1.

The experimental results clearly show that the

proposed face recognition methods using low-

dimensional features (either real-value or binary)

have consistently produced good matching accuracy

on both ORL and Yale data. In this study, we have

also investigated the dependency of face recognition

accuracy on the different number of Hamming de-

scriptor dimension and plotted the results in Figure

Figure 8: Accuracy and Hamming descriptor dimensional-

ity diagram on ORL and Yale data. Both are tested from 16

dimensions to 64 dimensions.

In general, the higher the Hamming descriptor di-

mension used, the better the matching accuracy. The

accuracy increases sharply from 16 dimension to 32

dimension. After 32 dimension, the accuracy in-

creases smoothly.

As the similarity computation of Hamming de-

scriptors is based on bit operation, the time for cal-

culating distance between extracted descriptors is

largely reduced. Table 2 gives the average time per-

formance on computing descriptors’ distance of each

image pair based on SIFT descriptors and our learned

Hamming descriptors.

From Table 2, we can see that our Hamming de-

Table 2: Average time consumption on computing descrip-

tors’ distance of each image pair.

Database Origianl SIFT HS-64 HS-32

Yale 0.62s 0.25s 0.22s

ORL 0.075s 0.028s 0.020s

scriptor largely reduce the time on computing descrip-

tor distance. The 32 dimensional Hamming descrip-

tor achieves almost 3 times accelaration on similarity

computation compared with SIFT descriptor based on

grid method, while increasing the accuracy.

6 CONCLUSIONS

It is always challenging to improve the matching ac-

curacy and reduce the computational cost simulta-

neously in face recognition applications. In the in-

troduction section, we have described the motivation

of using the projected Hamming descriptors for face

recognition. For this purpose of dealing with such

issue, we have developed a novel method for face

recognition problems which uses a new projection

function combined with a weighting function to re-

duce the high dimensionality of SIFT features.

Our proposed method offers a good solution to

handle the large datasets with enormous features,

owning to its ability of fast computing and small

memory requirement. In this study, the new face

recognition method were fulﬁlled in two ways: (1)

using a projection function to transform original SIFT

features into a low dimensional space, and (2) using

a more sophisticated projecting function for generat-

ing Hamming descriptors which reduces the memory

requirement and improves the computational speed.

To optimize the descriptors, we introduced a new fea-

tures weighting method to identify informative de-

scriptors. The weighting methods is simple to imple-

ment and performs very well on the two benchmark

datasets, ORL and Yale data in our experiment.

The experimental results suggest that our new pro-

posed method can be an efﬁcient face recognition sys-

tem to achieve high accurate matching rate with im-

proved computational speed.

REFERENCES

Ahonen, T., Hadid, A., and Pietikainen, M. (2006). Face

description with local binary patterns: Application to

face recognition. TPAMI, 28(12).

Belhumeur, P., Hespanha, J., and Kriegman, D. (1997).

Eigenfaces vs. ﬁsherfaces: Recognition using class

speciﬁc linear projection. TPAMI, 19:711–720.

Bicego, M., Lagorio, A., Grosso, E., and Tistarelli, M.

(2006). On the use of sift features for face authen-

tication. In CVPR Workshop, pages 35–41.

D.Lowe (2004). Distinctive image features from scale-

invariant keypoints. IJCV, 60(2):91–110.

Fernandez, C. and Vicente, M. (2008). Face recognition us-

ing multiple interest point detectors and sift descrip-

tors. In FG.

Fischler, M. A. and Bolles, R. C. (1981). Random sample

consensus: A paradigm for model ﬁtting with appli-

cations to image analysis and automated cartography.

Communications of the ACM, 24(6).

Gao, S., Tsang, I. W.-H., and Chia, L.-T. (2010). Kernel

sparse representation for image classiﬁcation and face

recognition. In ECCV.

Geng, C. and Jiang, X. (2011). Face recognition based on

the multi-scale local image structures. Pattern Recog-

nition, 44(10-11).

Jiang, X. (2011). Linear subspace learning-based dimen-

sionality reduction. IEEE Signal Processing Maga-

zine, 28(2):16–26.

Kri

zaj, J.,

Struc, V., and Pave

c, N. (2010). Adaptation

of sift features for robust face recognition. In Image

Analysis and Recognition, volume 6111, pages 394–

404.

Liu, J., Li, B., and Zhang, W.-S. (2012). Feature extrac-

tion using maximum variance sparse mapping. Neural

Computing and Applications.

Lu, G.-F., Lin, Z., and Jin, Z. (2010). Face recognition us-

ing discriminant locality preserving projections based

on maximum margin criterion. Pattern Recognition,

43(10).

Luo, J., Ma, Y., Takikawa, E., Lao, S., Kawade, M., and

Lu, B.-L. (2007). Person-speciﬁc sift features for face

recognition. In ICASSP.

Majumdar, A. and Ward, R. (2009). Discriminative sift fea-

tures for face recognition. In CCECE.

Mian, A. S., Bennamoun, M., and Owens, R. (2008). Key-

point detection and local feature matching for textured

3d face recognition. IJCV, 79(1).

Philbin, J., Isard, M., Sivic, J., and Zisserman, A. (2010).

Descriptor learning for efﬁcient retrieval. In ECCV.

Rosenberger, C. and Brun, L. (2008). Similarity-based

matching for face authentication. In ICPR.

Samaria, F. and Harter, A. (1994). Parameterisation of a

stochastic model for human face identiﬁcation. In

ICCV Workshop.

Soyel, H. and Demirel, H. (2011). Localized discriminative

scale invariant feature transform based facial expres-

sion recognition. Computers & Electrical Engineer-

ing.

Strecha, C., Bronstein, A., Bronstein, M., and Fua, P.

(2012). Ldahash: Improved matching with smaller

descriptors. TPAMI, 34:66–78.

Strecha, C., Pylvanainen, T., and Fua, P. (2010). Dy-

namic and scalable large scale image reconstruction.

In CVPR.

Turk, M. and Pentland, A. (1991). Face recognition using

eigenfaces. Cognitive Neurosicence, 3(1):71–86.

Wright, J. and Hua, G. (2009). Implicit elastic matching

with random projections for pose-variant face recog-

nition. In CVPR.

Yang, T. and Kecman, V. (2010). Face recognition with

adaptive local hyperplane algorithm. Pattern Analysis

and Applications, 13.

Zhang, Q., Chen, Y., Zhang, Y., and Xu, Y. (2008). Sift im-

plementation and optimization for multi-core systems.

In IPDPS.