VLSI Wavelet Denoising of Neural Signals

Critical Appraisal of Different Algorithmic Solutions for Threshold Estimation

Nicola Carta, Danilo Pani and Luigi Raffo

DIEE - Dept. of Electrical and Electronic Engineering, University of Cagliari, Via Marengo 3, 09123 Cagliari, Italy

Keywords:

Wavelet Denoising, Neural Signal Processing, FPGA, Design Tools.

Abstract:

Wavelet denoising represents a common preprocessing step for several biomedical applications exposing low

SNR. When the real-time requirements are joined to the fulﬁlment of area and power minimization for wear-

able/implantable applications, such as for neuroprosthetic devices, only custom VLSI implementations can

be adopted. In this case, every part of the algorithm should be carefully tuned. The usually overlooked part

related to threshold estimation is deeply analysed in this paper, in terms of required hardware resources and

functionality, exploiting Xilinx System Generator for the design of the architecture and the co-simulation. The

analysis reveals how the widely used Median Absolute Deviation (MAD) could lead to hardware implementa-

tions highly inefﬁcient compared to other dispersion estimators demonstrating better scalability, relatively to

the speciﬁc application.

1 INTRODUCTION

Real-time biomedical signal processing aims at ex-

tracting the information embedded into a physiolog-

ical measurement, typically in order to aid the diag-

nosis, monitor a patient or control an electronic de-

vice that, at a certain level, interacts with the patient.

With the increasing integration capabilities and the

advancements in CMOS processes, it is progressively

more common to require wearable or implantable

electronics for such a processing. Applications like

electrocardiography (ECG) (Baig et al., 2013) and

electroencephalography (EEG) (Casson et al., 2010)

often require these features. However, the low band-

width of these signals and the relatively low num-

ber of channels (except for very speciﬁc applications

like potential surface mapping or high density EEG)

impose looser constraints compared to other applica-

tions like invasive neural signal processing.

The aforementioned requirements can be solved

by the development of a low-power Application

Speciﬁc Integrated Circuit (ASIC). Compared to

microprogrammed solutions involving the use of

microcontrollers or low-power digital signal pro-

cessors (DSP), ASIC design requires highly spe-

ciﬁc skills and a longer development time (Mon-

tani et al., 2003), unfortunately leading to non-

ﬂexible architectures. Some tools for automatic

creation of hardware description language (HDL)

designs have been presented to address such is-

sues (e.g. ORCC, http://orcc.sourceforge.net/ (Nezan

et al., 2012) or the commercial Xilinx System Gener-

ator, http://www.xilinx.com/tools/sysgen.htm). Even

though unable to signiﬁcantly address the low-power

requirements, these tools enable rapid prototyping

with the possibility of exploiting an alternative lan-

guage/method rather than HDL in the design phase

(Palumbo et al., 2012). The integration with well-

known tools such as Simulink enables a faster de-

velopment and, leveraging on parameterized HDL li-

braries, good performance in terms of area and power

can be also achieved.

In this paper, Xilinx System Generator has been

chosen for its rapid prototyping advantage, evaluat-

ing the main performance ﬁgures associated to the

hardware implementation of a wavelet denoising al-

gorithm used for neural signal processing (Diedrich

et al., 2003). The ASIC implementation of this algo-

rithm would be particularly useful in a multichannel

neural signal processing context, especially for neu-

ral prostheses (Citi et al., 2008) which must be able

to work exploiting batteries as power source. At the

same time, it allows highlighting the possible pitfalls

hidden in the straightforward creation of an architec-

ture from its typical algorithmic version. In particular,

the threshold estimation stage is marginally consid-

ered in the largest part of the applications, usually ex-

ploiting ﬁxed precomputed thresholds (Kuzume et al.,

Carta N., Pani D. and Raffo L..

VLSI Wavelet Denoising of Neural Signals - Critical Appraisal of Different Algorithmic Solutions for Threshold Estimation.

DOI: 10.5220/0004865700450052

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2014), pages 45-52

ISBN: 978-989-758-013-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

2004) or preferably opting for the estimation of the

standard deviation of the noise by the Median Abso-

lute Deviation (MAD), known to be a robust estima-

tor of the dispersion in presence of outliers. Such an

approach is challenged here, revealing how it could

lead to very inefﬁcient or even infeasible architec-

tures. The discussion is supported by the results in

terms of a preliminary FPGA implementation, eval-

uating the performance onto an open neural signals

database (Quiroga et al., 2004).

2 WAVELET DENOISING

Wavelet denoising is a non-linear ﬁltering technique

usually adopted in presence of a Gaussian noise

whose spectrum overlaps the useful signal bandwidth.

It consists of a sub-band decomposition of the sig-

nal, thresholding (introducing the non-linearity) and

recomposition. The input signal is decomposed in

its low-frequency and high-frequency bands, respec-

tively called “approximation” and “detail”. The ap-

proximation is split again in the same way repeatedly

until the level N of decomposition has been reached.

Being the Nyquist frequency of the approximation

one half of that of the incoming signal, the sample rate

can be reduced (decimated approach) so that the same

ﬁlters can be used in every level. Alternatively, the

sample rate can be preserved upsampling in each level

the ﬁlter coefﬁcients of the previous one, in the so

called algorithme

a trous scheme (Holschneider et al.,

1990). Such a redundant approach leads to the same

time resolution in every level and to time invariance

(Cohen and Kovacevic, 1996). When the N-th level

has been computed, all the details are thresholded ei-

ther hard or soft, respectively whether the samples of

the detail signals are simply cleared to zero if below

the threshold or also the samples above threshold are

modiﬁed by subtracting the value of the threshold it-

self.

Recomposition exploits the mirrored version of

the corresponding decomposition ﬁlters (orthogonal

wavelets) or different ﬁlters (bi-orthogonal wavelets),

every couple of ﬁlters taking an approximation and

the related thresholded detail, producing an approx-

imation signal by averaging sample-wise their out-

puts. Only Finite Impulse Response (FIR) ﬁlters are

used, whose impulse responses depend on the chosen

mother wavelet.

2.1 Threshold Estimation

Several methods for calculating the threshold have

been presented in literature. The choice of the thresh-

old inﬂuences the quality of the denoising so much

that even data-speciﬁc approaches have been pre-

sented so far (Medina et al., 2003). The threshold can

be ﬁxed (Kuzume et al., 2004) or adaptive (Radovan

et al., 2013), the same or different for all the details.

In particular, adaptive thresholds are typically com-

puted estimating the rms or the standard deviation σ

of the signal at the different levels of the decomposi-

tion and then correcting it by a multiplicative factor.

Different multiplicative factors have been derived and

are preferred by different authors, as for the Minimax

(Citi et al., 2008), Stein’s Unbiased Risk (Mahmoud

et al., 2008) or Universal (Bahoura and Ezzaidi, 2012)

methods. Due to the robustness to the presence of out-

liers, usually the preferred method is to estimate σ by

the median absolute deviation (MAD), deﬁned as:

MAD = median

(|X

− median

)|) (1)

Due to the high-pass nature of the detail signals,

it is common to implement the MAD as simply the

median of the absolute value of the details:

MAD = median

(|X

|) (2)

It has been proved that MAD ≈ 0.6745σ. Nev-

ertheless, the MAD is preferred for the aforemen-

tioned robustness, especially in neural signal process-

ing, where the neural spikes can be considered as

partly composed of outlier samples in recordings with

a good signal to noise ratio (SNR). Such an approach,

which is perfect for off-line processing, overlooks the

real computational complexity of the median opera-

tor in case of continuous adaptation. This approach

has been challenged by some authors trying to de-

velop efﬁcient implementations for biomedical signal

processing (Pani et al., 2011; Zhang et al., 2011). In

the following sections, the adoption of the MAD and

the sample standard deviation on a sliding window is

compared not only in terms of denoising quality, but

also in terms of feasibility in the perspective of a low-

power real-time implementation as needed for an im-

plantable unit for the control of a neuroprosthetic de-

vice (Citi et al., 2008), using as a testbed a prototypi-

cal FPGA implementation programmedexploitingthe

Xilinx System Generator tool.

3 METHODS

As starting point, we consider a stationary wavelet

denoising trellis (“algorithme

a trous”). In order to

keep low the memory requirements in the perspective

FPGA implementation, the simple Haar wavelet has

been chosen, requiring very small ﬁlters. Considering

an input signal sampled at 12kHz as in (Pani et al.,

BIODEVICES2014-InternationalConferenceonBiomedicalElectronicsandDevices

2011), with 4 levels and removing the last approxi-

mation signal, a high-pass overall behaviour able to

reject the low-frequency components below 375Hz,

outside the bandwidth of neural signal, can be ob-

tained. In order to evaluate the impact of the thresh-

olding stage, no speciﬁc optimizations have been

made at the level of the ﬁlter banks for decomposi-

tion and recomposition. The FIR ﬁlters have been

implemented in the transposed direct-form I, insert-

ing registers with delay equal to increasing powers of

2 between the internal adders to perform the required

oversampling process in the different stages.

As we already stated above, the choice of the

threshold can have an impact on the quality of the de-

noising. However the repercussions in terms of hard-

ware requirements need to be carefully evaluated, as

we will discuss hereafter. In this exemplary applica-

tion, we consider two alternative solutions which are

based respectively on the calculation of:

• the MAD of the signal, using either a combinato-

rial or an iterative approach;

• the sample standard deviation σ of the signal.

As scaling factor, the Universal one has been

adopted, so that:

θ =

MAD

0.6745

2logM (3)

in the ﬁrst case, and:

θ = σ

2logM (4)

in the second one. M is the length of the signal frame

in terms of number of samples.

In order to provide adaptiveness in an on-line sce-

nario, both the ﬁrst and the second solution have been

adapted to work on a sliding window of variable size,

with an overlap of three quarters of the overall win-

dow length. In the ﬁrst case, this requires sorting the

new window every time in order to extract the me-

dian, however in the second case a faster solution can

be implemented. Starting from the technique used in

(Pani et al., 2011) and thanks to the zero-mean nature

of the high-pass detail signals, for each N new input

samples in the window, the related sum of squares for

the j-th decomposition level is computed as:

∑

n=1

[n] (5)

and then used to determine σ for the 4 times larger

windows as:

σ =

4N − 1

∑

k=1

(6)

Thanks to the sliding window approach, the

threshold value is updated every N sampling periods

(M = 4× N). The longer the observation window, the

better the estimation accuracy, provided that instanta-

neous variations (neural spikes) do not inﬂuence the

threshold computation. Such a processing can be del-

egated to a host processor picking up the detail signals

samples at the ﬁlters output and computing the var-

ious thresholds. However, when a non-microcoded

solution is pursued, because of the need to fulﬁl the

real-time and low-power constraints, threshold esti-

mation can be performed by dedicated cost-effective

hardware. In this case, the complexity depends on

both the chosen threshold estimation method and the

length of the observation window M.

3.1 Architecture Design using Xilinx

System Generator

In order to evaluate the different solutions from

a hardware perspective, starting from a high-level

model with an acceptable complexity even for re-

searchers not accustomed to HDL modelling, it is pos-

sible to use tools such as Xilinx System Generator. In

this way, the user-friendly environment of Simulink

can be exploited both to create the hardware design

and to perform accurate co-simulations taking into ac-

count the hardware implementation of a part of the

system under test.

The tools allow to choose whether to use the hard-

ware blocks coded by the user (providing the HDL

ﬁle) or those provided by Xilinx. The latter only

require to deﬁne the internal signal representation

(ﬁxed-point, unsigned or signed as 2’s complement,

etc.) as for the desired functionality, whereas the for-

mer must adhere to a standard interface mainly requir-

ing an enable signal for each input clock to synchro-

nize the modules inside the model. When the design

has been completely created, the set of the hardware

blocks can be mapped on a real FPGA board in order

to evaluate the percentage of used resources and the

behaviour by hardware/software co-simulations. This

is very useful to accelerate the simulation time com-

pared to the totally software case.

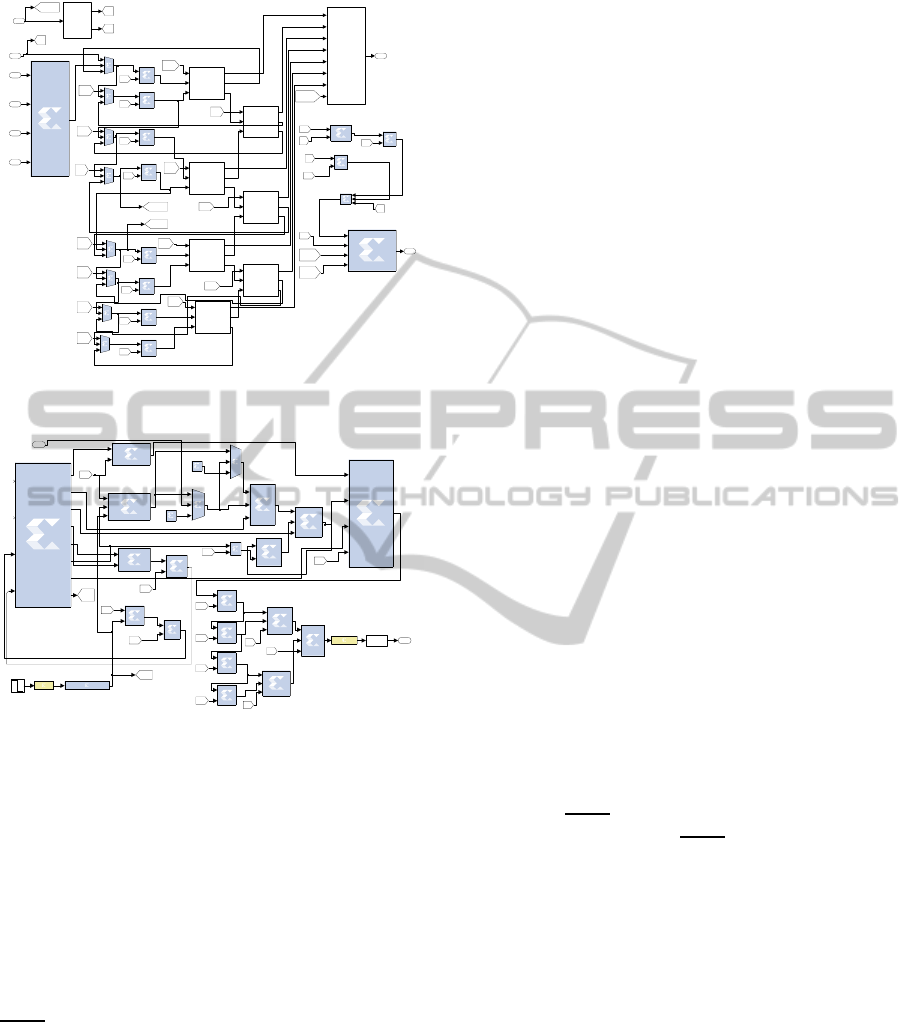
The wavelet denoising algorithm, created exploit-

ing the Xilinx System Generator tool, is shown in

Fig. 1. The Gateway In and the Gateway Out blocks

delimit the hardware part of the Simulink model,

deﬁning the interface signals to be mapped on the var-

ious pins available on the FPGA. The System Gen-

erator block ﬁxes the co-simulation parameters, the

Simulink system period, the target board to map the

hardware sub-model, and so on. In our tests, a Xilinx

Virtex-5 LX330 has been chosen for its considerable

VLSIWaveletDenoisingofNeuralSignals-CriticalAppraisalofDifferentAlgorithmicSolutionsforThreshold

Estimation

threshold_est4

In1

Out1

threshold_est3

In1

Out1

threshold_est2

In1

Out1

threshold_est1

In1

Out1

denoised

Out

Terminator

Signal From

easynoise01

Scope

Hard_Thres4

thr

twc1

Hard_Thres3

thr

twc1

Hard_Thres2

thr

twc1

Hard_Thres1

thr

twc1

H4(z)

In1

Out1

H4’(z)

In1

Out1

H3(z)

In2

Out2

H3’(z)

In2

Out2

H2(z)

In1

Out1

H2’(z)

In1

Out1

H1(z)

In1

Out1

H1’(z)

In1

Out1

G4(z)

In1

Out1

G4’(z)

In1

Out1

G3(z)

In2

Out2

G3’(z)

In2

Out2

G2(z)

In1

Out1

G2’(z)

In1

Out1

G1(z)

In2

Out2

G1’(z)

In2

Out2

Down Sample4

−1

↓266752

Down Sample3

−1

↓266752

Down Sample2

−1

↓266752

Down Sample1

−1

↓266752

Delay2

−14

Delay1

−12

Delay

−8

Data In

CMult6

x 0.5

CMult5

x 0.5

CMult4

x 0.5

CMult3

x 0.5

CMult2

x 0.5

CMult1

x 0.5

AddSub3

a + b

AddSub2

a + b

AddSub1

a + b

System

Generator

Figure 1: Simulink model of the chosen wavelet denoising scheme using System Generator blocks.

thr

Mult

a × b

Med

Med(x)

Constant

4.27459716796875

Abs

abs(x)

Figure 2: The Simulink Model of the Threshold Estimator

block with the constant deﬁned as for the case of M=64

samples per window.

Med(x)

Sort9

Sort8

Sort7

Sort6

Sort5

Sort4

Sort3

Sort23

Sort22

Sort21

Sort20

Sort2

Sort19

Sort18

Sort17

Sort16

Sort15

Sort14

Sort13

Sort12

Sort11

Sort10

Sort1

Sort

Delay9

−1

Delay8

−1

Delay7

−1

Delay6

−1

Delay12

−1

Delay11

−1

Delay10

−1

CMult8

x 0.5

AddSub

a + b

Figure 3: The Simulink Model of the sorter using an un-

folded combinatorial approach for windows with M=8 sam-

ples.

amount of available resources.

3.2 Threshold Estimator

Implementation

In case the

MAD is used, the System Generator im-

plementation involves the extraction of the absolute

value of each input samples, the computation of the

median value of the incoming windows of M input

samples and the multiplication by a constant, as de-

ﬁned in (3). The corresponding Simulink model is

depicted in Fig. 2. The median value calculation re-

quires the hardware implementation of a sorting al-

gorithm which represents a costly operation from a

hardware point of view.

A ﬁrst possible solution can be the unfolded sorter

presented in (Bahoura and Ezzaidi, 2012), for which

the Simulink model considering windows of N = 8

input samples is presented in Fig. 3. The basic sorting

cell makes the comparison between two inputs A and

B and swaps them if A < B. It is possible to demon-

strate that, if the comparators work in parallel, M − 1

steps are sufﬁcient to properly perform the sorting of

M elements. The output is updated in a combinatorial

way every time a sample arrives in input at the sam-

pling frequency f

, after the proper shift of the values

saved into the registers needed to prepare the input

samples for the processing. The

MAD is computed as

the arithmetic mean of the two central elements of the

sorted array for an even number of samples.

This solution presents several pitfalls from a hard-

ware implementation perspective. In particular there

is a clear scalability issue related to the enlargement

of the observation window. In this case, the increas-

ing internal critical path determined by the cascade

of comparators limits the maximum operating fre-

quency, beyond the penalty associated to the huge

amount of hardware resources.

To overcome such problems, an iterative (folded)

approach to the sorter able to reuse the same resources

at each step, similar to that proposed in (Martinez

et al., 2005) about the Burrows-Wheeler transform

but adapted to the wavelet denoising case, can be

used. In this case, the sorting strategy uses only two

levels of comparators. At the beginning, the swaps are

performed only for the registers related to odd adja-

cencies, activating only the ﬁrst level of comparators.

If the vector is not yet sorted, at the next iteration only

the comparators of the second level are active, and so

on until the sorting process is completed. It is possi-

ble to demonstrate that the number of necessary steps

is M/2 if M is the number of samples to sort. Figure 4

shows the iterative scheme.

The swp signal coming out from the comparator

block is used to specify that the two inputs have been

swapped. The samples in input to the parallel sorter,

belonging to each observation window, are temporar-

ily saved into a single-port memory. Immediately af-

ter the last sample of the window has been saved in

BIODEVICES2014-InternationalConferenceonBiomedicalElectronicsandDevices

median

Ready_Flag

we2

sample_counter

clr

reset8

RST

reset7

RST

reset6

RST

reset58

RST

reset5

RST

reset4

RST

reset3

RST

reset2

RST

reset1

RST

reset

RST

rst

−1

rst

−1

median calculator

rst

medianaout

MED_B

MED_A

level activator

en_comp

1st lev

2nd lev

en_median

delayed_ready flag

Subsystem3

In1

In2

In3

In4

In5

In6

In7

lev_sel

Out1

Single Port RAM

addr

data

rst

−1

Register7

rst

−1

Register6

rst

−1

Register5

rst

−1

Register4

rst

−1

Register3

rst

−1

Register2

rst

−1

Register1

rst

−1

rst

−1

Mux7

sel

Mux6

sel

Mux5

sel

Mux4

sel

Mux3

sel

Mux2

sel

Mux1

sel

Mux

sel

Logical2

and

Goto6

LEV_SEL

Goto5

SEL

Goto4

EN2

Goto3

EN1

Goto2

MED_B

Goto1

MED_A

From9

[SEL]

From8

[SEL]

From7

[SEL]

From6

[EN1]

From5

[EN1]

From4

[EN1]

From3

[EN1]

From2

[EN2]

From14

[LEV_SEL]

From13

[SEL]

From12

[SEL]

From11

[SEL]

From10

[SEL]

From1

[EN2]

From

[EN2]

Comparator7

swp

Comparator6

swp

Comparator5

swp

Comparator4

swp

Comparator3

swp

Comparator2

swp

Comparator1

swp

address

en input

lev selector

Data

rst

en_median

Figure 4: The Simulink Model of the sorter using an itera-

tive approach for windows with M=8 samples.

Out1

to−sqrt

Out

sum

rst

−1

sel_generator

rst

clr_reg

hit_sample

sel

sample counter

clr

rst

new sample

rst hit_sample

count4

clr

controller

rst

hit_sample

hit_window

hit_buffer

addr_inc

en_mul

en_add

en_count4

clr_count4

clr_reg

en_s_adder

address incr

inc

rst

address

Step

Single Port RAM

addr

data

rst

−1

Register7

rst

−1

Register6

rst

−1

Register5

rst

−1

Register4

rst

−1

Register3

rst

−1

Register2

rst

−1

Mux1

sel

Mux

sel

Mult

a × b

−1

Logical

Goto1

Goto

RST

From9

From8

From7

From6

RST

From5

RST

From4

RST

From3

RST

From2

RST

From14

RST

From11

RST

From10

RST

From1

RST

From

RST

Fcn

f(u)

Constant1

Constant

AddSub3

a + b

−1

AddSub2

a + b

−1

AddSub1

a + b

−1

AddSub

a + b

−1

In1

square

dataout

current sample

data_in

Nth

Figure 5: The Simulink Model of the Threshold Estimator

block based on the calculation of the sample standard devi-

ation.

this memory, its content is copied into the registers

and the sorting process can start. When all the swp

signals are equal to 0 during the last iteration, the in-

put vector is correctly sorted. A ﬁnite state machine,

one for each Threshold Estimator block (i.e. one for

each decomposition level), is used to control the vari-

ous phases of the process.

In order to compare the hardware characteristics

of these models of threshold estimation based on the

MAD against those of a traditional sample standard

deviation as described above, an hardware model has

been designed also for such an approach. Figure 5

shows the Simulink model for this implementation.

Every time an input sample arrives, it is squared and

added to the current value of s

. After N samples, the

ﬁnal value of s

is saved in one of the 4 locations of

the single-port RAM used as circular buffer in order

to determine the correct value of σ over the sliding

window.

Regardless the chosen approach, the value of the

threshold θ is sent in input to the Thresholder block,

able to apply the hard thresholding on the detail sam-

ples. It should be also considered that the value of θ

is different for the various levels.

4 EXPERIMENTAL RESULTS

Before analysing the results in terms of hardware re-

sources which are necessary for the different solu-

tions presented above, such solutions have been eval-

uated from a functional perspective. A publicly avail-

able dataset of simulated neural signals obtained from

real physiological action potentials recorded from an-

imals at the central nervous system level has been

used (Quiroga et al., 2004). The synthetic signals are

obtained by linearly mixing an artiﬁcial sequence of

real spikes from three neurons to other spikes at ran-

dom times and amplitudes, representativeof the back-

ground activity (of tunable intensity) of the neurons at

a greater distance from the recording electrodes. The

sampling frequency has been scaled to 12kHz and the

useful bandwidth is declared to be in the range 300Hz

- 3kHz.

4.1 Functional Evaluation

The different versions of the whole wavelet denoising

system have been mapped on the target FPGA in or-

der to evaluate, by hardware-software co-simulations,

the system performance under real conditions. Fig-

ure 6 shows in the ﬁrst row the neural signal with a

low level of background noise used as input for the

two hardware implementations based on the calcula-

tion of the

MAD and of the σ (the two versions of

the one implementing the MAD produce the same re-

sults). The next rows present the related outputs con-

sidering observation windows of M = 4× 64 samples.

It is possible to see that for both solutions, the

wavelet denoising is able to remove, after an initial

transient, the background noise added to the neural

signal without cutting signiﬁcant spikes. The same

performance can be achieved using the same input

signal but with a stronger background noise for which

it is difﬁcult to identify the various spikes on the raw

signal, as can be shown in the ﬁrst row of the Fig. 7.

Even using neural signals with very low SNR, the two

implementations behave similarly preserving the rel-

evant spikes.

Then, we considered the possibility of enlarging

the observation window in order to provide a more

signiﬁcant frame for computing the statistics on the

signal. For example, Fig. 8 shows the outputs of the

VLSIWaveletDenoisingofNeuralSignals-CriticalAppraisalofDifferentAlgorithmicSolutionsforThreshold

Estimation

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

−1

−0.5

0.5

Time [sec]

WD input

(a) Input Signal

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

−1

−0.5

0.5

Time [sec]

WD output with MAD

(b) WD output using the MAD-based threshold

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

−1

−0.5

0.5

Time [sec]

WD output with Std Dev

Figure 6: Wavelet Denoising input and outputs: low level

noise, N=64 samples.

two solutions using

MAD and σ in the case of win-

dows of N = 128 samples and a low level of back-

ground noise. The initial transient is obviously longer

in comparison to the previous cases.

We also analysed the trend of the thresholds in

output from the same decomposition level for differ-

ent observation window lengths, for the two hardware

solutions. The aim is to verify which is the minimum

value of N, considering a sliding window length of

4× N, that allows obtaining a good denoising.

As can be noticed from Fig. 9, after a variable

transient period according to the chosen value of N,

the longer the observation window the better the sta-

bility of the threshold, not inﬂuenced by the presence

of the neural spikes of interest. In fact, in the case of

N = 128, the threshold estimation assumes an almost

constant trend; the goal should be that of selecting

the solution which provides the best compromise in

terms of threshold estimation and required hardware

resources.

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

−1

−0.5

0.5

Time [sec]

WD input

(a) Input Signal

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

−1

−0.5

0.5

Time [sec]

WD output with MAD

(b) WD output using the MAD-based threshold

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

−1

−0.5

0.5

Time [sec]

WD output with Std Dev

Figure 7: Wavelet Denoising input and outputs: high level

noise, N=64 samples.

4.2 Hardware Figures of Merit

Thanks to the possibilities offered by Xilinx System

Generator, also to map the implemented designs on

real hardware, in this case the Xilinx FPGA Virtex-5

LX330 device, we evaluated pros and cons in terms

of necessary hardware resources for the different so-

lutions presented above. The ﬁnal goal is to determine

which is the best solution allowing to achieve a good

accuracy with limited area and power consumption, in

the light of the realization of a VLSI chip implement-

ing such a processing stage for an implantable unit in

the neuroprosthetic ﬁeld.

Synthesis results are presented in Table 1, which

shows the percentage of available slices and Look-up

Tables (LUTs) needed for the three considered thresh-

old estimation blocks only, since the remainder of the

wavelet denoising implementation is the same regard-

less of this stage.

The solution based on the combinatorial (un-

folded)

MAD implementation, as highlighted in Ta-

ble 1, is absolutely inefﬁcient, taking into account it

BIODEVICES2014-InternationalConferenceonBiomedicalElectronicsandDevices

Table 1: FPGA synthesis results for the Threshold Estimator varying the length of the observation window.

N f

max

[MHz] Slice Registers LUTs

32 417.34 156 / 207360 (0.07%) 80 / 207360 (0.04%)

64 416.61 157 / 207360 (0.07%) 82 / 207360 (0.04%)

128 416.02 160 / 207360 (0.07%) 84 / 207360 (0.04%)

unfolded MAD 8 417.08 558 / 207360 (0.27%) 20270 / 207360 (9.77%)

folded MAD

32 242.78 2493 / 207360 (1.20%) 7164 / 207360 (3.45%)

64 246.70 4932 / 207360 (2.38%) 14377 / 207360 (6.93%)

128 221.42 9806 / 207360 (4.73%) 28861 / 207360 (13.91%)

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

−1

−0.5

0.5

Time [sec]

WD input

(a) Input Signal

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

−1

−0.5

0.5

Time [sec]

WD output with MAD

(b) WD output using the MAD-based threshold

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

−1

−0.5

0.5

Time [sec]

WD output with Std Dev

Figure 8: Wavelet Denoising input and outputs: low level

noise, N=128 samples.

has been presented only for N = 8, with the usual

4-times larger observation window. A rough esti-

mation of the hardware resources required in case

of N = 32 would lead to more than 330kLUT over

the 207360 available ones, thus exceeding the con-

siderable amount of physical resources on the target

FPGA. The huge amount of LUTs, compared to the

folded version, is incompatible with a real implemen-

tation in the context of this application, taking into

account that the observation window length should be

large enough to properly estimate the statistics of a

signal sampled at 12kHz.

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

0.2

0.4

0.6

0.8

Time [sec]

Threshold Amplitude

N = 32

N = 64

N = 128

(a) MAD-based solution

0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

0.2

0.4

0.6

0.8

Time [sec]

Threshold Amplitude

N = 32

N = 64

N = 128

(b) σ-based solution

Figure 9: Threshold variation over time using different

lengths of the observation window.

FPGA synthesis results demonstrate that the

wavelet denoising solution based on the threshold es-

timation by the sample standard deviation allows min-

imizing the necessary hardware resources regardless

the length of the observation window. Furthermore,

the usage of slices and LUTs of the

MAD-based solu-

tion, even using a folded approach, is clearly incom-

patible with an efﬁcient implementation of this pro-

cessing stage, especially compared to the same data

related to the σ-based implementations.

5 CONCLUSIONS

This paper highlights how the choice of the thresh-

old estimation technique, more than having an inﬂu-

ence on the quality of the wavelet denoising algo-

rithm, has signiﬁcant reverberations on the feasibility

and efﬁciency of a custom VLSI architecture aimed at

an implantable chip in the context of neural prosthe-

ses. The comparison between a sample standard devi-

ation and the widespread

MAD reveals similar func-

VLSIWaveletDenoisingofNeuralSignals-CriticalAppraisalofDifferentAlgorithmicSolutionsforThreshold

Estimation

tional performancewith dramatically better character-

istic of the former in terms of hardware implementa-

tion, regardless the

MAD is implemented as a combi-

natorial trellis as suggested by some authors or in a

more efﬁcient folded version. The paper also stresses

the beneﬁt of using hardware-software co-simulations

tools such as Xilinx System Generator for rapid proto-

typing and veriﬁcation on FPGA, which represents a

value added for the research in rapidly evolving ﬁelds

such as neural engineering, overcoming the limits of

the traditional HDL coding.

ACKNOWLEDGEMENTS

The research leading to these results has received

funding by the Region of Sardinia in the ELoRA

project (Fundamental Research Programme, L.R.

7/2007, grant agreement CRP-60544), by the Euro-

pean Commission in the NEBIAS project (FP7, FET

Proactive, grant agreement 611687), by Italian Gov-

ernment in the HANDBOT project (PRIN 2010/11,

prot. 2010YF2RY

003) and by the Italian Ministry of

Health in the NEMESIS project (Young Researchers,

grant agreement 064/GR-2009-1591615).

REFERENCES

Bahoura, M. and Ezzaidi, H. (2012). FPGA-

implementation of discrete wavelet transform with

application to signal denoising. Circuits, Systems,

and Signal Processing, 31(3):987–1015.

Baig, M. M., Gholamhosseini, H., and Connolly, M. J.

(2013). A comprehensive survey of wearable and

wireless ECG monitoring systems for older adults.

Medical & Biological Engineering & Computing,

51(5):485–495.

Casson, A., Yates, D., Smith, S., Duncan, J., and Rodriguez-

Villegas, E. (2010). Wearable electroencephalogra-

phy. Engineering in Medicine and Biology Magazine,

IEEE, 29(3):44–56.

Citi, L., Carpaneto, J., Yoshida, K., Hoffmann, K.-P., Koch,

K. P., Dario, P., and Micera, S. (2008). On the use of

wavelet denoising and spike sorting techniques to pro-

cess electroneurographic signals recorded using intra-

neural electrodes. Journal of Neuroscience Methods,

172:294–302.

Cohen, A. and Kovacevic, J. (1996). Wavelets: the

mathematical background. Proceedings of the IEEE,

84(4):514–522.

Diedrich, A., Charoensuk, W., Brychta, R., Ertl, A., and

Shiavi, R. (2003). Analysis of raw microneurographic

recordings based on wavelet de-noising technique

and classiﬁcation algorithm: wavelet analysis in mi-

croneurography. IEEE Trans Biomed Eng, 50(1):41–

50.

Holschneider, M., Kronland-Martinet, R., Morlet, J., and

Tchamitchian, P. (1990). A real-time algorithm for

signal analysis with the help of the wavelet transform.

In Wavelets, pages 286–297. Springer Berlin Heidel-

berg.

Kuzume, K., Niijima, K., and Takano, S. (2004). FPGA-

based lifting wavelet processor for real-time signal de-

tection. Signal Processing, 84(10):1931–1940.

Mahmoud, M. I., Dessouky, M. I. M., Deyab, S., and

Elfouly, F. H. (2008). Signal denoising by wavelet

packet transform on FPGA technology. Special Issue

of Ubiquitous Computing and Communication Jour-

nal Bioinformatics and Image.

Martinez, J., Cumplido, R., and Feregrino, C. (2005). An

FPGA-based parallel sorting architecture for the Bur-

rows Wheeler transform. In International Conference

on Reconﬁgurable Computing and FPGAs, ReConFig

2005.

Medina, C., Alcaim, A., and Jr., J. A. (2003). Wavelet de-

noising of speech using neural networks for threshold

selection. Electronics Letters, 39(25):1869–1871.

Montani, M., Marchi, L. D., Marcianesi, A., and Speciale,

N. (2003). Comparison of a programmable DSP and

FPGA implementation for a wavelet-based denoising

algorithm. In Proc. IEEE 46th Midwest Symposium

on Circuits and Systems, volume 2, pages 602–605.

Nezan, J., Siret, N., Wipliez, M., Palumbo, F., and Raffo,

L. (2012). Multi-purpose systems: A novel dataﬂow-

based generation and mapping strategy. In Proc. IEEE

International Symposium on Circuits and Systems (IS-

CAS), pages 3073–3076.

Palumbo, F., Carta, N., Pani, D., Meloni, P., and Raffo, L.

(2012). The multi-dataﬂow composer tool: genera-

tion of on-the-ﬂy reconﬁgurable platforms. Journal of

Real-Time Image Processing, pages 1–17.

Pani, D., Usai, F., Citi, L., and Raffo, L. (2011). Impact of

the approximated on-line centering and whitening in

OL-JADE on the quality of the estimated fetal ecg. In

Proc. of the 5th International IEEE/EMBS Conference

on Neural Engineering (NER), pages 44–47.

Quiroga, R. Q., Nadasdy, Z., and Ben-Shaul, Y. (2004). Un-

supervised spike detection and sorting with wavelets

and superparamagnetic clustering. Neural Comput.,

16(8):1661–1687.

Radovan, S., Saˇsa, K., Dejan, K., and Goran, D. (2013). Op-

timization and implementation of the wavelet based

algorithms for embedded biomedical signal process-

ing. Computer Science and Information Systems,

10:502–523.

Zhang, M., Deng, R., Ma, Z., and Zhang, M. (2011). A

FPGA-based low-cost real-time wavelet packet de-

noising system. In Proc. of 2011 Int. Conf. on

Electronics and Optoelectronics (ICEOE), volume 2,

pages V2–350–V2–353.

BIODEVICES2014-InternationalConferenceonBiomedicalElectronicsandDevices