
Paired Indices for Clustering Evaluation
Correction for Agreement by Chance
Maria José Amorim
1
and Margarida G. M. S. Cardoso
2
1
Dep. of Mathematics, ISEL and Inst. Univ. de Lisboa (ISCTE-IUL), BRU-IUL, Av. Forças Armadas, Lisboa, Portugal.
2
Dep. of Quantitative Methods and BRU-UNIDE, ISCTE Busines School-IUL, Av. das Forças Armadas, Lisboa, Portugal.
Keywords: Adjusted Indices, Indices of Paired Agreement, Clustering Evaluation.
Abstract: In the present paper we focus on the performance of clustering algorithms using indices of paired agreement
to measure the accordance between clusters and an a priori known structure. We specifically propose a
method to correct all indices considered for agreement by chance – the adjusted indices are meant to provide
a realistic measure of clustering performance. The proposed method enables the correction of virtually any
index – overcoming previous limitations known in the literature - and provides very precise results. We use
simulated datasets under diverse scenarios and discuss the pertinence of our proposal which is particularly
relevant when poorly separated clusters are considered. Finally we compare the performance of EM and K-
Means algorithms, within each of the simulated scenarios and generally conclude that EM generally yields
best results.
1 INTRODUCTION
In the present study we focus on the use of indices of
paired agreement to measure accordance between
two partitions of the same data and propose a
method to handle agreement by chance.
This contribution aims to fill a gap in the
literature since recent alternative solutions that have
been proposed to address this issue - e.g. (Albatineh,
2010) or (Albatineh and Niewiadomska -Bugaj,
2011) - are limited in scope. We resort to diverse
indices of paired agreement – Rand, Russell and
Rao, Gower and Legendre, Jaccard, Czekanwski,
Goodman and Kruskal, Sokal and Sneath, Fowlkes
and Mallows – and illustrate the capacity of the
proposed method to adjust virtually any index for
agreement by chance.
In order to illustrate the usefulness of the
proposed method we compare the performance of
two well-known clustering tools: the Expectation
Maximization (EM) and the K-Means (KM)
algorithms. The EM provides the estimation of a
finite mixture model - (Dempster et al., 1977) and,
for example, (O´Hagan et al., 2012). The KM
algorithm, a (dis)similarity-based clustering method,
was independently discovered in different scientific
fields and is still a widely used clustering tool ((Jain,
2010), (Shamir and Tishby, 2010)).
We conduct clustering external validation trying
to measure the fit between a clustering structure
captured in cluster analysis and the ground truth.
The numerical experiments conducted resort to
simulated data sets and consider diverse clustering
scenarios.
1.1 Indices of Paired Agreement
between Partitions
Similarity indices have been used in various
domains for a long time: e.g. in clustering ecological
species (Jaccard, 1908), in plant genetics (Meyeri et
al., 2004) or in documents clustering (Chumwatana
et al., 2010). Several similarity indices can be used
to measure the agreement between two partitions of
the same data - P
K
and P
Q
with K and Q groups,
respectively. These are generally designated by
Indices of Agreement (IA) - see ((Gower and
Legendre, 1986), (Milligan and Cooper, 1986)).
Some of the IA are based on the number of pairs
of observations that both partitions allocate (or not)
to the same cluster – these are Indices of Paired
Agreement (IPA). In the present study, diverse IPA
are used to measure the degree of agreement
between partitions. They can be determined from a
similarity matrix A - a 2×2 matrix, where element
a=A(1,1) represents the number of pairs of
164
Amorim M. and G. M. S. Cardoso M..
Paired Indices for Clustering Evaluation - Correction for Agreement by Chance.
DOI: 10.5220/0004868301640170
In Proceedings of the 16th International Conference on Enterprise Information Systems (ICEIS-2014), pages 164-170
ISBN: 978-989-758-027-7
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

observations both partitions agree to allocate in the
same group; b=A(1,2) represents the number of pairs
that only belong to the same group in partition P
K
;
c=A(2,1) represents the numbers of pairs that only
belong to the same group in partition P
Q
; d=A(2,2)
represents the number of pairs of observations both
partitions agree to allocate to different groups. The
values of a, b, c and d can be calculated from the
cross-classification table between the two partitions
being considered (see equations 1 to 4). The cross-
classification table is a K*Q matrix, whose (k,q)th
1
2
2
(1)
1
2
.
1
2
(2)
1
2
.
1
2
(3)
2
(4)
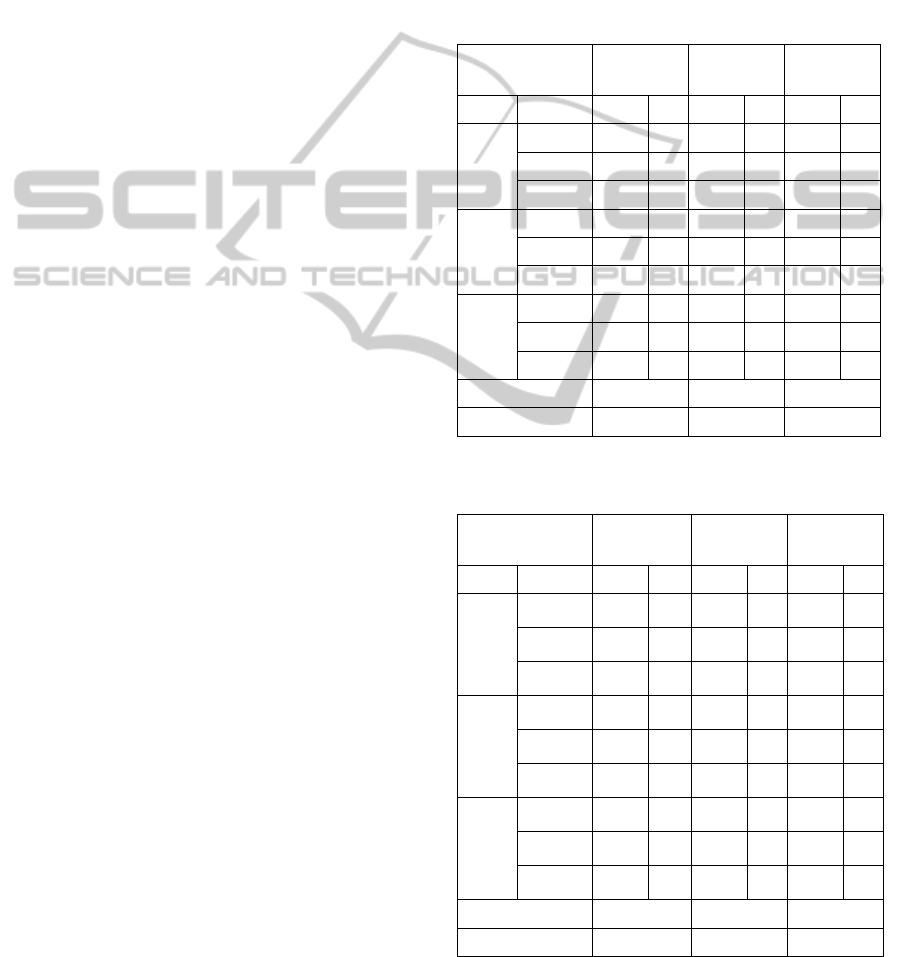
Table 1: Indices of paired agreement.
IPA
L Family
R
(Rand, 1971)
RR
(Russell and Rao, 1940)
GL ×
(Gower and Legendre, 1986)
J ×
(Jaccard, 1908)
C
(Czekanwski, 1932)
GK ×
(Goodman and Kruskal, 1954)
SoS ×
(Sokal and Sneath, 1963)
SS2 ×
(Sokal and Sneath, 1963)
FM
(Fowlkes and Mallows, 1983)
element - n
kq
- is the number of observations in the
intersection of group C
k
of P
K
(k=1…K) and C
q
of
P
Q
(q=1…Q), n
k.
and n
.q
represent the matrix’s rows
and columns totals (respectively) and n the number
of observations.
In the present work we consider the indices of
paired agreement in Table 1. The indices SoS and
SS2 can be calculated using the equations (5) and
(6), respectively, the others indices equations can be
found in references mentioned in Table 1.
(5)
2
2
(6)
1.2 Correcting Indices for Agreement
by Chance
In the context of clustering validation, indices of
agreement (IA) are used to measure the agreement
between partitions drawn from slightly modified
data sets to decide upon a clustering solution
stability, or to measure the agreement between
clustering solutions and the real partition (external
validation). The relevance of clustering validation is
underlined by (Hennig, 2006), for example.
The agreement between two partitions –
summarized in the corresponding cross-
classification table –can, however, be due to chance.
Therefore, in order to adequately evaluate the degree
of agreement between two partitions, indices of
agreement must be corrected to exclude agreement
by change. (Hubert and Arabie, 1985) were the first
to address this issue regarding the Rand index. For
correction, they considered the mean of this paired
index under the null hypothesis (H
0
) of no
association between the partitions to be compared,
conditional on the row and column table totals -
hypothesis of restricted independence. The adjusted
index is then:
1
(7)
Adj
M
(IPA) is bounded by 1 and takes the value
zero when the observed index - IPA
obs
– is equal to
the expected value under H
0
.
In general, the exact IPA mean, under H
0
, can be
determined considering all the cross-classification
tables under the hypothesis of restricted
independence. However, this is only feasible for
relatively small tables with small observed counts,
due to computational complexity (Krzanowski and
Marriott, 1994).
Under H
0
, the probability of observing the
associated cross-classification table can be modelled
by the Multivariate Hypergeometric distribution
(Halton, 1969) and the conditional probability of the
value n
kq
given the values in the previous rows and
columns can be modelled by the Hypergeometric
distribution. Thus, the conditional expected value of
n
kq
given previous entries and the row and column
totals can be calculated under H
0
. In fact, one can
determine the means and variation of all IPA that are
linear functions of the sum of the squares of the n
kq
i.e. all indices belonging to the L Family, namely the
R, RR, C and FM indices in
Table 1- see (Albatineh,
PairedIndicesforClusteringEvaluation-CorrectionforAgreementbyChance
165
2010) for more details. (Albatineh and
Niewiadomska-Bugaj, 2011) proposed an alternative
approach for some indices - SS2, J and GL - that are
not members of the L Family. They expressed J and
SS2 as functions of C, and GL as function of R, and
approximately computed their expected values.
Despite the diverse approaches to handle the
correction for agreement by chance there are various
IPA that are not covered by the procedures so far
proposed - GK and SoS, for example. Therefore we
propose a methodology that can deal with the
correction of any IPA for agreement by chance.
2 THE PROPOSED METHOD
In the present work, the expected value of each IPA
is estimated using the average of its values
corresponding to 17,000 cross-classifications tables
generated under H
0
- see (Amorim and Cardoso,
2010). For each generated table, the IPA values are
determined which enables obtaining the empirical
IPA distribution (under H
0
) and the corresponding
descriptive statistics.
The 17,000 cross-classifications tables generated
ensure that average estimates have 99% confidence
(Agresti et al., 1979).
The advantage of the proposed approach is that it
can be applied to virtually all indices– see also
(Amorim and Cardoso, 2012) where a similar
procedure was used for Mutual Information Indices.
In order to evaluate the performance of the IPA
in this study (seeTable 1), several scenarios are
considered:
Simulated data sets with Gaussian 2, 3 and 4
latent groups with 2, 3 or 4 Gaussian distributed
variables and with 500, 800 and 1100 observations,
respectively.
Mixtures with balanced and unbalanced
clusters’ weights.
Diverse degrees of clusters’ overlapping:
poorly-separated, moderately-separated and well-
separated clusters, where the degree of overlap is the
sum of misclassification probabilities (Maitra and
Melnykov, 2010).
The R MixSim package is used to obtain the
simulated data (Maitra and Melnykov, 2010). Thirty
simulated data sets are obtained in each of the 18
scenarios. Cluster analysis is performed using the
Expectation-Maximization algorithm implemented
in the Rmixmod package (Lebret et al, 2012) and the
K-means algorithm implemented in the IBM SPSS
Statistics software.
3 DATA ANALYSIS AND
RESULTS
In this section we present the results referring to the
simulated 3 clusters’ data sets. The corresponding
distributional parameters are presented in Tables 2
and 3. The results obtained refer to all scenarios
previously indicated in section 2.
Table 2: Balanced simulated data sets distributional
parameters.
Data set Poor Moderate Weel
Group Variable Mean Var Mean Var Mean Var
1
(30%)
X1 10.5 3.5 11.9 1.1 10.5 1.0
X2 2.3 0.5 2.5 0.3 2.5 1.3
X3 7.8 2.0 8.0 0.9 4.3 1.8
2
(30%)
X1 10.0 3.0 9.8 1.2 15.0 2.2
X2 2.5 0.3 1.5 0.3 4.0 1.2
X3 7.0 1.0 6.8 0.7 7.0 1.5
3
(40%)
X1 9.5 2.0 11.8 1.4 7.0 2.3
X2 2.0 0.4 2.0 0.4 6.2 1.6
X
3
7.5 1.2 8.9 0.7 2.5 1.7
Average overlap 0.633 0.140 0.019
Max. overlap 0.653 0.516 0.029
Table 3: Unbalanced simulated data sets distributional
parameters.
Data set Poor Moderate Weel
Group Variable Mean
Var
Mean Var Mean Var
1
(60%)
X1
11.0 2.2 12.3 1.1 14.3 0.7
X2
5.3 0.8 6.4 0.6 7.0 0.2
X3
7.8 1.8 8.8 1.1 9.2 0.3
2
(30%)
X1
10.0 2.0 11.0 1.0 12.7 0.5
X2
4.5 0.5 5.0 0.5 5.0 0.4
X3
7.2 1.4 7.5 0.8 7.6 0.3
3
(10%)
X1
9.4 1.8 9.5 0.9 11.0 0.5
X2
4.0 0.4 3.7 0.4 3.5 0.3
X
3
7.0 1.5 6.6 0.7 6.0 0.2
Average overlap 0.632 0.143 0.021
Max. overlap 0.868 0.215 0.115
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
166
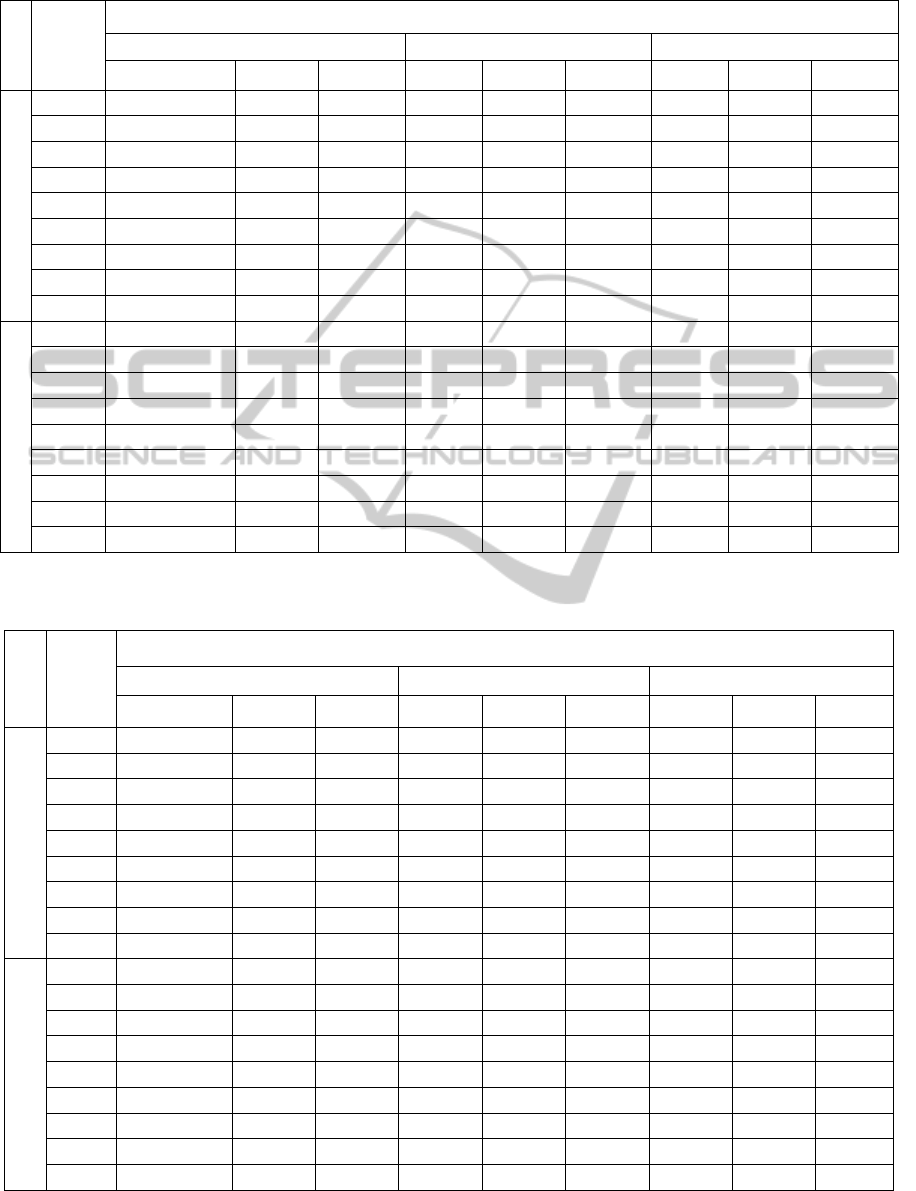
Table 4: IPA simulated, distributional and approximated expectations (values are averaged over the 30 datasets and
correspond to external validation of EM clusters).
Dataset-
IPA
Dataset - separation
Poor Moderate Weel
sim distrib approx sim distrib approx sim distrib approx
Balanced
Rand 0.464 0.464 0.521 0.521 0.552 0.552
RR 0.209 0.209 0.148 0.148 0.115 0.115
GL 0.632 0.631 0.684 0.687 0.711 0.716
J 0.275 0.270 0.232 0.224 0.204 0.195
C 0.431 0.431 0.376 0.376 0.339 0.339
GK 0.000 0.000 0.000
SoS 0.212 0.228 0.224
SS2 0.160 0.140 0.132 0.106 0.114 0.086
FM 0.453 0.453 0.381 0.381 0.339 0.339
Unbalanced
Rand 0.500 0.500 0.505 0.505 0.504 0.504
RR 0.229 0.229 0.206 0.206 0.209 0.209
GL 0.666 0.668 0.671 0.673 0.670 0.672
J 0.313 0.309 0.293 0.289 0.296 0.292
C 0.476 0.476 0.453 0.453 0.457 0.457
GK 0.000 0.000 0.000
SoS 0.246 0.248 0.248
SS2 0.186 0.172 0.172 0.155 0.174 0.157
FM 0.477 0.477 0.454 0.454 0.457 0.457
Table 5: IPA simulated, distributional and approximated expectations (values are averaged over the 30 datasets and
correspond to external validation of KM clusters).
Dataset-
IPA
Dataset – separation
Poor Moderate Weel
sim distrib approx sim distrib approx sim distrib approx
Balanced
R
0.552 0.552 0.551 0.551 0.552 0.552
RR
0.115 0.115 0.116 0.116 0.115 0.115
GL
0.711 0.716 0.710 0.715 0.711 0.716
J
0.204 0.195 0.205 0.196 0.204 0.195
C
0.339 0.339 0.341 0.341 0.339 0.339
GK
0.000 0.000 0.000
SoS
0.224 0.225 0.224
SS2
0.114 0.086 0.114 0.087 0.114 0.086
FM
0.339 0.339 0.341 0.341 0.339 0.339
Unbalanced
R
0.515 0.515 0.514 0.514 0.506 0.506
RR
0.152 0.152 0.158 0.158 0.198 0.198
GL
0.680 0.683 0.679 0.681 0.672 0.674
J
0.239 0.231 0.246 0.238 0.285 0.280
C
0.386 0.386 0.394 0.394 0.443 0.443
GK
0.000 0.000 0.000
SoS
0.235 0.237 0.246
SS2
0.136 0.110 0.140 0.115 0.166 0.148
FM
0.390 0.390 0.398 0.398 0.444 0.444
PairedIndicesforClusteringEvaluation-CorrectionforAgreementbyChance
167

Table 6: IPA observed and adjusted Means and the corresponding coefficients of variation (values are averaged over the 30
datasets and correspond to external validation of EM clusters).
Dataset-
IPA
Dataset – separation
Poor
Moderate
Weel
obsM cv adjM cv obsM cv adjM cv obsM cv adjM cv
Balanced
R 0.483 0.131 0.038 0.655 0.710 0.102 0.400 0.236 0.974 0.006 0.943 0.014
RR 0.219 0.262 0.012 0.629 0.242 0.124 0.110 0.205 0.327 0.015 0.239 0.018
GL 0.649 0.091 0.050 0.642 0.828 0.068 0.464 0.219 0.987 0.003 0.955 0.011
J 0.293 0.108 0.024 0.658 0.459 0.085 0.293 0.249 0.927 0.018 0.908 0.022
C 0.453 0.084 0.038 0.655 0.628 0.060 0.400 0.236 0.962 0.009 0.943 0.014
GK 0.101 0.555 0.101 0.554 0.724 0.175 0.724 0.175 0.998 0.001 0.998 0.001
SoS 0.234 0.199 0.028 0.636 0.485 0.146 0.333 0.257 0.943 0.014 0.927 0.018
SS2 0.172 0.126 0.014 0.661 0.299 0.107 0.191 0.262 0.864 0.033 0.847 0.038
FM 0.476 0.121 0.040 0.637 0.636 0.051 0.406 0.225 0.962 0.009 0.943 0.014
Unbalanced
R 0.605 0.062 0.211 0.362 0.847 0.025 0.690 0.064 0.990 0.004 0.980 0.009
RR 0.282 0.152 0.069 0.373 0.377 0.056 0.215 0.072 0.452 0.029 0.307 0.021
GL 0.753 0.039 0.260 0.348 0.917 0.014 0.747 0.053 0.995 0.002 0.985 0.006
J 0.416 0.126 0.151 0.384 0.711 0.053 0.591 0.083 0.979 0.009 0.970 0.013
C 0.585 0.091 0.211 0.362 0.830 0.032 0.690 0.064 0.989 0.005 0.980 0.009
GK 0.409 0.338 0.409 0.338 0.934 0.025 0.934 0.025 1.000 0.000 1.000 0.000
SoS 0.366 0.128 0.158 0.381 0.715 0.051 0.621 0.077 0.981 0.008 0.974 0.011
SS2 0.264 0.156 0.096 0.403 0.553 0.078 0.460 0.107 0.959 0.018 0.950 0.021
FM 0.587 0.093 0.212 0.362 0.831 0.032 0.690 0.063 0.989 0.005 0.980 0.09
Table 7: IPA observed and adjusted Means and the corresponding coefficients of variation (values are averaged over the 30
datasets and correspond to external validation of KM clusters).
Dataset-
IPA
Dataset – separation
Poor
Moderate
Weel
obsM cv adjM cv obsM cv adjM cv obsM cv adjM cv
Balanced
R
0.567 0.007 0.035 0.272 0.704 0.019 0.341 0.083 0.968 0.008 0.929 0.017
RR
0.123 0.024 0.009 0.273 0.193 0.037 0.087 0.080 0.323 0.014 0.235 0.018
GL
0.724 0.005 0.044 0.269 0.826 0.011 0.400 0.075 0.984 0.004 0.944 0.014
J
0.221 0.024 0.021 0.275 0.394 0.044 0.238 0.095 0.910 0.021 0.888 0.028
C
0.362 0.020 0.035 0.272 0.565 0.032 0.341 0.083 0.953 0.011 0.929 0.017
GK
0.077 0.269 0.077 0.268 0.635 0.062 0.635 0.062 0.997 0.001 0.997 0.001
SoS
0.243 0.023 0.025 0.275 0.438 0.045 0.276 0.093 0.930 0.017 0.910 0.022
SS2
0.124 0.027 0.012 0.278 0.246 0.055 0.148 0.106 0.836 0.039 0.815 0.045
FM
0.362 0.020 0.035 0.272 0.565 0.032 0.341 0.082 0.953 0.011 0.929 0.017
Unbalanced
R
0.550 0.018 0.072 0.223 0.695 0.048 0.373 0.182 0.943 0.100 0.883 0.218
RR
0.170 0.032 0.020 0.219 0.249 0.089 0.108 0.189 0.416 0.162 0.274 0.234
GL
0.710 0.011 0.092 0.217 0.820 0.028 0.439 0.161 0.968 0.057 0.901 0.188
J
0.274 0.029 0.046 0.228 0.450 0.108 0.272 0.219 0.889 0.196 0.850 0.270
C
0.430 0.022 0.072 0.223 0.620 0.073 0.373 0.182 0.930 0.127 0.883 0.218
GK
0.155 0.218 0.155 0.218 0.682 0.114 0.682 0.114 0.967 0.075 0.967 0.075
SoS
0.274 0.032 0.051 0.231 0.469 0.105 0.304 0.207 0.895 0.184 0.862 0.250
SS2
0.159 0.033 0.026 0.232 0.292 0.143 0.177 0.256 0.834 0.271 0.804 0.325
FM
0.435 0.023 0.073 0.222 0.625 0.070 0.378 0.177 0.932 0.123 0.884 0.214
In Tables 4 and 5 we present the comparative
precision of the proposed simulation based
approach: the corresponding averages (under H
0
)
match the distributional averages whenever they are
available - see (Albatineh, 2010) – and are similar to
the approximated expected values - see (Albatineh
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
168

and Niewiadomska-Bugaj, 2011). The correction of
observed indices values, in Tables 6 and 7, obeys to
formula (7).
The results regarding external validation of EM
and KM clustering algorithms are reported in Tables
6 and 7. The diverse IPA are affected differently by
the adjustment - the GL index is clearly the most
affected by correction. Also, correction for change is
particularly essential when considering poorly
separated clusters.
As expected, the averages of simulated values,
under H
0
, of the GK index are null (Goodman and
Kruskal, 1954). The R and C indices values are
equal after adjustment which is in accordance with
(Albatineh and Niewiadomska-Bugaj, 2006). We
also conclude that, after adjustment, FM values are
very similar to R and C values.
4 DISCUSSION AND
PERSPECTIVES
In the present paper we focus on the correction of
indices of paired agreement (IPA) between two
partitions.
When comparing two partitions – e.g. when
performing clustering validation and comparing
clusters estimated and real clusters – agreement
between them may be due to chance. This issue was
first addressed by (Hubert and Arabie, 1985)
referring to a specific measure of agreement - the
Rand index of paired agreement. These authors
provided a new adjusted Rand index excluding
agreement by chance. Naturally, there are numerous
IPA and this issue should be addressed when using
any index. Recently, (Albatineh, 2010), for example,
identified a family of paired indices and provided
analytic formulas for their correction, using the
corresponding averages under the hypothesis of
independence. However, analytic correction cannot
be provided for many indices – e.g. for the Jaccard
index (a very old and well-known index) or the
Gower and Legendre index, a more recent one.
As an alternative approach for IPA correction,
we propose using the simulation of crosstabs to
estimate the average of any index under the
hypothesis of restricted independence i.e. subject to
constraints of marginal totals (including the number
of observations in the known clusters and the
estimated ones). We generate 17,000 tables for the
estimation of each average. Finally, we correct the
observed IPA using their estimated average and use
normalization so that all values can be compared.
Nine IPA are analysed. The main contribution of this
study is therefore to provide a method that is able to
correct virtually any IPA for agreement by chance.
When an analytic solution is available for correction
(based on distributional assumptions), the
differences between IPA analytic averages and
averages provided by the proposed method are
insignificant (at most 0.0001) which shows the
method’s precision.
To illustrate the usefulness of the proposed
method for the indices' adjustment, we conduct
external validation of the EM and KM algorithms
within diverse scenarios.
According to the results obtained we identified
notorious differences between the observed and
adjusted indices when trying to capture a clustering
structure originated in a poorly separated original
mixture. This fact clearly demonstrates the
pertinence of indices’ correction. In fact, for difficult
(impossible?) clustering tasks the observed indices
clearly overestimate the clustering performance,
while the adjusted indices translate the poor
agreement with original clusters, despite of some
variability which, we believe, is realistic.
For the moderately separated components, the
agreement by chance factor yields minor correction
to the paired indices, and when “easy” clusters
(with a good separation) are considered, correction
for chance is almost insignificant.
Performance of the EM algorithm is generally
better. The gap between EM and KM is clearer in
the case of unbalanced clusters. For “easy”
clustering tasks, the KM and EM perform alike.
The results obtained underline the need to use
adjusted indices, corrected for agreement by chance
when conducting evaluation of (any) clustering
algorithms’ performance based on agreement with
the original structure. Additional clustering
algorithms and indices can be used in the future.
In future research, the distributions of alternative
corrected indices should be further investigated for
electing the most useful ones – those evidencing the
least biased distributions and the easiest to interpret.
REFERENCES
Agresti, A., Wackerly, D. & Boyett, J. M., 1979. Exact
conditional tests for cross-classifications:
approximation of attained significance levels.
Psychometrika, 44, 75-83.
Albatineh, A. N., Niewiadomska-Bugaj, M. & Mihalko,
D., 2006. On Similarity Indices and Correction for
Chance Agreement. Journal of Classification, 23, 301-
313.
PairedIndicesforClusteringEvaluation-CorrectionforAgreementbyChance
169

Albatineh, A. N., 2010. Means and variances for a family
of similarity indices used in cluster analysis. Journal
of Statistical Planning and Inference, 140, 2828-2838.
Albatineh, A. N. & Niewiadmska-Bugaj, M., 2011.
Correcting Jaccard and other similarity indices for
chance agreement in cluster analysis. Advances in
Data Analysis and Classification, 5, 179-200.
Amorim, M. J. &Cardoso, M. G. M. S., 2010. Limiares De
Concordância Entre Duas Partições. Livro de Resumos
do XVIII Congresso Anual da Sociedade Portuguesa
de Estatística, 47-49.
Amorim, M. J. P. C. & Cardoso, M. G. M. S., 2012.
Clustering cross-validation and mutual information
indices. In: Ana Colubi, K. F., Gil Gonzalez-
Rodriguesand Erricos John Kontoghiorghes, ed. 20th
International Con-ference on Computational Statistics
(COMPSTAT 2012), 2012 Limassol, Cyprus. The
International Statistical Institute/International
Association for Statistical Computing, 39-52.
Chumwatana, T., Wong, K. W. & Xie, H., 2010. A SOM-
Based Document Clustering Using Frequent Max
Substrings for Non-Segmented Texts. J. Intelligent
Learning Systems & Applications,, 2, 117-125.
Czekanowski, J., 1932. "Coefficient of racial likeness" and
"durchschnittliche Differenz". Anthropologischer
Anzeiger, 14, 227-249.
Dempster, A. P., Laird, N. M. & Rubin, D. B., 1977.
Maximum likelihood from incomplete data via the EM
algorithm.Journal of the Royal Statistical Society.
Series B (Methodological), 1-38.
Everit, B., Landau, S. & Leese, M. 2001. Cluster Analysis,
London, Arnold.
Fowlkes, E. B. &mallows, C. L., 1983. A method for
comparing two hierarchical clusterings.Journal of the
American Statistical Association, 78, 553-569.
Goodman, L. A. & Kruskal, W. H., 1954. Measures of
Association for Cross Classifications. Journal of the
American Statistical Associations, 49.
Gower, J. C. & Legendre, P., 1986. Metric and Euclidean
Properties of Dissimilarity Coefficients. Journal of
Classification, 3.
Halton, J. H., 1969. A rigorous derivation of the exact
contingency formula. In:Proceedings of the
Cambridge Philosophical Society. Cambridge Univ
Press, 527-530.
Hennig, C., 2006. Cluster-wise assessment of cluster
stability. Research report nº 271, Department of
Statistical Science, University College London.
Hubert, L. and Arabie, P. 1985. Comparing partitions.
Journal of classification,
2, 193-218.
Jaccard, 1908. Nouvelles Recerches sur la Distribuition
Florale. Bulletin de la Societé Vaudoise de Sciences
Naturells, 44, 223-370.
Jain, A. K., 2010. Data clustering: 50 years beyond K-
means. Pattern Recognition Letters, 31, 651-666.
Krzanowski, W. J. & Marriott, F. H. C., 1994.
Multivariate analysis, Edward Arnold London.
Lebret, R., S., L., Langrognet, F., Biernacki, C., Celeux,
G. & Govaert, G., 2012. Rmixmod: The r package of
the model-based unsupervised, supervised and semi-
supervised classification mixmod library.http://cran.r-
project.org/web/ packages/Rmixmod/index.html.
Maitra, R. & Melnykov, V., 2010. Simulating data to
study performance of finite mixture modeling and
clustering algorithms. Computational and Graphical
Statistics, 19, 354-376.
Meyeri, A. D. S., Garcia, A. A. F., Souza, A. P. & JR., C.
L. D. S., 2005. Comparison of similarity coefficients
used for cluster analysis with dominant markers in
maize (Zea mays L). Genetics and Molecular Biology,
27, 83-91.
Milligan, G. W. & Cooper, M. C., 1986. A Study of
Comparability of External Criteria for Hierarchical
Cluster Analysis. Multivariate Behavioral Reserch,
21, 441-458.
O’Hagan, A., Murphy, T. B. & Gormley, I. C., 2012.
Computational aspects of fitting mixture models via
the expectation–maximization algorithm. Compu-
tational Statistics and Data Analysis, 56, 3843-3864.
Rand, W. M., 1971. Objective Criteria for the Evaluation
of Clustering Methods. Journal of the American
Statistical Association, 66, 846-850.
RusseL, P. F. & Rao, T. R. 1940. On Habitat and
Association of Species of Anophelinae Larvae in
South-Eastern Madras. J. Malar. Inst. India, 3, 153-
178.
Shamir, O. and tishby, N., 2010. Stability and model
selection in k-means clustering. Mach Learn, 80, 213-
244.
Sokal, R. R. and Sneath, P. H., 1963. Principles of
Numerical Taxonomy, San Francisco CA: Freeman.
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
170
