
A Revisited Model for the Real Time Traffic Management
Astrid Piconese
1
, Thomas Bourdeaud’Huy
2
, Mariagrazia Dotoli
1
and Slim Hammadi
2
1
DEE, Department of Electrical Engineering and Information Science, Politecnico di Bari, Bari, Italy
2
LAGIS, Laboratoire d’Automatique, G´enie Informatique et Signal,
´
Ecole Centrale de Lille, Lille, France
Keywords:
Railway Systems, Real-time Optimization, Regional Networks, Single-track, Centralized Traffic Control,
Linear Programming.
Abstract:
The real-time trafficmanagement allow to solve unexpected disturbances that occur along a railway line during
the normal developement of the traffic. The original timetable is restored through the rescheduling process.
Despite the increase of real-time decision support tools for trains dispatchers that enable a better use of rail in-
frastructure, real-time traffic management received a limited scientific attention. In this paper, we deal with the
real time traffic management for regional railway networks, mainly single tracks, in which a centralized traffic
control system is installed. The rescheduling problem is presented as a Mixed Integer Linear Programming
Model which resolution allows to carry out the rescheduling process in a very short computational time.
1 INTRODUCTION
A railway system is a complex system with many
interacting processes that depend on technical de-
vices, human behavior, external environment, and
therefore contains many risks of disturbances. The
usual method how railways manage their traffic per-
formance is through a carefully designed plan of op-
erations, defining several months in advance routes,
orders and timing for all trains. This process, called
off-line timetabling, is followed by a real-time traf-
fic management which consists in managing distur-
bances that may occur during the ordinary function-
ing of the network.
Once a delayed train deviates from its original
schedule, it may propagateits delay to other trains due
to infrastructure, signaling or timing conflicts. Ma-
jor disturbances may influence the off-line plan of op-
erations that should be subject to short-term adjust-
ments in order to minimize the negative effects of the
disturbances. Possible traffic control actions include
changing dwell times at scheduled stops, changing
train speeds along lines, or adjusting train orders at
junctions, stations and passing points. Other control
actions involve major modifications such as changing
train routes or even canceling scheduled train jour-
neys. The main goal of the real-time dispatching is
to minimize trains delays, while satisfying the traf-
fic regulation constraints, and ensuring compatibility
with the current position of each train, see (D’Ariano,
2008).
In this paper we deal with real-time traffic control
problem for a regional single-track railway where an
operating system called Centralized Traffic Control
(CTC) is installed. The CTC provides a centralized
control for signals and switches within a limited ter-
ritory, controlled from a single control console. The
command is carried out by the Train Dispatcher (TD).
The train dispatcher observes the status of the ter-
ritory – i.e. occupation of line sections, location of
trains, etc. – in a continuous manner and collects in-
formation; meanwhile, he communicates with the up-
per level decision-makers and the staff in the territory
in order to exchange decisions taken. In case of an un-
planned event and emergency he takes a decision and
makes necessary actions in accordance with the rules
and regulations pre-defined by the railway authority,
see (
˙
Ismail, 1999).
The TD may benefit from appropriate decision
support system, such as scheduling algorithms, to per-
form a real-time simulation and evaluation of traf-
fic under disturbances in order to quickly reschedule
train movements and to reduce delays from a global
perspective.
It is important to find a good compromise between
the solution quality, the time horizon of the traffic
prediction, and the computational effort. If a short
time horizon is adopted, only few trains, and few con-
flicts, can be detected and solved with short computa-
tion times. On the other hand, a longer time horizon
139
Piconese A., Bourdeaud’huy T., Dotoli M. and Hammadi S..
A Revisited Model for the Real Time Traffic Management.
DOI: 10.5220/0004869701390150
In Proceedings of the 3rd International Conference on Operations Research and Enterprise Systems (ICORES-2014), pages 139-150
ISBN: 978-989-758-017-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

leads to a larger number of trains running in the sys-
tem, in order to eliminate completely the propagation
of the disturbance. There is a tradeoff between the
size of the time horizon of traffic prediction (bigger
time horizon meaning better quality) and the compu-
tational time. In fact, in a small time horizon the real-
time dispatching does not take into account conflict-
ing trains outside the time horizon. On the other hand,
a conflict arising far in the future may not be as rele-
vant as a closer conflict, since other unforeseen events
could still affect the further conflict, see (D’Ariano,
2008). In a small time horizon, the computational
time is smaller because datas are limited.
Usually the train dispatcher reschedules the in-
volved trains, depending on the known duration of
the disturbance. He bases his decisions on his own
knowledge, resolving a conflict at a time when it oc-
curs, and then manually rebuilds the timetable, with
a considerable waste of time and no certainty that its
decisions will lead to an optimal solution.
Building on the formalism given in (Dotoli et al.,
2013), we present a model that solves the reschedul-
ing problemforregionalpassenger transport networks
with stations of equal importance, where the CTC sys-
tem is installed. We formulate the problem as a Mixed
Integer Linear Programming Problem (MILP).
In the original model the new timetable after the
disturbance is obtained by minimizing train delays
in all the stations programmed in their path, while
considering constraints regarding travel times, stop
times at stations, safety standards and network capac-
ity. The model is applied to a limited time horizon
that is choosen by the analyst. In order to solve con-
flicts that may occur in the rescheduled timetable af-
ter the time horizon, an iterative heuristic algorithm is
applied. The heuristic algorithm solves a conflict at
the time when it occurs; priority is given to the train
with the highest traveling time, namely the longest
presence on the line. The computational time for
limited time horizons is of the order of seconds, but
the heuristic algorithm requires an elevated computa-
tional time that depends on the number of trains and
the complexity of the raiway line. The methodology
provides a decision support system to the train dis-
patcher that has to take decisions in order to restore
traffic and limit inefficiencies for passengers.
We adapt the previous methodology to regional
networks mainly made of single tracks and take into
account the constraints imposed by the railway infras-
tructure and the time constraints imposed by the ini-
tial schedule.
The revised model solves all conflicts that arise
along the railway line after the occurrence of the
disturbance; the heuristic algorithm is therefore no
longer applied. The rescheduled timetable is estab-
lished in a shorter time, then discomfort for passen-
gers is restricted and the quality of the transport ser-
vice is increased.
To show its effectiveness, we study the problem
in a particular section of a railway network located in
Southern Italy, see (FSE - Ferroviedel Sud Est, 2013).
The FSE network is constituted by single tracks with
few double track segments and in some stations only
one train can stop or pass through.
The paper is organized as follows. In Section 2 we
present the problem formalization. In Section 3 the
mathematical model for the resolution of the problem
is proposed. In section 4 we present the application
of the model to the case study of the FSE railway net-
work. Finally, Section 5 contains some concluding
remarks and suggestions for further research.
2 PROBLEM FORMALIZATION
2.1 Initial Scheduling
Definition 1 (Railway Network). A railway network
is defined by a set of segments on which trains runs.
Segment (b
i
): A segment b is a railway section
between two points. We define by B =
{b
1
, b
2
, . . . , b
B
} = {b
i
}
i∈[[1,B]]
the set of segments.
B denote the cardinality of the set B. The set of
segments is partitioned into the subset B
s
corre-
sponding to segments into a station, and B
c
corre-
sponding to the subset of rail connections outside
stations.
Track (v
j
): Let b be a segment ∈ B. We define by
V
b
= {v
b
1
, v
b
2
, . . . v
b
V
b
} = {v
b
j
}
j∈[[1,V
b
]]
the set of par-
allel tracks in b. The set of all tracks in the railway
network is denoted by V. V and V
b
denote respec-
tively the cardinality of V and V
b
for a given seg-
ment b. Given a track v ∈ V, we denote by b
v
its
corresponding segment.
Circulations in a railway network are defined by a
set of trains. Train’s path is made of an ordered set of
movements.
Definition 2 (Trains and Movements). We assume
that the train’s length is compatible with the length
of all tracks that compose the railway line. Trains are
thus defined as follows.
Train (t
k
): The set of trains using the railway
network is denoted as T = {t
1
,t
2
, . . . , t
T
} =
{t
k
}
k∈[[1,T]]
. T denotes the cardinality of T.
Train Direction (d
t
): Each train is defined by a di-
rection parameter expressing the position of its
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
140

destination station. Let t be a train ∈ T. We de-
note by d
t
= 0 the direction of a train which head
goes to the north (a.k.a. “even trains”) of the rail-
way line, and d
t
= 1 of a train running to the south
(a.k.a. “odd trains”).
Movement (µ
p
): A movement indicates the request
for a track by a train. Let t be a train ∈ T. We de-
fine by M
t
= {µ
t
1
, µ
t
2
, . . . , µ
t
M
t
} = {µ
t
p
}
p∈[[1,M
t
]]
the
ordered set of movements of train t. M
t
denotes
the cardinality of M
t
. µ
t
first
= µ
t
1
and µ
t
last
= µ
t
M
t
denote respectively the first and the last element
in M
t
. We define by M the set of all movements
on the railway line and by M
last
the set of the last
movements of each train.
Train movements are defined by several parameters.
Movement Direction: All movements µ of a train t
share the same direction as their train, denoted as
d
µ
:
∀t ∈ T, ∀µ ∈ M
t
, d
µ
= d
t
(1)
Track and Segment of a movement (b
µ
, v
µ
): Each
movement µ of a train is scheduled in an unique
segment b
µ
∈ B. We denote by M
b
the set of
movements scheduled in the same segment b ∈ B.
Each movement µ ∈ M must be scheduled in a
track of the segment b
µ
, denoted as v
µ
, according
to the following constraint:
∀t ∈ T, ∀µ ∈ M
t
, v
µ
∈ V
b
µ
(2)
Reference Schedule Times (α
ref
µ
, δ
ref
µ
, γ
ref
µ
): Each
train movement µ is associated to reference times
corresponding to its initial schedule. Let t ∈ T
be a train and µ ∈ M
t
one of its movements.
We define three reference times α
ref
µ
, δ
ref
µ
, γ
ref
µ
∈ N,
where:
- α
ref
µ
is the starting time of µ as established in the
initial schedule, expressed in minutes taking as
reference a time T
0
∈ N.
- δ
ref
µ
is the duration of µ (expressed in minutes)
if it occurs in a rail connection, i.e. the mini-
mum running time defined in the initial sched-
ule. This quantity is equal to 0 if the movement
occurs in a station. Formally:
∀t ∈ T, ∀µ ∈ M
t
, b
µ
∈ B
s
⇒ δ
ref
µ
= 0 (3)
- γ
ref
µ
is the duration of a movement µ (in minutes)
if it occurs in a station, i.e. the minimum stop-
ping time defined in the initial schedule. This
quantity is equal to 0 is the movement occurs in
a rail connection. Formally:
∀t ∈ T, ∀µ ∈ M
t
, b
µ
∈ B
c
⇒ γ
ref
µ
= 0 (4)
Using such notations, the time interval during
which a movement µ reserves its track can be ex-
pressed as [[α
ref
µ
, α
ref
µ
+δ
ref
µ
+γ
ref
µ
= β
ref
µ
]]. Two con-
secutive movements must be scheduled according
to these intervals, thus we have:
∀t ∈ T, ∀p ∈ [[1, M
t
[[, (5)
α
ref
µ
p+1
= α
ref
µ
p
+ δ
ref
µ
p
+ γ
ref
µ
p
In order to reduce the size of the initial problem we
could use only one variable ζ = γ + δ to represent
movements duration. However, even if such formu-
lation would reduce the number of initial variables,
the size of the problem after the presolve phase would
remain unchanged, since modern solvers are able to
detect such redundant variables. For clarity, we de-
cided thus to keep using two different variables γ and
δ to represent movementduration respectively in a rail
connection and in a station.
Definition 3 (Security Constraints). Since several
trains run at the same time on a railway network, sev-
eral constraints must be verified to ensure the security
of circulations.
Track Occupation Constraints: A track cannot be
occupied by two trains at the same time. Such re-
striction can be expressed formally by constrain-
ing any pair of movements using the same track to
be scheduled on disjoint timing intervals:
∀t
1
,t
2
∈ T, ∀µ
i
∈ M
t
1
, ∀µ
j
∈ M
t
2
,
v
µ
i
= v
µ
j
⇒ [[α
ref
µ
i
, β
ref
µ
i
]] ∩ [[α
ref
µ
j
, β
ref
µ
j
]] = ∅ (6)
Safety Times (∆
m
, ∆
f
): The safety time is the sepa-
ration time that has to elapse between two move-
ments µ
i
, µ
j
on the same track (i.e. between a
train leaving one track and another one entering
the same track). We denote by ∆
m
∈ N the safety
time required if trains meet and ∆
f
∈ N if one
train is following the other one. ∆
m
and ∆
f
are
expressed in the same time units as γ
ref
and δ
ref
.
These time delays must occur between the end of
the first movement (denoted as β
ref
µ
i
) and the start
of the otherone (denoted as α
ref
µ
j
). Formally, safety
time constraints can be expressed as follows:
∀b ∈ B, ∀µ
i
, µ
j
∈ M
b
v
µ
i
= v
µ
j
∧ d
µ
i
= d
µ
j
⇒
(
α
ref
µ
j
≥ β
ref
µ
i
+ ∆
f
∨ α
ref
µ
i
≥ β
ref
µ
j
+ ∆
f
(7)
v
µ
i
= v
µ
j
∧ d
µ
i
6= d
µ
j
⇒
(
α
ref
µ
j
≥ β
ref
µ
i
+ ∆
m
∨ α
ref
µ
i
≥ β
ref
µ
j
+ ∆
m
(8)
ARevisitedModelfortheRealTimeTrafficManagement
141
Note such constraints renforce the constraint (6)
since they induce a separation delay between the
time intervals of two movements on the same
track.
A rail transport service on a railway line is graph-
ically represented by a cartesian graph, representing
the safety constraints.
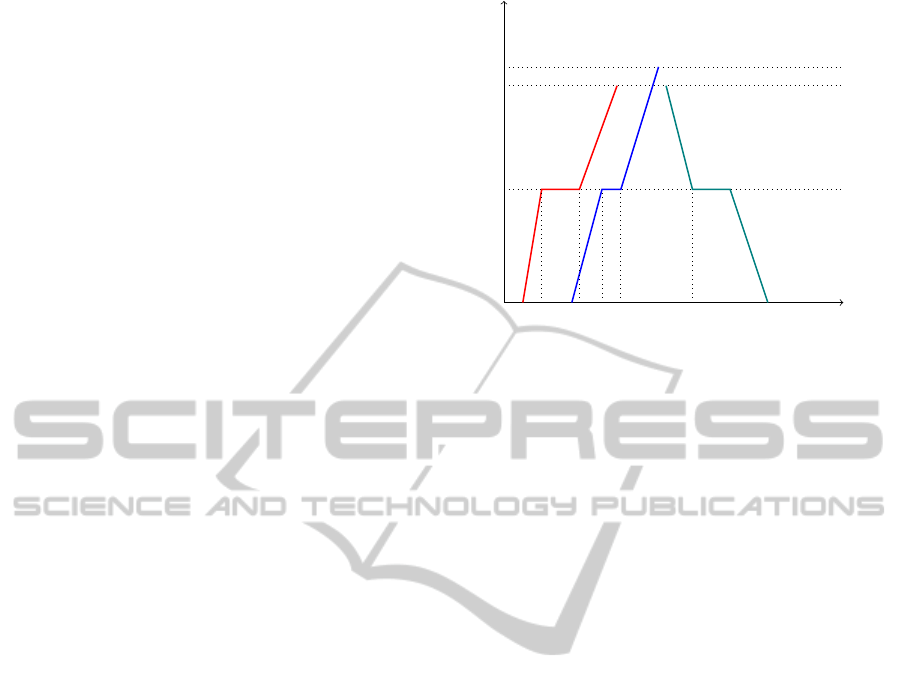
Graphic Timetable: The graphic timetable is a
cartesian graph that represents the situation of a
railway schedule for a day, see (Vicuna, 1989).
The diagram shows all movements, scheduled and
safety times.
The time line is plotted on the x axis. The rail-
way line (space) is plotted on the y axis. Inside
stations, tracks are represented by dashed lines
parallel to the x axis. Trains are represented by
an oblique broken line which orientation indicates
train direction. For instance, train lines are ori-
ented from bottom to up for even trains that travel
from south to north (i.e. to the station on the upper
end of the y axis).
Figure 1 represents the graphic timetable of three
trains t
1
, t
2
and t
4
. Train t
1
is directed to the
South, while t
2
and t
4
travel in the opposite di-
rection. The railway line is made of 5 segments:
single-tracked stations b
1
and b
3
, double-tracked
station b
5
and single-tracked rail connections b
2
and b
4
. Track sets for the five segments are de-
fined by: V
b
1
= {v
1
}, V
b
2
= {v
1
}, V
b
3
= {v
1
, v
2
},
V
b
4
= {v
1
}, V
b
5
= {v
1
}. Train’s paths are defined
by sets: M
t
1
= (µ
t
1
1
, µ
t
1
2
, µ
t
1
3
), M
t
2
= (µ
t
2
1
, µ
t
2
2
, µ
t
2
3
),
M
t
4
= (µ
t
4
1
, µ
t
4
2
, µ
t
4
3
). All trains cross station b
3
that
is single-tracked. As shown, safety times are ap-
plied when two trains occupy the same track of a
segment. ∆
f
is the safety time that has to elapse
between the end of the movement µ
t
2
2
and the be-
ginning of µ
t
4
2
, where t
2
and t
4
travel in the same
direction. ∆
m
is the safety time that has to elapse
between the end of µ
t
4
2
and the beginning of µ
t
1
2
,
where t
1
and t
4
travel in opposite direction.
2.2 Disturbances Issues
When a disturbance occurs along the railway net-
work, that compromises the normal traffic operation,
a rescheduling process must be accomplished taking
into account time constraints imposed by the initial
schedule.
Definition 4 (Disturbance). A disturbance denotes
the deviation of a train t
d
∈ T from its original sched-
ule due to an unforeseen situation, concerning one of
its movements µ
d
∈ M
t
d
.
t
2
t
4
t
1
time
Segment
b
1
b
2
b
3
b
4
b
5
µ
t
2
1
µ
t
2
2
µ
t
2
3
µ
t
4
1
µ
t
4
2
µ
t
4
3
µ
t
1
1
µ
t
1
2
µ
t
1
3
α
ref
µ
t
2
1
β
ref
µ
t
2
1
∆
m
∆
f
Figure 1: Graphic Timetable.
Disturbance Duration and Reference Time:
When a disturbance occurs, a disturbance refer-
ence time T
d
is defined as the first time on which
the disturbance has an impact on the schedule of
the others trains, i.e. the reference ending time of
the disturbed movement. If only one disturbance
affects one movement µ
t
d
d
∈ M
t
d
of a train t
d
along
the railway line, T
d
is defined as:
T
d
= β
ref
µ
d
We denote by ∆
d
the disturbance duration ex-
pressed in minutes. The impact of a disturbance
on the movement is expressed by an increase of
the value of parameter δ or γ depending on the na-
ture of the segment on which the disturbance oc-
curs. For instance, if b
µ
d
∈ B
c
, δ
′
µ
d
= δ
ref
µ
d
+ ∆
d
.
Conversely, if b
µ
d
∈ B
s
, γ
′
µ
d
= γ
ref
µ
d
+ ∆
d
.
If two independent disturbances affect two differ-
ent trains along the line, T
d
is defined as the mini-
mum final time of movements affected by the per-
turbation. Let t
d
1
and t
d
2
be two trains affected by
the disturbance. Let µ
d
1
∈ M
t
d
1
and µ
d
2
∈ M
t
d
2
be
the perturbed movements. T
d
is defined as:
T
d
= min
n
β
ref
µ
d
1
, β
ref
µ
d
2
o
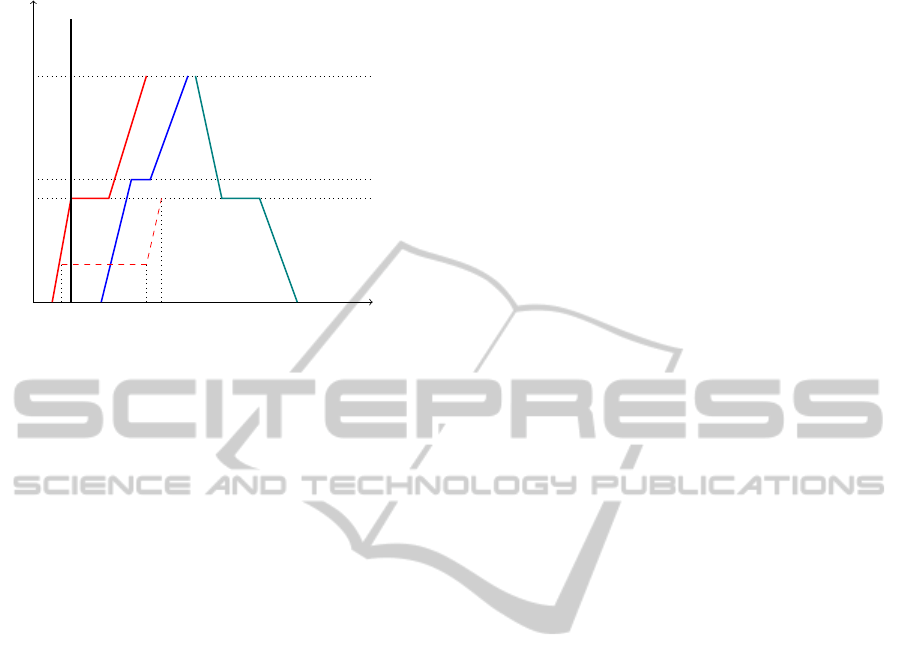
Figure 2 represents a railway line made of three
station (b
1
, b
3
and b
5
) and two single-tracked rail
connections (b
2
and b
4
). A disturbance occurs in
b
2
and affects only the movement µ
t
2
1
∈ M
t
2
. Ref-
erence time T
d
coincides with β
ref
µ
t
2
1
. The dashed
line shows the movement µ
t
2
1
after the end of the
rescheduling process. The recheduled crossing
time δ
ef f
µ
t
2
1
is equal to the reference time δ
ref
µ
t
2
1
in-
creased by the disturbance duration ∆
d
. The ef-
fective path of movement µ
t
2
1
interferes with the
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
142
t
2
t
4
t
1
time
Segment
b
1
b
2
b
3
b
4
b
5
µ
t
2
1
µ
t
2
2
µ
t
2
3
α
ref
µ
t
2
1
T
d
≡ β
ref
µ
t
2
1
β
eff
µ
t
2
1
∆
d
Figure 2: Disturbance of t
2
.
path of another movement in the segment b
2
that
has to be rescheduled.
Effective Schedule Times: In order to take into ac-
count the effect of the disturbance on the subse-
quent movements on the railway network, we in-
troduce for any movement its effective scheduled
times denoted by α
eff
, δ
eff
and γ
eff
∈ N. Obviously,
movements which final date β is scheduled before
T
d
are not altered. Formally:
∀t ∈ T, ∀µ ∈ M
t
s.t.β
ref
µ
≤ T
d
,
α
eff
µ
= α
ref
µ
δ
eff
µ
= δ
ref
µ
γ
eff
µ
= γ
ref
µ
(9)
Effective Time Constraints: These new scheduled
times must allow to absorb the perturbation by
delaying the initial reference times, according to
their respective segment types, following con-
straints (3) and (4). Formally, these previous
equations become:
∀t ∈ T, ∀µ ∈ M
t
s.t.β
ref
µ
> T
d
,
b
µ
∈ B
s
⇒
α
eff
µ
≥ α
ref
µ
δ
eff
µ
= δ
ref
µ
= 0
γ
eff
µ
≥ γ
ref
µ
(10)
b
µ
∈ B
c
⇒
α
eff
µ
≥ α
ref
µ
δ
eff
µ
≥ δ
ref
µ
γ
eff
µ
= γ
ref
µ
= 0
(11)
Effective schedule time must also obviously fol-
low the sequencing constraint (5) and safety con-
straints (6), (7) and (8).
Time Horizon (H): The time horizon H is the term
planning in which the rescheduling operations are
carried out. It consists of a given number of
timetable minutes in which a given number of
trains are scheduled on the railway line. Move-
ments after the time horizon are not taken into ac-
count in the rescheduling process, even if they be-
long to trains of which first movements belong to
the time horizon.
Of course, depending on the density of traffic at
the time of the disturbance, and its duration, the num-
ber of disturbed movements can vary considerably.
In this paper, we consider all the scheduled move-
ments of the day but one of our objective functions
can be designed to minimize the number of resched-
uled trains.
In the following section, we present the Mixed In-
teger Linear Programming Model that allows to solve
the rescheduling problem, i.e. to give a value to each
effective scheduled time while respecting the safety
constraints and optimizing practical criteria.
3 MATHEMATICAL MODELING
3.1 Decision Variables
We introduce additional variables and constants used
to express the problem in a linear way.
- X
µ,v
∈ {0, 1}
M×V
is the variable that identifies the
track v on which a movement µ occurs. X
µ,v
=
ϕ(v = v
µ
) where the function ϕ(C) is the indica-
tor ϕ(C) = 1 if the condition C is verified, 0 oth-
erwise.
- X
before
µ
i
,µ
j
∈ {0, 1}
M×M
is the variable that charac-
terizes the chronological order of two movements
µ
i
, µ
j
if they use the same segment. X
before
µ
i
,µ
j
=
ϕ(µ
i
is scheduled before µ
j
).
- X
delay
t
∈ {0, 1}
T
is the variable that specify if a
train t deviates from its original schedule and is
therefore delayed. X
delay
t
= ϕ(β
ef f
> β
ref
).
- X
delay
µ
∈ {0, 1}
T
is the variable that specify if a
movement µ deviates from its original schedule
and is therefore delayed. X
delay
µ
= ϕ(β
ef f
> β
ref
).
- B ∈ N is a sufficiently large positive constant.
- H ∈ N is a parameter that defines the size of the
time horizon.
By definition, the previous decisions variables are
subject to constraints characterizing their physical
sense.
• Any movement can only be scheduled on one
track of its segment, consequently:
∀µ ∈ M,
∑
v∈V
b
µ
X
µ,v
= 1 (12)
ARevisitedModelfortheRealTimeTrafficManagement
143

• Two movements scheduled on the same segment
must be ordered:
∀b ∈ B, ∀µ
i
, µ
j
∈ M
b
, (13)
X
before
µ
i
,µ
j
+ X
before
µ
j
,µ
i
= 1
Safety constraints presented above must be ex-
pressed using those variables in linear way.
3.2 Linearization of Safety Constraints
Security constraints (6), (7) and (8) are expressed
through the use of additional variables and constraints
in order to obtain a linear formulation.
3.2.1 Tracks Occupation Constraints
Constraint (6) specifies that a track v cannot be oc-
cupied by several movements at the same time. Con-
straints (7) and (8) express a separation delay must
elapse between two movements occupying the same
track. These conditions can be expressed by the fol-
lowing equations:
∀b ∈ B, ∀µ
i
, µ
j
∈ M
b
s.t. d
µ
i
= d
µ
j
, ∀v ∈ V
b
, (14)
β
eff
µ
i
− α
eff
µ
j
+ ∆
f
≤ B·
3− X
before
µ
i
,µ
j
− X
µ
i
,v
− X
µ
j
,v
∀b ∈ B, ∀µ
i
, µ
j
∈ M
b
s.t. d
µ
i
6= d
µ
j
, ∀v ∈ V
b
, (15)
β
eff
µ
i
− α
eff
µ
j
+ ∆
m
≤ B·
3− X
before
µ
i
,µ
j
− X
µ
i
,v
− X
µ
j
,v
Note for any pair of movements µ
i
, µ
j
, two in-
stances of the previous equations (14) and (15) are
considered in the mathematical model depending of
the the order of movements: (µ
i
, µ
j
) or (µ
j
, µ
i
).
The previous equation expresses that if two move-
ments µ
i
, µ
j
occurs on the same track, and if X
before
µ
i
,µ
j
=
1, then µ
i
must end before the start of µ
j
. If X
before
µ
i
,µ
j
= 0
or µ
i
and µ
j
do not occur in the same track, equation
(14) and (15) are trivially verified.
The disjunction operator ∨ in equations(7) and (8)
is taken into account by the boolean variable X
before
µ
i
,µ
j
that denotes the two possible alternatives.
3.3 Objective Functions
The optimization problem compares four alternative
objective functions defined as follows:
Obj
1
:min
∑
µ
i
∈M
(β
eff
µ
i
− β
ref
µ
i
) (16)
Obj
2
:min
∑
µ
i
∈M
last
(β
eff
µ
i
− β
ref
µ
i
) (17)
Obj
3
:min
∑
t∈T
X
t
delay
(18)
Obj
4
:min
∑
µ∈M
X
µ
delay
(19)
- Obj
1
minimizes the delay of the traffic (i.e. the
sum of the delays of all the movements trains in
the railway line).
- Obj
2
minimizes the total final delay of the traffic
(i.e. the final delays when trains arrive at their
final destination, or rather the last stop considered
within the rescheduling time horizon).
- Obj
3
minimizes the number of delayed trains.
- Obj
4
minimizes the number of delayed move-
ments for each train.
When Obj
3
or Obj
4
is used, we introduced five
additional constraints (20) to (24) as follows:
∀t ∈ T, β
eff
µ
t
last
− β
ref
µ
t
last
≤ B· X
t
delay
(20)
∀t ∈ T, β
eff
µ
t
last
− β
ref
µ
t
last
> 1+ B·
X
t
delay
− 1
(21)
∀t ∈ T, ∀µ ∈ M
t
⇒ α
eff
µ
≤ H (22)
∀t ∈ T, ∀µ ∈ M
t
⇒ δ
eff
µ
≤ H (23)
∀t ∈ T, ∀µ ∈ M
t
⇒ γ
eff
µ
≤ H (24)
Constraints (20) and (21) specify that if the
rescheduled ending time of the train coincides with its
reference time, the train is not delayed and X
t
delay
= 0.
Conversly, if one movement of a train is delayed,
the last movement is necessarily delayed according
to equations (10), (11) and equation (21) implies that
X
t
delay
= 1.
Constraints (22), (23) and (24) mean that move-
ments scheduled in the analyzed time horizon, after
the rescheduling process must start within the same
time horizon. This constraint prevents that the trains
are postponed for a long time or even suppressed by
moving outside the considered time horizon.
When Obj
4
is used, constraints (20) (resp. (21))
are replaced by constraints (25) (respectively (26))
that refers to all movements on the line.
∀µ ∈ M, β
eff
µ
− β
ref
µ
≤ B· X
t
delay
(25)
∀µ ∈ M, β
eff
µ
− β
ref
µ
> 1+ B·
X
t
delay
− 1
(26)
The full model is given in Figure 3.
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
144

Let (B, V) be a railway network, T a set of trains with their schedules and (µ
d
, ∆
d
, T
d
) the characteristics of a disturbance
occuring on the system. The mixed integer linear programming model MILP is defined by:
Obj
1
Minimize
∑
µ∈M
β
eff
µ
− β
ref
µ
(27)
Obj
2
Minimize
∑
µ∈M
last
β
eff
µ
− β
ref
µ
(28)
Obj
3
Minimize
∑
t∈T
X
delay
t
(29)
Obj
4
Minimize
∑
µ∈M
X
delay
µ
(30)
Subject to:
∀t ∈ T, ∀µ ∈ M
t
s.t. b
µ
∈ B
s
, δ
eff
µ
= 0 (31)
∀t ∈ T, ∀µ ∈ M
t
s.t. b
µ
∈ B
c
γ
eff
µ
= 0 (32)
∀t ∈ T, ∀p ∈ [[1, M
t
[[, α
eff
µ
p+1
− α
eff
µ
p
− δ
eff
µ
p
− γ
eff
µ
p
= 0 (33)
∀t ∈ T, ∀µ ∈ M
t
s.t. β
ref
µ
≤ T
d
, α
eff
µ
= α
ref
µ
(34)
∀t ∈ T, ∀µ ∈ M
t
s.t. β
ref
µ
≤ T
d
, δ
eff
µ
= δ
ref
µ
(35)
∀t ∈ T, ∀µ ∈ M
t
s.t. β
ref
µ
≤ T
d
, γ
eff
µ
= γ
ref
µ
(36)
∀t ∈ T, ∀µ ∈ M
t
s.t. β
ref
µ
> T
d
and b
µ
∈ B
s
, α
eff
µ
≥ α
ref
µ
(37)
∀t ∈ T, ∀µ ∈ M
t
s.t. β
ref
µ
> T
d
and b
µ
∈ B
s
, δ
eff
µ
= δ
ref
µ
(= 0) (38)
∀t ∈ T, ∀µ ∈ M
t
s.t. β
ref
µ
> T
d
and b
µ
∈ B
s
, γ
eff
µ
≥ γ
ref
µ
(39)
∀t ∈ T, ∀ µ ∈ M
t
s.t. β
ref
µ
> T
d
and b
µ
∈ B
c
, α
eff
µ
≥ α
ref
µ
(40)
∀t ∈ T, ∀ µ ∈ M
t
s.t. β
ref
µ
> T
d
and b
µ
∈ B
c
, δ
eff
µ
≥ δ
ref
µ
(41)
∀t ∈ T, ∀ µ ∈ M
t
s.t. β
ref
µ
> T
d
and b
µ
∈ B
c
, γ
eff
µ
= γ
ref
µ
(= 0) (42)
γ
eff
µ
d
= γ
ref
µ
d
+ ∆
d
(43)
δ
eff
µ
d
= δ
ref
µ
d
+ ∆
d
(44)
∀µ ∈ M,
∑
v∈V
b
µ
X
µ,v
= 1 (45)
∀b ∈ B, ∀µ
i
, µ
j
∈ M
b
, X
before
µ
i
,µ
j
+ X
before
µ
j
,µ
i
= 1 (46)
∀b ∈ B,∀µ
i
, µ
j
∈ M
b
, s.t. d
µ
i
= d
µ
j
, ∀v ∈ V
b
, β
eff
µ
i
− α
eff
µ
j
+ B·
X
before
µ
i
,µ
j
+ X
µ
i
,v
+ X
µ
j
,v
≤3· B− ∆
f
(47)
∀b ∈ B,∀µ
i
, µ
j
∈ M
b
, s.t. d
µ
i
6= d
µ
j
, ∀v ∈ V
b
, β
eff
µ
i
− α
eff
µ
j
+ B·
X
before
µ
i
,µ
j
+ X
µ
i
,v
+ X
µ
j
,v
≤3· B− ∆
m
(48)
∀t ∈ T, β
eff
µ
t
last
− B·X
t
delay
≤ β
ref
µ
t
last
(49)
∀t ∈ T, β
eff
µ
t
last
− B·X
t
delay
> β
ref
µ
t
last
− B (50)
∀µ ∈ M, β
eff
µ
− B·X
t
delay
≤ β
ref
µ
(51)
∀µ ∈ M, β
eff
µ
− B·X
t
delay
> β
ref
µ
− B (52)
∀t ∈ T, ∀µ ∈ M
t
, α
eff
µ
≤ H (53)
∀t ∈ T, ∀µ ∈ M
t
, δ
eff
µ
≤ H (54)
∀t ∈ T, ∀µ ∈ M
t
, γ
eff
µ
≤ H (55)
Figure 3: Mixed Integer Linear Programming Model.
Constraints (31) - (32) express that if a movement
occurs in a station (resp. in a rail connaction) the ef-
fective running time (res. the effective stopping time)
is null.
Constraint (33) specifies that each train movement
is directly succeeded by the next one, that means that
when a train leaves a track, it instantly begins to oc-
cupy the next one.
Constraints (34), (35) and (36) ensure that move-
ments scheduled completely before the occurrence of
the disturbance remain unchanged.
Constraints (37) to (39) (resp.(40) to (42)) enforce
the restrictions related to planned stops (respectively
to planned running times) and the consequent earliest
ARevisitedModelfortheRealTimeTrafficManagement
145
possible departure time.
Constraint (43) (resp. (44)) means that the run-
ning time of perturbed movements (respectively the
stopping time) is increased according to disturbance
duration.
Constraint (45) means that each movement has to
use exactly one track of its segment.
Constraint (46) implies that two movements
scheduled on the same segment must be ordered.
Constraints (47) - (48) mean that if several move-
ments have to use the same track of a segment, a
safety time (∆
f
or ∆
m
) must elapse between the end
of the first movement and the beginning of the second
one.
Constraints (49)-(50) (resp. (51)- (52)) denote if
a train (respectively a movement) is delayed. Con-
straints (53) to (55) enforce the beginning and the du-
ration of a movement within the time horizon. These
constraints are active only when Obj
3
(respectively
Obj
4
) is applied.
4 NUMERICAL EXPERIMENTS
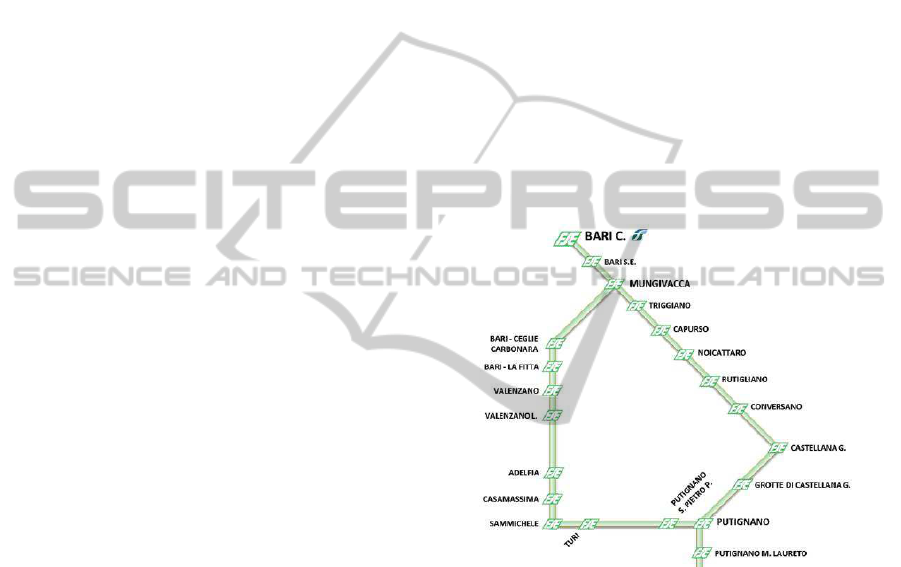
The presented model is applied to Ferrovie del Sud
Est (FSE), the largest public transport company op-
erating in the Apulia region of Southern Italy. We
analyze the railway ring connecting Mungivacca and
Putignano stations (Figure 4), where a CTC system is
installed. The operation system is installed in Mun-
givacca station that is independent, not controlled by
the CTC, as is Putignano, whereby these stations are
not studied here. In particular, we refer to the line
1 of the railway ring – passing through Conversano
– that is single tracked except for the line connect-
ing Noicattaro to Rutigliano, that is double tracked.
Moreover, Grotte di Castellana is a single track sta-
tion, not chaired by an operator. 24 even trains and 22
odd trains run on the railway line during a day. We as-
sume a safety time ∆
m
= 3 min for two trains traveling
in opposite directions and a time ∆
f
= 1 min for trains
in the same direction. In attempt to evaluate the op-
timality of the algorithm, we used IBM CPLEX 12.5
installed and run on an Intel Core 2 Duo 1.83 GHz
CPU and 3 GB RAM, under Windows with the model
formulated in AMPL.
4.1 One Disturbance on the Line
We consider a real data set referring to a train going
from Putignano to Mungivacca that stops along the
line that connects Castellana G. and Conversano due
to a disturbance occurring at 7:50 am. That same dis-
turbance event is used for all the experiments but with
different disturbance sizes ∆
d
and solved with differ-
ent time horizons H. Various disturbance times are
been considered, ranging from 10 to 50 minutes. A
time horizon of H minutes means that movementsthat
should have started (according to the initial timetable)
H minutes or more after the instant at which the dis-
turbance occurs are not considered in the computa-
tion. Time horizons are expressed in minutes and
take values equal to 30, 60, 90, 120, 180, 240, 300,
360, 420, 480, 540, 600 and 1440. The main aspects
considered to present results are Obj
1
, Obj
2
, Obj
3
,
Obj
4
that correspond respectively to sum of delays
for all train movements, delay of the last movement
of each train, number of rescheduled trains and num-
ber of rescheduled movements. All operational times
are given in minutes. CT refers to computational time
given in seconds. N and V refers to number of vari-
ables and constraints before and after the presolve
phase.
Figure 4: Ther railway ring used for the scenarios.
4.1.1 Overall Analysis
When only one disturbance occurs on the railway
line, results from experiments using the four objec-
tive functions for all different disturbance size (∆
d
)
and time horizons (H) are presented in Table 5.
The methodology is applied to a real case study in
which the occurence of short-term disturbance on the
railway line is frequent, this is not a trivial problem.
The model provides a proactive approach to solve, in
real time, problems that occur on the railway line.
The computational time (CT) for all time horizons
and disturbance sizes is of the order of a few sec-
ond. Comparison between different time horizons is
done in order to demonstrate that the model is able to
quickly solve even considerables problems that take
into account all trains on the railway line. In fact,
the highest value of CT (equal to 69.77 seconds) is
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
146

obtained using Ob j
1
for H = 1440 and ∆
d
= 45 min-
utes. This means that if a disturbance lasting 45 min-
utes occurs along the line, in just over a minute the
train dispatcher can obtain the rescheduled timetable
for the 24 hours following the occurrence of the fault.
The speed of resolution is a very important factor for
the presented problem, since the main objective of the
real-time traffic management is to quickly establish
a new timetable, in order to minimize the inconve-
nience for passengers.
Compared to the previous methodology used in
(Dotoli et al., 2013) there is an improvement due to a
reduction of total delay, number of rescheduled trains
and computational time. The objective of this model
is the minimization of delay of all movements. In Ta-
ble 1 we compare results of the rescheduling process
obtained with the application of the actual and the
previous methodology (AM, PM) when ∆
d
= 30 min-
utes and H = 180 minutes. We noticed that Ob j
1
is
unchanged for all subsequent values of time horizon.
This means that the delay caused by the disturbance is
absorbed within the 180 minutes after its occurrence.
For the previous methodology, we present values ob-
tained for H = 30 minutes in addition to values ob-
tained with the application of the heuristic algorithm
after the time horizon. CT refers only at the optimiza-
tion procedure.
By analyzing values we observe that with the
actual methodology the new timetable is computed
in 0.72 seconds. Three trains are involved in the
rescheduling process for a total delay of 608 minutes.
Previous methodology required 10.74 seconds to ob-
tain the new timetable within a 30 minutes window
after the occurrence of the fault. 10 trains are involved
in the rescheduling process and total delay is equal to
665 minutes. Actual methodology allows to obtain
the optimal solution with an exact approach, with-
out the application of the heuristic algorithm which
does not always provide optimal results. We should
also take into account that solvers used by the two
methodology are different. MATLAB with GLPK
used by the previous methodologyis replaced by IBM
CPLEX in the actual one. Resolution methods used
by the two solvers are different as well as their per-
formance. The previous methodology has obtained an
improvement compared to the current practice used
by the train dispatcher; the actual methodology pro-
vides a further amelioration. This is in line with ob-
jectives of the real-time traffic management.
4.1.2 Comparison between Objective Functions
We compare values obtained using the four objective
functions for H = 1440 and ∆
d
= 50 minutes, shown
in Table 2. We analyze the time horizon of 1440 min-
utes because the complexity of the problem is high
due to the presence, in the rescheduling process, of
all trains movements on the railway line until the end
of the day.
Lowest values in terms of total delay are obtained
using Obj
1
. Comparing results obtained with the first
and the second objective function we notice that al-
though the value of Obj
2
is the same, Obj
1
changes.
In particular, Obj
1
obtained while Obj
2
is greater.
The reason is simple: in this case, minimizing the
delay of the last movement of a train, the second ob-
jective function increases the number of its delayed
movements. This means that although values of Obj
3
are unchanged using the first and the second objec-
tive function, values of Obj
4
varies. In general, Obj
2
increases the arrival time at intermediate stations, in
order to minimize the delay at the last station of trains
path. In this case, there are no differences between
values of Obj
1
and Obj
2
obtained using Obj
3
and
Obj
4
. Extending the analysis to all time horizons, we
notice that in some cases (e.g. H = 180 and ∆
d
= 50
minutes) there is a difference between the two values,
due to the fact that these objective functions does not
take into account the exact dealy of trains. Thus, any
solution showing the same number of delayed trains is
optimal, whatever the value of Ob j
1
and Obj
2
. Mul-
ticriteria objective functions should be used to obtain
an unique optimal solution. The minimization of the
number of delayed trains (respectively movements)
may imply an increase of the total delay of resched-
uled trains.
Extending the analysis to values obtained in all
time horizons (H) and for all disturbance size (∆
d
) we
notice that minimizing Obj
1
provides better results in
terms of Ob j
1
and Ob j
2
. Minimizing Obj
4
provides
better values in terms of Obj
3
and Obj
4
.
4.1.3 Impact of Constraints (22), (23) and (24)
In order to prove the necessity of constraints (22),
(23) and (24) when using Ob j
3
and Obj
4
, we present
a simple railway line made by 7 segments on which
circulate 5 trains, represented in Figure 5. Railway
line is made by 4 single-tracked connection segment
(b
1
,b
3
,b
5
and b
7
) between 3 double-tracked stations
(b
2
, b
4
and b
6
). Trains t
1
and t
3
are directed to the
South, while t
2
, t
4
and t
6
travel in the opposite direc-
tion.
Table 1: Comparison between actual and previous method-
ology.
Obj
1
Obj
3
CT
Our Methodology 608 3 0.72
Dotoli et al. 665 10 10.74
ARevisitedModelfortheRealTimeTrafficManagement
147
Table 4: Two independent disturbances.
FirstDisturbance SecondDisturbance TwoDisturbances Sum
Obj
1
Obj
2
Obj
3
Obj
4
CT
Obj
1
Obj
2
Obj
3
Obj
4
CT
Obj
1
Obj
2
Obj
3
Obj
4
CT
Obj
1
Obj
2
Obj
3
Obj
4
CT
Obj
1
516 61 1 9 13.43 308 61 3 26 17.98 824 122 4 35 31.41 824 122 4 36 17.95
Obj
2
516 61 1 9 11.95 308 61 3 26 17.63 824 122 4 35 29.58 826 122 4 36 19.83
Obj
3
516 61 1 9 9.08 336 71 1 5 9.81 852 132 2 14 18.89 871 132 2 14 9.16
Obj
4
516 61 1 9 10.42 336 71 1 5 12.21 852 132 2 14 22.63 871 132 2 14 10.12
t
1
t
2
t
3
t
4
t
6
T
d
= 07 : 35
time
Segment
b
1
b
2
b
3
b
4
b
5
b
6
b
7
Figure 5: Disturbance of t
1
.
Table 2: Comparison between the four objective functions
with H = 1440 and ∆
d
= 50.
Obj
1
Obj
2
Obj
3
Obj
4
Obj
1
829 854 878 878
Obj
2
81 81 91 91
Obj
3
3 3 1 1
Obj
4
33 39 11 11
CT 30.07 16.86 6.56 26.18
Table 3: Results from experiments using Obj
3
without and
with additional constraints.
Obj
1
Obj
2
Obj
3
Obj
4
CT
WT 10040 10000 1 5 0.01
W 50 10 1 5 0.01
A disturbance occurs in the segment b
5
at 07:35
am and affects the train t
1
. We analyze a problem
with time horizon H = 25 minutes and a disturbance
size ∆
d
= 10 minutes. The same scenarios have been
solved without (WT) and with (W) the additional con-
straints using Obj
3
. Results are presented in Table 3.
By analyzing values of Ob j
1
and Obj
2
we notice
that despite the number of rescheduled trains is un-
changed, without the additional constraints the depar-
ture or the duration of some movements is delayed
for a long time. This means that minimizing Obj
3
tends to postpone movements of trains involved in the
rescheduling process at the end of the time horizon, in
order to affect the lowest number of trains on the line.
In the example, t
1
is the only delayed train. By in-
troducing additional constraints, values of Obj
1
(and
consequently Ob j
2
) are lower because the system is
forced to reschedule movements within the time hori-
zon. The number of rescheduled trains remains un-
changed.
4.2 Two Disturbances on the Line
When two independent disturbances occur on the rail-
way line, the rescheduling process of the first distur-
bance does not influence the rescheduling process of
the second one. We consider the same railway line
presented in Section 4 and we suppose that two in-
dependent disturbances occur at T
d
= 09 : 00 a.m.
respectively in the line that connects Rutigliano to
Conversano stations (segment b
9
) and Conversano to
Castellana G. (segment b
11
). We consider a time hori-
zon H = 1440 minutes and a disturbance size ∆
d
= 50
minutes.
First, we solve the problem considering only the
disturbance that occurs in the segment b
9
and that af-
fects a train directed from Putignano to Mungivacca
station.
Then, we solve the problem considering only the
disturbance that occurs in the segment b
11
and that
affects a train directed from Mungivacca to Putignano
station.
Finally, we solve the problem considering the two
disturbances at the same time. We compare results
with those given by the sum of values obtained solv-
ing the two problems separately.
Table 4 presents values of Obj
1
, Ob j
2
, Obj
3
,
Obj
4
and CT for the four scenarios.
By comparing values obtained from simultaneous
resolution with those obtained from the sum of in-
dividual resolutions of disturbances, i.e. values pre-
sented in the third and the fourth block of Table 4,
we notice that the simultaneous resolution provides
a better result in terms of computational time for all
objective functions. However, the the sum of individ-
ual resolutions provides an improvement in terms of
Obj
1
and Ob j
4
using the four objective functions. In
particular by applying Obj
1
, there is a reduction of
the number of rescheduled movements and by apply-
ing Obj
2
, there is also a reduction of total delay. By
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
148

Table 5: Results of analysis using Obj
1
, Obj
2
, Obj
3
and Obj
4
for all H and ∆
d
.
Tot. PrSlv ∆
d
= 10 ∆
d
= 15 ∆
d
= 20 ∆
d
= 25 ∆
d
= 30 ∆
d
= 35 ∆
d
= 40 ∆
d
= 45 ∆
d
= 50
H
#V
#C
#V
#C
Obj
Obj
1
Obj
2
Obj
3
Obj
4
CT
Obj
1
Obj
2
Obj
3
Obj
4
CT
Obj
1
Obj
2
Obj
3
Obj
4
CT
Obj
1
Obj
2
Obj
3
Obj
4
CT
Obj
1
Obj
2
Obj
3
Obj
4
CT
Obj
1
Obj
2
Obj
3
Obj
4
CT
Obj
1
Obj
2
Obj
3
Obj
4
CT
Obj
1
Obj
2
Obj
3
Obj
4
CT
Obj
1
Obj
2
Obj
3
Obj
4
CT
30 6316 6555 1957 1897 1 70 10 1 7 0.04 105 15 1 7 0.04 140 20 1 7 0.03 175 25 1 7 0.06 210 30 1 7 0.03 245 35 1 7 0.04 280 40 1 7 0.03 315 45 1 7 0.03 350 50 1 7 0.10
30 6316 6555 1172 1897 2 70 10 1 7 0.05 105 15 1 7 0.05 140 20 1 10 0.08 175 25 1 10 0.01 210 30 1 10 0.05 245 35 1 10 0.03 280 40 1 10 0.16 315 45 1 10 0.03 350 50 1 10 0.06
30 6316 7047 1960 1897 3 70 10 1 7 0.14 105 15 1 7 0.47 140 20 1 7 0.05 175 25 1 7 0.05 210 30 1 7 0.03 245 35 1 7 0.05 280 40 1 7 0.05 315 45 1 7 0.05 350 50 1 7 0.05
30 6472 7359 1972 1921 4 70 10 1 7 0.06 105 15 1 7 0.03 140 20 1 7 0.05 175 25 1 7 0.03 210 30 1 7 0.05 245 35 1 7 0.05 280 40 1 7 0.03 315 45 1 7 0.05 350 50 1 7 0.20
60 7636 8190 2675 2818 1 110 10 1 11 0.07 211 23 3 25 0.09 296 31 2 19 0.09 367 36 2 21 0.09 428 43 2 13 0.08 433 43 2 13 0.07 450 45 2 13 0.09 515 55 2 13 0.06 580 65 2 13 0.06
60 7636 8190 2675 2818 2 110 10 1 11 0.06 211 23 3 19 0.08 300 31 2 21 0.09 367 38 3 21 0.12 428 43 2 21 0.18 437 43 2 23 0.09 450 45 2 23 0.09 470 55 2 26 0.09 610 56 1 26 0.08
60 7636 8758 2678 2814 3 110 10 1 11 0.06 304 38 2 19 0.09 300 31 2 19 0.08 531 61 2 13 0.08 667 75 2 19 0.08 595 56 1 11 0.06 600 56 1 11 0.06 605 56 1 11 0.08 610 56 1 11 0.09
60 7816 9118 2690 2831 4 110 10 1 11 0.07 304 38 2 19 0.12 502 69 2 13 0.09 567 79 2 13 0.08 428 43 2 13 0.11 595 56 1 11 0.08 600 56 1 11 0.08 605 56 1 11 0.09 610 56 1 11 0.08
90 8920 10074 3401 3995 1 110 10 1 11 0.12 266 31 2 21 0.30 310 31 2 21 0.20 431 44 6 44 0.23 512 51 5 34 0.21 517 55 5 34 0.20 554 58 4 32 0.30 697 76 3 28 0.28 751 69 1 11 0.45
90 8920 10074 3401 3995 2 110 10 1 11 0.12 289 31 2 21 0.12 310 31 2 23 0.05 431 44 6 23 0.90 540 55 4 23 0.20 517 55 5 34 0.16 572 58 5 34 0.22 752 69 1 35 0.23 751 69 1 35 0.20
90 8920 10712 3380 3937 3 110 10 1 11 0.06 913 83 1 11 0.17 891 83 1 11 0.18 913 83 1 11 0.18 891 83 1 11 0.18 892 83 1 11 0.17 913 83 1 11 0.12 878 83 1 11 0.18 913 83 1 11 0.20
90 9122 11916 3436 4848 4 110 10 1 11 0.08 913 83 1 11 0.20 891 83 1 11 0.22 913 83 1 11 0.20 913 83 1 11 0.23 892 83 1 11 0.22 891 83 1 11 0.22 751 69 1 11 0.18 913 83 1 11 0.23
120 10519 12275 4345 5762 1 110 10 1 11 0.20 266 31 2 21 0.42 310 31 2 21 0.28 477 46 7 67 0.51 586 68 5 39 0.36 591 68 5 39 0.36 616 69 5 39 0.56 753 82 5 45 0.73 814 80 2 18 0.88
120 10519 12275 4345 5762 2 110 10 1 11 0.17 289 31 2 21 0.50 310 31 2 23 0.37 477 46 7 23 0.40 604 59 6 23 0.45 609 59 6 35 0.40 672 65 6 35 0.55 839 80 2 36 1.18 838 80 2 39 0.62
120 10519 12996 4192 5290 3 110 10 1 11 0.14 864 82 2 18 0.45 406 47 2 18 0.40 864 82 2 18 0.40 857 82 2 18 0.40 864 83 2 18 0.28 847 80 2 18 0.28 878 82 2 18 0.30 830 81 2 18 0.26
120 10748 13454 4279 5467 4 110 10 1 11 0.18 855 82 2 18 0.44 864 83 2 18 0.72 856 82 2 18 0.50 833 80 2 18 0.50 863 82 2 18 0.36 861 82 2 18 0.33 863 82 2 18 0.30 830 81 2 18 0.31
180 13051 16644 5925 9048 1 110 10 1 11 0.3 266 31 2 21 0.95 310 31 2 21 0.50 523 48 8 90 0.83 608 76 3 29 0.72 613 76 3 29 0.62 638 77 3 29 1.17 829 81 3 33 0.51 829 81 3 33 1.40
180 13051 16644 5925 9048 2 110 10 1 11 0.31 267 31 2 21 1.12 310 31 2 23 0.60 523 48 8 23 0.73 714 65 8 23 0.68 719 65 8 35 0.80 825 73 8 35 1.30 853 81 3 36 1.68 853 81 3 39 0.99
180 13051 17485 5916 9008 3 110 10 1 11 0.17 875 91 1 11 0.64 875 91 1 11 0.65 875 91 1 11 0.64 875 91 1 11 0.61 875 91 1 11 0.61 875 91 1 11 0.67 875 91 1 11 0.64 948 91 1 11 0.48
180 13318 18019 6037 9249 4 110 10 1 11 0.20 875 91 1 11 0.70 875 91 1 11 0.72 875 91 1 11 0.75 875 91 1 11 0.81 875 91 1 11 0.69 875 91 1 11 0.80 875 91 1 11 0.75 875 91 1 11 0.72
240 18149 21612 7721 13225 1 110 10 1 11 0.31 266 31 2 21 3.01 310 31 2 21 0.98 523 48 8 90 1.87 608 76 3 29 1.99 613 76 3 29 1.64 638 77 3 29 2.20 829 81 3 33 8.16 829 81 3 33 8.35
240 15804 43004 5376 24173 2 110 10 1 11 0.30 267 31 2 21 2.24 314 31 2 23 1.46 523 48 8 23 1.31 716 65 8 23 1.56 721 65 8 35 1.50 820 73 8 35 2.11 855 81 3 36 2.84 853 81 3 39 1.98
240 15804 22574 7684 13117 3 110 10 1 11 0.31 875 91 1 11 0.70 875 91 1 11 0.78 875 91 1 11 0.15 875 91 1 11 0.84 875 91 1 11 0.78 875 91 1 11 0.90 875 91 1 11 0.81 875 91 1 11 0.96
240 16110 23186 7844 13436 4 110 10 1 11 0.36 875 91 1 11 0.95 875 91 1 11 0.90 875 91 1 11 0.95 875 91 1 11 0.90 875 91 1 11 1.01 875 91 1 11 0.99 875 91 1 11 0.90 875 91 1 11 1.01
300 17528 25234 8889 16141 1 110 10 1 11 0.57 266 31 2 21 3.91 310 31 2 21 2.31 523 48 8 90 2.88 608 76 3 29 2.77 613 76 3 29 2.56 638 77 3 29 2.96 829 81 3 33 7.05 829 81 3 33 5.04
300 17528 25234 8889 16141 2 110 10 1 11 0.37 289 31 2 21 2.04 318 31 2 26 1.23 523 48 8 23 1.90 716 65 8 23 2.42 721 65 8 35 1.95 820 73 8 35 2.43 854 81 3 36 3.62 853 81 3 39 2.01
300 17528 26266 8892 16115 3 110 10 1 11 0.40 875 91 1 11 1.01 875 91 1 11 0.89 875 91 1 11 0.98 875 91 1 11 0.94 875 91 1 11 1.01 875 91 1 11 1.07 875 91 1 11 0.93 875 91 1 11 1.06
300 17856 26922 9074 16478 4 110 10 1 11 0.44 875 91 1 11 1.25 875 91 1 11 1.17 875 91 1 11 1.20 875 91 1 11 1.34 875 91 1 11 1.25 875 91 1 11 1.23 875 91 1 11 1.12 875 91 1 11 1.22
360 20240 30791 10762 20933 1 110 10 1 11 0.78 266 31 2 21 3.04 310 31 2 21 1.77 523 48 8 90 3.44 608 76 3 29 3.33 613 76 3 29 2.85 638 77 3 29 4.29 829 81 3 33 12.48 829 81 3 33 5.55
360 20240 30791 10762 20933 2 110 10 1 11 0.51 319 31 2 21 3.20 324 31 2 23 2.07 523 48 8 23 2.48 716 65 8 23 2.92 721 65 8 35 2.84 820 73 8 36 4.47 855 81 3 36 4.37 854 81 3 39 4.70
360 20240 31929 10575 20491 3 110 10 1 11 0.87 875 91 1 11 1.34 875 91 1 11 1.22 875 91 1 11 1.30 875 91 1 11 1.18 875 91 1 11 1.38 875 91 1 11 1.26 875 91 1 11 1.34 875 91 1 11 1.32
360 20602 32653 10791 20922 4 110 10 1 11 1.12 875 91 1 11 1.48 875 91 1 11 1.57 875 91 1 11 1.51 875 91 1 11 1.48 875 91 1 11 1.64 875 91 1 11 1.46 875 91 1 11 1.40 875 91 1 11 1.64
420 23226 37541 12889 26619 1 110 10 1 11 0.98 266 31 2 21 3.52 310 31 2 21 2.29 523 48 8 90 5.66 608 76 3 29 4.76 613 76 3 29 3.66 638 77 3 29 6.50 829 81 3 33 19.40 829 81 3 33 10.28
420 23226 37541 12889 26619 2 110 10 1 11 0.68 289 31 2 21 3.80 314 31 2 23 3.20 523 48 8 23 3.43 716 65 2 23 3.57 721 65 8 35 3.40 840 73 8 35 5.27 853 81 3 36 6.32 853 81 3 39 4.15
420 23226 38787 12892 26585 3 110 10 1 11 0.69 875 91 1 11 1.73 875 91 1 11 1.62 875 91 1 11 1.68 875 91 1 11 1.64 875 91 1 11 1.73 875 91 1 11 1.80 875 91 1 11 1.65 875 91 1 11 1.81
420 23622 39579 13142 27084 4 110 10 1 11 0.76 875 91 1 11 2.03 875 91 1 11 2.06 875 91 1 11 2.07 875 91 1 11 2.12 875 91 1 11 2.07 875 91 1 11 1.60 875 91 1 11 1.88 875 91 1 11 2.12
480 26152 44235 14868 32237 1 110 10 1 11 1.74 266 31 2 21 5.52 310 31 2 21 2.71 523 48 8 90 5.21 608 76 3 29 4.66 613 76 3 29 4.62 638 77 3 29 8.70 829 81 3 33 31.04 829 81 3 33 9.70
480 26152 44235 14868 32237 2 110 10 1 11 1.36 267 31 2 21 5.63 324 31 2 23 4.08 523 48 8 23 4.93 716 65 8 23 4.85 721 65 8 35 4.77 820 73 8 35 7.63 853 81 3 36 8.05 853 81 3 39 6.47
480 26152 45601 14729 31903 3 110 10 1 11 1.35 876 91 1 11 2.54 876 91 1 11 2.21 876 91 1 11 2.18 876 91 1 11 2.18 876 91 1 11 2.14 876 91 1 11 2.18 876 91 1 11 2.26 876 91 1 11 2.21
480 26586 46469 15017 32478 4 110 10 1 11 1.57 876 91 1 11 2.40 876 91 1 11 2.37 876 91 1 11 2.43 876 91 1 11 2.37 876 91 1 11 2.40 876 91 1 11 2.30 876 91 1 11 2.42 876 91 1 11 2.42
540 29808 53122 17727 40361 1 110 10 1 11 1.66 266 31 2 21 12.53 310 31 2 21 4.30 523 48 8 90 7.72 608 76 3 29 6.75 613 76 3 29 8.83 638 77 3 29 12.96 829 81 3 33 30.15 829 81 3 33 18.48
540 29808 53122 17727 40361 2 110 10 1 11 1.72 267 31 2 21 7.58 314 31 2 24 5.55 523 48 8 24 2.14 716 65 8 24 5.60 721 65 8 36 6.16 820 73 8 36 9.36 853 81 3 36 10.98 853 81 3 39 7.59
540 29808 54588 17314 39441 3 110 10 1 11 1.74 875 91 1 11 2.71 875 91 1 11 2.80 875 91 1 11 2.73 875 91 1 11 2.93 875 91 1 11 2.70 875 91 1 11 2.79 875 91 1 11 3.85 875 91 1 11 2.87
540 30274 55520 17634 40080 4 110 10 1 11 1.87 875 91 1 11 2.87 875 91 1 11 2.99 875 91 1 11 2.92 875 91 1 11 3.00 875 91 1 11 2.94 875 91 1 11 3.32 875 91 1 11 3.07 875 91 1 11 3.20
600 33335 61819 20398 48293 1 110 10 1 11 2.07 266 31 2 21 12.87 310 31 2 21 4.60 523 48 8 90 10.12 608 76 3 29 8.52 613 76 3 29 8.13 638 77 3 29 10.15 829 81 3 33 38.12 829 81 3 33 15.33
600 33335 61819 20398 48293 2 110 10 1 11 2.15 267 31 2 21 8.92 321 31 2 24 7.84 523 48 8 24 6.86 716 65 8 24 6.58 721 65 8 36 7.06 834 73 8 36 10.75 867 81 3 36 12.45 853 81 3 39 9.41
600 33335 63394 20131 47675 3 110 10 1 11 2.23 877 91 1 11 3.26 877 91 1 11 3.66 878 91 1 11 3.54 877 91 1 11 3.43 877 91 1 11 3.60 877 91 1 11 3.45 877 91 1 11 3.54 877 91 1 11 3.62
600 33836 64396 20486 48384 4 110 10 1 11 2.12 877 91 1 11 3.46 877 91 1 11 3.54 878 91 1 11 3.66 877 91 1 11 3.60 877 91 1 11 3.62 877 91 1 11 3.70 877 91 1 11 3.52 877 91 1 11 3.73
1440 48247 101160 32059 84305 1 110 10 1 11 3.85 266 31 2 21 22.40 310 31 2 21 9.17 523 48 8 90 19.81 608 76 3 29 17.08 613 76 3 29 16.55 638 77 3 29 20.23 829 81 3 33 69.77 829 81 3 33 30.07
1440 48247 101160 32059 84305 2 110 10 1 11 3.96 266 31 2 21 21.60 332 31 2 23 17.94 523 48 8 24 14.43 716 65 8 24 14.24 721 65 8 36 14.22 820 73 8 34 22.37 853 81 3 36 24.27 854 81 3 39 16.86
1440 48247 103146 31766 83615 3 110 10 1 11 4.40 878 91 1 11 6.60 878 91 1 11 7.08 878 91 1 11 6.32 878 91 1 11 6.58 878 91 1 11 6.97 878 91 1 11 6.95 878 91 1 11 8.47 878 91 1 11 6.56
1440 48879 104428 32252 84586 4 110 10 1 11 2.99 878 91 1 11 5.63 878 91 1 11 5.27 878 91 1 11 6.64 878 91 1 11 9.64 878 91 1 11 14.21 878 91 1 11 14.28 878 91 1 11 11.23 878 91 1 11 26.18
ARevisitedModelfortheRealTimeTrafficManagement
149

using Obj
3
and Obj
4
, there is a decrease of values
of Obj
1
. However, it is interesting to note that when
multiple independent disturbances occur on the line,
it is possible to decompose the problem in indepen-
dent subproblems. In this way, the train dispatcher
can give priority to the rescheduling of trains which
paths include stations where a higher level of service
is required or that have to comply connections with
other trains. One could expect that two disturbances
would be more difficult to solve but, according to the
first experiments, this is not the case. More particu-
larly, the time needed to solve the first disturbance is
greater than the time needed to solve both, perhaps
due to number of embedded variables. More explicit,
we are in progress to verify that.
5 CONCLUSIONS AND
PERSPECTIVES
In this paper, we propose a formalization of the
rescheduling real-time problem for a regional single-
tracked railway network in which a CTC control sys-
tem is installed. We propose a mathematical model
that operates as a decision support system for the train
dispatcher. The main goal is to find a decision support
system for the train dispatcher that is able to restore
normal traffic conditions after the occurrence of a dis-
turbance and to provide an adequate level of service
to passengers. We analyze four alternative objective
functions in order to find the optimal solution that is
a good compromise between total delay, number of
rescheduled trains and computational time.
There are many perspectives for this work:
- increase the complexity of the analysis, consider-
ing a greater number of disturbances on the line
that occur at different times and have different
size.
- introduce robustness in the rescheduling process.
A robust rescheduled timetable is less subject to
change if a new disturbance occurs on the railway
line.
- perform a structural analysis of the railway line
in order to verify if there are independent sectors
in which it is possible to predetermine an optimal
solution to applied when a disturbance occours.
- introduceindicators of the complexity of the prob-
lem in order to assess the sensibility of the com-
putational time with these parameters.
- include a resolution strategy that allow the cancel-
lation of a train when the delay that it would accu-
mulate along the line exceeds a certain threshold.
- study other resolution methods most suitable to
the complexity of the problem, such as constraints
programming, able toproduce a setof possible so-
lutions.
REFERENCES
D’Ariano, A. (2008). Real-Time Train Dispatching: Mod-
els, Algorithms and Applications. PhD thesis, Fac-
ulty of Civil Engineering and Geosciences, Delft Uni-
versity of Technology, Department of Transport and
Planning.
Dotoli, M., Epicoco, N., Falagario, M., Piconese, A., Scian-
calepore, F., and Turchiano, B. (2013). A real time
traffic management model for regional railway net-
works under disturbances. In 9th annual IEEE Confer-
ence on Automation Science and Engineering , Madi-
son, USA.
FSE - Ferrovie del Sud Est (2013). Fse - ferrovie del sud est
e servizi automobilistici. http://www.fseonline.it.
˙
Ismail, S. (1999). Railway traffic control and train schedul-
ing based on inter-train conflict management. Trans-
ports Research, Part B, 33:511–534.
Vicuna, G. (1989). Organizzazione e tencica ferroviaria.
Vol. II. CIFI; Collegio Ingegneri Ferroviari Italiani,
Roma.
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
150
