Online Non-rigid Structure-from-Motion based on a Keyframe

Representation of History

Simon Donn

e, Ljubomir Jovanov, Bart Goossens, Wilfried Philips and Aleksandra Pi

zurica

Department of Telecommunications and Information Processing (TELIN), Ghent University, Ghent, Belgium

Keywords:

Computer Vision, On-line 3D Reconstruction, Non-rigid Structure-from-Motion, Subset Selection.

Abstract:

Non-rigid structure-from-motion in an on-line setting holds many promises for useful applications, and off-line

reconstruction techniques are already very advanced. Literature has only recently started focusing on on-line

reconstruction, with only a handful of existing techniques available. Here we propose a novel method of

history representation which utilizes the advances in off-line reconstruction. We represent the history as a set

of keyframes, a representative subset of all past frames. This history representation is used as side-information

in the estimation of individual frames. We expand the history as previously unseen frames arrive and compress

it again when its size grows too large. We evaluate the proposed method on some test sequences, focusing on

a human face in a conversation. While on-line algorithms can never perform as well as off-line methods as

they have less information available, our method compares favourably to the state of the art off-line methods.

1 INTRODUCTION

One of the most important problems in computer vi-

sion today is the reconstruction of the 3D geometry of

a scene based on one or more cameras capturing 2D

image sequences. Non-rigid structure-from-motion

is one of the fundamental computer vision problems,

with a large number of potential applications such as:

• 3D video: conversion of 2D movies into 3D,

• Human-computer interface (HCI): pose and ges-

ture estimation of the user,

• Minimal-invasion surgery: extraction of 3D infor-

mation from laparoscopic images to provide sur-

geons with more detailed information.

These are only some important applications of these

techniques, illustrating the importance of accurate

and on-line 3D reconstruction. In this paper we fo-

cus on a teleconference scenario: we wish to create a

more immersive user experience by only using a sin-

gle 2D camera. The goal is to estimate the 3D co-

ordinates for a series of feature points from an input

stream of their corresponding 2D observations, and to

do so in an on-line fashion.

The input 2D coordinates are assumed to be rea-

sonably accurate, but our model includes input noise,

for example from feature tracker inaccuracies. This

paper focuses on the case of only one camera. We

make no further assumptions about this camera: it

may be either static or moving compared to the ob-

ject and we do not restrict ourselves to a given cam-

era model in this stage, either perspective or ortho-

graphic.

We say that the (external) feature tracker detects

J feature points on the surface and that the camera is

represented by C parameters. Accordingly, in each

frame we wish to estimate 3J 3D coordinates and

C camera parameters using 2J observed 2D coordi-

nates: the problem is ill-posed without any restric-

tions on the possible solutions. The two major chal-

lenges are ﬁnding the best solution to this ill-posed

problem and doing so in an on-line fashion. While the

existing literature offers a plethora of solutions to the

ill-posed problem in an off-line scenario, on-line non-

rigid structure-from-motion has only recently been re-

ceiving attention with just a handful of publications at

the time of writing (Paladini et al., 2010; Agudo et al.,

2012; Tao et al., 2013).

2 EXISTING METHODS

Non-rigid structure-from-motion is in itself an ill-

posed problem: at each input frame we wish to esti-

mate 3J +C unknowns based on only 2J input values,

where the camera parameters may or may not include

movement depending on the speciﬁcs of the method

used. To lower the amount of unknowns that need to

723

Donné S., Jovanov L., Goossens B., Philips W. and Pižurica A..

Online Non-rigid Structure-from-Motion based on a Keyframe Representation of History.

DOI: 10.5220/0004871407230731

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (PANORAMA-2014), pages 723-731

ISBN: 978-989-758-004-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Illustration of a shape basis extracted with a shape space method.

be estimated, we assume a certain degree of knowl-

edge about the scene. The various methods are gener-

ally classiﬁed by the type of knowledge they assume.

2.1 Template-based Methods

The ﬁrst option is to assume that the object being re-

constructed is well-known and that all of its possi-

ble behaviours are collected into a so-called template.

As illustrated in the literature, a linear space can ade-

quately represent deformations of a real, physical ob-

ject such as a human face (Blanz and Vetter, 1999;

Wang and Lai, 2008; Paysan et al., 2009). Such a tem-

plate effectively restricts the possible 3D point clouds

of the object to a K-dimensional subspace of the 3J-

dimensional space, with the template containing the

known subspace basis. This means we must estimate

K +C unknowns based on 2J input values, which is

more likely to be well-determined. Naturally, the di-

mensionality of the subspace is assumed to be signif-

icantly lower than 3J. If this were not the case, there

is little advantage from a template-based method.

2.2 Shape Basis Methods

Unfortunately, templates are often missing due to the

lack of any accurate knowledge about the deforming

object. We must therefore make less stringent as-

sumptions to reduce the number of unknowns. A re-

laxation of the assumption of the template methods

is that the possible constellations of the object’s point

cloud are indeed restricted to a K-dimensional sub-

space, but that the basis of this subspace is unknown

and must be estimated as well.

In this case K +C unknowns have to be estimated

for each frame, as well as 3JK unknowns globally for

the subspace basis (Bregler et al., 2000). Figure 1

shows an example of an estimated shape basis, and we

can see that this is similar to what one would expect a

template to contain.

In the seminal work of (Bregler et al., 2000) the

shape basis and the coefﬁcients are extracted through

matrix factorization. Several methods improve this

seminal method, either in the method of estimation

or in the modelling of the object. Some of the most

important approaches consist of:

- an extension to non-linear manifolds for the pos-

sible constellations (Rabaud and Belongie, 2008;

Shaji and Chandran, 2008; Fayad et al., 2009; Go-

tardo and Martinez, 2011a);

- the use of a perspective rather than an ortho-

graphic camera model (Xiao and Kanade, 2005;

Hartley and Vidal, 2008);

- the use of Bayesian estimation (Torresani et al.,

2008; Zhou et al., 2012);

- the handling of missing data points (Lee et al.,

2011).

One of these approaches, probabilistic principal

component analysis (PPCA) (Torresani et al., 2008)

is one of the best performing methods when in the in-

put is perturbed by noise, courtesy of its explicit noise

modelling. It is the one we choose to champion for the

shape basis methods in later comparisons. Moreover,

this method is computationally faster than most other

methods, which is another point of importance con-

sidering our goal of an on-line reconstruction. This

method is explained in more detail later in this sec-

tion, because our proposed method relies on the same

modelling and on the same approach for the actual re-

construction.

To the best of our knowledge there exist, at of

the time of writing, only a handful of on-line non-

rigid structure-from-motion methods in the literature.

In (Paladini et al., 2010), the authors perform off-line

reconstruction on a bootstrap sequence, which results

in an initial estimate for the shape basis. Afterwards

this basis is used to estimate the subsequent frames

sequentially. The shape basis is then expanded us-

ing principal component analysis (PCA). While the

shape basis representation from (Paladini et al., 2010)

tends to collect a large amount of noise over time

in noise-perturbed sequences as it will keep adding

bases based on noises, it works well in the noise-free

case. The authors of (Tao et al., 2013) utilize an adap-

tation of PCA more suited for sequential use: Incre-

mental PCA (IPCA). They use a frame window to step

through the input sequence and update the shape ba-

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

724

sis using IPCA. Their method requires a training in-

put set to estimate the prior distribution of shape basis

weights, however. Lastly, the use of an adapted Finite

Elements Method (FEM) is proposed (Agudo et al.,

2012). The major drawback of this FEM method is

that it requires an initialisation step wherein the ob-

ject behaves rigidly. This is a valid assumption in a

large number of cases, but we will focus on scenarios

where this requirement is not necessarily fulﬁlled.

2.3 Trajectory Basis Methods

Whereas shape basis approaches attempt to model

spatial coherence, trajectory basis methods exploit

temporal coherence: there is a high correlation be-

tween subsequent locations of a given point. These

methods model the point trajectories as elements of a

K-dimensional subspace. The optimal basis for each

input sequence can be estimated through principal

component analysis (PCA), but research has shown

this basis largely coincides with that of the discrete

cosine transform (DCT) (Akhter et al., 2011; Akhter

et al., 2008). A related method models the cam-

era as smoothly moving rather than the points: Col-

umn Space Fitting (Gotardo and Martinez, 2011b),

which we classify under trajectory basis methods in

this overview. It ﬁrst estimates the camera behaviour

and then uses this knowledge to perform reconstruc-

tion more effectively. It is chosen to champion for the

trajectory basis methods in later comparisons.

2.4 Details of PPCA

Because our method uses the estimation framework

from (Torresani et al., 2008) we repeat the basics

here. This approach is based on the Bayesian mod-

elling of the tracking errors and the input noise. Let

us s

j,t

as the 3D coordinates of point j, d

as the 3D

camera translation, R

as the camera matrix and c

the camera scaling factor,(all in the t

frame). Un-

der the assumption of Gaussian measurement noise

j,t

∼ N (0;σ

I) we can then express the 2D obser-

vation p

j,t

of the j

point as a weak-perspective pro-

jection:

j,t

|{z}

2×1

= c

|{z}

2×3

( s

j,t

|{z}

3×1

+ d

|{z}

3×1

) + n

j,t

|{z}

2×1

(1)

In matrix notation, the observed locations of all

points in a given frame t are concatenated vertically

into p

|{z}

2J×1

= G

|{z}

2J×3J

( s

|{z}

3J×1

+ D

|{z}

3J×1

) + n

|{z}

2J×1

(2)

In this equation, G

contains J copies of c

on its

diagonal, and other entities are the vertically concate-

nated versions of their counterparts in Equation 1. We

now assume s

to be an element of a K-dimensional

manifold:

|{z}

3J×1

= s

|{z}

3J×1

+ V

|{z}

3J×K

|{z}

K×1

where s is an average 3D shape, and V holds the shape

basis vectors in its columns, which are weighted with

the deformation coefﬁcients contained in z

Subsequently, the authors of (Torresani et al.,

2008) place a Gaussian prior on the deformation

weights: z

∼ N (0;I). The estimation of R

, s, V and

then amounts to a Bayesian scheme, which is called

probabilistic principal component analysis (PPCA).

Speciﬁcally, an expectation-maximization (EM) op-

timization is used for estimating the various parame-

ters. One ﬁnal remark must be given about the local-

isation: without any ﬁxed reference system, the loca-

tion of the camera and the object are only estimated

up to an afﬁne transform. For ease of use we will as-

sume that the center of the observed object is the ori-

gin (and that this center does not ﬂuctuate markedly

due to deformations). We will then express any move-

ment of either the real-life camera or the real-life ob-

ject as movements of our virtual camera, ﬁxing the

object’s center at the virtual origin.

3 THE PROPOSED ON-LINE

RECONSTRUCTION

We can identify two large elements in any on-line

method: a method for history representation and one

for the sequential processing of the input. In an ini-

tial attempt for on-line reconstruction method we per-

formed the EM update equations using the informa-

tion from a sliding temporal window for all of the

unknowns. Due to small frame windows and slow-

moving cameras, this strategy typically resulted in a

degeneration of the shape basis and the resulting re-

construction because the frame window did not con-

tain enough vantage points for the object. In this

case, the latest estimations of the various unknowns

were used as a history representation: obviously this

history representation was too simplistic. This sec-

tion comprises the selection of a representative sub-

set, both on artiﬁcial 2D point clouds and our speciﬁc

problem, and the overview of our proposed method.

OnlineNon-rigidStructure-from-MotionbasedonaKeyframeRepresentationofHistory

725

3.1 History Representation with

Keyframes

A key element of any sequential or on-line algorithm

is the need to remember past input. Clearly, it is in-

tractable to simply memorize all past frames of a the-

oretically inﬁnite sequence. We propose to use a set of

keyframes as a representation of all past input frames;

a sparse sampling of history, so to speak. We ex-

tract the shape basis for the shape subspace required

for the reconstruction from this history representation,

but we retain the entire subset as the history represen-

tation. The challenge is now the selection of such a set

of representative frames from all of the input frames.

3.1.1 General Subset Selection

The main goal of the keyframe selection procedure is

to select a set of frames which represent all the possi-

ble deformations of the object from as many vantage

points as possible. In order to achieve this goal, the

selection procedure should exclude all of the frames

that do not contribute any additional information to

the shape basis, eliminating duplicate frames from the

keyframe set.

A subset of representative frames is selected from

the full set, having much fewer elements. Due to the

combinatorial explosion, the number of possible ways

to select a subset from a larger set grows very quickly

with the size of the full set. Therefore, an exhaus-

tive comparison of all possible subsets of keyframes

is implausible and we resort to a heuristic subset se-

lection. Assuming that we can represent the elements

of the set as points in a Euclidean space, our goal is to

select a subset, the elements of which are uniformly

distributed throughout the bounds of the full set.

To select a subset with a given metric, we use

backward elimination. By starting from the full set

and removing one element at a time according to a

local criterion we remove the element whose exclu-

sion from the subset results in the best change of the

metric, e.g. one of the two elements lying closest to-

gether when maximizing the minimum distance: the

one lying closest to the rest of the subset.

We illustrate four different metrics to maximize:

the minimum distance between any two elements of

the subset, the mean distance between all elements of

the subset, the mean distance between the elements of

the subset and those of the full set, and the differential

entropy of the subset. These metrics are heuristically

chosen so that their maximization results either in a

uniform density over the bounds (the minimum dis-

tance and the entropy), or in an accurate representa-

tion of the bounds (the mean distance).

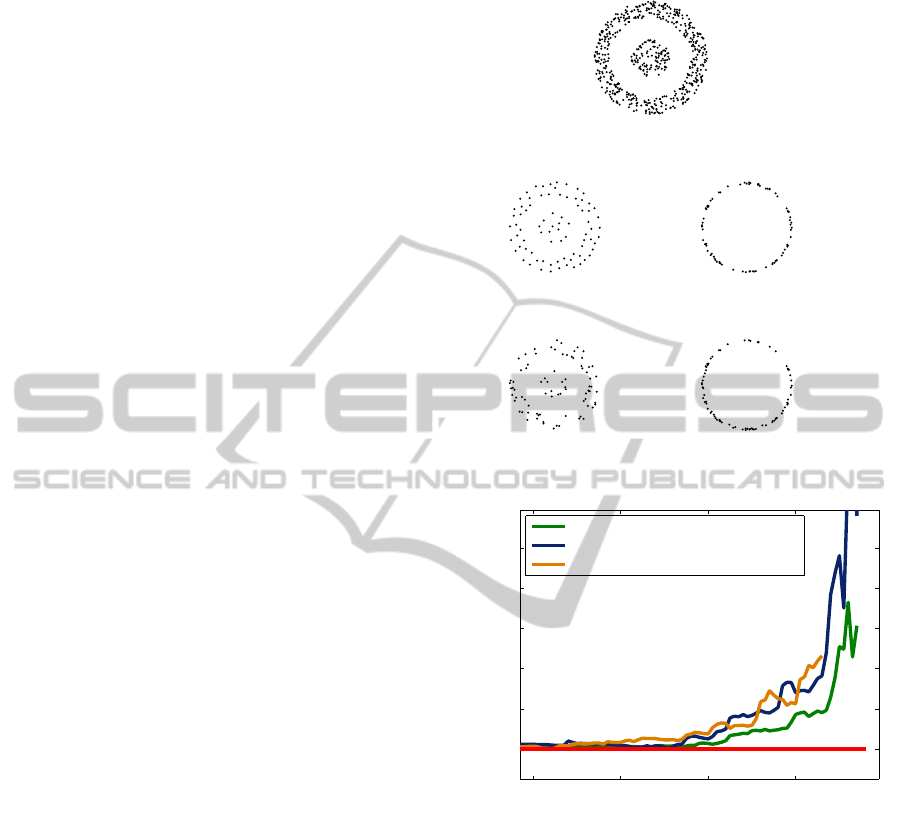
Full set

Minimum distance Mean distance to the subset

Mean distance to the full setEntropy

Figure 2: Demonstration of the subset selection metrics on

an artiﬁcial 2D point cloud.

240 260 280 300

1.2

1.4

1.6

1.8

Number of frames removed

Euclidean reconstruction error

(normalized)

Distance in the shape space

Distance in the camera manifold

Entropy in the combined manifold

Figure 3: Keyframe selection using several metrics. The

input sequence is a 316-frame sequence of a person talking

from (Torresani et al., 2008).

The mean distance to the full set is included be-

cause it is computationally faster than the mean dis-

tance to the subset. For the ﬁrst three metrics we re-

quire a meaningful distance to be deﬁned between any

two elements in the set, a drawback the differential

entropy does not suffer from. To estimate the differ-

ential entropy, we use a Matlab wrapper for the TIM,

an open-source C++ library for efﬁcient estimation of

information-theoretic measures (Rutanen, 2011).

The result of each of these strategies on the selec-

tion of a representative subset for an artiﬁcial 2D point

cloud are shown in Figure 2. We can see that maxi-

mizing the minimum distance between any two points

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

726

in the subset yields the most representative cloud,

while maximizing the mean distance represents the

edges well. The entropy metric gives disappointing

results, which we assume largely to be the result of

the difﬁculty of estimating the entropy of a continu-

ous variable based on a small number of samples.

3.1.2 Subset Selection for Keyframe Selection

Results shown in Figure 2 demeonstrate that it is pos-

sible to select a representative subset of 2D points

from a much larger set. In this section we investi-

gate whether this result also holds for selecting a set

of keyframes from the full set of frames, as illustrated

in Figure 4. The set of keyframes is said to be rep-

resentative to the full set if the reconstruction error is

not signiﬁcantly affected by restricting the estimation

of the shape basis to the set of keyframes rather than

the full set. To this end, three metrics for the selection

of keyframes are investigated:

- the minimum distance in the shape space,

- the minimum distance in the camera manifold,

- the entropy in the combined shape-camera space.

We use the Euclidian distance between deformation

coefﬁcients as the distance metric in the shape space.

In the camera manifold, the distance between two

camera parameter vectors is deﬁned as the euclidean

distance between a given unit vector transformed to

the cameras’ reference system. The differential en-

tropy is retained as a metric in this paper because it

allows us to combine the deformation coefﬁcients and

the camera parameters into a single metric, which is

not straightforward using distance-based metrics and

would require extensive research.

Figure 3 shows that the minimum distance on the

shape manifold results in a lower reconstruction error

than the other methods, indicating that the observa-

tion of the different deformations is more important

to the overall accuracy than the observation from dif-

ferent vantage points. The results were obtained on a

316-frame sequence from (Torresani et al., 2008) con-

sisting of a person talking to the camera. At each step,

we eliminate the frame which maximizes the respec-

tive metric and perform PPCA reconstruction restrict-

ing the estimation of the shape basis to the keyframes.

Figure 3 also shows that for keyframe set sizes of

about 35 frames there is little loss in accuracy.

3.2 Overview of the Proposed

Algorithm

We start by performing a 3D reconstruction of a boot-

strap sequence with an existing, off-line, reconstruc-

tion method. For this, any off-line reconstruction al-

gorithm can be used, but we have chosen the PPCA

method (Torresani et al., 2008) for simplicity. The

length of the bootstrap sequence must be chosen with

some care: choosing it too short will result in a rough

initialization, while choosing it too long will increase

the initialisation time. For the sequences used in

this paper we have found a bootstrap length of 60

frames to be a good middle ground. We select a

subset of frames from the bootstrap sequence which

accurately represents the whole of the bootstrap se-

quence, through the already discussed keyframe se-

lection. A rough initial reconstruction can be per-

formed for the bootstrap window (through a limita-

tion of the iteration count), which is sufﬁcient for

keyframe selection and which we improve only for

the selected keyframes.

Throughout the execution of the program we will

add frames to the keyframe set, and we cull the

keyframe set using the subset selection whenever its

cardinality exceeds a certain imposed size (heuristi-

cally chosen to be 1.5 times the initial size). The

initial history size is also chosen manually, and tests

have shown (see for example Figure 3) that a set of 30

frames is an acceptable choice.

For the on-line processing, we reconstruct each

frame sequentially using the shape basis we have ex-

tracted from the keyframe set, initialising the camera

matrix using the last estimated value. This consists of

alternately optimizing the camera parameters and the

deformation coefﬁcients for a set number of iterations

using the update steps from (Torresani et al., 2008).

In the next step we add the newly processed frame

to the keyframe set if it represents a deformation or

vantage point which is not yet represented in said set,

i.e. if the subset selection metric does not lower sig-

niﬁcantly when including the newly processed frame.

At the point where the keyframe set has changed sig-

niﬁcantly, i.e. it has grown to a predeﬁned threshold,

we select a new subset of the large keyframe set to

serve as the new history representation from now on.

Finally, we extract an updated shape basis from the

updated history and continue with the on-line process-

ing. The update of the keyframe set and the extraction

of the new shape basis can be done in parallel with

the on-line reconstruction using parallel programming

paradigms (OpenMP or GPGPU). An overview of the

proposed algorithm is given in the form of a ﬂowchart

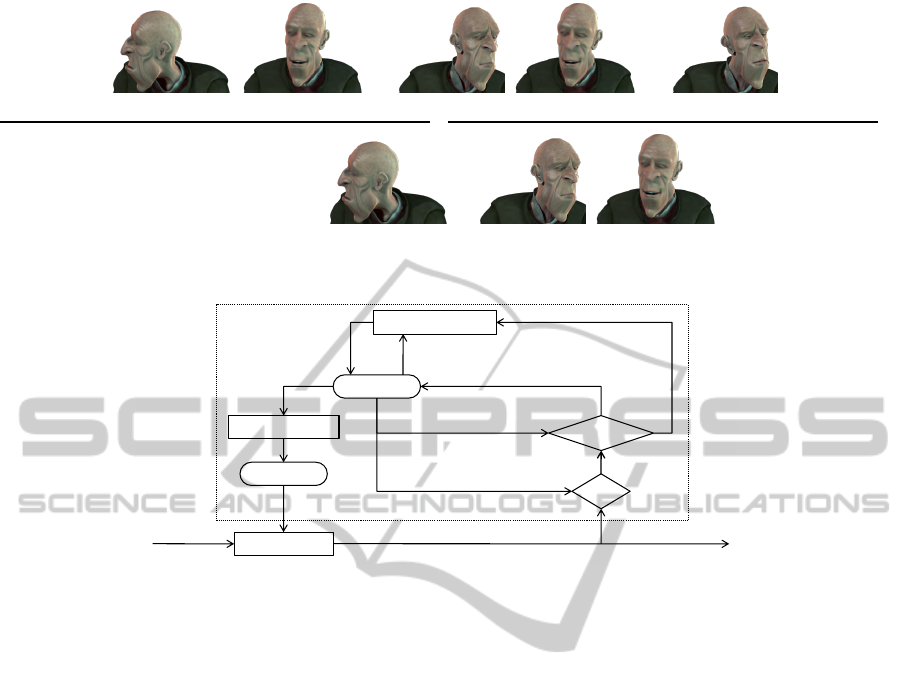
in Figure 5.

3.3 GOP Processing

Estimating the 3D shape one frame at a time incurs a

large amount of overhead, because we are performing

OnlineNon-rigidStructure-from-MotionbasedonaKeyframeRepresentationofHistory

727

| {z }

Figure 4: Illustration of how the keyframe selection should work: any duplicate or near identical frames should be eliminated.

Images courtesy of the open-source video Elephant’s Dream (Team, 2006), featuring the character Proog.

estimation

frame input

HISTORY

keyframes

yes

new?

too many?

add

yes

3D output

subset selection

replace

shape basis

basis estimation

Figure 5: Overview of our proposed method.

calculations on small matrices: the overhead of the

calculations is large compared to the complexity of

the calculations. Group-of-pictures (GOP) process-

ing is possible in the proposed method due to the na-

ture of the optimization equations, which results in a

lower average overhead per frame. Processing multi-

ple frames at the same time comes with the disadvan-

tage of a higher latency, and therefore the end-user

will have to decide which point of the trade-off is op-

timal for their particular application.

To illustrate the relationship between GOP size,

processing speed and latency, we vary the GOP size

from 1 to 10 and scatter the points (FPS

, Latency

)

in our Matlab implementation, as visible in Figure 6.

The latency displayed in the graph is the minimum

latency: to compute it we ignore the fact that the ﬁrst

frame of a GOP must wait until the last frame of its

GOP is observed until the estimation of the GOP can

begin. Therefore, the displayed latency is the latency

for the last frame of a GOP. The actual choice of the

GOP size depends on the application: a large GOP

size may be applicable to off-line reconstruction of

a very long sequence because current off-line recon-

struction methods typically scale badly with rising se-

quence length, in computational complexity and/or

required memory. In this case, latency is of little inter-

est and the goal is to maximize the throughput while

avoiding the high memory use and complexity of off-

line methods.

4 RESULTS

4.1 Quantitative Results

In this section we present the result of the pro-

posed approach and compare it to some state-of-the-

art methods. It is important to note that the proposed

method is restricted to causal processing of the in-

put sequence: we reconstruct frame t using only the

observations from frames 1 through t. The existing

methods work off-line on the whole video sequence

and are not restricted by causality: for a more fair

comparison we can restrict these to causal reconstruc-

tion as well. We do this because we want to focus

our evaluation on the effectiveness of our history rep-

resentation. Assuming the methods are allocated a

bootstrap window of B frames, we can restrict them

to causal workings by reconstructing frame t using

only the frames 1, . . . , t. Clearly, this is not a prac-

tical way to perform reconstruction, but it gives an

indication of the performance of other methods in a

causal setting. Figure 7 shows the comparison be-

tween the proposed method and some state-of-the-

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

728

40 45 50 55 60

100

150

200

Frames per second (FPS)

Latency (ms)

Figure 6: Relationship between GOP size, processing speed

and minimum latency. Each data point is labeled by the

GOP size responsible for it.

0 0.5 1 1.5 2

0.02

0.04

0.06

0.08

0.1

Noise energy (%)

Euclidean reconstruction error

PPCA [14]

CSF [19]

Proposed method

Figure 7: Causal comparison between two existing methods

and our proposed method. The input sequence is consists of

a person talking, courtesy of (Torresani et al., 2008).

art methods (Gotardo and Martinez, 2011b; Torre-

sani et al., 2008). While the proposed method can

never perform a reconstruction of the same accuracy

as its off-line variant, because it does not retain the

same amount of information on previous frames, our

proposed method still compares favourably to the off-

line PPCA method and outperforms other state of the

art methods. Our proposed method has also inherited

the noise robustness of the Bayesian modelling from

the off-line PPCA, as illustrated by the equality of the

slopes.

These graphs of course do not reﬂect the immense

advantage of the on-line aspect of our method. There

is no entry for the ﬁrst online method by (Paladini

et al., 2010) because it uses a threshold for the error

as an indicator of whether or not the model should

be expanded. The resulting line in the graph is there-

fore constant and does not reﬂect the downsides of

the method (extraordinary computational complexity

with rising noise). The graph was produced by per-

turbing the 316-frame sequence from (Torresani et al.,

2008) with zero-mean Gaussian noise (AWGN), re-

constructing the perturbed sequence with the vari-

ous methods and afterwards computing the average

3D error between the reconstructed point cloud and

the ground truth. The speciﬁc parameter values for

our method were: a 60-frame bootstrap length, a 40-

frame history representation size and 25 EM iterations

per frame.

4.2 Qualitative Results

Figure 8 puts these reconstruction errors into perspec-

tive: all three methods manage an accurate recon-

struction of the face from the sequence from (Tor-

resani et al., 2008). We also present a reconstruc-

tion by the three methods of the sequence extracted

from Elephant’s Dream (Team, 2006) in Figure 9. For

this comparison, we extract the projected points from

the video’s source and pass them as input to the re-

construction methods. Because the full mesh of the

Proog’s face has over 4000 points, we manually se-

lected a subset of 197 points to perform reconstruc-

tion on. After reconstruction, the resulting 3D mesh

is visualized by using the original texture from the

movie sources.

5 CONCLUSIONS

In this paper we have proposed a new method

for on-line non-rigid structure-from-motion based on

keyframe selection. While the literature on off-line

3D reconstruction has received a lot of attention and

several accurate techniques exist, relatively few ven-

tures have been made concerning on-line operation.

A new method of history representation using a set

of keyframes is described and evaluated, comparing

favourably to existing methods, performing similarly

to its off-line variant and outperforming other off-line

state-of-the-art methods.

We see two clear options for future work on on-

line non-rigid structure-from-motion: improving the

history representation and improving the estimation

of the separate frames. Sequential statistical estima-

tion, which is used to great effect in other ﬁelds, may

offer a more theoretical approach to history repre-

sentation. On the other hand, the estimation of the

separate frames can no doubt beneﬁt from existing

methods in off-line reconstruction. The exploitation

of the temporal coherence through implementation of

a linear dynamic system as in (Torresani et al., 2008),

OnlineNon-rigidStructure-from-MotionbasedonaKeyframeRepresentationofHistory

729

CSF

PPCA

Proposed method

Figure 8: Visual comparison between three methods. The top row shows the original view point, and the bottom row shows

an alternate view point. Lines and points show the projection of reconstructed 3D points and their connections, while small

circles are centered around the ground truth locations.

(a) Original movie (b) CSF (c) PPCA (d) Proposed method

Figure 9: Visual comparison between two existing methods and our proposed method on a sequence extracted from Elephant’s

Dream (Team, 2006).

the PPCA-speciﬁc improvement of the camera update

equation as in (Qu et al., 2012), or other techniques

from off-line state-of-the-art offer possibilities for im-

provement.

ACKNOWLEDGEMENTS

The research for this paper was started in a master’s

thesis at Ghent University (at the TELIN department)

and ﬁnished during the start of a PhD funded by the

BOF under grant number 01D21213. Special thanks

go to Erwin Six and Donny Tytgat at the Alcatel Bell

Labs in Antwerp for their help and insights during the

early stages of the research.

REFERENCES

Agudo, A., Calvo, B., and Montiel, J. (2012). 3d reconstruc-

tion of non-rigid surfaces in real-time using wedge el-

ements. In Computer Vision ECCV 2012. Workshops

and Demonstrations, volume 7583 of Lecture Notes

in Computer Science, pages 113–122. Springer Berlin

Heidelberg.

Akhter, I., Sheikh, Y., Khan, S., and Kanade, T. (2011).

Trajectory space: A dual representation for nonrigid

structure from motion. IEEE Transactions on Pattern

Analysis and Machine Intelligence (TPAMI).

Akhter, I., Sheikh, Y. A., Khan, S., and Kanade, T. (2008).

Nonrigid structure from motion in trajectory space. In

Neural Information Processing Systems.

Blanz, V. and Vetter, T. (1999). A morphable model for

the synthesis of 3d faces. In Proceedings of the 26th

annual conference on Computer graphics and inter-

active techniques, SIGGRAPH ’99, pages 187–194,

New York and NY and USA. ACM Press/Addison-

Wesley Publishing Co.

Bregler, C., Hertzmann, A., and Biermann, H. (2000). Re-

covering non-rigid 3d shape from image streams. In

Computer Vision and Pattern Recognition and 2000.

Proceedings. IEEE Conference on, volume 2, pages

690 –696 vol.2.

Fayad, J., Bue, A. D., de Agapito, L., and Aguiar, P. (2009).

Non-rigid structure from motion using quadratic de-

formation models. In BMVC. British Machine Vision

Association.

Gotardo, P. and Martinez, A. (2011a). Kernel non-rigid

structure from motion. In Computer Vision (ICCV)

and 2011 IEEE International Conference on, pages

802 –809.

Gotardo, P. F. and Martinez, A. M. (2011b). Computing

smooth time trajectories for camera and deformable

shape in structure from motion with occlusion. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 33:2051–2065.

Hartley, R. and Vidal, R. (2008). Perspective nonrigid shape

and motion recovery. In In Proc. European Confer-

ence on Computer Vision, pages 276–289.

Lee, S. J., Park, K. R., and Kim, J. (2011). A sfm-based

3d face reconstruction method robust to self-occlusion

by using a shape conversion matrix. Pattern Recogn.,

44(7):1470–1486.

Paladini, M., Bartoli, A., and Agapito, L. (2010). Se-

quential non-rigid structure-from-motion with the 3d-

implicit low-rank shape model. In Proceedings of the

11th European conference on Computer vision: Part

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

730

II, ECCV’10, pages 15–28, Berlin and Heidelberg.

Springer-Verlag.

Paysan, P., Knothe, R., Amberg, B., Romdhani, S., and Vet-

ter, T. (2009). A 3d face model for pose and illumina-

tion invariant face recognition. In Advanced Video and

Signal Based Surveillance and 2009. AVSS ’09. Sixth

IEEE International Conference on, pages 296 –301.

Qu, C., Gao, H., and Ekenel, H. K. (2012). Rotation up-

date on manifold for non-rigid structure from motion.

IEEE International Conference on Image Processing.

Rabaud, V. and Belongie, S. (2008). Re-thinking non-rigid

structure from motion. In Computer Vision and Pat-

tern Recognition and 2008. CVPR 2008. IEEE Con-

ference on, pages 1 –8.

Rutanen, K. (2011). Tim, information-theoretic measures

in matlab. http://www.cs.tut.ﬁ/ timhome/tim/tim.htm.

Shaji, A. and Chandran, S. (2008). Riemannian manifold

optimisation for non-rigid structure from motion. In

Computer Vision and Pattern Recognition Workshops

and 2008. CVPRW ’08. IEEE Computer Society Con-

ference on, pages 1 –6.

Tao, L., Mein, S. J., Quan, W., and Matuszewski, B. J.

(2013). Recursive non-rigid structure from motion

with online learned shape prior. Computer Vision and

Image Understanding, 117(10):1287 – 1298.

Team, O. O. M. (2006). Elephant’s dream.

http://www.elephantsdream.org/.

Torresani, L., Hertzmann, A., and Bregler, C. (2008). Non-

rigid structure-from-motion: Estimating shape and

motion with hierarchical priors. IEEE Transactions

on Pattern Analysis and Machine Intelligence.

Wang, S.-F. and Lai, S.-H. (2008). Estimating 3d face

model and facial deformation from a single image

based on expression manifold optimization. In Pro-

ceedings of the 10th European Conference on Com-

puter Vision: Part I, ECCV ’08, pages 589–602,

Berlin and Heidelberg. Springer-Verlag.

Xiao, J. and Kanade, T. (2005). Uncalibrated perspective

reconstruction of deformable structures. In Proceed-

ings of the Tenth IEEE International Conference on

Computer Vision - Volume 2, ICCV ’05, pages 1075–

1082, Washington and DC and USA. IEEE Computer

Society.

Zhou, H., Li, X., and Sadka, A. (2012). Nonrigid structure-

from-motion from 2-d images using markov chain

monte carlo. Multimedia and IEEE Transactions on,

14(1):168 –177.

OnlineNon-rigidStructure-from-MotionbasedonaKeyframeRepresentationofHistory

731