Multi-entity Bayesian Networks for Treasuring the Intangible

Cultural Heritage

Giannis Chantas, Spiros Nikolopoulos and Ioannis Kompatsiaris

Information Technologies Institute, Centre for Research and Technology - Hellas, Thessaloniki, Greece

Keywords:

First-Order Logic, Multi-entity Bayesian Networks, Knowledge Modeling, Intangible Cultural Heritage.

Abstract:

In this paper, we propose the use of Multi-entity Bayesian networks (MEBNs) for modeling the knowledge

and analyzing the content pertaining to the domain of Intangible Cultural Heritage (ICH). MEBNs provide

a rigorous knowledge representation framework in conjunction with reasoning and probabilistic inference

capabilities. There are mainly two reasons motivating the use of MEBNs in the domain of ICH. The ﬁrst is

that MEBNs extend ﬁrst-order logic with the ability to model uncertainty. The second reason is the capability

of MEBN to adapt to speciﬁc situations by providing custom, situation speciﬁc Bayesian networks. Finally,

we use an example to demonstrate the potential efﬁciency of MEBNs in the domain of ICH.

1 INTRODUCTION

The term intangible cultural heritage (ICH) (UN-

ESCO, 2013) refers to valuable traditional art forms

and creative practices, such as singing, dancing,

craftsmanship, etc. Preserving the knowledge cap-

tured by these human treasures (as called by UN-

ESCO) is considered particularly important and the

use of technology to achieve this objective has re-

cently become a popular research topic.

In this paper, we highlight the usefulness of an ef-

ﬁcient knowledge representation scheme in facilitat-

ing the preservation procedure of ICH. We are moti-

vated by the fact that expert domain knowledge can

boost the automated analysis of ICH content and pro-

pose the use of a sophisticated tool like Multi-entity

Bayesian Networks (MEBNs) for allowing preserva-

tion to go beyond the mere digitization of ICH mani-

festations.

ICH manifestations can be captured in a multi-

modal fashion, using sensors of various types, such as

visual (2D/3D), auditory, motion, etc. Furthermore,

the knowledge regarding the ICH domain is diverse,

vast and intricate. For the efﬁcient analysis of the

captured and digitized content, the expert knowledge

plays a crucial role. Thus, this knowledge has to be

precisely represented in a digitized environment and

in a feasible to exploitation manner. A major difﬁ-

culty in representing such knowledge is the inherent

ambiguity and uncertainty in concepts prevalent, not

only the ICH domain, but almost in every real world

environment being modeled. For instance, the steps

performed during a traditional dance, although their

number is certain, the way that they are followed by

the performers may vary with respect to the region,

epoch, or even the individual. Moreover, the number

of concepts to be detected is rarely a priori known.

Indeed, the number of dances and dance steps, songs

and singers, etc, varies per situation.

Ontologies (Staab and R. Studer, 2009) are used

extensively for knowledge representation. An ontol-

ogy provides knowledge representation of a domain

through digital means in a formal language. In this

way, the use of this knowledge for the analysis of

new content, i.e., reasoning, is feasible. Represen-

tation in an ontology is usually based on the descrip-

tion logic (DL), a variant of ﬁrst-order logic (Davis,

1990) (FOL). However, the expressivity of DL is not

sufﬁcient to solve the problem of uncertainty in ICH

knowledge.

In order to overcome this obstacle, various works

have been proposed that enable logic-based represen-

tation schemes to express uncertainty using probabil-

ity theory. The model we propose for this endeavor

in this paper is MEBN (Laskey, 2008). MEBN is

the outcome of the cross-fertilization of ﬁrst-order

logic and probability theory. MEBN adopt proba-

bility theory as a means to model uncertainty. First-

order Bayesian logic (FOBL) is an extension of FOL,

enabling MEBN to extend BN by being more ﬂex-

ible to adapt to speciﬁc situations that arise. More

speciﬁcally, with FOBL, a MEBN can be instantiated

796

Chantas G., Nikolopoulos S. and Kompatsiaris I..

Multi-entity Bayesian Networks for Treasuring the Intangible Cultural Heritage.

DOI: 10.5220/0004875407960802

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (IAMICH-2014), pages 796-802

ISBN: 978-989-758-004-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

to a situation speciﬁc Bayesian network (SSBN) that

models the situation that has been recorded as evi-

dence in the environment being modeled. This over-

comes the rigid and non-ﬂexible nature of Bayesian

networks.

In the next section, we provide the necessary the-

oretical background knowledge about FOL, Bayesian

networks (BN) and ontologies. Then, in Section 3 we

describe the concept of MEBN as a knowledge rep-

resentation and analysis model for the ICH domain.

Moreover, an example of the application of MEBN

is given that demonstrates the advantages of such a

choice. In Section 4, existing literature related to ICH

domain knowledge modeling is provided. In sections

5 and 6, a discussion and conclusions are given, re-

spectively.

2 BACKGROUND

2.1 First-Order Logic

First-Order logic (FOL) (Davis, 1990) is by far the

most commonly used, studied, and implemented logi-

cal system. FOL is a formal system used to deﬁne the-

ories in mathematics, computer science and other sci-

entiﬁc ﬁelds, and it is a very important concept, both

from a theoretical and a practical viewpoint. FOL can

also be used as a rigorous foundation of knowledge

representation schemes.

A theory in ﬁrst-order logic consists of the ax-

ioms, expressed as sentences in the FOL language,

in conjunction with the sentences that are derived

from the axioms according to the reasoning rules, i.e.,

the theorems or valid sentences. In practice, when a

FOL theory is implemented in a computer, axioms are

stored as data structures and the reasoner that evalu-

ates the truth-value of a sentence has the form of a

computer program.

Theories are expressed using the FOL language.

The main components of the FOL language are con-

stants, variables, functions and predicates. Variables

are placeholders of constants. Functions return a con-

stant given their input arguments. Predicates are an

essential component of FOL (the reason that it is

also called predicate logic), since they are used to

deﬁne relations between other components, such as

variables and constants. For example the predicates

parents(John,Mary,George), may state that John and

Mary are parents of George. What also makes FOL

a strongly expressive language are the rules, such

as ”sibling(X,Y):- parent(X,X1,X2) AND(Y,X1,X2)”.

This rule states that any two persons X, Y are siblings

if they have the same parents.

An interpretation of a FOL theory gives a seman-

tic meaning to each constant, predicate and function

(formulas). More speciﬁcally, an interpretation maps

each formula to a speciﬁc nominal entity, constraints

each predicate to relate with each other entities be-

longing to a speciﬁc set, and relates a function to a

function of the domain. A set containing all instanti-

ated formulas of a FOL theory is called an interpre-

tation. Note that, there can be many interpretations,

since instantiations vary.

However, FOL does not provide expressivity to

model uncertain knowledge, let alone a suitable rig-

orous reasoning mechanism. This is a consequence

of the fact that each interpretation mentioned above

shares equal validity with the others. As we will see

in 3, the key feature of MEBN is the assignment of

a probability to every interpretation. This is achieved

with the ﬁrst-order Bayesian logic (FOBL) language.

2.2 Bayesian Networks

Bayesian networks (BN) are stochastic models that

have been applied successfully to problems where un-

certainty is prevalent. Bayesian networks are directed,

acyclic graphical (DAG) models (Whittaker, 2009).

More speciﬁcally, a BN consists of random variables,

represented by nodes in a DAG, along with their re-

lations determining the structure of the DAG. More-

over, a conditional probability distribution is deﬁned

for each variable. Formally, a Bayesian network con-

sists of the following:

• N random variables, denoted by x = {x

, ..., x

• A graph G (which is a DAG), deﬁned by the set

G = {E, V }, where V is the set of vertices and E

the set of directed edges. Each vertex corresponds

to a x

and each edge indicates a parent-child rela-

tion between the two connected variables.

• A joint probability distribution of x, given by:

p(x) =

∏

i=1

p(x

|pa

). (1)

p(x

|pa

) is the local conditional probability of x

, ∀i

and pa

the set of parents of x

. The joint distribution

of x in written in (1) in its so-called product form.

This is possible due to the acyclicity and directivity

of G.

When modeling with BNs, we assume that a ran-

dom variable x

corresponds to a measurable attribute

of a real world entity, e.g., the average temperature

of a country in a speciﬁc day. Nevertheless, unmea-

surable concepts (such as people names, etc.) can be

modeled with natural numbers. x

can take a ﬁnite or

(un)countably inﬁnite amount of values. Denoting by

Multi-entityBayesianNetworksforTreasuringtheIntangibleCulturalHeritage

797

the set of possible values, we write that x

∈ {D

Using this terminology, p(x) is a distribution that as-

signs a probability to every possible conﬁguration of

x = {x

, ..., x

Inference in Bayesian Networks is a crucial pro-

cess in order to make them practical and exploit their

modeling efﬁciency. Inference in BN mainly refers to

the process of estimating the posterior distribution of

a subset of the random variables, given the observed

values of another subset. The observations are direct

evidence that we obtain from the real world we model

with the speciﬁc BN. In other words, Bayesian infer-

ence is the mechanism that offers estimation of the

unknownn variables, given certain, observed values

of other variables. Given the observations x

, the ob-

jective of inference is to estimate the posterior proba-

bility distribution of a set of unobserved (hidden) ran-

dom variables x

, using Bayes rule.

However, the straightforward use of Bayes rule for

inference is rarely practical, due to the high computa-

tional complexity of the algorithm in real world sce-

narios. There are many algorithms that offer tractable

inference, such as belief propagation (where inference

is not necessarily exact), variational approximate in-

ference (Bishop, 2006) (mostly used for continuous

variables), etc. Lastly, we should note that infer-

ence provides conclusions about the variables being

modeled after the presence of new evidence. During

training, the conditional probability distributions are

found. Of course, there are cases where an expert

can provide explicitly such distributions. Typically

though, a BN is constructed prior to that, using train-

ing data and a suitable training algorithm (e.g., max-

imum likelihood). The serious disadvantage of BN

networks when used for knowledge representation is,

once they are designed, their structure is kept ﬁxed.

Thus, since in real world scenarios the modeled en-

vironment changes, BN are seriously handicapped to

adapt to speciﬁc situations.

2.3 Ontologies

Ontologies have been extensively used as knowledge

representation schemes of a domain, including cul-

tural heritage (Baader et al., 2003). The most no-

table example is the CIDOC Conceptual Reference

Model (CRM) (Doerr, 2003), which is a well-known

knowledge representation ontology aiming to facili-

tate heterogeneous cultural heritage information ex-

change (tangible or not). It was developed under the

guidance of the International Committee for Docu-

mentation (CIDOC) of the International Council of

Museums (ICOM). In September 2006, it was ac-

cepted as ISO 21127. CICDOC CRM aims to model

the knowledge regarding cultural objects available at

museums, which can be of various forms of art, geo-

graphical place, and epoch. The standardized CIDOC

CRM ontology is mainly used as a common cultural

information exchange framework.

Moreover, an ontology for analyzing traditional

dances based on the Laban notational system for hu-

man body movement is proposed in (Ioannidis, 2011).

Analysis is based on knowledge represented using an

ontology. However, the ontology is non-probabilistic,

as well as the reasoning performed for the analysis.

Since ontologies are based on classical logic, i.e.,

the DL language, they enjoy the expressivity for

deﬁning complex knowledge and concepts of a do-

main. However, they lack the ability to express

knowledge with probabilistic terms. In the next sec-

tion, we propose MEBN as a model that overcomes

this difﬁculty.

3 MULTI-ENTITY BAYESIAN

NETWORKS

Multi-entity Bayesian networks are the outcome of

the combination of Bayesian Networks with FOL. In

other words, in MEBN, the capability of BN to model

uncertainty is combined with the expressivity of FOL.

From a stochastic Bayesian modeling perspective, the

objective of using MEBN is to built situation speciﬁc

BN (SSBN) that are customized according to the snap

shot of the environment in this situation. In MEBN,

FOL is extended to FOBL, which is used to express

and represent knowledge. This overcomes the BN

shortcoming of being very rigid and not ﬂexible to

model dynamic environments.

More speciﬁcally, from the FOL perspective,

FOBL extends FOL with the ability to model uncer-

tainty. A MEBN theory, expressed with FOBL, is the

probabilistic analogous of a FOL theory. The key fea-

ture enabling a MEBN theory to model uncertainty is

the treatment of sentences (e.g., predicates/relations)

as random variables that can be instantiated to a spe-

ciﬁc value, belonging to a ﬁnite set. For example,

the sentence weatherGood(X,T) means that at time

T the weather is good for the X activity to be per-

formed, but when treated as random variable it may

take one of the following instances: cloudy, sunny,

warm, according to a probability distribution. In the

simplest case, a random variable can be Boolean, e.g.,

weatherGood(T) is a random variable that indicates

that the weather is good or not at time T . The random

variables/sentences represent attributes of entities and

relations among them. In MEBN, the random vari-

ables comprise a DAG, where each random variable

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

798

depends only on its parents. A set with all random

variables being instantiated is called an interpretation

of the MEBN theory. Thus, the joint probability that

combines all the local conditional distributions of the

random variables assigns a probability to each inter-

pretation.

From a Bayesian perspective, a MEBN the-

ory (MTheory) is a collection of MEBN fragments

(MFrags). An MFrag is the analogous of a BN node,

since it includes resident nodes, for which a local

conditional distribution is deﬁned. These variables

are conditioned on the input nodes, i.e., their the an-

cestors. Note that every input node in an MFrag is

a resident node in another MFrag, which is called

home MFrag. Thus, each MFrag is a fragment of the

global Bayesian network consisting of all MFrag of

the MTheory. Another component of an MFrag is the

context terms which are used to specify logical con-

straints for the instantiations of the ordinary logical

variables. We must note that, an ordinary variable

can have multiple instantiations for a single MThe-

ory interpretation. Since the random variables have

logic variables (or functions) as arguments, the result-

ing SSBN contains multiple random variables, one for

each argument instantiation. Nevertheless, local dis-

tributions can be designed with the ability to take into

account the volatile number of parents. Note that this

is the core mechanism provided by FOBL for the con-

struction of SSBN.

The ultimate goal of modeling with MEBN is in-

ference, which provides us with the ability to ana-

lyze observations, taken from the real world and draw

conclusions. Inference is performed in SSBN that

result based on evidence. There are two steps in

SSBN construction. In the ﬁrst step, new evidence

are incorporated in the MTheory by instantiating or-

dinary variables, which enables the construction of

the SSBN that models the speciﬁc situation. Other

evidence are observations of a subset of the random

variables. Thus, before inference, these variables are

instantiated to their observations (i.e., they are the ob-

served variables). Then, Bayesian inference provides

the posterior probability distribution of the unknown

random variables we want to estimate. This posterior

distribution can also be used to learn the conditional

distributions the target random variables.

With this position paper, we aim to highlight

MEBN as a knowledge representation and analysis

tool for the ICH domain. Speciﬁcally, our goal is to

recognize ICH concepts, such as dance types, singing

styles, etc., in ICH content, based on their formal def-

inition in a knowledge representation schema. This

schema has been developed with consultation from

the domain knowledge experts and it is expected to

boost the analysis performance. The concepts meant

to be detected are manifested in ICH content by per-

formers (singers, dancers, etc.), which content comes

with various modalities, e.g., audio, video, motion.

Thus, we deal with multimodal analysis.

There are two main reasons we propose MEBN

for this task. The ﬁrst is the uncertainty modeling ca-

pability and the second is the situation speciﬁc con-

struction of BN that MEBN provides. For example,

regarding uncertainty, a movement pattern in a tra-

ditional dance is not always deterministically driven,

since people may chose to follow a variant of the stan-

dard dance movement. Another source of uncertainty

arises also from the inaccuracy of the basic concept

detection algorithms, e.g., some steps that comprise

the dance may not be detected. The second reason

is that, usually, it is not a priori known how many

dancers, singers, or even dances and songs are mani-

fested in a particular timespan of ICH content. SSBN

construction using FOBL can be proven very beneﬁ-

cial for dynamic modeling of such situations.

A concise example of MEBN usage for multi-

modal traditional dance modeling is presented in Fig-

ure 1. In this ﬁgure, an MTheory is presented consist-

ing of three MFrags. The ”Dance” MFrag contains

one input random variable, DanceType, with its states

being the ”dance type” instances (Tsamiko, Calus,

etc.). The resident random variables of this MFrag

are Steps(d,t1), Steps(d,t2), MusicTempo(d). The ﬁrst

two denote a sequence of steps and the third the mu-

sic tempo accompanying the dance. Due to the re-

cursive deﬁnition of the steps, there can be numer-

ous steps, depending on the number of the time vari-

ables instances. These instances depend on the ev-

idence being found in the ICH content (i.e., the time

instants). Let us suppose a particular variable instanti-

ation in order to demonstrate the mechanism that pro-

duces an SSBN. For simplicity of the demonstration,

we will work only with the Dance MFrag. Suppose

that the following logical entities have been found

as evidence: T 0, T 1, T 2, Dance1. This means that

only one dance is performed. d=Dance, starting at

time T 0 and ending at T 2 (T 0, T 1, T2 is an ordered

sequence of time instants). Regarding random vari-

ables, the observations are three consecutive steps, re-

sulting in the instantiations Step(Dance1,T0)=Right,

Step(Dance1,T1)=Right, Step(Dance1,T2)=Left, and

one tempo MusicTempo(Dance1)=Slow. The partial

SSBN produced by these instantiations is depicted in

Figure 2.

The instantiated random variables in the SSBN

of Figure 2 are the observed variables. The goal is

to estimate the posterior distribution of the Dance-

Type variable given the observations. This is achieved

Multi-entityBayesianNetworksforTreasuringtheIntangibleCulturalHeritage

799

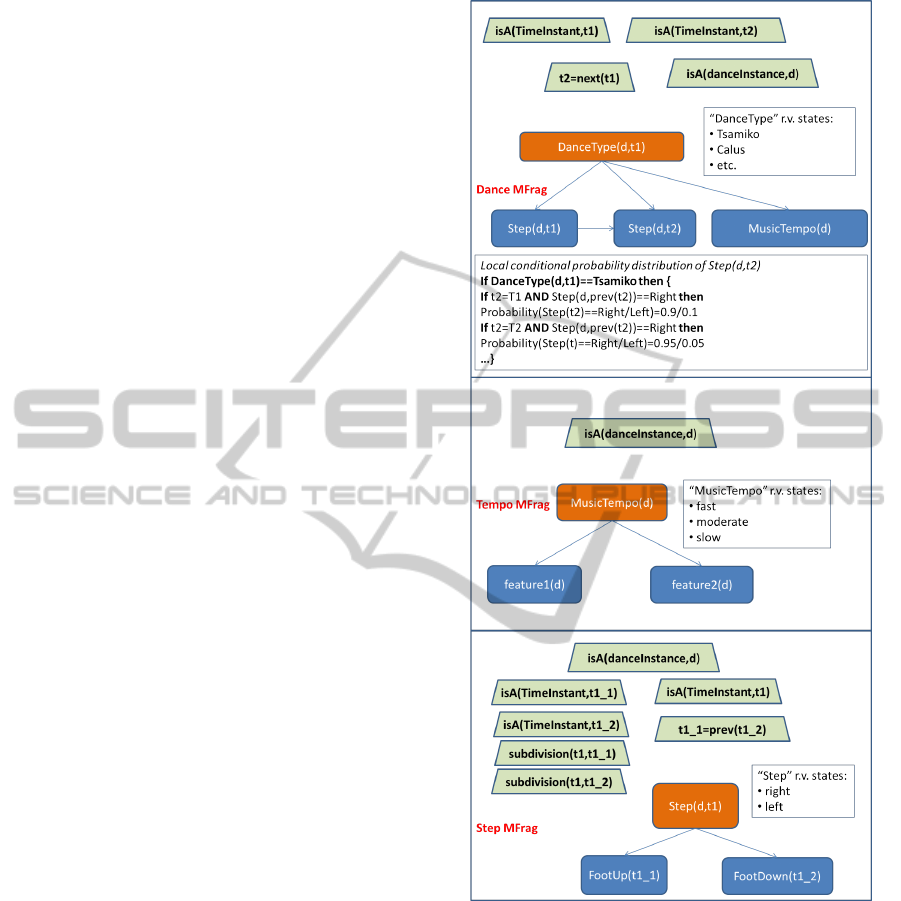
through Bayesian inference, based on the local condi-

tional distribution of the Step variables, which is de-

picted in the Steps MFrag, and the MusicTempo local

distribution. All these distributions are conditioned

on the DanceType variable. In addition, each Step

variable is conditioned on the previous, except that

for which (t

= T 0). Note that, in a more general ex-

ample, the SSBN would contain nodes from various

MFrags.

4 EXISTING LITERATURE

A number of models similar to MEBN have been

developed that represent probabilistic knowledge.

OOBN models (Koller and Pfeffer, 1997) have been

proposed as an alternative to standard BN for over-

coming the inherent inﬂexible structure of BN. An

OOBN object is an extension of a node in BN and

it is a collection of attributes of a domain. This ren-

ders OOBN more ﬂexible than BN to be customized

to situations that arise. Also, OOBN enjoy many ben-

eﬁts similar to that of object oriented programming,

such as model re-use.

Probabilistic relational models (PRMs) (Pfeffer,

2000) extend Bayesian networks more efﬁciently than

OOBN. In particular, they introduce the concept of

properties, and relations between them. Like a MEBN

theory, a PRM represents a probability distribution

over possible interpretations. Practically, the distribu-

tion assigns a probability to every possible relation in-

stantiations of the relational schema. Inference algo-

rithms in PRMs can provide, apart from the distribu-

tion, also the structure and the uncertainty underlying

it. However, OOBN and PRM expressivity is inferior

to MEBN, mainly due to the context constraints used

to enforce logical contraints on the model variables.

In (Milch and Russell, 2007), a survey about pro-

gramming languages combining, similar with FOBL,

logic and probability can be found. In these lan-

guages, inference based on probability is integrated in

the reasoning mechanism of this language. However,

there are serious limitations in this type of modeling,

such as the explicit deﬁnition of local distributions,

which renders them sub-optimal for our purpose when

compared to MEBN.

Ontologies with probabilistic extensions have

been used for ICH knowledge representation. For ex-

ample, in (Mallik et al., 2011), ontology-based map-

ping of cultural heritage content to ICH concepts

is proposed. More speciﬁcally, an ontology-based

framework is proposed that facilitates the represen-

tation of the ICH concepts, their properties and the

relationships among them. The concepts are charac-

Figure 1: MEBN example for traditional dance knowledge

representation: MTheory consisting of three MFrags. Ran-

dom variable color meaning: orange is ”input”, blue is ”res-

ident”, green is ”context constraints”. Only the local distri-

bution of Steps(d,t2) is depicted.

teristics/features (low or high level) that constitute the

semantics of the ICH content. Thus, the ontology

used in this framework includes descriptions of do-

main concepts, which descriptions are given formally

with terms of related low-level audio-visual features,

appearing in the multimedia ICH content. In this way,

a convenient semantic interpretation of the multime-

dia data is enabled. Moreover, a custom language,

the Multimedia Web Ontology Language (MOWL),

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

800

Figure 2: Example partial SSBN for evidence t =

{T 0, T 1, T 2}, d = Dance1.

is used to encode the domain knowledge.

In a closely related work (Mallik et al., 2008),

a semi-automatic ontology construction methodol-

ogy for ICH knowledge modelling is proposed. Par-

ticularly, in this work, the aim is to complement

the knowledge assisted framework for the seman-

tic analysis of cultural Indian dances presented in

(Mallik et al., 2011), i.e., detection of speciﬁc dance

styles and moves in multimedia with cultural content.

Bayesian networks and probabilistic inference for the

automatic analysis of the relations among the con-

cepts deﬁned and described by ICH experts is pro-

posed to this end. Note, however, that although the

ontology is constructed using probabilistic methods,

i.e., as a BN of concepts and relations, the BN re-

mains unchanged. This is a serious modeling handi-

cap, which does not appear in MEBN.

5 DISCUSSION

The main challenges that we expect to encounter by

the application of MEBNs for ICH are discussed next.

First and foremost, a major challenge is, as stated

previously, the inherent uncertainty in ICH knowl-

edge. This stems from the fact that there are many

cases where the performers implement an ICH ac-

tivity (e.g., dance, singing) in a non-determenistic

manner. For example, during the peformance of a

traditional dance, although the number of the steps

and their characteristics, e.g., direction, are prede-

ﬁned, the execution of each step may vary per person

and/or occasion, for this speciﬁc dance. Moreover, in

a dance, ﬁgures are performed spontaneously, rather

in a predeﬁned pattern. Thus, one aspect of this chal-

lenge is the inability of an expert to deﬁne rigously

some parts of the ICH activity that are inherently un-

certain and difﬁcult to be described with deterministic

terms. To demonstrate that using the previous exam-

ple, although the direction of each step can be strictly

deﬁned (e.g., left or right), it is sometimes not feasible

to describe quantitatively the height of the foot from

the ground during a step, the step length, or even a

precise motion trajectory of the dancers. With MEBN

we can model this uncertain knowlege using the rig-

orous framework of probabilities and Bayesian net-

works.

Lastly, the fact that MEBNs incorprate the con-

cept of ontologies into their modeling part enables

the systematical collection and formal representation

of the multiple concepts of ICH knowledge. Thus,

with MEBN we aim to also exploit the useful fea-

ture of ontologies to facilitate a convenient and with a

non prone to errors developement of the ICH knowl-

edge representation part. Thus, MEBN combine, for

this speciﬁc problem, the advantages of both worlds,

i.e., knowledge expression and representation on the

framework of ontologies and modeling uncertainty

using probabilistic models (BN).

6 CONCLUSIONS

In this paper, we propose MEBN as an answer to the

need of representing ICH domain knowledge and as a

theoretical and practical tool to model the concepts

and their relation between them. A key feature of

MEBN that we ﬁnd very useful for this case is their

built-in capability to express uncertainty that is inher-

ently present to the ICH concepts, as these are deﬁned

by the knowledge experts. Moreover, with MEBN

we can model the temporal evolution of attributes of

an ICH domain, such as the evolution of steps in a

dance or the variations of pitch in a musical perfor-

mance. Lastly, we mention models similar in spirit

with MEBN that merge ﬁrst order logic with proba-

bilistic models.

ACKNOWLEDGEMENTS

The research leading to these results has received

funding from the European Community’s Sev-

enth Framework Programme (FP7-ICT-2011-9) under

grant agreement no FP7-ICT-600676 ”i-Treasures:

Intangible Treasures - Capturing the Intangible Cul-

tural Heritage and Learning the Rare Know-How of

Living Human Treasures”.

REFERENCES

Baader, F., Calvanese, D., McGuinness, D., Nardi, D., and

Patel-Schneider, P. F. (2003). The Description Logic

Handbook: Theory, Implementation and Applications.

Cambridge University Press.

Multi-entityBayesianNetworksforTreasuringtheIntangibleCulturalHeritage

801

Bishop, C. M. (2006). Pattern Recognition and Ma-

chine Learning (Information Science and Statistics).

Springer-Verlag New York, Inc.

Davis, E. (1990). Representations of Commonsense Knowl-

edge. San Mateo, California: Morgan Kaufmann.

Doerr, M. (2003). The cidoc conceptual reference model:

an ontological approach to semantic interoperability

of metadata. AI Magazine, 69:(3): 75–92.

Ioannidis, K. E. R. Y. (2011). A labanotation based ontol-

ogy for representing dance movement. In 9th Interna-

tional Gesture Workshop, Athens, Greece, May.

Koller, D. and Pfeffer, A. (1997). Object-oriented bayesian

networks. In Uncertainty in Artiﬁcial Intelligence:

Proceedings of the Thirteenth Conference, San Fran-

cisco, CA: Morgan Kaufmann.

Laskey, K. B. (2008). Mebn: A language for ﬁrst-order

bayesian knowledge bases. Artiﬁcial Intelligence,

172:(2–3), 140178.

Mallik, A., Chaudhuri, S., and Ghosh, H. (2011).

Nrityakosha: Preserving the intangible heritage of in-

dian classical dance. ACM Journal on Computing and

Cultural Heritage, 4:(3), 11.

Mallik, A., Pasumarthi, A. P., and Chaudhury, S. (2008).

Multimedia ontology learning for automatic anno-

tation and video browsing. In 1st ACM Interna-

tional Conference on Multimedia Information Re-

trieval (MIR’08), New York,.

Milch, B. and Russell, S. (2007). First-order probabilis-

tic languages: Into the unknown. In In Proc. of

the 16th International Conference on Inductive Logic

Programming, pages 10–24.

Pfeffer, A. (2000). Probabilistic Reasoning for Complex

Systems. Stanford, CA, Stanford University.

Staab, S. and R. Studer, e. (2009). Handbook on Ontologies,

chapter 23. International Handbooks on Information

Systems, Springer.

UNESCO (2013). Convention of the safeguarding of in-

tangible cultural heritage of unesco, 2003. URL:

http://www.unesco.org/culture/ich/index.php.

Whittaker, J. (2009). Graphical models in applied multi-

variate statistics. Wiley Publishing.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

802