
Weighted Sum-rate Maximization for Multi-user Mimo-OFDM
Downlink with ZF-DPC Methods
P. Krishna
1
, T. Anil Kumar
2
and K. Kishan Rao
3
1
Department of ECE, SVS Institute of Technology, Hanamkonda, Warangal, India
2
Department of ECE, SR Engineering College, Hasanparthy, Warangal, India
3
Vaagdevi College of Engineering, Boll kkunta, Warangal, India
Keywords: Multi-user MIMO, Zero-Forcing (ZF), Dirty-paper Coding (DPC) Weighted Sum-rate, SNR.
Abstract: Multi -user MIMO techniques were born due to the urge of high data rates and spectral efficiency in 4G
systems. For scenarios with a large number of users to be served in one cell, high capacity gains can be
achieved by transmitting independent data streams to different users sharing the same time -frequency
resources through the use of MIMO precoding. Linear precoding is employed in MU-MIMO
communication system to improve the system capacity and to minimize the receiver complexity. The
previous works on optimization algorithm to design a linear precoder to maximize the system capacity is
assumed to have perfect channel state information (CSI) at the base station (BS).However the CSI available
at the BS is imperfect due to channel estimation errors. With enough channel state information (CSI) at the
transmitter, MIMO precoding allows to increase multi-user diversity gain. However, without a correct
precoding vector selection, the interference between users can seriously degrade the overall network data
rate. In a close-loop configuration, the base station (BS) receives from each user the preferred precoding
vector and modulation and coding scheme (MCS).To achieve the highest multi -user diversity gains and
avoid users interference, the BS needs to recalculate the precoding vector and MCS for each user. Weighted
sum rate maximization is also considered, and qualification of throughput difference between two strategies
is performed. In this process, it is shown that allocating the user powers in direct proportional to user
weights asymptotically maximizes weight sum rate. The goal of this paper is to investigate the performance
and complexity of state -of-the - art methods for calculation of precoding vectors such as zero –forcing (ZF)
or mean square error (MMSE) and Dirty paper Coding(DPC).
1 INTRODUCTION
Multiple input -multiple output (MIMO) techniques
are essential features in 3GPP LTE and LTE -A
systems in order to achieve high data rates and high
system capacity. When a large number of users need
to be served in one cell, high capacity gains can be
achieved by transmitting independent data streams
to different users sharing the same time - frequency
resources. This is called multi - user MIMO (MU -
MIMO) and it can be realized through the use of
MIMO precoding. Several precoding techniques
applicable to the LTE standard have been introduced
and discussed in the past few years (Zhou et al.,
2009); (Cho et al., 2010); (Schwarz et al., 2010);
(PHILIPS, 2007); (Schwarz et al., 2010); (Ribeiro et
al., 2008); (Liu et al., 2012).
In a closed-loop configuration, the receiving user
obtains downlink channel state information (CSI) by
calculating three values that are feed backed to the
base station (BS): channel quality indicator (CQI),
rank indicator (RI), and precoding matrix indicator
(PMI). With this information, the BS becomes aware
of the channel quality of the users and can therefore
choose the proper transmit modulation and coding
schemes (MCS) for each of them. On the other hand,
the PMI shows the precoding vector preferred by the
user according to a certain criterion, for example,
mutual information. However, these CSI feedback
values reported by each user do not consider the
interference created to the rest of the users on the
same time-frequency resources. The base station
should recalculate the PMI and MCS in order to
avoid user interference. If we directly apply the CSI
values feed backed by the users in a MU-MIMO
transmission, the system performance can be
14
Krishna P., Anil Kumar T. and Kishan Rao K..
Weighted Sum-rate Maximization for Multi-user Mimo-OFDM Downlink with ZF-DPC Methods.
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

degraded significantly due to interferences between
users.
Dirty paper coding (DPC) was proved to achieve
the capacity region of the multiple antenna broadcast
channel (BC). However, implementation of DPC
requires significant complexity at both transmitter
and receiver, and the problem of finding practical
dirty paper codes close to the capacity limit is still
open. On the other hand, linear precoding is a low
complexity but suboptimal transmission technique
(with complexity roughly equivalent to point-to-
point multiple- input–multiple-output (MIMO)) that
is able to transmit the same number of data streams
as a DPC-based system. Linear precoding therefore
achieves the same multiplexing gain (which
characterizes the slope of the capacity versus SNR
curve) as DPC, but incurs an absolute rate/power
offset relative to DPC.
2 SYSTEM MODEL
We consider an MU-MIMO system with one BS and
K mobile station (MS), where the BS is equipped
with M antennas and each MS with N antennas. The
point-to multipoint MU-MIMO system is employed
in downlink transmission. We consider the channel
as the flat fading MIMO channel with Rayleigh
distribution. Assuming that the transmitted signal is
linearly precoded at the base station, the vector of
the received signals at the K receivers is given by:
(1)
Where, H is the KXM channel matrix, x is the vector
consisting K independent streams of data With zero
mean and normalized variance and n is and additive
white Gaussian noise vector. Due to errors
introduced by channel estimation, reciprocity
mismatch, quantization or delay we assume that the
base station has only an estimate of the true channel
response H that we denoted by H
.In the channel
estimation model that we consider here
HH
H
(2)
Where given the estimated channel matrix
, we
assume that the estimation error matrix H
has K*M
independent elements with zero mean and estimation
error variance denoted by
. Also we assume that H
is independent of the data vector x and the Gaussian
noise vector n.
……
(3)
√
……
√
(4)
Where x is the transmitted symbol vector with K
data streams, W is the precoding matrix with K
Precoding vectors, and [ ·]
T
denotes the matrix
transposition.
=
(5)
The channel matrix
can be assumed as the virtual
channel matrix of user k after precoding. At the
receiver, a linear receiver
is exploited to detect
the transmit signal for the user k. The detected signal
of the k
th
user is
(6)
The linear receiver
can be designed by ZF or
MMSE criteria, and linear MMSE will obtain better
performance. In order to simplify the analysis, the
power allocation is assumed as = p/k/N0 and linear
MMSE MIMO detection is used in this paper as
.
.
.
-1
(7)
Where I is identity matrix.
.
(8)
SINR
H
H
T
∑
H
H
T
,
(9)
3 HIGHEST SNR SUM-RATE
CALCULATIONS
In this section, we compute the affine
approximations to the dirty paper coding sum rate
and the linear precoding sum rate at high SNR. In
the following section, these expressions are used to
quantify the sum rate degradation incurred by linear
precoding relative to DPC.
3.1 Dirty Paper Coding
The sum rate by DPC, which achieves the sum
capacity, can be written by the duality of the MIMO
broadcast channel (BC) and the MIMO multiple-
access channel (MAC)
,
(10)
Where
represents the transmit covariance
matrices in the dual MAC. No closed –form
solutions to (10) is know to exist, but it has shown
that
,
convergence to the capacity of the
point-point MIMO channel with transfer matrix H
WeightedSum-rateMaximizationforMulti-userMimo-OFDMDownlinkwithZF-DPCMethods
15
whenever :
Theorem1: When and H has full row rank
→
,
.
.
0
(11)
Using this result we can make a few important
observations regarding the optimal covariance
matrices at high SNR. Since
.
.
(12)
Choosing each of the dual MAC covariance matrices
as
in (10) achieve the sum capacity at
asymptotically high SNR.Thus uniform power
allocation across the KN antennas in the dual MAC
is asymptotically optimal an approximation for the
sum rate can be defined as:
,
≅
|
(13)
Where ≅ refers to equivalence in the limit (i.e., the
difference between both sides converges to zero
as→∞).Since the MIMO BC and the
point-to-point MIMO channel are equivalent at
high SNR (Theorem 1), the high SNR results
developed in (PHILIPS, 2007) directly apply to the
sum capacity of the MIMO BC channel.
4 RESULT ANAYSIS
Figure 1 plots the ZF and DPC throughputs for two
five receiver systems. In a five-transmit-antenna/five
receiver system (M = K = 5,N = 1), The figure
shows that it gives accurate results throughout the
entire SNR range. Throughput curves for a (M =
10,K = 5,N = 1) system are also shown.
Figure 1: DPC vs ZF at High SNR.
The ZF power penalty is only 1.26 dB, which is
reasonably close to the asymptotic penalty of 1.67
dB, increasing the number of transmit antennas from
5 to 10 shifts the sum capacity curve by 5.59 dB, but
improves the performance of ZF by 9.88 dB. This is
because ZF gains the increase in the sum capacity,
along with the significantly decreased ZF penalty
due to the increased number of transmit antennas
(5.55 dB to 1.26 dB). Thus adding transmit antennas
has the dual benefit of increasing the performance of
DPC as well as reducing the penalty of using low-
complexity ZF.
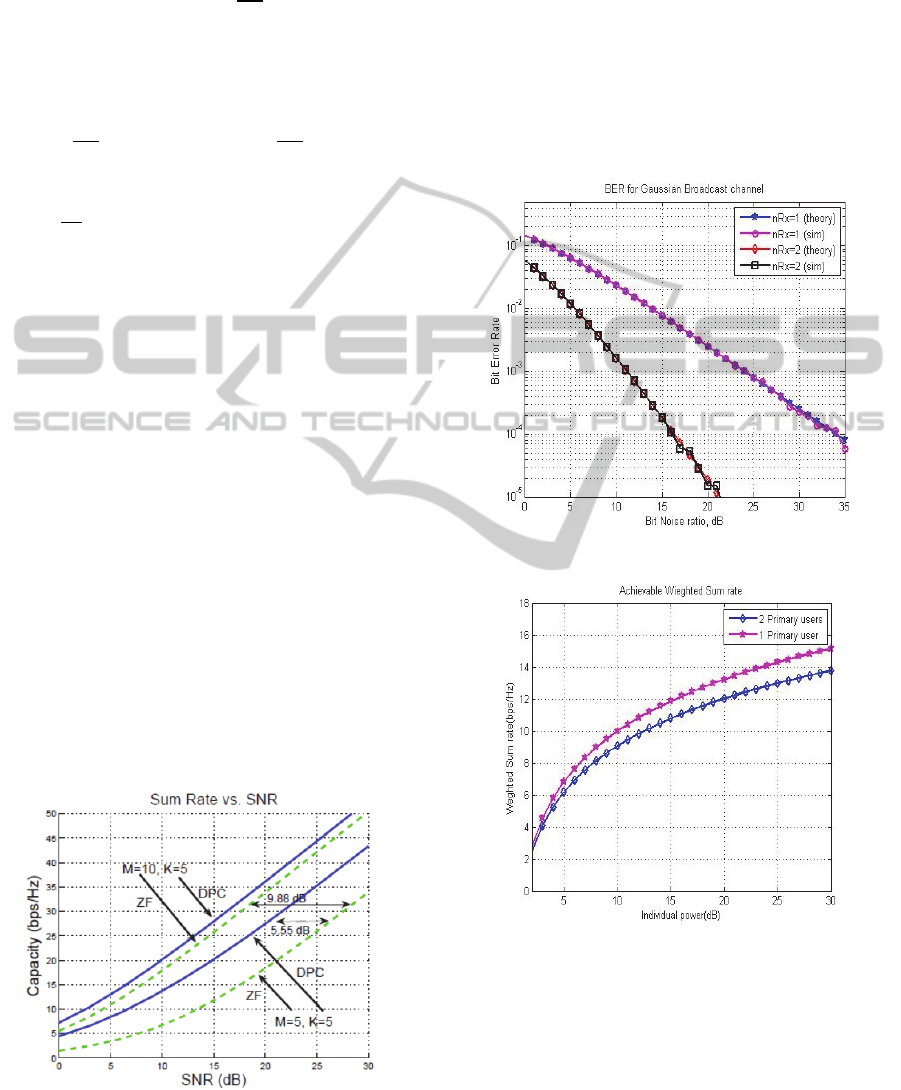
Figure 2: BER for Gaussian error BC channel.
Figure 3: Achievable weighted sum-rate.
5 CONCLUSIONS
We have investigated the difference between the
throughputs achieved by DPC relative to those
achieved with linear precoding strategies. When the
aggregate number of receive antennas is equal or
slightly less than the number of transmit antennas,
PECCS2014-DoctoralConsortium
16

linear precoding incurs a rather significant penalty
relative to DPC, but this penalty is much smaller
when the number of transmit antennas is large
relative to the number of receive antennas.
Additionally, one interesting finding is that
allocating power directly proportional to user
weights is asymptotically optimal for DPC at high
SNR. This simple yet asymptotically optimal power
policy may prove to be useful in other setting such
as opportunistic scheduling.
REFERENCES
Y. Zhou, B. Clerckx and S. Kim, "Flexible Multi-user
MIMO with Limited Feedback" IEEE Vehicular
Technology Conference (VTC Spring), Barcelona,
Spain, April 26 -29, 2009.
Yong Soo Cho, Jaekwon Kim, Won Young Yang, and
Chung G. Kang, “MIMO - OFDM Wireless
Communications with MATLAB,” Wiley, 2010
S. Schwarz, C. Mehlf ̈uhrer, and M. Rupp, “Calculation of
the spatial preprocessing and link adaption feedback
for 3GPP UMTS/LTE,” in Wireless Advanced
(WiAD), 2010 6th Conference on, (London, UK), June
2010.
Philips,“Definition of PMI / CQI feedback calculation for
MUMIMO,” R1-07 3141, 3GPP TSG RAN WG1
#49bis,Orlando, U.S.A., 25
th
-29th June 2007
S. Schwarz, M. Wrulich, and M. Rupp, “Mutual
Information based of the Precoding Matrix Indicator
for 3GPP UMTS/LTE,” in Proc. IEEE Workshop on
Smart Antennas 2010, (Bremen, Germany),February
2010.
Ribeiro, C.B. Hugl, K. , Lampinen, M. ,Kuusela, M. ,
“Performance of linear multi - user MIMO precoding
in LTE System,” ISWPC, May 7 -9, 2008
Lingjia Liu, Runhua Chen, Stefan Geirhofer, Krishna
Sayana, Zhihua Shi, and Yongxing Zhou, “Downlink
MIMO in LTE -Advanced: SU - MIMO vs. MU -
MIMO,” IEEE Communications Magazine, Feb. 2012,
pp. 140 - 147.
A. Lozano, A. M. Tulino, and S. Verdú, “High SNR
power offset in multiantenna communication,” IEEE
Trans. Inf. Theory, vol. 51, no. 12, pp. 4134–4151,
Dec. 2005.
WeightedSum-rateMaximizationforMulti-userMimo-OFDMDownlinkwithZF-DPCMethods
17
