De Novo Short Read Assembly Algorithm with Low Memory Usage

Yuki Endo

, Fubito Toyama

, Chikafumi Chiba

, Hiroshi Mori

and Kenji Shoji

Graduate School of Engineering, Utsunomiya University, Yoto 7-1-2, Utsunomiya, Tochigi, 321-8585, Japan

Faculty of Life and Environmental Sciences, University of Tsukuba, Tennoudai 1-1-1, Tsukuba, Ibaraki 305-8572, Japan

Keywords:

Bioinfomatics, Next Generation Sequencing, De Novo Assembly

Abstract:

Determining whole genome sequences of various species has many applications not only in biological system,

but also in medicine, pharmacy and agriculture. In recent years, the emergence of high-throughput next-

generation sequencing technologies has dramatically reduced time and costs for whole genome sequencing.

These new technologies provide ultrahigh throughput with lower unit data cost. However, the data are very

short length fragments of DNA. Thus, developing algorithms for merging these fragments is very important.

Merging these fragments without reference data is called de novo assembly. Many algorithms for de novo

assembly have been proposed in recent years. Velvet, one of the algorithms, is famous because it has good

performance in terms of memory and time consumption. But memory consumption increases dramatically

when the size of input fragments is huge. Therefore, it is necessary to develop algorithm with low memory

usage. In this paper, we propose an algorithm for de novo assembly with lower memory. In our experiments

using E.coli K-12 strain MG 1655, memory consumption of the proposed algorithm was one-third of that of

Velvet.

1 INTRODUCTION

Determining whole genome sequences of various

species has many applications not only in biologi-

cal system, but also in medicine, pharmacy and agri-

culture. In recent years, the emergence of high-

throughput next-generation sequencer (NGS) tech-

nologies has dramatically reduced time and costs for

whole genome sequencing. These new technologies

provide ultrahigh throughput with lower unit data

cost. However, many very small fragments (fewer

than 100 base pair) of DNA are sequenced in these

technologies. The fragments are typically called

reads. The precision of NGS is not perfect. Therefore,

the reads obtained by NGS might include sequencing

errors. Thus, developingalgorithms for mergingthese

reads is very important. Merging these reads without

reference data is called de novo assembly.

The de novo assembly algorithms can be classi-

ﬁed into two approaches by its features : overlap-

layout-consensus (OLC) and de Bruijn graph. OLC

approaches relies on an overlap graph. Edena (Her-

nandez et al., 2008), MIRA (Chevreux et al., 2004),

Celera (Miller et al., 2008), SSAKE (Warren et al.,

2007), and VCAKE (Jeck et al., 2007) assemblers

are based on OLC approach. In OLC strategy, pair-

wise overlaps are found by all-againtst-all pair-wise

comparison. Overlap graphs are constructed from

pair-wise overlaps. In overlap graphs, a vertex rep-

resents a read and an edge denotes an overlap be-

tween two connected vertices (reads). Consensus se-

quences are determined by tracing paths in the graph.

On the other hand, Velvet (Zerbino and Birney, 2008),

ABySS (Simpson et al., 2009), ALLPATHS (Butler

et al., 2008), and SOAPdenovo (Li et al., 2010) as-

semblers are based on de Bruijn graph approach. In

the de Bruijn graph, a vertex represents a sequence of

k bases (k-mer), where k is any positive integer. An

edge represents an overlap of k-1 bases. Thus, two

connected vertices denote a k-1 overlap between their

vertices (k-mers). After the de Bruijn graph was con-

structed from reads obtained by NGS, contigs are de-

termined by tracing paths in the graph. The de Bruijn

graph approach is most widely applied to the short

reads from Solexa and SOLiD platforms. In this ap-

proach, ﬁxed-length (k-1) overlaps are found and re-

dundant k-mers (subsequence) are compressed. Thus,

it is suitable for assembling vast quantities of short

reads. Velvet is one of the most popular de novo as-

sembler based on the de Bruijn graph. However mem-

ory consumption increases dramatically when the size

of input reads is huge (more than several gigabytes).

Therefore it is hard to use Velvet for huge scale as-

sembly.

215

Endo Y., Toyama F., Chiba C., Mori H. and Shoji K..

De Novo Short Read Assembly Algorithm with Low Memory Usage.

DOI: 10.5220/0004881002150220

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2014), pages 215-220

ISBN: 978-989-758-012-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

In this paper, we propose an algorithm for huge

scale de novo assembly with low memory usage. Al-

though our algorithm is based on de Bruijn graph ap-

proach in the same way as Velvet, edge information

is not kept in main memory. Thus, the amount of

memory can be reduced greatly in our method. In

our experiments using E.coli K-12 strain MG 1655,

the results showed that maximum memory consump-

tion of the proposed algorithm was one-third that of

Velvet. Furthermore, the running time of proposed

method was also faster than that of Velvet.

2 AN ASSEMBLY ALGORITHM

WITH LOW MEMORY USAGE

In this paper, we propose an algorithm for huge scale

de novo assembly with low memory usage. Figure 1

shows the outline of our algorithm. First, all k-mers

obtained by dividing reads are recorded. At the same

time, the number of occurrences of each k-mer is also

counted. Second, the de Bruijn graph is constructed

using k-mers. Then, the graph is partitioned into sub-

graphs such that the subgraph has a simple path or a

simple cycle. The simple path is a path in the graph

which does not have repeating vertices or edges. The

subgraphs are connected to make a larger simple path.

The number of occurrences of a k-mer is used to se-

lect a connection path. Finally, contigs are generated

by tracing vertices in the each connected graphs.

2.1 Extraction of k-mers

k-mers are extracted from all reads. They are kept in

database in memory as “k-mer integer”. As shown

in Table 1, k-mer integer is a representation of one-

to-one correspondence between k-mer and integer.

Speciﬁcally, bases “A”, “C”, “G”, and “T” correspond

to quaternary digits 0, 1, 2, and 3 respectively. Thus, a

k-mer sequence is expressed as a quaternary numeral.

For example, a 5-mer base sequence “ACGTA” is con-

verted to the quaternary number 01230. Then, it is

converted to the decimal number 108. Thus, 108 is

k-mer integer corresponding to “ACGTA”. If a k-mer

sequence is represented by a string, memory would

be needed k bytes. In the k-mer integer representa-

tion, the amount of memory for k-mer sequences can

be reduced to one fourth of that of the string repre-

sentation. Using k-mer integer is not only superior

to memory usage, but also to processing time. For-

ward and reversecomplement k-mer sequences are re-

garded as the same sequence in our method. Either of

the two complementary sequences is registered in the

database on main memory.

Figure 1: Outline of the proposed method.

In this work, k-mer integer and the number of oc-

currences of the k-mer corresponding to the k-mer in-

teger are kept in main memory. In order to achieve

low memory usage, other data (such as edges in de

Bruijn graph) is not kept in the memory. K-mer se-

quence in which the number of occurrences of the

sequence is small (less than a threshold) is not used

in the graph construction because it is suspected that

such k-mer sequences contain sequencing errors. In

our experiments, the threshold was set to 5. Figure

2 shows the extraction of k-mer and the contents of

database in the proposed method.

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

216

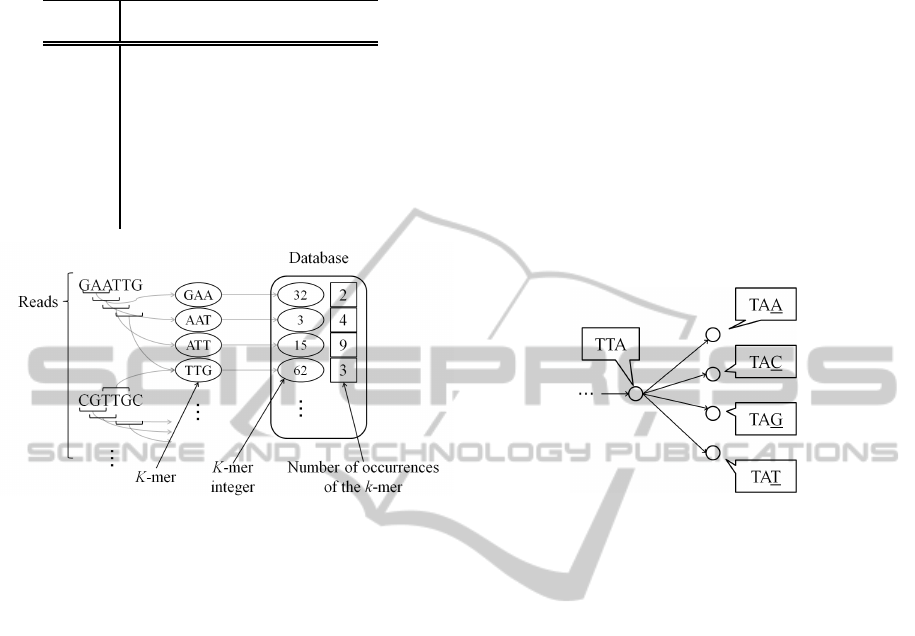
Table 1: k-mer sequence corresponding to k-mer integer

(in case of 5-mer).

k-mer Quaternary Binary

k-mer integer

(decimal)

AAAAA 0 0 0

AAAAC

1 1 1

AAAAG

2 10 2

AAAAT

3 11 3

AAACA

10 100 4

AAACC

11 101 5

AAACG

12 110 6

AAACT

13 111 7

AAAGA

21 1000 8

AAAGC

22 1001 9

Figure 2: Extraction of k-mer and the contents of database

in the proposed method (in case of 3-mer).

2.2 Graph Construction

The de Bruijn graph is constructed using k-mers. In

the de Bruijn graph, each vertex represents a k-mer.

An edge represents an overlap of k-1 bases. Thus,

two connected vertices denote a k-1 overlap between

their vertices (k-mers). For example, there is an edge

between the two vertices corresponding to “ACGTA”

and “CGTAC”. The direction of the edge is from

“ACGTA” to “CGTAC”.

The contigs are generated by tracing vertices in

the de Bruijn. However, de Bruijn graph constructed

from short reads has numerous branches and cycles.

Therefore, it is difﬁcult to ﬁnd the paths from which

contigs are constructed. The details of the method to

ﬁnd out such paths are described in Section 2.3.

In conventional algorithms using de Bruijn graph,

when the graph is constructed, edge information

about which vertices are connected to each other is

also kept in main memory. Since there are many

edges in the graph, keeping the edge information con-

sumes a huge amount of memory. In this paper,

the edge information is not kept in main memory.

Thus, although computational time for assembly is

increased, memory usage can be reduced. The ex-

istence of the edge is calculated only when it is re-

quired. Speciﬁcally, the vertices which are connected

by a directed edge from a vertex have only 4 types of

k-mers because the k-mers which are represented by

the connected vertices overlap by k-1 bases as shown

in Fig. 3. Thus, the connected vertices (k-mer se-

quences) can be obtained by checking four values of

k-mer integer in the database. By using this method,

although processing time to check the values of k-mer

integer is increased, memory for keeping connection

edge data is not required. Only the data of vertices

are kept in the database. Thus, the amount of mem-

ory can be reduced greatly in our method. The graph

construction is ﬁnished by registering the values of k-

mer integer from k-mer sequences and the number of

occurrences of each k-mer on our database.

Figure 3: Example of 4 types of k-mers which are connected

to the current vertex (in case of 3-mer).

2.3 Edge Removal

As mentioned in Section 2.2, the constructed graph

has numerous branches and cycles. Consequently,

it is important to select the edges on the path from

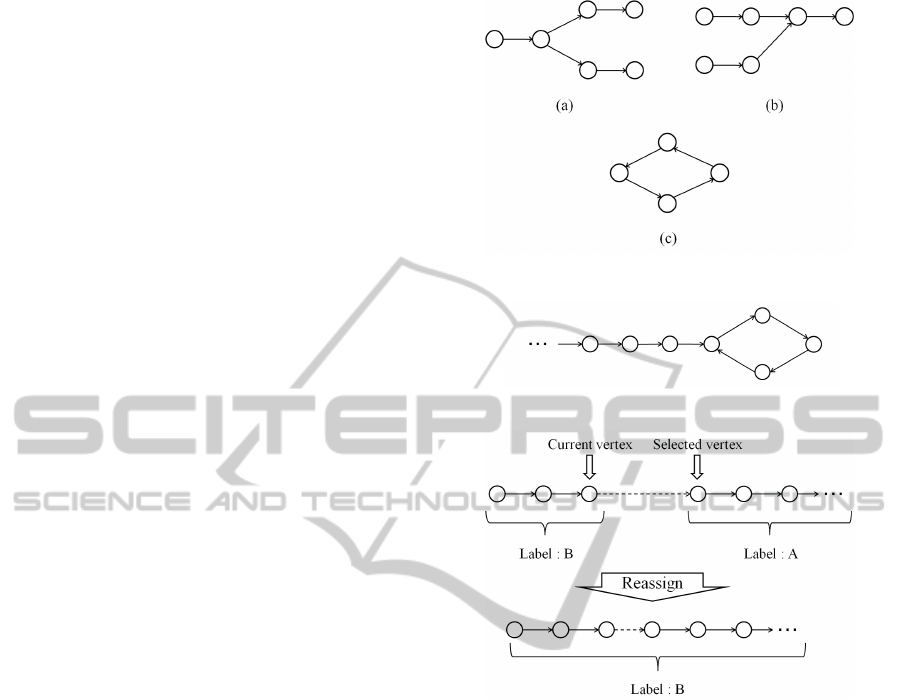
which a contig is constructed. Figure 4 shows exam-

ples of branches. A vertex has multiple edges in Fig.

4 (a). A vertex has multiple edges from other vertices

in Fig. 4 (b). Although the outdegree of the vertices

with branches is two in Fig. 4, the maximum number

of the out degree is four. Figure 4 (c) shows an ex-

ample of a cycle. Actually, these branches and cycles

are intricately intertwined. A path from the directed

graph in which branches and cycles are included is

needed to generate a contig. It is necessary to deter-

mine the unique simple path based on some criteria.

The edge removal process is as follows.

1. A start vertex (k-mer) which has the largest num-

ber of occurrences is selected.

2. The start vertex is set to the current vertex.

3. The existence of the vertices which are connected

to the current vertex is checked.

(a) If one connected vertex is found, the vertex is

set to the current vertex. Go to 3.

(b) If multiple connected vertices are found, one of

them is set to the current vertex. The details of

DeNovoShortReadAssemblyAlgorithmwithLowMemoryUsage

217

the vertex selection are described in later in this

section. Go to 3.

vertex is regarded as the end vertex. Go to 4.

4. The existence of the vertices which are not se-

lected yet is checked.

(a) If the vertices which are not selected are found,

the new start vertex which has the largest num-

ber of occurrences is selected from the vertices

which are not selected yet. Go to 2.

(b) If the vertices which are not selected are not

found, the process is ﬁnished.

In this process, the vertices which are included in a

path are assigned to same label. A path from the start

vertex to the end vertex represents a subgraph. Multi-

ple subgraphs are created in this process;

The details of the vertex selection in which

branches and cycles are included are described as be-

low. When there are multiple out going edges from

the current vertex as shown Fig. 4 (a), the edge con-

nected to the vertex in which the number of occur-

rences of k-mer is the largest is selected and the other

outgoing edges are removed. When there are multi-

ple incoming edges as shown in Fig. 4 (b), the edge

is selected by the same process and other incoming

edges are removed. In this edge selection process,

when the difference of occurrences of k-mer between

the selected vertex and unselected vertices is less than

a threshold, the current vertex is regarded as the end

vertex and new start vertex is selected again. When

the label of the selected vertex is the same as that of

the current vertex as shown in Fig. 4 (c) (in the case

of cycle), the current vertex is regarded as the end ver-

tex. In many cases, a cycle is a part of a path as shown

in Fig. 5. The vertices which are in the cycle are as-

signed to the new label in this case. Thus, a cycle is

separated from the current scanning path.

Furthermore, there is the case in which the se-

lected vertex has been assigned to other label as

shown in Fig. 6. In this case, all the vertices in the

path which has the selected vertex are reassigned to

the label of the current vertex.

2.4 Subgraph Connection and Contig

Construction

To construct a longer path, subgraphs obtained by the

process described in previous section are connected.

The outline of the subgraph connection process is as

follows. First, a subgraph with simple path is se-

lected. The subgraphs with the longest path is se-

lected from subgraphs which have not been selected.

Figure 4: Examples of branches and cycle.

Figure 5: Example of a cycle which is a part of a path.

Figure 6: Example of the label reassignment.

However the subgraph with a simple cycle can be se-

lected more than once. This subgraph is set to the start

subgraph. Next, the subgraph in which the start vertex

or the end vertexare connected to the end vertexor the

start vertex of the selected subgraph are searched. The

details of connection of the subgraph with a simple

cycle are described in later in this section. This pro-

cess is realized by checking k-mer integer described

in the previous section. If such subgraph is found,

the start (end) vertex is connected to the end (start)

vertex, and the two subgraph are merged into a sin-

gle subgraph. This graph expanding process is re-

peated while merging graph exists. If there are multi-

ple subgraphs which can be connected, the subgraph

with longer simple path is connected. Figure 7 shows

an example of connecting subgraphs. The example

in this ﬁgure is the case of left side connection. The

same process is repeated on the right side.

In addition, the subgraph with a simple cycle is

connected as shown in Fig. 8. In this ﬁgure, The ver-

tex v

is start vertex of subgraph G

path

with a simple

path. The vertex v

is contained in subgraph G

cycle

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

218

with a simple cycle. If the k-mers of the vertex v

and

overlap each other, the vertex v

which connected

to v

is checked. (v

is also contained G

cycle

.) v

and

are regarded as the start( or end) vertex. Then, the

path

and G

cycle

are merged. If the vertex v

is con-

nected to other vertex which is included in other sub-

graph, These subgraphs are merged again as shown in

Fig. 8.

Figure 7: Example of subgraphs connection.

Figure 8: Example of the connection of subgraph with a

simple cycle.

After the subgraph connection, the list of the ver-

tices is obtained by tracing the path which is included

in a subgraph. The contig is generated by merging k-

mers which are referenced from the vertices as shown

in Fig. 9. The ﬁnal contigs are obtained by repeating

this process for all subgraphs. In our experiments, the

contigs which are longer than a threshold are output.

In our experiments, the threshold was set to length of

the reads.

3 EXPERIMENTAL RESULTS

To evaluate the performance of the proposed method,

we compare the performance of our method with that

of Velvet which is one of the most popular de novo

assembler based on the de bruijn graph. E.coli K-

12 strain MG 1655 for which the complete DNA se-

quence is known was used in our experiments. The

Figure 9: Generation of contigs.

sequence length is approximately 4.6Mbp. The real

dataset with 35bp reads was made by a computer from

the complete DNA sequence of E.coli K-12 strain

MG 1655. Experiments were conducted using reads

(35bp) that generated by the NGS from the genome.

Experiments were run with the k-mer size of 19, 21,

23, 25, 27, 29, and 31. We assessed the maximum

memory consumption, the running time, the contig

length, and the accuracy of contigs.

Figure 10 and Fig. 11 show the maximum mem-

ory usage and the running time for each k-mer, re-

spectively. As shown in Fig. 10, the memory usage of

the proposed algorithm is one-third of that of Velvet.

Therefore, the purpose of this research was achieved

because the amount of memory was reduced greatly.

Moreover the average running time of the proposed

method was approximately 41% of that of Velvet. In

the proposed method, the connection between vertices

is checked each time when a path is traced. Thus,

the running time to ﬁnd the connection between ver-

tices is increased. However, since the path tracing

algorithms for resolving branches and cycles is very

simple, the average running time was faster in the

proposed method. In addition, the running time was

shortened according to the increase of the k-mer size.

On the other hand, the change of the k-mer size had

hardly inﬂuence on the memory.

Table 2 shows the results of the contig quantity of

the proposed method and Velvet. Maximum length,

N50 length, the number of contigs, and total bases

are shown in Table 2. The N50 length is deﬁned as

the length of the shortest contig such that the sum of

contigs of equal length or longer is at least 50% of

the total length of all contigs. Table 3 shows the re-

sults of the accuracy of the contigs. Percentage of

the genome covered and average error rate are shown

in Table 3. The maximum length of the proposed

method was shorter than that of Velvet as shown in Ta-

ble 2. Moreover, N50 length of the proposed method

was shorter than that of Velvet. The main reason for

these results is that the path tracing algorithm for re-

DeNovoShortReadAssemblyAlgorithmwithLowMemoryUsage

219

solving branches and cycles is very simple in the pro-

posed method. Thus, the maximum length and N50

length would be better by modifying the path trac-

ing algorithm. On the other hand, the error rate of

the proposed method was lower than that of Velvet.

The genome coverage was slightly lower than that of

Velvet. These results indicate that there are not large

differences in the contig quantity from path tracing

algorithms.

Figure 10: Comparison of maximum memory consumption.

Figure 11: Comparison of running time.

Table 2: Comparison of quantity of contigs.

Maximum

length (bp)

N50

(bp)

# of

contigs

Total

(bp)

Proposed method 74,708 17,038 631 4,560,202

Velvet

81,421 22,870 754 4,544,229

Table 3: Comparison of precision of contigs.

Genome

covered (%)

Average

error rate (%)

Proposed method 99.59 5.71

Velvet

99.89 7.29

4 CONCLUSIONS

In this paper, we propose an algorithm for huge scale

de novo assembly with low memory usage. In our ex-

periments using E.coli K-12 strain MG 1655, the re-

sults showed that maximum memory consumption of

the proposed algorithm was one-third that of Velvet.

Furthermore, the running time of proposed method

was also faster than that of Velvet. These results

showed that the proposed method outperformed Vel-

vet for the memory and the running time. On the other

hand, contig quality obtained by the proposed method

was slightly worse than that of Velvet. To improve

the accuracy of the contigs, we need to modifying the

path tracing algorithm in the future works.

REFERENCES

Butler, J., MacCallum, I., Kleber, M., Shlyakhter, I. A.,

Belmonte, M. K., Lander, E. S., Nusbaum, C., and

Jaffe, D. B. (2008). ALLPATHS: de novo assembly

of whole-genome shotgun microreads. Genome Res.,

18(5):810–820.

Chevreux, B., Pﬁsterer, T., Drescher, B., Driesel, A. J.,

Muller, W. E., Wetter, T., and Suhai, S. (2004). Us-

ing the miraEST assembler for reliable and automated

mRNA transcript assembly and SNP detection in se-

quenced ESTs. Genome Res., 14(6):1147–1159.

Hernandez, D., Francois, P., Farinelli, L., Osteras, M., and

Schrenzel, J. (2008). De novo bacterial genome se-

quencing: millions of very short reads assembled on a

desktop computer. Genome Res., 18(5):802–809.

Jeck, W. R., Reinhardt, J. A., Baltrus, D. A., Hicken-

botham, M. T., Magrini, V., Mardis, E. R., Dangl,

J. L., and Jones, C. D. (2007). Extending assembly

of short DNA sequences to handle error. Bioinformat-

ics, 23(21):2942–2944.

Li, R., Zhu, H., Ruan, J., Qian, W., Fang, X., Shi, Z., Li,

Y., Li, S., Shan, G., Kristiansen, K., Li, S., Yang, H.,

Wang, J., and Wang, J. (2010). De novo assembly

of human genomes with massively parallel short read

sequencing. Genome Res., 20(2):265–272.

Miller, J. R., Delcher, A. L., Koren, S., Venter, E., Walenz,

B. P., Brownley, A., Johnson, J., Li, K., Mobarry,

C., and Sutton, G. (2008). Aggressive assembly of

pyrosequencing reads with mates. Bioinformatics,

24(24):2818–2824.

Simpson, J. T., Wong, K., Jackman, S. D., Schein, J. E.,

Jones, S. J., and Birol, I. (2009). ABySS: a parallel

assembler for short read sequence data. Genome Res.,

19(6):1117–1123.

Warren, R. L., Sutton, G. G., Jones, S. J., and Holt, R. A.

(2007). Assembling millions of short DNA sequences

using SSAKE. Bioinformatics, 23(4):500–501.

Zerbino, D. R. and Birney, E. (2008). Velvet: algorithms for

de novo short read assembly using de Bruijn graphs.

Genome Res., 18(5):821–829.

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

220