Analytical Modeling for Performance Evaluation of ASE Noise-impaired

Direct-detection Single-sideband Multi-band Optical OFDM Systems

Pedro Cruz, Tiago Alves and Adolfo Cartaxo

Optical Communications and Photonics Group, Instituto de Telecomunicac¸

oes, Instituto Superior T

ecnico,

Universidade de Lisboa, 1049-001 Lisboa, Portugal

Keywords:

Orthogonal Frequency Division Multiplexing (OFDM), Direct-Detection, Multi-band, Single-Sideband,

Ampliﬁed Spontaneous Emission (ASE) Noise, Optical Signal-to-Noise Ratio, Bit Error Ratio.

Abstract:

An analytical model for performance evaluation of ampliﬁed spontaneous emission noise-impaired direct-

detection single-sideband multi-band (MB) optical orthogonal frequency division multiplexing (OFDM) sys-

tems is proposed. The bit error ratio (BER) is used as ﬁgure of merit for performance evaluation, and is

obtained through an analytical relationship between the electrical signal-to-noise ratio (SNR) and the optical

SNR. The effectiveness of the analytical model is veriﬁed through comparison of the BER estimates provided

by the analytical model with the ones obtained using numerical simulation and the exhaustive Gaussian ap-

proach. Excellent agreement of the BER results is veriﬁed when distortion does not affect signiﬁcantly the

MB-OFDM signal performance.

1 INTRODUCTION

Orthogonal frequency division multiplexing (OFDM)

has been widely appointed as a powerful solution

to provide capacity granularity and switching capa-

bilities in optical networks (Cvijetic, 2012; Blouza

et al., 2011; Christodoulopoulos et al., 2011). Flexi-

ble bandwidth allocation was also identiﬁed as one of

the main advantages of OFDM-based networks (Arm-

strong, 2009; Shieh, 2011). Optical communication

systems have also exploited the advantages of high

spectral efﬁciency and resilience to linear ﬁber ef-

fects that OFDM can offer (Armstrong, 2009; Low-

ery et al., 2006). Two different optical OFDM ﬂavors

have been considered in the literature: i) coherent-

detection, where a local oscillator, hybrid couplers

and several photodetectors are employed at the op-

tical receiver, and ii) direct-detection, where only

one photodetector is required at the receiver. For

systems where cost is of primary concern, such as

in metropolitan networks, OFDM systems employing

direct-detection are preferred (Kim et al., 2012).

Although optical OFDM systems have been

widely studied, the implementation of multi-band

OFDM (MB-OFDM) using direct-detection is a rela-

tively new concept (Peng et al., 2012; Li et al., 2013).

A high-speed (> 100 Gb/s) MB-OFDM system using

a direct-detection optical OFDM superchannel (sev-

eral OFDM bands) with dual carriers at both sides of

the superchannel is proposed in (Peng et al., 2012)

for long-haul networks. In that work, an analytical

form to get the optimum carrier-to-signal power ra-

tio is obtained in optical back-to-back, where only

linear noise is considered. This kind of analytical

formulation is of special interest as it allows obtain-

ing a ﬁrst estimate of system performance without

requiring extensive numerical simulations to acquire

the results. Although the system presented in (Peng

et al., 2012) has high spectral efﬁciency, it is quite

challenging to implement this MB-OFDM system in

ﬂexible metropolitan networks mainly due to huge re-

quirements for the receiver front-end bandwidth. The

optical OFDM superchannel proposed in (Li et al.,

2013), which is a variant of the MB-OFDM direct-

detection long-haul system of (Peng et al., 2012), pro-

poses the use of multiple carriers along the super-

channel. In (Li et al., 2013), a carrier supports a

few OFDM bands, targeting ultra-high capacity with

more relaxed receiver front-end bandwidth require-

ments, when comparing with the system of (Peng

et al., 2012). These two MB-OFDM systems (Peng

et al., 2012; Li et al., 2013) have proposed and

demonstrated effective direct-detection solutions for

long-haul networks. This paper considers a different

MB-OFDM system, where one carrier supports one

OFDM band. In this system, the pair OFDM band-

134

Cruz P., Alves T. and Cartaxo A..

Analytical Modeling for Performance Evaluation of ASE Noise-impaired Direct-detection Single-sideband Multi-band Optical OFDM Systems.

DOI: 10.5220/0004881301340141

In Proceedings of 2nd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2014), pages 134-141

ISBN: 978-989-758-008-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

carrier is selected by optical ﬁltering before direct de-

tection, reducing the required bandwidth of the front-

end receiver signiﬁcantly, when comparing with the

receiver bandwidth requirements of the systems pre-

sented in (Peng et al., 2012) and (Li et al., 2013). This

MB-OFDM system presents some challenges that re-

quire investigation, such as the crosstalk originated by

the ﬁnite selectivity of the optical ﬁlters or the effect

of increasing the spectral efﬁciency by reducing the

gap between the carrier and the OFDM band on the

system performance.

In this work, the performance of an ampliﬁed

spontaneous emission (ASE) noise-impaired direct-

detection single-sideband (SSB) MB-OFDM system

employing a virtual carrier per OFDM signal is ana-

lytically modeled, by using the bit error ratio (BER)

as ﬁgure of merit. Operation in optical back-to-back

is considered, as optical ﬁber impairments should not

present remarkable inﬂuence on the performance of

SSB systems.

2 SYSTEM DESCRIPTION

The model considered to describe the MB-OFDM

system in optical back-to-back is presented in Fig. 1.



ASE Noise

Loader



Band

Pass

Filter



 



DFB Laser

SSB

Filter

OFDM

Receiver

Band

Selector

SSB Transmitter

Band Receiver



MB-OFDM

Transmitter

Figure 1: MB-OFDM system model in optical back-to-

back. ASE - ampliﬁed spontaneous emission; DFB - dis-

tributed feedback; MZM - Mach-Zehnder modulator; PIN -

positive-intrinsic-negative; SSB - single-sideband.

The radiofrequency (RF) MB-OFDM signal gen-

erated at the MB-OFDM transmitter is composed by

OFDM signals (or bands) and N

RF carriers (or

virtual carriers - VCs), as depicted in Fig. 2.

The MB-OFDM system considers one VC per

OFDM band. Each pair band-VC does not interfere in

frequency with the corresponding neighboring pairs.

The virtual-carrier-to-band gap (VCBG) is selected

in order to avoid the signal-signal beat interference

(SSBI) originated by the photodetector square-law. A

MB-OFDM system design with the VC at a higher



Filter

DFB Laser

...

VC 1

VC 2

VC N

VCBG

MZM

Figure 2: Simpliﬁed scheme of a MB-OFDM signal, with

bands and N

VCs. VCBG - virtual-carrier-to-band gap.

frequency than the corresponding OFDM band is con-

sidered. At the SSB transmitter, the optical signal is

generated by a distributed feedback (DFB) laser and

the MB-OFDM signal modulates that optical signal

using a chirpless Mach-Zehnder modulator (MZM),

biased at quadrature point. The optical signal at the

MZM output is then ﬁltered by a SSB ﬁlter, creating

a SSB signal. This allows overcoming the chromatic

dispersion-induced power fading impairment caused

by the square-law photodetection of a double-sided

optical signal transmitted along a dispersive medium.

After SSB ﬁltering, an ASE noise loader adds optical

noise to the MB-OFDM signal. After ASE noise ad-

dition, the band and VC to be dropped at the receiver

are selected by the band selector (BS) optical ﬁlter.

The band receiver is composed by a positive-intrinsic-

negative (PIN) photodetector, a band pass ﬁlter (BPF)

and an OFDM receiver. The PIN converts the opti-

cal signal to an electrical signal. The BPF removes

the out-of-band noise and ﬁlters the received OFDM

signal, and the OFDM receiver digitally-converts and

demodulates the electrical signal.

3 ANALYTICAL MODELING

In this section, the analytical modeling of the signal

and noise power along the MB-OFDM system is per-

formed. The main objective is to obtain analytical ex-

pressions for the optical signal-to-noise ratio (OSNR)

and the electrical signal-to-noise ratio (ESNR) at the

BPF output. With these expressions, fast BER esti-

mates can be obtained to provide insight on the perfor-

mance of SSB MB-OFDM systems employing direct-

detection.

The RF signal at the MZM input, v

(t), can be

written as:

(t) = [s

(t) + A

(t)]

| {z }

(t)

RMS,imp

RMS,s

(t)

, (1)

with

(t) =

∑

n=1

b,n

(t)

RMS,s

b,n

(t)

, (2)

AnalyticalModelingforPerformanceEvaluationofASENoise-impairedDirect-detectionSingle-sidebandMulti-band

OpticalOFDMSystems

135

and

(t) =

∑

n=1

v,n

(t)

RMS,s

v,n

(t)

, (3)

where s

(t) is the sum of all up-converted N

OFDM

band signals, A

is the amplitude of each VC, s

(t)

is the sum of all N

VCs, s

b,n

(t) is the n-th OFDM

band, V

RMS,s

b,n

(t)

is the root-mean-square (RMS) volt-

age of s

b,n

(t), s

v,n

(t) is the n-th VC, V

RMS,s

v,n

(t)

is the

RMS voltage of s

v,n

(t), s

(t) is the MB-OFDM signal,

RMS,s

(t)

is the RMS voltage of s

(t), and V

RMS,imp

the RMS voltage imposed to the MB-OFDM signal at

the MZM input. As a note, v

(t) can be written as:

(t) = s

b,e

(t) + s

v,e

(t), (4)

with











b,e

(t) =

RMS,imp

RMS,s

(t)

(t),

v,e

(t) =

RMS,imp

RMS,s

(t)

(t),

(5)

and the mean power of v

(t), p

, is given by:

= V

RMS,imp

. (6)

The output electrical ﬁeld of a chirpless MZM,

MZM

(t), can be expressed as:

MZM

(t) = E

cos



[−V

+ v

(t)]



exp( j2πν

t),

(7)

where E

is the optical ﬁeld at the MZM input, V

the MZM bias voltage, V

is the voltage required to

switch between the maximum and the minimum of

the MZM power transmission characteristic, and ν

the optical frequency.

Considering a linearized MZM by applying the

Taylor series ﬁrst-order approximation around zero

with respect to v

(t), and that the MZM is biased

at quadrature point (V

= V

/2), the linearized output

ﬁeld, e

MZM,l

(t), can be written as:

MZM,l

(t) = E

√

(t)

exp( j2πν

t).

(8)

Using Eqs. 4 and 5, and knowing that:

(

(t)

= N

RMS,s

(t)

= N

(1 + A

(9)

the mean power at the linearized MZM output,

MZM,l

, can be expressed as:

MZM,l

|{z}

RMS,imp

1 + A

| {z }

RMS,imp

1 + A

| {z }

, (10)

where p

is the optical carrier mean power, p

is the

mean power of all the VCs, and p

is the mean power

of all the OFDM bands.

Two important power ratios can be determined

from Eq. 10, which are the virtual-carrier-to-band

power ratio (VBPR) and the optical-carrier-to-band

power ratio (OBPR). These ratios are important be-

cause they have a signiﬁcant impact on the perfor-

mance of the MB-OFDM signal. The VBPR is given

by:

VBPR =

v,n

b,n

= A

, (11)

and the OBPR can be written as:

OBPR =

(1 + VBPR)

RMS,imp

, (12)

where p

v,n

= p

and p

b,n

= p

are the mean

power of the VC n and the OFDM band n, respec-

tively.

After electro-optical conversion, SSB ﬁltering is

performed and the lower sideband and lower VC are

removed. After some calculations, the mean power at

the SSB ﬁlter output, p

SSB

, can be expressed as:

SSB

= p

. (13)

Afterwards, an ASE noise loader is added to the

signal at the SSB ﬁlter output. Hence, it is important

to deﬁne the OSNR after noise loading (NL).

Considering that the ASE noise is zero-mean

additive-white-Gaussian and is present in the parallel

(k) and perpendicular (⊥) polarization directions, and

that the signal ﬁeld at the SSB ﬁlter output is polar-

ized in the parallel direction, the low pass equivalent

(LPE) of the ﬁeld after NL, e

(t), can be expressed

as:

(t) =



SSB,k

(t) + n

I,k

(t) + jn

Q,k

(t)



I,⊥

(t) + jn

Q,⊥

(t)

⊥

(14)

where e

SSB,k

(t) is the OFDM signal ﬁeld at the SSB

ﬁlter output in the k polarization deﬁned by u

, n

I,k

(t)

and n

Q,k

(t) are the I and Q noise components in the k

polarization, respectively, and n

I,⊥

(t) and n

Q,⊥

(t) are

PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology

136

the I and Q noise components in the ⊥ polarization

deﬁned by u

⊥

, respectively.

Assuming that each one of the four noise com-

ponents has a constant power spectral density (PSD)

given by S

ASE

, the optical noise mean power in a

bandwidth B

after NL, p

n,NL

, can be expressed as:

n,NL

= 4 S

ASE

. (15)

Usually, B

corresponds to a reference bandwidth of

0.1 nm, which is approximately 12.5 GHz.

The OSNR is deﬁned as the ratio between the sig-

nal power after NL, p

s,NL

(which is equal to the signal

power at the SSB ﬁlter output, p

SSB

), and the noise

mean power, p

n,NL

, in the reference bandwidth B

after NL. Considering Eqs. 13 and 15, the OSNR is

then expressed as:

OSNR =

s,NL

n,NL

SSB

n,NL

ASE

. (16)

After ASE noise loading, the BS is used to select

the OFDM band and VC that will be photodetected

(dropped). The BS is an ideal optical ﬁlter, with trans-

fer function H

BS,n

( f ) and impulse response h

BS,n

(t),

that only selects the n-th OFDM signal and the n-th

VC. The LPE of H

BS,n

( f ) can be written as:

BS,n

( f ) = rect



f − f



, (17)

where B

is the BS bandwidth and f

is the center

frequency of the BS given by:

max

+ f

min

v,n



RF,n

−



, (18)

where f

v,n

is the n-th VC frequency, f

RF,n

is the n-th

band central frequency, f

max

and f

min

are the maxi-

mum and minimum frequencies of the passband of the

BS, respectively, and B

is the OFDM signal band-

width.

The LPE of the signal at the BS output, e

BS,n

(t),

can be expressed as:

BS,n

(t) = e

(t) ~ h

BS,n

(t) =

BS,n,k

(t) + n

I,k

(t) + jn

Q,k

(t)

I,⊥

(t) + jn

Q,⊥

(t)

⊥

(19)

where ~ denotes the convolution operation, e

BS,n,k

(t)

is the ﬁeld, at the BS output, of the n-th OFDM signal

and n-th VC in the k polarization, n

I,k

(t) and n

Q,k

(t)

are the ﬁltered I and Q noise components in the k po-

larization, respectively, and n

I,⊥

(t) and n

Q,⊥

(t) are

the ﬁltered I and Q noise components in the ⊥ po-

larization, respectively. The ﬁeld e

BS,n,k

(t) is given

by:

BS,n,k

(t)=

√

RMS,imp

RMS,s

(t)

RMS,s

b,n

(t)

b,n

(t)+

RMS,imp

RMS,s

(t)

RMS,s

v,n

(t)

v,n

(t)

exp( j2πν

t),

(20)

with

b,n

(t) = s

I,n

(t)cos(2π f

RF,n

t)−

−s

Q,n

(t)sin(2π f

RF,n

t),

(21)

and

v,n

(t) =

√

2cos(2π f

v,n

t + φ

), (22)

where s

I,n

(t) is the low pass in-phase (I) component

of the OFDM signal of band n, s

Q,n

(t) is the low pass

quadrature (Q) component of the OFDM signal of

band n, and φ

is the VC initial phase.

The ﬁeld e

BS,n,k

(t) has a mean power, p

BS,n

, given

as follows:

BS,n

+ p

v,n

b,n

. (23)

After band selection, the signal is photodetected.

The PIN model used in this work is a square modu-

lus function with responsivity R

of 1 A/W. The pho-

tocurrent at the PIN output, i

PIN,n

(t), can be written

as:

PIN,n

(t) = |e

BS,n

(t)|



BS,n,k

(t) + n

I,k

(t) + jn

Q,k

(t)



I,⊥

(t) + jn

Q,⊥

(t)



(24)

After some calculations, the PIN output current

can be separated in two groups: the signal-dependent

current and the noise-dependent current. The signal

dependent current, denoted as i

s,PIN

(t), is given by:

s,PIN

(t) =





RMS,imp

RMS,s

b,n

(t)

RMS,s

(t)



I,n

(t) + s

Q,n

(t)



√

RMS,imp

RMS,s

b,n

(t)

RMS,s

v,n

(t)

RMS,s

(t)

(t) +

RMS,imp

RMS,s

v,n

(t)

RMS,s

(t)





(25)

AnalyticalModelingforPerformanceEvaluationofASENoise-impairedDirect-detectionSingle-sidebandMulti-band

OpticalOFDMSystems

137

with

(t) = s

I,n

(t)cos[2π( f

v,n

− f

RF,n

)t]+

+ s

Q,n

(t)sin[2π( f

v,n

− f

RF,n

)t].

(26)

The ﬁrst term of i

s,PIN

(t) is the SSBI, the second term

is the received OFDM signal, and the third term is the

direct-current (DC) component. The Fourier trans-

form of i

s,PIN

(t), I

s,PIN

( f ), is given by:

s,PIN

( f ) =





RMS,imp

RMS,s

b,n

(t)

RMS,s

(t)

( f ) +

√

RMS,imp

RMS,s

b,n

(t)

RMS,s

v,n

(t)

RMS,s

(t)

( f ) +

RMS,imp

RMS,s

v,n

(t)

RMS,s

(t)

δ( f )





(27)

with S

( f ) = F {s

I,n

(t) + s

Q,n

(t)} and S

( f ) =

F {s

(t)}, where F {·} denotes the Fourier trans-

form. The noise-dependent current, denoted as

n,PIN

(t), where the noise-noise beat terms were ne-

glected, can be expressed as:

n,PIN

(t) = e

BS,n,k

(t)

I,k

(t) − jn

Q,k

(t)

BS,n,k

(t)

I,k

(t) − jn

Q,k

(t)

∗

(28)

In order to obtain the noise PSD at the PIN out-

put, S

n,PIN

( f ), the Fourier transform of the auto-

correlation function of i

n,PIN

(t) must be evaluated.

After performing some calculations, S

n,PIN

( f ) is

given by:

n,PIN

( f ) = 2S

ASE

BS,n

( f + f

v,n

)

BS,n

(−f + f

v,n

)

BS,n

(29)

After photodetection, a BPF is used to remove the

SSBI and the DC component from the photodetected

signal. The BPF transfer function, H

BPF

( f ), is given

by:

BPF

( f ) = rect



f − f

RF,n

+ f

v,n



+ rect



f + f

RF,n

− f

v,n



(30)

where B

is the BPF bandwidth, which is equal to

the OFDM signal bandwidth. The Fourier transform,

s,BPF

( f ), of the signal at the BPF output, can be ex-

pressed as:

s,BPF

( f ) = I

s,PIN

( f )H

BPF

( f ),

(31)

which is approximately given by:

s,BPF

( f ) ≈

√

RMS,imp

RMS,s

b,n

(t)

RMS,s

v,n

(t)

RMS,s

(t)

( f )H

BPF

( f ).

(32)

After some calculations, the mean power of I

s,BPF

( f ),

s,BPF

, can be written as:

s,BPF

v,n

b,n

. (33)

The noise power at the BPF output can be obtained

from the PSD of the noise at the PIN output (Eq. 29)

as:

n,BPF

+∞

−∞

n,PIN

( f )

BPF

( f )

d f =

= 4 p

BS,n

ASE

, (34)

where B

is the bandwidth of the low pass ﬁlter at the

receiver (which has the greatest frequency limitation).

The ESNR is deﬁned as the ratio between the sig-

nal power, p

s,BPF

, and the noise mean power, p

n,BPF

at the BPF output. Considering Eqs. 33 and 34, the

ESNR is then given by:

ESNR =

s,BPF

n,BPF

v,n

b,n



v,n

+ p

b,n



ASE

. (35)

4 PERFORMANCE EVALUATION

METRIC

The ﬁgure of merit used in this study to categorize

the system performance is the BER, which can be es-

timated as a function of the ESNR with the following

expression (Peng et al., 2012):

BER =

1 −

√

log

(

√

erfc





3ESNR log

(

√

(M −1)log

(M)





(36)

where erfc(·) is the complementary error function,

and M is the number of distinct symbols of the

quadrature amplitude modulation format. Know-

ing that p

b,n

= N

OBPR, p

b,n

= N

VBPR,

PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology

138

b,n

= N

, p

= V

RMS,imp

, and using Eqs. 35

and 16, the ESNR can be expressed as:

ESNR =

VBPR

(VBPR + 1)

OSNR, (37)

with

2π

+ 8V

. (38)

Some important conclusions can be derived from

Eq. 37. Keeping p

constant, the ESNR of one

band is inversely proportional to N

, which means

that transmitting more than one band will require an

OSNR increase proportional to the number of bands

to achieve the same performance as when only one

band is transmitted. An increase of VBPR will also

lead to a higher required OSNR, to achieve the same

performance obtained with low VBPR. This is be-

cause the power attributed to the OFDM band de-

creases and the power assigned to the VC increases,

meaning lower ESNR.

5 NUMERICAL RESULTS

The effectiveness of the proposed analytical model

for MB-OFDM systems is assessed by comparing its

estimates with the ones of numerical simulation us-

ing MATLAB. The OSNR that leads to a BER =

−3

(OSNR

req

) and the BER itself are used as ﬁg-

ures of merit. To assess the analytical method (AM)

accuracy, the BER obtained with the AM is com-

pared with the BER retrieved from numerical simu-

lation (NS) using the exhaustive Gaussian approach

(EGA) (Alves and Cartaxo, 2010). In the analysis,

each OFDM symbol has 128 subcarriers, each OFDM

band has a bit rate of 5 Gb/s and a bandwidth of 2.5

GHz, the maximum total bit rate (assuming a maxi-

mum of 4 bands) is 20 Gb/s, and the following param-

eters are ﬁxed: M = 4, V

= 5V, B

= 2.5 GHz, B

12.5 GHz, f

RF,n

∈ [2.25,8.25,14.25,20.25] GHz and

v,n

∈ [6, 12, 18, 24] GHz with n ∈[1,2,3,4].

The linearized MZM with the relationship be-

tween the applied voltage and ﬁeld at the MZM output

given by Eq. 8 is used in the numerical results. A par-

ticular study, in which a real MZM is considered in

the simulation, is also performed and explicitly men-

tioned. The target of this particular study is to assess

the validity range of the AM in presence of MZM dis-

tortion. With the real MZM, is important to impose

that the VC frequencies are multiple of f

v,1

(in this

work, f

v,1

= 6 GHz), in order to guarantee that the

inter-modulation products of the VCs do not interfere

with the OFDM bands.

The number of bands affects signiﬁcantly the per-

formance of the MB-OFDM system, as it was con-

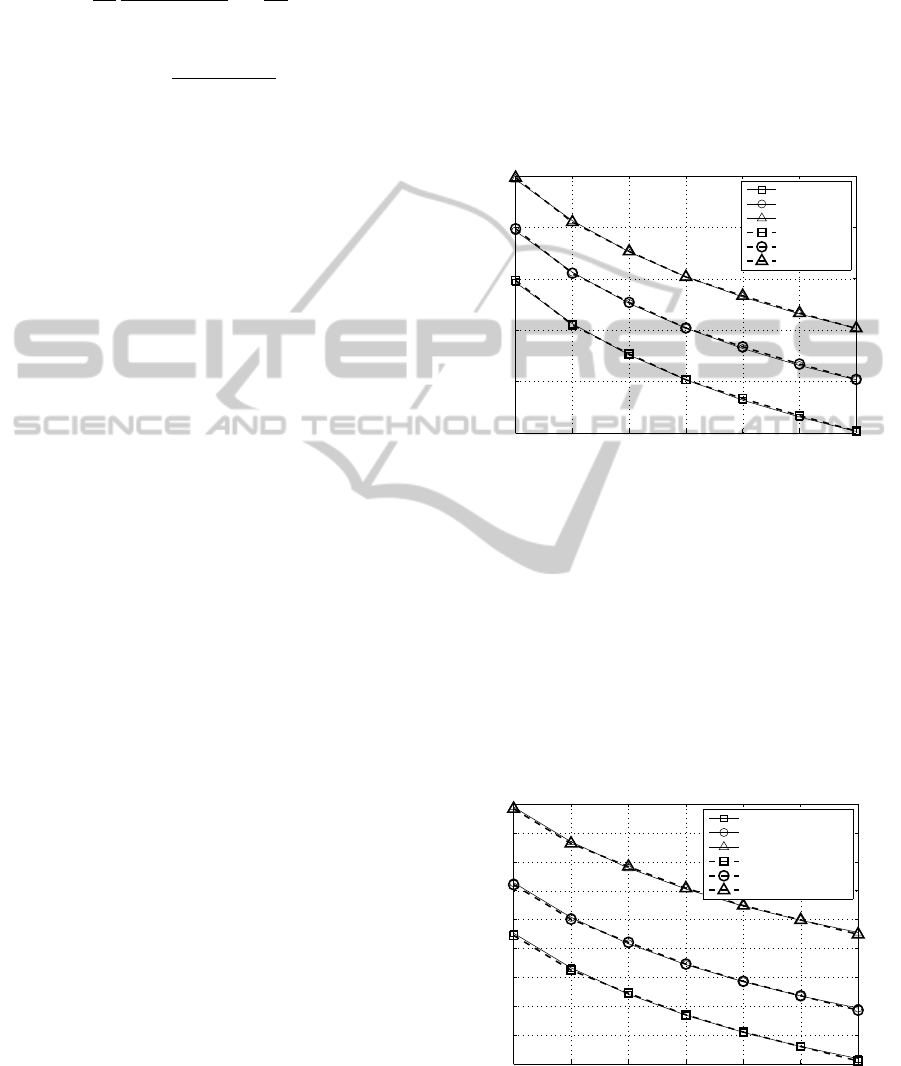
cluded through analysis of Eq. 37. Fig. 3 shows the

OSNR

req

as function of V

RMS,imp

for N

= [1,2,4], ob-

tained with the AM and with NS. A VBPR of 15 dB

is imposed. Fig. 3 shows that the AM results have

excellent agreement with the ones obtained with NS.

Fig. 3 also demonstrates that when N

doubles, the

OSNR

req

increases 3 dB. Fig. 3 shows also that in-

creasing V

RMS,imp

leads to a OSNR

req

decrease, which

is valid for this system because it does not exhibit

MZM distortion.

750 1000 1250 1500 1750 2000 2250

RMS,imp

[mV]

OSNR

req

[dB]

NB = 1 (AM)

NB = 2 (AM)

NB = 4 (AM)

NB = 1 (NS)

NB = 2 (NS)

NB = 4 (NS)

Figure 3: OSNR

req

as function of V

RMS,imp

for N

[1,2, 4], with AM (solid lines) and NS (dashed lines), with

a ﬁxed VBPR of 15 dB.

Another parameter besides N

that inﬂuence sig-

niﬁcantly the performance results is the VBPR. Fig. 4

shows the OSNR

req

as function of V

RMS,imp

for VBPR

= [3, 9, 15] dB, with the AM and with NS. The MB-

OFDM system has four bands (N

= 4). Fig. 4 shows

an excellent agreement between the AM results and

the NS results. Fig. 4 also shows that increasing

VBPR leads to an increase of the OSNR

req

. This in-

crease is higher for higher VBPRs.

750 1000 1250 1500 1750 2000 2250

RMS,imp

[mV]

OSNR

req

[dB]

VBPR = 3 dB (AM)

VBPR = 9 dB (AM)

VBPR = 15 dB (AM)

VBPR = 3 dB (NS)

VBPR = 9 dB (NS)

VBPR = 15 dB (NS)

Figure 4: OSNR

req

as function of V

RMS,imp

for VBPR =

[3,9, 15] dB, with AM (solid lines) and NS (dashed lines),

and with N

= 4.

AnalyticalModelingforPerformanceEvaluationofASENoise-impairedDirect-detectionSingle-sidebandMulti-band

OpticalOFDMSystems

139

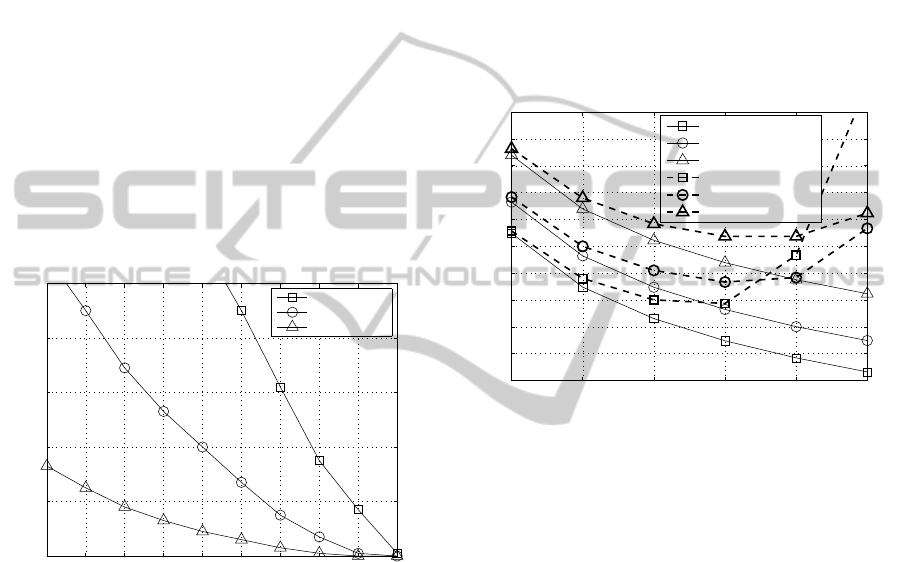
In the results of Figs. 3 and 4, the VCBG is se-

lected in order to avoid the SSBI overlapping with the

received OFDM band. However, it is important to

verify the resilience of the AM when PIN distortion

interferes with the information-bearing signal, as a

smaller VCBG means more spectral efﬁciency. Fig. 5

shows the BER as function of the VCBG width in

GHz, for VBPR = [3,9,15] dB and V

RMS,imp

= 1500

mV. The OSNR is 22.4 dB for VBPR = 3 dB, 25.9 dB

for VBPR = 9 dB and 31.1 dB for VBPR = 15 dB.

With these OSNR levels and as the AM does not take

into account the PIN distortion, the BER obtained us-

ing the AM is 10

−3

for all VCBG widths. Therefore,

Fig. 5 only shows the NS results. Fig. 5 shows that

the SSBI caused by the PIN affects the performance

when the VCBG width is lower than the bandwidth of

the OFDM signal, as the SSBI spectrum overlaps the

OFDM signal spectrum. Fig. 5 shows also that the

BER degrades more substantially for lower VBPRs.

This is because lower VBPR levels leads to more

SSBI power.

0.25 0.5 0.75 1 1.25 1.5 1.75 2 2.25 2.5

−3

−2.8

−2.6

−2.4

−2.2

−2

VCBG width [GHz]

log

BER

VBPR = 3 dB

VBPR = 9 dB

VBPR = 15 dB

Figure 5: BER as function of the VCBG width, for VBPR

= [3, 9,15] dB and V

RMS,imp

= 1500 mV, with NS. With the

AM, the BER is 10

−3

for all VCBG widths.

The results shown in Figs. 3, 4 and 5 present the

effects of ASE noise and PIN distortion on the perfor-

mance. However, the effects of MZM distortion were

not considered in the simulation in those results as a

linearized MZM is assumed in the analytical formu-

lation. To illustrate the impact of MZM nonlinearity

on the required OSNR and assess the validity range of

the AM presented in this work, a real MZM described

by Eq. 7 is considered in the simulation.

Fig. 6 shows the OSNR

req

as function of the

RMS,imp

, for VBPR = [3,9, 15] dB, and for the ﬁrst

band which is the most affected by MZM distortion.

The MB-OFDM system has four bands (N

= 4), and

a VCBG width of 2.5 GHz is imposed. Fig. 6 shows

that the MZM distortion causes a performance degra-

dation as the RMS voltage increases. For RMS volt-

ages around 400 mV, the minimum OSNR

req

is ob-

tained. From the simulation results, the minimum

OSNR

req

for VBPR = 3 dB is 38 dB, for VBPR = 9

dB is 40 dB, and for VBPR = 15 dB is 45 dB. The er-

ror committed by the AM in the minimum OSNR

req

approximately 4 dB for VBPR = 3 dB and for VBPR

= [9,15] dB is approximately 3 dB. The analytical

modeling of this work assumes noise-impaired MB-

OFDM systems. Hence distortion-impaired systems

are not well described by this model. This occurs for

RMS,imp

higher than approximately 200 mV, which in

modulation index (V

RMS,imp

in percentage) is 4%.

100 200 300 400 500 600

RMS,imp

[mV]

OSNR

req

[dB]

VBPR = 3 dB (AM)

VBPR = 9 dB (AM)

VBPR = 15 dB (AM)

VBPR = 3 dB (NS)

VBPR = 9 dB (NS)

VBPR = 15 dB (NS)

Figure 6: OSNR

req

as function of the V

RMS,imp

, for VBPR

= [3, 9,15] dB. A MB-OFDM system with 4 bands (N

= 4)

is considered. A real MZM is considered in the simulation.

6 CONCLUSIONS

An analytical model for performance evaluation

of ASE noise-impaired direct-detection SSB MB-

OFDM systems has been proposed. The effective-

ness of the analytical model has been veriﬁed through

comparison with numerical simulation using the EGA

to evaluate the BER. Excellent agreement in the BER

results when MZM and PIN distortion do not in-

terfere with the MB-OFDM signal has been shown.

When PIN distortion is affecting the MB-OFDM sig-

nal, the analytical model provides more accurate es-

timates for high VBPRs. When MZM distortion is

interfering with the MB-OFDM signal, the analytical

model presents a deviation in the required OSNR not

exceeding 1 dB, for modulation indexes lower than

4%. The analytical modeling for distortion-impaired

MB-OFDM systems, as well as the MB-OFDM sys-

tem optimization in order to achieve the best required

OSNR, will be reported elsewhere.

PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology

140

ACKNOWLEDGEMENTS

The work of Pedro Cruz was supported by Fundac¸

para a Ci

encia e a Tecnologia from Portugal un-

der Contract SFRH/BD/85940/2012 and by projects

MORFEUS-PTDC/EEI-TEL/2573/2012 and PEst-

OE/EEI/LA0008/2013.

REFERENCES

Alves, T. and Cartaxo, A. (2010). Extension of the exhaus-

tive gaussian approach for BER estimation in exper-

imental direct-detection OFDM setups. Microwave

and Optical Technology Letters, 52(12):2772–2775.

Armstrong, J. (2009). OFDM for optical communications.

Journal of Lightwave Technology, 27(3):189–204.

Blouza, S., Karaki, J., Brochier, N., Rouzic, E., Pincemin,

E., and Cousin, B. (2011). Multi-band OFDM for op-

tical networking. In Proceedings of the International

Conference on Computer as a Tool. IEEE.

Christodoulopoulos, K., Tomkos, I., and Varvarigos, E.

(2011). Elastic bandwidth allocation in ﬂexible

OFDM-based optical networks. Journal of Lightwave

Technology, 29(9):1354–1366.

Cvijetic, N. (2012). OFDM for next-generation optical

access networks. Journal of Lightwave Technology,

30(4):384–398.

Kim, S., Seo, K., and Lee, J. (2012). Spectral efﬁcien-

cies of channel-interleaved bidirectional and unidirec-

tional ultradense WDM for metro applications. Jour-

nal of Lightwave Technology, 30(2):229–233.

Li, Z., Xiao, X., Gui, T., Yang, Q., Hu, R., He, Z., Luo,

M., Li, C., Zhang, X., Xue, D., You, S., and Yu, S.

(2013). 432-Gb/s direct-detection optical OFDM su-

perchannel transmission over 3040-km SSMF. IEEE

Photonics Technology Letters, 25(15):1524–1526.

Lowery, A., Du, L., and Armstrong, J. (2006). Orthogo-

nal frequency division multiplexing for adaptive dis-

persion compensation in long haul WDM systems.

In Proceedings of the Optical Fiber Communications

Conference, number PDP39. OSA.

Peng, W., Morita, I., Takahashi, H., and Tsuritani, T.

(2012). Transmission of high-speed (>100 Gb/s)

direct-detection optical OFDM superchannel. Journal

of Lightwave Technology, 30(12):2025–2034.

Shieh, W. (2011). OFDM for ﬂexible high-speed op-

tical networks. Journal of Lightwave Technology,

29(10):1560–1577.

AnalyticalModelingforPerformanceEvaluationofASENoise-impairedDirect-detectionSingle-sidebandMulti-band

OpticalOFDMSystems

141