An Improved Parallel Algorithm Using GPU

for Siting Observers on Terrain

Guilherme C. Pena

, Marcus V. A. Andrade

, Salles V. G. Magalh˜aes

W. R. Franklin

and Chaulio R. Ferreira

Departamento de Inform´atica, Universidade Federal de Vic¸osa (UFV), Vic¸osa, MG, Brazil

Electrical, Computer, and Systems Engineering Dept., Rensselaer Polytechnic Institute (RPI), Troy, N.Y., U.S.A.

Keywords:

Siting, Terrain Visibility, Viewshed, GPU Parallel Algorithm.

Abstract:

This paper presents an efﬁcient method to determine a set of observers (that is, where to site them) such

that a given percentage of a terrain is visually covered. Our method extends the method proposed in (Franklin,

2002) including a local search heuristic efﬁciently implemented using dynamic programming and GPU parallel

programming. This local search strategy allows to achieve a higher coverage using the same number of

observers as the original method and thus it is possible to obtain a given coverage using a smaller number of

observers. It can be an important improvement since an observer can represent an expensive facility such as a

telecommunication tower. The proposed method performance was compared with that of other methods and

the tests showed that it can be more than 1200 times faster than the sequential implementation (with no use

of dynamic programming and no GPU parallel programmming) and, also, more than 20 times faster than a

previous parallel method presented in (Magalh˜aes et al., 2011).

1 INTRODUCTION

A large amount of high-resolution geographic data

has become available because of the recent ad-

vances in remote sensing. Thus, the development

of advanced techniques to process these data has

been required by Geographic Information Science

(GIS) (Laurini and Thompson, 1992). The Earth sur-

face elevation (terrain) data are usually represented

approximately by a digital elevation matrix (DEM)

that stores the elevations of regularly sampled terrain

points. Elevations of intermediate points are usually

approximated using some interpolation process (Li

et al., 2005).

An important group of GIS applications concerns

visibility, i.e., determining the set of points that are

visible from some particular point, called observer.

The observer can be located at some height above

the terrain. These applications include telecommu-

nications, environmental planning, autonomous vehi-

cle navigation and military monitoring (Franklin and

Ray, 1994; Li et al., 2005; Nagy, 1994; Andrade et al.,

2011). One important related problem is the siting

of a given number of observers in order to optimally

“cover the terrain”. These observers may represent

radio, TV, Internet or mobile phone towers, or mon-

itoring cameras or towers (Ben-Moshe, 2005; Ben-

Shimol et al., 2007). As described in (Nagy, 1994),

this is an NP-Hard problem and, therefore, there is no

known efﬁcient algorithm to ﬁnd its optimal solution.

However, even obtaining approximate solutions

for this optimization problem demands a long pro-

cessing time, particularly when processing large

quantities of data. One way to reduce this processing

time is to design parallel algorithms based on general

purpose graphics processing units (GPGPUs), which

are present in most current graphics cards.

This paper deals with an instance of the multiple

observers siting problem where the goal is to deter-

mine a set of observers on a terrain represented by

an elevation matrix such that these observers together

can achieve a given visual coverage of the terrain. In

(Franklin, 2002), the author presented a solution for

this problem based on greedy strategy and, in this pa-

per, we extend that method including a local search

heuristic based on a swapping strategy to achieve a

better terrain coverage using the same number of ob-

servers. As the main contribution of this paper, this

heuristic was implemented in parallel using Graphics

Processing Units (GPUs) and dynamic programming.

The extended method proposed in this paper,

named SiteGSM (from Site using GPU’s shared mem-

367

Pena G., Andrade M., Magalhães S., Franklin W. and Ferreira C..

An Improved Parallel Algorithm Using GPU for Siting Observers on Terrain.

DOI: 10.5220/0004884303670375

In Proceedings of the 16th International Conference on Enterprise Information Systems (ICEIS-2014), pages 367-375

ISBN: 978-989-758-027-7

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

ory), was compared with some other methods for

siting observers on terrain such as (Franklin, 2002;

Franklin and Vogt, 2006; Magalh˜aes et al., 2010a;

Magalh˜aes et al., 2011) and, as the tests showed,

our method achieves a better performance than all of

them: it is faster than (Magalh˜aes et al., 2010a; Ma-

galh˜aes et al., 2011) (in some cases, more than 20

times faster than both) or it can use a smaller num-

ber of observers than (Franklin, 2002; Franklin and

Vogt, 2006) to cover the terrain (which may represent

an important improvement since the observer can be

an expensive facility as, for example, a communica-

tion tower).

2 BACKGROUND

2.1 Terrain Visibility Deﬁnitions

A terrain represents a region of the earth surface

where the terrain’s value at any point is the elevation

of the corresponding point of the earth surface above

a reference ellipsoid called the geoid that represents

sea-level. For this paper, a terrain is represented by a

matrix of elevation posts on a square grid, whose ver-

tical and horizontal spacing is uniform either in dis-

tance, e.g., 10m, or in angle, e.g. 1 arc-second.

An observer is a point in the space that “wants”

to see or communicate with other points in the space,

called targets. As usual, the notations for observer

and target are O and T. The base points of O and T

are the points on the geoid directly below O and T

respectively, which are denoted as O

and T

. Both

O and T are at height h ≥ 0 above O

and T

. All

symbols that appear in this work are shown in table 2.

The radius of interest, R, of O is the radius of the

circle centered on O

that contains all points that can

be seen by the observer in the absence of obstructions.

E.g., if O is a radio transmitter, R is a function of the

transmitter power and receiver sensitivity. For con-

venience, R is usually compared to the distance be-

tween O

and T

rather than between O and T, which

is equivalent when h is much smaller than the radius

of the earth.

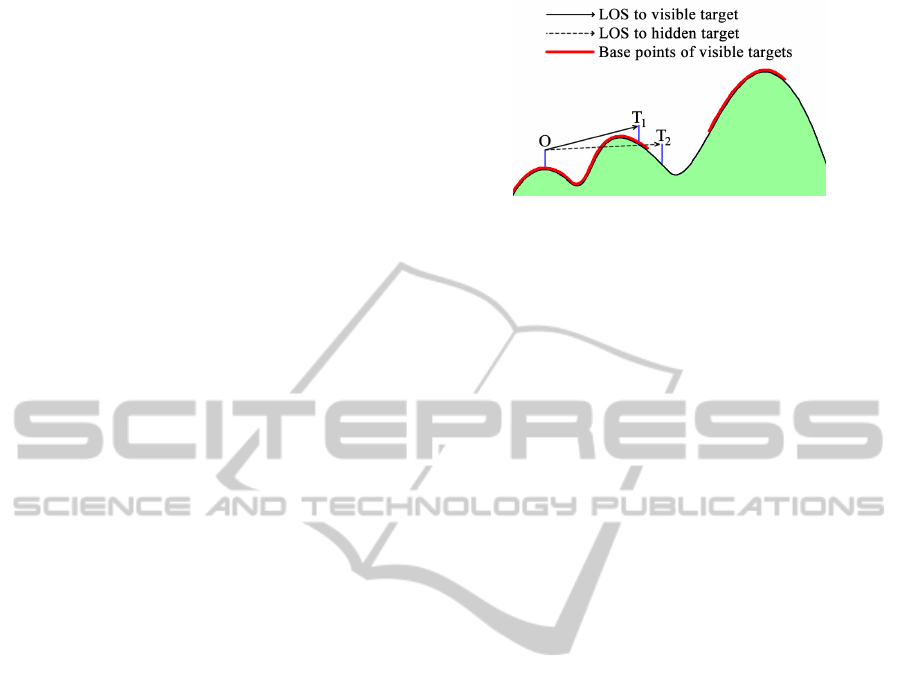
A target T is visible from O iff |T

− O

| ≤ R and

there is no terrain point blocking the line segment,

called the Line of Sight (LOS), between O and T; see

Figure 1. In this Figure, T

is visible from O but T

not.

The viewshed, V, of O is the set of base points

whose corresponding targets are visible from O. In

general, V is stored as a bit matrix where 0 represents

a non-visible point and 1 represents a visible point.

Figure 1: Visibility queries using a line of sight.

The visibility index, ω, of O is the number of tar-

gets that are visible from O. Points with a large ω are

usually good candidate places to site observers in or-

der to maximize the area of the terrain that is seen by

at least one observer (Franklin and Ray, 1994).

The joint viewshed, V , of a set of observers S =

} is the union of the individual viewsheds V

, i.e.,

the bitwise-or of their bit matrices.

The joint visibility index, Ω, of S is the number of

targets in the terrain that are visible from at least one

observer in S . Usually, Ω is normalized as a percent-

age of the terrain area.

Multi-observer siting means optimizing the loca-

tions of a set of observers such that Ω is as large as

possible. This is an NP-Hard problem (Nagy, 1994)

and has important practical facilities-location applica-

tions, such as siting mobile phone towers, ﬁre moni-

toring towers, and radar systems.

In this paper we will consider the following equiv-

alent multi-observer siting problem: to obtain a set of

observers whose joint visibility index Ω is, at least, a

given percentage of the terrrain.

2.2 Parallel Programming Using

General Purpose GPU

The programming architectures that allow using

GPU units’ parallel computing power (as, for ex-

ample, the Compute Uniﬁed Device Architecture

(CUDA) (NVIDIA, 2013)) have led to the develop-

ment of many algorithms that achieve high computa-

tion performances.

CUDA has made possible the development of al-

gorithms to solve time-consuming problems using the

large number of parallel multiprocessors as well as

the high memory bandwidth provided by GPUs. To

accomplish high-performance computing, it is neces-

sary to develop parallel algorithms that are totally or

partially executed on the GPU.

The CUDA-enabled graphics cards are composed

of multiple processors, more speciﬁcally, Single In-

struction Multiple Data (SIMD) processors called

Stream Multiprocessors (SMs), which allow the ex-

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

368

Figure 2: Comparison between GPUs and CPUs structures.

Source: (NVIDIA, 2013)

ecution of multiple parallel threads. Thus, GPU pro-

cessors can efﬁciently execute instructions involving

many operations with data parallelism, i.e., when the

same operation is applied to different data.

According to NVIDIA, GPUs can provide greater

processing powerthan CPUs because they are special-

ized in performing parallel tasks involving many cal-

culations. On the other hand, the CPUs are designed

to perform tasks involving execution ﬂow control and

data cache. The physical difference between both ar-

chitectures can be visualized in Figure 2: GPUs dedi-

cate most of their area for processing units (in green),

while CPUs dedicate most of their area for execution

control and data cache (in yellow and orange, respec-

tively).

A CUDA application consists in code that is exe-

cuted on CPU and functions (called kernels) that are

executed on GPU. The GPU is able to do parallel pro-

cessing by creating threads such that each thread may

execute the kernel operations in different data. Thus,

the GPU is used as a coprocessor that is able to per-

form certain tasks more efﬁciently than the CPU.

3 RELATED WORK

There are some important work related to the problem

addressed on this paper. In (Ben-Moshe, 2005), the

author presented an algorithm to site facilities using

an approach based on radio locator, frequency alloca-

tion and connectivity. The input includes a weighted

set of demand locations, a set of feasible facility lo-

cations and a distance function that measures the cost

of travel between a pair of locations. In (Ben-Shimol

et al., 2007), the authors described an algorithm to

site a minimal set of ﬁxed-access relay antennas on

a given terrain to generate the communication links

between multiple base stations. Although the goal of

these two works is not to achieve a given coverage of

the terrain, they are related to the problem addressed

on this paper because they use some important con-

cepts related to our approach.

Other papers describing solutions to site observers

on terrains are (Franklin and Vogt, 2004a; Franklin

and Vogt, 2004b; Franklin and Vogt, 2006). They are

based on the method Site proposed in (Franklin, 2002)

which is described in section 4 and, as mentioned be-

fore, this method uses a greedy strategy to site ob-

servers on a terrain. In (Magalh˜aes et al., 2010b),

the method Site was extended to process huge ter-

rains stored in external memory where the main idea

is to subdivide the terrain in smaller pieces (subre-

gions) and process each piece in the internal memory.

In order to consider the inﬂuence of observers sited

near to the borders of the subregions, each subregion

is augmented with a band of width R (the observer ra-

dius of interest) around it. Additionally, the viewshed

representation used in the original method Site was

improved to require a smaller amount of memory.

In (Magalh˜aes et al., 2010a; Magalh˜aes et al.,

2011) were presented two additional methods to site

observer on terrains. They are described in section 5

and both are based on the method Site. In (Magalh˜aes

et al., 2010a), the original method Site was extended

including a local search heuristic to try to reduce the

number of observers selected to achieve the desired

coverage. In (Magalh˜aes et al., 2011), some routines

used in the method proposed in (Magalh˜aes et al.,

2010a) were implemented in parallel using GPU.

In this paper, we present a more efﬁcient paral-

lel implementation of the method described in (Ma-

galh˜aes et al., 2010a) that uses a faster implementa-

tion (in parallel) of the local search. In section 5, we

present a better description of the method proposed in

this paper and also, the differences with the method

presented in (Magalh˜aes et al., 2011).

4 THE SITE METHOD

Considering that the observer siting problem is NP-

Hard, Franklin (Franklin, 2002; Franklin and Vogt,

2006) proposed an approximate heuristic solution,

called Site, to ﬁnd a set of observers to cover the ter-

rain. More precisely, this method uses a greedy ap-

proach to obtain a set S of observers such that a given

percentage of the terrain is covered. Initially, S = {}

and a set P = {P

} of candidate observers is selected.

Then, at each step, the P

that will most increase the

current joint visibility index of S is inserted into S .

As described in (Franklin, 2002), the details are as

follows.

1. Estimate the visibility index of each point in the

terrain M. More precisely, determine the points

that have a certain minimum visibility index with

a certain conﬁdence level. This may be achieved

by sampling random targets.

AnImprovedParallelAlgorithmUsingGPUforSitingObserversonTerrain

369

2. Compute P = {P

} as the set of points with the

largest visibility indices. However, do not se-

lect two points that are too close together, since

their viewsheds will probably overlap consider-

ably, and hence, some of them will be redundant.

3. Compute V

, the viewshed of each P

4. Initialize S = {}. This will accumulate the set of

actual observers S ⊆ P .

5. Initialize V , the joint viewshed of S , that is, the

union of the viewsheds of all P

in S .

6. Repeat the following until a termination condi-

tion is satisﬁed. Typical conditions require |S| to

achievea certain maximum, or V to achievea cer-

tain minimum of visible points.

(a) Iterate through P to ﬁnd the P

that will cause

the joint visibility index Ω to increase the most.

That involves repeatedly counting the number

of 1 bits in the union of the joint viewshed V

and V

(b) Insert that P

into S and update V .

5 OBSERVER SITING IN GPU

In (Magalh˜aes et al., 2010a) was presented an ex-

tension of the method Site, named Site+, where

some heuristics were included to achieve a same

terrain coverage using fewer observers. In order

to make these heuristics more efﬁcient, the method

SiteGPU (Magalh˜aes et al., 2011) implemented the

following operations in GPU: (1) computing the vis-

ibility index of viewsheds; (2) ﬁnding the candidate

observer that will most increase the visibility index

of a joint viewshed; and (3) computing the union of

viewsheds. In this implementation it was used the

following strategy: all data (the viewsheds and joint

viewsheds) were kept in the GPU global memory and

the heuristics were executed on CPU. Thus, the GPU

was used as a coprocessor to efﬁciently perform oper-

ations requested by the heuristics.

Also, to accelerate the viewshed operations, in

SiteGPU the viewsheds were represented as a small

piece of the terrain matrix. More precisely, each view-

shed was represented by a (2R+ 1) × (2R+ 1) matrix

where R is the radius of interest of the observer which

is sited on this matrix center. That strategy improves

the algorithm efﬁciency because the points outside the

observer’s radius of interest are not considered, since

they are, by deﬁnition, not visible.

The main operation performed by Site+ is the

swap heuristic that tries to increase the joint visibility

index of the current partial solution without changing

the number of observers selected. The basic idea is

to check whether swapping a selected observer (in the

current partial solution) with another observer didn’t

selected yet will increase the joint visibility index.

This checking step considers all pairs composed by

one observer in the partial solution and another one

not in that solution and selects the pair that causes the

highest contribution for the joint visibility index.

Notice that increasing the joint visibility index

of a partial solution can reduce the number of steps

required by the greedy strategy to achieve the ﬁnal

solution and, thus, the required coverage could be

achieved using a smaller number of observers (that

could be an importantimprovementsince the observer

can be an expensive facility, such as a cellular tower).

But, on the other hand, this local search performs sev-

eral viewshed operations and it is often the bottleneck

of both Site+ and SiteGPU.

In this paper we propose a more efﬁcient method,

named SiteGSM, to site observers on terrain. It is

based on Site+ and includes a faster implementa-

tion of the local search using dynamic programming

and GPU’s shared memory which is much faster than

the GPU’s global memory (used by SiteGPU). It is

important to mention that both methods Site+ and

SiteGSM obtain exactly the same solution, that is,

the same number of observers (sited on same terrain

places) and, of course, the same terrain coverage. The

difference is that SiteGSM is much faster than Site+.

5.1 The Local Search - Swap

Given a set with n candidate observers, let A =

, ·· · , V

} be the set with their corresponding view-

sheds, that is, V

is the viewshed of observer i and let S

be a subset of A with k viewsheds representing an ini-

tial solution for the observer siting problem. The goal

of the swap heuristic is to iteratively change S in or-

der to increase the joint visibility index while keeping

constant the number of observers in S.

The local search method is based on the concept

of neighborhood of a solution which can be deﬁned as

follows: given a solution S =



, ·· · , V



, a neigh-

bor of S is a solution S

′

where an element of S is re-

placed by another element not in S. See Figure 3. In

each iteration the current solution is replaced by its

best neighbor (the one with highest visibility index).

The process of replacing the current solution with

its best neighbor is repeated until it is obtained a so-

lution having no better neighbor, which is a local op-

timum.

To simplify the notation, a solution S =

, ·· · , V

} will be written as S = {i

, ·· · , i

} in-

dicating that the solution is, in fact, correspond to

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

370

Figure 3: Given A = {V

, V

}, S

′

are the neighbors

of the solution S = {V

, V

the joint viewshed of the observers whose indices are

, ·· · , i

. Thus, the heuristic may be implemented

(sequentially) as follows: given the set of candidate

viewsheds A = {V

, ·· · , V

}, let S be a solution com-

posed of k viewsheds, i.e., S = {i

, ·· · , i

} such that

the joint viewshed of S is V

⊕ · ·· ⊕V

where ⊕ rep-

resents the union operation between two viewsheds.

Furthermore, let V

be the joint viewshed of all

viewsheds in S exceptV

. In each iteration, the neigh-

bors of S are generated in order to ﬁnd the best solu-

tion for the next iteration. The visibility indices of the

neighbor solutions are calculated by computing the

number of visible points in V

⊕V

for r = 1···k and

j = 1· ·· n with j 6= r.

The most time-consuming step in this heuristic is

computing the joint visibility index for each neighbor

solution. Algorithm 1 presents the code for this step

that computes the number of visible points in V

⊕V

(for all r = 1···k and j = 1··· n; j 6= r) and stores

them in the element Vix[r][ j]. In the next step, this

matrix will be used to ﬁnd the best neighbor of S.

For efﬁciencyimprovement, in this work the view-

sheds are packed in 64-bit words (where each word

represents the visibility of 64 points). Thus, the view-

shed unions and visibility indices can be computed

using, respectively, bitwise-or operator and bit pop-

ulation count functions, which are available in the

hardware of most current computers.

5.2 An Efﬁcient Swap Heuristic

Implementation

Notice that, to generate V

, for r = 1· ··k, Algo-

rithm 1 performs Θ(k

) union operations ⊕, where

each union operation involves Θ(vsize) positions in

the viewshed matrices. But, as described below, this

step can be improved considerably using dynamic

programming.

Given a solution S = {i

, ·· · , i

}, i.e., V

⊕ ··· ⊕

Algorithm 1 : Calculate the Vix matrix where vsize is

the number of points in each viewshed, k is the num-

ber of observers in the solution S and n is the num-

ber of candidate observers. The output is matrix Vix,

where Vix[r][ j] is the joint visibility index of a solu-

tion replacing observer r with j.

1: Vix[k][n] ← {{0}}

2: V [k][vsize] ← {{0}}

3: for r ← 1to k do

4: for m ← 1to k do

5: if r 6= m then

6: for w ← 1to VSize do

7: V [r][w] ← V [r][w] or V[S[m]][w]

8: end for

9: end if

10: end for

11: end for

12: for r ← 1to k do

13: for j ← 1to n do

14: for w ← 1to vsize do

15: Vix[r][ j] ←Vix[r][ j]+(V [r][w] orV[ j][w])

16: end for

17: end for

18: end for

19: return Vix

, for each r ∈ {1, ·· · , k}, we have V

= (V

⊕ ·· ·⊕

r−1

)⊕(V

r+1

⊕···⊕V

). Doing λ

−

= V

⊕···⊕V

r−1

and λ

= V

r+1

⊕···⊕V

we can observe that both λ

−

and λ

can be obtained by the following recurrence

relations:

−

0 and λ

−

= λ

−

r−1

⊕V

r−1

for all r ∈ 2, ··· , k

0 and λ

= V

r+1

⊕ λ

r+1

for all r ∈ 1, ··· , k− 1

For example, Figure 4 illustrates V

computation

for k = 5: in this ﬁgure, each row r represents the

value of V

where the elements in the left of the r-

th column represents λ

−

and in the right, λ

. Notice

that λ

−

can be computed by joining the viewsheds V

and V

(which is the value of λ

−

) with viewshed V

On the other hand, the λ

values can be computed in

similar way using the reverse order.

Based on these recurrence relations, Algorithm 2

uses dynamic programming to compute a matrix V

that stores V

, for r = 1·· ·k. Notice that this algo-

rithm performs only Θ(k) viewshed unions and can

replace the piece of code composed by lines 2 to 11

in Algorithm 1 where are performed Θ(k

) viewshed

unions.

In SiteGSM, the Algorithm 2 was implemented

in GPU using the following strategy: the viewsheds

were kept in GPU’s global memory and, then, the

AnImprovedParallelAlgorithmUsingGPUforSitingObserversonTerrain

371

Figure 4: Matrix illustrating V

in a solution with k = 5

observers.

union of viewsheds (loop in lines 3, 9 and 15 of Algo-

rithm 2) were performed using GPU’s threads, that is,

each thread performs a bitwise-or operation with one

element of a viewshed and the corresponding element

of another viewshed.

Algorithm 2 : Compute the matrix V that stores V

for r = 1··· k using a dynamic programming strategy.

1: V

[k][vsize] ← {{0}}

2: for r ← 2 to k do

3: for w ← 1 to vsize do

4: V

[r][w] ← V

[r− 1][w] or V[S[r− 1]][w]

5: end for

6: end for

7: V

[k][vsize] ← {{0}}

8: for r ← k− 1 to 1 do

9: for w ← 1 to vsize do

10: V

[r][w] ← V

[r+ 1][w] or V[S[r+ 1]][w]

11: end for

12: end for

13: V [k][vsize] ← {{0}}

14: for r ← 1 to k do

15: for w ← 1 to vsize do

16: V [r][w] ← V

[r][w] or V

[r][w]

17: end for

18: end for

After computing V

, the next step is to compute

the joint visibility index of the neighbor solutions, as

performed by lines 12 to 18 in Algorithm 1. A staight-

forward implementation of this step in GPU was pre-

sented in (Magalh˜aes et al., 2011), where all view-

sheds are kept in the GPU’s global memory and, then,

each element of matrix Vix (that stores the joint vis-

ibility index) is computed using a parallel algorithm

to overlap a pair of viewsheds followed by a parallel

reduction operation to determine the number of visi-

ble points. However, this strategy does not take ad-

vantage of the GPU performance efﬁciently because

it requires too many accesses to the global memory,

which is much slower than other memories such as

the shared memory.

In order to make a better use of the GPU mem-

ory hierarchy, we propose a new strategy based on

a fast GPU matrix multiplication algorithm. Notice

that the joint visibility index, that is, the Vix matrix,

is obtained in lines 12 to 18 of Algorithm 1, where

the matrices V and V are overlapped using a bitwise-

or operation. In this case, the two matrices are swept

in a row major order, but the matrices could be reor-

ganized such that the overlapping could be computed

using an access pattern similar to matrix multiplica-

tion. More precisely, line 15 in Algorithm 1 can be

replaced with

Vix[r][ j] ← Vix[r][ j] + V [r][w] or V

[w][ j]

where V

is the transposed matrix of V.

Thus, the Vix matrix can be computed using a sim-

ple adaptation of some very fast algorithm for matrix

multiplication in GPU. In particular, we adapted the

algorithm presented in (NVIDIA, 2013), replacing the

multiplication operation by a bitwise-or followed by

a binary population count operation. This algorithm

subdivides the matrices into blocks, which are loaded

iteratively in the GPU’s shared memory as the multi-

plication process is performed. Therefore, most of the

algorithm accesses are to the shared memory which is

much faster than the global memory.

Additionally, since the viewsheds matrices are,

usually, sparse (the points outside the observer’s ra-

dius of interest are always non visible), we adapted

the matrix multiplication algorithm to avoid loading

and processing matrix blocks where all the elements

are 0.

6 EXPERIMENTAL RESULTS

The method SiteGSM was implemented in

C++/CUDA and compiled using nvcc 4.0 with

maximum optimization level (-O3). It was compared

against SiteGPU (Magalh˜aes et al., 2011) and against

Site+ (Magalh˜aes et al., 2010a), a sequential CPU

version with no use of dynamic programming. The

tests were executed on a computer with Dual Intel

Xeon E5-2687 3.1GHz, 128GiB of memory and

GPU NVidia Tesla Kepler K20x with 6GiB of global

memory, 48KB of shared memory per block and

2688 CUDA processing cores running Ubuntu 12.04

LTS.

The tests used different datasets obtained from

NASA SRTM webpage: a terrain with 1201 × 1201

points (90-meter resolution SRTM3 terrain) repre-

senting a region of the Minas Gerais state in Brazil

and another terrain with 3601×3601points (30-meter

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

372

Figure 5: Observers sited in terrain 1201

with desired cov-

erage 25% and radii of interest: 100 (a), 200 (b) and 300 (c).

The observers are indicated by yellow triangles and visible

points are showed in red.

resolution SRTM1 terrain) representing a region of

the New Jersey state in USA.

The initial set P of candidate observers for each

terrain was computed using steps 1 to 3 of the Site

method proposed by (Franklin, 2002) and described

in section 4. The Site was set up to select 1000 candi-

dates for the smaller terrain and 3000 candidates for

the larger one, as in (Magalh˜aes et al., 2011). Also,

the viewsheds of all candidate observers were com-

puted using the same viewshed algorithm used by

Site, with the observers and target points sited 30 me-

ters above the terrain. This value was chosen because,

in general, it is the height of real towers, as for exam-

ple, communication antennas (Delmellea et al., 2005).

The observer siting methods were tested using

radii of interest 100, 200 and 300 points for the ﬁrst

terrain; and 200, 300 and 400 points for the second

terrain. For each terrain, the desired coverages (joint

visibility indices) were 75%, 85% and 95% of the ter-

rain area. Figure 5 shows three examples, with radii

of interest 100, 200 and 300 and desired coverage of

25%, indicating how observers were sited on the ter-

rain.

Table 1 presents the processing time (in seconds)

spent by each method. Column #Obs shows the num-

ber of observers sited in each case and the SiteGSM’s

speedup is shown in parentheses. The symbol * repre-

sents a case for which the set P of candidate observers

is not enough to achieve the desired coverage. The

symbol ∞ indicates those cases where the processing

time is greater than 7 hours.

As the tests showed, in all cases, the method

SiteGSM proposed in this paper was faster than

SiteGPU (Magalh˜aes et al., 2011) - in some cases,

more than 20 times - and, as expected, much faster

than the Site+ (more than 1200 times). Notice that,

in almost all cases, the higher the desired coverage,

the higher the speedup. This can be explained by the

fact that higher coverages require more observers and

consequently more viewsheds must be processed.

While much faster than Site+, SiteGSM obtains

the same solution as the former and, as presented in

(Magalh˜aes et al., 2010a), the Site+ can achieve sim-

ilar terrain coverage as the original Site using about

10% less observers. This can be an important (eco-

nomic) improvement since the observers can repre-

sent some expensive facility, as for example, a com-

munication antenna.

7 CONCLUSION

We presented an efﬁcient implementation of a heuris-

tic to site observers on terrains to achieve a given cov-

erage of this terrain. The method is based on an exten-

sion of Site (Franklin, 2002), where it was included a

local search strategy that tries to improve the cover-

age obtained by a ﬁxed number of observers. This lo-

cal search was implemented in parallel using graphics

processing units and also dynamic programming.

As the tests showed, the method described in this

paper is more efﬁcient than a previous method pre-

sented in (Magalh˜aes et al., 2011) and, in some cases,

AnImprovedParallelAlgorithmUsingGPUforSitingObserversonTerrain

373

Table 1: Processing time (in seconds) of three methods: two parallel methods using GPU (SiteGSM and SiteGPU) and a

sequential one (Site+) to site observers on terrains with different sizes considering different radii of interest (R) to achieve

some desired coverages (Ω).

Ter. R Ω #Obs.

Processing Time (in sec.)

SiteGSM SiteGPU Site+

1201

100

75% 162 12 180 (15.0) 11010 (917.5)

85% 299 33 545 (16.5) ∞ (-)

95% * * * (-) * (-)

200

75% 55 3 35 (11.7) 1304 (434.7)

85% 97 6 104 (17.3) 4020 (670.0)

95% 323 48 888 (18.5) ∞ (-)

300

75% 34 2 19 (9.5) 479 (239.5)

85% 62 4 70 (17.5) 1826 (456.5)

95% 216 28 566 (20.2) 19408 (693.1)

3601

200

75% 81 76 422 (5.6) ∞ (-)

85% 97 110 708 (6.4) ∞ (-)

95% 125 183 1341 (7.3) ∞ (-)

300

75% 36 28 160 (5.7) ∞ (-)

85% 42 41 276 (6.7) ∞ (-)

95% 54 66 523 (7.9) ∞ (-)

400

75% 20 14 81 (5.8) 14867 (1061.9)

85% 24 19 124 (6.5) 22869 (1203.6)

95% 30 30 270 (9.0) ∞ (-)

Table 2: Table of notations.

Symbol Description

O Observer

T Target

Observer’s base point

Target’s base point

h Height of an observer or target above terrain

R Radius of interest of an observer

V Viewshed of an observer

ω Visibility index of an observer

S Set of observers

V Joint viewshed of a set of observers

Ω Joint visibility index of a set of observers

P Set of candidate observers

n Number of candidate observers

A Set of candidate observers

S Subset of A

k Number of observers in S

′

Neighbor solution of S

, ··· , i

Observers Indices

⊕ Union operation between two viewsheds

Viewshed of the observer k in S

Joint viewshed of all viewsheds in S except V

vsize Number of points in each viewshed

Vix[r][ j] Joint visibility index of a solution replacing observer r with j

−

Union between the viewsheds V

···V

r−1

Union between the viewsheds V

r+1

···V

more than 20 times faster. Also, it is up to 1200 times

faster than the corresponding sequential implementa-

tion.

This is an interesting contribution since the ex-

tended method Site+ using local search heuristic can

achieve a desired coverage using a smaller number of

observers than the original Site and thus, better solu-

tions can be generated faster.

As a next step, to improve the proposed method

performance even more, we will try to reduce the

viewshed matrix size using only a bounding box con-

taining the observer radius of interest. Thus, it will be

possible to reduce the volume of data to be processed

and, in this case, it seems that we could compute the

joint visibility indices adapting a GPU sparse matrix

multiplication algorithm.

ACKNOWLEDGEMENTS

This work was partially supported by FAPEMIG,

CNPq, CAPES, GAPSO and NSF IIS-1117277.

REFERENCES

Andrade, M. V. A., Magalh˜aes, S. V. G., Magalh˜aes, M. A.,

Franklin, W. R., and Cutler, B. M. (2011). Efﬁcient

viewshed computation on terrain in external memory.

GeoInformatica, 15(2):381–397.

Ben-Moshe, B. (2005). Geometric Facility Location Opti-

mization. PHD thesis, Ben-Gurion University, Israel,

Department of Computer Science.

Ben-Shimol, Y., Ben-Moshe, B., Ben-Yehezkel, Y., Dvir,

A., and Segal, M. (2007). Automated antenna posi-

tioning algorithms for wireless ﬁxed-access networks.

Journal of Heuristics, 13(3):243–263.

Delmellea, E. M., Rogersonb, P. A., Akellad, M. R., Battae,

R., Blattf, A., and Wilsonf, G. (2005). A spatial model

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

374

of received signal strength indicator values for auto-

mated collision notiﬁcation technology. Transporta-

tion Research Part C: Emerging Technologies, 13(5-

6):432–447.

Franklin, W. R. (2002). Siting observers on terrain. In

Springer-Verlag, editor, In D. Richardson and P. van

Oosterom editors, Advances in Spatial Data Han-

dling: 10th International Symposium on Spatial Data

Handling, pages 109–120.

Franklin, W. R. and Ray, C. (1994). Higher isn’t necessar-

ily better: Visibility algorithms and experiments. In

Advances in GIS research: sixth international sympo-

sium on spatial data handling, volume 2, pages 751–

770. Edinburgh.

Franklin, W. R. and Vogt, C. (2004a). Efﬁcient multiple

observer siting on large terrain cells. GIScience 2004.

Franklin, W. R. and Vogt, C. (2004b). Multiple observer

siting on terrain with intervisibility or lo-res data. In

XXth Congress, International Society for Photogram-

metry and Remote Sensing, Istanbul, pages 12–23.

Franklin, W. R. and Vogt, C. (2006). Tradeoffs when multi-

ple observer siting on large terrain cells. In Springer-

Verlag, editor, 12th International Symposium on Spa-

tial Data Handling, pages 845–861.

Laurini, R. and Thompson, D. (1992). Fundamentals od

Spatial Information Systems. Academic Press.

Li, Z., Zhu, Q., and Gold, C. (2005). Digital terrain model-

ing: principles and methodology. CRC Press.

Magalh˜aes, S. V. G., Andrade, M. V. A., and Ferreira, C.

(2010a). Heuristics to site observers in a terrain repre-

sented by a digital elevation matrix. In GeoInfo, pages

110–121.

Magalh˜aes, S. V. G., Andrade, M. V. A., and Ferreira, R. S.

(2011). Using gpu to accelerate heuristics to site ob-

servers in dem terrains. In IADIS Applied Computing

(AC 2011), pages 127–133. Rio de Janeiro.

Magalh˜aes, S. V. G., Andrade, M. V. A., and Franklin,

W. R. (2010b). An optimization heuristic for siting

observers in huge terrains stored in external memory.

In Hybrid Intelligent Systems (HIS), 2010 10th Inter-

national Conference on, pages 135–140. IEEE.

Nagy, G. (1994). Terrain visibility. Computers & graphics,

18(6):763–773.

NVIDIA (2013). CUDA programming guide. NVIDIA Cor-

poration, July.

AnImprovedParallelAlgorithmUsingGPUforSitingObserversonTerrain

375