
AIV: A Heuristic Algorithm based on Iterated Local Search and Variable
Neighborhood Descent for Solving the Unrelated Parallel Machine
Scheduling Problem with Setup Times
Matheus Nohra Haddad
1
, Luciano Perdig˜ao Cota
1
, Marcone Jamilson Freitas Souza
1
and Nelson Maculan
2
1
Departamento de Computac¸˜ao, Universidade Federal de Ouro Preto, Ouro Preto, Brazil
2
Programa de Engenharia de Sistemas e Computac¸ ˜ao, Universidade Federal do Rio de Janeiro, Rio de Janeiro, Brazil
Keywords:
Unrelated Parallel Machine Scheduling, Iterated Local Search, Random Variable Neighborhood Descent,
Makespan.
Abstract:
This paper deals with the Unrelated Parallel Machine Scheduling Problem with Setup Times (UPMSPST). The
objective is to minimize the maximum completion time of the schedule, the so-called makespan. This problem
is commonly found in industrial processes like textile manufacturing and it belongs to N P -Hard class. It is
proposed an algorithm named AIV based on Iterated Local Search (ILS) and Variable Neighborhood Descent
(VND). This algorithm starts from an initial solution constructed on a greedy way by the Adaptive Shortest
Processing Time (ASPT) rule. Then, this initial solution is refined by ILS, using as local search the Random
VND procedure, which explores neighborhoods based on swaps and multiple insertions. In this procedure,
here called RVND, there is no fixed sequence of neighborhoods, because they are sorted on each application of
the local search. In AIV each perturbation is characterized by removing a job from one machine and inserting
it into another machine. AIV was tested using benchmark instances from literature. Statistical analysis of
the computational experiments showed that AIV outperformed the algorithms of the literature, setting new
improved solutions.
1 INTRODUCTION
This paper deals with the Unrelated Parallel Machine
Scheduling Problem with Setup Times (UPMSPST),
which can be formally defined as follows. Let N =
{1,...,n} be a set of jobs and let M = {1,...,m} be
a set of unrelated machines. The UPMSPST con-
sists of scheduling n jobs on m machines, satisfy-
ing the following characteristics: (i) Each job j ∈ N
must be processed exactly once by only one machine
k ∈ M. (ii) Each job j ∈ N has a processing time p
jk
which depends on the machine k ∈ M where it will
be allocated. (iii) There are setup times S
ijk
, between
jobs, where k represents the machine on which jobs
i and j are processed, in this order. (iv) There is a
setup time to process the first job, represented by S
0jk
.
The objective is to minimize the maximum comple-
tion time of the schedule, the so-called makespan or
also denoted by C
max
. Because of such characteris-
tics, UPMSPST is defined as R
M
| S
ijk
| C
max
(Graham
et al., 1979). In this representation, R
M
represent the
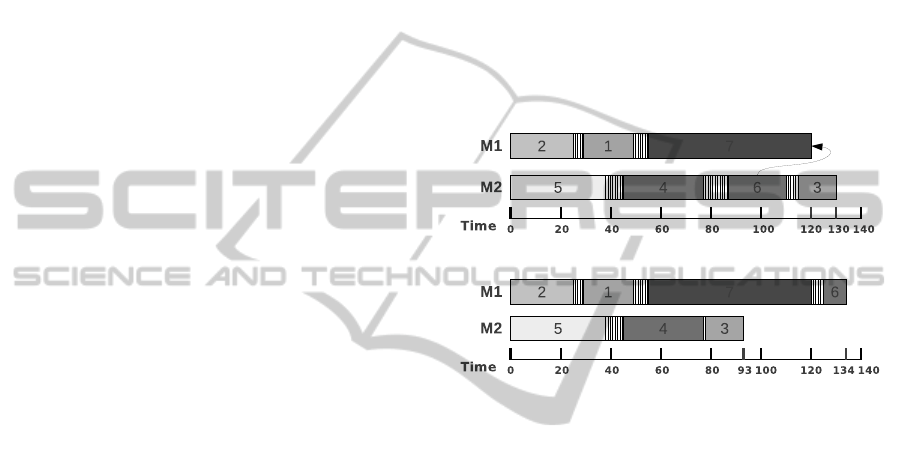
Figure 1: An example of a possible schedule.
unrelated machines, S
ijk
the setup times and C
max
the
makespan. Figure 1 illustrates a schedule for a test
problem composed by two machines and seven jobs.
In Table 1 are presented the processing times of these
jobs in both machines. The setup times of these jobs
in these machines are showed in Table 2 and Table 3.
It can be observed that in machine M1 the jobs 2,
1 and 7 are allocated in this order. In machine M2 the
schedule of the jobs 5, 4, 6 and 3, in this order, is also
perceived by this figure. The cross-hatched areas of
the figure represent the setup times between jobs and
the numbered areas the processing times. On the line
below the schedule there is the timeline, in which the
times 120 and 130 represent the completion times of
each machine.
376
Nohra Haddad M., Perdigão Cota L., Jamilson Freitas Souza M. and Maculan N..
AIV: A Heuristic Algorithm based on Iterated Local Search and Variable Neighborhood Descent for Solving the Unrelated Parallel Machine Scheduling
Problem with Setup Times.
DOI: 10.5220/0004884603760383
In Proceedings of the 16th International Conference on Enterprise Information Systems (ICEIS-2014), pages 376-383
ISBN: 978-989-758-027-7
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Processing times in machines M1 and M2.
M1 M2
1 20 4
2
25 21
3 28 14
4
17 32
5 43 38
6
9 23
7 58 52
Table 2: Setup times in machine M1.
M1
1 2 3 4 5 6 7
1 2 1 8 1 3 9 6
2 4 7 6 3 7 8 4
3
7 3 4 2 3 5 3
4 3 8 3 5 5 2 2
5
8 3 7 9 6 5 7
6 8 8 1 2 2 1 9
7
1 4 5 2 3 5 1
Table 3: Setup times in machine M2.
M2
1 2 3 4 5 6 7
1 3 4 6 5 9 3 2
2 1 2 6 2 7 7 5
3
2 6 4 6 8 1 4
4 5 7 8 3 2 5 6
5
7 9 5 7 6 4 8
6 9 3 5 4 9 8 3
7
3 2 6 1 5 6 7
As the job 6 is allocated to machine M2 its pro-
cessing time p
62
will be 23. Its predecessor and its
successor are the jobs 4 and 3, respectively. So, in this
example, are computed the times S
462
= 5 and S
632
=
5. Thus, it can be calculated the completion time of
machine M1 as S
021
+ p
21
+S
211
+ p
11
+S
171
+ p
71
=
120. Equivalently it is also calculated the comple-
tion time of machine M2 as S
052
+ p
52
+ S
542
+ p
42
+
S
462
+ p
62
+S
632
+ p
32
= 130. After the calculation of
the completion times of machines M1 and M2, it can
be concluded that the machine M2 is the bottleneck
machine. In other words, M2 is the machine that has
the highest completion time, the makespan.
The UPMSPST appears in many practical sit-
uations, one example is the textile manufacturing
(Pereira Lopes and de Carvalho, 2007). On the other
hand, the UPMSPST is in N P -Hard class, as it is
a generalization of the Parallel Machine Schedul-
ing Problem with Identical Machines and without
Setup Times (Karp, 1972; Garey and Johnson, 1979).
The theoretical and practical importance instigate the
study of the UPMSPST. Under these circumstances,
finding the optimal solution for UPMSPST using ex-
act methods can be computationally infeasible for
large-sized problems. Thus, metaheuristics and local
search heuristics are usually developed to find good
near optimal solutions.
In order to find these near optimal solutions for
the UPMSPST, this paper proposes the development
of an algorithm based on Iterated Local Search – ILS
(Lourenc¸o et al., 2003) and Variable Neighborhood
Descent – VND (Mladenovic and Hansen, 1997).
This algorithm is called AIV, it starts from an initial
solution constructed on a greedy way by the Adaptive
Shortest Processing Time – ASPT rule. Then, this ini-
tial solution is refined by ILS, using as local search
the Random VND procedure. In this procedure, here
called RVND, there is no fixed sequence of neighbor-
hoods, because they are sorted on each application of
the local search. In (Souza et al., 2010) the authors
showed the effectiveness of RVND over the conven-
tional VND.
AIV was tested using benchmark instances from
(de Optimizaci´on Aplicada, 2011) and the computa-
tional results showed that it is able to produce better
solutions than the algorithms found in literature, with
lower variability and setting new upper bounds for the
majority of instances.
The rest of this paper is structured as follows.
Firstly, works that inspired the development of this
paper are described. Then, the methodology used for
the deployment of this paper is presented. The com-
putational results are shown on sequence. Finally, this
paper is concluded and possible proposals to be ex-
plored are described.
2 LITERATURE REVIEW
In literature are found several works that seek to ad-
dress the UPMSPST and similar problems. These ap-
proacheswere inspirations for the development of this
paper.
(Weng et al., 2001) propose the development of
seven heuristics with the objective of minimizing the
weighted mean completion time. In (Kim et al.,
2003), a problem with common due dates is addressed
and four heuristics are implemented for minimizing
the total weighted tardiness. (Logendran et al., 2007)
aim to minimize the total weighted tardiness, consid-
ering dynamic releases of jobs and dynamic availabil-
ity of machines and they used four dispatching rules
in order to generate initial solutions and a Tabu Search
as the basis for the development of six search algo-
rithms. This problem is also addressed in (Pereira
AIV:AHeuristicAlgorithmbasedonIteratedLocalSearchandVariableNeighborhoodDescentforSolvingtheUnrelated
ParallelMachineSchedulingProblemwithSetupTimes
377

Lopes and de Carvalho, 2007), where a Branch-and-
Price algorithm is developed.
More recent references are found when deal-
ing with the UPMSPST. (Al-Salem, 2004) created
a Three-phase Partitioning Heuristic, called PH. In
(Rabadi et al., 2006) it is proposed a Metaheuristic
for Randomized Priority Search (Meta-RaPS). (Helal
et al., 2006) bet in Tabu Search for solving the
UPMSPST. (Arnaout et al., 2010) implement the Ant
Colony Optimization (ACO), considering its applica-
tion to problems wherein the ratio of jobs to machines
is large. In (Ying et al., 2012) it is implemented a
Restricted Simulated Annealing (RSA), which aims
to reduce the computational effort by only perform-
ing movements that the algorithm consider effective.
In (Chang and Chen, 2011) is defined and proved a
set of proprieties for the UPMSPST and also imple-
mented an Genetic Algorithm and a Simulated An-
nealing using these proprieties. A hybridization that
joins the Multistart algorithm, the VND and a mathe-
matical programming model is made in (Fleszar et al.,
2011). (Vallada and Ruiz, 2011) solve the UPMSPST
using Genetic Algorithms, with two sets of parame-
ters, the authors implemented two algorithms, GA1
and GA2. In (Vallada and Ruiz, 2011), the authors
created and provided test problems for the UPMSPST
(de Optimizaci´on Aplicada, 2011). Also in (de Op-
timizaci´on Aplicada, 2011) are presented the best
known solutions to the UPMSPST so far.
3 METHODOLOGY
3.1 The AIV Algorithm
The proposed algorithm, named AIV, combines the
heuristic procedures Iterated Local Search (ILS) and
Random Variable Neighborhood Descent (RVND).
The main structure of AIV is based on ILS, using the
RVND procedure to perform the local searches.
A solution s in AIV is represented as a vector of
lists. In this representation there is a vector v whose
size is the number of machines (m). Each position of
this vector contains a number that represents a ma-
chine. The schedule of the jobs on each machine is
represented by a list of numbers, where each number
represents one job.
In AIV, a solution s is evaluated by the completion
time of the machine that will be the last to conclude
their jobs, the so-called makespan.
The pseudo-code of AIV is presented in Algo-
rithm 1.
The Algorithm 1 has only two input parameters:
1)timesLevel, which represents thenumber of times
Algorithm 1: AIV.
1 input : timesLevel, executionTime
2 currentTime ← 0;
3 Solution s, s’, bestSol;
4 s ←
ASPT()
;
5 s ←
RVND(
s
)
;
6 bestSol ← s;
7 level ← 1;
8 Update currentTime;
9 while currentTime < executionTime do
10 s’ ← s;
11 times ← 0;
12 maxPerturb ← level + 1;
13 while times < timesLevel do
14 perturb ← 0;
15 s’ ← s;
16 while perturb < maxPerturb do
17 perturb ++;
18 s
′
←
perturbation(
s’
)
;
19 end
20 s
′
←
RVND(
s’
)
;
21 if f(s
′
) < f(s) then
22 s ← s’;
23
updateBest(
s, bestSol
)
;
24 times ← 0;
25 end
26 times ++;
27 Update currentTime;
28 end
29 level ++;
30 if level ≥ 4 then
31 level ← 1;
32 end
33 end
34 return bestSol;
in each level of perturbation; 2) executionTime, the
time in milliseconds that limits the execution of the
algorithm.
First of all, AIV begins initializing the variable
that controls the time limit, currentTime (line 2).
Next, it initializes three empty solutions: the current
solution s, the modified solution s
′
and the solution
that will store the best solution found bestSol (line 3).
In line 4 a new solution is created based on
the Adaptive Shortest Processing Time (ASPT) rule
(see subsection 3.2). Then, this new solution passes
through local searches at line 5, using the RVND
module (see subsection 3.4).
In the next step, the current best known solution,
bestSol, is updated (line 6) and the level of perturba-
tions is set to 1 (line 7).
After all these steps, the execution time is recalcu-
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
378

lated in line 8.
The iterative process of ILS is situated in lines 9 to
33 and it finishes when the time limit is exceeded. A
copy of the current solution to the modified solution
is made in line 10.
In lines 11 and 12 the variable that controls
the number of times in each level of perturbation
(times) is initialized, as well as the variable that limits
the maximum number of perturbations (maxPerturb).
The following loop is responsible to control the num-
ber of times in each level of perturbation (lines 13-
28).
The next loop, lines 16 to 19, executes the pertur-
bations (line 18) in the modified solution. The num-
ber of times this loop is executed depends on the level
of perturbation. With the perturbations accomplished,
the new solution obtained is evaluated and the RVND
procedure is applied in this new solution until a local
optimum is reached, in relation to all neighborhoods
adopted in RVND.
In lines (21-25) it is verified if the changes made
in the current solution were good enough to continue
the search from it. When the time is up, in bestSol
will be stored the best solution found by AIV.
The following subsections present details of the
each module of AIV.
3.2 Adaptive Shortest Processing Time
The Adaptive Shortest Processing Time (ASPT) rule
is an extension of the Shortest Processing Time rule
(Baker, 1974).
In ASPT, firstly, it is created a set N = {1, ..., n}
containing all jobs and a set M = {1,...,m} that con-
tains all machines.
From the set N, the jobs are classified according to
an evaluation function g
k
. This function is responsible
to obtain the completion time of the machine k. Given
a Candidate List (CL) of jobs, it is evaluated, based on
the g
k
function, the insertion of each of these jobs in
all positions of all machines. The aim is to obtain in
which position of what machine that the candidate job
will produce the lowest completion time, that is, the
g
min
.
If the machine with the lowest completion time
has not allocated any job yet, its new completion time
will be the sum of the processing time of the job to be
inserted with the initial setup time for such job.
If this machine has some job, its new completion
time will be the previous completion time plus the
processing time of the job to be inserted and the setup
times involved, if it has sequenced jobs before or af-
ter.
This allocation process ends when all jobs are as-
signed to some machine, thus producing a feasible
solution, s. This solution is returned by the heuris-
tic. The algorithm is said to be adaptive because the
choice of a job to be inserted depends on the preexist-
ing allocation.
3.3 Neighborhood Structures
Three neighborhoodstructures are used to explore the
solution space. These structures are based on swap
and insertion movements of the jobs.
• The first neighborhood, N
1
, is analyzed with mul-
tiple insertions movements, which are character-
ized by removing a job from a machine and insert
it into a position on another machine, including
the machine to which the job was already allo-
cated.
• The search in the second neighborhood, N
2
, is
made by swap movements of the jobs between dif-
ferent machines.
• The third and final neighborhood, N
3
, is based on
swap movementsof the jobs on the same machine.
3.4 Random Variable Neighborhood
Descent
The Random Variable Neighborhood Descent –
RVND procedure (Souza et al., 2010; Subramanian
et al., 2010) is a variant of the VND procedure
(Mladenovic and Hansen, 1997).
Each neighborhood of the set {N
1
,N
2
,N
3
} de-
scribed in section 3.3 defines one local search. Un-
like VND, the RVND explores the solution space us-
ing these three neighborhoods in a random order. The
RVND is finished when it is found on a local optimum
with relation to the three considered neighborhoods.
Following are described the local searches proce-
dures used in RVND.
3.4.1 Local Search with Multiple Insertion
The first local search uses multiple insertions move-
ments with the strategy First Improvement. In this
search, each job of each machine is inserted in all po-
sitions of all machines.
The selection of the jobs to be removed respects
the allocation order in the machines. That is, initially,
the first job is selected to be removed, then the second
job until all jobs from a machine are chosen. The ma-
chines that will have their jobs removed are selected
based on their completion times. The search starts
AIV:AHeuristicAlgorithmbasedonIteratedLocalSearchandVariableNeighborhoodDescentforSolvingtheUnrelated
ParallelMachineSchedulingProblemwithSetupTimes
379
with machines with higher completion times to ma-
chines with lower completion times.
By contrast, the insertions are made from ma-
chines with lower completion times to machines with
higher completion times. The jobs are inserted start-
ing from the first position and stopping at the last po-
sition.
The movement is accepted if the completion times
of the machines involved are reduced. If the comple-
tion time of a machine is reduced and the completion
time of another machine is added, the movement is
also accepted. However, in this case, it is only ac-
cepted if the value of reduced time is greater than the
value of time increased.
It is noteworthy that even in the absence of im-
provement in the value of makespan, the movement
can be accepted. Upon such acceptance of a move-
ment, the search is restarted and only ends when it
is found a local optimum, that is, when there is no
movement that can be accepted in the neighborhood
of multiple insertion.
3.4.2 Local Search with Swaps Between
Different Machines
The second local search makes swap movements be-
tween different machines. For each pair of existing
machines are made every possible swap of jobs be-
tween them.
Exchanges are made from machines that have
higher completion times to machines with lower com-
pletion times. The acceptance criteria are the same
as those applied in the first local search. If there are
reductions in completion times on two machines in-
volved, then the movement is accepted. If the reduced
value of the completion time of a machine is larger
than the completion time plus another machine, the
movement is also accepted. Once a movement is ac-
cepted, the search stops.
3.4.3 Local Search with Swaps on the Same
Machine
The third local search applies swap movements on
the same machine and uses the strategy Best Improve-
ment.
The machines are ordered from the machine that
has the highest value of completion time to the ma-
chine that has the lowest value of completion time.
For each machine, starting from the first, all pos-
sible swaps between their jobs are made. The best
movement is accepted if the completion time of the
machine is reduced and, in this case, the local search
is repeated from this solution; otherwise, the next ma-
chine is analyzed.
This local search only ends when no improve-
ments is found in 30% of the machines.
3.5 Efficient Evaluation of The
Objective Function
The evaluation of an entire solution after every move-
ment, insertion or swap, demands a large computa-
tional effort.
Aiming to avoid this situation, it was created a
procedurethat evaluatesonly the processing and setup
times involvedin the movements. In this way, in order
to obtain the new completion time of each machine it
is necessary few additions and subtractions.
Figure 2: Example of an insertion movement.
Figure 2 represent an example of an insertion
movement, based on Fig. 1 and tables 1, 2 and 3.
Figure 2 shows the removal of the job 6 from ma-
chine M2 and its insertion after job 7 on machine M1.
The new completion time of machine M2 is obtained
by subtracting from its previous value the process-
ing time of job 6 p
62
and also subtracting the setup
times involved, S
462
and S
632
. The addition of a the
setup time S
432
is made to the completion time of
machine M2. In machine M1, the processing time
of job 6 p
61
and the setup time S
761
are included in
the new completion time. It is not necessary to do
a subtraction from the completion time of machine
M1, because job 7 is the last to be processed and
no setup time is required. Then, the new comple-
tion time of machine M1 is M1 = 120+ 9+ 5 = 134
and the new completion time of machine M2 is M2 =
130− 23− 10− 5+ 1= 93.
Although the given example is for an insertion
movement, it is trivial to apply the same procedure
for a swap movement.
3.6 Perturbations
A perturbation is characterized by applying an inser-
tion movement in a local optimum, but this movement
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
380

differs when inserting the job in another machine. The
job will be inserted into its best position, that is, in the
position that will produce the lowest completion time.
Doing so, sub parts of the problem are optimized after
each perturbation. The machines and the job involved
are chosen randomly.
In AIV, the number of perturbations applied to a
solution is controlled by the level of perturbation. A
level l of perturbation consists in the application of
l + 1 insertion movements. The maximum level al-
lowed for the perturbations is set to 3.
If AIV generates timeslevel perturbed solutions
without an improvement in the current solution the
perturbation level is increased. If an improvement of
the current solution is found, the level of perturbation
is set to its lowest level (l = 1).
4 COMPUTATIONAL RESULTS
Using a set of 360 test problems from (de Opti-
mizaci´on Aplicada, 2011) the computational tests
were performed. This set of test problems involves
combinations of 50, 100 and 150 jobs with 10, 15 and
20 machines. There are 40 instances for each combi-
nation of jobs and machines. The best known solu-
tions for each of these test problems are also provided
in (de Optimizaci´on Aplicada, 2011).
AIV was developed in C++ language and all ex-
periments were executed in a computer with Intel
Core i5 3.0 GHz processor, 8 GB of RAM memory
and in Ubuntu 12.04 operational system.
The input parameters used in AIV were: the
number of iterations on each level of perturbation:
timeslevel = 15 and the stop criterion: Time
max
,
which is the maximum time of execution, in millisec-
onds, obtained by Eq. 1. In this equation, m repre-
sents the number of machines, n the number of jobs
and t is a parameter that was tested with three values
for each instance: 10, 30 and 50. It is observed that
the stop criterion, with these values of t, was the same
adopted in (Vallada and Ruiz, 2011).
Time
max
= n× (m/2) × t ms (1)
With the objective to verify the variability of fi-
nal solutions produced by AIV it was used the metric
given by Eq. 2. This metric is used to compare algo-
rithms. For each algorithm Alg applied to a test prob-
lem i is calculated the Relative Percentage Deviation
RPD
i
of the solution found
¯
f
Alg
i
in relation to the best
known solution f
∗
i
.
In this paper, the algorithm AIV was executed 30
times, for each instance and for each value of t, cal-
culating the Average Relative Percentage Deviation
RPD
avg
i
of the RPD
i
values found. In (Vallada and
Ruiz, 2011) the algorithms were executed 5 times for
each instance and for each value of t.
RPD
i
=
¯
f
Alg
i
− f
∗
i
f
∗
i
(2)
In Table 4 are presented, for each set of instances,
the RPD
avg
i
values obtained for each value of t =
10,30, 50 by AIV and also it contains the RPD
avg
i
val-
ues obtained by GA1 and GA2, both proposed in (Val-
lada and Ruiz, 2011). To our knowledge, the results
reported in the literature for this set of test problems
are only presented in (Vallada and Ruiz, 2011) and
the best algorithms tested by the authors were GA1
and GA2.
There are three values of RPD
avg
i
separated by a
’/’ for each set of instances in the table. Each sepa-
ration represents tests results with different values of
t, 10/30/50. If a negative value is found, it means
that the result reached by AIV outperformed the best
value found in (Vallada and Ruiz, 2011) on their ex-
periments.
Table 4: Average Relative Percentage Deviation of the al-
gorithms AIV, GA1 and GA2 with t = 10/30/50.
Instances
AIV
1
GA1
2
GA2
2
50 x 10 3.69/1.83/1.30 13.56/12.31/11.66 7.79/6.92/6.49
50 x 15
1.52/-0.77/-1.33 13.87/13.95/12.74 12.25/8.92/9.20
50 x 20
5.26/2.01/1.65 12.92/12.58/13.44 11.08/8.04/9.57
100 x 10
5.06/2.93/2.00 13.11/10.46/9.68 15.72/6.76/5.54
100 x 15
1.80/-0.40/-1.29 15.41/13.95/12.94 22.15/8.36/7.32
100 x 20
0.52/-1.64/-2.89 15.34/13.65/13.60 22.02/9.79/8.59
150 x 10
3.77/1.99/1.07 10.95/8.19/7.69 18.40/5.75/5.28
150 x 15
1.83/-0.24/-1.04 14.51/11.93/11.78 24.89/8.09/6.80
150 x 20
-1.04/-3.10/-4.00 13.82/12.66/12.49 22.63/9.53/7.40
RPD
avg
2.49/0.29/-0.50 13.72/12.19/11.78 17.44/8.02/7.35
1
Executed on Intel Core i5 3.0 GHz, 8 GB of RAM, 30 runs for each instance
2
Executed on Intel Core 2 Duo 2.4 GHz, 2 GB of RAM, 5 runs for each instance
The best values of RPD
avg
are highlighted in
bold. It is remarkable that AIV is the algorithm
that found the best results. Not only it has im-
proved the majority of best known solutions, but
also it wins in all sets of instances. A table with
all the results found by AIV and also the previous
best know values for the UPMSPST can be found
in http://www.decom.ufop.br/prof/marcone/projects/
upmsp/Table
AIV.ods.
The box plot, Figure 3, contains all the RPD
avg
values for each algorithm. It is notable that 100% of
the RPD values encountered by AIV outperform the
ones obtained by both GA1 and GA2 algorithms. By
the way, it is observed that 75% of solutions found by
AIV are near the best known solutions.
In order to verify if exist statistical differences
between the RPD values it was applied an analysis
of variance (ANOVA) (Montgomery, 2007). This
analysis returned, with 95% of confidence level and
AIV:AHeuristicAlgorithmbasedonIteratedLocalSearchandVariableNeighborhoodDescentforSolvingtheUnrelated
ParallelMachineSchedulingProblemwithSetupTimes
381

AIV GA1 GA2
−5 0 5 10 15 20 25
Algorithms
RPD_avg
Figure 3: Box plot showing the RPD
avg
of the algorithms.
threshold = 0.05, that F(2, 78) = 76.01 and p = 2 ×
10
−16
. As p < threshold, exist statistical differences
between the RPD values.
A Tukey HSD test, with 95% of confidence level
and threshold = 0.05, was used for checking where
are these differences. Table 5 contains the differences
in the average values of RPD (diff), the lower end
point (lwr), the upper end point (upr) and the p-value
(p) for each pair of algorithms.
The p-value shows that when comparing AIV to
GA1 there is a statistical difference between them,
because it was less than the threshold. The same
conclusion can be achieved when comparing AIV to
GA2. However, when GA1 is compared to GA2 they
are not statistically different from each other, since
the p-value was greater than the threshold.
Table 5: Results from Tukey HSD test.
Algorithms diff lwr upr p
GA1-AIV 11.803704 9.324312 14.2830956 0.0000000
GA2-AIV 10.177407 7.698016 12.6567993 0.0000000
GA2-GA1 -1.626296 -4.105688 0.8530956 0.2659124
By plotting the results from the Tukey HSD test
(Fig. 4) it is more noticeable that AIV is statistically
different from both GA1 and GA2, as their graphs do
not pass through zero. The largest difference appears
when comparing AIV with GA1, where AIV remark-
ably wins. Also when making a comparison between
AIV and GA2 the results show a better performance
of AIV.
Comparing algorithms GA1 and GA2 it can be
perceived that they are not statistically different from
each other, because the graph passes through zero.
Thus, with a statistical basis it can be concluded,
within the considered instances, that AIV is the best
algorithm on obtaining solutions for UPMSPST.
0 5 10 15
GA2−GA1 GA2−AIV GA1−AIV
95% family−wise confidence level
Differences in mean levels of Algorithm
Figure 4: Graphical results from Tukey HSD test.
5 CONCLUSIONS
The Unrelated Parallel Machine Scheduling Problem
with Setup Times (UPMSPST) is an important prob-
lem that is practical and theoretical. Because of that,
this paper studied the UPMSPST, aiming to the min-
imization of the maximum completion time of the
schedule, the makespan.
In order to solve the UPMSPST it was proposed
an algorithm based on Iterated Local Search (ILS)
and Variable Neighborhood Descent (VND). This al-
gorithm was named AIV. This algorithm implements
the Adaptive Shortest Processing Time (ASPT) rule
in order to create an initial solution. The Random
Variable Neighborhood Descent (RVND) procedure
was used to perform the local searches, randomly ex-
ploring the solution space with multiple insertions and
swap movements. A perturbation in AIV is an appli-
cation of an insertion movement.
AIV was used in test problems from literature and
the results were compared to two genetic algorithms,
GA1 and GA2, both developed in (Vallada and Ruiz,
2011). Statistical analysis of the computational re-
sults showed that AIV is able to produce, in aver-
age, 100% of better solutions than both genetic al-
gorithms. AIV was also able to generate new lower
bounds for these test problems. Thus, it can be con-
cluded that AIV is a great choice when dealing with
the UPMSPST.
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
382

It is proposed for future works that AIV will be
tested on the entire set of test problems available in
(de Optimizaci´on Aplicada, 2011). An improvement
that will be studied is an incorporation of a Mixed
Integer Programming(MIP) model to AIV for solving
related sub problems.
ACKNOWLEDGEMENTS
The authors thank the Brazilian agencies FAPEMIG
and CNPq, and the Universidade Federal de Ouro
Preto (UFOP) for the financial support on the devel-
opment of this work.
REFERENCES
Al-Salem, A. (2004). Scheduling to minimize makespan on
unrelated parallel machines with sequence dependent
setup times. Engineering Journal of the University of
Qatar, 17(1):177–187.
Arnaout, J., Rabadi, G., and Musa, R. (2010). A two-
stage ant colony optimization algorithm to minimize
the makespan on unrelated parallel machines with
sequence-dependent setup times. Journal of Intelli-
gent Manufacturing, 21(6):693–701.
Baker, K. R. (1974). Introduction to Sequencing and
Scheduling. John Wiley & Sons.
Chang, P. and Chen, S. (2011). Integrating dominance prop-
erties with genetic algorithms for parallel machine
scheduling problems with setup times. Applied Soft
Computing, 11(1):1263–1274.
de Optimizaci´on Aplicada, S. (2011). A web site
that includes benchmark problem data sets and
solutions for scheduling problems. Available at
http://soa.iti.es/problem-instances.
Fleszar, K., Charalambous, C., and Hindi, K. (2011).
A variable neighborhood descent heuristic for
the problem of makespan minimisation on unre-
lated parallel machines with setup times. Jour-
nal of Intelligent Manufacturing, 23(5):1949–1958.
doi:10.1007/s10845-011-0522-8.
Garey, M. and Johnson, D. (1979). Computers and in-
tractability: A guide to the theory of np-completeness.
WH Freeman & Co., San Francisco, 174.
Graham, R., Lawler, E., Lenstra, J., and Kan, A. (1979).
Optimization and approximation in deterministic se-
quencing and scheduling: a survey. Annals of discrete
Mathematics, 5(2):287–326.
Helal, M., Rabadi, G., and Al-Salem, A. (2006). A tabu
search algorithm to minimize the makespan for the
unrelated parallel machines scheduling problem with
setup times. International Journal of Operations Re-
search, 3(3):182–192.
Karp, R. M. (1972). Reducibility among combinatorial
problems. Complexity of Computer Computations,
40(4):85–103.
Kim, D. W., Na, D. G., and Frank Chen, F. (2003). Un-
related parallel machine scheduling with setup times
and a total weighted tardiness objective. Robotics and
Computer-Integrated Manufacturing, 19:173–181.
Logendran, R., McDonell, B., and Smucker, B. (2007).
Scheduling unrelated parallel machines with
sequence-dependent setups. Computers & Oper-
ations research, 34(11):3420–3438.
Lourenc¸o, H. R., Martin, O., and St¨utzle, T. (2003). Iter-
ated local search. In Glover, F. and Kochenberger, G.,
editors, Handbook of Metaheuristics, volume 57 of In-
ternational Series in Operations Research & Manage-
ment Science, pages 321–353. Kluwer Academic Pub-
lishers, Norwell, MA.
Mladenovic, N. and Hansen, P. (1997). Variable neighbor-
hood search. Computers and Operations Research,
24(11):1097–1100.
Montgomery, D. (2007). Design and Analysis of Experi-
ments. John Wiley & Sons, New York, NY, fifth edi-
tion.
Pereira Lopes, M. J. and de Carvalho, J. M. (2007). A
branch-and-price algorithm for scheduling parallel
machines with sequence dependent setup times. Eu-
ropean Journal of Operational Research, 176:1508–
1527.
Rabadi, G., Moraga, R. J., and Al-Salem, A. (2006). Heuris-
tics for the unrelated parallel machine scheduling
problem with setup times. Journal of Intelligent Man-
ufacturing, 17(1):85–97.
Souza, M., Coelho, I., Ribas, S., Santos, H., and Mer-
schmann, L. (2010). A hybrid heuristic algorithm
for the open-pit-mining operational planning prob-
lem. European Journal of Operational Research,
207(2):1041–1051.
Subramanian, A., Drummond, L., Bentes, C., Ochi, L., and
Farias, R. (2010). A parallel heuristic for the vehicle
routing problem with simultaneous pickup and deliv-
ery. Computers & Operations Research, 37(11):1899–
1911.
Vallada, E. and Ruiz, R. (2011). A genetic algorithm for the
unrelated parallel machine scheduling problem with
sequence dependent setup times. European Journal of
Operational Research, 211(3):612–622.
Weng, M. X., Lu, J., and Ren, H. (2001). Unrelated parallel
machine scheduling with setup consideration and a to-
tal weighted completion time objective. International
Journal of Production Economics, 70:215–226.
Ying, K.-C., Lee, Z.-J., and Lin, S.-W. (2012). Makespan
minimisation for scheduling unrelated parallel ma-
chines with setup times. Journal of Intelligent Manu-
facturing, 23(5):1795–1803.
AIV:AHeuristicAlgorithmbasedonIteratedLocalSearchandVariableNeighborhoodDescentforSolvingtheUnrelated
ParallelMachineSchedulingProblemwithSetupTimes
383
