
Code Size and Accuracy-aware Synthesis of Fixed-point Programs
for Matrix Multiplication
Matthieu Martel
1,2,3
, Amine Najahi
1,2,3
and Guillaume Revy
1,2,3
1
Univ. Perpignan Via Domitia, DALI, F-66860, Perpignan, France
2
Univ. Montpellier II, LIRMM, UMR 5506, F-34095, Montpellier, France
3
CNRS, LIRMM, UMR 5506, F-34095, Montpellier, France
Keywords:
Automated Code Synthesis, Matrix Multiplication, Fixed-point Arithmetic, Certified Numerical Accuracy.
Abstract:
In digital signal processing, many primitives boil down to a matrix multiplication. In order to enable savings in
time, energy consumption, and on-chip area, these primitives are often implemented in fixed-point arithmetic.
Various conflicting goals undermine the process of writing fixed-point codes, such as numerical accuracy, run-
time latency, and size of the codes. In this article, we introduce a new methodology to automate the synthesis
of small and accurate codes for matrix multiplication in fixed-point arithmetic. Our approach relies on a
heuristic to merge matrix rows or columns in order to reduce the synthesized code size, while guaranteeing
a target accuracy. We suggest a merging strategy based on finding closest pairs of vectors, which makes it
possible to address in a few seconds problems such as the synthesis of small and accurate codes for size-64
and more matrix multiplication. Finally, we illustrate its efficiency on a set of benchmarks, and we show that
it allows to reduce the synthesized code size by more than 50% while maintaining good numerical properties.
1 INTRODUCTION
Embedded systems are usually dedicated to one or
few tasks that are often highly demanding on com-
putational resources. Examples of computational ap-
plications widely deployed on these targets include
discrete transforms (DCT, FFT, and digital filters) as
well as image processing. Since floating-point imple-
mentations are costly in hardware resources, embed-
ded system programmers prefer the fixed-point arith-
metic (Yates, 2009). Indeed, the latter requires no
specific hardware, relies on integer arithmetic only,
and is highly efficient in terms of execution speed and
energy consumption. Besides, in such systems, the
accuracy is often critical, and there is a real need for
the design of numerically certified basic blocks.
However, there are currently two hurdles to the
widespread use of fixed-point arithmetic. First, fixed-
point programming is a tedious process that requires
a high degree of expertise since the programmer is
in charge of such arithmetical details as alignments
and overflow prevention. Second, the low dynamic
range of fixed-point numbers compared to floating-
point numbers led to a persistent belief that fixed-
point computations are inherently unsafe and should
be confined to uncritical applications. For all of these
reasons, the fixed-point arithmetic has been for long
limited to small and simple enough problems. In this
article, our goal is to overcome these limitations for
the case of matrix multiplication which is a widely
deployed basic block in embedded applications.
For this purpose, we suggest and implement a
novel methodology to automate the synthesis of tight
and accurate codes for matrix multiplication that
lends itself naturally to matrix-vector multiplication.
In fact, a classical n×n matrix multiplication requires
n
2
dot-products. For the sake of accuracy, each dot-
product may rely on a particular optimized fixed-point
code, leading to large code sizes. The challenge is
therefore to reduce the number of synthesized dot-
products without harming the overall accuracy of ma-
trix multiplication. Our contribution is a novel strat-
egy to carefully select and merge close enough rows
and columns of the input matrices in order to reduce
the number of synthesized dot-products, while guar-
anteeing a certain accuracy bound. This methodol-
ogy is implemented in an automated tool and allows
to quickly and easily treat problems previously con-
sidered intractable or unsuitable for this arithmetic.
For instance, writing a code for the accurate mul-
tiplication of size-64 matrices is almost impossible
to achieve by hand since it involves various trade-
204
Martel M., Najahi A. and Revy G..
Code Size and Accuracy-aware Synthesis of Fixed-point Programs for Matrix Multiplication.
DOI: 10.5220/0004884802040214
In Proceedings of the 4th International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2014), pages
204-214
ISBN: 978-989-758-000-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

offs between code size, runtime latency, and accuracy.
Moreover, to increase the level of confidence in the
synthesized codes, our tool uses an analytic method-
ology based on interval arithmetic (Moore et al.,
2009) to compute strict bounds on the roundoff er-
rors and to guarantee the absence of overflow. With
each synthesized code, it provides an accuracy cer-
tificate that bounds the accuracy errors due to finite
wordlength effects, and that can be checked using the
formal verification tool Gappa
1
(Melquiond, 2006).
Although many work on linear algebra routines in
fixed-point arithmetic exists, to our knowledge, this
article is the first one where certified fixed-point tech-
niques are applied to such large problems, as size-64
matrix multiplication. Indeed (Nikolic et al., 2007)
deals with the transformation from floating-point to
fixed-point of matrix decomposition algorithms for
DSPs and (Golub and Mitchell, 1998) with the im-
plementation of matrix factorization algorithms for
the particular C6x VLIW processor, while (Mehlhose
and Schifferm
¨
uller, 2009) and (Irturk et al., 2010)
discuss matrix inversion for the C64x+ DSP core
and FPGAs, respectively. For the matrix multiplica-
tion, (Syed M. Qasim, 2010) present a hardware im-
plementation of a matrix multiplier optimized for a
Virtex4 FPGA, which mainly relies on a large matrix-
vector block to handle large matrices. Yet another
FPGA architecture is presented in (Sotiropoulos and
Papaefstathiou, 2009), that uses parallel DSP units
and multiplies sub-matrices, whose size has been op-
timized so as to fully exploit the resources of the
underlying architecture. In (Campbell and Khatri,
2006) a delay and resource efficient methodology is
introduced to implement a FPGA architecture for ma-
trix multiplication in integer/fixed-point arithmetic.
These works suggest a variety of techniques to de-
termine and optimize fixed-point wordlengths. How-
ever, the roundoff error bounds in their methodologies
are computed a posteriori by simulating the fixed-
point design and comparing its output to that of a
floating-point design. Also when determining fixed-
point formats of intermediate variables, most of these
works use a technique introduced by Sung et al. (Kim
et al., 1998). This technique consists in using floating-
point simulation to estimate the range of intermediate
computations and convert the program to fixed-point
arithmetic. In (Nikolic et al., 2007), the Sung tech-
nique is used to suggest a number of linear algebra
routines. This simulation based technique has two
drawbacks: 1. Its duration is exponentially propor-
tional to the number of input variables. It is there-
fore impractical for large problems. 2. It provides no
strict guaranties that intermediate computations will
1
See http://gappa.gforge.inria.fr.
X
7
X
6
X
5
X
4
X
3
X
2
X
1
X
0
i = 3 f = 5
k = 8
Figure 1: Fixed-point number in Q
3,5
on k = 8 bits.
not overflow. On the other hand, the authors of (Lee
et al., 2006) use a more rigorous approach to generate
fixed-point codes for various problems. But we are
not aware of any automated implementation and their
examples do not supersede the size-8 DCT.
This article is organized as follows: After some
background on fixed-point arithmetic in Section 2,
Section 3 discusses two straightforward approaches
for synthesizing matrix multiplication programs.
Then our new strategy to synthesize codes that sat-
isfy certain tradeoff goals is presented in Section 4.
Finally Section 5 is dedicated to some experimental
benchmarks, before a conclusion in Section 6.
2 BACKGROUND ON
FIXED-POINT ARITHMETIC
This section presents our fixed-point arithmetic
model, including an error model, and it discusses the
numerical issues arising from the computation of dot-
products in this arithmetic.
2.1 Fixed-point Arithmetic Model
Fixed-point Number. Fixed-point arithmetic al-
lows one to represent a real value by means of an in-
teger associated to an implicit scaling factor. Let X be
a k-bit signed integer in radix 2, encoded using two’s
complement notation. Combined with a factor f ∈ Z,
it represents the real value x defined as follows:
x = X · 2
− f
.
In the sequel of this article, Q
i, f
denotes the for-
mat of a given fixed-point value represented using a
k-bit integer associated with a scaling factor f , with
k = i + f , as shown in Figure 1.
Hence a fixed-point variable v in Q
i, f
is such that:
v ∈ {V · 2
− f
} with (1)
V ∈ Z ∩[−2
k−1
,2
k−1
− 1],
by step of 2
− f
.
Set of Fixed-point Intervals. In practice, a fixed-
point variable v may lie in a smaller range than
the one defined in Equation (1). For instance, if
CodeSizeandAccuracy-awareSynthesisofFixed-pointProgramsforMatrixMultiplication
205

V ∈ Z ∩[−2
k−1
+2
k−2
,2
k−1
−2
k−2
] in Equation (1),
then v is still in the Q
i, f
format but with additional
constraints on the runtime values it can take. For this
reason, in this article, we denote by Fix the set of
fixed-point intervals, where each element has a fixed
format and an interval that narrows its runtime values.
Notice that unlike the exponent of floating-point
variables, the scaling factor of fixed-point variables
is fixed and is not encoded into the program. It is
known only by the programmer, who is in charge of
all the arithmetical details. For example, when adding
two fixed-point values, both operand points have first
to be aligned, that is, operands have to be set in the
same fixed-point format. This alignment may lead to
a potential roundoff error in finite precision.
2.2 Error Model in Fixed-point
Arithmetic
Let v, v
`
, and v
r
be three fixed-point variables in the
formats Q
i, f
, Q
i
`
, f
`
, and Q
i
r
, f
r
, respectively, and be an
operation in {+,−,×}:
v = v
`
v
r
.
For the sake of conciseness, we do not deal here
with the determination of fixed-point formats, but it
can be found in (Yates, 2009) or (Mouilleron et al.,
2013). Let us rather detail how we compute an inter-
val error(v) enclosing the error entailed by the evalu-
ation of v, where value(v) is an interval enclosing the
value of v.
• In absence of overflow, addition and subtraction
are error-free. Hence, for ∈ {+,−} we have:
error(v) = error(v
`
) error(v
r
).
• If the operation is a multiplication, we have:
error(v) = error
×
+ error(v
`
) ·error(v
r
)
+ error(v
`
) ·value(v
r
)
+ value(v
`
) ·error(v
r
),
where error
×
is the error entailed by the multipli-
cation itself. Usually in fixed-point arithmetic this
error is due to the truncation of the exact result of
the multiplication to fit in a smaller format with f
fraction bits. Hence we have:
error
×
= [2
−( f
`
+ f
r
)
− 2
− f
,0].
Most 32-bits DSP processors provide a 32 × 32
multiplier that returns the 32 most significant bits
of the exact result, which is the multiplier consid-
ered in this work.
Left shift entails no error but only a possible overflow.
However right shift may also be followed by the trun-
cation of the exact result to fit in a smaller format with
f fraction bits. Hence the evaluation of v = v
`
>> r en-
tails an error defined as follows:
error(v) = error(v
`
) +error
>>
with in practice:
error
>>
= [2
− f
`
− 2
− f
,0] and f = f
`
− r.
2.3 Synthesis of Dot-product Code in
Fixed-point Arithmetic
The code synthesized by our tool for matrix mul-
tiplication relies on dot-product evaluations as ba-
sic blocks. Besides the arithmetic model, the com-
putation order of summations when evaluating dot-
products has a great impact on the accuracy of the re-
sulting codes. This is a well-known issue in floating-
point arithmetic (Ogita et al., 2005),(Rump, 2009) but
the same holds for fixed-point arithmetic. Precisely,
summing n variables can be done using
∏
n−2
i=1
(2i +1)
different ways.
2
For example, there exists 945 differ-
ent schemes to implement a size-6 dot-product. Due
to this huge combinatorics, there is a need for heuris-
tics to address the issue of synthesizing accurate dot-
product codes.
Our approach relies on the use of the CGPE
3
li-
brary (Mouilleron and Revy, 2011). Introduced by
Revy et al., it was initially designed to synthesize
codes for polynomial evaluation, and it has been so far
extended to summation and dot-product. CGPE im-
plements the previous arithmetic model and embraces
some heuristics to produce fast and numerically cer-
tified codes, relying on k-bit integer arithmetic only.
Typically k ∈ {16,32, 64} and, for the rest of the ar-
ticle, we consider k = 32. CGPE takes as input an
interval of fixed-point values for each coefficient and
variable, a maximum error bound allowed for the code
evaluation, and some architectural constraints. Then
it outputs codes exposing a high degree of instruction-
level parallelism and for which we are able to bound
the evaluation error.
For dot-products, CGPE takes two size-n vectors
V
1
and V
2
whose elements belong to the vectors of
intervals
V
1
,V
2
∈ Fix
n
,
with Fix the set of fixed-point intervals defined in Sec-
tion 2.1. It computes fast and numerically certified
codes to implement V
1
· V
2
. In the sequel of the arti-
cle, we will refer to the routine DPSynthesis(V
1
,V
2
)
to compute automatically these codes.
2
See http://oeis.org/A001147.
3
See http://cgpe.gforge.inria.fr.
PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
206

3 STRAIGHTFORWARD
APPROACHES FOR THE
SYNTHESIS OF MATRIX
MULTIPLICATION PROGRAMS
Let A and B be two fixed-point interval matrices of
size m × n and n × p, respectively:
A ∈ Fix
m×n
and B ∈ Fix
n×p
.
In the article, we denote by A
i,:
and A
:, j
the i
th
row and
j
th
column of A, respectively, and A
i, j
the element of
the i
th
row and j
th
column of A.
We discuss now two straightforward approaches
for the synthesis of a fixed-point program to mul-
tiply A
0
and B
0
, where A
0
and B
0
are two matrices
that belong to A and B, that is, where each element
A
0
i,k
and B
0
k, j
belongs to the intervals A
i,k
and B
k, j
,
respectively. This consists in writing a program for
computing C = A · B, where C ∈ Fix
m×p
. Therefore,
∀i, j ∈ {1,·· · , m} × {1, · ·· , p}, we have:
C
i, j
= A
i,:
· B
:, j
=
n
∑
k=1
A
i,k
· B
k, j
, (2)
At the end of the section, we give some code size and
accuracy estimates for each approach.
3.1 Accurate and Compact Approaches
Following Equation (2), a first straightforward ap-
proach to write code for matrix multiplication con-
sists in synthesizing a program for each dot-product
A
i,:
· B
:, j
. Algorithm 1 below implements this ap-
proach, where DPSynthesis(A
i,:
,B
:, j
) produces a fast
and numerically certified code for the computation
of A
i,:
· B
:, j
.
Remark that Algorithm 1 issues m × p requests to
the DPSynthesis routine. At runtime, only one call
to each generated code will be issued, for a total of
m × p calls.
Algorithm 1: Accurate algorithm.
Input:
Two matrices A ∈ Fix
m×n
and B ∈ Fix
n×p
Output:
Code to compute the product A · B
Algorithm:
1: for 1 ≤ i ≤ m do
2: for 1 ≤ j ≤ p do
3: DPSynthesis(A
i,:
,B
:, j
)
4: end for
5: end for
Algorithm 2: Compact algorithm.
Algorithm:
1: U ← A
1,:
∪ A
2,:
∪ · · · ∪ A
m,:
, with U ∈ Fix
1×n
2: V ← B
:,1
∪ B
:,2
∪ · · · ∪ B
:,p
, with V ∈ Fix
n×1
3: DPSynthesis(U,V )
To significantly reduce the size of the whole pro-
gram, the computed codes could be refactored to eval-
uate more than one dot-product. Algorithm 2 below,
whose input and output are the same as Algorithm 1,
pushes this idea to the limits by merging element by
element the matrices A and B into a unique row U
and column V , respectively. Merging two fixed-point
intervals means computing their union. Using this ap-
proach, it issues a unique call to DPSynthesis at syn-
thesis. But, at runtime, m × p calls to the synthesized
code are still needed to evaluate the matrix product.
Let us now illustrate the differences between these
two algorithms by considering the problem of gener-
ating code for the product of the following two fixed-
point interval matrices:
A =
[−1000,1000] [−3000,3000]
[−1,1] [−1,1]
and
B =
[−2000,2000] [−2,2]
[−4000,4000] [−10,10]
,
where A
1,1
and B
1,1
are in the format Q
11,21
, A
1,2
in Q
12,20
, A
2,1
, A
2,2
, B
2,1
in Q
2,30
, B
1,2
in Q
3,29
, and
B
2,2
in Q
5,27
. Algorithm 1 produces 4 distinct codes,
denoted by DPCode
1,1
, DPCode
1,2
, DPCode
2,1
, and
DPCode
2,2
. On the other hand, Algorithm 2 first com-
putes U and V as follows:
U = A
1,:
∪ A
2,:
= ([−1000,1000][−3000,3000])
and
V = B
:,1
∪ B
:,2
=
[−2000,2000]
[−4000,4000]
.
Then, DPCode
U,V
is generated that evaluates the dot-
product of U and V . Table 1 summarizes the proper-
ties of the codes produced by both algorithms on the
example.
On the first hand, Table 1(a) shows that Algo-
rithm 1 produces codes optimized for the range of
its entries: it is clearly superior in terms of accuracy
since a dedicated code evaluates each runtime dot-
product. On the other hand, Table 1(b) shows that,
as expected, Algorithm 2 produces far less code: it
is is optimal in terms of code size since a unique dot-
product code is generated, but remains a worst-case in
terms of accuracy. Fixed-point arithmetic is primarily
CodeSizeandAccuracy-awareSynthesisofFixed-pointProgramsforMatrixMultiplication
207

Table 1: Numerical properties of the codes generated by algorithms 1 and 2 for the product A · B.
(a) Results for the 4 codes generated by Algorithm 1.
Dot-product A
1,:
· B
:,1
A
1,:
· B
:,2
A
2,:
· B
:,1
A
2,:
· B
:,2
Evaluated using DPCode
1,1
DPCode
1,2
DPCode
2,1
DPCode
2,2
Output format Q
26,6
Q
18,14
Q
15,17
Q
7,25
Certified error ≈ 2
−5
≈ 2
−14
≈ 2
−16
≈ 2
−24
Maximum error ≈ 2
−5
Average error ≈ 2
−7
(b) Results for the code generated by Algorithm 2.
Dot-product A
1,:
· B
:,1
A
1,:
· B
:,2
A
2,:
· B
:,1
A
2,:
· B
:,2
Evaluated using DPCode
U,V
Output format Q
26,6
Certified error ≈ 2
−5
Maximum error ≈ 2
−5
Average error ≈ 2
−5
used in embedded systems where the execution envi-
ronment is usually constrained. Hence even tools that
produce codes with guaranteed error bounds would be
useless if the generated code size is excessively large.
In this article, we go further than Algorithms 1 and 2,
and explore the possible means to achieve tradeoffs
between the two conflicting goals.
3.2 Code Size and Accuracy Estimates
The dot-product is the basic block of classical ma-
trix multiplication. In a size-n dot-product, regard-
less of the evaluation scheme used, n multiplications
and n − 1 additions are performed, since it can be
reduced to a size-n summation. Also, depending on
the formats of their operands, additions frequently re-
quire alignment shifts. Thus the number of shifts is
bounded by 2n and, in absence of overflow, it falls
to n. Hence 4n − 1 is a worst case bound on the
number of elementary operations (additions, multipli-
cations, and shifts) needed to evaluate a size-n dot-
product. Globally, (4n − 1) · t is a bound on the to-
tal size of a matrix multiplication code, where t ∈
{1,··· , m × p} is the number of generated dot-product
codes. On the previous example, this bound evaluates
to 28 for Algorithm 1 vs. 7 for Algorithm 2, since
n = 2, and t = 4 and 1, respectively.
As for accuracy estimates, given a matrix multi-
plication program composed of several DPCodes, the
maximum of all error bounds can be considered as a
measure of the numerical quality. However, exam-
ples can be found where this measure does not reflect
the numerical accuracy of all the codes. Consider for
instance the example of Section 3.1, where both algo-
rithms generate codes that have the same maximum
error bound (≈ 2
−5
), yet 3 of the 4 DPCodes gen-
erated by Algorithm 1 are by far more accurate than
this bound. For this reason, we may also rely on the
average error since we consider it as a more faithful
criterion to estimate the accuracy.
4 DYNAMIC CLOSEST PAIR
ALGORITHM FOR CODE SIZE
VS. ACCURACY TRADEOFFS
In this section, we discuss how to achieve code size
vs. accuracy tradeoffs, and the related combinatorics.
We finally detail our new approach based on rows and
columns merging and implemented in the Dynamic
Closest Pair algorithm.
4.1 How to Achieve Tradeoffs
On the first hand, when developing a numerical ap-
plication for embedded systems, the amount of pro-
gram memory available imposes an upper bound on
the code size. On the other hand, the nature of the ap-
plication and its environment help in deciding on the
required degree of accuracy.
Once these parameters set, the programmer tries
Algorithms 1 and 2. Either the accurate algorithm
(Algorithm 1) is not accurate enough: a solution we
do not discuss here consists in adapting the fixed-
point computation wordlengths to reach the required
accuracy, as in (Lee and Villasenor, 2009). Or the
compact algorithm (Algorithm 2) does not satisfy the
code size constraint: other solutions must be consid-
ered such as adding more hardware resources. Fi-
nally, the only uncertainty that remains is when Al-
gorithm 1 satisfies the accuracy constraint but has a
large code size while Algorithm 2 satisfies the code
size bound but is not accurate enough. This case ap-
peals for code size vs. accuracy tradeoffs.
Recall that m × p dot-product calls are required
at runtime. To evaluate them using less than m × p
DPCodes, it is necessary to refactor some DPCodes
so that they would evaluate more than one runtime
dot-product. This amounts to merging certain rows
and/or columns of the input matrices together. Obvi-
ously, it is useless to go as far as compressing the left
and right matrices into one row and column, respec-
tively, since this corresponds to Algorithm 2. Our idea
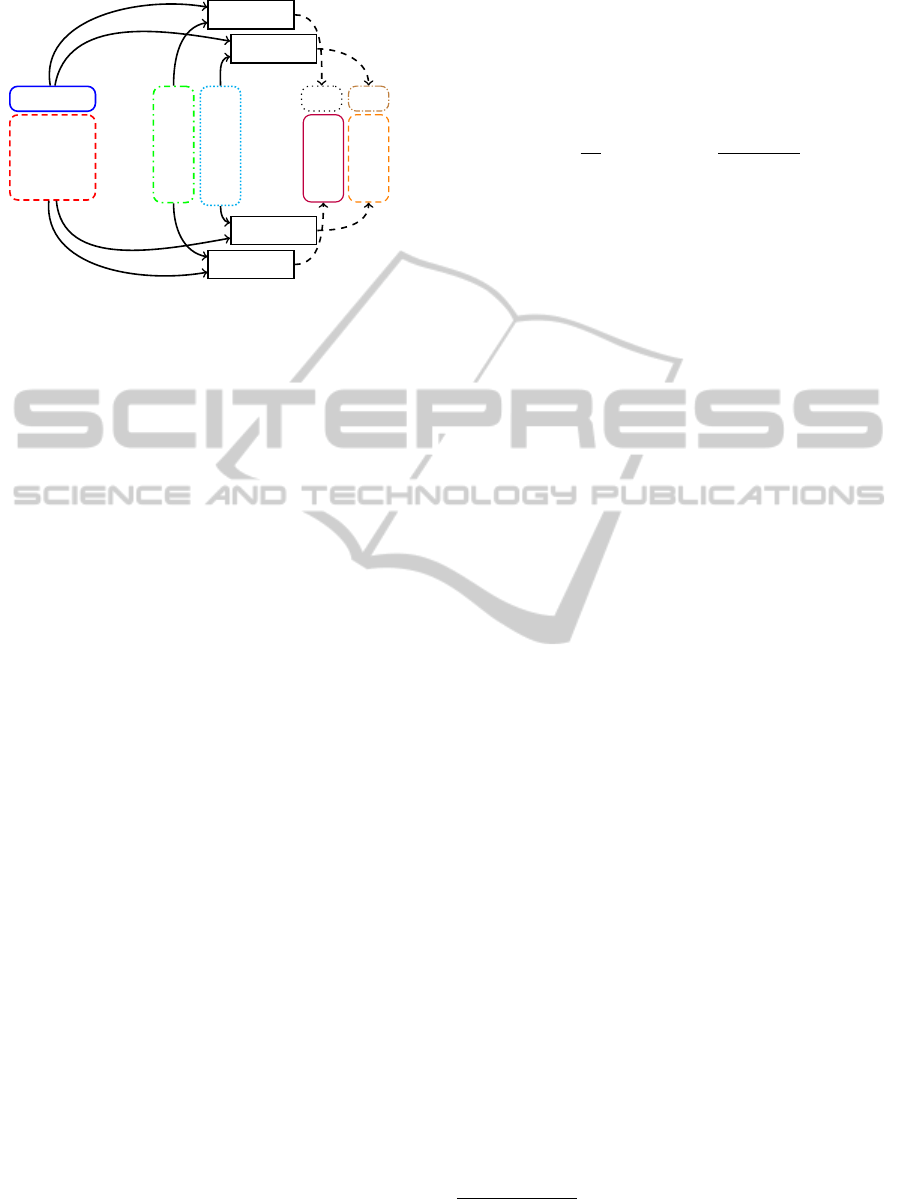
is illustrated by Figure 2 on a 4 × 4 matrix multipli-
PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
208
• • • •
• • • •
• • • •
• • • •
×
• • • •
• • • •
• • • •
• • • •
=
• • • •
• • • •
• • • •
• • • •
DPCode
1
DPCode
2
DPCode
3
DPCode
4
Figure 2: Merging strategy on a 4 ×4 matrix multiplication.
cation. In this example, each matrix is compressed
into a 2 × 2 matrix, as shown by the differently col-
ored and shaped blocks. In this case, the number of
required codes is reduced from 16 to 4. For exam-
ple, DPCode
1
has been particularly optimized for the
computation of A
1,:
· B
:,1
and A
1,:
· B
:,2
, and will be
used exclusively for these at runtime.
4.2 Combinatorial Aspect of the
Merging Strategy
Let A and B be two fixed-point interval matrices of
size m × n and n × p, respectively:
A ∈ Fix
m×n
and B ∈ Fix
n×p
,
and their two associated sets of vectors
S
A
= {A
1,:
,··· , A
m,:
} and S
B
= {B
:,1
,··· , B
:,p
}.
In our case, the problem of finding an interesting code
size vs. accuracy tradeoff reduces to finding partitions
of the sets S
A
and S
B
into k
A
≤ m and k
B
≤ p subsets,
respectively, such that both of the following condi-
tions hold:
1. the code size bound σ is satisfied, that is:
(4n − 1) · k
A
· k
B
< σ,
2. and the error bound ε is guaranteed, that is:
ε
matrix
< ε,
where ε
matrix
is either the minimal, the maximal, or
the average computation error depending on the
certification level required by the user.
Remark that, given the partitions of S
A
and S
B
, the
first condition is easy to check. However in order to
guarantee the error condition, we must compute the
error bound using CGPE.
A benefit of formulating the refactoring strategy
in terms of partitioning is the ability to give an upper
bound on the number of possible dot-product merg-
ings. Indeed, given a non-empty set S of k vectors,
the number of different ways to partition S into k
0
≤ k
non-empty subsets of vectors is given by the Stirling
number
4
of the second kind
k
k
0
, defined as follows:
k
k
0
=
1
k
0
!
k
0
∑
j=0
(−1)
k
0
− j
k
0
!
j!(k
0
− j)!
j
k
.
However, k
0
is a priori unknown and can be ∈
{1,··· , k}. The total number of possible partitions of
a set of k vectors is therefore given by the following
sum, commonly referred to as the Bell number:
5
B(k) =
k
∑
k
0
=1
k
k
0
.
Finally, in our case, the total number of partitionings
is defined as follows:
P (m, p) = B(m) · B(p) − 2, (3)
where m× p is the size of the resulting matrix. Notice
that we exclude two partitions:
1. The partition of S
A
and S
B
into respectively m and
p subsets which correspond to putting one and
only one vector in each subset. This is the par-
titioning that leads to Algorithm 1.
2. The partition of S
A
and S
B
into one subset each.
This partitioning leads to Algorithm 2.
Observe that even for small matrix sizes, the
number P in Equation (3) is huge: P (5, 5) = 2702,
P (10,10) ≥ 2
33
, and P (64,64) ≥ 2
433
. Therefore,
aggressive heuristics will be necessary to tackle this
problem. In the following, we introduce a method
based on finding closest pairs of vectors according to
a certain metric. This allows to find partitions that
achieve the required tradeoff.
4.3 Dynamic Closest Pair Algorithm
Merging two fixed-point interval vectors U and V
component-wise yields a vector whose ranges are
larger than those of U and V . This eventually leads to
a degradation of the accuracy if the resulting vector is
used to generate some DPCodes. In the extreme, this
is illustrated by Algorithm 2 in Section 3.1. Therefore
the underlying idea of our approach is that of putting
together, in the same subset, row or column vectors
that are close according to a given distance or crite-
rion. Hence we ensure a reduction in code size while
maintaining tight fixed-point formats, and thus guar-
anteeing a tight error bound.
4
See http://oeis.org/A008277.
5
See http://oeis.org/A000110.
CodeSizeandAccuracy-awareSynthesisofFixed-pointProgramsforMatrixMultiplication
209

I
1
I
2
d
H
(I
1
,I
2
)
(a) Hausdorff distance.
I
1
I
2
d
W
(I
1
,I
2
)
(b) Width criterion.
Figure 3: Illustration of distances between two intervals.
Many metrics can be used to compute the distance
between two vectors. Below, we cite two mathemat-
ically rigorous distances that are suitable for fixed-
point interval arithmetic: the Hausdorff and the fixed-
point distances. However, as our method does not use
the mathematical properties of distances, any criterion
that may discriminate between pairs of fixed-point in-
terval vectors may be used. For instance, although not
a distance, the width criterion introduced below was
used in our experiments.
Hausdorff Distance. A fixed-point interval vari-
able corresponds to a rational discrete interval. It fol-
lows that the Hausdorff distance (Moore et al., 2009),
widely used as a metric in interval arithmetic, can be
applied to fixed-point interval variables. Given two
fixed-point intervals I
1
and I
2
, this distance d
H
(I
1
,I
2
)
is defined as follows:
d
H
: Fix × Fix → R
+
d
H
(I
1
,I
2
) = max
I
1
− I
2
,
I
1
− I
2
,
where I
1
and I
1
stand for the lower and upper bound
of the interval I
1
, respectively. Roughly, this distance
computes the maximum increase suffered by I
1
and
I
2
when computing their union I
1
∪ I
2
, as illustrated
on Figure 3(a).
Fixed-point Distance. Contrarily to Hausdorff’s
distance which reasons on the intervals defined by
the fixed-point variables, the fixed-point distance uses
only their fixed-point formats. As such, it is slightly
faster to compute. Given two fixed-point intervals I
1
and I
2
, this distance d
F
(I
1
,I
2
) is defined as follows:
d
F
: Fix × Fix → N
d
F
(I
1
,I
2
) =
|
IntegerPart(I
1
) − IntegerPart(I
2
)
|
.
Analogously to Hausdorff distance, this distance
computes the increase in the integer part suffered by
I
1
and I
2
when computing their union I
1
∪ I
2
.
Width Criterion. Given two fixed-point intervals
I
1
and I
2
, our third metric computes the width of the
interval resulting from the union I
1
∪ I
2
, as illustrated
on Figure 3(b). Formally, it is defined as follows:
d
W
: Fix × Fix → R
+
d
W
(I
1
,I
2
) =
I
1
∪ I
2
− I
1
∪ I
2
.
Algorithm 3: Dynamic Closest Pair algorithm.
Input:
Two matrices A ∈ Fix
m×n
and B ∈ Fix
n×p
An accuracy bound C
1
(ex. average error bound is < ε)
A code size bound C
2
A metric d
Output:
Code to compute A · B s.t. C
1
and C
2
are satisfied,
or no code otherwise
Algorithm:
1: S
A
← {A
1,:
,..., A
m,:
}
2: S
B
← {B
:,1
,..., B
:,p
}
3: while C
1
is satisfied do
4: (u
A
,v
A
),d
A
← f indClosestPair(S
A
,d)
5: (u
B
,v
B
),d
B
← f indClosestPair(S
B
,d)
6: if d
A
≤ d
B
then
7: remove(u
A
,v
A
,S
A
)
8: insert(u
A
∪ v
A
,S
A
)
9: else
10: remove(u
B
,v
B
,S
B
)
11: insert(u
B
∪ v
B
,S
B
)
12: end if
13: for (A
i
,B
j
) ∈ S
A
× S
B
do
14: DPSynthesis(A
i
,B
j
)
15: end for
16: end while
17: /* Revert the last merging step. */
18: /* Check the bound C
2
. */
Notice that although the metrics are introduced as
functions of two fixed-point intervals, we generalized
them to fixed-point interval vectors by considering ei-
ther the component-wise max or average value.
Given one of the above metrics and a set S of vec-
tors, we are able to implement the f indClosestPair
routine that returns the closest pair of vectors in S.
There are several ways to implement such a routine.
A O(n
2
) naive approach would compare all the pos-
sible pairs of vectors. But, depending on the dis-
tance used, optimized implementations may rely on
the well established fast closest pair of points algo-
rithms (Shamos and Hoey, 1975), (Cormen et al.,
2009, §33).
Nevertheless, our contribution lies mainly in the
design of Algorithm 3 which is based on a dynamic
search of a code that satisfies an accuracy bound C
1
and code size bound C
2
.
Here, we assume that Algorithm 1 satisfies the
accuracy bound C
1
, otherwise, no smaller code sat-
isfying C
1
could be found. Therefore, Algorithm 3
PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
210

Table 2: Weight matrices considered for the benchmarks.
Name W
i, j
Heat map
Center 2
max(i, j,n−1−i,n−1− j)−bn/2c
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
Edges 2
min(i, j,n−1−i,n−1− j)
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
Rows / Columns 2
bi/2c
2
b j/2c
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
Random 2
rand(0,bn/2c−1)
2 4 6 8 10 12 14 16
2
4
6
8
10
12
14
16
starts with two sets of m and p vectors respectively,
corresponding to the rows of A and the columns of
B. As long as the bound C
1
is satisfied, each step
of the while loop merges together the closest pair of
rows or columns, and thus decrements the total num-
ber of vectors by 1. At the end of Algorithm 3, if
the size of the generated code satisfies the code size
bound C
2
, a tradeoff solution has been found. Other-
wise, Algorithm 3 failed to find a code that satisfies
both bounds C
1
and C
2
. This algorithm was imple-
mented in the FPLA tool,
6
that relies on CGPE and
work is in progress to enhance it with more linear al-
gebra routines. Section 5 studies the efficiency of this
algorithm on a variety of fixed-point benchmarks.
5 NUMERICAL EXPERIMENTS
In this section, we illustrate the efficiency of our
heuristics, and the behaviour of Algorithm 3 as well as
the impact of the distance and the matrix size through
a set of numerical results.
5.1 Experimental Environment
Experiments have been carried out on an Intel Xeon
Quad Core 3.1 GHz running the GNU/Linux environ-
ment. In our experiments, we used 3 structured and
1 unstructured benchmarks. For structured bench-
marks, the large coefficient distributions through-
out the matrices follow different patterns. This is
achieved through weight matrices, as shown in Ta-
ble 2 where W
i, j
corresponds to the element of row i
and column j of the considered weight matrix.
Notice, that the dynamic range defined as
max(W
i, j
)/min(W
i, j
) is the same for all benchmarks,
and is equal to 2
bn/2c
. The reason we did not di-
rectly use these matrices in our experiments is that
the 3 first patterns correspond to structured matrices
in the usual sense and that better algorithms to multi-
ply structured matrices exist (Mouilleron, 2011). To
6
FPLA: Fixed-Point Linear Algebra.
obtain random matrices where the large coefficients
are still distributed according to the pattern described
by the weight matrices, we computed the Hadamard
product of Table 2 matrices with normally distributed
matrices generated using Matlab
R
’s randn function.
Finally, notice that the matrices obtained this way
have floating-point coefficients. In order to get fixed-
point matrices, we first converted them to interval ma-
trices by considering the radius 1 intervals centered
at each coefficient. Next, the floating-point intervals
are converted into fixed-point variables by consider-
ing the smallest fixed-point format that holds all the
interval’s values.
5.2 Efficiency of the Distance based
Heuristic
As a first experiment, let us consider 2 of the previ-
ous benchmarks: centered and random square matri-
ces of size 6. For each, we build two matrices A and B
and observe the efficiency of our closest pair heuris-
tic based approach by comparing the result of Algo-
rithm 3 to all the possible codes. To do so, we com-
pute all the possible row or column mergings: from
Equation (3) and including the two degenerated cases,
for size-6 matrices, there are 41 209 such mergings.
For each of these, we synthesize the codes for com-
puting A·B, and determine the average error. This ex-
haustive experiment took approximately 2h15min per
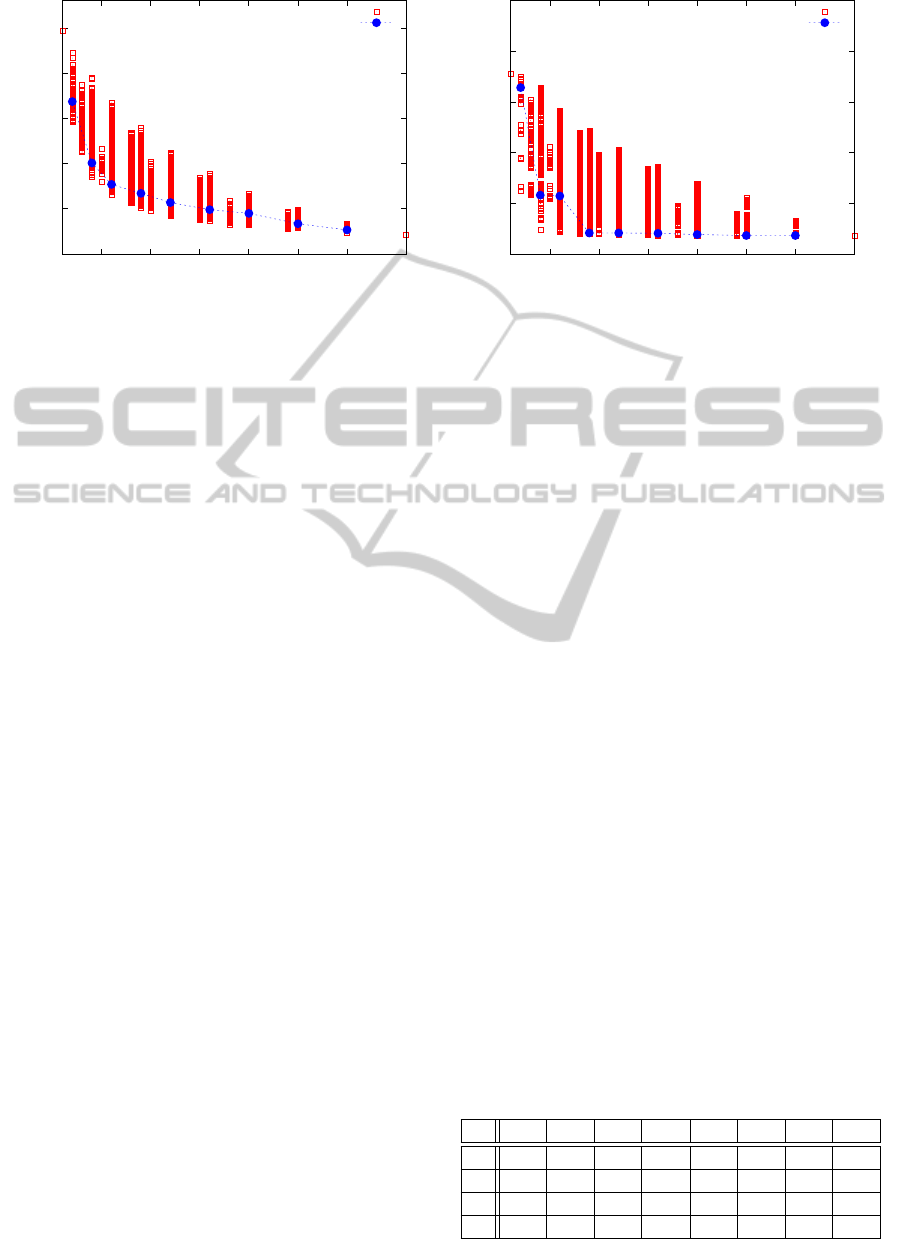
benchmark. Figure 4 shows the average error of the
produced codes according to the number of DPCodes
involved. Next we ran our tool using Hausdorff’s
distance to observe the behavior of Algorithm 3 and
recorded all the intermediate steps. This took less
than 10s for each benchmark and corresponds to the
dark blue dots in Figure 4. Notice on both sides the
accurate algorithm which produces 36 dot-products
and the compact algorithm which produces only 1
dot-product. Notice also that Algorithm 3 is an it-
erative and deterministic algorithm. Once it goes in
a wrong branch of the result space, this may lead to
a code having an average error slightly larger than
the best case. This can be observed on Figure 4(b):
the first 6 steps produce code with very tight aver-
age error, but step 7 results in a code with an average
error of ≈ 10
−3
while the best code has an error of
≈ 5 · 10
−4
. As a consequence, the following of the
algorithm gives a code with an error of ≈ 3 · 10
−3
in-
stead of ≈ 10
−3
for the best case.
Despite this, these experiments show the interest
of our heuristic approach. Indeed we may observe
that, at each step, the heuristic merges together 2 rows
of A or 2 columns of B to produce a code having in
most cases an average error close to the best case.
CodeSizeandAccuracy-awareSynthesisofFixed-pointProgramsforMatrixMultiplication
211
0
0.005
0.01
0.015
0.02
0.025
1 5 10 15 20 25 30 36
Average error
Number of dot-products used
Average error
Algorithm 3 run result
(a) Random matrices.
0
0.001
0.002
0.003
0.004
0.005
1 5 10 15 20 25 30 36
Average error
Number of dot-products used
Average error
Algorithm 3 run result
(b) Center matrices.
Figure 4: Average error according to the number of dot-product codes.
This is particularly the case on Figure 4(a) for random
benchmarks. Moreover, Algorithm 3 converges to-
ward code having good numerical quality much faster
than the exhaustive approach.
5.3 Impact of the Metric on the
Tradeoff Strategy
In this second experiment, we consider 25 × 25 matri-
ces. For each benchmark introduced above, 50 differ-
ent matrix products are generated, and the results ex-
hibited are computed as the average on these 50 prod-
ucts. To compare the different distances, we consider
the average accuracy bound: for each metric, we var-
ied this bound and used Algorithm 3 to obtain the
most compact codes that satisfy it. Here we ignored
the code size bound C
2
by setting it to a large enough
value. Also, in order to show the efficiency of the
closest pair strategy, we compare the codes generated
using Algorithm 3 with those of an algorithm where
the merging of rows and columns is carried out ran-
domly. Figure 5 shows the results of running FPLA.
First notice that, as expected, large accuracy
bounds yield the most compact codes. For instance,
for all the benchmarks, no matter the distance used,
if the target average accuracy is > 2
−9.5
, one DP-
Code suffices to evaluate the matrix multiplication.
This indeed amounts to using Algorithm 2. Also as
expected and except for few values, when used with
one of the distances above, our algorithm produces
less DPCodes than with the random function as a dis-
tance. Using the average width criterion, our algo-
rithm is by far better than the random algorithm and
yields on the center and rows/columns benchmarks a
significant reduction in code size, as shown on Fig-
ures 5(a) and 5(c). For example, for the center bench-
mark, when the average error bound is set to 2
−16
, our
algorithm satisfies it with only 58 DPCodes, while the
random algorithm needs 234 DPCodes. This yields a
code size reduction of up to 75%. Notice also that
globally, the center benchmark is the most accurate.
This is due to the fact that few rows/columns have
a high dynamic range. On Figures 5(b) and 5(d), in
the edges as well as random benchmarks, all of the
rows and columns have a high dynamic range which
explains in part why these benchmarks are less accu-
rate than the center benchmark. These experiments
also suggest that average based distances yield tighter
code than max based ones.
5.4 Impact of the Matrix Size
In this third experiment, we study the influence of
the matrix sizes on the methodology presented above.
To do so, we consider square matrices of the center
benchmark with sizes 8, 16, 32, and 64, where each
element has been scaled so as these matrices have
the same dynamic range. We run Algorithm 3 using
average width criterion with different average error
bounds from 2
−21
to 2
−14
. Here the bound C
2
has
also been ignored. For each of these benchmarks, we
determine the number of DPCodes used for each av-
erage error, as shown in Table 3 (where “−” means
“no result has been found”).
This shows clearly that our method is extensible to
large matrices, since it allows to reduce the size of the
problem to be implemented, while maintaining a good
Table 3: Number of DPCodes for various matrix sizes.
2
−21
2
−20
2
−19
2
−18
2
−17
2
−16
2
−15
2
−14
8 24 6 1 1 1 1 1 1
16 − 117 40 16 3 1 1 1
32 − − 552 147 14 2 1 1
64 − − − 2303 931 225 48 1
PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
212

0
50
100
150
200
250
300
350
400
450
500
2
-17
2
-16
2
-15
2
-14
2
-13
2
-12
Number of dot-product codes
Average error bound
Average width criterion
Max width criterion
Average Hausdorff criterion
Max Hausdorff criterion
Average fixed criterion
Max fixed criterion
Random criterion
(a) Center matrices.
0
100
200
300
400
500
600
2
-14
2
-13
2
-12
2
-11
2
-10
2
-9
Number of dot-product codes
Average error bound
Average width criterion
Max width criterion
Average Hausdorff criterion
Max Hausdorff criterion
Average fixed criterion
Max fixed criterion
Random criterion
(b) Edges matrices.
0
100
200
300
400
500
600
2
-16
2
-15
2
-14
2
-13
2
-12
2
-11
2
-10
Number of dot-product codes
Average error bound
Average width criterion
Max width criterion
Average Hausdorff criterion
Max Hausdorff criterion
Average fixed criterion
Max fixed criterion
Random criterion
(c) Rows/Columns matrices.
0
100
200
300
400
500
600
2
-16
2
-15
2
-14
2
-13
2
-12
2
-11
Number of dot-product codes
Average error bound
Average width criterion
Max width criterion
Average Hausdorff criterion
Max Hausdorff criterion
Average fixed criterion
Max fixed criterion
Random criterion
(d) Random matrices.
Figure 5: Number of dot-product codes generated by each algorithm for increasing average error bounds.
numerical quality. For example, the 64 × 64 accu-
rate matrix multiplication would use 4096 DPCodes.
Using our heuristic, we produce a code with 2303
DPCodes having an average error bounded by 2
−18
,
that is, a reduction of about 45%. Remark that
no code with average error bound of 2
−19
is found,
which means that even the accurate algorithm (Algo-
rithm 1) has an error no tighter than 2
−19
: we can con-
clude that our heuristic converges towards code hav-
ing an error close to the best case, but with half less
DPCodes. Remark finally that it falls to 1 DPCode if
we target an error bound of 2
−14
.
6 CONCLUSIONS
In this article, we discussed the automated synthesis
of small and accurate programs for matrix multiplica-
tion in fixed-point arithmetic. More particularly, we
presented a new strategy based on the merging of row
or column vectors of the matrices, so as to reduce the
size of the generated code while guaranteeing a cer-
tain error bound is satisfied. We also suggested cri-
teria to decide which vectors are to be merged. The
efficiency of this approach has been illustrated on a
set of benchmarks. It remains now to validate this ap-
proach and the synthesized codes on real digital signal
processing applications (including State Space filter
realizations or MP3 compression).
In addition, the further research direction is three-
fold. As a first direction, it would be interesting to
study the possibility of extending this approach to
tri-matrix multiplication, widely used in DSP appli-
cations (ALshebeili, 2001),(Qasim et al., 2008), and
even to matrix chain multiplications or matrix powers.
In this work, we only deal with the basic matrix mul-
tiplication algorithm. As a second direction, we could
investigate the interest of using other families of ma-
trix multiplication algorithms, such as those based on
blocking, and the impact on a fixed-point implemen-
tation. Finally, fixed-point arithmetic is widely used
for implementing linear algebra algorithms on hard-
ware providing no floating-point unit. In this sense,
another research direction would be the automated
CodeSizeandAccuracy-awareSynthesisofFixed-pointProgramsforMatrixMultiplication
213

synthesis of such algorithms in fixed-point arithmetic,
like matrix inversion, for these particular hardware
and the adaptation of the techniques presented here
to such particular problems.
ACKNOWLEDGEMENTS
The work was supported by the ANR project DE-
FIS (Ing
´
enierie Num
´
erique et S
´
ecurit
´
e 2011, ANR-
11-INSE-0008).
REFERENCES
ALshebeili, S. A. (2001). Computation of higher-order
cross moments based on matrix multiplication. Jour-
nal of the Franklin Institute, 338(7):811–816.
Campbell, S. J. and Khatri, S. P. (2006). Resource and de-
lay efficient matrix multiplication using newer FPGA
devices. In Proceedings of the 16th ACM Great Lakes
Symposium on VLSI, GLSVLSI ’06, pages 308–311,
New York, NY, USA. ACM.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein,
C. (2009). Introduction to Algorithms (3. ed.). MIT
Press.
Golub, G. and Mitchell, I. (1998). Matrix factorizations in
Fixed Point on the C6x VLIW architecture. Techni-
cal report, Stanford University, Standford, California,
USA.
Irturk, A., Benson, B., Mirzaei, S., and Kastner, R. (2010).
GUSTO: An automatic generation and optimization
tool for matrix inversion architectures. ACM Trans.
Embed. Comput. Syst., 9(4):32:1–32:21.
Kim, S., il Kum, K., and Sung, W. (1998). Fixed-point
optimization utility for C and C++ based digital sig-
nal processing programs. In IEEE Trans. Circuits and
Systems II, pages 1455–146.
Lee, D.-U., Gaffar, A., Cheung, R. C. C., Mencer, O.,
Luk, W., and Constantinides, G. (2006). Accuracy-
guaranteed bit-width optimization. Computer-Aided
Design of Integrated Circuits and Systems, IEEE
Transactions on, 25(10):1990–2000.
Lee, D.-U. and Villasenor, J. D. (2009). Optimized Custom
Precision Function Evaluation for Embedded Proces-
sors. IEEE Transactions on Computers, 58(1):46–59.
Mehlhose, M. and Schifferm
¨
uller, S. (2009). Efficient
Fixed-Point Implementation of Linear Equalization
for Cooperative MIMO Systems. 17th European Sig-
nal Processing Conference (EUSIPCO 2009).
Melquiond, G. (2006). De l’arithm
´
etique d’intervalles
`
a la
certification de programmes. PhD thesis,
´
ENS Lyon.
Moore, R. E., Kearfott, R. B., and Cloud, M. J. (2009). In-
troduction to Interval Analysis. SIAM.
Mouilleron, C. (2011). Efficient computation with struc-
tured matrices and arithmetic expressions. PhD the-
sis, Univ. de Lyon - ENS de Lyon.
Mouilleron, C., Najahi, A., and Revy, G. (2013). Auto-
mated Synthesis of Target-Dependent Programs for
Polynomial Evaluation in Fixed-Point Arithmetic.
Technical Report 13006.
Mouilleron, C. and Revy, G. (2011). Automatic Generation
of Fast and Certified Code for Polynomial Evaluation.
In Proc. of the 20th IEEE Symposium on Computer
Arithmetic (ARITH’20), Tuebingen, Germany.
Nikolic, Z., Nguyen, H. T., and Frantz, G. (2007). Design
and Implementation of Numerical Linear Algebra Al-
gorithms on Fixed-Point DSPs. EURASIP J. Adv. Sig.
Proc., 2007.
Ogita, T., Rump, S. M., and Oishi, S. (2005). Accurate Sum
and Dot Product. SIAM J. Sci. Comput., 26(6):1955–
1988.
Qasim, S. M., Abbasi, S., Alshebeili, S., Almashary, B., and
Khan, A. A. (2008). FPGA Based Parallel Architec-
ture for the Computation of Third-Order Cross Mo-
ments. International Journal of Computer, Informa-
tion and Systems Science, and Engineering, 2(3):216–
220.
Rump, S. M. (2009). Ultimately Fast Accurate Summation.
SIAM J. Sci. Comput., 31(5):3466–3502.
Shamos, M. I. and Hoey, D. (1975). Closest-point problems.
In FOCS, pages 151–162.
Sotiropoulos, I. and Papaefstathiou, I. (2009). A fast par-
allel matrix multiplication reconfigurable unit utilized
in face recognitions systems. In Field Programmable
Logic and Applications, 2009. FPL 2009. Interna-
tional Conference on, pages 276–281.
Syed M. Qasim, Ahmed A. Telba, A. Y. A. (2010). FPGA
Design and Implementation of Matrix Multiplier Ar-
chitectures for Image and Signal Processing Applica-
tions. International Journal of Computer Science and
Network Security, 10(2):168–176.
Yates, R. (2009). Fixed-Point Arithmetic: An Introduction.
Digital Signal Labs.
PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
214
