
Self-organizing Maps for Event-Related Potential Data Analysis
Luk
´
a
ˇ
s Va
ˇ
reka and Pavel Mautner
Department of Computer Science and Engineering, University of West Bohemia, 22 Univerzitn
´
ı, Pilsen, Czech Republic
Keywords:
Event-Related Potentials, P300, Self-Organizing Maps, BCI.
Abstract:
Event-Related Potentials (ERPs) and especially the P300 component have been gaining attention in brain-
computer interface design and neurobiological research. The detection of the P300 component in electroen-
cephalographic signal is challenging since its signal-to-noise ratio is very low. Instead of using traditional
supervised pattern recognition, this paper discusses using unsupervised neural networks for the P300 classi-
fication purposes. To validate the proposed approach, a method for the P300 detection based on matching
pursuit and self-organizing maps is proposed and evaluated. The results may be applied to the design of
brain-computer interfaces.
1 INTRODUCTION
Exogenous event-related potentials (ERPs) are elec-
trical changes recorded from the brain as it makes the
decision or initiates the response. (Picton et al., 1995)
In experiments, event-related potentials are trig-
gered by stimulation while recording electroen-
cephalographic (EEG) signal. There are several ERP
components, differing by latency (time delay after the
stimulus onset) and polarity. Both parameters are typ-
ically reflected by naming conventions (e.g. the N100
is an ERP with a negative amplitude located approxi-
mately 100 ms after the stimulus onset). (Luck, 2005)
Event-related potentials with higher latencies tend
to occur in association with specific experiment
paradigms. For example, oddball paradigm (Luck,
2005) is commonly used for the P300 elicitation.
In this technique, low-probability target stimuli are
mixed with high-probability non-target stimuli. Both
stimuli trigger a reaction which can be measured and
detected shortly after the event in the EEG signal
and consists of multiple ERP components. However,
the target stimuli tend to cause a different reaction,
with the P300 waveform (sometimes referred to as
the P3 component) being most significant. This wave-
form (and especially its sub-component P3b (Polich,
2007)) is probably related to the process of decision
making - it is elicited when the subjects classifies
the last stimulus as the target (for example by silent
counting). The P300 is usually the strongest ERP
component and it occurs approximately 250 - 450 ms
after the target stimulus as a positive peak. This ERP
component is frequently used in brain-computer in-
terfaces. (Luck, 2005)
Many different pattern recognition algorithms
have been proposed for brain-computer interfaces
(BCIs). BCIs allow the paralyzed users to communi-
cate with the outside world without using their mus-
cles, i.e. their intention is read from their EEG sig-
nal directly. For example, the P300 speller stimulates
the user with a matrix containing letters. Rows and
columns randomly flash. When the user acknowl-
edges the letter he/she is indented to write, the row
flash is followed by the P300 component that can be
detected in the signal.
Unfortunately, ERP components including the
P300 component are usually hidden in EEG noise,
i.e. signal-to-noise ratio is very low. This problem
is commonly addressed by averaging together subse-
quent trials. Random EEG activity is suppressed and
non-random ERP components time-locked to stimuli
stand out (Luck, 2005). Fig. 1 shows an example of
averaged event-related potentials for target and non-
target stimuli.
This paper discusses the problems of state-of-the-
art P300 BCI systems and proposes a new approach
towards the P300 detection based on self-organizing
maps. The benefits of this approach are discussed.
Furthermore, the validity of proposals was verified
on an experimental off-line BCI system. Match-
ing pursuit was used for feature extraction and self-
organizing maps were used for classification.
State of the art of the field is presented in Sec-
tion 1.1. The new approach is proposed in Section
387
Va
ˇ
reka L. and Mautner P..
Self-Organizing Maps for Event-Related Potential Data Analysis.
DOI: 10.5220/0004885103870392
In Proceedings of the International Conference on Health Informatics (HEALTHINF-2014), pages 387-392
ISBN: 978-989-758-010-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Comparison of averaged EEG responses to non-
target stimuli (Xs) and target stimuli (Os). The ensemble
averaging is necessary, otherwise the event-related poten-
tials could hardly be distinguished from noisy EEG signal.
There is a clear P3b component following the Os stimuli.
Negative is plotted upward (Luck, 2005).
1.2. Section 2 presents an experimental off-line BCI
system to evaluate the previously formulated hypoth-
esis. To describe the method, theoretical background
is introduced in Sections 2.1.1 and 2.1.2. Section 2.2
describes the process of data acquisition. The method
for pattern recognition is described in Section 2.3. In
Section 2.4, the proposed method is evaluated. The
paper is concluded in Section 3.
1.1 State of the Art
The P300 speller has been studied extensively and is
one of the well established BCI systems. However,
a recent review of the field (Mak et al., 2011) con-
cludes that more work still needs to be done to opti-
mize the speed and accuracy before the P300 speller is
practical to use with disabled patients. This becomes
even more relevant when considering that paralyzed
patients can display widely varying P300 responses
between subjects. A reliable BCI system must be able
to adapt to the unique ERP responses of each sub-
ject and to handle the variations between trials within
a subject. When using traditional supervised pattern
recognition techniques, it is common to train the BCI
system for each new subject, allowing it to only learn
the characteristics of his/her ERP responses. There-
fore, some approaches might have difficulty if they
use a priori information to make assumptions about
the temporal and spatial characteristics of the standard
P300 response, especially when applied to abnormal
ERPs from paralyzed patients. (Cashero, 2012)
Therefore, the universal BCI system should not
only rely on a priori information about expected
event-related response, but should also be able to
adapt and to provide reasonable accuracy for differ-
ent subjects.
1.2 Using Unsupervised Neural
Networks
In the paper, using unsupervised neural networks
(UNNs), e.g. self-organizing maps, will be explored.
When traditional supervised learning methods are
used, all attention is concentrated on separating the
classes using class labels, and any other information
is ignored by the classifier. Instead of using class
labels from a supervisor, unsupervised neural net-
works learn representation of different kinds of data
types that occur in the data sets. Since no assump-
tions of the class structure of the data are made, the
networks may discover new clusters that have not
been apparent before. Therefore, the method may
also contribute to understand the related feature vec-
tors. Self-organizing maps were successfully applied
to recognition of topographic patterns of EEG spectra
in (Joutsiniemi et al., 1995). Six classes in total were
used, for continuous alpha activity, flat EEG, theta ac-
tivity, eye movements, muscle activity and bad elec-
trodes contact. The authors concluded that SOMs
were able to recognize similar topographic patterns in
different EEGs, also in EEGs not used for the training
of the map. According to (Lotte et al., 2007), Learn-
ing Vector Quantization is the closest approach that
has been investigated regarding P300 BCIs. In (Liang
and Bougrain, 2008), supervised LVQ1 has success-
fully been applied to the P300 data. This further sup-
ports the hypothesis that similar models may be ben-
eficial for P300 BCIs.
Unsupervised ANN, e.g. self-organizing maps
can be trained on the data from a simple odd-ball
experiment. At least two clusters and possibly also
a ”noise” cluster should appear after training. One
cluster is expected to be associated with target fea-
tures, another one with nontarget features and in ad-
dition, the rest will probably be undecidable. An
expert can associate the clusters with classification
classes, or training features with known classes can
be propagated through the network to create the as-
sociations. For each subject, the clusters will be dis-
tributed differently over the map. The percentage of
training features that will be associated with the un-
decidable cluster may indicate to which extent the
subject is suitable for P300 BCIs. The trained neu-
ral network could be applied to a more complex BCI
HEALTHINF2014-InternationalConferenceonHealthInformatics
388

paradigm, e.g. the P300 speller. If the classification
class of a single trial pattern cannot be decided, the
trial can be averaged with the next corresponding trial
to gradually increase signal to noise ratio.
2 EXPERIMENTAL OFF-LINE
BCI SYSTEM
To evaluate the benefits of using UNNs for the P300
detection, an experimental off-line BCI system was
designed and evaluated on P300 datasets. Pattern
recognition was based on matching pursuit and self-
organizing maps.
2.1 Theoretical Background
2.1.1 Signal Decomposition using Matching
Pursuit
Matching pursuit is an algorithm used for continu-
ous EEG signal processing (Durka and Blinowska,
1995). However, its use for event-related potential
data processing has been discussed only in a few pub-
lications (Tomas Rondik and Mautner, 2011).
It decomposes any signal into a linear expansion
of waveforms. These waveforms are selected from a
redundant dictionary of functions. At each iteration,
a waveform is chosen in order to best match the sig-
nificant structures of the signal. Typically, this part is
approximated by a Gabor atom, which has the highest
scalar product with the original signal, and then it is
subtracted from the signal (Mallat and Zhang, 1993).
This process is repeated until the whole signal is ap-
proximated by Gabor atoms with an acceptable error.
Suppose we have a function g as follows:
g(t) = e
−πt
2
(1)
The Gabor atom has the following definition:
g
s,u,v,w
(t) = g(
t − u
s
)cos(vt + w) (2)
where s means scale, u latency, v frequency and w
phase. These four parameters define each individual
atom.
After a given amount of iterations, the signal is
decomposed into a set of Gabor atoms.
Although matching pursuit is traditionally based
on Gabor atoms, it is also possible to apply the same
principal to any other normalized base. For example,
in this paper, we focus on Gaussian base, i.e. Gabor
base with both v and w parameters set to 0. This base
also resembles the shape of event-related potentials
(Luck, 2005). Furthermore, it is less complex and
thus matching with Gaussian base has lower compu-
tational complexity.
2.1.2 Self-organizing Maps
Self-Organizing Maps (SOMs) are neural networks in
the unsupervised-learning category.
SOM converts complex, nonlinear statistical re-
lationship between high-dimensional data items into
simple geometric relationship on a low-dimensional
display. To allow this, a topological structure among
the cluster units is assumed. There are m cluster units,
arranged typically in a two-dimensional array and the
input signals are n-tuples. (Kohonen, 1989)
The weight vector of a cluster unit, commonly
referred to as a codebook vector, serves as an input
pattern associated with that cluster. During the self-
organization process, the cluster unit whose weight
vector matches the input pattern most closely (typi-
cally, by means of the square of the minimum Eu-
clidean distance) is chosen as the winner. The win-
ning unit and typically also its neighboring units (in
terms of topology of the cluster units) update their
weights. The weight vectors of the neighboring units
do not have to be close to the input pattern. The ar-
chitecture and algorithm that follow for the net can be
used to cluster a set of p continuous-valued vectors
x = (x
1
, x
2
, .., x
n
) into m clusters. (Fausett, 1994)
2.2 Data Acquisition
2.2.1 Stimulation Device
The experiments that were used to produce the data
for this paper were based on three-stimulus-paradigm.
The subjects were visually stimulated with three high
power Light-Emitting Diodes (LEDs) differing by
their color: red, green and yellow. Fig. 2 shows the
stimulation LED module. The core of the stimula-
tor is an 8bit micro-controller that generates required
stimuli. It also generates additional synchronization
signals for an EEG recorder. The stimulator is de-
scribed in more detail in (Dudacek et al., Sept).
Figure 2: Stimulation device with flashing diodes.
Self-OrganizingMapsforEvent-RelatedPotentialDataAnalysis
389
2.2.2 Experimental Setup
Six healhy individuals (4 males and 2 females, univer-
sity students, aged 22-29) participated in our experi-
ment. The following setting of the stimulation device
was used: each diode flashed once a second and each
flash took 500 ms. The probabilities of the red, green
and yellow diodes flashing were 75%, 20% and 5%,
respectively. The subjects were sitting 1 m from the
stimulation device for 20 minutes. They were asked
to sit comfortably, not to move and to limit their eye
blinking. They were instructed to pay attention to the
scenario and not to perform another task-relevant cog-
nitive or behavioral activity.
2.3 Pattern Recognition
Pattern recognition algorithm was designed as a pro-
cess consisting of feature extraction and subsequent
clustering of the features. The features were extracted
to correspond to the ERP components. Clustering
and subsequent analysis were used to separate various
P300 component candidates on the map and to tag the
corresponding SOM codebook vectors. This allowed
the SOM to act as a P300 classifier on a testing data-
set.
2.3.1 Preprocessing and Feature Extraction
The input signal was split into epochs using stimuli
markers. For the P300 classification purposes, only
the data associated with target and non-target stimuli
(green and red diodes flashing) were extracted. Given
the sampling frequency of 1 kHz and the fact that each
epoch started 100 ms before the stimulus onset and
ended 1 s afterwards, 1100 samples were needed for
the epoch description. The samples corresponding to
the first 100 ms were used only for baseline correc-
tion (adjusting these values to average zero). The re-
maining samples were crucial for the procedure itself.
Each sample is a real number, corresponding to its
recorded voltage value in µV. From each stimulus, the
epochs corresponding to the channel Cz were saved.
From each measured subject, 10% of the target and
nontarget epochs were randomly chosen and merged
into a training data-set. The remaining epochs were
used for evaluation. The preprocessing of the epochs
continued in the following steps:
1. The extracted epochs were randomly shuffled.
2. The epochs damaged by eye-blinking artifacts
were automatically removed according to the am-
plitude criterium (Luck, 2005) with the decision
threshold being set to 45 µV .
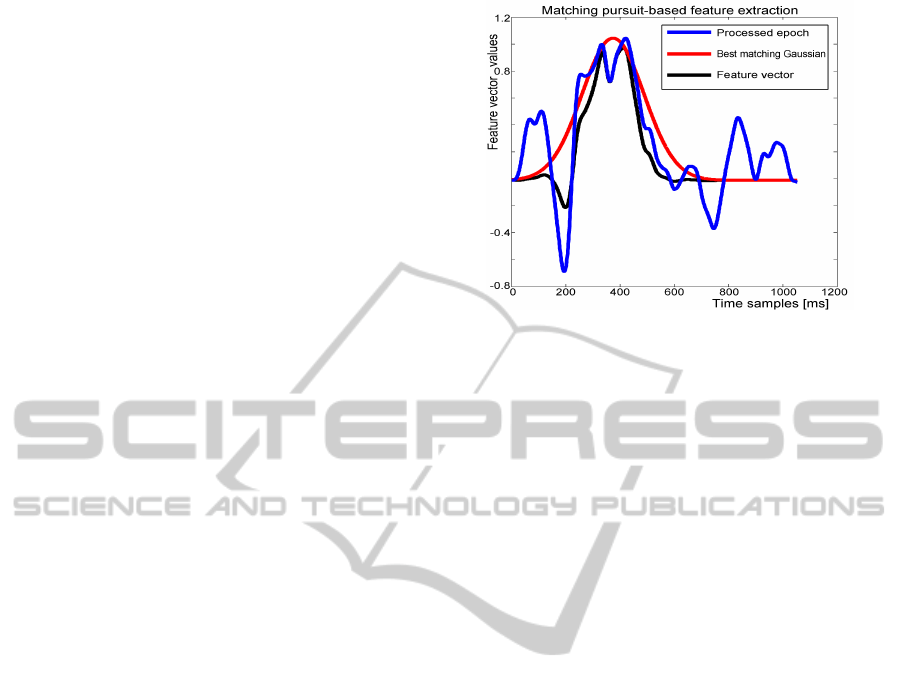
Figure 3: The figure depicts how each single feature vector
is extracted from the preprocessed epoch (blue). Matching
pursuit selects the best matching Gaussian atom. The atom
that was selected in the first iteration is depicted in red. To
get the feature vector (plotted in black), element-by-element
multiplication of the epoch with the selected Gaussian atom
was calculated.
3. Each epoch was band-pass-filtered with the cut-
off frequencies of 0.2 and 10 Hz to improve
signal-to-noise ratio.
4. The signal was downsampled by factor of 4.
As the next step, matching pursuit with Gaussian
base was applied to the pre-processed signal. Five it-
erations were calculated. However, to extract possible
components, matching pursuit atoms were not con-
sidered ERP components directly. Instead, the ERP
component candidates c were estimating using Equa-
tion 3.
c(t) = abs(a(t))s(t) (3)
In Equation 3, a is the current atom decomposed
by matching pursuit, s is the preprocessed epoch, and
t corresponds to time samples. An example is shown
in Fig. 3.
Finally, the scales of the features were normalized.
2.3.2 Clustering
For the implementation of self-organizing maps,
SOM Toolbox (Vesanto et al., 2000) was used. Self-
organizing map was trained with the training feature
vectors obtained using the procedure described above.
The size of the map was automatically adjusted to
18 x 20. Both rough training phase and fine-tuning
of the network were calculated to optimize cluster-
ing. Fig. 4 shows the codebook vectors of the SOM
network. Note that there appears to be a cluster of
vectors corresponding to the P300 component.
To separate the P300 component candidates,
cross-correlation between the codebook vectors of the
HEALTHINF2014-InternationalConferenceonHealthInformatics
390

Figure 4: All weight vectors from SOM cluster units are
plotted in the upper plot. Note that many of them have
latency and polarity that correspond to the P300 compo-
nent. Unlike the other codebook vectors, these vectors cor-
respond to non-random activity time-locked to stimuli. The
bottom plot only depicts the codebook vectors that were
tagged as the P300 candidates.
Table 1: Accuracy of classification using the trained SOM
network.
Subject ID Accuracy (Standard deviation) (%)
86 71.4 (3.6)
93 71.0 (3.6)
94 75.1 (3.4)
98 70.6 (3.6)
99 71.6 (3.6)
100 73.2 (3.5)
SOM and the P300 component (approximated by the
appropriately scaled Gaussian function) was calcu-
lated, but only in the corresponding time intervals
where the P300 component can be located (i.e. 250
- 450 ms after the stimulus (Luck, 2005)). Maximum
correlation coefficient was compared with a thresh-
old. The threshold represents the decision border be-
tween two classification classes (the P300 component
detected/not detected). The threshold was empirically
set to 0.03. Any cluster unit that was associated with
a higher maximum correlation coefficient, was tagged
as the P300 candidate cluster unit. The histogram in
Fig. 6 illustrates the threshold decision problem.
2.4 Evaluation of the Off-line BCI
System
To evaluate the proposed classification algorithm, the
following procedure was designed.
Feature vectors from the testing data-set were ex-
tracted using the procedure described above (exclud-
ing matching pursuit decomposition). Then, the fea-
ture vectors were applied to the trained SOM. For
each single feature vector, it was verified, if the SOM
Figure 5: This figure illustrates how the trained SOM re-
sponds to the testing data-set. To see the difference, only
target epochs (i.e. containing the P300), or only non-target
epochs (i.e. containing smaller P300 components) were ap-
plied to the SOM network. On the left, it is clearly ob-
servable, that more than half of the features are correctly
detected as targets. However, some feature vectors were
misclassified. In the non-target area, the features are more
equally spread. In absolute values, slightly more feature
vectors were classified as containing the P300 than in the
target group. However, since there are much more non-
targets than targets, in relative values, the percentage of mis-
classification for non-target is lower. If the output matches
the expected output, it is depicted in green, otherwise it is
depicted in blue.
correctly decided whether the feature vector belongs
to the P300 cluster, or not. The decision was based
on comparing the tag of the feature with the tag of the
winning cluster unit. Tab. 1 contains the results. For
all subjects, the accuracy is over 70% for single tri-
als. Fig. 5 illustrates how the SOM responded to the
testing data.
3 CONCLUSIONS AND FUTURE
WORK
The suggested method has proven to be suitable for
the P300 component detection in single EEG chan-
nels. In the future, improving the method using spa-
tial filtering may be further explored and tested. In
addition, a seed corresponding to the expected target
response may be inserted into the network with the
expectation that the target patterns will be associated
with the neurons positioned nearby. This would allow
the researcher to control the process of clustering.
ACKNOWLEDGEMENTS
This work was supported by the UWB grant SGS-
2013-039 Methods and Applications of Bio- and
Medical Informatics.
Self-OrganizingMapsforEvent-RelatedPotentialDataAnalysis
391

(a) Cross-correlation histogram (b) The P300 cluster in the SOM
Figure 6: The histogram illustrates how the normalized Gaussian function scaled to resemble the P300 component correlates
with the SOM codebook vectors. The threshold was set to 0.03 and any cluster units that were associated with higher
correlations were tagged as the P300 component candidates (in red). Fig. 6(b) shows the distribution of the P300 candidates
on the map. The cluster units in red belong to the P300 component cluster.
REFERENCES
Cashero, Z. (2012). Comparison of Eeg Preprocessing
Methods to Improve the Performance of the P300
Speller. Proquest, Umi Dissertation Publishing.
Dudacek, K., Mautner, P., Moucek, R., and Novotny, J.
(Sept.). Odd-ball protocol stimulator for neuroinfor-
matics research. In Applied Electronics (AE), 2011
International Conference on, pages 1–4.
Durka, P. and Blinowska, K. (1995). Analysis of EEG
transients by means of matching pursuit. Annals of
Biomedical Engineering, 23(5):608–611.
Fausett, L., editor (1994). Fundamentals of neural net-
works: architectures, algorithms, and applications.
Prentice-Hall, Inc., Upper Saddle River, NJ, USA.
Joutsiniemi, S. L., Kaski, S., and Larsen, A. T. (1995). Self-
organizing map in recognition of topographic patterns
of EEG spectra. IEEE Transactions on Biomedical
Engineering, 42:1062–1068.
Kohonen, T. (1989). Self-organization and associative
memory: 3rd edition. Springer-Verlag New York, Inc.,
New York, NY, USA.
Liang, N. and Bougrain, L. (2008). Non-identity Learning
Vector Quantization applied to evoked potential de-
tection. In Deuxi
`
eme conf
´
erence franc¸aise de Neuro-
sciences Computationnelles, ”Neurocomp08”, Mar-
seille, France. ISBN : 978-2-9532965-0-1.
Lotte, F., Congedo, M., L
´
ecuyer, A., Lamarche, F., and Ar-
naldi, B. (2007). A review of classification algorithms
for EEG-based brain-computer interfaces. Journal of
neural engineering, 4(2).
Luck, S. (2005). An introduction to the event-related poten-
tial technique. Cognitive neuroscience. MIT Press.
Mak, J. N., Arbel, Y., Minett, J. W., McCane, L. M., Yuk-
sel, B., Ryan, D., Thompson, D., Bianchi, L., and
Erdogmus, D. (2011). Optimizing the P300-based
brain-computer interface: current status, limitations
and future directions. Journal of Neural Engineering,
8(2):025003+.
Mallat, S. and Zhang, Z. (1993). Matching pursuit with
time-frequency dictionaries. IEEE Transactions on
Signal Processing, 41:3397–3415.
Picton, T. W., Lins, O. G., and Scherg, M. (1995). The
recording and analysis of event-related potentials. In
Boller, F. and Grafman, J., editors, Handbook of Neu-
ropsychology, volume 10, pages 3–73. Elsevier, Ams-
terdam.
Polich, J. (2007). Updating P300: an integrative the-
ory of P3a and P3b. Clinical neurophysiology,
118(10):2128–2148.
Tomas Rondik, Jindrich Ciniburk, R. M. and Mautner,
P. (2011). Erp components detection using wavelet
transform and matching pursuit algorithm. In Applied
Electronics 2011, pages 1–4.
Vesanto, J., Himberg, J., Alhoniemi, E., and Parhankangas,
J. (2000). Self-organizing map in matlab: the som
toolbox. In In Proceedings of the Matlab DSP Con-
ference, pages 35–40.
HEALTHINF2014-InternationalConferenceonHealthInformatics
392
