
Multi-objective Optimization of Investment Strategies
Based on Evolutionary Computation Techniques, in Volatile Environments
Jose Matias Pinto, Rui Ferreira Neves and Nuno Horta
Instituto de Telecomunicações, Instituto Superior Técnico, Torre Norte, Piso 10, Lisboa, Portugal
Keywords: Multi-objective Optimization, Stock Market Forecast, Technical Analysis, Financial Markets, Moving
Average, Time Series Prediction.
Abstract: In this document, the use of a multi-objective evolutionary system to optimize an investment strategy based
on the use of Moving Averages is proposed to be used on stock markets, able to yield high returns at
minimal risk. Fair and established metrics are used to both evaluate the return and the risk of the optimized
strategies. The Pareto Fronts obtained with the training data during the experiments conducted outperform
both B&H strategy and the classical approaches that consider solely the absolute return. Additionally, the
PF obtained show the inherent trade-off between risk and returns. The experimental results are evaluated
using data coming from the principal world markets, namely, the main stock indexes of the most developed
economies, such as: NASDAQ, S&P500, FTSE100, DAX30 and NIKKEI225. Although, the experimental
results suggest that the positive connection between the gains with training and testing data, usually
assumed in the single-objective proposals, is not necessarily true for all cases.
1 INTRODUCTION
Besides some unfavourable judgments (Korczak et
al., 2002), Technical Indicators (TI) are still widely
used as tools to do the technical analysis of financial
markets, exploiting the existence of trends to
establish potential buy, sell or hold conditions. This
study is notoriously tricky for a number of reasons,
though (Achelis, 2000) has made a complete
reference that fully explains the most important TI's
one can identify and use. Anyway, the main
difficulty of TI usage is still deciding its suitable
parameter values, as number of days of periods, and
this, in order to take advantage of the market and
improve your likelihood of success.
Thus, evolutionary computation appears as a
highly suitable alternative to extend technical
analysis of financial markets to tune the parameters
of some chosen TI (or set of TI's), so that, the
desired goals are achieved, at maximum extent
possible. In this environment, what the system
should do, can be viewed as some kind of predicting
future stock prices. Consequently, in this context,
evolutionary computation emerges as a stochastic
search technique able to deal with highly
complicated and non-linear search spaces.
In the last decade, several financial crises have
occurred with large consequences on the valorisation
of financial assets. Therefore emerges the principal
motivation for this paper: tune an Investment or
Trading Strategy (TS) able to achieve both the
highest returns with the minimal risk.
One of the goals of this work is to tune a TS to
present the highest returns as existing single
objective based approaches, and concurrently reduce
the risk. The proposed framework is tested using
data from the main stock indexes of the most
developed economies, such as NASDAQ, S&P500,
FTSE100, DAX30 and NIKKEI225; then the results
are presented, and some possible conclusions
outlined.
The next section will present the related work
using GA and the various TS's currently used in
Technical Analyses. In Section 3 the methodology,
the roles of the most relevant modules used to build
the proposed framework, and the chromosome
encoding are outlined. The TS adopted in this study
and the metrics used to evaluate the evolved TS are
also presented in this section. Section 4 presents the
results and the most relevant outcomes are
highlighted. Finally, in section five, the conclusions
of this study are presented.
480
Matias Pinto J., Ferreira Neves R. and Horta N..
Multi-objective Optimization of Investment Strategies - Based on Evolutionary Computation Techniques, in Volatile Environments.
DOI: 10.5220/0004889204800488
In Proceedings of the 16th International Conference on Enterprise Information Systems (ICEIS-2014), pages 480-488
ISBN: 978-989-758-027-7
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK
Stock market analysis has been one of the most
attractive and active research fields, where many
Machine Learning techniques have been used.
Generally speaking, one can distinguish two
methods for anticipating future stock prices and the
time to buy or sell; one is Technical Analysis
(Murphy, 1999) and the other is Fundamental
Analysis (Graham et al., 2003). Fundamental
Analysis look at stock prices using financial
statement of each company, economic trend and so
on; requires a large set of financial and accounting
data, difficult to obtain and both released with some
delay and often suffers of low consistency.
Technical Analysis numerically analyzes the past
movement of stock prices, is based on the use of
technical stock market indicators that work on a
series of data, usually stock prices or volume,
(Achelis, 2000) is accurate, on time, and relativity
easy to obtain. Consequently, this work will be
focused on the use of Technical Analysis to
anticipate future stock price movements.
Many approaches based on evolutionary
computation have been proposed and applied to
diverse fields of financial to predict worth trends. In
an attempt to summarize, in most of the works, the
generated returns are exclusively used as the only
fitness metric, without accounting for the related
risk. Some examples are the use of GAs to optimize
TI's parameters (Fernández-Blanco et al., 2008), or
to develop TS based on TI's (Bodas-Sagi et al.,
2009), (Gorgulho et al., 2011).
According to what was stated for the first time in
1952 (Markowitz, 1952), any TS should have the
highest possible profit with the feasible minimal
risk. Sadly, these two metrics are intrinsically
conflicting by virtue of the risk-returns trade-off.
Some articles propose the combination of the two
conflicting objectives into one single metric, in
particular (Bodas-Sagi & al., 2009) use the Chicago
Board Options Exchange (CBOE) Volatility Index
(VIX) as an estimate of risk. Also, (Schoreels & al.,
2006) propose the use of a Capital Asset Pricing
Model (CAPM) (William, 1964) system, based on
portfolio theory (Markowitz, 1952) to reduce risk
trough balanced selection of securities. More
recently (Pinto et al., 2011) propose and study
several alternatives to the classical fitness evaluation
functions.
A Multi-Objective system to maximize the total
returns and to minimize the risk as the exposure to it
is proposed by (Chiam et al., 2009). The framework
is tested using data gotten from one stock market,
the Singapore Exchange stock market (Straits Times
Index (STI)). Hence, some of the conclusions drawn
on this study could be attributed to the market used
to test it. Moreover, the metric used to evaluate the
return is peculiarly unusual; so, it is difficult, to
compare the presented results with the results
presented by other alternative applications.
3 METHODOLOGY
The proposed system consists of a Multi Objective
Genetic Algorithm coupled with a market return
evaluation module that does the fitness evaluation,
and this, based on the estimation of the two
conflicting objectives, on the chosen market, and on
the specified period.
3.1 Strategy and Parameters
The strategy tested on this work was the Moving
Average Crossover (MAC), which is based on the
use of two Moving Averages (MA), with different
periods. One, formed by the MA with the shorter of
the two periods is called the "Fast MA”, and the
other, with the longer period is the "Slow MA". The
"Fast MA" reflects changes earlier than does the
"Slow MA". A buying (or sell short) signal is
generated when the Fast MA crosses over the Slow
MA. Conversely, sell (or a buy short) signal is
generated when the Fast MA crosses under the Slow
MA.
After defining the strategy, it is necessary to
define the parameters of the MAC, which in the case
are the type of the MA’s and the corresponding
period. It is important to stress that, for the type of
MA to use, the GA has also the freedom to choose
between a Simple or an Exponential MA.
Although it is common to tune the parameters of
one single TI and then use it to generate buy and sell
signals, for both long and short positions, in this
article, the option of using a separate set of
parameters for each of the possible actions was
taken; to specify: "enter long"; "exit long"; "enter
short"; and "exit short".
Some pre-processing of the historical data is also
done. This applies for instance to the MA periods,
which are calculated at program start and are limited
to the following set of Simple or Exponential MA's:
1, 4, 8, 12, 14, 16, 20, 24, 28, 32, 36, 40, 55, 60, 65,
70, 75, 80, 85, 90, 95, 100, 110, 120, 130, 140, 150,
160, 170, 180, 190, 200 and 250 days. This set of
periods has been chosen because it covers the most
widely used, long and short-term MA periods, found
Multi-objectiveOptimizationofInvestmentStrategies-BasedonEvolutionaryComputationTechniques,inVolatile
Environments
481

on books and recommended by experts (Achelis,
2000).
3.2 Genetic Encoding
The chromosome must represent the MAC indicator
used, this way one MAC chromosome is represented
by two genes: one represents the type and the period
of the Fast MA and the other does the same for the
Slow. These entries are natural numbers in the
interval of values between 0 and 65 as it encodes, in
one single entry (integer variable) the type of MA
and its period. In Table 1 is represented the
chromosome structure.
Table 1: Chromosome representation.
Parameters
Enter long
position
Exit long
position
Exit short
position
Enter short
position
Fast
MA
Slow
MA
Fast
MA
Slow
MA
Fast
MA
Slow
MA
Fast
MA
Slow
MA
Chromosome
0..65 0..65 0..65 0..65 0..65 0..65 0..65 0..65
3.3 Fitness Evaluation
The fitness evaluation process is concerned with
simulating the performance of the each trading agent
in the evolving population and calculating the
corresponding total returns and the related risk. The
resultant fitness values of the trading agent must be
evaluated under some established and fair metric, as
will be discussed in the next subsections.
3.3.1 Return Metric
The profits generated by a given TS can be
measured in different ways, as will be seen next:
For instance, the potential profits can be estimated
by simply summing the area under the total asset
graph during the trading period (Schoreels et al.,
2005). Alternatively, another return metric could be
the final (total) assets; this means the available
capital plus the value of all holdings, at the end of
the investment period (Kendall et al., 2003). Sadly,
both above metrics have the nuisance that they are
always attached to the initial cash invested.
Therefore, an alternative metrics exists that
considers its relative value and is known as Return
on Investment (ROI),. This metric is a ratio and
represents the money gained or lost on an
investment relative to the amount of money
invested. ROI is usually expressed as a percentage,
and for one period, by definition, is calculated
according with equation 1. “Profit” is the amount of
money gained or lost and “Initial_Investment” is the
money invested.
_
_
1
_
Profit
ROI
Initial Investiment
F
inal_Assets Initial_Investiment
Initial Investiment
Final_Assets
Initial Investiment
(1)
ROI still has the trouble that, for multi-period
investment, it is difficult to compare it with the
results one would get in one single period.
Therefore, a metric that could be compared with
similar alternative investments should be used
instead. This way, in this article, the Annualized
ROI, will be used. The Annualized ROI is nothing
more than the “Geometric Average of the Ratio of
the Returns” also known as the "True Time-
Weighted Rate of Returns". Mathematically, for an
investment lasting for N periods, with full
reinvestment, is computed as exposed in equation 2;
in this equation, N is the number of periods, more
exactly, the number of years, the investment lasts.
() ( 1)1
N
Anualised ROI ROI
(2)
3.3.2 Risk Metrics
Risk is usually seen as the volatility or the
uncertainty of the expected returns over the
investment period. Therefore, the linked risk of any
investment technique can be estimated in several
ways, as will be examined subsequently.
The most traditional risk metric is inherited from
statistics and from Markowitz Mean-Variance
Model (Markowitz, 1952), and consists in the use of
the variance of the results as a gauge for the risk.
This variance can be calculated using the standard
deviation or the variance between the returns, this
statistical measure of the dispersion of the results is
usually named, in finance, as volatility.
Instead, risk can be computed as the exposure to
it (Weissman, 2005). Specifically, it can be
measured by the proportion of trading days when a
position is maintained open on the market, and is,
mathematically, the ratio between the time the agent
is on the market and the total trading time available.
Essentially, staying longer in the market corresponds
to a higher exposure to risk, like market crashes and
other disastrous events, while shorter periods on the
market correspond to a lower risk exposure and
greater liquidity (as the capital is engaged for a
smaller time).
Alternative metrics for the risk can be found on
the literature, as, for instance, the use of some risk-
adjusted return metric, as the Sharpe ratio, Sortino
ratio, Sterling ratio (SR), Calmar ratio (CR) or also
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
482

VIX which compute the net profitability after
discounting the associated risk (Korczak et al.,
2004). In short, the preceding risk metrics are in
reality alternative methods to combine into one
single objective (or metric) the two conflicting
objectives faced on this kind of problems (risk and
return).
Therefore, in the remaining of this paper, the risk
exposure will be used as the risk metric.
3.4 Optimisation Kernel
This study is concerned with the Evolutionary
Optimization of a TS treated as a multi-objective
problem, so the Optimisation Kernel is based on a
version of a state of the art multi-objective
evolutionary algorithm: Non Dominated Sorting
Genetic Algorithm 2 (NSGAII) (Deb et al, 2002).
NSGAII parameters are as follows: population size
500, the crossover probability fixed to 0.8 and
parents selected by tournament selection. Each run
on training data continued for 300 generations and
the probability of real mutation set to 0.1.
3.5 The Investment Simulator
The Investment Simulator or Market Return
Evaluation Module simulates an investment in the
user specified index including long and short
positions. Stock market index, which it could buy
(“go long”), sell it and stay out of the market (“Out”)
or even sell if it didn’t own any (“go short”) hoping
to profit from a decline in the price of the assets
between the sale and the repurchase.
Since daily data was available, the training
consisted in formulating an TS, give to the agent
some initial cash to spend, and every day simulate
the performance of the agent; having it to buy or sell
(“long” or “short”) the total cash available, if the
conditions defined on its encoded strategy are met.
Transaction costs were not included in the
simulation, as dividends not too. Environment is also
assumed discrete and deterministic in a liquid
market.
4 RESULTS
A multi-objective evolutionary optimization of a TS
is studied in this essay what involves the
maximization of a Return Metric and the
minimization of the related Risk Metric. In this kind
of problems the optimal solutions exist in the form
of a set of tradeoffs known as the Pareto-optimal set
(PF); and any objective belonging to a solution in
the optimal set cannot be improved without
degrading at least one of the others objectives.
An example of a possible PF is illustrated in
Figure 1, and this represents clearly the risk-return
trade-off or Efficient Frontier always faced in this
kind of problems.
Figure 1: Risk Return Trade-off.
On this illustration, each point denotes a Strategy
evolved by the GA. The black circles and the white
crosses represent non-dominated and dominated
solutions respectively. The set formed by the former
solutions is the Pareto optimal solution set because
their returns cannot be improved further without
compromising risk. In the context of single objective
optimization where return is the only goal, the
evolutionary process will ultimately drive the
solutions towards the extreme point B. This is not
applicable to conservative investors, who may prefer
a lower risk at a cost of lower returns. Point A
represents the extreme case of a conservative
investor with zero returns due to his total risk
adversity.
4.1 Training and Testing Data Sets
The system was tested using historical daily prices
from the stock indexes: S&P 500, FTSE 100, DAX
30, NIKKEI 225 and NASDAQ.
The period of time chosen for training was from
3 Jan. 2000 to 31 Dec. 2007. This time period was
assumed sufficient to evolve a competitive
population as it exhibited significant movement,
including several boom and crash periods. For out of
sample and testing period, two years of data was
used, and it was from 2 Jan. 2008 to 31 Dec. 2009.
Multi-objectiveOptimizationofInvestmentStrategies-BasedonEvolutionaryComputationTechniques,inVolatile
Environments
483

4.2 Analysis of the Training
Performance
Figure 2 present the PF's evolved for the 5 indexes
tested in this study, in one of the experimental runs
performed. Though the various solutions sets vary in
terms of Pareto dominance and optimality, all
clearly illustrate the inherent trade-off between
return and risk. Furthermore, the trading agents
evolved are able to generate high returns in open
positions less than 100% of the trading period, for
instance, the observable annualized ROI near or
above 10% with risk exposure around 0.6.
Figure 2: Evolved Pareto Fronts for the five Indexes
Tested.
In Financial Computing when analyzing the
performance of a given TS, it is common to compare
it against the “Buy & Hold” (B&H) and “Sell &
Hold” (S&H) strategies. When the ROI performance
of the evolved TS (see figure 2) is compared against
both B&H and S&H approaches (see B&H and S&H
annualised ROI calculation on Table 2), during the
training period, it is easy to conclude that, in this
context, both B&H and S&H strategies are
undoubtedly suboptimal. It is also important to
remind that both, B&H and S&H, strategies
correspond to a risk exposure of 1 (one); since the
capital is all time engaged.
In Figure 3 is presented an example of the eight-
year financial data used to optimize the strategy, in
the current case is the FTSE100 index. The line
labelled “Buy & Hold” characterizes the
performance of the B&H strategy; this same line is
coincident with the current index evaluation at close
price. On this same illustration, the performance of
the S&H strategy is exposed by the curve tagged
“Sell & Hold”. An example of the trading
performance of one of the optimized strategies is
also shown on this figure, by the line labelled
“Trained Chromosome”. On the same illustration the
X axis is the time, and on the Y axis is the assets
evaluation.
Table 2: Annualized ROI for B&H and S&H strategies in
the training period.
NIKKEI
225
FTSE
100
S&P500 DAX30 NASDAQ
B&H
Absolute
Return
-3695.08 - 206.00 13.14 1316.56 -1478.87
B&H ROI
[%]
- 19.44% - 3.09% 0.90% 19.50% - 35.80%
B&H
Annualized
ROI [%]
-2.67% -0.39% 0.11% 2.25% -5.39%
S&H
Absolute
Return
3695.08 206.00 -13.14 -1316.56 1478.87
S&H ROI
[%]
19.44% 3.09% - 0.90% - 19.50% 35.80%
S&H
Annualized
ROI [%]
2.25% 0.38% -0.11% -2.67% 3.90%
Figure 3: Example of daily closing prices and the
performance of one trained agent, for FTSE100 index, in
the training period.
In order to have a better insight about the data and
results, 30 (thirty) experimental runs were
performed, the results collected, and then, discrete
intervals of 0.1 of risk exposure considered. With
this data, plots like the one shown in Figure 4 were
gotten.
Figure 4: Annualised ROI in discrete intervals of 0.1 Risk
Exposure, observed with DAX index.
Figure 4 plots an example of the observed
distribution of the Annualized ROI in function of the
risk exposure. This illustration shows the First
Quartile of data (Q1), the Third Quartile of data
(Q3), as well the Median, with the whiskers located
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
484
respectively at 10% and 90% of data, and this for the
results observed, with training data. Again, the risk-
returns trade-off is evident, since the average of the
Annualized ROI increases for higher levels of risk
exposure. The lack of solutions in the risk exposure
range of 0.1 to 0.2 can be due to the difficulty in
optimizing the chosen TI to exploit the price
movements in order to create strategies in this
region. Similar plots, identical the one shown, were
also observed for the further indexes also tested in
this study.
4.3 Correlation Analysis of Training
and Testing Performance
The results presented in the previous subsection
showed that it is possible to tune a TS to attain
attractive returns at various levels of risk exposure.
Despite this, the great effectiveness of any approach
will depend on being able to extend these interesting
returns to unseen data, which is usually recognized
as its generalization performance.
In order to evaluate the engine generalization
performance, the available trading data is portioned
into two independent sets of data, this means:
training and testing data sets, as explained in
subsection 4.1. In the training phase of the
evolutionary process, the TS will be trained, tuned
and evaluated using only training data. After being
trained, the developed strategies obtained in the final
generation will be then applied to the testing data set
and its generalization performance is evaluated. This
is an indicator of the framework real effectiveness in
getting good results using unseen data.
The plot of the risk-returns PF's for the training
data gotten in one of the experimental run is
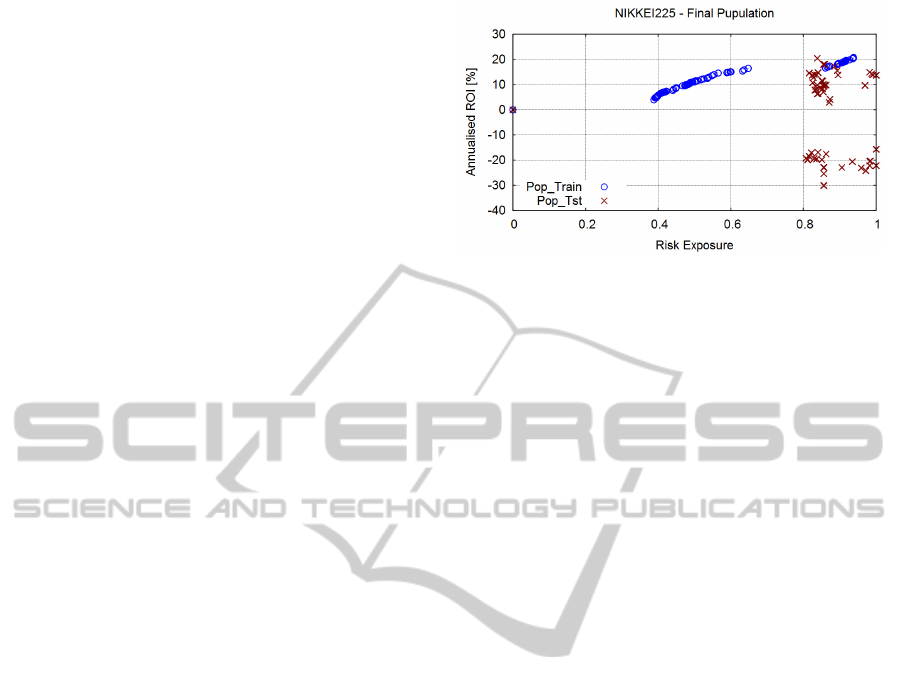
presented in Figure 5. The marks labelled
“Pop_Train” represent the final population evolved
after 400 generations, while the points tagged
“Pop_Tst” represent the results of this same
population when applied to the testing data set.
The example shown on Figure 5 is for the
NIKKEI index, but similar plots were observed with
the further indexes also tested.
Again, in this plot, the risk-returns trade-off is
evident with the training data. However, such
correlation disappears when the same strategy is
applied to the testing data. For instance, annualized
ROI of 15% are realizable at a risk level of 0.6 with
the training data, while big losses are gotten at the
same level of risk with the testing data. This low
relation between training and testing results was also
observed in previous studies (Korczak et al., 2004),
(Chiam et al, 2009).
Figure 5: Pareto Fronts observed with training and testing
data.
The most evident conclusion from this figure is that
positive returns with the training data do not
necessarily match to positive returns with the testing
data.
Hence, it urges the need to better understand
how the training and testing data correlate together,
in order to examine the generalization performance
of the evolved TS's. This suggests that a correlation
analysis between the four variables involved should
be conducted; to name: training ROI, training risk,
testing ROI and testing risk.
To better clarify the results, 30 independent
experimental runs were performed and with the
results observed in these experimental runs, the
graphs shown in Figure 6 where build. On this
graphs the variables are plotted and its potential
correlations can be visually inspected. Once more,
the plot of training ROI and training risk accurately
shows the risk-returns trade-off. While an almost
random plot is obtained when the testing returns
against the testing risk are plotted, therefore this
suggests the existence of low correlation between
training ROI and testing ROI.
Contrasting to the traditional theory in single-
objective approaches where higher training returns
are coupled with higher testing returns, this
relationship is missing from these plots. Instead,
higher training returns correspond to increased
volatility in the observed testing returns; this is
clearly observable in the graph of Figure 7. This
figure plots the quartiles of data (Q1-Q3), the
median, as well the whiskers located respectively at
10 and 90% of the observed results, when the
training returns are divided in discrete intervals of
5%. On this figure the median of the testing returns
does not boost when the values of training returns
increase. In its place, there is a visible increase in the
variance of the results, denoted by largest vertical
lines (both whiskers and boxes).
Multi-objectiveOptimizationofInvestmentStrategies-BasedonEvolutionaryComputationTechniques,inVolatile
Environments
485

0
5
10
15
20
25
30
0 0.2 0.4 0.6 0.8 1
Train Annualized ROI [%]
Test Time on Market
0
5
10
15
20
25
30
-0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4
Train Annualized ROI [%]
Test Annualized ROI
0
5
10
15
20
25
30
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Train Annualized ROI [%]
Train Time on Market
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 0.2 0.4 0.6 0.8 1
Train Time on Market
Test Time on Market
-40
-30
-20
-10
0
10
20
30
40
0 0.2 0.4 0.6 0.8 1
Test Annualized ROI [%]
Test Time on Market
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
-0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4
Train Time on Market
Test Annualized ROI
Figure 6: Plots showing the correlation between training returns, training risk, testing returns and testing risk.
Figure 7: Statistical distribution of testing returns at
discrete intervals of the training returns for DAX index.
In conclusion, the positive correlation typically
implicit in conventional single-objective approaches,
to do the optimization of TS's, between training and
testing returns, is not necessarily true for all cases.
Figure 8: Distribution of testing returns at discrete
intervals of training risk for DAX index.
Similar conclusions can be extracted from the
plot shown in Figure 8 where the testing returns
observed in the 30 independent runs are resumed at
discrete intervals of 0.1 training risk. Again, the
median of the testing returns does not increase when
the training risk increases.
Although, a steady increase is clearly observable
in the variance of the test returns is clear from the
plots (Figures 8 and 9), what confirms the claim that
higher training returns correspond to increased
volatility in the test returns results.
Figure 9 shows the number of solutions gotten in
each interval of test risk exposure (scale at left)
together with the Std. Dev. gotten with both the
training data and testing data (scale at right). The
apparent drop in the test results volatility for risk
Figure 9: Number of Solutions and Standard deviation of
the testing returns at discrete intervals of 0.1 risk exposure
for DAX Index.
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
486

level above 0.8 is statistically irrelevant as there are
few solutions in this region. The plots presented
were built with the DAX results, but similar plots
were also observed for the remaining four indexes
also tested in this study.
4 CONCLUSIONS
This document presented and investigated a multi-
objective evolutionary approach to do the
optimization of a set of TS’s. In this work, fair and
established metrics were used to both evaluate the
return and the related risk. Both metrics were
simultaneously optimized and a popular TI
frequently used by real-world professionals was
used as the building block of the core strategy.
Furthermore, the TS’s were trained, and afterwards
tested, using data coming from five main stock
indexes, representative of the world most developed
economies. The PF’s obtained by the algorithm
using testing data correctly depict the intrinsic trade-
off between risk and return.
The low correlation between training returns and
testing returns conducted to deceptive results when
the testing results are analyzed, what suggests a low
potential in the framework generalization capability.
Consequently, the experimental results suggest that
the positive connection between training and testing
returns usually assumed in conventional single-
objective approaches may not necessarily hold true
for all cases.
Anyway, some interesting conclusions can be
extracted, namely the conclusion that higher training
returns correspond to increased volatility in the
testing results. The MAs have the disadvantage of
being a trend follower indicator, so the signals one
can get from such indicator are always with some
delay. Further tests should be accomplished, using
other TI and the achieved results should be seen as a
benchmark to further improvements with the use of
other TI, or even the use of multi TI strategies.
REFERENCES
Achelis, S. B., 2000. Technical Analysis from A to Z, 2nd
Edition, McGraw-Hill, New York, 2nd Edition, New
York, (October 2, 2000).
Bodas-Sagi, Diego J., Fernández, Pablo, Hidalgo, J.
Ignacio, Soltero, Francisco J., Risco-Martín, José L.,
2009. Multiobjective Optimization of Technical
Market Indicators. In Proceedings of the 11th Annual
Conference Genetic and Evolutionary Computation
Conference (GECCO). Montreal, Canada, 1999–2004.
Chiam, Swee Chiang, Tan, Kay Chen, Mamun, Abdullah
Al, 2009. Investigating technical trading strategy via
an multi-objective evolutionary platform. In Expert
Systems with Applications. 36, 7, (Sep., 2009), 10408-
10423.
Deb, Kalyanmoy, Pratap, Amrit, Agrawal, Samir,
Meyarivan, T., 2002. A fast and elitist multi-objective
genetic algorithm: NSGA-II. In IEEE Transactions on
Evolutionary Computation. IEEE Computer Society,
Washington, DC, USA, 6, 2, (Apr, 2002), 182-197.
Fernández-Blanco, Pablo, Bodas-Sagi, Diego J., Soltero,
Francisco J., Hidalgo, J. Ignacio, 2008. Technical
Market Indicators Optimization Using Evolutionary
Algorithms. In Proceedings of the 2008 GECCO
conference on Genetic and evolutionary computation
(GECCO). Atlanta, Georgia. USA, 1851-1857.
Gorgulho, António, Neves, Rui, Horta, Nuno, 2011.
Applying a GA kernel on optimizing technical
analysis rules for stock picking and portfolio
composition. In Expert Systems with Applications
(ESWA). 38, 11, (October 2011), 14072–14085.
Graham, Benjamin, Zweig, Jason, Buffett, Warren E.,
2003. The Intelligent Investor, Revised edition, Collins
Business, Revised edition, (July 8, 2003).
Kendall, Graham, Su, Yan, 2003. A multi-agent Based
Simulated Stock Market – Testing on Different Types
of Stocks. In Proceedings of the 2003 Congress on
Evolutionary Computation (CEC’03). 4, 2298-2305.
Korczak, J.J., Lipinski, Piotr, 2004. Evolutionary Building
of Stock Trading Experts in a Real-Time System. In
Proceedings of the 2004 Congress on Evolutionary
Computation (CEC 2004). Portland, USA, (19-23
June, 2004), 940-947.
Korczak, Jerzy, Roger, Patrick, 2002. Stock Timing Using
Genetic Algorithms in Applied Stochastic models. In
Business and Industry. 18, (January 15, 2002), 121-
134.
Markowitz, Harry M., 1952. Portfolio Selection. In The
Journal of Finance. 7, 1, (Mar., 1952), 77-91.
Murphy, John J., 1999. Technical Analysis of Financial
Markets, Prentice Hall Press, New York Institute of
Multi-objectiveOptimizationofInvestmentStrategies-BasedonEvolutionaryComputationTechniques,inVolatile
Environments
487

Finance, New York. (January 4, 1999).
Pinto, J., Neves, R. F., Horta, N., 2011. Fitness function
evaluation for MA trading strategies based on genetic
algorithms. In Proceedings of the 13th annual
conference companion on Genetic and evolutionary
computation (GECCO '11). ACM, New York, NY,
USA, 819-820.
Schoreels, Cyril, Garibaldi, Jonathan M., 2005. A
comparison of adaptive and static agents in equity
market trading. In Proceedings of the EEE/WIC/ACM
International Conference on Intelligent Agent
Technology (IAT '05). Compiegne, France, 393-399.
Schoreels, Cyril, Garibaldi, Jonathan M., 2006. Genetic
algorithm evolved agent-based equity trading using
Technical Analysis and the Capital Asset Pricing
Model. In Proceedings of the 6th International
Conference on Recent Advances in Soft Computing
(RASC2006). Canterbury, UK, 194-199.
Weissman, Richard L., 2005. Mechanical Trading
Systems: Pairing Trader Psychology with Technical
Analysis, Wiley Trading. Wiley Trading.
William, F. Sharpe, 1964. Capital Asset Prices: A Theory
of Market Equilibrium under Conditions of Risk. In
The Journal of Finance. 19, 3, (Sep., 1964), Blackwell
Publishing, American Finance Association, 425-442.
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
488
