
Continuous Core Body Temperature Estimation via SURFACE
Temperature Measurements using Wearable Sensors
Is it Feasible?
Kumar Saurabh
1,4
, Hiteshwar Rao
3
, Bharadwaj Amrutur
2,3
and Asokan Sundarrajan
1,3
1
Department of Instrumentation & Applied Physics, Indian Institute of Science, Bangalore, India
2
Department of Electrical Communication Engineering, Indian Institute of Science, Bangalore, India
3
Robert Bosch Centre for Cyber Physical Systems, Indian Institute of Science, Bangalore, India
4
Robert Bosch Engineering & Business Solutions Ltd, Bangalore, India
Keywords: Core Body Temperature, Hypothermia, Wearable Sensors.
Abstract: Core body temperature is an important indicator of well being of humans. The commonly used methods and
sites of measurement do not lend well for continuous measurement at home. However, continuous
monitoring using non-invasive, small, low cost sensors could have many applications like detection of
hypothermia and fever in low birth weight neonates in rural settings. We investigate the feasibility of
making such measurements using only skin temperature sensors. Our initial sensor prototype is composed of
flexible materials, with embedded high precision thermistors and is based on dual heat flux technique. Our
initial experiments show that the reliable estimation of core temperature under varying ambient conditions
and at different measurement sites is a challenge, but promising. Further work is needed to combine results
from experimental measurements and theoretical simulations to provide good insights and enable accurate
estimation of core body temperature for long term monitoring at home.
1 INTRODUCTION
Even though pulmonary artery temperature is
considered to be the gold standard for core
temperature measurement, it is not used for general
clinical practice. Rectal temperature is close to this
but poses severe constraints due to invasiveness and
concerns about hygiene even though continuous
monitoring probes are available. Digital
thermometers for oral and axillary temperature
measurements have replaced the traditional mercury
in glass thermometers and provide relatively quicker
and easier measurements. However, these are meant
for manual use and do not suit continuous
monitoring needs. Recently, tympanic thermometers
based on infrared measurements have become
popular as they are fast and easy to use. However,
different studies show different results regarding
their accuracy in comparison to the pulmonary artery
temperature (Hooper & Andrews 2006). There have
been some attempts to integrate it into a head gear
similar to headphones (Boano, Lasagni & Roemer
2013). Other techniques like radiometric sensing
(Bonds, Gerig, Weller & Herzig 2012) have been
evaluated. Conductive textiles have been used for
monitoring temperature of neonates in Neonatal
Intensive Care Units (Chen, Dols, Oetomo & Feijs
2010). However, none of these are suitable for
continuous temperature monitoring of neonates at
home due to inconvenience in use, complexity of the
device or power requirements. Skin temperature is
the easiest to measure in a non-invasive manner
using simple sensors. However, single point
measurements of skin temperature vary significantly
with the ambient conditions. As the
thermoregulation of neonates is not well developed,
using fixed offsets to skin temperature would add to
the errors. Hence there is a need for reliable
estimation of core temperature from skin
temperature measurement to develop low cost
sensors that are accurate and reliable for remote
monitoring applications.
181
Saurabh K., Rao H., Amrutur B. and Sundarrajan A..
Continuous Core Body Temperature Estimation via SURFACE Temperature Measurements using Wearable Sensors - Is it Feasible?.
DOI: 10.5220/0004889901810186
In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2014), pages 181-186
ISBN: 978-989-758-013-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 CORE BODY TEMPERATURE
ESTIMATION FROM BODY
SURFACE MEASUREMENTS
One of the earliest efforts to develop a sensor for
core body temperature measurement from surface
measurements has been based on zero heat flow
method (Fox, Solman, Isaacs & MacDonald 1973).
The method uses a heater to create a zone of zero
heat flux such that the skin temperature under the
sensor reaches the core temperature. Studies have
shown the effectiveness of this method except
during exceptional rapid cooling or heating as the
response time is around 15 to 20 minutes when
applied to forehead (Togawa 1985). There have been
other attempts to evaluate the effectiveness of this
scheme for different applications (Zeiner et.al. 2010)
(Teunissen et.al. 2011). However, the use of a
heating element creates problems for applications
which involve mobility and require low power
consumption. New technique which does not involve
the use of heater and is based on a double sensor has
been reported for monitoring heat strains (Gunga
et.al. 2008) and also for space applications (Gunga
et.al. 2009). The design uses two temperature
sensors separated by an insulating layer whose
thermal conductivity is known. By measuring the
skin temperature and the temperature at the upper
sensor and knowing the thermal conductivity of
human tissue, the core temperature can be
calculated. However, this technique still requires the
correct knowledge of the thermal conductivity of the
epidermal tissues where the sensor is placed.
Another solution has been proposed using two heat
flow channels in parallel (Kitamura, Zhu, Chen &
Nemoto 2010). This work avoids the dependence on
knowledge of the thermal properties of tissue below
the sensor. Its performance has been compared to the
zero heat flux method. Further work has been
presented to improve the response time (Sim, Lee,
Baek & Park 2012). These present interesting ideas
for use in continuous monitoring applications.
However, additional constraints on materials of the
device to conform to body contour have to be added
for it to be acceptable for long term use on neonates.
Also, correspondence between experimental
measurements and theoretical correctness and
assumptions has to be established. We explore these
aspects by considering sensors for neonates. We
study the accuracy under varying conditions and at
different sites of measurement using both
simulations and experiments.
2.1 The Device Structure
For the device to be easily acceptable to parents for
long term use, it has to be such that it does not leave
any mark on the neonate’s skin. Also, it cannot be
taped to the skin as regular application and removal
of tapes create redness. Using a hard metal contact at
the skin interface or an inflexible material for the
sensor cover, would create problems. Hence using a
soft material that bends to conform to the body
contour and also ensure that the sensor is in contact
with the skin is a good option.
PolyDimethylsiloxane (PDMS) can be used as the
material for the device. PDMS provides both
flexibility and biocompatibility. Hence it can be
placed on the delicate skin of neonates over long
periods of time. Another major advantage provided
by PDMS is that it is highly hydrophobic. This
makes it very good for usage where it is likely to be
exposed to water or urine.
We use Dow Corning’s Sylgard 184 elastomer
kit for the purpose. Two different ratios of base and
curing agent have been used for two different layers
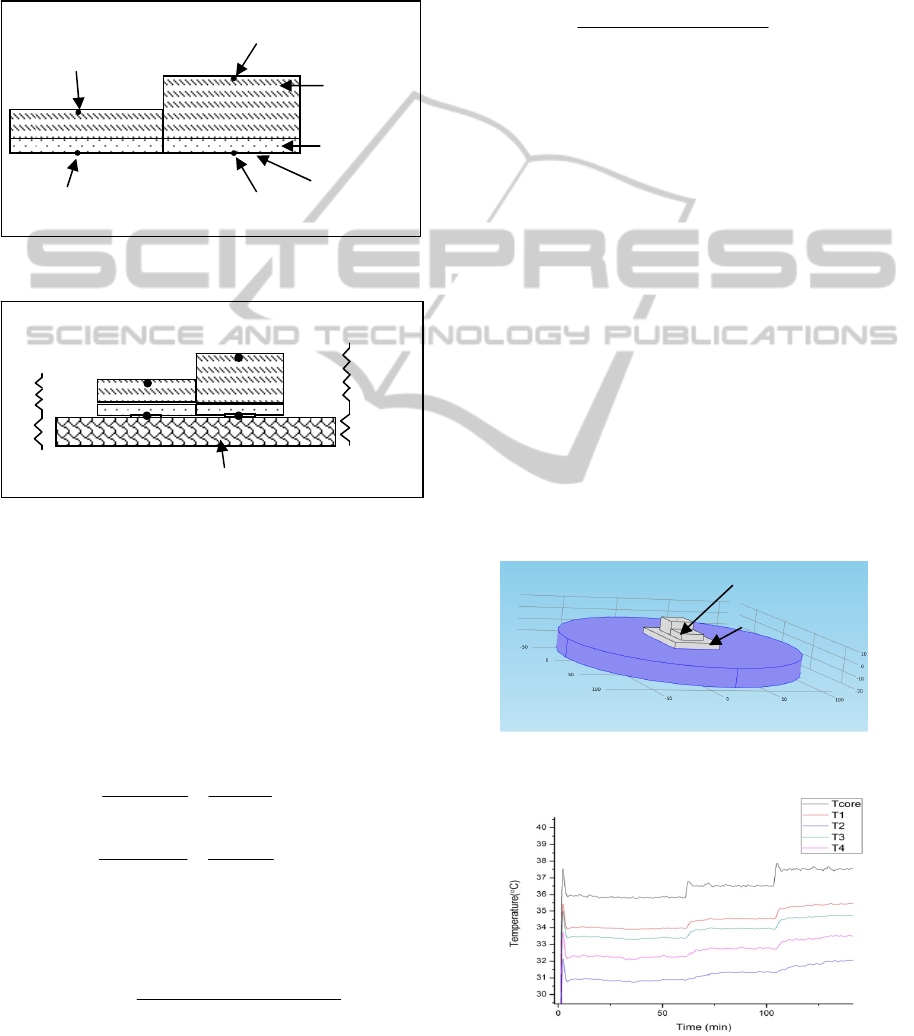
of the sensor (shown in Fig 1). For the layer that is
contact with the skin, base elastomer to curing agent
ratio of 10:0.4 is used while and for the top layer, a
ratio of 10:1 is used. The top layer is prepared first
and the lower layer is added after partial curing of
the first layer. This ensures that the two layers bind
together. By following this method, the need for
complex surface modification techniques like use of
oxygen plasma to improve adhesion between the
layers is avoided. The lower layer provides adhesion
to the skin surface and the upper layer provides the
rigidity needed for the sensor. Also, the lower layer
is softer and does not leave any mark when placed
on the skin. Experiments were performed with
different ratios of base and curing agent. It was
observed that a ratio of 10:0.2 provides better
adhesion over a longer time. But the layer is too soft
and can get easily damaged. The ratio of 10:0.4
provides adhesion while being strong enough for
long term use. However, the adhesion of the sensor
is not enough to hold it for a long time over
prolonged removal and placement cycles especially
in the presence of oil or dirt on the skin surface.
Hence a belt has been provided on the side of sensor.
In the presence of a belt, the adhesion is enough to
ensure contact of the sensor with the skin to get
reliable measurements with low pressure from the
belt on the skin. Instead of using IC based
temperature sensors as used in prior work, we use
high precision thermistors (MF51E103E3950). Since
the device can be made in very controlled manner
BIODEVICES2014-InternationalConferenceonBiomedicalElectronicsandDevices
182
with respect to composition and size of moulds, the
thermal properties can be ensured for every device
and extensive calibrations for each sensor would not
be needed after it is in final form. The device also
has an integrated SOC (BLE112) from Bluegiga
Technologies for data acquisition and Bluetooth
®
low energy communication with a gateway device.
Figure 1: Device Structure.
Figure 2: Schematic of device placed on skin and
analogous equivalent circuit with two parallel heat flow
channels and thermal resistances network.
Following the concept as proposed by Kitamura
et.al., heat flow in the two channels can be modelled
using an equivalent thermal resistance network with
two parallel heat flow paths where R1 and R2 are
the respective thermal resistance of the two channels
and Rs is the thermal resistance of skin and
subcutaneous tissue.
1
211
R
TT
Rs
TTcore
(1)
2
433
R
TT
Rs
TTcore
(2)
When the temperatures T1 and T3 (as shown in Fig.
2) are measured close to each other as is the case
here, the core temperature can be calculated as
T
core
= T1 +
KTTTT
TTTT
*)43()21(
)13(*)21(
(3)
where K = R1/R2. Hence the dependence on
knowledge of thermal resistivity of skin and
subcutaneous tissue can be eliminated. The equation
in the published work by Kitamura and used in some
of the work that used the concept has slight error in
the denominator term. We have used a corrected
equation (equation 3). K can be obtained
experimentally by applying a fixed temperature for
Tcore and measuring T1, T2, T3, and T4 as
K=
)43(*)1(
)21(*)3(
TTTTcore
TTTTcore
(4)
2.2 Experimental Setup
and Measurements
To verify the concept, experiments have to be
performed to simulate different core temperatures.
To simulate the effect of skin and human tissues
experiments were tried using different phantoms.
Phantoms made from gelatine (obtained from
porcine cells) as well as poly vinyl alcohol were
tried. However, when these were exposed to
continuous heating especially above 36 degrees for
long durations (30-40minutes), the physical
properties started changing due to loss of water
content. This made it difficult to conduct the
experiments. Hence PDMS (10:1) was used instead
as it has thermal conductivity of 0.15 W/m K which
is very close to that of skin and fat. The sensor was
placed on a PDMS layer of thickness 5mm which in
turn was placed on a well controlled hot plate to
simulate the core temperature.
Figure 3: Experimental Setup.
Figure 4: Measured Temperatures during experiment.
PDMS (10:1)
PDMS (10:0.4)
Aluminum tape
Thermistor 2
Thermistor 4
Thermistor 1
Thermistor 3
T1
T2
T3
T4
R1
Rs
Tcore
Rs
R2
Tcore
Skin and tissue
Hot Plate
Device
Layer simulating
skin and tissues
ContinuousCoreBodyTemperatureEstimationviaSURFACETemperatureMeasurementsusingWearableSensors-Isit
Feasible?
183
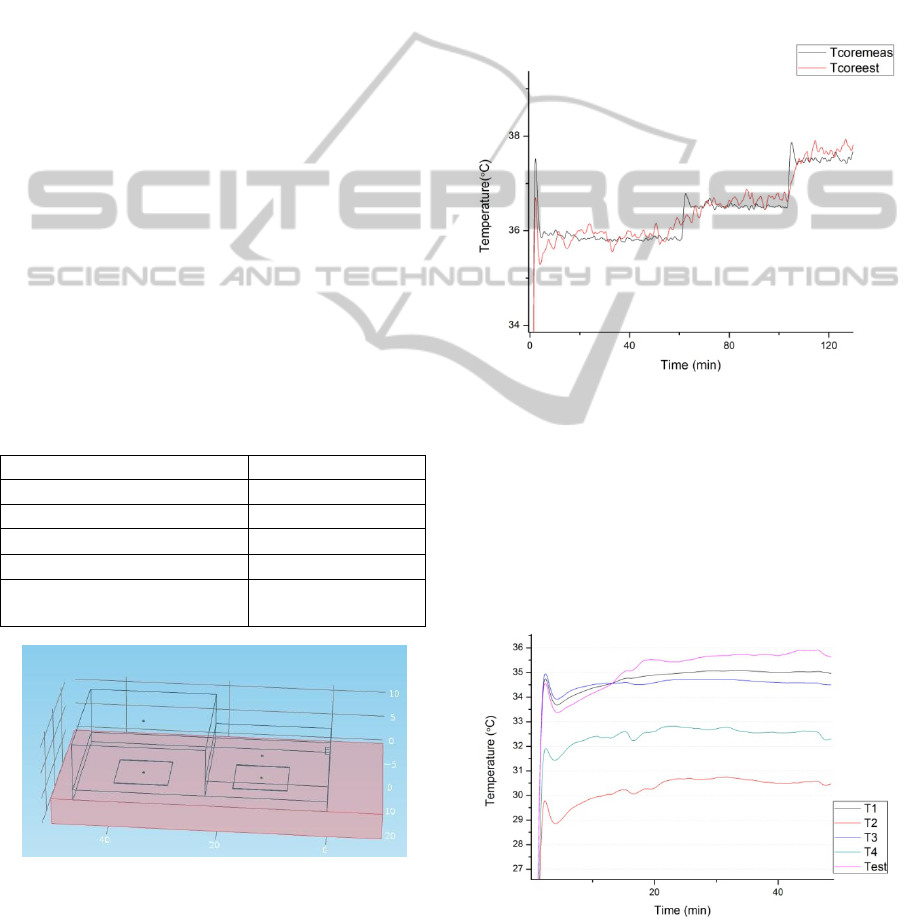
Three temperature points of 36C, 36.5C and
37.5C were used to cover the normal body
temperature range. Based on the measurements as
shown in Fig 4, the value of K was obtained as 3.5
for all three temperature points.
Calculation of Tcore is very sensitive to the
temperature difference T3-T1. Hence, it justifies the
use of high precision thermistors instead of IC based
temperature sensors as used in earlier work.
2.3 Heat Transfer Simulation
A three dimensional sensor model was created using
COMSOL
TM
as shown in Fig. 3 and heat transfer
simulation was performed to verify the feasibility of
using the concept. In the model, the sensor was
composed of PDMS blocks with four domain point
probes placed at the bottom and top surfaces similar
to that in fig 1. The simulation was performed by
placing it on another PDMS layer similar to the
experimental setup. The bottom boundary of the
lower PDMS layer was assigned the temperature
equivalent to Tcore. Radiation and convection was
specified at the top surface. The convective heat
transfer coefficient was kept very low to have
simulation equivalent to still air in the room. The
parameters were specified as follows and ambient
temperature was specified as 25C which was same
for experimental measurements.
Parameter Value
Thermal Conductivity (k)
0.15 W/(mK)
Density (ρ) 0.97 Kg/m
3
Heat Capacity (Cp)
1460 J/(KgK)
Surface Emissivity ()
0.9
Convective heat transfer
coefficient (h)
2.5 W/(m
2
K)
Figure 5: COMSOL model.
3 RESULTS AND DISCUSSION
Using the value of K as 3.5 obtained in the
experiment, the applied core temperature was
estimated. The mean error was less than 0.2C for
the experimental temperature range. The results are
shown in Fig 4. Intentionally, smoothing is not
performed to show that there are minor fluctuations
in temperature as the core temperature itself has
fluctuations due to the involved PID control of the
hot plate. The response of the sensor is quite fast to
step changes in temperature and hence it can track
varying temperatures with a delay of less than 5
minutes even for step changes.
Figure 6: Comparison of applied Tcore and Estimated
Tcore.
The sensor was placed on the forehead on four
different days and timings to measure the
performance. It takes approximately 20-30minutes
for the temperature to stabilise. This is similar to the
time mentioned in earlier work. Hence, the choice of
PDMS as the material does not increase the
measurement time.
Figure 7: Measurement on forehead.
It is important to compare the measured temperature
to other standard sites of measurement used in
BIODEVICES2014-InternationalConferenceonBiomedicalElectronicsandDevices
184
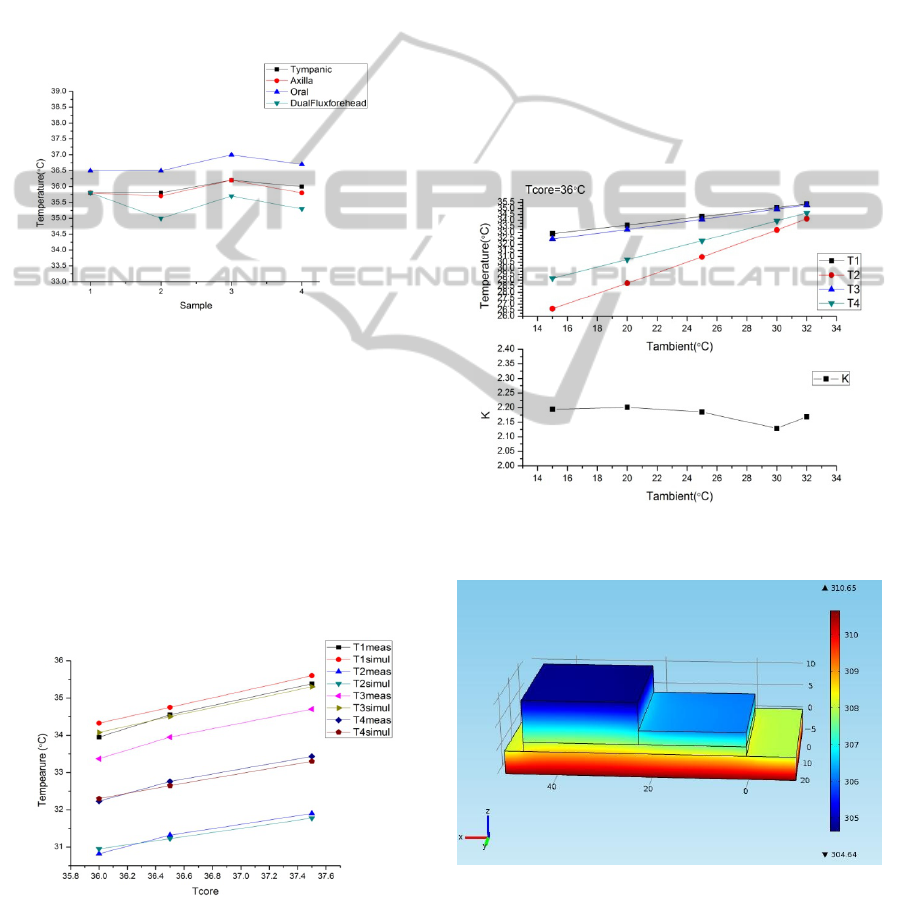
regular clinical use. Tympanic temperature was
measured using an infrared tympanic thermometer
(Omron MC510) and the oral and axillary
temperatures were measured using a digital
thermometer (Neclife). The results show that the
obtained temperatures using dual flux method is
usually lower compared to all three measurements.
However, the variation is consistent across different
temperatures. However, concrete conclusions cannot
be derived based on these measurements as no
temperatures in the hypothermic and fever ranges
were measured.
Figure 8: Comparison of temperature measurements using
different methods and sites of measurement.
Comparison of experimental results and theoretical
simulations can help in improving the design of the
sensor. Hence, a comparison of COMSOL
simulation results and experimental measurements
for the different temperatures measured within the
sensor is presented in Fig 9. T2 and T4 match very
closely for all three points. However, T1 and T3 are
higher is simulation than in experiment. One of the
reasons could be the contact resistance between the
hot plate and the lower PDMS layer.
Figure 9: Comparison of measured temperatures within
the device and COMSOL simulations.
The temperature at different boundaries can be seen
in the simulation results in Fig 11. During
simulation, it can be easily noticed that the presence
of a metallic contact (aluminium foil in this case) at
the bottom layer impacts the absolute value of
temperatures even though it does not significantly
affect the difference in temperatures. Also, there is
significant impact of selection of convection
boundaries.
Since simulation assumes, perfect contact, this
can impact the values. The K value obtained in
simulation 2 as expected. In simulation this value
does not vary significantly over ambient
temperatures ranging from 15C to 32C as seen in
fig. 10. However, as the ambient temperature
increases, T1-T3 becomes very small and hence in
experimental measurements, inaccuracies in the
thermistor calibration can have a significant impact
on the estimated temperature.
Figure 10: Temperatures T1, T2, T3, T4 and the values of
K with varying ambient temperatures.
Figure 11: Temperature at different boundaries in the
COMSOL simulation.
ContinuousCoreBodyTemperatureEstimationviaSURFACETemperatureMeasurementsusingWearableSensors-Isit
Feasible?
185

4 CONCLUSIONS AND FUTURE
WORK
The choice of PDMS as the material and a simple
geometry does not adversely affect the sensor
characteristics compared to results mentioned in
earlier work. However, it is required to understand
in details the reasons for differences in experimental
values and theoretical simulations including the
possibility to overcome the effects of contact
resistance which is dependent on contact resistance
without affecting the flexibility of the sensor. Also,
the effect of ambient variations and convection are
important for accuracy of the sensor. A much more
detailed model is required to compensate for these as
compared to the simple thermal resistance network
model. It might be useful to use dynamic models to
infer the change in ambient conditions and, if
possible, the context of measurements to reduce the
possibility of false alarms. Another important aspect
that has not been studied so far is the use at a
measurement site other than the forehead. If the
sensor can be used at a location between the
abdomen and chest, it can be coupled with other
vital parameter measurements on a single sensing
device. However, the layer of adipose tissues is
significantly lesser for neonates and hence data
obtained on adults and neonates could vary.
Another very important aspect for future work is
to develop a good model incorporating multiple
tissue layers and blood perfusion using Penne’s Bio-
heat equations instead of simple heat transfer
models. It could be interesting if some of the
parameters can be learnt from data obtained through
continuous measurements and be able to predict
conditions like increased blood perfusion due to
exposure to cold and compensate for differences in
core temperature measurements. It would also help
in validating the assumption that the effective
thermal resistance of tissue below the sensor is same
for both parallel heat flow channels.
ACKNOWLEDGEMENTS
We acknowledge the funding provided by Robert
Bosch Centre for Cyber Physical Systems at Indian
Institute of Science, Bangalore to carry out this
work.
REFERENCES
Bonds Q., Gerig J., Weller, T. M., Herzig P., 2012.
Towards core body temperature measurement via
close proximity radiometric sensing. IEEE Sensors
Journal. 12 (3).
Boano, C. A., Lasagni, M., & Roemer, K., 2013. Non-
invasive measurement of core temperature in marathon
runners. Proceedings of the 10th International
Conference on Wearable and Implantable Body
Sensor Networks.
Chen, W., Dols, S., Oetomo, S. B., Feijs, L., 2010.
Monitoring body temperature of newborn infants at
neonatal intensive care units using wearable sensors.
In BodyNets’2010. Fifth Interntional Conference on
Body Area Networks.
Fox, R. H., Solman A. J., Isaacs R., Fry A. J. &
MacDonald I.C. 1973. A new method for monitoring
deep body temperature from the skin surface. Clinical
Science. 44 p. 81-86.
Gunga et.al. 2008. A non-invasive device to continuously
monitor heat strains in humans. Journal of Thermal
Biology. 33. p. 297-307.
Gunga et.al. 2009. The Double Sensor - A non-invasive
device to continuously monitor core temperature in
humans on earth and in space. Respiratory Physiology
and Neurology. 169S. p. 63-68.
Hooper, V. D. & Andrews, J. O., 2006. Accuracy of
noninvasive core temperature measurement in acutely
ill adults: The state of the science. Biological Research
for Nursing. 8. p. 24-34.
Kitamura, K. I., Zhu, X., Chen, W., Nemoto, T. 2010.
Development of a new method for the noninvasive
measurement of deep body temperature without a
heater. Medical Engineering & Physics. 32. p. 1-6.
Mullany, L. C., 2010. Neonatal hypothermia in low
resource settings. Seminars in Perinatology. 34. p.426-
433.
Sim S.Y., Lee W. K., Baek H. J. and Park K.S. 2012. A
non-intrusive temperature measuring system for
estimating deep body temperature in bed. In 34
th
annual conference of the IEEE EMBS.
Teunissen et.al. 2011. Non-invasive continuous core
temperature monitoring by zero heat flux.
Physiological Measurements. 32. p. 559-570.
Togawa, T. 1985. Body Temperature Measurement. Clin.
Phys. Physiol. Meas. 6(2). p. 83-108.
Zeiner et.al. 2010. Non-invasive continuous cerebral
temperature monitoring in patients treated with mild
therapeutic hypothermia: An observational pilot study.
Resuscitation. 81. p. 861-866.
BIODEVICES2014-InternationalConferenceonBiomedicalElectronicsandDevices
186
