Extending the Hybridization of Metaheuristics with Data Mining

to a Broader Domain

Marcos Guerine, Isabel Rosseti and Alexandre Plastino

Institute of Computing, Federal Fluminense University, Niterói, 24210-240 Rio de Janeiro, Brazil

Keywords:

Hybrid Metaheuristic, Data Mining, GRASP, 1-PDTSP.

Abstract:

The incorporation of data mining techniques into metaheuristics has been efﬁciently adopted to solve several

optimization problems. Nevertheless, we observe in the literature that this hybridization has been limited to

problems in which the solutions are characterized by sets of (unordered) elements. In this work, we develop a

hybrid data mining metaheuristic to solve a problem for which solutions are deﬁned by sequences of elements.

This way, we extend the domain of combinatorial optimization problems which can beneﬁt from the com-

bination of data mining and metaheuristic. Computational experiments showed that the proposed approach

improves the pure algorithm both in the average quality of the solution and in execution time.

1 INTRODUCTION

Over the last decades, strategies based on metaheuris-

tics have been proposed to solve a large set of hard op-

timization problems, achieving sub-optimal solutions

in an acceptable computational time. Each meta-

heuristic is supported by a different paradigm and of-

fers mechanisms to escape from local optimal solu-

tions (Gendreau and Potvin, 2010).

A trend in metaheuristic research is to combine

components of classical metaheuristics, providing ro-

bust hybrid heuristics (Talbi, 2002). Moreover, con-

cepts and processes from other research areas may

also be used to improve metaheuristics. An example

of this latter case is a hybrid version of the GRASP

metaheuristic which incorporates a data mining (DM)

process, called Data Mining GRASP (DM-GRASP

for short) (Ribeiro et al., 2004).

GRASP (Feo and Resende, 1995), which stands

for Greedy Randomized Adaptive Search Procedures,

is an iterative metaheuristic that has been success-

fully applied to a large class of optimization prob-

lems (Festa and Resende, 2009a; Festa and Resende,

2009b). Each GRASP iteration is divided into two

phases. First, a feasible solution is built into a con-

struction phase. Then, in a second phase, its neigh-

bourhood is explored by a local search procedure in

order to ﬁnd a better solution. The best solution found

over all iterations is taken as result.

In its original form, GRASP has independent it-

erations that do not use information about solutions

from previous iterations. Because of this, GRASP is

considered memoryless. In order to overcome this

weakness, some ideas on keeping track of recurrent

good sub-optimal solutions and ﬁxing variables have

been successfully investigated, e.g., adaptive mem-

ory (Fleurent and Glover, 1999), vocabulary building

(Berger et al., 2000) and path relinking (Resende and

Ribeiro, 2005).

Based on the hypothesis that patterns found in

good quality solutions may be used to guide the

exploration of the solution space, the hybrid DM-

GRASP metaheuristic was proposed (Ribeiro et al.,

2004; Ribeiro et al., 2006). Data mining refers to the

automatic extraction of knowledge from datasets, ex-

pressed in terms of patterns or rules (Han and Kam-

ber, 2011). Some techniques that extract these pat-

terns or rules have been used to improve state-of-the-

art metaheuristics for different optimization problems

(Plastino et al., 2011; Santos et al., 2008).

The main idea of this hybridization is to mine a

subset of elements that frequently occur in an elite

set of high quality solutions and use these patterns

to guide the search in the solution space. This ap-

proach was ﬁrst introduced by (Ribeiro et al., 2004;

Ribeiro et al., 2006), combining a frequent itemset

mining technique with GRASP metaheuristic, and ap-

plying it to the set packing problem, achieving very

promising results both in terms of solution quality

and computational time. This framework was also

evaluated in other problems, such as the maximum

diversity problem (Santos et al., 2005), the efﬁcient

395

Guerine M., Rosseti I. and Plastino A..

Extending the Hybridization of Metaheuristics with Data Mining to a Broader Domain.

DOI: 10.5220/0004891303950406

In Proceedings of the 16th International Conference on Enterprise Information Systems (ICEIS-2014), pages 395-406

ISBN: 978-989-758-027-7

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

server replication for reliable multicast problem (San-

tos et al., 2006b), the p-median problem (Plastino

et al., 2009; Plastino et al., 2011) and recently to the

2-path network design problem (2PNDP) (Barbalho

et al., 2013).

All these applications of DM-GRASP have a com-

mon property: their solutions are represented by sub-

sets of elements, without setting any ordering. In the

p-median problem, for example, the order of the cho-

sen facilities does not change the solution. However,

in some optimization problems the order is essential,

which is the case of the one-commodity pickup-and-

delivery travelling salesman problem (1-PDTSP).

In this work, we propose the incorporation of

a data mining technique into an existing heuris-

tic for the 1-PDTSP, based on both GRASP meta-

heuristic and the local improvement Variable Neigh-

borhood Descent (VND), developed by (Hernández-

Pérez et al., 2009). We intend to show, as the main

contribution of this work, that the hybridization of

metaheuristics with data mining is successfully ap-

plied not only to problems in which solutions are rep-

resented by a subset of elements, but also to problems

in which solutions are represented by a sequence of

elements, considering the order. Extensive computa-

tional analysis shows that the addition of a data min-

ing module into the original heuristic outperforms the

pure algorithm both in terms of the solution quality

and computational efforts.

The remainder of this work is organized as fol-

lows: Section 2 presents the 1-PDTSP and some re-

lated work. In Section 3, the GRASP/VND heuris-

tic proposed in (Hernández-Pérez et al., 2009) for the

1-PDTSP is revised. Section 4 describes how the hy-

brid data mining technique is adapted to consider the

order of custumers and how this technique is inserted

into the original heuristic. In Section 5, computa-

tional results obtained by this strategy and the original

GRASP/VND are compared. Finally, Section 6 pro-

vides the conclusions and some future work is pointed

out.

2 THE OPTIMIZATION

PROBLEM

Introduced by (Hernández-Pérez and Salazar-

González, 2004a), the 1-PDTSP consists of a

generalization of the well-known travelling sales-

man problem (TSP) by associating to each city (or

customer) a demand of a given product. As in the

TSP, each customer must be visited exactly once

by a capacitated vehicle, minimizing the distance

route for the vehicle and satisfying the customers’

requirements without violating vehicle capacity. The

order of this path over the customers is important

to both the quality and viability of the route. The

exchanging of two or more clients in a path, for

example, may affect all other clients and the entire

solution might become infeasible.

When the vehicle capacity is extremely large, the

1-PDTSP coincides with the TSP and, hence, is N P-

Hard. Moreover, the veriﬁcation of the existence of a

feasible solution to a given instance is N P -Complete.

On the other hand, check if a given solution is feasible

is a linear task (Hernández-Pérez, 2004).

(Hernández-Pérez and Salazar-González, 2004a)

presented an integer linear programming formulation

for the 1-PDTSP. Let G = (V,A) be a complete

graph, where V = {1, . ..,n} is the vertex set and

A = {(i, j) : i, j ∈ V } the arc set between all vertices.

Each vertex i ∈ V is associated to an integer demand

, with q

< 0 for a delivery customer and q

> 0 for

pickup customers. The travel distance c

i j

from i to

j is given for all pairs of locations. For each sub-

set S ⊂ V , let δ

(S) = {(i, j) ∈ A : i ∈ S, j /∈ S} and

−

(S) = {(i, j) ∈ A : i /∈ S, j ∈ S} be, respectively, the

set of arcs going out from and in to S.

Vehicle capacity is represented by Q and q

is de-

mand of the depot. The latter can be considered as

a customer that receives or provides an amount of

goods to ensure that equation q

= −

∑

i=2

is sat-

isﬁed.

Equation 1 guarantees the overall ﬂow conserva-

tion for 1-PDTSP solutions.

∑

∀i∈V:q

∑

∀i∈V:q

= 0 (1)

Let x

i j

be a binary decision variable that indicates

whether the arc (i, j) is (x

i j

= 1) or not (x

i j

= 0) in the

solution and f

i j

a continuous variable indicating the

ﬂow through arc (i, j) ∈ A. The mathematical formu-

lation for 1-PDTSP is given below.

min

∑

(i, j)∈A

i j

(2)

subject to:

∑

(i, j)∈δ

({i})

i j

= 1, ∀i ∈ V (3)

∑

(i, j)∈δ

−

({i})

i j

= 1, ∀i ∈ V (4)

∑

(i, j)∈δ

(S)

i j

≥ 1, ∀S ⊂ V (5)

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

396

∑

(i, j)∈δ

({i})

i j

−

∑

(i, j)∈δ

−

({i})

i j

= q

, ∀i ∈ V (6)

0 ≤ f

i j

≤ Qx

i j

, ∀(i, j) ∈ A (7)

The objective function presented in Equation 2

aims at minimizing the total sum of costs (travel dis-

tance) in the solution. Constraints (3) and (4) ensure

that each customer must be visited once. Equation (5)

prohibits subcycles and disconnected routes by ensur-

ing that for each client subset there will be at least one

arc going out from it. Equation (6) guarantees that

each customer is attended in relation to its demand by

assuming that this value is exactly the difference be-

tween the ﬂows going in and out from this customer.

Finally, constraint (7) deﬁnes the domain of ﬂow vari-

ables, ranging from zero to the capacity of the vehicle.

The 1-PDTSP has some real practical applications

in the repositioning scenario (Hernández-Pérez and

Salazar-González, 2004a). For example, this problem

arises from a given store that needs to restock some of

its products in its whole set of stores. Let’s suppose

that some stores have an amount of products left in

stock while in other stores the same product is lack-

ing. Then one could move products from the former

store to the latter so that both are attended.

There are a few methods to solve the 1-PDTSP

in the literature. (Hernández-Pérez and Salazar-

González, 2004a) described an exact branch-and-

cut algorithm to solve instances with up to 60 cus-

tomers. The same authors proposed two heuristics

(Hernández-Pérez and Salazar-González, 2004b) to

deal with bigger instances. The ﬁrst one consists of

a local search to provide a primal upper bound to the

previous branch-and-cut algorithm, and the second is

the same branch-and-cut considering only a subset of

variables, associated to promising edges, and hence

reducing the search space.

A new version of the branch-and-cut method

was developed later (Hernández-Pérez and Salazar-

González, 2007) with a new set of restrictions for the

problem, based on some valid inequalities of the ca-

pacitated vehicle routing problem. (Martinovic et al.,

2008) presented a Simulated Annealing, modiﬁed and

iterative, that uses a greedy randomized construction.

(Hernández-Pérez et al., 2009) proposed a hybrid

heuristic based on GRASP and VND. The initial so-

lution is built iteratively, selecting a new client over

a restricted candidate list to be inserted at the end of

the path. The single local search phase of the GRASP

is replaced by a VND procedure that contains a mod-

iﬁed version of 2-opt and 3-opt moves. In Section 3,

we revise this approach in detail.

(Zhao et al., 2009) presented a Genetic Algorithm

composed by a new constructive heuristic to gener-

ate the initial population and a local search proce-

dure to speed up the convergence of the search. (Paes

et al., 2010) proposed a multi-start algorithm based

on GRASP (as constructive phase), ILS (as main

method) and VND procedure with a random order of

neighbourhoods (as local search).

Recently, (Mladenovi

c et al., 2012) developed

an algorithm based on the Variable Neighbourhood

Search (VNS) that uses a new and efﬁcient way to

verify the viability of solutions. This check uses a

binary indexed tree that stores speciﬁc data on the so-

lutions to reduce the computational effort on the local

search phase.

In the next section we review the hybrid

GRASP/VND heuristic proposed by (Hernández-

Pérez et al., 2009). This heuristic was chosen as the

base of the proposed data mining hybrid strategy be-

cause it is a competitive heuristic for the 1-PDTSP

and because the GRASP has been successfully com-

bined with data mining procedures (Ribeiro et al.,

2004; Ribeiro et al., 2006; Santos et al., 2005; San-

tos et al., 2006b; Barbalho et al., 2013).

3 GRASP/VND HEURISTIC FOR

THE 1-PDTSP

The hybrid heuristic presented in (Hernández-Pérez

et al., 2009) has the same structure of a classic

GRASP metaheuristic, as shown in the Algorithm 1.

This strategy consists of a main loop, where the ter-

mination criterion is the number of iterations. Each

iteration of this loop has a construction phase (line 4)

and a local search phase (line 5). At the end, after

all iterations, a post-optimization phase is run, using

another local search procedure (line 10) trying to im-

prove the best overall solution found.

Algorithm 1: Hybrid GRASP/VND for 1-PDTSP.

1: GRASP/VND ( maxIter )

2: f (s

∗

) ← ∞;

3: for iter = 1 until maxIter do

4: s ← ConstructionGRASP();

5: s ← V ND

(s);

6: if s is feasible and f (s) < f (s

∗

) then

7: s

∗

← s ;

8: end if;

9: end for;

10: s

∗

← V ND

∗

);

11: return s

∗

;

ExtendingtheHybridizationofMetaheuristicswithDataMiningtoaBroaderDomain

397

In the construction phase, one client is selected at

random to be the depot. After that, clients are inserted

iteratively at the end of the path as below. In each iter-

ation, clients that can be feasibly inserted into the so-

lution under construction are sorted by their distance

to the last customer in the solution, and only the ﬁrst

l elements will be part of the restricted candidate list

(RCL). If there is no client that can be feasibly added

to the path, the RCL is built by the ﬁrst l closest cus-

tomers to the one at the end of the current solution.

Finally, one client of the RCL is chosen at random

and inserted at the end of the path. The construction

ends when all clients are in the solution.

The local search phase, named V ND

, is based

on the variable neighbourhood descent procedure

(Mladenovi

c and Hansen, 1997), which consists of

applying multiple neighbourhood structures to a given

solution in a predeﬁned order, and whenever the cur-

rent solution is improved, the procedure returns to the

ﬁrst neighbourhood structure. The VND

is made by

two classic moves, 2-opt and 3-opt, modiﬁed to ac-

cept infeasible solutions as a start point. These moves

are applied in the following order. First, the 2-opt

heuristic, which removes two non-adjacent edges and

inserts them in another way to build a new route. And

next, the 3-opt, which is almost the same as the previ-

ous one, but handling three edges.

After the end of the main loop, the post-

optimization phase is performed with another VND

procedure, named V ND

, which is applied to the best

solution found so far. The V ND

consists of two

other neighbourhood structures based on the Rein-

sertion move, also well-known for TSP. This move

is divided into two smaller structures, applied in this

order: ﬁrst, the Reinsertion Forward, that removes a

client and reinserts it in a position after its original

position, and secondly, Reinsertion Backward, simi-

lar to the ﬁrst one but the removed client is reinserted

in a previous position.

In the next section, we present the proposed

data mining hybrid heuristic for the 1-PDTSP,

called DM-GRASP/VND, which is a hybrid ver-

sion of the GRASP/VND metaheuristic presented in

(Hernández-Pérez et al., 2009) with a data mining

technique.

4 THE HYBRID DATA MINING

PROPOSAL: DM-GRASP/VND

The data mining area offers several techniques to ex-

tract patterns and rules from databases. Among them,

Frequent Itemset Mining (FIM) techniques extracts

subsets of items that appear frequently in a dataset

of transactions, where each transaction is a subset of

elements from the application domain.

In this work, the dataset is a set of sub-optimal

solutions, also called an elite set. Each transaction

corresponds to a solution of the 1-PDTSP. The main

idea is to use a FIM technique to mine patterns from

the elite set and use them to guide the construction of

new solutions.

The proposed hybrid DM-GRASP/VND heuristic

is divided into two main phases. The ﬁrst one is called

the elite set generation phase and consists of execut-

ing n pure GRASP/VND iterations which generate a

set of different solutions, storing the d best solutions

in the elite set. For this reason, the elite set can be

viewed as a long term memory added to the original

GRASP/VND heuristic.

Having built the elite set, an intermediate step is

executed to apply a FIM technique and obtain the pat-

terns. At this point, it is important to remember that

a solution of the 1-PDTSP is a sequence of elements

and their order is important, which makes the use of

a FIM technique not directly applicable. To allow the

use of a FIM technique, we propose to transform the

solutions of the elite set in a way that each solution

is represented by a set of elements, but without losing

its sequence.

For each pair of consecutive clients (i and j) from

a solution, an arc (i, j) is generated, mapping each so-

lution to a set of arcs. After that, we can apply a FIM

technique to mine patterns over the elite set, selecting

the l p largest patterns. Each pattern mined consists

of a group of arcs that appeared together in at least

sup

min

solutions of the elite set, a parameter known as

minimum support. The quantity and size of the mined

patterns may vary according to this parameter.

Inside a pattern, an arc (i, j) has an origin client

i and a destination client j. Moreover, one can ﬁnd

that, in the same pattern, two or more arcs may be

consecutive and can be easily connected to set up a

bigger route segment, named path segment (PS). This

way, each pattern is made of one or more PS.

The second phase of the DM-GRASP/VND pro-

posed consists of executing other n iterations, replac-

ing the original construction phase by an adapted con-

struction which uses the patterns extracted in the ﬁrst

phase to build new solutions.

Algorithm 2 presents the adapted construction. In

each construction, one pattern p from the l p patterns

is selected in a round-robin way (line 2). After that,

one PS from p is chosen, ps (line 3). In the ﬁrst use

of p, we chose the largest PS, in the second, the next

largest one, and so on.

Once ps is chosen, the construction is guided as

follows. We identify all the solutions from the elite set

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

398

Algorithm 2: Adapted construction using mined pat-

terns.

1: AdaptedConstruction( listOfPatterns, ES)

2: p ← SelectPattern(listOfPatterns);

3: ps ← SelectPS(p);

4: s

cho

← SelectSolutionWithPS(ps,ES);

5: s ← ExtractSubroute(ps,s

cho

);

6: s ← ConstructionGRASP(s);

7: return s;

that contains ps as a subroute and choose one at ran-

dom, s

cho

(line 4). The solution s to be built initially

receives a part of s

cho

which holds all clients from the

depot until the end of ps on s

cho

(line 5). From now

on, a distinct route is built, inserting unvisited clients

at the end of the solution, applying the same idea of

the original constructive heuristic (line 6).

Algorithm 3 presents the hybrid heuristic with

data mining. The main modiﬁcation regarding Al-

gorithm 1 is represented by lines 9, 11, and 13. It

is possible to see that this algorithm consists of two

loops that are almost identical to the main loop of

Algorithm 1, using half the number of iterations in

each one. The elite set is built in the ﬁrst loop (line

9), the data mining process is called between those

loops (line 11) and the new construction heuristic is

performed in the second phase (line 13).

Algorithm 3: Hybrid heuristic with data mining.

1: DM-GRASP/VND ( maxIter, sup

min

, d, l p)

2: f (s

∗

) ← ∞; ES ←

3: for iter = 1 until maxIter/2 do

4: s ← ConstructionGRASP();

5: s ← V ND

(s);

6: if s is feasible and f (s) < f (s

∗

) then

7: s

∗

← s ;

8: end if;

9: UpdateEliteSet(s,ES,d);

10: end for;

11: listOfPatterns ← Mine(ES,sup

min

,l p);

12: for iter = 1 until maxIter/2 do

13: s ← AdaptedConstruction(listOfPatterns,ES);

14: s ← V ND

(s);

15: if s is feasible and f (s) < f (s

∗

) then

16: s

∗

← s ;

17: end if;

18: end for;

19: s

∗

← V ND

∗

);

20: return s

∗

;

In the next section we present the computational

experiments conducted with both GRASP/VND and

DM-GRASP/VND strategies.

5 COMPUTATIONAL RESULTS

In this section, the computational results obtained for

GRASP/VND and the proposed DM-GRASP/VND

are presented and compared. Since the GRASP/VND

original implementation was not available, we had to

develop it based on (Hernández-Pérez et al., 2009).

Both heuristics were coded in C++, using the g++

version 4.6.3 compiler and all tests were carried out

on a personal computer with Intel

Core

i5 CPU

650 @ 3.20GHz with 4GB RAM and running Linux

Fedora version 15. The parallel capability of the pro-

cessor was not used.

In order to evaluate the algorithms, we used a set

of instance problems for the 1-PDTSP provided by

(Hernández-Pérez et al., 2009). This set contains a

few randomly generated instances from 100 to 500

clients, using a vehicle capacity equal to 10. These

instances are the biggest in terms of number of clients

and the most difﬁcult in terms of vehicle capacity. The

maximum number of iterations (maxIter), the elite

set size (d), the minimum support value (sup

min

) and

the number of patterns selected (l p) are, respectively,

200, 10, 20% and 10. Except for the number of the

iterations, which was chosen according to the original

parameter reported in (Hernández-Pérez et al., 2009),

the others were deﬁned based on the settings used in

(Plastino et al., 2011).

The remainder of this section is organized thus:

ﬁrst, we compare the computational results obtained

by both strategies and then check whether the dif-

ferences of mean values reached by the evaluated

algorithms are statistically signiﬁcant. Finally, we

present some additional analysis on the computational

experiments to illustrate the behaviour of the DM-

GRASP/VND after the mining step.

5.1 Comparing GRASP/VND and

DM-GRASP/VND

In this section, we report the computational results ob-

tained for the GRASP/VND and DM-GRASP/VND

approaches, comparing the best solutions reached, the

average cost solution values obtained, and the aver-

age running times required by each method. Both

GRASP/VND and DM-GRASP/VND were run 10

times with a different random seed in each run.

In Table 1, the results related to the quality of the

solutions obtained are shown. The ﬁrst column shows

the instance identiﬁer. The second and ﬁfth columns

have the best cost values obtained by the original

and the DM-GRASP/VND approaches, respectively.

The third and seventh columns present the average

cost values obtained by them. The fourth and ninth

ExtendingtheHybridizationofMetaheuristicswithDataMiningtoaBroaderDomain

399

Table 1: Computational results for GRASP/VND and DM-GRASP/VND.

Instances

GRASP/VND DM-GRASP/VND

Best Average Average Best Diff % Average Diff % Average Diff %

Solution Solution Time (s) Solution Best Solution Average Time (s) Time

n100q10A 12369 12514.4 4.01 11915 -3.67 12375.5 -1.11 2.97 -25.98

n100q10B 13668 13885.7 3.86 13596 -0.53 13823.1 -0.45 2.77 -28.07

n100q10C 14619 14810.8 4.01 14310 -2.11 14603.0 -1.40 2.85 -28.92

n100q10D 14806 14993.4 4.15 14666 -0.95 14772.7 -1.47 3.12 -24.76

n100q10E 12594 12819.7 3.94 12018 -4.57 12587.1 -1.81 2.63 -33.27

n100q10F 12082 12297.2 3.57 11891 -1.58 12125.1 -1.40 2.67 -25.24

n100q10G 12344 12623.4 3.84 12176 -1.36 12481.5 -1.12 2.71 -29.56

n100q10H 13405 13590.7 3.72 13362 -0.32 13459.8 -0.96 2.68 -27.93

n100q10I 14512 14715.9 3.74 14514 0.01 14698.0 -0.12 2.60 -30.58

n100q10J 13700 13992.0 4.00 13713 0.09 13905.9 -0.62 2.99 -25.28

Group Average -1.50 -1.05 -27.96

n200q10A 18707 19053.1 34.34 18319 -2.07 18725.7 -1.72 24.00 -30.10

n200q10B 19046 19406.7 33.27 18689 -1.87 19273.4 -0.69 21.90 -34.18

n200q10C 17445 17740.2 37.19 17430 -0.09 17630.7 -0.62 27.45 -26.17

n200q10D 22428 22772.4 33.65 22047 -1.70 22524.4 -1.09 22.69 -32.58

n200q10E 20409 20738.2 36.77 20323 -0.42 20639.7 -0.47 24.63 -33.02

n200q10F 22483 22709.4 37.10 22295 -0.84 22615.9 -0.41 27.22 -26.63

n200q10G 18585 18855.3 34.72 18147 -2.36 18735.5 -0.64 21.81 -37.16

n200q10H 22165 22588.2 39.85 21907 -1.16 22348.4 -1.06 26.65 -33.12

n200q10I 19533 19859.3 34.22 19362 -0.88 19504.1 -1.79 22.76 -33.47

n200q10J 20179 20471.6 32.80 20011 -0.83 20244.1 -1.11 23.15 -29.42

Group Average -1.22 -0.96 -31.59

n300q10A 24942 25148.1 136.01 24392 -2.21 24738.4 -1.63 92.17 -32.23

n300q10B 24413 24802.3 133.15 24347 -0.27 24595.0 -0.84 89.63 -32.68

n300q10C 23212 23418.2 142.24 22838 -1.61 23170.2 -1.06 92.90 -34.69

n300q10D 27080 27614.3 147.46 26325 -2.79 27113.1 -1.82 99.18 -32.74

n300q10E 28643 28914.2 147.16 27980 -2.31 28425.1 -1.69 99.90 -32.11

n300q10F 25843 26213.9 143.07 25592 -0.97 25895.3 -1.22 108.49 -24.17

n300q10G 25631 25814.5 144.66 25105 -2.05 25413.8 -1.55 108.70 -24.86

n300q10H 23590 23795.3 138.41 23143 -1.89 23512.1 -1.19 93.02 -32.79

n300q10I 26018 26358.4 136.85 25444 -2.21 25965.2 -1.49 94.40 -31.02

n300q10J 24050 24466.0 140.90 23806 -1.01 24139.1 -1.34 98.85 -29.84

Group Average -1.73 -1.38 -30.71

n400q10A 33087 33266.8 393.04 32170 -2.77 32620.1 -1.94 282.19 -28.20

n400q10B 26677 26797.2 347.47 26107 -2.14 26395.1 -1.50 246.68 -29.01

n400q10C 30394 30682.2 399.14 29838 -1.83 30235.7 -1.46 269.07 -32.59

n400q10D 25814 26267.5 400.79 25291 -2.03 25750.1 -1.97 264.62 -33.98

n400q10E 26795 27313.9 355.53 26393 -1.50 26824.5 -1.79 260.04 -26.86

n400q10F 28107 28910.0 361.85 28188 0.29 28539.2 -1.28 256.23 -29.19

n400q10G 25697 26220.6 398.57 25113 -2.27 25492.7 -2.78 279.50 -29.88

n400q10H 27158 27773.1 393.40 26813 -1.27 27238.1 -1.93 278.53 -29.20

n400q10I 30115 30898.7 387.77 30208 0.31 30549.5 -1.13 263.87 -31.95

n400q10J 27655 28059.0 383.00 26921 -2.65 27536.1 -1.86 268.10 -30.00

Group Average -1.59 -1.76 -30.08

n500q10A 29874 30661.4 825.94 29558 -1.06 30246.4 -1.35 579.69 -29.82

n500q10B 28559 29042.9 846.08 28253 -1.07 28583.9 -1.58 573.82 -32.18

n500q10C 32360 33162.5 867.24 32065 -0.91 32569.1 -1.79 577.93 -33.36

n500q10D 32750 33074.3 863.71 32117 -1.93 32484.5 -1.78 593.99 -31.23

n500q10E 32298 32667.1 881.04 31704 -1.84 32263.6 -1.24 598.28 -32.09

n500q10F 30856 31354.6 813.26 30432 -1.37 30991.2 -1.16 511.36 -37.12

n500q10G 28879 29123.4 885.22 28357 -1.81 28642.5 -1.65 597.69 -32.48

n500q10H 38579 39023.5 849.81 37926 -1.69 38350.5 -1.72 596.57 -29.80

n500q10I 32718 33217.7 858.72 32330 -1.19 32624.5 -1.79 547.15 -36.28

n500q10J 32407 33131.7 873.12 32530 0.38 32720.7 -1.24 576.76 -33.94

Group Average -1.25 -1.53 -32.83

Overall Average -1.46 -1.34 -30.63

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

400

columns show the average execution time (in sec-

onds) for the GRASP/VND and DM-GRASP/VND.

The sixth, eighth and tenth columns report the per-

centual difference (Diff %) of the DM-GRASP/VND

over the GRASP/VND for each criteria, as evaluated

by Equation 8.

Di f f % =

DM-GRASP/VND − GRASP/VND

GRASP/VND

(8)

The intermediate rows show the partial averages

of the percentual differences for each group of the

same size instances and the last row of the table

presents the overall average of the percentual differ-

ences. The smallest values considering the best solu-

tion, the average solution and the average time, i.e.,

the best results among them, are bold-faced.

These results show that the proposed DM-

GRASP/VND method produced better solutions in

less computational time for almost all instances. Only

in ﬁve out of 50 instances, the DM-GRASP/VND did

not outperform GRASP/VND in terms of best solu-

tion found, giving an overall percentual difference of

1.46%, and being on average 30.63% faster than the

original method. In terms of average quality of the

solution, the average percentual difference between

these heuristics was of 1.34%.

There are two main reasons for the faster be-

haviour of DM-GRASP/VND. First, the adapted con-

struction is faster than the original one because it uses

a subroute of an existing high-quality solution. Sec-

ondly, the quality of the solutions constructed after the

data mining process is usually better than that of the

original construction and, therefore, makes the local

search effort considerably smaller.

5.2 Analysis of Statistical Signiﬁcance

In order to verify whether or not the differences

of mean values obtained by the evaluated strategies

shown in Table 1 are statistically signiﬁcant, we em-

ployed the Non-parametric Friedman test technique

(Siegel and Castellan Jr, 1988), with a p-value equal

to 0.05. This test is usually applied to compare al-

gorithms with some random features and identify if

the difference in performance between them is due to

random causes.

Table 2 shows the number of better average so-

lutions found by each strategy, for each group of the

same size instances. The number of cases where p-

value is less than 0.05 is shown in brackets. When

comparing DM-GRASP/VND with GRASP/VND,

we see that the DM-GRASP/VND obtained the best

result for all the instances and, in almost all cases, the

difference is statistically signiﬁcant. These results in-

dicate the superiority of the proposed strategy.

Table 2: Analysis of statistical signiﬁcance.

Algorithm

Instance Group

n100 n200 n300 n400 n500

GRASP/VND 0 (0) 0 (0) 0 (0) 0 (0) 0 (0)

DM-GRASP/VND 10(6) 10(4) 10(7) 10(9) 10(8)

The Wilcoxon-Mann-Whitney non-parametric

test was also applied to check if the DM-

GRASP/VND method could ﬁnd better solutions

than the original approach. According to (Siegel and

Castellan Jr, 1988), this statistical test is commonly

used when two independent samples are analysed

and whenever it is necessary to have a statistical

test to reject the null hypothesis (i.e., there are no

signiﬁcant differences between these two samples),

with a signiﬁcance level of α (i.e., it is possible to

reject the null hypothesis with the probability of

(1 − α) × 100%). Two hypotheses were used in this

test:

• null hypothesis (H0): there are no signiﬁcant dif-

ferences between the solutions found by DM-

GRASP/VND and the original method; and

• alternative hypothesis (H1): there are signiﬁcant

differences between the solutions found by DM-

GRASP/VND and the original algorithm.

Considering the results shown in Table 1, using

the R package (The R Project for Statistical Comput-

ing, 2013), it is possible to reject H0 with α = 2.2 ×

−16

. Thus, with a probability greater than 99%, we

can conclude that there are signiﬁcant differences be-

tween the solutions found by DM-GRASP/VND and

GRASP/VND heuristics.

5.3 Complementary Analysis

Figures 1 and 2 illustrate the behaviour of the

construction and local search phases, for both

GRASP/VND and DM-GRASP/VND, in terms of the

solution cost values obtained, along the execution of

1000 iterations for the n500q10G instance with a spe-

ciﬁc random seed. We could see that, as the 1-PDTSP

is a minimization problem, the local search reduces

the cost of the solution obtained by the construction

phase.

In Figure 1, we notice that the GRASP/VND

heuristic behaves similarly throughout the iterations.

Furthermore, we could also see that the GRASP/VND

and the DM-GRASP/VND (see Figure 2) has exactly

the same behaviour until the 500th iteration, where

the data mining procedure is executed. From this

ExtendingtheHybridizationofMetaheuristicswithDataMiningtoaBroaderDomain

401

point on, the quality of the solutions obtained by DM-

GRASP/VND, both in construction and local search

procedures, is improved.

50000

100000

150000

200000

250000

300000

350000

0 500 1000

Cost

Iteration

Construction

Local Search

Figure 1: Cost X iteration plot of GRASP/VND for instance

n500q10G.

50000

100000

150000

200000

250000

300000

350000

0 500 1000

Cost

Iteration

Construction

Local Search

Figure 2: Cost X iteration plot of DM-GRASP/VND for

instance n500q10G.

Towards making visible the improvement of the

local search phase after the data mining call, we ex-

panded Figures 1 and 2, as shown in Figures 3 and

4. In them, each algorithm presents the cost of so-

lution obtained along 1000 iterations, but we reduce

the gap in the cost axis for the values from 27000 to

33000. By looking at Figure 3, we can see that the

GRASP/VND heuristic has found only a few solu-

tions with cost less than 29000 throughout the itera-

tions. However, the DM-GRASP/VND approach, af-

ter the 500th iteration, reached several solutions with

cost less than 29000 (see Figure 4). We can also

notice that the DM-GRASP/VND strategy constructs

initial solutions, which are based on the adapted con-

struction method, as good as those already explored

by the local search phase.

27000

28000

29000

30000

31000

32000

33000

0 250 500 750 1000

Cost

Iteration

Construction

Local Search

Figure 3: Cost X iteration enlarged plot of GRASP/VND

for instance n500q10G.

27000

28000

29000

30000

31000

32000

33000

0 250 500 750 1000

Cost

Iteration

Construction

Local Search

Figure 4: Cost X iteration enlarged plot of DM-

GRASP/VND for instance n500q10G.

An additional experiment was run to evalu-

ate the time required for GRASP/VND and DM-

GRASP/VND to achieve a solution as good as a tar-

get solution value. Each strategy was run 100 times

(with different random seeds) until a target solution

cost value was reached for a speciﬁc instance. The

instance n500q10G was used, with the target value

equal to 29123. For each seed, the time (in seconds)

in which the target was reached is plotted, as shown

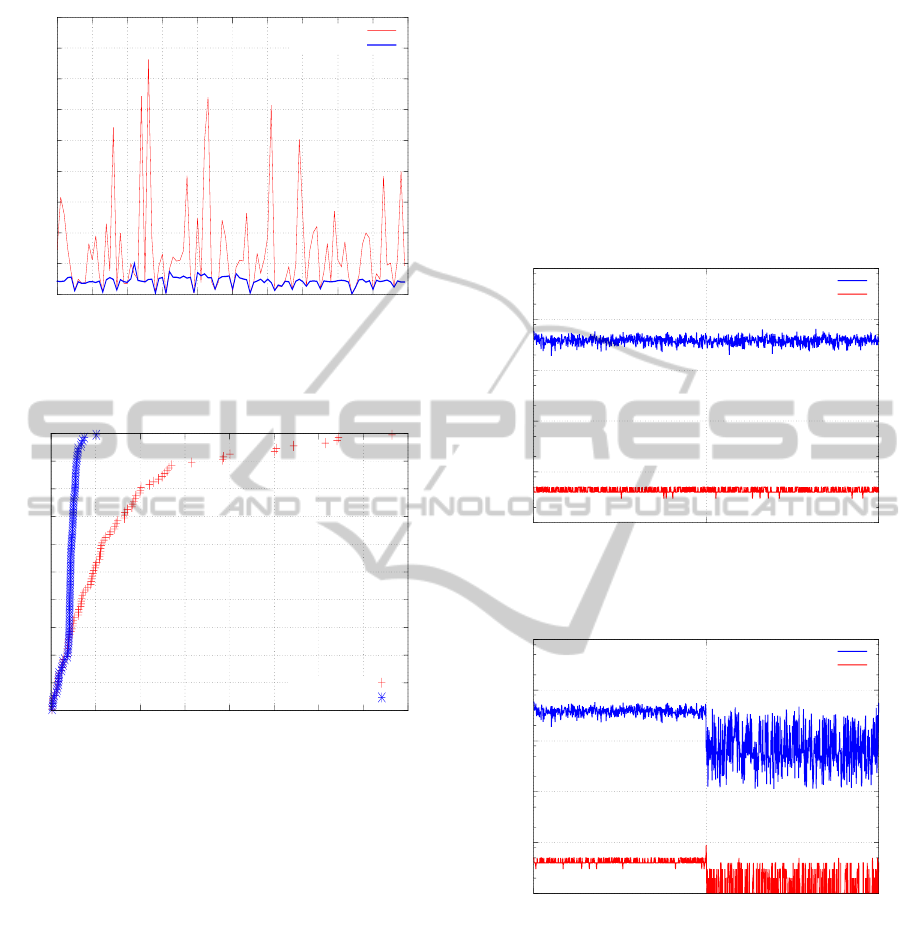
in Figure 5. We see that in almost all executions

the DM-GRASP/VND reached the target before the

GRASP/VND.

Figure 6 presents another comparison between

these algorithms, based on the time-to-target plots

(TTT-plots) (Aiex et al., 2007), which are used to

analyse the behaviour of algorithms with some ran-

dom components. These plots show the cumulative

probability, vertical axis, for an algorithm to reach a

preﬁxed target solution in the indicated running time,

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

402

1000

2000

3000

4000

5000

6000

7000

8000

9000

0 10 20 30 40 50 60 70 80 90 100

Time (s)

Seed

GRASP/VND

DM-GRASP/VND

Figure 5: Analysis of convergence with a target for instance

n500q10G.

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 1000 2000 3000 4000 5000 6000 7000 8000

Cumulative probability

Time to target solution (s)

GRASP/VND

DM-GRASP/VND

Figure 6: Time-to-target plot for a target for instance

n500q10G.

as deﬁned by the horizontal axis.

In the TTT-plots experiment, we sorted out the ex-

ecution times required for each algorithm to reach a

solution at least as good as a target solution (these

times were already shown in Figure 5). Then, the i-

th sorted running time, t

, is associated with a prob-

ability p

= (i − 0.5)/100 and points z

= (t

, p

) are

plotted. We see that the proposed strategy outper-

forms the pure GRASP/VND. The cumulative proba-

bility for DM-GRASP/VND to ﬁnd, for example, the

preﬁxed target in 1000 seconds is almost 100% while

the same probability for the pure GRASP/VND is of

about 55%.

Figures 7 and 8 illustrate the running time spent

by the construction and the local search phases

of both algorithms evaluated for the n500q10G in-

stance. While the computational time required by the

GRASP/VND for both construction and local search

phases is the same throughout the iterations (see Fig-

ure 7), the hybrid DM-GRASP/VND method man-

aged a signiﬁcant time reduction after the 500th iter-

ation, when the data mining call occurs. This time

reduction, seen in Figure 8, for both construction

and local search phases, corroborates the fact that the

adapted construction is faster than the original con-

struction. It also shows that the local search bene-

ﬁts from the patterns making the DM-GRASP/VND

strategy converge faster.

0.001

0.01

0.1

100

0 500 1000

Time (s)

Iteration

Local Search

Construction

Figure 7: Time X iteration plot of one execution of

GRASP/VND for instance n500q10G.

0.001

0.01

0.1

100

0 500 1000

Time (s)

Iteration

Local Search

Construction

Figure 8: Time X iteration plot of one execution of DM-

GRASP/VND for instance n500q10G.

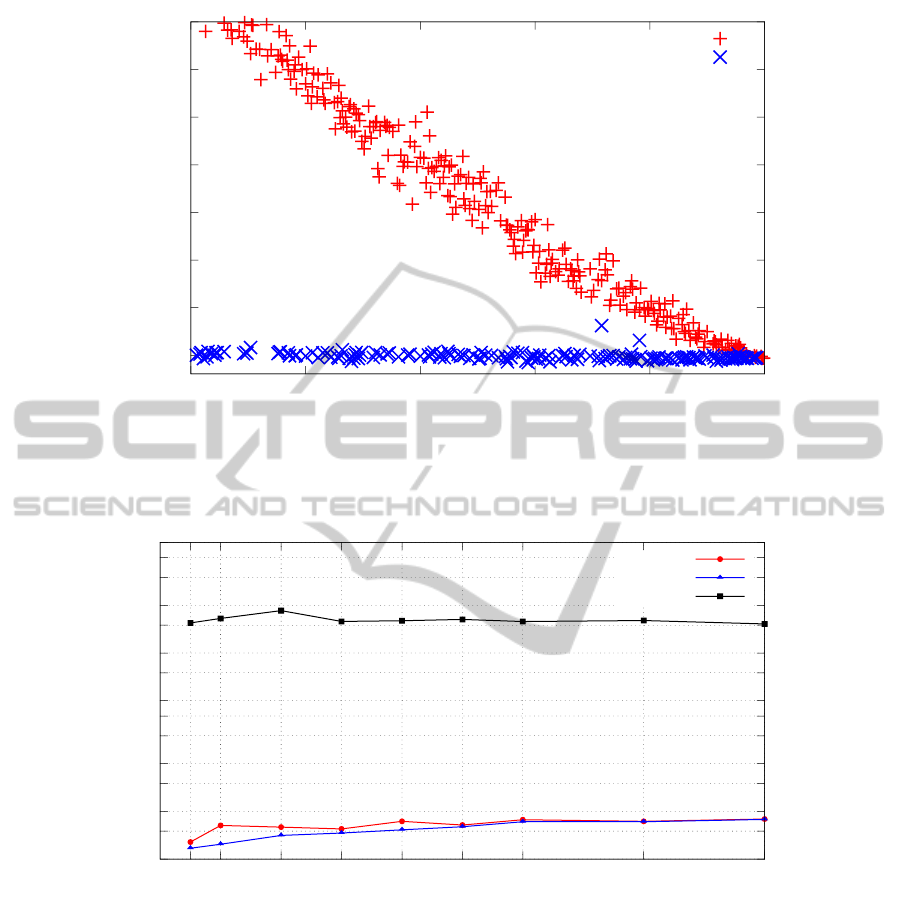
In Figure 9, we analyze the impact of ﬁxing clients

in the adapted construction, which depends on how

far from the depot a pattern is ﬁxed, i.e., patterns

far from the depot ﬁx more clients in the adapted

construction, while patterns closer to the depot ﬁx

less clients. This ﬁgure indicates that the larger the

amount of clients ﬁxed, the smaller the cost of the so-

lution is.

In the last experiment, each strategy was run with

100, 200, 400, 600, 800, 1000, 1200, 1600, and 2000

iterations, evaluating the best solution, average qual-

ExtendingtheHybridizationofMetaheuristicswithDataMiningtoaBroaderDomain

403

30000

40000

50000

60000

70000

80000

90000

100000

0 100 200 300 400 500

Cost

Number of ﬁxed clients

Construction

Local Search

Figure 9: Solution cost with different number of ﬁxed clients in the construction phase for instance n500q10G.

1.5

100

100 200 400 600 800 1000 1200 1600 2000

Percentual diﬀerence (%)

Iteration

Percentual diﬀerence over GRASP/VND

Best

Average

Time

Figure 10: Variating number of iterations.

ity of the solution and computing time for execution.

Figure 10 shows the percentual difference of DM-

GRASP/VND over GRASP/VND for each of the cri-

teria. We see that the percentual difference for best

solution and average quality of solution rose as more

iterations were performed, stabilizing apparently only

after 1200 iterations. As regards execution time, the

percentual difference varies slightly, though always

remaining above 30%.

6 CONCLUSIONS

The hybridization of GRASP heuristics with data

mining techniques has been successfully applied to

different combinatorial optimization problems. Until

now, all the problems explored had in common the

fact that their solutions were characterized by a set

of elements. We showed, as the main contribution of

this work, that this hybridization can also be applied

to problems in which solutions are represented by a

sequence of elements.

In this work we developed a hybrid data mining

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

404

heuristic for the 1-PDTSP (called DM-GRASP/VND)

by incorporating a frequent itemset mining technique

into a GRASP/VND existing algorithm, as presented

in (Hernández-Pérez et al., 2009). The experimen-

tal results showed that the DM-GRASP/VND method

outperformed the GRASP/VND strategy as the for-

mer was able to obtain better solutions in less compu-

tational time.

As future work, the goal is to implement a multi-

mining version of the DM-GRASP/VND, running

the data mining procedure more than once. This

idea, successfully applied in other hybrid data min-

ing strategies (Barbalho et al., 2013; Plastino et al.,

2013), consists of executing the data mining method

whenever the elite set becomes stable.

ACKNOWLEDGEMENTS

The authors would like to thank CNPq and CAPES

for the partial support of this research work.

REFERENCES

Agrawal, R. and Srikant, R. (1994). Fast algorithms for

mining association rules. In Proceedings of 20

In-

ternational Conference on VLDB, pages 487–499.

Aiex, R. M., Resende, M. G. C., and Ribeiro, C. C. (2007).

Ttt plots: A perl program to create time-to-target

plots. Optimization Letters, 1:355–366.

Barbalho, H., Rosseti, I., Martins, S. L., and Plastino,

A. (2013). A hybrid data mining GRASP with

path-relinking. Computers & Operations Research,

40:3159–3173.

Berger, D., Gendron, B., Potvin, J.-Y., Raghavan, S., and

Soriano, P. (2000). Tabu search for a network loading

problem with multiple facilities. Journal of Heuris-

tics, 6:253–267.

Feo, T. A. and Resende, M. G. C. (1995). Greedy random-

ized adaptive search procedures. Journal of Global

Optimization, 6:109–133.

Festa, P. and Resende, M. G. C. (2009a). An annotated bib-

liography of GRASP part I: Algorithms. International

Transactions in Operational Research, 16:1–24.

Festa, P. and Resende, M. G. C. (2009b). An annotated bib-

liography of GRASP part II: Applications. Interna-

tional Transactions in Operational Research, 16:131–

172.

Fleurent, C. and Glover, F. (1999). Improved construc-

tive multistart strategies for the quadratic assignment

problem using adaptive memory. INFORMS Journal

on Computing, 11:198–204.

Gendreau, M. and Potvin, J.-Y. (2010). Handbook of Meta-

heuristics, volume 146 of International Series in Op-

erations Research & Management Science. Springer,

2nd edition.

Goethals, B. and Zaki, M. J. (2003). Advances in fre-

quent itemset mining implementations: Introduction

to FIMI03. In Goethals, B. and Zaki, M. J., editors,

Frequent Itemset Mining Implementations (FIMI’03),

Proceedings of the ICDM 2003 Workshop on Frequent

Itemset Mining Implementations. Melbourne, Florida,

USA. Available in http://CEUR-WS.org/Vol-90.

Han, J. and Kamber, M. (2011). Data Mining: Concepts

and Techniques. Morgan Kaufmann Publishers, 3rd

edition.

Han, J., Pei, J., and Yin, Y. (2000). Mining frequent pat-

terns without candidate generation. SIGMOD Record,

29:1–12.

Hernández-Pérez (2004). Travelling salesman problems

with pickups and deliveries. PhD thesis, University

of La Laguna, Spain.

Hernández-Pérez, H. and Salazar-González, J. (2004a).

A branch-and-cut algorithm for a traveling salesman

problem with pickup and delivery. Discrete Applied

Mathematics, 145:453–459.

Hernández-Pérez, H. and Salazar-González, J. (2004b).

Heuristics for the one commodity pickup-and-delivery

traveling salesman problem. Transportation Science,

38:245–255.

Hernández-Pérez, H. and Salazar-González, J. (2007). The

one-commodity pickup-and-delivery traveling sales-

man problem: Inequalities and algorithms. Networks,

50:258–272.

Hernández-Pérez, H., Salazar-González, J., and Rodríguez-

Martín, I. (2009). A hybrid GRASP/VND heuris-

tic for the one-commodity pickup-and-delivery travel-

ing salesman problem. Computers & Operations Re-

search, 36:1639–1645.

Martinovic, G., Aleksi, I., and Baumgartner, A. (2008).

Single-Commodity Vehicle Routing Problem with

Pickup and Delivery Service. Mathematical Problems

in Engineering, pages 1–18.

Mladenovi

c, N. and Hansen, P. (1997). Variable neigh-

borhood search. Computers & Operations Research,

24:1097–1100.

Mladenovi

c, N., Uroševi

c, D., Hanaﬁ, S., and Ili

c, A.

(2012). A general variable neighborhood search

for the one-commodity pickup-and-delivery travelling

salesman problem. European Journal of Operational

Research, 220:270–285.

Paes, B. C., Subramanian, A., and Ochi, L. S. (2010). Uma

heurística híbrida para o problema do caixeiro via-

jante com coleta e entrega envolvendo um único tipo

de produto. In Anais do XLII Simpósio Brasileiro

de Pesquisa Operacional, pages 1513–1524. (In Por-

tuguese).

Plastino, A., Barbalho, H., Santos, L., Fuchshuber, R., and

Martins, S. (2013). Adaptive and multi-mining ver-

sions of the DM-GRASP hybrid metaheuristic. Jour-

nal of Heuristics, pages 1–36.

Plastino, A., Fonseca, E. R., Fuchshuber, R., Martins, S. L.,

Freitas, A. A., Luis, M., and Salhi, S. (2009). A hybrid

data mining metaheuristic for the p-median problem.

In Proceedings of the SIAM International Conference

on Data Mining, pages 305–316.

ExtendingtheHybridizationofMetaheuristicswithDataMiningtoaBroaderDomain

405

Plastino, A., Fuchshuber, R., Martins, S. L., Freitas, A. A.,

and Salhi, S. (2011). A hybrid data mining meta-

heuristic for the p-median problem. Statistical Analy-

sis and Data Mining, 4:313–335.

Resende, M. G. C. and Ribeiro, C. C. (2005). GRASP with

path-relinking: Recent advances and applications. In

Ibaraki, T., Nonobe, K., and Yagiura, M., editors,

Metaheuristics: Progress as Real Problem Solvers,

volume 32 of Operations Research/Computer Science

Interfaces Series, pages 29–63. Springer.

Ribeiro, M. H., Plastino, A., and Martins, S. L. (2006). Hy-

bridization of GRASP metaheuristic with data mining

techniques. Journal of Mathematical Modelling Algo-

rithms, 5:23–41.

Ribeiro, M. H., Trindade, V. F., Plastino, A., and Martins,

S. L. (2004). Hybridization of GRASP metaheuristics

with data mining techniques. In Proceedings of the

ECAI workshop on hybrid metaheuristics, pages 69–

78.

Santos, H. G., Ochi, L. S., Marinho, E. H., and Drummond,

L. M. A. (2006a). Combining an evolutionary algo-

rithm with data mining to solve a single-vehicle rout-

ing problem. Neurocomputing, 70:70–77.

Santos, L. F., Martins, S. L., and Plastino, A. (2008).

Applications of the DM-GRASP heuristic: a survey.

International Transactions in Operational Research,

15:387–416.

Santos, L. F., Milagres, R., Albuquerque, C. V., Martins,

S. L., and Plastino, A. (2006b). A hybrid GRASP with

data mining for efﬁcient server replication for reliable

multicast. In Proceedings of the IEEE GLOBECOM

conference, pages 1–6.

Santos, L. F., Ribeiro, M. H., Plastino, A., and Martins,

S. L. (2005). A hybrid GRASP with data mining for

the maximum diversity problem. In Proceedings of

the International Workshop on Hybrid Metaheuristics,

volume 3636 of Lecture Notes in Computer Science,

pages 116–127, Barcelona, Spain.

Siegel, S. and Castellan Jr, N. J. (1988). Nonparametric

Statistics for the Behavioral Sciences. McGraw-Hill,

2nd edition.

Talbi, E.-G. (2002). A taxonomy of hybrid metaheuristics.

Journal of Heuristics, 8:541–564.

The R Project for Statistical Computing (2013).

http://www.r-project.org/, last visit in 10/18/2013.

Zhao, F., Li, S., Sun, J., and Mei, D. (2009). Genetic al-

gorithm for the one-commodity pickup-and-delivery

traveling salesman problem. Computers & Industrial

Engineering, 56:1642–1648.

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

406