
TrieMotif
A New and Efficient Method to Mine Frequent K-Motifs from Large Time Series
Daniel Y. T. Chino
1
, Renata R. V. Gonc¸alves
2
, Luciana A. S. Romani
2
,
Caetano Traina Jr.
1
and Agma J. M. Traina
1
1
Institute of Mathematics and Computer Science, University of S
˜
ao Paulo, S
˜
ao Carlos, Brazil
2
Cepagri-Unicamp, Campinas, Brazil
3
Embrapa Agriculture Informatics, Campinas, Brazil
Keywords:
Time Series, Frequent K-Motif, AVHRR-NOAA Images.
Abstract:
Finding previously unknown patterns that frequently occur on time series is a core task of mining time series.
These patterns are known as time series motifs and are essential to associate events and meaningful occurrences
within the time series. In this work we propose a method based on a trie data structure, that allows a fast and
accurate time series motif discovery. From the experiments performed on synthetic and real data we can see
that our TrieMotif approach is able to efficiently find motifs even when the size of the time series goes longer,
being in average 3 times faster and requiring 10 times less memory than the state of the art approach. As a
case study on real data, we also evaluated our method using time series extracted from remote sensing images
regarding sugarcane crops. Our proposed method was able to find relevant patterns, as sugarcane cycles and
other land covers inside the same area.
1 INTRODUCTION
The large volume of time series continually generated
by a variety of sensors, climate models and stock mar-
kets demands fast methods to take advantage of such
amount of data. The information contained in time
series databases is a rich source for decision making
tasks demanded by the owners of such data. One of
the main tasks when mining time series is to find the
motifs present therein, that is, to find patterns that fre-
quently occurs in time series. By finding motifs, it
is possible to mine association rules aimed at spotting
patterns indicating that some events frequently lead to
others.
Existing applications involving time series, such
as stock market analysis, are not yet able to record all
the factors that govern the data organized in the time
series, such as political and technological factors. On
the contrary, climate variations nowadays have most
of its governing factors being recorded, using sens-
ing equipments such as satellites and ground-based
weather stations. However, the diversity of data avail-
able makes it hard to discover complex patterns that
can support more robust analyzes. In this scenario,
finding motifs assumes an even greater importance.
In this work we took advantage of real time se-
ries extracted from remote sensing imagery contain-
ing Normalized Difference Vegetation Index (NDVI)
measurements. The NDVI time series present the veg-
etative strength of the plantation (Rouse et al., 1973).
To follow the development of a crop is strategic for
agribusiness practices in Brazil, since agriculture is
the country’s main asset. The accurate monitoring of
agriculture in the whole world have become more and
more important specially due to climate change im-
pacts. The “food safety” issue has concerned gov-
ernments from several countries and the development
of new technologies for monitoring, as well as the
proposition of mitigation and adaptation measures,
are crucial. In this sense, remote sensing can be an im-
portant tool to improve the fast detection of changes
in the land cover besides to aid at monitoring the crop
cycle.
Since the volume of time series databases as well
as the length of the series is growing at a very fast
pace, it is mandatory to develop algorithms and meth-
ods that can deal with time series in the scenario of
big data. In this paper we present a new method to
extract motifs from time series and a new algorithm
to index them in a trie data structure that performs
well over large time series, which is up to 3 times
faster than the state-of-the-art method. We evaluated
60
Chino D., Gonçalves R., Romani L., Traina Jr. C. and Traina A..
TrieMotif - A New and Efficient Method to Mine Frequent K-Motifs from Large Time Series.
DOI: 10.5220/0004891900600069
In Proceedings of the 16th International Conference on Enterprise Information Systems (ICEIS-2014), pages 60-69
ISBN: 978-989-758-027-7
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

the proposed TrieMotif over both synthetic and real
time series and obtained very promising results.
This paper is organized as follows. Section 2 sum-
marizes the main concepts used as the basis to de-
velop our work. Section 3 describes our proposed
method and Section 4 discusses its evaluation. Sec-
tion 5 shows the TrieMotif performance on real data
obtained from remote sensing images and Section 6
concludes this paper.
2 BACKGROUND AND RELATED
WORKS
A time series motif is a pattern that occur frequently.
They were first defined in (Lin et al., 2002) and a gen-
eralized definition was given in (Chiu et al., 2003). In
this section we recall these definitions and notations,
as they will be used in this paper. First we begin with
a definition of time series:
Definition 1. Time Series: A time series T =
t
1
, . . . ,t
m
is an ordered set of m real-valued variables.
Since we want to find patterns that frequently oc-
cur along a time series, we will not work with the
whole time series, we are aiming only at parts of a
time series, which are called subsequences and are de-
fined as follows.
Definition 2. Subsequence: Given a time series T
of length m, a subsequence S
p
of T is a sampling
of length n < m of contiguous positions from T be-
ginning at position p, that is, S
p
= t
p
, . . . ,t
p+n−1
for
1 ≤ p ≤ m − n + 1.
In order to find frequent patterns, we need to de-
fine a matching between patterns.
Definition 3. Match: Given a distance function
D(S
p
, S
q
) between two subsequences, a positive real
number R (range) and a time series T containing a
subsequence S
p
and a subsequence S
q
, if D(S
p
, S
q
) ≤
R then S
q
is called a matching subsequence of S
p
.
On subsequences of the same time series, the best
matches are probably subsequences that are slightly
shifted. Matching between two overlapped subse-
quences is called a trivial match. Figure 1 illustrates
the idea of a trivial match. The trivial match is defined
as follows:
Definition 4. Trivial Match: Given a time series T ,
containing a subsequence S
p
and a matching subse-
quence S
q
, we say that S
q
is a trivial match to S
p
if ei-
ther p = q or if there is no subsequence S
q
0
beginning
at q
0
such that D(S
p
, S
q
0
) > R, and either q < q
0
< p
or p < q
0
< q. That is, if two subsequences overlaps,
-30
-20
-10
0
10
20
30
0 20 40 60 80 100 120 140 160 180
Time
S
q
Trivial Match
Figure 1: The best matches of a subsequence S
q
are proba-
bly the trivial matches that occur right before or after S
q
.
there must exist a subsequence between them that is
not a match.
These definitions allow defining the Frequent K-
Motif problem. First, all subsequences are extracted
using a sliding window. Then, since we are inter-
ested in patterns, each subsequence is z-normalized
to have zero mean and one standard deviation (Keogh
and Kasetty, 2003). The K-Motif is defined as fol-
lows.
Definition 5. Frequent K-Motifs: Given a time series
T , a subsequence of length n and a range R, the most
significant motif in T (1-Motif ) is the subsequence
F
{1}
that has the highest count of non-trivial matches.
The K
th
most significant motif in T (K-Motif ) is the
subsequence F
{K}
that has the highest count of non-
trivial matches, and satisfies D(F
{K}
, F
{i}
) > 2R, for
all 1 ≤ i < K.
The Nearest Neighbor motif was defined by
Yankov et al. (Yankov et al., 2007), and it represents
the closest pair of subsequences. In our proposed
work, we focus on the Frequent K-Motif problem and
we will be referring to them as K-Motif. Since the K-
Motifs are unknown patterns, a brute-force approach
would compare every subsequence with each other.
This approach has quadratic computational cost since
it requires O(m
2
) calls to the distance function.
An approach to reduce the complexity of this
problem employs dimensionality reduction and dis-
cretization of the time series (Lin et al., 2002).
The SAX (Symbolic Aggregate approXimation) tech-
nique allows time series of size n to be represented by
strings of arbitrary size w (w < l) (Lin et al., 2003).
For a given time series, SAX consists of the follow-
ing steps. Firstly, the time series is z-normalized, so
that the data follow normal distribution (Goldin et al.,
1995). Next, the normalized time series is converted
into the Piecewise Aggregate Approximation (PAA)
TrieMotif-ANewandEfficientMethodtoMineFrequentK-MotifsfromLargeTimeSeries
61
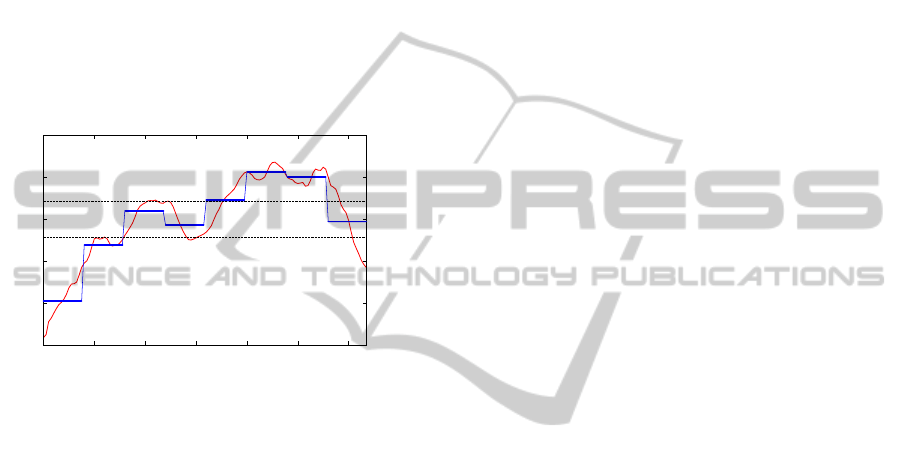
representation, decreasing the time series dimension-
ality (Keogh et al., 2001). The time series is then re-
placed with w values corresponding to the average of
the respective segment. Thus, in the PAA representa-
tion, the time series is divided into w continuous seg-
ments of equal length. Finally, the PAA representa-
tion is discretized into a string with an alphabet of size
a > 2. Figure 2 shows an example of a time series sub-
sequence of size n = 128 discretized using SAX with
w = 8 and a = 3. It is also possible to compare two
SAX time series using the MINDIST function. The
MINDIST lower bounds the Euclidean distance (Lin
et al., 2007), warranting no false dismissals (Falout-
sos et al., 1994).
-3
-2
-1
0
1
2
0 20 40 60 80 100 120
Time
A
B
B
B
A
C
C
C
Figure 2: A time series subsequence of size n = 128 is re-
duced to a PAA representation of size w = 8 and then is
mapped to a string of a = 3 symbols AABBCCCB.
Chiu et al. proposed a fast algorithm based on
Random Projection (Chiu et al., 2003). Each sub-
sequence of a time series is discretized using SAX.
The discretized subsequences are mapped into a ma-
trix, where each row points back to the original po-
sition of the subsequence on the time series. Then,
the algorithm uses the random projection to com-
pute a collision matrix, which counts the frequency
of subsequence pairs. Through the collision matrix,
the subsequences are checked on the original domain
seeking for motifs. Although fast, the collision ma-
trix is quadratic on the length of the time series, re-
quiring a high amount of memory. Also using the
SAX discretization, Li and Lin (Li and Lin, 2010;
Li et al., 2012) proposed a variable length motif dis-
covery based on grammar induction. Catalano et al.
(Catalano et al., 2006) proposed a method that works
on the original domain of the data. The motifs are
discovered in linear time and constant memory costs
using random sampling. However, this approach can
lead to poor performance for long time series with in-
frequent motifs (Mohammad and Nishida, 2009).
Several works proposed to solve the motif discov-
ery problem taking advantage of tree data structures.
Udechukwu et al. proposed an algorithm that uses
a suffix tree to find the Frequent Motif (Udechukwu
et al., 2004). The time series are discretized consid-
ering the slopes between two consecutive measures.
The symbols are chosen according to the angle be-
tween the line joining the two points and the time
axis. Although this algorithm do not require to set
the length of the motif, the algorithm is affected by
noise. A suffix tree was also used to find motifs in
multivariate time series (Wang et al., 2010). Keogh
et al. solved a similar problem to the motif discovery
using a trie structure to find the most unusual subse-
quence in a time series (Keogh et al., 2007).
Our proposed TrieMotif algorithm is up to 3 times
faster and requires up to 10 times less memory than
the state-of-the-art approach, because TrieMotif se-
lects only the candidates that are most probably a
match to a motif. Using this approach, TrieMotif
reduces the number of unnecessary distance calcula-
tions.
3 OUR PROPOSAL: TrieMotif
ALGORITHM
In this section we present the TrieMotif algorithm,
which aims at finding the top K-Motifs. The TrieMo-
tif algorithm consists of three stages:
• First, all subsequences are extracted from the time
series and converted into a symbolic representa-
tion;
• The subsequences are indexed using a Trie and
a list of possible non trivial matches (candidates)
are generated for each subsequence using the Trie
index;
• The distances between the motif candidates on the
original time series are calculated.
On the first stage, all subsequences S
i
of size
n are extracted using a sliding window and are z-
normalized. These subsequences pass through a di-
mensionality reduction process to reduce the compu-
tational cost on the next stage. A subsequence of size
n can be represented as a sequence of size w, via the
PAA algorithm. On the next step of this stage, sub-
sequences are converted into a symbolic representa-
tion. This representation is obtained by dividing the
interval of the subsequence values into a equal size
bins, where each bin receives a symbol. Each value in
the subsequence is converted into the symbol of the
corresponding bin. Figure 3 shows an example that
converts a subsequence S of size m = 128 and val-
ues between [−2.83, 1.36] into a string of size w = 8
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
62

using an alphabet a of 3 symbols. Initially the subse-
quence passes through a dimensionality reduction via
PAA with w = 8. Then, assuming a = 3, three bins are
created: A = [−2.83, −1.43), B = [−1.43, −0.03) and
C = [−0.03, 1.36]. Notice, that we kept the zero mean
and the standard deviation requirements. Finally, the
symbolic representation of S is
ˆ
S = ABCBCCCB.
-3
-2
-1
0
1
2
-20 0 20 40 60 80 100 120
Time
A
B
C
A
B
B
B
C
C
C
C
Figure 3: A time series subsequence of size m = 128 is con-
verted into a string of a = 3 symbols and size w = 8.
To find the top K-Motifs, the brute force algorithm
would calculate the distance of each subsequence S
q
to every other subsequence. Our proposal reduces the
number of distance calculations by selecting only can-
didates S
i
that may be a match – the trivial matches
are discarded on the next stage. To select the candi-
dates we index all subsequences (already represented
as a string) in a trie. For example, consider the subse-
quences S
1
, S
2
, S
3
and S
4
, w = 4 and a = 4, as shown
in Figure 4. As they are processed in the first stage,
they become
ˆ
S
1
= AABD,
ˆ
S
2
= BABD,
ˆ
S
3
= ABDA
and
ˆ
S
4
= DCCA respectively. Figure 5 shows how the
trie is built.
An exact search on the trie would return candi-
dates faster, but some candidates S
i
that are a match
could be discarded. If we search for candidates of
ˆ
S
1
,
although
ˆ
S
2
is probably a match, it would not be se-
lected. To solve this problem, we modified the exact
search on the trie to a range-like search. On the ex-
act search, when the algorithm is processing the j
th
element of
ˆ
S
q
(
ˆ
S
q
[ j]), it only visits the path of the
trie where Node
symbol
=
ˆ
S
q
[ j]. In our proposed ap-
proach, we associate numerical values to the symbols.
For example, A is equal to 1, B is equal to 2, and so
on. Therefore, we can take advantage of closer values
to compute the similarity when comparing the sym-
bols. On our modified search, the algorithm also vis-
its paths where |
ˆ
S
q
[ j] − Node
symbol
| ≤ δ. That is, if
ˆ
S
q
[ j] = B and δ = 1, the algorithm visits the paths of
A, B and C (one up or one down). As backtracking all
possible paths might be computationally expensive,
we exploit pruning of unwanted paths by indexing the
elements of the strings in a non-sequential order. This
approach is interesting, because time series measures
over a short period tend to have similar values. For
example, if in a given time there is a B symbol, prob-
ably the next symbol might be A, B or C (even in large
alphabets). Taking that into account, we interleave el-
ements from the beginning and the end of the string,
i.e, the first symbol, then the last symbol, then the
second and so on.
Figure 5 shows how the modified search behave
when searching for candidates to
ˆ
S
1
. On the first level,
ˆ
S
1
[1] = A and the algorithm will visit the paths of the
symbols A and B. On the next level,
ˆ
S
1
[4] = D and
it will visit the paths of C and D. This process is
repeated until it reaches a leaf node. In this exam-
ple, it will return the candidates
ˆ
S
1
and
ˆ
S
2
, but
ˆ
S
3
and
ˆ
S
4
will not be checked. Figures 5 and 6 also show
that changing the order of the elements can reduce the
backtracking. If the subsequences were indexed using
the sequential order, our modified search would also
visit the path of
ˆ
S
3
for at least one more level, while
changing the order, this path is never visited.
A B
C
D
S1 = AABD
S2 = BABD
S3 = ABDA
S4 = DCCA
A B
C
D A B
C
D A B
C
D
A B
C
D A B
C
D A B
C
D
S1[1] = A
S1[2] = A
S1[3] = B
S1[4] = D
1 2 3 4
A B
C
D
A B
C
D
S3
A B
C
D
S2
A B
C
D
S1
A B
C
D
S4
Figure 5: By selecting candidates using our modified
search, the algorithm backtracks only on nodes of the paths
of the strings
ˆ
S
1
and
ˆ
S
2
.
A B
C
D
S1 = AABD
S2 = BABD
S3 = ABDA
S4 = DCCA
A B
C
D A B
C
D A B
C
D
A B
C
D A B
C
D A B
C
D
S1[1] = A
S1[2] = A
S1[3] = B
S1[4] = D
1 2 3 4
A B
C
D
A B
C
D
S3
A B
C
D
S2
A B
C
D
S1
A B
C
D
S4
Figure 6: Creating the trie index using normal order in-
creases the backtracking, since the algorithm visits part of
the path of the string
ˆ
S
3
.
The basic idea of this stage is shown in Figure 7.
Non-trivial matches subsequences S
i
might have val-
ues near S
q
, so basically, the range search algorithm
TrieMotif-ANewandEfficientMethodtoMineFrequentK-MotifsfromLargeTimeSeries
63

-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0 2 4 6 8 10 12 14
Time
S
1
S
2
S
3
S
4
(a) Original time series.
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0 2 4 6 8 10 12 14
Time
S
1
Ŝ
2
Ŝ
3
Ŝ
4
Ŝ
A
B
C
D
(b) PAA representantion.
Figure 4: Symbolic conversion process of the subsequences S
1
, S
2
, S
3
and S
4
to the strings
ˆ
S
1
= AABD,
ˆ
S
2
= BABD,
ˆ
S
3
=
ABDA and
ˆ
S
4
= DCCA.
sets an upper and a lower limit to define an area con-
taining these subsequences.
On the last stage, after obtaining a list of candi-
dates for each S
q
, we calculate the distance between
S
q
and S
i
on the original time series domain, discard-
ing trivial matches of S
q
. On this stage we also make
sure that the K-Motifs satisfy Definition 5.
Algorithm 1 shows the TrieMotif algorithm to lo-
cate the top K-Motifs. First, all subsequences S
i
are
converted into a symbolic representation
ˆ
S
i
and every
ˆ
S
i
is indexed in the Trie index. Through the Trie in-
dex, we can reduce the number of non-trivial match
calculations by generating a set C of the possible can-
didates for every
ˆ
S
i
. Then, we check on the original
time series domain if the subsequences C
j
in C satis-
fies D(S
i
,C
j
) ≤ R and it is not a trivial match. Since
it is not possible to know the top K most frequent
motifs before computing every subsequence, we store
the motif on a list (ListO f Moti f ). On the last step
of the algorithm, we also need to check if the top K-
Motifs satisfies the Definition 5. To do so, we sort the
ListO f Moti f by the number of non-trivial matches in
decreasing order. Thus, the most frequent motifs ap-
pear on the beginning of the list. Thereafter we iterate
through the sorted ListO f Moti f and whenever F
{i}
satisfies the Definition 5, we insert F
{i}
in the result
set TopKMoti f , otherwise F
{i}
is discarded.
To improve the efficiency of the method, we also
calculate every distance using the “early abandon-
ment” approach. Note that, although we presented
a method to discretize the time series subsequences,
the TrieMotif algorithm also support others symbolic
discretizations, such as the SAX algorithm. In those
cases, and if the distance function is the Euclidean
one, it is possible to take advantage of the low com-
plexity of the MINDIST and discard calculations on
the original time series whenever MINDIST (
ˆ
S
q
,
ˆ
S
i
) >
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
0 10 20 30 40 50 60 70 80
Time
S
q
Figure 7: Subsequences S
i
that satisfy D(S
q
, S
i
) ≤ R are
possibly in the highlighted area.
R, since the MINDIST is a lower bound to the Eu-
clidean distance.
4 SYNTHETIC DATA ANALYSIS
To validate our method, we performed tests on a syn-
thetic time series generated by random walk of size
m = 1, 000. We also embedded a motif of size 100
in four different positions of the time series. Figure 8
shows the embedded motif and its variants. The mo-
tifs were planted on positions 32, 287, 568 and 875, as
shown in Figure 9. We ran the TrieMotif using the bin
discretization method with n = 100, R = 2.5, w = 16,
a = 4 and δ = 1. As expected, the TrieMotif was able
to successfully find the motif on the planted positions.
Knowing that our method is able to find the em-
bedded motifs, we made a series of experiments
varying the length of the time series to evaluate the
method efficiency. We compared our method with the
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
64

Algorithm 1 : K-TrieMotif Algorithm.
Input: T , n, R, w, a, δ, K
Output: List of the top K-Motif
1: ListO f Moti f ←
/
0
2: for all Subsequence S
i
with size n of T do
3:
ˆ
S
i
← ConvertIntoSymbol(S
i
, w, a)
4: Insert
ˆ
S
i
in the Trie index
5: end for
6: for all Subsequence
ˆ
S
i
of T do
7: C ← GetCandidatesFromTrie(
ˆ
S
i
, δ)
8: Moti f S ←
/
0
9: for all C
j
∈ C do
10: if NonTrivialMatch(S
i
, C
j
, R) then
11: Add C
j
to Moti f S
12: end if
13: end for
14: Insert Moti f S in the ListO f Moti f
15: end for
16: Sort ListO f Moti f by size in decreasing order
17: TopKMoti f s ←
/
0
18: k ← 0
19: for all (F
{i}
∈ ListO f Moti f ) and (k < K) do
20: if (Distance(F
{i}
, F
{l}
) ≤ 2R), ∀F
{l}
∈
TopKMoti f then
21: Discard F
{i}
22: else
23: Insert F
{i}
in TopKMoti f
24: k++
25: end if
26: end for
27: return TopKMoti f
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
0 10 20 30 40 50 60 70 80 90 100
Time
Original Motif
Variation 1
Variation 2
Variation 3
Figure 8: Planted motif and its variants into a longer dataset
for evaluation tests.
brute force algorithm and with a Random Projection
method, since it used extensively and is the basis of
others algorithms in the literature. We searched for
motifs of size n = 100 and used the Euclidian dis-
tance. For both Random Projection and TrieMotif we
-60
-40
-20
0
20
40
60
80
0 100 200 300 400 500 600 700 800 900 1000
Time
Time Series
Motif
Figure 9: A random walk time series with the implanted
motif (blue).
used the same parameters for the discretization, a = 4
and w = 16. We ran the Random Projection with 100
iterations. For the TrieMotif, we used both bin and
SAX representations with δ = 1. We varied the time
series length from 1, 000 to 100, 000. Each set of pa-
rameters were tested using 5 different seeds for the
random walk. All tests were performed 5 times, total-
izing 25 executions. The wall clock time and memory
usage measurements were taken from these 25 runs of
the algorithm. The presented values correspond to the
average of the 25 executions. Due to time limitations,
the brute-force algorithm was not executed for time
series with lengths above 40, 000. The experiments
were performed in an HP server with 2 Intel Xeon
5600 processors with 96 GB of main memory, under
CentOS Linux 6.2. All methods (TrieMotif, Random
Projection and Brute-force) were implemented using
the C++ programming language. The efficiency com-
parison is shown in Figure 10 and the memory usage
is shown on Figure 11.
0
500
1000
1500
2000
2500
3000
3500
0 10 20 30 40 50 60 70 80 90 100
Time (seconds)
Time Series Length (x1000)
TrieMotif (SAX)
TrieMotif (Bin)
Random Projection
Brute-force
Figure 10: Efficiency comparison of the TrieMotif with
brute force and Random Projection.
As expected, both Random Projection and
TrieMotif performed better than the brute-force ap-
TrieMotif-ANewandEfficientMethodtoMineFrequentK-MotifsfromLargeTimeSeries
65

proach. For time series of length below 10, 000, both
Random Projection and the TrieMotif had a simi-
lar performance. However, as the time series length
grows, the TrieMotif presented a better performance.
This result is due to the fact that TrieMotif selects
only the candidates that are probably a match of a
motif, reducing the number of unnecessary distance
calculations. It is also possible to notice a better per-
formance of the TrieMotif using the SAX representa-
tion. The TrieMotif also consumes less memory than
the Random Projection, since the Random Projection
algorithm needs at least m
2
memory for the collision
matrix. From Figure 11, we can see that the memory
requirements of our method is significantly less de-
manding than Random Projection, requiring 10 times
less memory than the state of the art (the Random Pro-
jection approach).
0
5
10
15
20
25
30
35
40
0 10 20 30 40 50 60 70 80 90 100
Memory Usage (GB)
Time Series Length (x1000)
TrieMotif
Random Projection
Brute-force
Figure 11: Comparison of maximum memory usage of the
TrieMotif and Random Projection.
5 REAL DATA EXPERIMENTS
We also performed experiments using data from real
applications. For this evaluation, we extracted data
from time series of remote sensing images gathered
by AVHRR/ NOAA satellite (Advanced Very High
Resolution Radiometer/National Oceanic and Atmo-
spheric Administration). These images correspond to
monthly measures of the Normalized Difference Veg-
etation Index (NDVI), which indicates the soil vegeta-
tive vigor represented in the pixels of the images and
is strongly correlated with biomass. We used images
of the S
˜
ao Paulo state, Brazil (Figure 12), correspond-
ing to the period between April 2001 and March 2010.
From these images, we extracted 174,034 time series
of size 108. Each time series corresponds to a pair of
latitude and longitude of the S
˜
ao Paulo state, exclud-
ing the coastal region. In order to find the motifs in
a time series database, we created a longer time se-
ries by concatenating all time series. The TrieMotif
algorithm was created using this longer time series. It
is important to highlight that in the subsequence ex-
traction, on the first stage, we avoided creating subse-
quences containing parts of two distinct time series,
that is, the end of a time series concatenated to the
beginning of the next one.
Figure 12: State of S
˜
ao Paulo, Brazil.
The S
˜
ao Paulo state was divided into 5 regions
of interest (Figure 13). The regions were obtained
through a clustering algorithm and the results were
analyzed by specialists in the agrometeorology and
remote sensing fields. According to them, region 1
corresponds to water and urban areas, regions 2 and
3 correspond to a mixture of crops (excluding sugar-
cane) and grassland, region 4 corresponds to sugar-
cane crops and region 5 to forest. Figure 14 shows
a summary of each region of interest and the number
of time series in each region. The S
˜
ao Paulo state is
one of the greatest producers of sugarcane in Brazil.
In this work, we consider complete sugarcane cycles
of approximately one year, each of which starting in
April and ending in March, thus, we looked for the
top 4-Motifs of size n = 12 (annual measures). We
ran the TrieMotif algorithm using the bin discretiza-
tion with R = 1.5, w = 4, a = 4 and δ = 1. The exper-
iments were performed using the same computational
infrastructure of the synthetic data.
Figures 15, 16, 17, 18 and 19 show the top 4-Motif
for each region of interest. The plots are not normal-
ized due to the specialists restrictions for analyzing
them. The 1-Motif found on region 1 (Figure 15(a))
has a pattern with low values and variation, which ex-
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
66

Figure 13: The S
˜
ao Paulo state was divided into 5 regions of interest. Region 1 (purple) corresponds to water/cities, Region
2 and 3 (blue and green respectively) to a mixture of crops and grassland, Region 4 (yellow) is sugarcane crop and Region 5
(red) corresponds to forest. The black lines represent the political counties of the state. The south of the state is a forest nature
federal reserve.
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
Mar May Jul Sep Nov Jan
NDVI
Time
(a) 1-Motif
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
Apr Jun Aug Oct Dec Feb
NDVI
Time
(b) 2-Motif
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
Apr Jun Aug Oct Dec Feb
NDVI
Time
(c) 3-Motif
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
Dec Feb Apr Jun Aug Oct
NDVI
Time
(d) 4-Motif
Figure 15: Top 4-Motif for Region of interest 1.
Region Color # of Series Represents
1 Purple 2,804 Water and Cities
2 Blue 55,815
Grassland and
Mixture of Crops
3 Green 50,785
4 Yellow 48,301 Sugarcane crops
5 Red 16,329 Forest
Figure 14: Number of time series in each region of interest.
perts say correspond to urban regions. The other Mo-
tifs found in region 1 (Figures 15(b), 15(c) and 15(d))
have a pattern that corresponds to water regions. Fig-
ures 16 and 17 show patterns with a higher value of
NDVI and with a high variation, which specialists at-
tribute to agricultural areas.The top 3-Motifs found on
region 4 (see Figures 18(a), 18(b) and 18(c)) is clearly
recognized by agrometeorologists as a sugarcane cy-
cle, with its high values of NDVI on April and low
values on October. Since sugarcane harvesting begins
in April, the NDVI slowly starts to decrease in this
period. On October, the harvest finishes and the soil
remains exposed, thereafter the NDVI has the lowest
value. From October to March, the sugarcane grows
and the NDVI increases again. Figure 19 shows a pat-
tern with high values of NDVI and low variations, cor-
responding to the expected forest behavior, where the
NDVI follows the local temperature variation.
The TrieMotif algorithm obtained interesting re-
sults, finding patterns that were not expected by the
specialists. According to them, for some regions, the
4-Motifs found do not resemble with the expected pat-
terns. The 4-Motifs found on both regions 2 and 3
(Figures 16(d) and 17(d) respectively) indicates the
presence of sugarcane and the 4-Motif found on re-
gion 4 (Figure 18(d)) does not resemble a sugarcane
cycle. This result indicates the need for a further in-
spection in the areas where these patterns occur.
TrieMotif-ANewandEfficientMethodtoMineFrequentK-MotifsfromLargeTimeSeries
67

0
0.2
0.4
0.6
0.8
Jan Mar May Jul Sep Nov
NDVI
Time
(a) 1-Motif
0
0.2
0.4
0.6
0.8
Sep Nov Jan Mar May Jul
NDVI
Time
(b) 2-Motif
0
0.2
0.4
0.6
0.8
Jul Sep Nov Jan Mar May
NDVI
Time
(c) 3-Motif
0
0.2
0.4
0.6
0.8
May Jul Sep Nov Jan Mar
NDVI
Time
(d) 4-Motif
Figure 16: Top 4-Motif for Region of interest 2.
0
0.2
0.4
0.6
0.8
Dec Feb Apr Jun Aug Oct
NDVI
Time
(a) 1-Motif
0
0.2
0.4
0.6
0.8
Jun Aug Oct Dec Feb Apr
NDVI
Time
(b) 2-Motif
0
0.2
0.4
0.6
0.8
Aug Oct Dec Feb Apr Jun
NDVI
Time
(c) 3-Motif
0
0.2
0.4
0.6
0.8
Apr Jun Aug Oct Dec Feb
NDVI
Time
(d) 4-Motif
Figure 17: Top 4-Motif for Region of interest 3.
0
0.2
0.4
0.6
0.8
Dec Feb Apr Jun Aug Oct
Time
(a) 1-Motif
0
0.2
0.4
0.6
0.8
Apr Jun Aug Oct Dec Feb
NDVI
Time
(b) 2-Motif
0
0.2
0.4
0.6
0.8
Aug Oct Dec Feb Apr Jun
NDVI
Time
(c) 3-Motif
0
0.2
0.4
0.6
0.8
Jun Aug Oct Dec Feb Apr
NDVI
Time
(d) 4-Motif
Figure 18: Top 4-Motif for Region of interest 4.
0
0.2
0.4
0.6
0.8
Jun Aug Oct Dec Feb Apr
NDVI
Time
(a) 1-Motif
0
0.2
0.4
0.6
0.8
Jan Mar May Jul Sep Nov
NDVI
Time
(b) 2-Motif
0
0.2
0.4
0.6
0.8
Oct Dec Feb Apr Jun Aug
NDVI
Time
(c) 3-Motif
0
0.2
0.4
0.6
0.8
Jan Mar May Jul Sep Nov
NDVI
Time
(d) 4-Motif
Figure 19: Top 4-Motif for Region of interest 5.
6 CONCLUSIONS
Finding patterns in time series is highly relevant for
applications where both the antecedent and the con-
sequent events are recorded as time series. This is the
case of climate and agrometeorological data, where
it is known that the next state of the atmosphere de-
pends in large amount of its previous state. Today,
a large network of sensing devices, such as satellites
recording both earth and solar activities, as well as
ground-based whether monitoring stations keep track
of climate evolution. However, the large amount of
data and their diversity makes it hard to discover com-
plex patterns able to support more robust analyzes. In
this scenario, is is very important to have powerful
and fast algorithms to help analyzing the that data.
In this paper we proposed TrieMotif, a novel tech-
nique that provides, in an integrated framework, an
automated technique to extract frequent patterns in
time series as K-Motifs. It reduces the resolution of
the data, speeding up the sub-sequence comparison
operations, indexes them in a trie structure and adopts
heuristics commonly employed by the meteorologists
to prune from the similarity search operations those
branches that do not represent interesting answers. In
this way, our technique is able to select only candidate
subsequences that have high probability to match a
motif, thus, reducing the number of comparisons per-
ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems
68

formed.
Experiments performed over data from both syn-
thetic and real applications showed that our technique
indeed perform in average 3 times faster them the
state of the art approach (Random Projection), includ-
ing the best methods previously available. It also re-
quires less memory, and the experiments revealed that
it requires up to 10 times less memory than the com-
petitor methods. We presented the results to special-
ists in the field (meteorologists), that confirmed that
the results are indeed correct and useful for their day-
to-day activities to process climate data. For future
works, we intend to explore data from larger regions,
as the whole Brazil and South America. We also in-
tend to explore data from different sensors in order to
evaluate improvements that may be needed.
ACKNOWLEDGEMENTS
The authors are grateful for the financial support
granted by FAPESP, CNPq, CAPES, SticAmsud, Em-
brapa Agricultural Informatics, Cepagri/Unicamp and
Agritempo for data.
REFERENCES
Catalano, J., Armstrong, T., and Oates, T. (2006). Dis-
covering Patterns in Real-Valued Time Series. In
F
¨
urnkranz, J., Scheffer, T., and Spiliopoulou, M., ed-
itors, Knowledge Discovery in Databases: PKDD
2006, volume 4213 of Lecture Notes in Computer Sci-
ence, pages 462–469. Springer Berlin Heidelberg.
Chiu, B., Keogh, E., and Lonardi, S. (2003). Probabilis-
tic discovery of time series motifs. In Proceedings
of the ninth ACM SIGKDD international conference
on Knowledge discovery and data mining, KDD ’03,
pages 493–498, New York, NY, USA. ACM.
Faloutsos, C., Ranganathan, M., Manolopoulos, Y., and
Manolopoulos, Y. (1994). Fast subsequence match-
ing in time-series databases. In Proceedings of the
ACM SIGMOD International Conference on Manage-
ment of Data, pages 419–429, Minneapolis, USA.
Goldin, D. Q., Kanellakis, P. C., and Kanellakis, P. C.
(1995). On similarity queries for time-series data:
Constraint specification and implementation. In Pro-
ceedings of the 1st International Conference on Prin-
ciples and Practice of Constraint Programming, pages
137–153, Cassis, France.
Keogh, E., Chakrabarti, K., Pazzani, M., and Mehrotra, S.
(2001). Dimensionality reduction for fast similarity
search in large time series databases. Knowledge and
Information Systems, 3:263–286.
Keogh, E. and Kasetty, S. (2003). On the need for time
series data mining benchmarks: a survey and empir-
ical demonstration. In Data Mining and Knowledge
Discovery, volume 7, pages 349–371. Springer.
Keogh, E., Lin, J., Lee, S.-H., and Herle, H. (2007). Find-
ing the most unusual time series subsequence: algo-
rithms and applications. Knowledge and Information
Systems, 11(1):1–27.
Li, Y. and Lin, J. (2010). Approximate variable-length
time series motif discovery using grammar inference.
In Proceedings of the Tenth International Workshop
on Multimedia Data Mining, MDMKDD ’10, pages
10:1—-10:9, New York, NY, USA. ACM.
Li, Y., Lin, J., and Oates, T. (2012). Visualizing Variable-
Length Time Series Motifs. In SDM, pages 895–906.
SIAM / Omnipress.
Lin, J., Keogh, E., Lonardi, S., and Chiu, B. (2003). A sym-
bolic representation of time series, with implications
for streaming algorithms. In Proceedings of the 8th
ACM SIGMOD workshop on Research issues in data
mining and knowledge discovery, DMKD ’03, pages
2–11, New York, NY, USA. ACM.
Lin, J., Keogh, E., Patel, P., and Lonardi, S. (2002). Finding
motifs in time series. In In the 2nd Workshop on Tem-
poral Data Mining, at the 8th ACM SIGKDD Interna-
tional Conference on Knowledge Discovery and Data
Mining, International Conference on Knowledge Dis-
covery and Data Mining, Edmonton, Alberta, Canada.
ACM.
Lin, J., Keogh, E. J., Wei, L., and Lonardi, S. (2007). Ex-
periencing sax: a novel symbolic representation of
time series. Data Mining and Knowledge Discovery,
15:107–144.
Mohammad, Y. and Nishida, T. (2009). Constrained Motif
Discovery in Time Series. New Generation Comput-
ing, 27(4):319–346.
Rouse, J. W., Haas, R. H., Schell, J. A., and Deering, D. W.
(1973). Monitoring vegetation systems in the great
plains with ERTS. In Proceedings of the Third ERTS
Symposium, pages 309–317, Washington, DC, USA.
Udechukwu, A., Barker, K., and Alhajj, R. (2004). Discov-
ering all frequent trends in time series. In Proceedings
of the winter international synposium on Information
and communication technologies, WISICT ’04, pages
1–6. Trinity College Dublin.
Wang, L., Chng, E. S., and Li, H. (2010). A tree-
construction search approach for multivariate time se-
ries motifs discovery. Pattern Recognition Letters,
31(9):869–875.
Yankov, D., Keogh, E., Medina, J., Chiu, B., and Zordan,
V. (2007). Detecting time series motifs under uniform
scaling. In Proceedings of the 13th ACM SIGKDD
international conference on Knowledge discovery and
data mining, KDD ’07, pages 844–853, New York,
NY, USA. ACM.
TrieMotif-ANewandEfficientMethodtoMineFrequentK-MotifsfromLargeTimeSeries
69
