A Framework for the Discovery of Predictive Fix-time Models

Francesco Folino, Massimo Guarascio and Luigi Pontieri

Institute ICAR, National Research Council (CNR), via P. Bucci 41C, 87036 Rende, CS, Italy

Keywords:

Data Mining, Prediction, Business Process Analysis, Bug Tracking.

Abstract:

Fix-time prediction is a key task in bug tracking systems, which has been recently faced through the deﬁnition

of inductive learning methods, trained to estimate the time needed to solve a case at the moment when it is

reported. And yet, the actions performed on a bug along its life can help reﬁne the prediction of its (remaining)

ﬁx time, possibly with the help of Process Mining techniques. However, typical bug-tracking systems lack any

task-oriented description of the resolution process, and store ﬁne-grain records, just capturing bug attributes’

updates. Moreover, no general approach has been proposed to support the deﬁnition of derived data, which

can help improve considerably ﬁx-time predictions. A new methodological framework for the analysis of bug

repositories is presented here, along with an associated toolkit, leveraging two kinds of tools: (i) a combination

of modular and ﬂexible data-transformation mechanisms, for producing an enhanced process-oriented view of

log data, and (ii) a series of ad-hoc induction techniques, for extracting a prediction model out of such a view.

Preliminary results on the bug repository of a real project conﬁrm the validity of our proposal and, in particular,

of our log transformation methods.

1 INTRODUCTION

In general, issue tracking systems (a.k.a. “trou-

ble/incident ticket” systems) are commonly used in

real collaboration environments in order to manage,

maintain and help resolve various issues in an organi-

zation/community. A popular sub-class of these sys-

tems it that of bug tracking systems, aimed at support-

ing the ﬁxing of bugs in software artifacts, and widely

used in complex software-development projects, es-

pecially in the open-source world.

A key task in such a context amounts to accurately

foreseeing a bug ﬁx time (i.e. the time needed to

eventually solve the bug). This problem recently at-

tracted the attention of data-mining researchers (An-

balagan and Vouk, 2009; Marks et al., 2011; Pan-

jer, 2007), who tried to extract either a discrete (i.e.

classiﬁcation-oriented) or continuous (i.e. regression-

oriented) ﬁx-time predictor, out of historical bug logs.

Current solutions rely on standard propositional pre-

diction methods, while regarding each bug record as a

tuple encoding all information available when the bug

was initially reported, and labelled with a discrete or

numerical (target) ﬁx-time value. In this way, the rich

amount of log data collected across the life of each

bug — including any change made to bug properties,

like its priority,criticality, status, or assignee — is dis-

regarded, despite it may well help update, at run-time,

the prediction of (remaining) ﬁx times.

The analysis of activity logs is the general aim of

Process Mining research (van der Aalst et al., 2003),

which recently started facing right the induction of

predictive process models (van der Aalst et al., 2011;

Folino et al., 2012; Folino et al., 2013). However,

these approaches need a mapping of log records to

well-speciﬁed process tasks, which are rarely deﬁned

in real systems, where the logs typically register only

the sequence of changes made to a bug’s attributes. In

fact, despite many systems support the design of bug-

handling workﬂows, these are rarely used in real ap-

plications. Moreover, different bug repositories tend

to exhibit heterogeneous data schemes (even if built

with the same system, such as, e.g., Bugzilla), by

virtue of the possibility, offered by most tracking plat-

forms, to customize the data ﬁelds of bugs.

In this work, we propose a comprehensive

methodological framework for the analysis of bug

data and, in particular, for the discovery of ﬁx times,

which allows for taking full advantage of bug at-

tributes and bug modiﬁcation records, so overcom-

ing the limitations of current solutions. In particular,

in order to help the analyst grasp a suitable abstrac-

tion level over bug histories, we deﬁne a modular set

of parametric data-transformation methods for con-

verting each bug history into a process trace (where

update records are abstracted into higher-level activ-

Folino F., Guarascio M. and Pontieri L..

A Framework for the Discovery of Predictive Fix-time Models.

DOI: 10.5220/0004897400990108

In Proceedings of the 16th International Conference on Enterprise Information Systems (ICEIS-2014), pages 99-108

ISBN: 978-989-758-027-7

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

ities), and for possibly enriching these traces with

derived/aggregated data. In this way, a high-quality

process-orientedview of bug histories can be obtained

and analyzed with existing (or novel) process min-

ing methods, in order to eventually build a predictive

model, capable to estimate, at run-time, the remain-

ing ﬁx time of a bug. The approach has been imple-

mented in a system prototype, offering an integrated

and extensible set of data-transformation and predic-

tive learning tools.

By virtue of its generality and ﬂexibility, the pro-

posed approach can be applied proﬁtably to a variety

of real-life bug repositories, while allowing the ana-

lyst to customize the discovery of a ﬁx-time model

to the speciﬁc data schema and business rules of the

repository under analysis. Moreover, as the approach

only assumes that each log event represents a modi-

ﬁcation to a case attribute, it can be easily extended

to analyze the logs of other lowly-structured process

management systems (such as, e.g., issue-tracking

systems or data-centric transactional systems).

The rest of the paper is structured as follows. Sec-

tion 2 summarizes some relevant related works, and

the main points of novelty of our proposal. After in-

troducing a few basic concepts in Section 3, we illus-

trate, in Section 4, our core log-abstraction methods.

The overall discovery approach and the implemented

system are presented in Sections 5 and 6, respectively.

We then discuss a series of tests in Section 7, and draw

some concluding remarks in Section 8.

2 RELATED WORK

Previous approaches to the forecasting of bug ﬁx

times mainly rely on the application of classical learn-

ing methods, devised for analysing propositional data

labelled with a discrete or numerical target. In par-

ticular, linear regressors and random-forest classi-

ﬁers were trained in (Anbalagan and Vouk, 2009) and

in (Marks et al., 2011), respectively, in order to pre-

dict bug lifetimes, using different bug attributes as

input variables. Different standard classiﬁcation al-

gorithms were exploited instead in (Panjer, 2007) to

the same purpose. Decision trees were also exploited

in (Giger et al., 2010) to estimate how promptly a new

bug report will receive attention. Moreover, a stan-

dard linear regression method was used in (Hooimei-

jer and Weimer, 2007) to predict whether a bug report

will be triaged within a given amount of time.

As mentioned above,none of these approaches ex-

plored the possibly to improve such a preliminary es-

timate subsequently, as long as the bug undergoes dif-

ferent treatments and modiﬁcations. The only (par-

tial) exception is the work in (Panjer, 2007), where

some information gathered after the creation of a bug

is used as well, but just for the special case of un-

conﬁrmed bugs, and up to the moment of their accep-

tation. On the contrary, we want to exploit the rich

amount of log data stored for the bugs (across their

entire life), in order to build a history-aware predic-

tion model, providing accurate run-time forecasts for

the remaining ﬁx time of new (unﬁnished) bug cases.

Predicting processing times is the goal of an

emerging research stream in the ﬁeld of Process Min-

ing, which speciﬁcally addresses the induction of

state-aware performance model out of historical log

traces. In particular, the discovery of an annotated

ﬁnite-state model (AFSM) was proposed in (van der

Aalst et al., 2011), where the states correspond

to abstract representations of log traces, and store

processing-time estimates. This learning approach

was combined in (Folino et al., 2012; Folino et al.,

2013) with a predictive clustering scheme, where the

initial data values of each log trace are used as de-

scriptive features for the clustering, and its associated

processing times as target features. By reusing ex-

isting induction methods, each discovered cluster is

then equipped with a distinct prediction model — pre-

cisely, an AFSM in (Folino et al., 2012), and classical

regression models in (Folino et al., 2013).

Unfortunately, these Process Mining techniques

rely on a process-oriented representation of system

logs, where each event refers to a well-speciﬁed task;

conversely, common bug tracking systems just regis-

ter bug attribute updates, with no link to resolution

tasks. To overcome this limitation, we try to help

the analyst extract high-level activities out of bug his-

tory records, by providing her/him with a collection

of data transformation methods, tailored to ﬁne-grain

attribute-update records, like those stored in bug logs.

The capability of derived data to improve ﬁx-

time predictions was pointed out in (Bhattacharya and

Neamtiu, 2011), where a few summary statistics and

derived properties were computed for certain Bugzilla

repositories, in a pre-processing phase. We attempt

to generalize such an approach, by devising an ex-

tensible set of data transformation and data aggrega-

tion/abstraction mechanisms, allowing to extract and

evaluate such derived features for a generic bug log.

3 PRELIMINARIES

In order to make the discourse concrete, let us fo-

cus on the structure of a bug repository developed

with Bugzilla (

http://www.bugzilla.org

), a general-

purpose bug-tracking platform, devoted to support

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

100

people in various bug-related tasks – e.g., keep track

of bugs, communicate with colleagues, submit/review

patches, and manage quality assurance (QA). Notice,

however, that this particular choice does not under-

mine the generality of our approach, since very simi-

lar bug tracking strategies take place in most real-life

software development/maintenance environments.

In typical Bugzilla applications, tasks are often

carried out in an unstructured manner, without be-

ing enforced by a prescriptive process model. Such

applications mainly looks like a repository, where an

extensible set of attributes are associated with a bug,

and possibly updated along its entire life.

For example, in the Bugzilla repository of project

Eclipse (used in our experiments), the main attributes

associated with each bug b are: who entered b into the

system (

reporter

); the last solver b was assigned to

(

assignee

); the

component

and

product

affected by

severity

’s and

priority

’s levels; the list of users

that must be kept informed on b’s progress (

); the

lists of other bugs depending on b (

dependsOn

), and

of related documents (

seeAlso

); a

milestone

; the

status

and

resolution

of b (both described below).

Few bug attributes (e.g.,

reporter

) are static,

whereas the others (e.g.,

status

resolution

assignee

) may change as long as the bug case

evolves. In particular, the

status

of a bug b may

take the following values: unconﬁrmed (i.e. b was

reported by an external user, and it needs to be

conﬁrmed by a project member), new (i.e. b was

opened/conﬁrmed by a project member), assigned

(i.e. b was assigned to a solver), resolved (i.e. a ﬁx

was made to b, but it needs to be validated), veriﬁed

(i.e. a QA manager has validated the ﬁx), reopened

(if the last ﬁx was judged incorrect), and closed. For

a resolved bug b, the

resolution

ﬁeld may take one

of these values: ﬁxed, duplicate (i.e. b is a duplicate

of another bug), works-for-me (i.e. b has been judged

unfounded), invalid, won’t-ﬁx.

In any Bugzilla repository, the whole history of a

bug is stored as a list of update records, all of which

share the same structure, consisting of ﬁve predeﬁned

ﬁelds (in addition to a bug identiﬁer): who (the per-

son who made the update), when (a timestamp for the

record), what (the attribute modiﬁed), removed (the

former value of that attribute) and added (the newly

assigned value). Figure 1 reports, as an example, the

update records of an Ecplise’s bug.

Bug Traces and Associated Data: The contents of

a bug repository can be viewed as a set of bug traces,

each storing the sequence of events recorded during

the life of the bug. As explained above, each of these

events concerns the modiﬁcation of a bug attribute,

Figure 1: Activity log for a single Bugzilla’s bug (whose ID

is omitted for brevity). Row groups gather “simultaneous”

update records (sharing the same timestamp and executor).

and takes the form of the records in Figure 1.

Let E be the universe of all possible bug events,

and T be the universe of all possible bug traces. For

any event e ∈ E, let who(e) and when(e), what(e),

removed(e), and added(e) be the executor, the times-

tamp, the attribute modiﬁed, the former valueand new

value stored in e, respectively.

For each (bug) trace τ ∈ T , let len(τ) be the

number of events stored in τ; moreover, for any i =

1 .. len(τ), let τ[i] be the i-th event of τ, and τ(i] ∈ T

be the preﬁx trace gathering the ﬁrst i events in τ.

Clearly, preﬁx traces have the same form as fully

unfolded traces (and yet belong to T ), but only rep-

resent partial bug histories. In actual fact, the preﬁx

traces of any bug allow us to look at the evolution of

that bug, across its whole life. For example, the activ-

ity log of Figure 1 (which just stores the history of one

bug) will be represented as a trace τ

consisting of 12

events, one for each of the update records (i.e. rows

of the table) in the ﬁgure; in particular, for the ﬁrst

event, it is who(τ

[1]) = svihovec, what(τ

[1]) =

added(τ

[1])) = {margolis,svihovec}.

As mentioned above, typical bug tracking systems

store several attributes for each bug instance (e.g.,

reporter

priority

, etc.), which may take differ-

ent values during its life. Let F

,.. . ,F

be all of the

attributes deﬁned for a bug. Then, for any (either par-

tial of completed) bug trace τ, let data(τ) be a tuple

storing the updated values of these attributes associ-

ated with τ (i.e. the values taken by the correspond-

ing bug after the last event of τ), and data(τ)[F

] be the

value taken by F

(for i = 1..n). Clearly, for any fully

unfolded bug trace τ, the data tuple of each sub-trace

τ(i] is a snapshot of the data associated with the bug

at the i-th step of its history (with i ∈ {1,.. .,len(τ)}).

Finally, a (bug) log L is a ﬁnite subset of T , while

the preﬁx set of L, denoted by P (L), is the set of all

possible preﬁx traces that can be extracted from L.

Fix-time Measurements and Models: Let ˆµ

T → R be an unknown function assigning a ﬁx-time

AFrameworkfortheDiscoveryofPredictiveFix-timeModels

101

value to any bug (sub-)trace. The value of ˆµ

clearly known over all P (L)’s traces, for any given

log L — indeed, for any log trace τ and preﬁx τ(i], it

is ˆµ

(τ(i]) = when(τ[len(τ)])− when(τ[i]). For exam-

ple, for the trace τ

(2], encoding the ﬁrst 2 events in

Figure 1, it is ˆµ

(τ

(2]) = when(τ[12]) − when(τ[2])

= 197 days (assuming that time spans are measured in

days).

A Fix-time Prediction Model (FTPM) is a model

approximating ˆµ, which can estimate the remaining

ﬁx time of a bug, based on its current trace. Learn-

ing such a model is an inductive problem, where the

training set is a log L, and the value ˆµ

(τ) of the target

measure is known for each (preﬁx) trace τ ∈ P (L).

4 CORE BUG TRACE

ABSTRACTION OPERATORS

In the discovery of an FTPM model we want to take

into account all bugs’ histories (i.e. all sequences of

update records), in addition to the intrinsic features of

the bugs (e.g., the affected product, severity level, re-

porter). Our core idea is to regard some of the actions

performed on a bug as a clue for the activities of an

unknown (bug resolution) process, in order to possi-

bly exploit Process Mining approaches. To this end,

we discard the na¨ıve idea of just deﬁning such activi-

ties as all possible changes to the status of a bug, since

this will lead to discard relevant events, such as the

(re-)assignment of the bug to a solver, or the modiﬁ-

cation of key properties (like its severity, criticality, or

category). On the other hand, we do not either adopt

the extreme solution of looking at all attribute updates

as resolution tasks, seeing as many of them are hardly

linked to ﬁx times, and they may even have a noise-

like effect on the discovery of ﬁx-time predictors.

The rest of this section presents a collection of

parametric data-transformation methods, which are

meant to turn bug histories into abstract traces of rel-

evant resolution activities, suitable for the application

of process-oriented prediction techniques.

Activity-oriented Event Abstraction: An event

abstraction function α is a function mapping each

event e ∈ E to an abstract representation α(e), which

captures relevant facets of the action performed. To

this end, in current process mining approaches, log

events are usually abstracted into their associated

tasks, possibly combined with other properties of

them (e.g., their executors), under the assumption that

the events correspond to the execution of work-items,

according to a workﬂow-oriented view of the process

analyzed.

In our framework, such a function α is right in-

tended to turn each bug-tracking event into a high-

level bug-resolution activity, by mapping the former

to a label that captures well its meaning. As a bug

system only tracks attribute-update events, the ana-

lyst is allowed to deﬁne this function in terms of their

ﬁelds (i.e. who, when, what, added, and removed).

The default instantiation of α, denoted by α, is

deﬁned as follows (with symbol + denoting the string

concatenation operator):

α(e) =







what(e)+ “:=”+added(e), if what(e) ∈

{

status

resolution

}

“∆”+what(e), otherwise

(1)

This particular deﬁnition of α focuses on what bug

attribute has been modiﬁed, while abstracting any

other event’s ﬁeld (namely, who, when, removed, and

added); as an exception, the assigned values are in-

cluded in the abstract representation when the update

involves the

status

resolution

, since such in-

formation can help characterize the current state of a

bug, and improve ﬁx-time predictions. For example,

for the ﬁrst two events of the bug trace τ

(gather-

ing all the records in Figure 1), it is

α(τ

[1]) = ∆

and

α(τ

[2]) = ∆

TargetMilestone

, while the activ-

ity label of the last event (τ

[12]) is

status

:=closed.

Different event abstraction functions can be de-

ﬁned by the analyst, in order to focus on other facets

of bug activities, or to change the level of detail,

depending on the speciﬁc bug attributes (and as-

sociated domains) available in the application sce-

nario at hand. For instance, with regard to the sce-

nario of Section 3, one may reﬁne the representa-

tion of severity-level changes by deﬁning two distinct

activity labels for them, say ∆Severity-Eclipse and

∆Severity-NotEclipse, based on the presence of sub-

string “eclipse” in the e-mail address of the person

who made the change.

Macro-event Criterion: In real bug tracking envi-

ronments, multiple ﬁelds of a bug are often modi-

ﬁed in a single access session, and the correspond-

ing activity records are all stored with the same

timestamp, in an almost arbitrary order. For exam-

ple, in our experimentation, we encountered many

cases where the closure of the bug (i.e. an event of

type

status

:=closed) preceded a “contemporaneous”

change of assignee (or a message dispatch).

Regarding each set of contemporaneous events as

one macro-event, the analyst can deﬁne three kinds

of data-manipulation rules, in order to rearrange them

based on their ﬁelds: (i) a predominance rule, assign-

ing different relevance levels to simultaneous events

(with the ultimate aim of purging off less relevant

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

102

Table 1: Default macro-event criterion: predominance, merging and sort rules over simultaneous events. No merging rules for

levels 2 and 3 (whose events are only reordered), and no sort rules for level-1 events (which are merged together) are deﬁned.

Predominance levels Merging rules Sort rules

(lev.) (bug attributes) (macro-event activity label) (ordering relation)

status

resolution

α(h , ,

status

, , i) + “+

′′

+α(h , ,

resolution

, , i) —

priority

severity

assignee

—

priority

severity

assignee

milestone

—

milestone

ones); (ii) a set of merging rules, indicating when two

or more contemporaneous events (with the same pre-

dominance level) must be merged together, and which

activity label must be assigned to the resulting aggre-

gated event; (iii) a set of sort rules, specifying an or-

dering relation over (non-purged and non-merged) si-

multaneous events.

Any combination of the above kinds of rules will

be collectively regarded, hereinafter, as a macro-

event criterion. The default instantiation of this cri-

terion is summarized in Table 1, where each event

is given a “predominance” level, only based on what

attribute was updated in the event. Such levels acts

as a sort of priority in the selection of events (the

lower the level, the greater the priority): an event

is eventually kept only if there is no simultaneous

event with a lower level than it. In particular, events

involving a change to the

status

resolution

hide

assignee

priority

severity

updates, which,

in their turn, hide changes to the

milestone

A merging rule is deﬁned in Table 1 only for 1-

level simultaneous events, which states that, when-

ever the

status

and

resolution

of a bug are mod-

iﬁed contemporarily, the respective events must be

merged into a single macro-event, labelled with the

concatenation of their associated activity labels. For

example, this implies that the ninth and tenth events

in Figure 1 will be merged together, and labelled with

the string “

state

:=resolved +

resolution

:=ﬁxed”.

Also the default sort rule (shown in the table as an

ordering relation <) only depends on the what ﬁeld,

and states that events involving attribute

milestone

must precede those concerning

, and that

priority

(resp.,

severity

) updates must precede

severity

(resp.,

assignee

) ones. In this way, e.g., the ﬁrst two

events in Figure 1 will be switched with one another.

Example 1. Let us apply all default log abstraction

operators introduced above (i.e. the event abstrac-

tion function in Equation 1 and the macro-event cri-

terion of Table 1) to the bug trace τ

encoding the

events in Figure 1. For the sake of conciseness,

let us only consider events involving the attributes

in Table 1. The resulting trace τ

′

consists of 8

events, which are associated with the following ac-

tivity labels, respectively: l

=“∆

milestone

”, l

=“∆

”,

= “∆

assignee

”, l

= “∆

”, l

= “∆

”, l

= “∆

assignee

”,

= “

status

:=resolved+

resolution

:=ﬁxed”, l

= “

status

:= closed”, where l

is the activity label of τ

′

[i]. The

respective timestamps (at 1-hour granularity) of these

events are: t

= t

=(2012-06-20 10EDT), t

=(2012-

06-20 22EDT), t

=(2012-06-21 11EDT), t

=(2012-06-

25 05EDT), t

=(2012-07-02 10EDT), t

=(2012-07-02

15EDT), t

=(2013-01-03 11EST). ⊳

State-oriented Trace Abstraction: For each trace

τ, a collection of relevant preﬁxes (i.e. sub-traces)

rp(τ) is selected, in order to extract an abstract rep-

resentation for the states traversed by the associ-

ated bug, during its life. Two strategies can be

adopted to this end, named event-oriented and block-

oriented. In the former strategy all possible τ’s pre-

ﬁxes are considered, i.e. rp(τ) = {τ(i] | i = 1. .. len(τ)},

whereas in the latter only preﬁxes ending with the last

event of a “macro-activity” are selected, i.e. rp(τ) =

{ τ(i] | 1 ≤ i ≤ len(τ) and when(τ[ j]) > when(τ[i]) ∀ j ∈

{i+ 1,. .. ,len(τ)} }.

Independently of the selection strategy, each trace

′

in rp(τ) is turned into a tuple state

(τ

′

), whose at-

tributes are all the abstract activities produced by a

given event abstraction function α (e.g., that in Eq. 1).

The value taken by each of these activities, say a, is

denoted by state(τ

′

)

[a] and computed as follows:

state

(τ

′

)[a]=

SUM

({δ(τ

′

[i])| α(τ

′

[i])=a,i=1..len(τ

′

)}) (2)

where δ is a function assigning an integer weight to

each event, based on its properties; by default it is (i)

δ(e) = |added(e)|, if e is not an aggregation of multi-

ple simultaneous events (i.e. it corresponds to one raw

update record) and e involves a multivalued attribute

(like

CC, seeAlso

), or (ii) δ(e) = 1 otherwise.

Any preﬁx trace τ

′

is hence encoded by an integer

vector in the space of the abstract activities extracted

by α, where each component accounts for all the oc-

currences, in τ

′

, of the corresponding activity. Such

a vector captures the state of a bug (at any step of its

evolution) through a summarized view of its history.

Example 2. Let us consider the trace τ

′

shown

in Example 1. The unfolding of this trace gives

rise to 8 distinct preﬁx sub-traces, denoted by

′

(1], τ

′

(2], ..., τ

′

(8]. Five distinct abstract ac-

tivities occur in these traces: a

=“∆

milestone

”,

=“∆

”, a

=“∆

assignee

”, a

=“

status

:=resolved+

resolution

:=ﬁxed)”, a

=“

status

:=closed”. As to trace

AFrameworkfortheDiscoveryofPredictiveFix-timeModels

103

abstractions, all components of state

(τ

′

(1]) (i.e.

the tuple encoding the state reached after the ﬁrst

step) are 0 but that associated with a

and a

, which

are state

(τ

′

(1])[a

] = 1, and state

(τ

′

(1])[a

] = 2.

— indeed, two values were added to

in the

ﬁrst macro-activity. If using the event-oriented

strategy, the above traces will generate 8 state tuples:

state

(τ

′

(1])=h1,2,0,0,0i, state

(τ

′

(2])=h1,2,1,0,0i,

state

(τ

′

(3])=h1,4,1,0,0i, state

(τ

′

(4])=h1,5,1,0,0i,

state

(τ

′

(5])=h1,5,2,0,0i, state

(τ

′

(6])=h1,5,2,1,0i,

state

(τ

′

(7])=h1,5,2,1,1i. ⊳

Such a state-oriented representation of a log L will

be eventually exploited to induce a ﬁx-time predictor

(i.e. a FTPM) for L, as explained in the next section.

5 DISCOVERY APPROACH

We can now illustrate our whole approach to the

discovery of a Fix-time Prediction Model (FTPM),

based on a given set of raw bug records. The approach

is illustrated in Figure 2 as a meta-algorithm, named

FTPM Discovery

, which encodes the main logical

steps of our (process-oriented) data-transformation

methodology, as well as the eventual application of

a predictive induction method to the transformed log.

The algorithm takes as input a bug repository,stor-

ing a collection of bug records (like those described

at the beginning of Section 3), along with a num-

ber of parameters concerning the application of data-

manipulation operators.

In order to apply the abstraction operators intro-

duced in Section 4, bug data are ﬁrst turned into a set

of bug traces (i.e. a bug log).

Based on a given ﬁltering criterion Φ, function

filterEvents

is used to possibly remove uninterest-

ing events (e.g., outliers or noisy data), which may

confuse the learner, and lead to poor predictions.

Function

handleMacroEvents

allows us to ap-

ply a given macro-event criterion Γ (such as that de-

scribed in Table 1) to rearrange each group of simulta-

neous log events according to the associated predom-

inance, reordering and/or merging rules.

The two following steps (Steps 4 and 5) are

meant to possibly associate each bug trace τ with

additional “derived” data, in order to complement

the original contents of data(τ) with context in-

formation. In fact, the insertion of such addi-

tional information was already considered in previous

bug analysis works (Hooimeijer and Weimer, 2007;

Marks et al., 2011), and was proven effective in

improving the accuracy of predictive models (Bhat-

tacharya and Neamtiu, 2011). Basically, function

deriveTraceAttributes

is devoted to insert new

Input: A collection B of bug records (cf. Section 3),

a ﬁltering criterion Φ, a macro-event criterion Γ, an

event abstraction function α, and a preﬁx selection

strategy S ∈ {

BLOCK, EVENT

}

Output: An FTPM (Fix-time Prediction Model) for B

Method: Perform the following steps:

1 Convert B into a log L of bug traces;

2 L :=

filterEvents

(L,φ);

3 L :=

handleMacroEvents

(L,Γ);

4 L :=

deriveTraceAttributes

(L);

5 L :=

refineTraceAttributes

(L);

6 if S =

BLOCK

then

7 RS:={τ(i]) | τ ∈ L,1 ≤ i ≤ len(τ), and

when(τ[ j]) > when(τ[i]) ∀ j ∈ N s.t. i < j ≤ len(τ)};

8 else

9 RS:= {τ(i]) | τ ∈ L, and 1 ≤ i ≤ len(τ)};

10 end if

11 M :=

mineFTPM

(RS,α);

12 return M.

Figure 2: Meta-algorithm

FTPM Discovery

derived trace attributes, deﬁned as some summarized

statistics over bug ﬁeld/trace collections. Conversely,

function

refineTraceAttributes

allows to trans-

form a number of (raw or derived) bugs/events at-

tributes, by turning each of them into a more expres-

sive attribute. Two kinds of capabilities are provided

by our framework to this end: (i) attribute enrich-

ment, which consists in extending the values of an

attribute with correlated information (extracted from

the same repository), and (ii) attribute aggregation,

which consists in reducing the dimensionality of an

attribute by partitioning its domain into classes. Fur-

ther details on the current implementation of both

functions are presented in the next section.

Steps 6-10 are simply meant to extract a set RS of

relevant (sub-)traces out of P (L), based on the cho-

sen selection strategy S. RS is then used by function

mineFTPM

as a training set, in order to eventually in-

duce an FTPM. To this end, as explained in Sec-

tion 4, each trace τ ∈ RS is converted into a tuple la-

belled with the ﬁx-time measurement µ

(τ), and en-

coding both the representation of τ’s state (w.r.t. the

given event abstraction function α), and its associ-

ated (augmented) data tuple data(τ). More precisely,

data(τ) and state

(τ) are used as descriptive/input

attributes, while regarding the actual remaining-time

value µ

(τ

′

) as the target of prediction.

At this point, a wide range of learning methods

(including those described in Section 2) can be used

to induce a regression or classiﬁcation model. As a

matter of fact, different solutions for carrying out this

task are available in the current implementation of our

approach, as described in detail in the next section.

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

104

6 PROTOTYPE SYSTEM

A prototype system was developed to fully implement

the approach presented above, and support the discov-

ery of high-quality FTPMs. In particular, the system

allows the analyst to ﬂexibly and modularly apply all

the data-processing operators presented in this work,

in an interactive and iterative way, as well as to deﬁne

and store (in a reusable form) new variants of them,

according to a template-based paradigm. The archi-

tecture of the system is shown in Figure 3.

Bugzilla

Repository

Bugzilla

Gateway

Resolution

Event Log

Trace

Abstraction

Simultaneous

Event

Rearrangement

Feature

Derivation

Enhanced

Event Log

Predictive

Models

Enhanced Trace Builder

Predictive

Clustering

Regression

Classification

Predictive Model Discovering

Data

Transformation

Rule Repository

Figure 3: Logical architecture of the system prototype.

Module Bugzilla Gateway is capable to extract

historical data stored in any Bugzilla repository

(through its web interface), and to convert them into

bug traces. The imported log, possibly cleaned (ac-

cording to suitable ﬁltering rules), is stored in the

Resolution Event Log. Notice that, in principle, the

system can be extended with analogous modules for

importing log data from different bug tracking plat-

forms.

The Enhanced Trace Builder module allows to ap-

ply various data-transformation criteria (possibly al-

ready stored in the Data-Transformation Rule Repos-

itory), in order to produce an enhanced version of the

log, more suitable for ﬁx time prediction. Specif-

ically, the Simultaneous Event Rearrangement sub-

module can be exploited to manipulate each group of

simultaneous events according to some macro-event

criterion, as discussed in Section 4. Conversely, the

Features Derivation sub-module helps possibly en-

rich all bug traces with additional (derived and/or ab-

stracted) context data. In any case, the Trace Abstrac-

tion block is eventually employed to build a state-

oriented abstraction for each selected (sub-)trace.

Each “reﬁned” log view obtained by way of the

above described functionalities, and stored in the En-

hanced Event Log repository, can be used as input

for module Predictive Model Discovering. To this

end, the abstracted traces are delivered to either the

Regression or Classiﬁcation module, based on which

learning task was chosen by the user. Preliminary to

the induction of a prediction model, the traces can be

possibly partitioned into groups by one of the predic-

tive clustering methods implemented by the Predic-

tive Clustering module, which will also produce a set

of decision rules for discriminating among the discov-

ered clusters. In this case, each cluster will be even-

tually equipped with a distinct ﬁx-time predictor.

Details on Built-in Derived and Abstracted Data:

The following context data are automatically inserted

by our system into each bug trace τ: (i) a collection of

rough workload indicators, storing the overall num-

ber of bugs currently opened in the system, and the

number of those pertaining the same product version

(resp., component and OS) as τ; (ii) an analogous col-

lection of counters for the bugs ﬁxed in the past year

(globally, and for the version/component/OS referred

to by τ); (iii) a “reputation” coefﬁcient, computed for

the reporter of τ as in (Bhattacharya and Neamtiu,

2011); (iv) the average ﬁx-time for various groups of

related bugs (e.g., those concerning the same project

or reporter as τ) and closed in the past year; (v) sev-

eral seasonality dimensions (such as, week-day and

month) derived from the date of the last event in τ.

As to the reﬁnement of data, the system im-

plements a speciﬁc attribute enrichment mechanism,

which allows to replace users’ identiﬁers (possibly

appearing, e.g., in who ﬁelds of bug history records,

or in certain bug attributes) with their respective e-

mail addresses — actually, no further information on

people is available in many real bug repositories. To

this end, a greedy matching procedurewas developed,

based on comparing any user ID with all the email ad-

dresses appearing in various attributes of the bugs.

A further semi-automated built-in procedure

available in the system allows instead to group the

values of a given bug attribute a, by heuristically ﬁnd-

ing a partitioning that exhibits high correlation with

ﬁx-time values, based on a given aggregation hierar-

chy – such a hierarchy can be already available for

the attribute (as in the case of email addresses and

software products, which follow implicit meronomi-

cal and taxonomical schemes, respectively), or can be

computed automatically (via an ad-hoc clustering ap-

proach). Essentially, the procedure tries to ﬁnd an op-

timal cut of the hierarchy, looking at the information

loss that is produced when real ﬁx-time values are ap-

proximated with the averages computed over the se-

lected nodes. Details are omitted for lack of space.

Details on Built-in Induction Methods: Several

alternative learning methods are currently imple-

mented in our system, which support the induction of

a FTPM, from a propositional training set like that

described in the previous section. These methods,

AFrameworkfortheDiscoveryofPredictiveFix-timeModels

105

ranging from classical regression methods to state-

aware Process Mining methods (van der Aalst et al.,

2011; Folino et al., 2012; Folino et al., 2013), are

listed next:

•

IBK

, a lazy (case-based) na¨ıve regression method,

implementing the k-NN procedure available in

Weka (Tan et al., 2005), using k = 1 and Euclidean

distance (and nominal attributes’s binarization);

•

RepTree

, implementing the homonymous

regression-tree learning method (Tan et al.,

2005), while using the variance reduction crite-

rion and 4-fold reduced-error pruning (as well

as with a minimum value of 0.001 and 2 for the

node variance and node coverage, respectively);

•

AFSM

, implementing the FSM-based learning

method in (van der Aalst et al., 2011), using no

history horizon and the multi-set trace abstraction

(which yields the same state codes as Eq. 2 with

unitary event weights, i.e. δ(e) = 1 ∀e ∈ E);

•

CATP

, implementing the approach in (Folino et al.,

2012), which ﬁrst builds a multi-target predictive

clustering for the bugs, using a greedy selection

of all the partial ﬁx-time values of each bug, and

then equip each cluster with an AFSM prediction

model (by reusing the previous method);

•

AATP-IBK

and

AATP-RepTree

, which combine a

multi-target predictive clustering procedure with

the base learners

IBK

and

RepTree

, respectively,

following the approach in (Folino et al., 2013);

•

CBTP 1Reg

(standing for “Clustering Based Time

Predictor with 1-dimensional Regression”), a

novel method which ﬁrst computes a regression

tree by way of algorithm

RepTree

, using each bug

as a single training instance, with its overall ﬁx-

time as target; a classic linear-regression model is

then learnt for each cluster.

Like in previous bug analysis works, the analyst

can also induce a classiﬁcation model for the pre-

diction of (discrete) ﬁx times, after deﬁning a set of

a-priori classes in terms of ﬁx-time ranges (possibly

with the help of automated binning tools). To this end,

a number of existing classiﬁer-induction algorithms

can be exploited, including the following ones:

•

J48

, the Weka’s implementation of classical

C4.5 (Quinlan, 1993) algorithm (with 3-fold re-

duced error pruning);

•

Random Forest

, implementing the algorithm

in (Breiman, 2001) for inducing a random forest

of decision trees (of size 10);

•

MRNB

, a two-phase induction method proposed

in (Costa et al., 2009), which follows a sort

of predictive-clustering strategy, where an ini-

tial rule-based classiﬁcation model is reﬁned by

equipping each leaf with a probabilistic classiﬁer.

7 CASE STUDY

This section discusses some tests performed with our

prototype system, concerning the induction of differ-

ent ﬁx-time predictors from real data, extracted from

the Bugzilla repository of project Eclipse. Two induc-

tion tasks were considered in the tests: (i) discover a

regression model for predicting numeric ﬁx-time val-

ues, and (ii) discover a classiﬁcation model, w.r.t. a

given set of time span classes.

Original Data and Derived Logs: A sample of

3906 bug records (gathered from January 2012 to

March 2013) was turned into a set of bug trace like

those described in Section 3. An explorative analysis

of this log showed that the length of full bug traces

ranges from 2 to 27, while bug ﬁx time ranges from

one day (i.e., a bug is opened and closed in the same

day) to 420 days, with an average of about 59 days.

In order to make this log more suitable for predic-

tion, we applied the basic event abstraction function

α of Eq. 1, so obtaining a ﬁrst “reﬁned” view L

over

the selected bug traces.

Four further log views, named L

,.. . ,L

, were

then derived from L

, by incrementally applying

the data-processing functions appearing in algorithm

FTPM Discovery

(cf. Figure 2).

A ﬁrst cleaned view L

, consisting of 2283 traces,

was produced by applying to L

a speciﬁc instantia-

tion of function

filterEvents

, removing the follow-

ing data: (i) bugs never ﬁxed, (ii) “trivial” bug cases

(i.e. all bugs opened and closed in the same day),

and (iii) trace attributes (e.g.,

version

whiteboard

and

milestone

) featuring many missing values, and

bug/event ﬁelds (e.g.

summary

) containing long texts.

In order to take advantage of the restructuring of

simultaneousevents, a view L

was produced by treat-

ing L

with the default implementation of function

hanldeMacroEvents

(based on the rules of Table 1).

View L

was obtained applying a number of

attribute derivation mechanisms available in our

system (as a built-in implementation of function

deriveTraceAttributes

) to L

was derived from L

through the built-in imple-

mentation of function

abstractTraceAttributes

In particular, all people identiﬁers in the

reporter

bug attribute were replaced with a number of re-

porters’ groups representing different organizational

units (namely, {oracle, ibm.us, ibm.no

us, vmware,

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

106

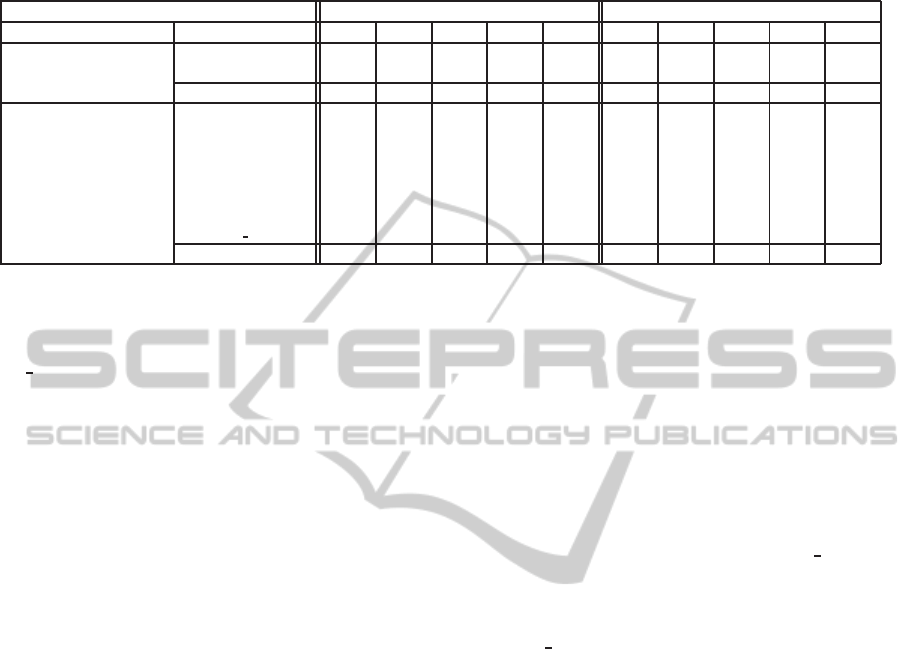
Table 2: Regression results on Eclipse bug data. Rows correspond to different FTPM induction methods, tested in two

learning settings: without and with bug history events. Columns L

,. .. ,L

correspond to different views of the original

dataset, each obtained by a speciﬁc combination of pre-processing operations, as explained in the text.

Predictors rmse mae

Setting Methods L

No Bug History (Baseline)

IBK

1.051 1.051 1.050 1.092 1.093 0.569 0.569 0.561 0.583 0.584

RepTree

0.973 0.973 0.970 0.966 0.925 0.562 0.562 0.552 0.547 0.546

Avg (no history) 0.973 0.973 0.970 0.966 0.925 0.562 0.562 0.552 0.547 0.546

History-aware

AFSM

1.123 1.027 1.010 1.010 1.010 0.717 0.640 0.647 0.647 0.647

CATP

0.967 0.873 0.880 0.737 0.640 0.510 0.467 0.440 0.380 0.320

IBK

0.983 0.823 0.807 0.793 0.803 0.430 0.360 0.360 0.347 0.360

AATP-IBK

1.003 1.007 0.827 0.800 0.710 0.437 0.473 0.367 0.353 0.310

RepTree

1.013 0.883 0.907 0.910 0.773 0.533 0.473 0.473 0.477 0.367

AATP-RepTree

0.970 0.930 0.887 0.783 0.657 0.510 0.530 0.437 0.390 0.313

CBPT 1Reg

0.947 0.900 0.750 0.700 0.547 0.490 0.453 0.383 0.350 0.280

Avg (history-aware) 1.001 0.920 0.867 0.819 0.734 0.518 0.485 0.444 0.420 0.371

other}), and extracted semi-automatically from e-

mail addresses. A similar approach was used

to produce a binary abstraction (namely {eclipse,

not

eclipse}) of attribute

assignee

, and an aggregate

representation of both

product

and

component

Regression Results: When facing the prediction of

ﬁx times by way of regression techniques, predic-

tion accuracy was evaluated through the standard er-

ror metrics root mean squared error (rmse) and mean

absolute error (mae). Both metrics were computed

via 10-fold cross validation, and normalized by the

average ﬁx time (59 days), for ease of interpretation.

Table 2 reports the normalized rmse and mae er-

rors obtained, with different numeric prediction meth-

ods available in our system (and described in Sec-

tion 6), on the ﬁve log views described above. Two

different learning setting were considered to this end:

using bug history information (originally registered

in terms of attribute-update events), and neglecting it.

Note that the latter setting is intended to provide the

reader with a sort of baseline, mimicking the approach

followed by previous ﬁx-time prediction works.

In general, it is easy to see that results obtained in

the ﬁrst setting (“no bug history”) — where only the

initial data of reported bugs are used as input variables

for the prediction — are rather poor, if compared to

the average ones obtained in the “history-aware” set-

ting. Indeed, the errors measured in the former setting

are quite high, no matter which inductive methods

(i.e.

IBK

RepTree

) is used, and which combination

of pre-processing operations are applied to the orig-

inal logs. Interestingly, this result substantiates our

claim that the exploitation of bug activity information

helps improve the precision of ﬁx-time forecasts.

On the other hand, in the second setting, both rmse

and mae errors tend to decrease when using more re-

ﬁned log views. In particular, substantial reductions

were obtained with the progressive introduction of

macro-event manipulations (view L

), and of derived

and abstracted data (views L

and L

, respectively).

By a ﬁner grain analysis, we can notice that this

trend is not followed by

AFSM

, which exhibits worse

performances than the other history-aware methods,

over all the log views. This bad behavior may be as-

cribed to the fact that

AFSM

does not exploit context

data, which instead seem to be a key factor of im-

provement for ﬁx-time prediction accuracy.

Very good results are obtained (in the history-

aware setting) when using some kind of predictive

clustering method, be it single-target (

CBPT 1Reg

and

RepTree

) or multi-target (

CATP

AATP-RepTree

and

AATP-IBK

). However, trace-centered clustering ap-

proaches (namely,

CATP

AATP-RepTree

AATP-IBK

and

CBTP 1Reg

) achieve better results than

RepTree

which considers all possible trace preﬁxes for the

clustering. In fact, the beneﬁt of using a clustering

procedure is quite evident in the case of

IBK

, which

generally gets worse achievements than any other ap-

proach, presumably due to its inability to fully exploit

derived data. Indeed, still focusing on the history-

aware setting, it can be noticed that the prediction ac-

curacy of

IBK

slightly increases when it is embedded

in the predictive clustering scheme of

AATP-IBK

Classiﬁcation Results: Let us ﬁnally show some of

the results obtained by facing the discovery of a ﬁx-

time predictor as a classiﬁcation problem, as com-

monly done in current literature. Two learning set-

tings are considered again, based on the possibility

to use bug-history data when inducing a classiﬁca-

tion model. The case where such data are disregarded

still plays here a sort of baseline, corresponding to

the approach followed in several ﬁx-time prediction

works (Giger et al., 2010; Marks et al., 2011).

Target classes were identiﬁed by discretizing – via

equal-depth binning – the ﬁx times of all bugs consid-

ered in the tests. These classes roughly correspond to

AFrameworkfortheDiscoveryofPredictiveFix-timeModels

107

Table 3: Accuracy results of different ﬁx-time classiﬁers on

a fully enhanced log (L

), derived from Eclipse bugs.

Predictors Accuracy Measures

Approach Methods P R F

No Bug History

J48

0.560 0.562 0.559

MRNB

0.582 0.583 0.582

Random Forest

0.538 0.541 0.539

Avg (no history) 0.560 0.562 0.560

History-aware

J48

0.736 0.728 0.726

MRNB

0.818 0.822 0.819

Random Forest

0.815 0.816 0.815

Avg (history-aware) 0.790 0.789 0.787

the following ranges: µ

≤ 1 day, 1 day < µ

≤ 10

days, 10 days < µ

≤ 2 months, and µ

> 2 months.

Table 3 reports the accuracy results obtained,

against the most reﬁned log view (i.e. L

)

, by

three different induction methods (namely,

J48

RandomForest

and

MRNB

) implemented in our sys-

tem. Three standard metrics were computed (via 10-

fold cross-validation) to evaluate models’ accuracy:

precision (P), recall (R) and the balanced F

score

(a.k.a. F-measure), deﬁned as F

= 2· P· R /(P+ R).

These ﬁgures conﬁrm that the exploitation of bug

history allows for improving neatly the accuracy of

discovered models, regardless of the learning method

and of the evaluation measure. In particular, very

good scores are achieved when using (on history-

aware logs) the

Random Forest

and

MRNB

methods.

8 CONCLUSIONS

A methodological framework for the prediction of

bug ﬁx times and an associated prototype system have

been proposed, which fully exploit bug attributes’

change logs. Provided with a rich collection of ﬂexi-

ble data-transformation methods, the analyst can ob-

tain a high-quality view of such logs, prior to apply-

ing Process Mining techniques to discover a process-

aware prediction model. Encouraging results were

obtained on some bug logs of a real open-source

project, which empirically prove the beneﬁts of ex-

ploiting bug update histories, and of employing our

data manipulation methods.

As to future work, we plan to extend our approach

in order to deal with long textual descriptions associ-

ated with bug/issue reports, as well as to predict other

process-oriented performance measures than the sole

ﬁx time (e.g., QoS or cost indicators). We will also

explore the application of our methods to the logs of

Less accurate models were extracted from the other

(less reﬁned) log views (namely, L

,. .. ,L

). Detailed re-

sults found in these cases are omitted for lack of space.

other kinds of data-centric and lowly-structured col-

laboration environments (such as, e.g., issue-tracking

and data-centered transactional systems).

REFERENCES

Anbalagan, P. and Vouk, M. (2009). On predicting the

time taken to correct bug reports in open source

projects. In Proc. of Int. Conf. on Software Mainte-

nance (ICSM’09), pages 523–526.

Bhattacharya, P. and Neamtiu, I. (2011). Bug-ﬁx time

prediction models: can we do better? In Proc.

of 8th Intl. Conf. on Mining Software Repositories

(MSR’11), pages 207–210.

Breiman, L. (2001). Random forests. Machine Learning,

45(1):5–32.

Costa, G., Guarascio, M., Manco, G., Ortale, R., and Ri-

tacco, E. (2009). Rule learning with probabilistic

smoothing. In Proc. of 11th Int. Conf. on Data Wareh.

and Knowl. Discovery (DaWaK’09), pages 428–440.

Folino, F., Guarascio, M., and Pontieri, L. (2012). Discover-

ing context-aware models for predicting business pro-

cess performances. In Proc. of 20th Intl. Conf. on Co-

operative Inf. Systems (CoopIS’12), pages 287–304.

Folino, F., Guarascio, M., and Pontieri, L. (2013). A

data-adaptive trace abstraction approach to the pre-

diction of business process performances. In Proc.

of 15th Intl. Conf. on Enterprise Information Systems

(ICEIS’13), pages 56–65.

Giger, E., Pinzger, M., and Gall, H. (2010). Predicting

the ﬁx time of bugs. In Proc. of 2nd Intl. Workshop

on Recommendation Systems for Software Engineer-

ing (RSSE’10), pages 52–56.

Hooimeijer, P. and Weimer, W. (2007). Modeling bug report

quality. In Proc. of 22nd IEEE/ACM Intl. Conf. on

Automated Software Engin. (ASE’07), pages 34–43.

Marks, L., Zou, Y., and Hassan, A. E. (2011). Studying

the ﬁx-time for bugs in large open source projects. In

Proc. of 7th Intl. Conf. on Predictive Models in Soft-

ware Engineering (Promise’11), pages 11:1–11:8.

Panjer, L. (2007). Predicting eclipse bug lifetimes. In Proc.

of 4th Intl. Workshop on Mining Software Repositories

(MSR’07), pages 29–.

Quinlan, J. R. (1993). C4.5: Programs for Machine Learn-

ing. Morgan Kaufmann Publishers Inc., San Fran-

cisco, CA, USA.

Tan, P.-N., Steinbach, M., and Kumar, V. (2005). Introduc-

tion to Data Mining. Addison-Wesley Longman.

van der Aalst, W., van Dongen, B., Herbst, J., Maruster,

L., Schimm, G., and Weijters, A. (2003). Workﬂow

mining: a survey of issues and approaches. Data &

Knowledge Engineering, 47(2):237–267.

van der Aalst, W. M. P., Schonenberg, M. H., and Song,

M. (2011). Time prediction based on process mining.

Information Systems, 36(2):450–475.

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

108