Recovering Software Layers from Object Oriented Systems

Alvine Boaye Belle

, Ghizlane El Boussaidi

and Hafedh Mili

Ecole de Technologie Superieure, Université du Quebec, Montreal, Canada

Laboratoire de Recherches en Technologies du Commerce Électronique (LATECE), UQAM,

Montreal, Canada

Keywords: Reverse Engineering, Architecture Recovery, Layering Principles, Optimization, Clustering, Software

Maintenance.

Abstract: Recovering the architecture of existing software systems remains a challenge and an active research field in

software engineering. In this paper, we propose an approach to recover the layered architecture of object

oriented software systems. To do so, our approach first recovers clusters corresponding to the various re-

sponsibilities of the system; the challenge in this context is to find the appropriate level of granularity of

these responsibilities. Then the recovered clusters are assigned to layers using an optimization algorithm

that exploits the principles of the layering architectural style. The approach was validated on five Java open

source systems.

1 INTRODUCTION

Software architecture is commonly defined as a set

of components and connectors (i.e., interactions

between components) that satisfy a set of functional

requirements and quality attributes (Shaw and Gar-

lan, 1996); (Bass et al., 2003). It is an abstract repre-

sentation that encompasses many complementary

static, runtime and allocation views of a software

system (Buschmann et al., 1996). Software architec-

tures are built by applying architectural styles which

describe families of systems (Shaw and Garlan,

1996). Examples of common architectural styles are

the layered, pipes and filters, client-server and ser-

vice-oriented styles; each of these styles has its own

vocabulary and constraints and promotes some spe-

cific quality attributes.

To appropriately support the evolution of an ex-

isting software system, we need to understand its

architecture. However the as-built architecture is

often insufficiently documented (Stoermer et al.,

2003). Moreover, this architecture has often deviated

from the initial design because of the changes un-

dergone by the system. Hence, a software architec-

ture recovery process is required to reconstruct and

document its architecture. The reconstructed archi-

tecture enables to understand the system, to restruc-

ture it as needed, and to constrain its future evolu-

tion. In the context of this paper, we are interested in

recovering layered architectures of object oriented

systems.

Several approaches were proposed to support the

recovery of layered architectures (e.g., (Laval et al.,

2012); (Hassan and Holt, 2002); (Sarkar et al.,

2009); (Andreopoulos et al., 2007) and (Scanniello

et al., 2010)). Most of these approaches propose

some heuristics to cluster elements of the system

under analysis into layers. For example, in both

(Sarkar et al., 2009) and (Laval et al., 2012), heuris-

tics to resolve cyclic dependencies are proposed,

while (Scanniello et al., 2010); (Laval et al., 2012)

and (Andreopoulos et al., 2007) propose heuristics

that exploit the number of fan-out and fan-in de-

pendencies of a module to assign it to the lowest or

highest-level layer. However, these heuristics may

result in architectures that are too permissive with

layering violations.

In this paper, we propose an approach to recover

the layered architecture of object oriented systems.

In particular, the approach first attempts to cluster

the packages of the system under analysis to build

the system’s responsibilities. The challenge, in this

context, is to find the appropriate level of granularity

of the clusters. The resulting responsibility clusters

are then assigned to layers so as to minimize the

violations to the layered style principles. To do so,

we propose a set of layers dependency metrics and

we use these metrics to formalize the layering of

responsibility clusters as an optimization problem.

Boaye Belle A., Boussaidi G. and Mili H..

Recovering Software Layers from Object Oriented Systems.

DOI: 10.5220/0004900400780089

In Proceedings of the 9th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE-2014), pages 78-89

ISBN: 978-989-758-030-7

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

The contribution of this paper is threefold: 1) a

clustering algorithm that aggregates software pack-

ages in order to recover the responsibilities of the

system at a given granularity; 2) a layering recovery

process that builds layers from the aggregated pack-

ages; and 3) the assessment of our approach using

five Java open-source systems.

The remainder of this paper is organized as fol-

lows. Section 2 states the problem inherent to the

layering recovery techniques. Section 3 describes

our layering recovery approach. In section 4, we

describe the results of an experiment of our ap-

proach on five systems. We discuss related works in

section 5 and we conclude in section 6.

2 PROBLEM STATEMENT

The layered style was described in many reference

books and papers (e.g., (Shaw and Garlan, 1996);

(Buschmann et al., 1996); (Clements et al., 2003)

and (Eeles, 2002)). It is a technique for decomposing

a software system into groups of subtasks where

each group of subtasks is at a particular level of

abstraction (Buschmann et al., 1996). In other

words, a layered architecture is an organized hierar-

chy where each layer is providing services to the

layer above it and serves as a client to the layer be-

low (Shaw and Garlan, 1996). The OSI reference

model (Zimmermann, 1980) is one of the most

known layered systems. In OSI, a layer uses services

provided by lower layers and adds value to them to

provide services needed by higher layers.

In an ideal layered architecture, a layer may only

use services of the next lower layer. This is referred

to as strict layering in (Buschmann et al., 1996) and

as closed layering in (Szyperski, 1998). This strict

ordering relation is often violated in practice; i.e.,

very often, layered systems allow a layer to use ser-

vices provided by any lower layer. Not restricting

the dependence of a layer to its lower adjacent layer

is considered as a regular feature in the open layer-

ing (Szyperski, 1998) and the relaxed layering

(Buschmann et al., 1996). However, it is considered

as a violation named a skip-call violation in (Sarkar

et al., 2009) and layer bridging in (Clements et al.,

2003). Exceptionally, a layer may need to rely on a

service offered by an upper layer. These dependen-

cies are called back-calls in (Sarkar et al., 2009) and

are discussed in (Clements et al., 2003) under the

name “upward usage”. However, the quality attrib-

utes promoted by the layered style (e.g., reuse, port-

ability, maintainability, understandability, and ex-

changeability) are no longer supported when layers

are allowed to use services of higher layers without

restriction (Clements et al., 2003). Therefore, the

structure of a layered architecture must be a directed

acyclic graph or at least a directed graph with very

few cycles connecting layers.

Many approaches have been proposed to recover

the software architecture. Most of them rely on clus-

tering, which is a common used technique to recon-

struct architecture (e.g., (Tzerpos and Holt, 2000);

(Mitchell et al., 2001); (Maqbool and Babri, 2007);

(Lung et al., 2004)). However, these approaches

target specific languages and systems and do not use

a standard representation of the data of the system

under analysis. As a consequence, resulting tools do

not interoperate with each other (Ulrich and New-

comb, 2010). Besides, most of the layering recovery

approaches attempt to recover the layered architec-

ture by relying on heuristics to resolve cyclic de-

pendencies (e.g., (Sarkar et al., 2009) and (Laval et

al., 2012)) or to layer modules according to the

number of their fan-in and fan-out dependencies

(e.g., (Scanniello et al., 2010); (Laval et al., 2012)

and (Andreopoulos et al., 2007)). However, these

heuristics are not based on layering principles and

may result in architectures that are too permissive

with layering violations.

To tackle these issues, we proposed in (Boaye-

Belle et al., 2013) a platform and language inde-

pendent approach which exploits the layering prin-

ciples to reconstruct the layered architecture of ob-

ject oriented software systems. For this purpose, we

extracted two layering principles from the layered

style: the responsibility principle and the abstraction

principle. The responsibility principle states that

each layer of the system must be assigned a given

responsibility (Eeles, 2002); (Buschmann et al.,

1996), so that the topmost layer corresponds to the

overall function of the system as perceived by the

final user and the responsibilities of the lower layers

contribute to those of the higher layers (Buschmann

et al., 1996). The abstraction principle states that the

layers of a system must be ordered according to the

abstraction criterion that rules the flow of communi-

cation between packages of the system. In (Boaye-

Belle et al., 2013), we relied on existing decomposi-

tion of object oriented systems into packages that we

assumed as being designed according to the respon-

sibility principle and we used the abstraction princi-

ple to specify a set of constraints on the layering of

these packages. These constraints were used to

translate the layering recovery process into an opti-

mization problem that we solved using a heuristic

search algorithm. Experimentations with this ap-

proach yielded encouraging results.

RecoveringSoftwareLayersfromObjectOrientedSystems

However, relying on existing decomposition of

systems into packages raised some issues when re-

covering the layers. In fact, when we flatten the

packages hierarchy, two children packages that are

nested within the same parent package might be

assigned to different layers during the recovery pro-

cess, ending for instance in two consecutive layers.

Such an assignment may be wrong depending on the

granularity of the parent package’s responsibility.

The nesting of child packages into the same parent

package indicates that they contribute to the same

general responsibility, and, depending on its granu-

larity, this responsibility may belong to one layer or

may spam several layers. This problem, also encoun-

tered by other layering recovery approaches (e.g.,

(Laval et al., 2012); (Hautus, 2002)), is illustrated by

Figure 1. In the latter, layers 3, 2, and 1, are respon-

sible of the system's visualization, logic, and data,

respectively. The packages view1.package1 and

view1.package2 are part of the package view1 which

contributes to layer 3’s responsibility. However, in

Figure 1, these two packages were assigned to con-

secutive layers to promote adjacent relationships

between layers (i.e., to promote reuse).

Figure 1: An example of packages' assignment to layers.

To address this issue, each group of packages be-

longing to the same layer's responsibility should be

clustered and assigned to the same level of abstrac-

tion (i.e., layer). In Figure 1, it would allow cluster-

ing view1.package1 and view1.package2 into a sin-

gle cluster that would have been assigned to layer 3.

Notice that when the responsibility of a layer is

complex, it is refined into finer responsibilities in

order to handle its complexity and ease its compre-

hensibility. Each resulting finer responsibility can in

turn be recursively refined until basic responsibili-

ties are obtained. The refinement of a layer's respon-

sibility can then lead to different granularities of

responsibilities, i.e. to responsibilities with various

degrees of complexity. Depending on its granularity,

each responsibility can be implemented by a number

of packages. Hence, to assign the responsibili-

ties/packages to the right layers, packages should be

clustered at the appropriate level of granularity. In

fact, if the granularity of the responsibilities is set to

a coarse level, the clustering process will produce

very few clusters with too many packages (Tzerpos

and Holt, 2000). This may lead to a very small num-

ber of layers and the resulting architecture will be

close to a monolithic one. If the responsibilities'

granularity is too fine, then the clustering process

will generate many clusters including hardly more

than one package. Assigning clusters to layers, in

this case, raises the same issues as discussed above

and illustrated by Figure 1. Therefore, tackling the

issue of clustering the packages at the appropriate

level of granularity will enable recovering the as-

built layered architecture of object oriented systems.

3 OVERVIEW OF THE

PROPOSED APPROACH

To recover the layering organization of a system, we

follow the three-step approach illustrated by Figure

2. The first step consists in retrieving the facts from

the system under analysis. To extract the system's

facts, we analyze its source code and generate plat-

form independent models that are compliant with the

Knowledge Discovery Metamodel (KDM). The

latter was introduced by the OMG (OMG Specifica-

tions, 2013) as a standard representation of legacy

systems. The KDM defines a meta-model for repre-

senting—at various levels of abstraction—all aspects

of existing legacy systems. This meta-model pro-

vides a common interchange format to ensure in-

teroperability between tools. In our context, we

parse the KDM models that we generated from the

source code, to retrieve packages and their relation-

ships. Dependencies between two packages are de-

rived from the dependencies between their respec-

tive classes (i.e., class references, inheritance, meth-

od invocation and parameters).

Once the system’s facts are extracted, we iterate

over steps 2 and 3 to recover the layering architec-

ture of the system. The second step of our approach

aims at clustering packages to build the responsibili-

ties of the system at a given granularity. To do so,

we build a responsibility tree of the system using its

packages’ namespaces and we define the granularity

of a given responsibility as the number of nodes that

have to be traversed from the root of the responsibil-

ity tree to the node corresponding to that responsibil-

ity (i.e., the level of the package representing the

responsibility in the tree). Depending on the targeted

granularity, clusters of packages are built from sub-

trees of nodes corresponding to that granularity. Step

2 is described in details in subsections 3.1 and 3.2.

In the third step of our approach, clusters obtained in

ENASE2014-9thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering

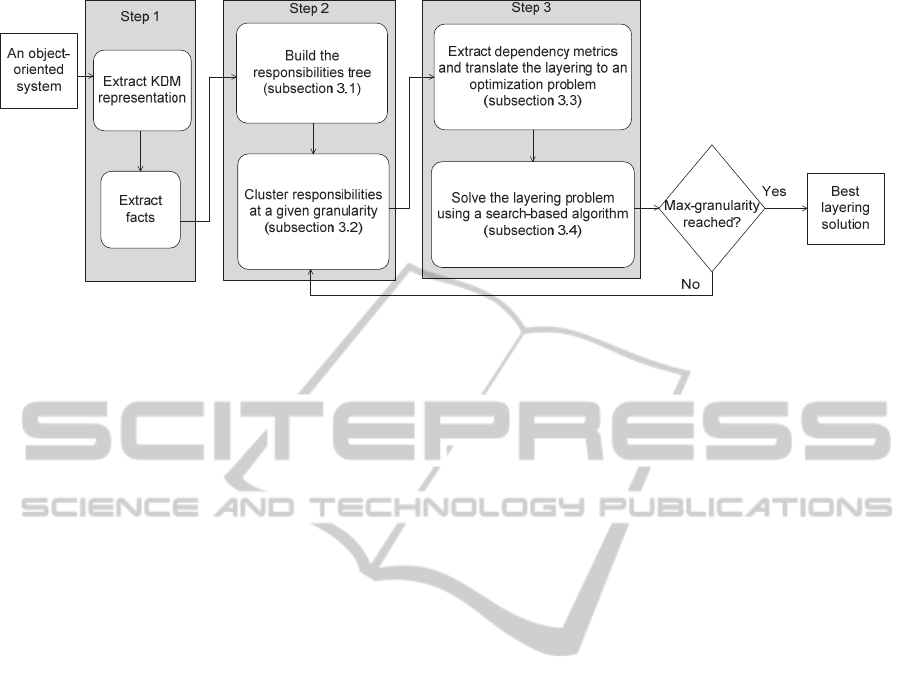
Figure 2: Overview of the proposed approach.

the second step are assigned to layers so as to mini-

mize the layers’ dependencies that violate the lay-

ered architecture (e.g., skip-calls and back-calls) and

maximize dependencies between adjacent layers that

we call adjacent dependencies. To do so, we intro-

duce a number of dependency metrics that are de-

rived from the abstraction principle introduced in

(Boaye-Belle et al., 2013). We use these metrics to

formalize the layering of clusters of packages as an

optimization problem that we solve using a search-

based algorithm. Step 3 is described in details in

subsections 3.3 and 3.4.

At the first iteration of steps 2 and 3, the granu-

larity of the responsibilities is set to 2. At each itera-

tion, the granularity of the responsibilities is in-

creased until it reaches the maximum value (i.e., the

height of the responsibilities tree minus one). The

layering solution obtained after each iteration is

evaluated and it is kept as the best layering solution

if its evaluation gives better results than the best

solution found at the previous iteration. A layering

solution is evaluated using a manual decomposition

of the system and a ratio computed as the number of

adjacent dependencies over the sum of all the de-

pendencies in the solution. We rely on this ratio to

compare two layering solutions instead of the abso-

lute number of adjacent dependencies since the

number of these dependencies varies depending on

the granularity of responsibilities.

3.1 Building the Responsibilities

Hierarchy

Some clustering techniques were proposed to create

subsystems that enable managing and understanding

the analyzed system (e.g., (Müller et al., 1993);

(Hassan and Holt, 2002); (Bowman and Holt, 1998)

and (Tzerpos and Holt, 1996)). These techniques

rely for instance on a system's documentation, on the

development team structure, on the directory struc-

ture of a system, and on the naming conventions

followed when naming a system's parts. The use of

naming information to aggregate packages into sub-

systems is the most common technique used by

these approaches (e.g., (Müller et al., 1993) and

(Hassan and Holt, 2002)). In fact, during the naming

of packages, the developers usually name each

package meaningfully, and they generally rely on

the package's functionality to do so. A package’s

name gives a hint about its role in the system (Clem-

ents et al., 2003). Therefore, the so-obtained naming

information usually gives some clues about the re-

sponsibilities of a system's packages. Of course,

naming information can only be useful if the devel-

opers of the system have followed naming conven-

tions (Müller et al., 1993).

All programming languages (e.g., SmallTalk,

C++ and Java) provide mechanisms to support vari-

ous kinds of namespaces (e.g., records, dictionaries,

objects) (Achermann and Nierstrasz, 2000) allowing

to name software entities. A namespace is a se-

quence of key-words that map labels to values

(Achermann and Nierstrasz, 2000) and identifies a

software entity (e.g., package). Packages that con-

tribute to the same responsibility usually have

namespaces beginning with the same subset of key-

words. In our context, we rely on namespaces to

reconstitute the hierarchy of a system's responsibili-

ties. This hierarchy can be seen as a responsibilities

tree that is built so that its root node is the subset of

key-words that appears at the beginning of each

package. The root node represents the overall func-

tionality of the system. The other nodes of the tree

are recursively built so that each path from the root

to a leaf describes the namespace of a package. Con-

cretely, intermediate nodes of the tree correspond to

responsibilities/packages with finer granularity than

the root node (i.e., responsibilities that have been

RecoveringSoftwareLayersfromObjectOrientedSystems

refined), while the leaves of the tree correspond to

the elementary responsibilities. To get from the root

to the nodes located at a given granularity of respon-

sibilities G, we need to cross (G-1) nodes.

Let us consider JHotDraw 7.0.6, a framework

developed with Java and whose packages'

namespaces are listed in table 1. Figure 3 shows the

responsibilities tree obtained using the key-words in

the packages namespaces of JHotDraw 7.0.6. The

value of the granularity of the root of the tree, which

is the sequence “org.jhotdraw”, is 1. Each path from

the root to a leaf corresponds to a package whose

namespace begins with “org.jhotdraw”. Packages

whose namespaces do not begin with the sequence

“org.jhotdraw” (e.g., “nanoxml” and

“net.n3.nanoxml”) are not included in the tree.

Figure 3: an example of the Responsibilities tree.

3.2 A Responsibilities-based Clustering

Algorithm

In order to build responsibilities-based clusters, we

rely on the responsibilities tree of the system built

using packages namespaces as explained above. We

traverse the responsibilities tree to select each sub-

tree rooted by a node located at a specified granu-

larity of responsibility. The packages whose

namespaces define paths to leaves located in a se-

lected sub-tree are put together in a cluster. Each of

the resulting clusters comprises packages contrib-

uting to the same granularity of responsibilities. The

algorithm describing this clustering process is illus-

trated by Figure 4. This algorithm takes as input the

set of packages of the analyzed system and the tar-

geted granularity of responsibilities at a given itera-

tion. As discussed above, we iterate over all possible

levels of granularities in our approach. The algo-

rithm returns the set of clusters of responsibilities

corresponding to the given granularity.

Table 1: JHotDraw Packages Namespaces.

No Packages namespaces Granularity

1 nanoxml -

2 net.n3.nanoxml -

3 org.jhotdraw.app.* 3

4 org.jhotdraw.app.action 3

5 org.jhotdraw.beans 2

6 org.jhotdraw.draw.* 3

7 org.jhotdraw.draw.action 3

8 org.jhotdraw.geom 2

9 org.jhotdraw.gui.* 3

10 org.jhotdraw.gui.datatransfer 3

11 org.jhotdraw.gui.event 3

12 org.jhotdraw.io 2

13 org.jhotdraw.samples.draw 3

14 org.jhotdraw.samples.net.* 4

15 org.jhotdraw.samples.net.figures 4

16 org.jhotdraw.samples.pert.* 4

17 org.jhotdraw.samples.pert.figures 4

18 org.jhotdraw.samples.svg.* 4

19 org.jhotdraw.samples.svg.action 4

20 org.jhotdraw.samples.svg.figures 4

21 org.jhotdraw.undo 2

22 org.jhotdraw.util.* 3

23 org.jhotdraw.util.prefs 3

24 org.jhotdraw.xml 2

The algorithm starts by determining the smallest

non-empty namespace common to the majority of

packages (line 1). Each package whose namespace

do not begin with the smallest namespace is re-

moved from the set of packages and put in a single-

ton cluster (lines 2 to 8). The latter is added to the

set of clusters (line 8). The algorithm then builds the

responsibilities tree from the set of remaining pack-

ages, considering the smallest common namespace

as the root of the tree (line 11). The tree nodes are

then recursively computed so that each path from the

root to a leaf describes the namespace of a package.

During the tree's construction, granularity values are

ENASE2014-9thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering

assigned to tree nodes, the root node having the

granularity value of 1. We then consider all nodes

whose granularity of responsibility is equal to the

input granularity of responsibilities (lines 12 to 13).

For each of these nodes, we build a cluster contain-

ing all the packages whose namespaces correspond

to leaves in the sub-tree rooted by the considered

node (line 14). The clustered packages are at the

same time removed from the remaining set of pack-

ages. Each resulting cluster is added to the set of

clusters (line 15). Finally, the packages remaining in

the set of packages are put in singleton clusters that

are in turn added to the set of clusters (lines 18 to

22).

Figure 4: A high level view of the clustering algorithm.

3.3 The Layering of Responsibilities as

an Optimization Problem

We rely on the abstraction principle introduced in

(Boaye-Belle et al., 2013) to assign levels to the

clusters obtained from the responsibilities clustering

step. In fact, our analysis of the layered style led us

to retain two properties that we need to comply with

when assigning clusters to layers:

1) The Layer abstraction uniformity property: clus-

ters assigned to the same layer must be at the

same abstraction level. The level of abstraction

of a component often refers to its conceptual dis-

tance from the “physical” components of the sys-

tem (Buschmann et al., 1996), i.e. hardware, da-

tabase, files and network.

2) Incremental layer dependency property: a cluster

assigned to a layer (j) must only rely on services

of the layer below (j-1). As discussed in the

problem statement, this property is the one that is

mostly violated, either through back-call or skip-

call dependencies between layers. Our analysis

of the various descriptions of the layered style

and several open source projects led us to con-

clude that this property should be stated in a way

that allows—to some extent—the skip-call and

back call violations. Hence, we relaxed this

property to “clusters of layer j-1 are mainly

geared towards offering services to clusters of

layer j”. This means that in the event when there

is some skip-call and back-call dependencies be-

tween layers, the number of these dependencies

must be insignificant compared to the number of

downward dependencies between adjacent lay-

ers.

To ensure compliance with the first property, the

clusters of the same layer should be at the same

distance from the “physical” or lowest layer clusters.

However, the existence of back-call and skip-call

dependencies introduces a discrepancy between the

clusters' distances, even when they belong to the

same layer. Hence, compliance with our first proper-

ty derives largely from compliance with our second

property which we will formalize using a set of met-

rics and constraints related to the dependencies be-

tween layers. These constraints will enable to trans-

late the layering problem into an optimization prob-

lem.

We define the index of use of a layer j by a layer

i as the number of dependencies directed from layer

i to layer j. This index is obtained by summing the

weights of the dependencies directed from each

cluster of layer i to each cluster of layer j. The de-

pendency between two clusters derives from the

dependencies between their respective packages. In

what follows, this index is labeled as:

 AdjacencyUse(i,j) when j = i-1. Adjacen-

cyUse(i,j) denotes the number of dependencies

directed from layer i to its adjacent lower layer j.

 SkipUse(i,j) when j < i-1. SkipUse(i,j) is the

number of skip-call dependencies directed from

layer i to layer j.

 BackUse(i,j) when i < j. BackUse(i,j) is the

number of back-call dependencies directed from

layer i to layer j.

 IntraUse(i) when i = j. IntraUse(i) is the number

of the dependencies inside layer i.

Figure 5 illustrates the calculation of the layer de-

pendency metrics for a system made of three layers

RecoveringSoftwareLayersfromObjectOrientedSystems

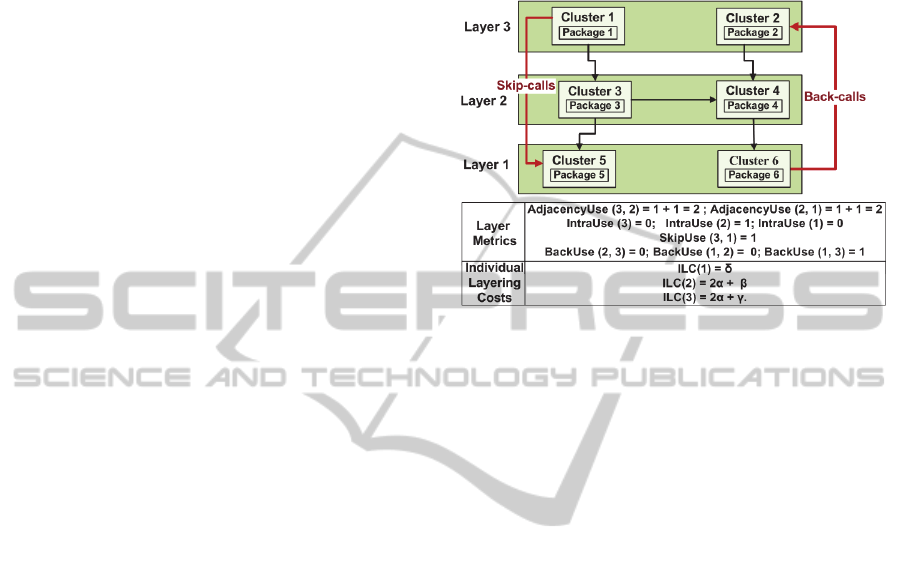
where all dependencies have the same weight (i.e., a

weight of 1). In accordance with the incremental

layer dependency property, we want to minimize the

number of skip-call and back-call dependencies.

This means that, apart from the upper layer adjacent

to layer j, we must minimize the index of use relat-

ing other layers to layer j. However, skip-calls are

often used for performance reasons and should be

more tolerated than the back-calls which lead to a

poorly structured system. These restrictions are for-

malized by the following constraint:

For all i, j, k | j<i and k<j-1, BackUse(j,i) ≤

SkipUse(j,k) ≤ AdjacencyUse(j, j-1)

(1)

Constraint (1) may be certainly satisfied when the

number of the layers of the system is very small (i.e.,

when layers are merged). However, dependencies

between clusters of the same layer are not recom-

mended unless otherwise stated (Bourquin and Kel-

ler, 2007) or when some concerns as portability need

to be addressed (Clements et al., 2003). Hence, we

subjoined to constraint (1) the following constraint

that limits the number of intra-dependencies of a

layer:

IntraUse(j) ≤ AdjacencyUse(j, j-1) (2)

The layer dependency metrics and constraints intro-

duced so far will be used to guide the process of

assigning the clusters of a given system to a set of

layers while rewarding the adjacency between layers

and keeping their intra-dependencies quite low and

minimizing the skip-calls and back-calls. For this

purpose, we define the individual layering cost

(ILC) of a given layer i of the system as follows:

ILC(i) αAdjacencyUse



i, i  1





βIntraUse







∑

SkipUsei, j







δ

∑

BackUsei, j





(3)

Where α, β, γ and δ are respectively the penalties

adjoined to the adjacent dependencies, the intra-

dependencies, the skip-call dependencies and the

back-call dependencies. For instance, in Figure 5,

ILC(3) = 2α + γ, as the third layer has two adjacent

dependencies and one skip-calls.

In order to penalize the undesired dependencies

and satisfy the two constraints defined before, the

penalty α must be lower than the other penalties. The

global layering cost LC of assigning the clusters of a

system to a set of n layers is then computed by

summing the individual layering cost for each layer i

of the system:

LC 

∑

ILCi





(4)

The lower LC is, the better the assignment of clus-

ters to layers is. Attempting to reconstruct a layered

architecture while minimizing its LC, is a problem

that can be solved by adapting a search-based algo-

rithm to reduce the search space.

Figure 5: Example of the calculation of the layer metrics

and the individual layering costs.

3.4 An Algorithm to Assign

Responsibilities to Layers

In order to build the optimal layering of software

systems, we choose to adapt the steepest ascent hill-

climbing technique (Mitchell et al., 2001) using our

LC (Eq. 4) as a fitness function. We focused on the

hill-climbing algorithm because it performs well in

the context of large systems and it has been success-

fully used in several approaches. The algorithm

works in an iterative way. It starts by an initial parti-

tion of the system’s modules into a set of clusters;

usually a randomly generated partition as in (Mitch-

ell et al., 2001). Modules are then moved between

clusters to improve the partition according to some

criterion. This criterion is based on maximizing or

minimizing a fitness function.

Figure 6 shows a high-level view of our adapta-

tion of this technique to the layering problem. It

starts with an initial partition consisting of a set of n

layers comprising the clusters resulting from the

clustering step. The uppermost layer is constituted

by the clusters having no incident dependencies; the

lowermost layer of this partition contains the clusters

having no outgoing dependencies; and the remaining

clusters are randomly assigned to intermediate lay-

ers. The so-called initial system is then considered as

the current solution of the algorithm (line 1). In the

following iterations (lines 3 to 20), all the neighbor-

ing solutions are created (line 6) and evaluated using

their cost (line 8). A neighbor solution is computed

by moving a single cluster from a layer A to a layer

ENASE2014-9thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering

B of the current solution, provided these two layers

are different. In order to compute the cost of each

neighbor, we set the values of α, β, γ and δ prior to

the application of the algorithm. The neighbor hav-

ing the lowest value of LC is considered as the best

neighbor of the iteration (lines 9 to 12) and accepted

as the current solution if its cost is lower than the

one of the current solution (lines 14 to 17). The algo-

rithm stops if the current solution cannot be im-

proved anymore (lines 18 and 19).

Figure 6: A high level view of our layering algorithm.

4 VALIDATION

The validation of our approach aimed at addressing

the two following questions: i) What is the correct

granularity of responsibility to consider when clus-

tering packages of a given system? This question is

meant to investigate the appropriate granularity of

responsibility that will help addressing the issues

raised in section 2. ii) What are the values of penal-

ties (α, β, γ and δ) that generate software layers that

correspond to the as-built architecture? The user

might try many combinations values before finding

the ones that best fit the analyzed system. Hence, our

goal through the second question is to reduce the set

of penalties’ values that the user could consider

when applying our layering recovery algorithm.

To validate our approach, we implemented a tool

within the Eclipse

environment. This tool is made

of three modules. The first one is a fact extractor

built atop of the MoDisco open source tool which

enables to generate a KDM representation of the

system under analysis. The KDM representation is

then used by our extractor to retrieve the system’s

packages and the dependencies between them. The

second module implements the clustering algorithm

to generate clusters from the extracted packages

according to the second step of our approach. In

particular, this module builds a module dependency

graph where nodes are clusters of packages and

edges are dependencies between the clusters which

are inferred from the dependencies between packag-

es. The module dependency graph enables the crea-

tion of an initial partition (i.e., initial layering solu-

tion) that is the input of the third module of our tool.

This third module implements our layering algo-

rithm.

4.1 Experiment

To assess our approach and answer the two research

questions discussed above, we conducted experi-

ments on five software projects. Some characteris-

tics of these projects are summarized in table 2. We

choose these projects because they are open-source

systems that are known to be layered systems. Table

3 shows the results of executing the approach on

these projects using three different setups. We indi-

cate for each setup the values of the penalties that

were used when applying the layering algorithm.

During these experiments, we set the adjacency

penalty (α) to 0 for all these setups; we reward

downward adjacent dependencies. Table 3 shows for

each setup, the best ratio (computed as the number

of adjacent dependencies over the sum of all the

dependencies in the solution as discussed in section

3) found for all the iterations of the approach on a

system and the corresponding granularity of respon-

sibilities.

Layered solutions obtained during the experi-

ment and that correspond to the as-built architectures

of the analyzed systems are in grayed cells in table

3. Interestingly, we can notice that setup 2 is the one

that yields the best results in terms of the ratio of

adjacent dependencies. The explanation lies in the

fact that since the clustering step has already re-

solved some cyclic dependencies, a quite high value

of the back-call penalty δ (e.g., δ =4) is sufficient to

resolve the remaining cyclic dependencies. In this

regard, having the intra-dependencies penalty β

higher than the skip-calls penalty γ in setup 2, avoids

putting the remaining cyclic dependencies in the

same layer at the expense of the adjacent dependen-

RecoveringSoftwareLayersfromObjectOrientedSystems

cies. This answers our second research question

regarding the set of values of penalties (α, β, γ and δ)

that generate software layers that correspond to the

as-built architecture.

Table 2: Projects statistics.

Project

Numb. of

files

LOC

Numb. of

packages

Package

dependencies

JFreeChart

1.0.14

596 209711 37

225

JHotDraw

7.0.6

310 51 801 24

JUnit 4.10 162 10 402 28

107

Rhino 1.7 237 132634 15

JEdit 4.3 488 138046 28

154

Setting the back-call penalty δ to a very high

value as in setup 3, will ensure assigning to the same

layer the majority of the clusters involved in cyclic

dependencies. Hence, we expected setup 3 to be

more appropriate for systems where the number of

cyclic dependency remains very high in spite of the

clustering step. For instance, JEdit 4.3 has a very

high number of cyclic dependencies and we ex-

pected that setup 3 would yield the best results for

that system. However, the best ratio found for JEdit

4.3 corresponds to setup 2. This discrepancy can be

explained by the fact that JEdit 4.3 has some omni-

present packages which bias the recovery process.

Among these omnipresent packages is the package

with the namespace org.gjt.sp.jedit.* which uses

many packages and is in turn used by many other

packages.

Regarding the first research question, we ob-

served that the majority of the best ratios of desired

dependencies (i.e., the ratios of adjacent dependen-

cies over the sum of all the dependencies in the solu-

tion) are obtained when the granularity of responsi-

bilities is assigned a value of 3. In fact, when the

granularity of the responsibilities is too coarse (e.g.,

granularity=1 or 2), the clustering step results in

very few clusters (e.g., 2 clusters in the case of Rhi-

no 1.7, JFreeChart 1.0.14 and jEdit 4.3) and the

layering step in a too small number of layers (i.e.,

one to two layers). Furthermore, experimentations

also showed that the more the level of responsibili-

ties considered for clustering is far from the root's

one (e.g., granularity =5), the more the ratios of

desired dependencies decrease.

Table 3: Layering results.

Rhino JHo

D. JUni

JEdi

JFree.

Setup 1:

α =0, β =1,

γ = 2, δ = 4

Ratio

77% 85.55% 67.32 % 51.78% 53%

Granularity

3 2 3 4 3

Setup 2:

α =0, β =2,

γ = 1, δ = 4

Ratio

84% 84.98% 67.32 % 64.00% 59%

Granularity

3 2 3 4 3

Setup 3:

α =0, β =2,

γ = 1, δ = 8

Ratio

77% 84.98% 67.32 % 60.08% 55.41%

Granularity

3 2 3 3 3

Figure 7: The layering results of JHotDraw 7.0.6.

ENASE2014-9thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering

This is due to the fact that the majority of the gener-

ated clusters are singletons (i.e., they contain one

package), which weakens and sometimes nullifies

the impact of the clustering process on the layering

recovery.

In case of JHotDraw 7.0.6, the best layering so-

lution is obtained using setup 1 and for a granularity

of responsibilities of value 2. This solution is illus-

trated by figure 7 and it is pretty close to the one that

was built through a manual decomposition of the

source code. JHotDraw constitutes an “exception” as

it was designed as an example of a well-designed

framework. It contains less cyclic dependencies than

the other projects and its analysis yields the best

desired ratio for all setups when compared to the

ratios of the other projects. Another interesting fact

that came to our attention is that in the case of JUnit

4.10, a granularity of responsibilities equals to 3

produces the best and an identical layering organiza-

tion for each of the 3 setups. This indicates that for

this system, the clustering step led to a stabilization

of the layering results.

4.2 Threats to Validity

To validate our approach, we performed our prelim-

inary experiments on open-source systems that were

known to be layered systems. And since it was diffi-

cult to find experts to decompose these systems, we

manually verified the experimentation results. Nev-

ertheless, as future work, we need to carry out exper-

iments on industrial legacy systems to assess the

usefulness of our approach and generalize the re-

sults. Besides, the object-oriented systems we ana-

lyzed were all developed in Java. However, using

the KDM standard to represent them makes our

approach language and platform-independent and

therefore applicable to other types of systems. An-

other issue that could hinder the applicability of our

approach is its dependence on the MoDisco tool’s

robustness and scalability. Using other tools to gen-

erate the KDM representations of the analyzed sys-

tems will help addressing this threat.

5 RELATED WORKS

Many approaches have focused on the architectural

reconstruction and they mostly rely on clustering

techniques. Various clustering-based approaches are

discussed in (Maqbool and Babri, 2007) and (Shtern

and Tzerpos, 2012). Most of these approaches aim at

finding a clustering of the system that optimizes the

modularity of resulting packages (e.g., (Lung et al.,

2004), (El Boussaidi et al., 2012)). Our work is more

related to the approaches proposed to recover or

analyze layered architectures (e.g., (Sarkar et al.,

2009); (Lague et al., 1998); (Laval et al., 2012);

(Scanniello et al., 2010); (Müller et al., 1993);

(Tzerpos and Holt, 1996)).

Laval et al., (2012) proposed an approach, called

oZone, which removes undesired cyclic dependen-

cies prior to the decomposition of a system into lay-

ers. For this purpose, they rely on two heuristics to

resolve dependencies that belong to cycles and im-

pede the finding of layers of a system. These de-

pendencies are tagged by the proposed algorithm

and they are ignored when building layers of the

system. In (Sarkar et al., 2009), the authors proposed

3 layering principles (skip-call, back-call and cyclic

dependency) and a set of metrics that measure the

violation of these principles. Although these princi-

ples are focused on detecting violations, they are

related to the layer abstraction uniformity and in-

cremental layer dependency properties as defined in

this paper. Nevertheless, unlike both (Laval et al.,

2012) and (Sarkar et al., 2009), we address the layer-

ing recovery process without relying on any heuris-

tic to resolve the cyclic dependencies problem.

Scanniello et al., (2010) proposed a semi-

automatic approach aiming at recovering software

layers. In their approach, the uppermost layer com-

prises the classes that rely on many other classes,

while the lowermost layer is made of the classes that

are used by many other classes. The middle layer

comprises in turn the remaining classes. In both

(Laval et al., 2012) and (Scanniello et al., 2010), it is

assumed that a module that does not have fan-out-

dependencies belongs to the lowest-level layer and

conversely a module that does not have fan-in de-

pendencies belongs to the highest-level layer. How-

ever, when a module represents a common subtask

exclusive to packages of a middle-level layer, this

module will not have any fan-out dependency but

still belongs to this middle-level layer. Likewise, a

module that starts some specific service of a middle-

layer may not have any fan-independency but still

belongs to this middle-level layer.

Lague et al., (1998) developed a framework for

analyzing layered systems to evaluate the coherence

between the description of the architecture given in

design documents and the actual source code's struc-

ture. Their framework relies on a set of questions for

evaluating the properties of a layered system and a

set of metrics that help answering these questions.

This empirical study has shown that strict layering is

not enforced in layered systems as skip-calls are

made extensively however there are no back-calls.

RecoveringSoftwareLayersfromObjectOrientedSystems

Though the framework does not support the recov-

ery of the layered architecture, its results helped us

adjust our skip-call cost parameter compared to the

intra and back-call cost parameters.

Tzerpos and Holt (1996) propose a “hybrid” pro-

cess to reconstruct software architectures. This pro-

cess is based on various steps including: selecting

the domain model; retrieving the facts from the

source code and from the files' names; clustering the

facts into subsystems based on naming conventions,

directory structure or automatic clustering tech-

niques; creating successive structural diagrams that

are refined by the developers. Müller et al., (1993)

propose an approach aiming at supporting users in

discovering, restructuring and analyzing subsystem

structures using a reverse engineering tool. The pro-

posed process involves the identification of the lay-

ered subsystem structures. The layered structure is

obtained through the clustering of system's packages

into building blocks using composition operations

among which the composition by name. Similarly to

(Tzerpos and Holt, 1996) and (Müller et al., 1993),

our layering recovery process involves a naming-

based clustering step. However, our clustering step

is focused on the recovery of the layers' responsibili-

ties while theirs targets the ease of the system's man-

ageability and understandability. Besides, in

(Tzerpos and Holt, 1996) and (Müller et al., 1993)

the maintainer has to intervene in most of the recov-

ery process's steps, while in our approach the main-

tainer only needs to validate the layering results.

6 CONCLUSION AND FUTURE

WORK

In this paper, we proposed an approach that aims at

recovering the layered architecture of object oriented

systems. This approach attempts to cluster the pack-

ages of the system under analysis to build clusters of

the system’s responsibilities. The resulting clusters

are then assigned to layers so as to minimize the

layers’ dependencies that violate the layered archi-

tecture and maximize dependencies between adja-

cent layers. To do so, we introduced a set of layers

dependency metrics and we used these metrics to

formalize the layering of clusters of packages as an

optimization problem. The challenge in this context

is to find the appropriate granularity to consider

when clustering responsibilities.

We applied the approach on five open-source

systems and we manually assessed the resulting

layered architectures. The results were very promis-

ing as illustrated in section 4. Our approach has two

main advantages: 1) it does not rely on heuristics to

resolve cyclic dependencies and 2) it is language and

platform independent as it relies on the KDM speci-

fication standard. Moreover, it supports the interac-

tion with users and domain experts to refine the

layering results.

While we continue to refine the principles and

metrics of our approach, we need to perform more

experiments and analyses to properly tune the penal-

ties used by our layering algorithm. In this context,

we intend to conduct experiments on industrial sys-

tems and get the feedback from these systems' ex-

perts in order to validate the resulting layered archi-

tectures and assess the usefulness of our approach.

In the short term, we plan to apply the approach on

larger open source systems (e.g., Mozilla and Ant)

and to compare our results with other approaches.

We also envision improving our fact extractor in

order to get a richer and more accurate representa-

tion of the analyzed systems.

REFERENCES

Ulrich, W., Newcomb, P., 2010. Information systems

transformation: Architecture-Driven Modernization

Case Studies.OMG Press.

Shaw, M., Garlan, D., 1996, Software Architecture: Per-

spectives on an Emerging Discipline. Prentice Hall.

Stoermer, C., O'Brien, L., Verhoef, C., 2003. Moving

Towards Quality Attribute Driven Software Architec-

ture Reconstruction. In WCRE, (Vol. 3, p. 46).

OMG Specifications: http://www.omg.org/ [accessed in

March 2013]

Clements, P., Garlan, D., Bass, L., Stafford, J., Nord, R.,

Ivers, J., & Little, R., 2003. Documenting Software

Architectures: Views and Beyond. Addison-Wesley.

Bass, L., Clements, P., Kazman, R., 2003. Software Archi-

tecture in Practice. Addison-Wesley.

Tzerpos, V., Holt, R.C., 2000. ACDC: An Algorithm for

Comprehension-Driven Clustering. In WCRE.

Mitchell, B., Traverso, M., Mancoridis, S., 2001. An ar-

chitecture for distributing the computation of software

clustering algorithms. In Software Architecture,

2001.Proceedings.Working IEEE/IFIP Conference

on (pp. 181-190).IEEE.

Buschmann, F., Meunier, R., Rohnert, H., Sommerlad, P.,

Stal, M., 1996. Pattern-Oriented Software Architec-

ture: A System of Patterns. John Wiley & Sons.

Maqbool, O., Babri, H.A., 2007. Hierarchical Clustering

for Software Architecture Recovery. TSE, vol.33,

no.11, pp.759-780.

Lung, C-H., Zaman M., Nandi, A., 2004. Applications of

Clustering Techniques to Software Partitioning, Re-

covery and Restructuring. JSS, vol. 73, pp. 227–244.

Shtern, M., Tzerpos, V., 2012. Clustering Methodologies

ENASE2014-9thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering

for Software Engineering. Advances in Software Engi-

neering.

Zimmermann, H., 1980. OSI Reference Model--The ISO

Model of Architecture for Open Systems Interconnec-

tion. IEEE Transactions on Communications, vol.28,

no.4, pp.425-432.

Szyperski, C., 1998. Component Software. Addison Wes-

ley.

Eeles, P., 2002. Layering Strategies. Rational Software

White Paper, TP 199.

Sarkar, S., G. Maskeri, S. Ramachandran, 2009. Discovery

of architectural layers and measurement of layering

violations in source code. JSS, Vol. 82 (11), pp. 1891-

1905.

El Boussaidi, G., Boaye-Belle, A., Vaucher, S., Mili, H.,

2012. Reconstructing Architectural Views from Lega-

cy Systems. In WCRE, 2012, pp. 345-354.

Bourquin, F., Keller, R.K, 2007. High-impact Refactoring

Based on Architecture Violations. In CSMR '07, pp.

149-158.

Lague, B., LeDuc, C., Le Bon, A., Merlo, E.,Dagenais,

M., 1998. An analysis framework for understanding

layered software architectures. In IWPC, pp. 37-44

Laval, J., Anquetil, N., Bhatti, M.U., Ducasse, S., 2012.

OZONE: Layer Identification in the presence of Cy-

clic Dependencies. Science of Computer Program-

ming.

Scanniello, G., D'Amico, A., D'Amico, C., D'Amico, T,

2010. Architectural layer recovery for software system

understanding and evolution. SPE vol. 40(10), pp.

897-916.

Hautus, E., 2002. Improving Java software through pack-

age structure analysis.In International Conference on

Software Engineering and Applications.

Müller, H. A., Orgun, M. A., Tilley, S.R., Uhl, J.S.,

1993. A reverse engineering approach to subsystem-

structure identification. Journal of Software Mainte-

nance: Research and Practice ;5(4):181–204.

Hassan, A. E., Holt, R. C, 2002. Architecture recovery of

web applications. ICSE, pp. 349-359

Tzerpos, V., Holt, R. C., 1996. A Hybrid process for re-

covering software architecture. In Proceedings of the

1996 conference of the Centre for Advanced Studies

on Collaborative research (p. 38). IBM Press. 1996.

Achermann, F., Nierstrasz, O., 2000. Explicit Namespac-

es. In Modular Programming Languages (pp. 77-89).

Springer Berlin Heidelberg. 2000.

Boaye-Belle, A., El Boussaidi, G., Desrosiers, C., Mili, H.,

2013. The Layered Architecture revisited: Is it an Op-

timization Problem?. In SEKE.

Andreopoulos, B., An, A., Tzerpos, V., Wang, X., 2007.

Clustering large software systems at multiple layers.

Information & Software Technology 49(3): 244-254.

RecoveringSoftwareLayersfromObjectOrientedSystems