
Genome Mapping by a 60-core Processor
Tomohiro Yasuda and Asako Koike
Central Research Laboratory, Hitachi, Ltd., 1-280, Higashi-koigakubo, Kokubunji-shi, Tokyo, Japan
Keywords:
Genome Mapping, Many-core Processor, Multi-threading, Vector Operations.
Abstract:
Next-generation sequencing (NGS) has drastically changed researches based on DNA sequencing with its
high throughput and low costs. Mapping sequences generated by NGS sequences onto reference genomes is
an indispensable step to find useful knowledge for biological researches or clinical applications. To accelerate
genome mapping by using a new many-core processor Xeon Phi, two major mapping programs, BWA and
Bowtie2, were ported to Xeon Phi in this study. Although vector operations of Xeon Phi are not compatible
with those of x86 processors, these incompatibilities were successfully circumvented. In a computational
experiment where the ported programs were evaluated, the performances of the ported BWA and Bowtie2
peaked when 120 and 60 threads were used, respectively. These results imply that performances of BWA and
Bowtie2 can be improved by using tens of processing cores.
1 INTRODUCTION
Next-generation sequencing (NGS) has drastically re-
duced the cost of DNA sequencing by producing an
unprecedented amount of data. For example, HiSeq
2500 of Illumina, Inc. produces 600 Gbp in a single
run, which is 200 times as much as the sequence of
the human genome. A number of projects that aim
to sequence genomes of large cohorts using NGS are
in progress all over the world. For sequence analysis
based on NGS, it is necessary to compare NGS se-
quences and reference genome sequences, detect po-
sitions on the genome where each NGS sequence is
derived from, and find the differences between NGS
sequences and reference genome sequences. This
process, called mapping, is indispensable for various
analysis. For example, detection of single nucleotide
polymorphisms (SNPs) or structural variations (SVs)
needs a mapping step (1000 Genomes Project Consor-
tium, 2010). Because an enormous amount of NGS
sequences need to be analyzed, fast mapping methods
are required.
In addition to acceleration of mapping by fast soft-
ware tools (Li and Homer, 2010; Hatem et al., 2013),
acceleration by hardware has a great impact. As pre-
dicted by Moore’s Law, the performanceof computers
has been steadily increasing. However, improving the
performance of a single processing core has become
quite difficult these days. Computing performance
has therefore recently been improved mainly by in-
creasing the number of processing cores. For high-
performance computing (HPC), using GPUs (graph-
ics processing units) is attracting attention and has
achieved great success. Such an approach, called
general-purpose computing on GPUs (or GPGPU
for short), has also been applied to sequence align-
ment (Manavski and Valle, 2008; Klus et al., 2012;
Liu et al., 2013). However, a lot of complex optimiza-
tion techniques are required to maximize the perfor-
mance of GPGPU. Rewriting software programs for
GPGPU is therefore a hard task.
In 2012, Intel Corp. released a coprocessor
called Xeon Phi, which contains 60 processing cores
and can execute 240 threads simultaneously. Each
core has an x86-architecture-based design, which
is widely used in PCs and servers. This design
is a unique advantage of Xeon Phi, because the
same programming model for widely used x86 pro-
cessors can be applied for Xeon Phi. In addi-
tion, Xeon Phi has high peak performance. It has
computing performance of 1 TFLOPS with a single
board. The fastest supercomputer at Top500 in June
2013 (http://www.top500.org/lists/2013/06/), Tianhe-2
of China, contains 48,000 Xeon Phi’s and offers33.86
PFLOPS. Moreover, a research that aims to apply
Xeon Phi to sequence alignment has recently been re-
ported (Kurtz et al., 2013).
To accelerate mapping, we ported two famous
mapping tools, Burrows-Wheeler Aligner (BWA) (Li
and Durbin, 2009) and Bowtie2 (Langmead and
227
Yasuda T. and Koike A..
Genome Mapping by a 60-core Processor.
DOI: 10.5220/0004901702270232
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2014), pages 227-232
ISBN: 978-989-758-012-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Major incompatibilities of vector operations supported by Xeon Phi and x86.
difference Xeon Phi x86(SSE2)
vector number of registers 32 8
register bit width of elements 32 bits 16 or 8 bits
number of elements 16 8 or 16
alignment of memory 32-byte aligned (vectors containing 16-bit integers), 16-byte aligned
addresses 16-byte aligned (vectors containing 8-bit integers)
saturation operations No Yes
result of comparison mask register vector register
Salzberg, 2012), to Xeon Phi. The aim of porting is
to obtain exactly the same mapping results of BWA
and Bowtie2 on Xeon Phi as on x86 processors within
a much shorter time. As shown below, it was ex-
perimentally confirmed that the performances of the
ported BWA and Bowtie2 went up drastically when
the number of threads increased. Although their peak
performances had to be improved, this study is the
first step towards the acceleration of mapping by us-
ing Xeon Phi.
2 INCOMPATIBILITIES
BETWEEN Xeon Phi AND x86
BWA and Bowtie2 both use Farrar’s algorithm (Far-
rar, 2007) to reduce processing times. This algo-
rithm accelerates a well-known dynamic program-
ming (DP) algorithm for sequence alignment (Smith
and Waterman, 1981; Gotoh, 1982), which calculates
the optimal alignment of two sequences. Farrar’s al-
gorithm exploits vector operations of x86 processors,
called Streaming SIMD Extension 2 (SSE2). A single
instruction of SSE2 can conduct one of arithmetic op-
erations, comparison operations, logical operations,
etc. for vectors containing multiple integers. Because
Farrar’s algorithm is used, the source codes of BWA
and Bowtie2 include tens or hundreds of SSE2 oper-
ations. Although Xeon Phi also supports vector op-
erations, they are not compatible with those of x86.
The differences between vector operations of Xeon
Phi and x86 are summarized in Table 1. To port BWA
and Bowtie2 to Xeon Phi, all vector operations of x86
must be converted to those of Xeon Phi.
Moreover, the sort function of the C++ standard
template library (STL), used by Bowtie2, has an in-
compatibility between Xeon Phi and x86 (Figure 1).
This incompatibility must also be eliminated to obtain
exactly the same mapping results.
㸸
㸸
VRUWUHVXOW
RI[
VRUWUHVXOW
RI;HRQ3KL
Figure 1: An example of inconsistent results obtained by
the sort function in STL. In this example, a set of integer
pairs were sorted. Each pair consisted of a coordinate on the
genome and a score. Many pairs had the same scores (−4 or
−5). Because only scores were considered during the sort,
the orders of the pairs with the same score were different.
For example, the 12-th pair in the x86 result appeared as the
5-th result in the Xeon Phi. This difference caused different
outputs of Bowtie2 on Xeon Phi and on x86.
3 RESOLVING
INCOMPATIBILITIES
The incompatibilitiesbetween x86 and Xeon Phi were
overcome as explained in the following. To imple-
ment vector operations, compiler intrinsics were used
in the ported programs as in the original BWA and
Bowtie2.
3.1 Incompatibilities of Vector Registers
Bit Width of Vector Elements. The bit width of
vector elements is 32 bits on Xeon Phi, which is wider
than the bit width on x86 (8 or 16 bits). Because any
8-bit or 16-bit integer can be represented by a 32-bit
integer, 32-bit operations were used instead of 8-bit
or 16-bit operations.
However, a result of calculation by a 32-bit oper-
ation differs from that by an 8-bit or 16-bit operation
when overflow occurs. This difference was resolved
by emulating saturation operations as described later.
BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
228
ϬϬϬϬϭϮϯϰ
ELWV
ELWV
ϭϮϯϰ
ϭϮ
ELWV
ϬϬϬϬϬϬϭϮ
ELWV
ELWV
ELWV
ELWV
ELWV
GRZQ
FRQYHUVLRQ
XS
FRQYHUVLRQ
GRZQ
FRQYHUVLRQ
XS
FRQYHUVLRQ
YHFWRU
HOHPHQW
LQDYHFWRU
UHJLVWHU
RI;HRQ3KL
YHFWRU
HOHPHQW
VWRUHGLQ
PHPRU\
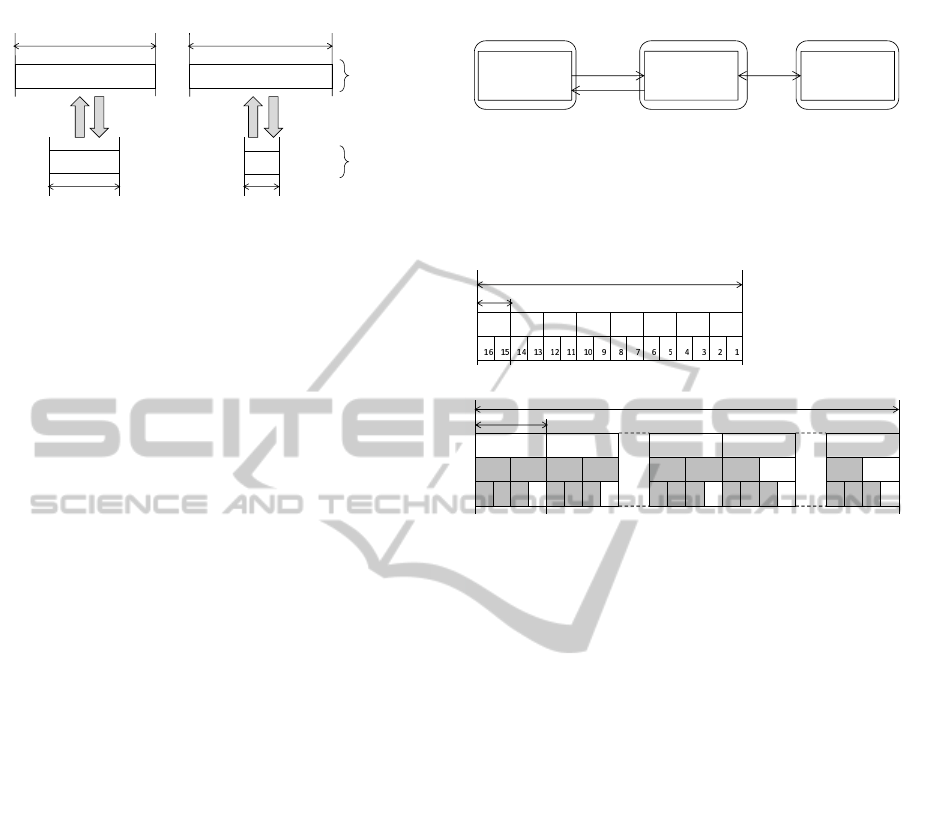
Figure 2: Up-conversion and down-conversion supported
by Xeon Phi. Both types of conversion change the bit width
of each element to fit it to the new vector. If the new bit
width is too small to store the element, the element is re-
placed by the maximum or the minimum value that can be
represented by the new bit width.
Alignment of Memory Addresses. Xeon Phi can
store a vector containing 32-bit integers in a vector on
memory containing 8-bit integers or 16-bit integers by
reducing the bit width of each element. This mecha-
nism is called down-conversion (Figure 2). The mem-
ory address for a vector containing 8-bit integers must
be 16-byte aligned, while the address for vectors con-
taining 16-bit integers must be 32-byte aligned. Simi-
larly, up-conversion converts a vector containing 8-bit
or 16-bit integers on memory into a vector containing
32-bit integers in a vector register. The address of an
up-converted vector on memory has to be aligned in
the same manner as that of a down-converted one.
In the original source codes of BWA or Bowtie2,
a memory address for a vector containing 16-bit in-
tegers may not be 32-byte aligned. This is not al-
lowed in Xeon Phi codes. To resolve this problem,
the following method (Figure 3) was adopted for min-
imizing the codes to be modified, because memory
addresses of vectors are 16-byte aligned in the orig-
inal source codes. Suppose that a vector containing
eight 32-bit integers that emulates a vector contain-
ing eight 16-bit integers is to be stored. First, a buffer
with enough size is prepared. Second, the vector con-
taining 32-bit integers is stored in this buffer as a
vector containing 16-bit integers by down-conversion.
Third, the stored vector is loaded as a vector contain-
ing sixteen 8-bit integers. Finally, the loaded vector
is stored in the final destination as a vector contain-
ing sixteen 8-bit integers that is an exact copy of the
vector stored in the buffer. Loading a vector was sim-
ilarly implemented.
Bits Shared by 16-bit and 8-bit Elements. A vec-
tor register of x86 is 128-bit wide and can be used
as either a vector containing eight 16-bit integers or a
vector containing sixteen 8-bit integers (Figure 4A).
Both vectors share all bits in a 128-bit vector register.
YHFWRU
FRQWDLQLQJHLJKW
ELWLQWHJHUV
YHFWRU
FRQWDLQLQJHLJKW
ELWLQWHJHUV
YHFWRU
FRQWDLQLQJHLJKW
ELWLQWHJHUV
YHFWRUUHJLVWHU
RI;HRQ3KL
EXIIHU
E\WHDOLJQHG
GHVWLQDWLRQDGGUHVV
E\WHDOLJQHG
GRZQ
FRQYHUVLRQ
XS
FRQYHUVLRQ
FRS\
DVDYHFWRU
RIVL[WHHQ
XQVLJQHG
ELW
LQWHJHUV
Figure 3: Memory access of a vector containing eight 16-bit
integers. Because the memory address of such a vector has
to be 32-byte aligned on Xeon Phi, such a vector is copied
from or to a 16-byte aligned address by using a buffer that
is 32-byte aligned.
Ă
ϭϲ
Ă
ϭϱ
Ă
ϵ
Ă
ϴ
Ă
ϭ
ď
ϴ
ď
ϭ
Đ
ϭϲ
Đ
ϭϱ
Đ
ϵ
Đ
ϴ
Đ
ϭ
ELWV
ELWV
ď
ϴ
ď
ϳ
ď
ϲ
ď
ϱ
ď
ϰ
ď
ϯ
ď
Ϯ
ď
ϭ
Đ
Đ Đ Đ Đ Đ Đ Đ Đ Đ Đ Đ Đ Đ Đ Đ
%YHFWRUUHJLVWHURI;HRQ3KL
$YHFWRUUHJLVWHURI[
ELWV
ELWV
Figure 4: Structures of vector registers of Xeon Phi and x86.
A: In the vector register of x86, a 16-bit element b
i
(1 ≤ i ≤
8) shares the same bits with 8-bit elements c
2i−1
and c
2i
.
B: In the vector register of Xeon Phi, a 32-bit element in
a vector, a
i
(1 ≤ i ≤ 16), is used to emulate both of 16-bit
elements b
i
and 8-bit elements c
i
in this study.
Therefore, two 8-bit elements c
1
and c
2
in Figure 4A,
for example, are stored in the same bits as a 16-bit ele-
ment b
1
. To obtain higher performance by exploiting
this fact, Bowtie2 uses a programming practice that
sets two flanking 8-bit elements to the same integer
k at once by setting one 16-bit element to an integer
256k + k. In our modified program ported to Xeon
Phi, however, vectors containing 16-bit integers and
those containing 8-bit integers share bits differently
(Figure 4B). Accordingly, such a programming prac-
tice of Bowtie2 was removed.
3.2 Emulation of Saturation Operations
Saturation operations are variations of arithmetic op-
erations. When positive overflow occurs, the result of
a saturation operation is replaced with the maximum
integer represented by the same bit width. Similarly,
when negative overflow occurs, the result of a satura-
tion operation is replaced with the minimum integer.
Because Xeon Phi does not support saturation opera-
tions, they were emulated in the following ways.
Max Operations and min Operations. A max op-
eration generates a new vector whose elements are
GenomeMappingbya60-coreProcessor
229

larger elements of those at the same positions in two
input vectors. A min operation similarly generates
a new vector containing smaller elements. Because
saturation operations forcedly replace results of arith-
metic operations with the maximum or the minimum
integer represented by the same bit width when over-
flow occurs, a max operation or a min operation was
inserted just after arithmetic operations to emulate
this replacement. In the case of vectors containing
signed 16-bit integers, for example, the modified op-
eration is explained with the following mathematical
expressions. Let a and b be input vectors, c be an
output vector, and x
i
be the i-th element in a vector x,
where x is one of a, b, and c. By using these notations,
the modified operation for addition is represented by
the following expression:
c
i
:= min{2
15
− 1, a
i
+ b
i
}.
Here, it is assumed that b
i
≥ 0 for all i. Similarly, for
subtraction,
c
i
:= max{−2
15
, a
i
− b
i
}.
Down-conversion. Down-conversion replaces any
32-bit element in a vector register with the maximum
or the minimum integer represented by the bit width
of the vector stored, if the element cannot be repre-
sented by the bit width. The rule of replacement is
the same as that of saturation operations. Therefore,
down-conversionwas used to emulate a saturation op-
eration if the result of a saturation operation was im-
mediately stored in the memory.
3.3 Comparison Operations
Both Xeon Phi and x86 support comparison opera-
tions, which compare each element of two vectors one
by one. In x86, the results of a comparison operation
is stored in a vector, whose element is set to −1 if
a specified condition is satisfied and to 0 otherwise.
For example, the equality of elements in two vec-
tors (1, 2, 3, 4, 5, 6, 7, 8) and (1, 2, 3, 4, 4, 3, 2, 1) is rep-
resented by a new vector (−1, −1, −1, −1, 0, 0, 0, 0).
Xeon Phi, on the contrary, stores the results of a com-
parison operation in a special register, called a mask
register. A mask register is 16-bit wide. Each bit in
the register correspondsto a comparison result of each
pair of corresponding elements in two compared vec-
tors. Because of this difference, all operations that
depend on the comparison results had to be rewritten.
Interestingly, the most of comparison operations
in the original Bowtie2 codes compare identical vec-
tors and determine their equality, resulting in a vec-
tor whose elements are all −1. In other words, com-
parison operations are used for the purpose of filling
vectors with −1. Such comparison operations were
replaced with a macro
_mm512_set1_epi32
, which
sets all elements in a vector to a given integer.
3.4 Other Incompatible Vector
Operations
In spite of the above-described rewriting, there were
extra x86 instructions not implemented in Xeon Phi.
These instructions were rewritten as follows.
Filling a Vector with a given Integer. Instruction
_mm_insert_epi16
sets a single specified element in
a vector to a given integer. On the other hand, instruc-
tion
_mm_shufflelo_epi16
swaps four rightmost el-
ements in a vector containing eight 16-bit integers.
They are not implemented in Xeon Phi and cannot be
easily replaced even with multiple instructions. How-
ever, these two instructions were always used together
for the purpose of setting all elements in a vector to
a given single integer. Therefore, they were replaced
with a single macro
_mm512_set1_epi32
that con-
ducts the desired operation.
Shifting Vector Elements to the Left. When ap-
plied to a vector a, instruction
_mm_slli_si128
mod-
ifies each element in a as follows:
a
k
:=
a
k−i
if k− i ≥ 1,
0 otherwise,
(1)
where i and k are non-negative integers such
that 1 ≤ i, k ≤ 16. When i = 1, for ex-
ample, a vector (a
16
, a
15
, a
14
, . . . , a
2
, a
1
) becomes
(a
15
, a
14
, a
13
, . . . , a
1
, 0).
Because i is always one in the source code of
BWA and Bowtie2, the instruction was emulated with
the following two steps. First, all elements except
the rightmost one are appropriately set by instruction
_mm512_permutevar_epi32
, which sets each ele-
ment in a vector to any element in the same vector.
In this step, a vector (a
16
, a
15
, a
14
, . . . , a
2
, a
1
) is modi-
fied to be (a
15
, a
14
, a
13
, . . . , a
1
, a
1
). Second, the right-
most element is set to zero by copying the rightmost
element in a vector whose elements are all zeros. A
mask register was used to implement this copy opera-
tion.
Shifting Vector Elements to the Right. Similarly,
_mm_srli_si128
modifies each element in a as fol-
lows:
a
k
:=
a
k+i
if k+ i ≤ n,
0 otherwise,
(2)
where n is the number of elements in a. Un-
like
_mm_slli_si128
,
_mm_srli_si128
is also used
BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
230
when i 6= 1 in the source codes of BWA and Bowtie2.
However,
_mm_srli_si128
is used only in the fol-
lowing two cases.
1. Setting all elements except the rightmost one to
zero:
To emulate the operation in this case, the right-
most element was copied to a vector whose ele-
ments are all zeros by using a mask register.
2. Choosing the largest element in a vector:
To emulate the operation in this case, a single
macro
_mm512_reduce_max_epi32
of Xeon Phi,
which conducts the desired operation by itself,
was used.
3.5 Sort Function of STL Library
The sort function and other functions called by the
sort function were extracted from the source code
of STL. The extracted functions were then integrated
into the source code of Bowtie2. This integration pro-
duced exactly the same mapping results on Xeon Phi
as on x86.
4 RESULTS OF EVALUATION
The ported BWA and Bowtie2 programs were eval-
uated on a Linux server with Xeon Phi 5110P (60
cores, 1.053 GHz, 8 GB RAM). NGS sequence data
used for evaluation were those of a Japanese per-
son (ERR246054) sequenced in the 1000 Genomes
Project (1000 Genomes Project Consortium, 2010).
They consisted of 1,809,507 pairs of NGS sequences
whose length was 100 bases each. Processing times
of BWA and Bowtie2 for 1, 4, 8, 16, 30, 60, 120, 240,
and 480 threads were measured. Whenever the exe-
cuted process finished normally, the mapping results
were exactly the same as the results obtained by the
original BWA and Bowtie2 on x86 processors.
To obtain mapping results, BWA must be in-
voked two times with aln subcommand, and once
with sampe subcommand. Because aln subcommand
is much more time consuming than sampe subcom-
mand, we focused on the processing time of aln sub-
command and evaluated its processing time as that of
BWA.
The processing times of mapping ERR246054 se-
quences onto chromosome 1 by the ported BWA and
Bowtie2 are shown in Figures 5 and 6 and listed in Ta-
ble 2. The performances went up almost proportion-
ally to the number of threads (up to 30 threads), and
peaked when 60 or 120 threads were used. However,
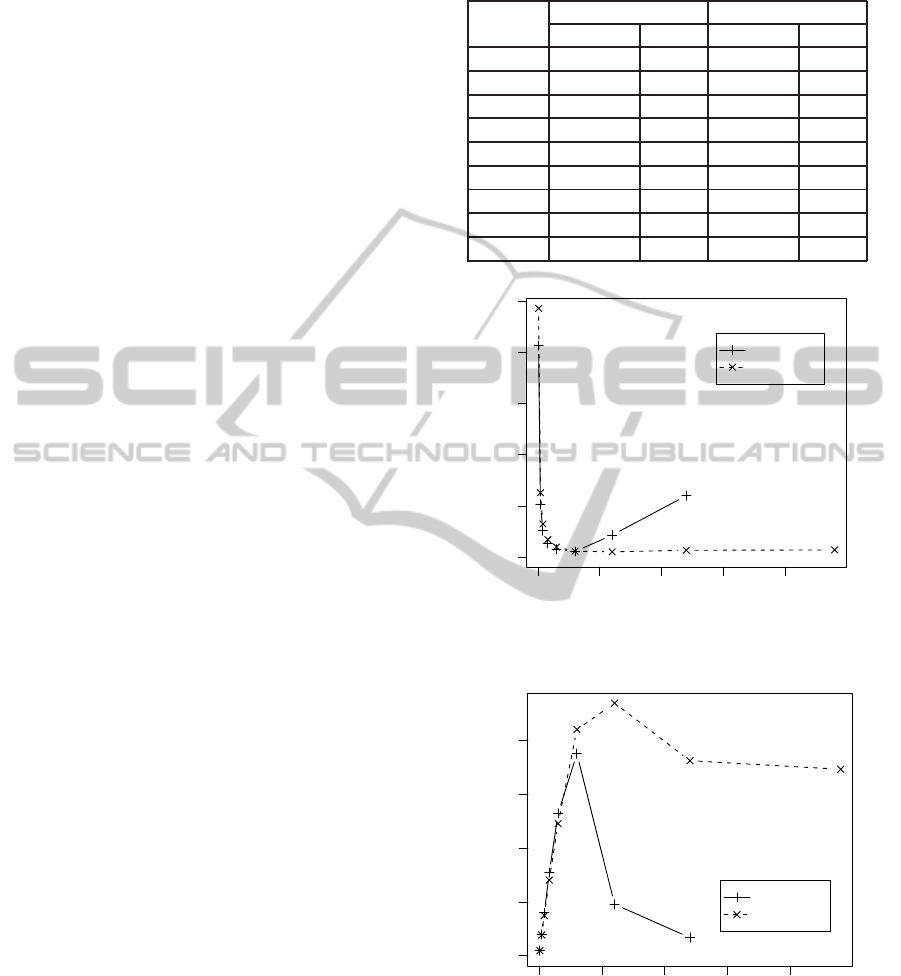
Table 2: Processing times for ERR246054. Bowtie2 did not
work with 480 threads. All times are in seconds.
no. processing time ratio
threads Bowtie2 BWA Bowtie2 BWA
1 8261 9723 1.0 1.0
4 2060 2516 4.0 3.9
8 1038 1295 8.0 7.5
16 534 688 15.5 14.1
30 312 395 26.5 24.6
60 220 231 37.6 42.1
120 860 207 9.6 47.0
240 2401 268 3.4 36.3
480 N/A 280 N/A 34.7
0 100 200 300 400
0 2000 4000 6000 8000 10000
number of threads
processing time [sec]
Bowtie2
BWA(aln)
Figure 5: Processing times for ERR246054.
0 100 200 300 400
0 10 20 30 40
number of threads
ratio of improvement
Bowtie2
BWA(aln)
Figure 6: Performance improvement for ERR246054.
using more than 120 threads deteriorated the perfor-
mance. One possible reason is that the amount of
communications between cores and the memory ex-
ceeded the capacity of the internal ring bus of Xeon
Phi when 120 or more threads were used. It can thus
GenomeMappingbya60-coreProcessor
231

be concluded that while Xeon Phi has 60 cores that
can execute four threads each, the number of threads
executed by each core should be one or two to get the
best performance on Xeon Phi for BWA and Bowtie2.
Meanwhile, a quad-core x86 CPU, Core i7 920
2.67GHz, did the same task by using eight threads
in 145 and 190 seconds for Bowtie2 and BWA, re-
spectively. Accordingly, this study is only the first
step towards acceleration of genome mapping by us-
ing Xeon Phi.
5 CONCLUDING REMARKS
Two well-known mapping tools, BWA and Bowtie2,
were ported to a many-core processor Xeon Phi. Pri-
mary obstacles in porting BWA and Bowtie2 were in-
compatibilities of vector operations used in these pro-
grams. These incompatibilities were circumvented by
emulating vector operations of x86 processors with
those of Xeon Phi. In a computational experiment,
it was confirmed that the more threads were used up
to 60 threads, the higher the performances of ported
programs were. The peak performances for BWA and
Bowtie2 were observed when 120 and 60 threads are
used, respectively. These results imply that using tens
of threads on the many-core processor Xeon Phi is
very much promising for accelerating mapping. In
addition, the ported programs successfully generated
exactly the same mapping results as the original BWA
and Bowtie2.
In future, the performances of BWA and Bowtie2
on Xeon Phi are expected to be further improved by
three ways. First, fully exploiting computation power
of Xeon Phi; for example, using all 32 vector regis-
ters at once. In this study, only vector operations of
x86 that has eight 128-bit vector registers were em-
ulated. Second, using Xeon Phi with x86 processors
in a coordinated manner. This enables x86 processors
and Xeon Phi to execute steps that fit their respective
architectures. Because the latest x86 processors are
faster than Xeon Phi for single-threaded processes,
steps that cannot be concurrently executed should be
done on x86 processors. Third, improving the rewrit-
ten code; for example, removing max operations and
min operations when results of mapping are not af-
fected by removal.
The hardware of Xeon Phi will also be updated.
The current release of Xeon Phi, codenamed Knights
Corner, is only the first product of a lineup of many-
core processors. It adopts a ring bus that becomes
a bottleneck when a large amount of data is moved
between cores and the memory. As new designs
come out, the architecture of Xeon Phi will evolve to
provide low-latency and high-bandwidth communica-
tions between cores.
REFERENCES
1000 Genomes Project Consortium (2010). A map of hu-
man genome variation from population-scale sequenc-
ing. Nature, 467(7319):1061–1073.
Farrar, M. (2007). Striped smith-waterman speeds database
searches six times over other simd implementations.
Bioinformatics, 23(2):156–161.
Gotoh, O. (1982). An improved algorithm for matching
biological sequences. Journal of Molecular Biology,
162(3):705 – 708.
Hatem, A., Bozdag, D., Toland, A., and Catalyurek, U.
(2013). Benchmarking short sequence mapping tools.
BMC Bioinformatics, 14:184.
Klus, P., Lam, S., Lyberg, D., Cheung, M., Pullan, G., Mc-
Farlane, I., Yeo, G., and Lam, B. (2012). Barracuda -
a fast short read sequence aligner using graphics pro-
cessing units. BMC Research Notes, 5:27.
Kurtz, M., Esteban, F. J., Hern´andez, P., Caballero, J. A.,
Guevara, A., Dorado, G., and G´alvez, S. (2013).
Many-core Tile64 vs. multi-core Intel Xeon: Bioinfor-
matics performance comparison. In VI Latin Ameri-
can Symposium on High Performance Computing HP-
CLatAm 2013, pages 134–144.
Langmead, B. and Salzberg, S. L. (2012). Fast gapped-read
alignment with Bowtie 2. Nat Meth, 9(4):357–359.
Li, H. and Durbin, R. (2009). Fast and accurate short read
alignment with Burrows-Wheeler transform. Bioin-
formatics, 25(14):1754–1760.
Li, H. and Homer, N. (2010). A survey of sequence
alignment algorithms for next-generation sequencing.
Briefings in Bioinformatics, 11(5):473–483.
Liu, Y., Li, J.-Y., Mao, Y.-Q., Wang, X.-L., and Zhao, D.-S.
(2013). A literature evaluation of CUDA compatible
sequence aligners. In Bioinformatics 2013.
Manavski, S. and Valle, G. (2008). CUDA compatible GPU
cards as efficient hardware accelerators for smith-
waterman sequence alignment. BMC Bioinformatics,
9(Suppl 2):S10.
Smith, T. and Waterman, M. (1981). Identification of com-
mon molecular subsequences. Journal of Molecular
Biology, 147(1):195 – 197.
BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
232
