
Multiagent Approach for Effective Disaster Evacuation
Yasuki Iizuka
1
, Katsuya Kinoshita
1
and Kayo Iizuka
2
1
Dept. of Mathematical Sciences, Tokai University, Hiratsuka, Japan
2
School of Network and Information, Senshu University, Kawasaki, Japan
Keywords:
Disaster Evacuation, Distributed Constraint Optimization Problem.
Abstract:
At times of disaster, or immediately prior to such periods, smooth evacuation is a key issues. However, it is
difficult to achieve, because people tend to panic when faced with disaster. This paper proposes a system that
supports effective evacuation from danger using the framework of the Distributed Constraint Optimization
Problem (DCOP). The use of the DCOP facilitates the assisted optimization of people’s evacuation timing
without a center server. This system enables assistance in terms of evacuation guidance to be given to relieve
congestion, by calculating evacuation timing via an ad-hoc network of evacuees’ mobile devices (phones, PCs,
etc.). In this paper, we focus on the formalization of the disaster evacuation problem and how to solve it using
the framework of the Distributed Constraint Optimization Problem.
1 INTRODUCTION
Much effort has been expended in improving dis-
aster prevention countermeasures. Although most
of the countermeasures that have been implemented
are classified as Public-help, which are implemented
by the public sector, many people survive in times
of disaster based on Self-help (countermeasures im-
plemented by individuals) and Mutual-help (counter-
measures implemented based on mutual help). There-
fore, Mutual-help and Self-help are attracting much
attention (CabinetOffice, 2011).
At times of disaster, or immediately prior to such
periods, smooth evacuation is a key issues. However,
it is difficult to achieve, because people tend to panic
when faced with disaster, crowding evacuation pas-
sageways of buildings in the event of fire and con-
gesting roads with cars containingpeople fleeing from
predicted hurricanes.
Therefore, although evacuation guidance is very
important, the disaster countermeasure office would
be unable to guide all evacuees intensively at the time
of a disaster. Evacuees need to take refuge based on
Mutual-help.
We aim to develop a the system that provides op-
timal evacuation guidance autonomously at the time
of a disaster. The system uses the mobile devices of
evacuees, performs distributed calculation using the
frameworkof the Distributed Constraint Optimization
Problem (DCOP), and does not need a center server.
In this paper, we focus on the formalization of the dis-
aster evacuation problem and how to solve it using the
frameworkof the Distributed Constraint Optimization
Problem.
2 DISASTER EVACUATION
The authors designed and developed a real-time dis-
aster information mapping system aimed at conjugat-
ing facilities such as university campuses for the pur-
pose of assisting Mutual-help (Iizuka et al., 2011).
This system is a web based system that can handle
disaster situation information in places such as uni-
versity campuses by level of detail, such as class-
rooms or laboratories in the school buildings by us-
ing Wi-Fi devices. It can aggregate the information
that is sent by users (informers), store it in a situation
database on the server and display a disaster situation
map to users on request. However, issues caused by
heavily-congested and crowded conditions were not
given sufficient consideration in the experiments de-
scribed above. In the case where an enormous num-
ber of evacuees have to move, or they have to pass
throughnarrowaisles, they may become confused and
evacuation may take longer. In such cases, a navigat-
ing system for evacuees would be effective, prevent-
ing them from rushing into a certain passageway, or
instructing them to wait just a few moments, in order
to meet the flow rate allowance.
223
Iizuka Y., Kinoshita K. and Iizuka K..
Multiagent Approach for Effective Disaster Evacuation.
DOI: 10.5220/0004905002230228
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 223-228
ISBN: 978-989-758-016-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Usage image of the disaster evacuation assist sys-
tem.
By using a system like that of (Iizuka et al., 2011),
people could know “which evacuation route is safe”
, the next issue is “how to evacuate safely and ef-
fectively.” However, smooth and effective evacua-
tion is not always easy. People tend to rush forward
to passageways that are perceived to be safe, which
results in congestion. The more people rush, the
greater the congestion. The provision of additional
appropriate information concerning evacuation guid-
ance may make it feasible to avoid congestion, and
shorten evacuation times.
Disaster countermeasures offices are set up in or-
ganizations in order to determine and provide ap-
propriate evacuation routes. However, planning and
providing appropriate information rapidly is not easy
with limited resources. Therefore, an effective disas-
ter evacuation assistance system is required to address
these issues.
Our proposed system facilitates the assisted opti-
mization of people’s evacuation timing, by estimat-
ing the location of evacuees. This system enables as-
sistance to be given in the form of evacuation guid-
ance to relieve congestion, by calculating evacuation
routes and timing via an ad-hoc network of evacuees’
mobile devices (phones, PCs, etc.), intercommunica-
tion function and location information. The mobile
devices must be equipped with wireless LAN (Wi-
Fi). Locations of evacuees are estimated by mobile
devices using the positional relationship between the
device and the wireless base station. The evacua-
tion route and timing of each evacuee are calculated
by distributed processing using the evacuees’ devices
connected by an ad-hoc network. The framework
of the Distributed Constraint Optimization Problem
(DCOP) is used in order to solve the problem. Figure
1 shows the concept of the system.
We assume the use of this system on a university
campus. University campuses have various unique
features and issues when considering disaster preven-
tion. For example, it is difficult to determine how
many people there are on campuses. There will be
many students studying in libraries, spare rooms, or
0
1
2
2
2
3
3
3
4
Agent
Destination
Evacuation zone
Figure 2: Model of evacuation zone.
cafeterias. Visitors can also use the open spaces. In
addition, administrative structural issues exist, which
are different from those in companies. University
campuses are a prime example of places that require
Mutual-help.
3 FORMALIZATION OF
EVACUATION
In this section we formalize the problem. The evacu-
ation covered in this paper is local adaptation evacu-
ation; we do not consider the planned evacuation of a
wide area
3.1 Formalization of Evacuation
In order to use the framework of the DCOP, it is
necessary formalize the disaster evacuation problem.
Thus, we considered the formalization as follows.
Evacuees with a mobile device are considered to
be agent A = {a
1
, ..., a
N
}.
P = ∪{p
1
, ..., p
M
} are the places from which peo-
ple must evacuate.
When agent a
l
is located in time t at place p
i
, it is
written as place(a
l
,t) = p
i
. L(t) is the set of places
of an agent who has not evacuated.
L(t) := ∪{place(a
i
,t) | place(a
i
,t) ∈ P } (1)
Agent a
i
is assumed to be capable of detecting the
number of nearby agents nr(a
i
).
At the time of a disaster, the situation is fluid. Peo-
ple may be unable to pass along a passage.
All places P
i
have a score of val(P
i
) ∈ N. This
score is assumed to decrease toward the refuge direc-
tion. It is assumed that the agent can search the evac-
uation routes, and calculate the scores for the areas
on the routes. In this paper, it is assumed that all the
agents’ score allocation is the same for simplification.
The above modeling can express P as a graph as
shown in Figure 2. At this time, utility function f of
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
224

Estimate of situation
planning
move
Time t
Using DCOP
Estimate of situation
planning
move
Time t+1
Estimate of situation
planning
move
Time t-1
Using DCOP
Using DCOP
Figure 3: Real-time planning problem.
the entire agent is as follows:
f(A,L ,t) :=
∑
{a
i
|place(a
i
,t)∈P }
val(place(a
i
,t))
nr(a
i
)
(2)
The numerator expresses the desire to evacuate, and
the denominator is a constraint to avoid congestion.
In this study, evacuation is considered to be a real-
time planning problem (shown in Figure 3.) The po-
sition after moving of the agent in time t + 1 may not
be the position that the system computed in the time t.
An agent may be unable to move according to the sit-
uation which a system cannot know, or an agent may
not follow the guidance of a system.
That is, the evacuation problem at time t is to solve
the following expression.
arg min
L
( f(A, L,t + 1) − f(A, L,t)) (3)
The above f(A,L ,t + 1) − f(A, L,t) is negative. By
solving this expression, the agent knows the appro-
priate evacuation timing. To solve this, we adopt the
DCOP framework.
It is necessary to consider the following conditions
further:
1. Short time to complete evacuation
2. Short continuous wait time of each agent
3. Fairness of the agent
3.2 Evacuation Problem as Distributed
Constraint Optimization Problem
The Distributed Constraint Optimization Problems
(DCOP) are the fundamental framework in dis-
tributed artificial intelligence and have recently at-
tracted considerable attention (Yokoo and Hirayama,
2000)D Algorithms used to solve DCOP include
ADOPT (Modi et al., 2005)C OptAPO (Mailler and
Lesser, 2004), DPOP (Petcu and Faltings, 2005)C
NCBB (Chechetka and Sycara, 2006), and distributed
stochastic search algorithms (DSA) (Zhang et al.,
2005). As for a complete algorithm, an optimum
solution is guaranteed, despite the extended comput-
ing time. When using DCOP for real-world prob-
lems, particularly when solving problems involv-
ing robotics and sensor networks, problems must
be solved in distributed environments with mini-
mal computationresources (Fitzpatrick and Meertens,
2001)(Zhang et al., 2005). Under such circumstances,
seeking an optimum solution with a complete algo-
rithm is not always the best method, and there is a
need for a fast and efficient approximation algorithm.
The Distributed Constraint Optimization Problem
(DCOP) is defined as a tuple < A, X, D, F > (Modi
et al., 2005)(Petcu and Faltings, 2005)D A set of vari-
ables X = {x
1
, x
2
, ..., x
n
} exists, each of which is as-
signed a value taken from a finite and discrete domain
D = {D
1
, D
2
, ..., D
n
}, and each of which is also as-
signed to multiple agents A = {a
1
, a
2
, ..., a
m
}. (n is
handled as n = m here for simplification purposes.)
Constraint function F = { f
ij
|D
i
×D
j
→ R} is defined
between x
i
and x
j
. The agent a
k
only has the follow-
ing information: information about x
k
, which is as-
signed to a
k
, and the cost function f
k∗
. In this case,
the purpose of DCOP is to obtain an assignment for
variable A that minimizes the summation of the cost
function F (A) =
∑
f
ij
(A) In DCOP, an assignment
A
o
that offers the minimum F (A
o
) amongst all pos-
sible assignments A is defined as the optimum solu-
tion. In DCOP, agents solve problems by exchanging
values of the variable through message transmission
with other agents whose variable are associated by
constraints. The framework of DCOP does not need a
center server in order to solve problems.
When treated as a distributed constraint optimiza-
tion problem, the evacuation problem can be consid-
ered as follows.
An agent has a variable to store the place to which
the agent should move. And the agent decides the po-
sition of the time t + 1 using DCOP in time t. This is
continuously performed as a real-time planning prob-
lem (Figure 3). The situation confirmation for every
step is indispensable. At this time, minimization of
Formula(2), i.e., minimization of Formula(3), is the
objective function. The denominator of Formula(2) is
the constraint of an agent’s move and can be described
by binomial constraint. The molecule of Formula(2)
becomes a unary constraint.
The above illustrate a simple application of
DCOP.
MultiagentApproachforEffectiveDisasterEvacuation
225
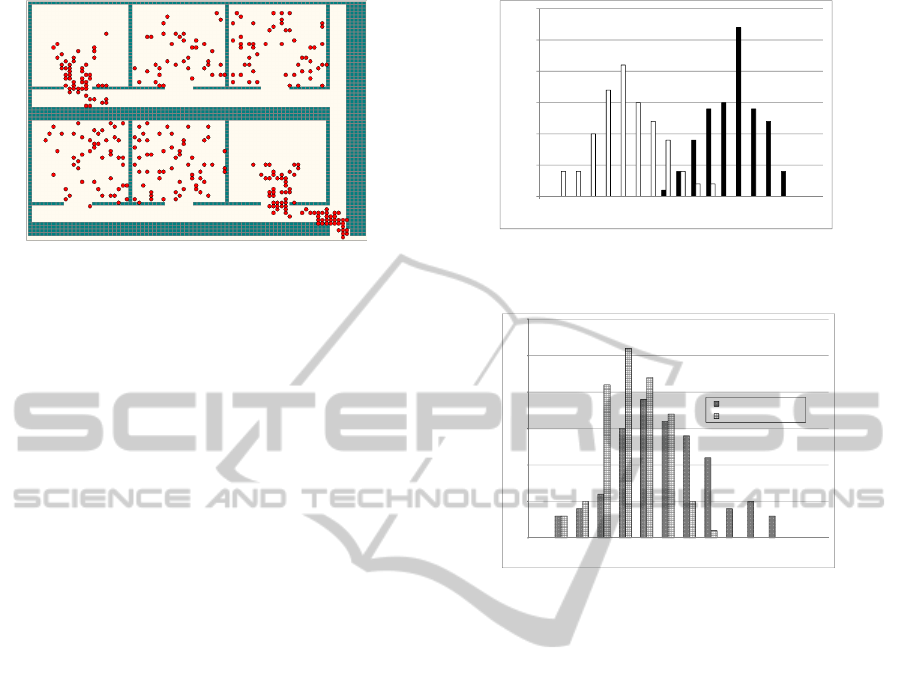
Figure 4: Multi-agent simulation of a disaster evacuation.
4 EXPERIMENT USING
MULTI-AGENT SIMULATION
A multi-agent simulation is often used for disaster
evacuation experiments, not only for disaster preven-
tion planning, but also building or city planning. We
conducted an experiment using multi-agent simula-
tion in order to investigate the validity of the proposed
system. In the experiment, we also investigated the
influence of an approximation algorithm to solve the
problem.
4.1 Experimental Conditions
We set up a 2-story school building with six rooms
for the experimental conditions. It was assumed that
the evacuation route was limited to only one accord-
ing to the disaster. The agents shall move rationally to
an evacuation place and agents move according to the
model of the crowd walking (Kaneda and Okayama,
2007). The evacuee’s psychological model is not used
in this experiment; the agent shall follow guidance if
guidance is available. The number of agents was set
to 400. The location of the classrooms and the simu-
lation image are shown in Figure 4.
Evacuation is started from the situation where
people are randomly distributed throughout the class-
rooms and passages. The evacuation guidance in this
experiment negotiates only the evacuation start timing
from each classroom by DCOP. If the population den-
sity of a passage becomes below the threshold value,
evacuation will be started from any one classroom on
each floor. DCOP shall be used for the selection of
the classroom that may start evacuation. In this ex-
periment, in order to solve DCOP, the approximation
algorithm DSA (Zhang et al., 2005) was used. It is
important to solve the problem in a short time in an
urgent situation such as disaster evacuation. In such
a case, an approximation algorithm is more suitable
0
5
10
15
20
25
30
250 254 258 262 266 270 274 278 282 286 290 294 298 302 306 310 314 318 322
Frequenc
y
Time(seconds)
Without guidance
With guidance
Figure 5: The frequency distribution of the evacuation com-
pletion time (with/without guidance).
0
5
10
15
20
25
30
250 254 258 262 266 270 274 278 282 286 290 294 298 302
Frequency
Time(seconds)
approximate solution
strict solution
Figure 6: The frequency distribution of the evacuation com-
pletion time (approximate solution/strict solution).
than complete algorithm. DSA is a randomized algo-
rithm.
4.2 Experimental Results
We compared evacuation completion time in cases
with and without evacuation guidance. If there is no
evacuation guidance, evacuation will be simultane-
ously started from all the classrooms, but if there is
evacuation guidance, evacuation will be started from
one classroom.
The simulation was performed 300 times under
this condition, and the frequency distribution of the
evacuation completion time of the result is shown in
Figure 5. The evacuation completion time was plot-
ted on the X-axis, and frequency was plotted on the
Y-axis. In this experimental result, when there was
evacuation guidance by DCOP, evacuation comple-
tion time decreased by about 10%. This effect should
change according to conditions such as the location of
the classrooms, width of the passage, etc.
The approximation algorithm DSA was used for
this experiment. For this reason, although evacua-
tion should have been ideally performed from any one
classroom of each floor, evacuation might have been
simultaneously performed from two classrooms. This
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
226

is a case where a strict solution cannot be found by
DSA.
The case where evacuationis performed only from
one classroom is called a strict solution. The fre-
quency distribution of only a strict solution is shown
in Figure 6. In the figure, the case of the approximate
solution was also plotted for comparison. Although a
significant difference was observed in these two as a
result of the t-test, the difference was very slight. In
this experiment, there were only three classrooms on
one floor, so the difference between the strict solution
and the approximate solution might be small.
5 RELATED WORK
(Lass et al., 2008) discussed the application of DCOP
to coordination in a disaster management situation.
Authorities must assign tasks and resources in dis-
aster scenarios; unfortunately accomplishing this in
real time is currently difficult. They argue the frame-
work of DCOP is uniquely suited to meet the require-
ments imposed of coordination mechanisms in these
settings. (Nguyen et al., 2012) extended DCOP to
Stochastic DCOP(SDCOP) in order apply it to dis-
aster management proposed by (Lass et al., 2008)D
In SDCOP, the constraint rewards are deterministic
values but are sampled from known probability dis-
tribution function called reward functions. And they
proposed an algorithm that solves SDCOP. These re-
searches are specialized in the resource (or shelter) as-
signment problem at the time of a disaster, and have
not made reference to evacuation guidance.
Evacuation problems can be modeled in dynamic
network flows (Hamacher and Tjandra, 2002)D The
standard approach to solving dynamic flow problems
is to transform the graph into a time-expanded net-
work. However, the expanded graph is larger.The
major computational bottlenecks are the time and
memory required to construct the expanded network.
Some heuristic algorithms have been proposed for
this problem (Hamacher and Tjandra, 2002)D (Lu
et al., 2005) considered capacity constrained routing
heuristics. (Hadzic et al., 2011) considered the prob-
lem of planning evacuation routes in deteriorating net-
works, where nodes become unavailable over time. In
these researchs of heuristic algorithms, it is assumed
that problem solving is performed in a non-distributed
environment.
There are also some related works concerning dis-
aster evacuation simulation systems using multi-agent
simulation (Burstedde et al., 2001) (Helbing et al.,
2000)(Shi et al., 2009).
6 CONCLUSIONS
We aim to develop a the system that provides optimal
evacuation guidance autonomously at the time of a
disaster. This system enables assistance to be given in
the form of evacuation guidance to relievecongestion,
by calculating evacuation routes and timing via an ad-
hoc network of evacuees’ mobile devices, without a
center server.
In this paper, the problem of disaster evacua-
tion was formalized and how to solve it using the
framework of the Distributed Constraint Optimiza-
tion Problem was examined. In the experiment us-
ing a multi-agent simulation, when evacuation guid-
ance using DCOP existed, the evacuation completion
time decreased by about 10%. And even when it was
solved with an approximation algorithm, the effect on
the evacuation completion time was small.
As the formalization in this paper is very simple, it
is necessary to introduce a more realistic model. The
fairness of an agent’s latency time, and minimizing
the total evacuation completion time should also be
written as a constraint. The fairness of latency time
will be realizable if an agent’s continuation latency
time is minimized. Therefore, it is necessary to write
the continuation latency time as a unary constraint.
Moreover, it is necessary to examine the guidance
method itself to ensure that people are able to follow
the guidance.
ACKNOWLEDGEMENTS
This work was supported in part by a JSPS Grant-in-
Aid for Scientific Research (25350481).
REFERENCES
Burstedde, C., Klauck, K., Schadschneider, A., and Zittartz,
J. (2001). Simulation of pedestrian dynamics using a
two-dimensional cellular automaton. Physica A: Sta-
tistical Mechanics and its Applications, 295(3):507–
525.
CabinetOffice (2011). Disaster Management In Japan.
Government of Japan.
Chechetka, A. and Sycara, K. (2006). No-commitment
branch and bound search for distributed constraint op-
timization. In Proceedings of the fifth international
joint conference on Autonomous agents and multia-
gent systems, pages 1427–1429. ACM.
Fitzpatrick, S. and Meertens, L. (2001). An experimen-
tal assessment of a stochastic, anytime, decentralized,
soft colourer for sparse graphs. In 1st Symposium on
Stochastic Algorithms: Foundations and Applications,
pages 49–64.
MultiagentApproachforEffectiveDisasterEvacuation
227

Hadzic, T., Brown, K. N., and Sreenan, C. J. (2011). Real-
time pedestrian evacuation planning during emer-
gency. In Tools with Artificial Intelligence (ICTAI),
2011 23rd IEEE International Conference on, pages
597–604. IEEE.
Hamacher, H. W. and Tjandra, S. A. (2002). Mathemat-
ical modelling of evacuation problems–a state of the
art. Pedestrian and evacuation dynamics, 2002(227-
266):1–2.
Helbing, D., Farkas, I., and Vicsek, T. (2000). Simu-
lating dynamical features of escape panic. Nature,
407(6803):487–490.
Iizuka, K., Iizuka, Y., and Yoshida, K. (2011). A real-time
disaster situation mapping system for university cam-
puses. In Ozok, A. and Zaphiris, P., editors, Online
Communities and Social Computing, volume 6778
of Lecture Notes in Computer Science, pages 40–49.
Springer Berlin / Heidelberg.
Kaneda, T. and Okayama, D. (2007). A pedestrian agent
model using relative coordinate systems. In Agent-
Based Approaches in Economic and Social Complex
Systems IV, pages 63–70. Springer.
Lass, R. N., Kopena, J. B., Sultanik, E. A., Nguyen, D. N.,
Dugan, C. P., Modi, P. J., and Regli, W. C. (2008).
Coordination of first responders under communication
and resource constraints. In Proceedings of the 7th
international joint conference on Autonomous agents
and multiagent systems-Volume 3, pages 1409–1412.
International Foundation for Autonomous Agents and
Multiagent Systems.
Lu, Q., George, B., and Shekhar, S. (2005). Capacity con-
strained routing algorithms for evacuation planning:
A summary of results. In Advances in spatial and tem-
poral databases, pages 291–307. Springer.
Mailler, R. and Lesser, V. (2004). Solving distributed con-
straint optimization problems using cooperative me-
diation. In in Proceedings of the Third International
Joint Conference on Autonomous Agents and Multia-
gent Systems, pages 438–445. IEEE Computer Soci-
ety.
Modi, P. J., Shen, W.-M., Tambe, M., and Yokoo, M.
(2005). Adopt: asynchronous distributed constraint
optimization with quality guarantees. Artif. Intell.,
(161):149–180.
Nguyen, D. T., Yeoh, W., and Lau, H. C. (2012). Stochas-
tic dominance in stochastic dcops for risk-sensitive
applications. In Proceedings of the 11th Interna-
tional Conference on Autonomous Agents and Multia-
gent Systems-Volume 1, pages 257–264. International
Foundation for Autonomous Agents and Multiagent
Systems.
Petcu, A. and Faltings, B. (2005). A scalable method for
multiagent constraint optimization. In IJCAI, vol-
ume 5, pages 266–271.
Shi, J., Ren, A., and Chen, C. (2009). Agent-based evacua-
tion model of large public buildings under fire condi-
tions. Automation in Construction, 18(3):338–347.
Yokoo, M. and Hirayama, K. (2000). Algorithms for dis-
tributed constraint satisfaction: A review. In Au-
tonomous Agents and Multi-Agent Systems, volume 3,
pages 198–212.
Zhang, W., Wang, G., Xing, Z., and Wittenburg, L. (2005).
Distributed stochastic search and distributed breakout:
properties, comparison and applications to constraint
optimization problems in sensor networks. Artif. In-
tell., (161):55–87.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
228
