SYNC-SOM

Double-layer Oscillatory Network for Cluster Analysis

A. V. Novikov and E. N. Benderskaya

Department of Computer Systems and Software Technologies, St.-Petersburg State Polytechnical University,

Polytechnicheskaya, St.-Petersburg, Russia

Keywords: Cluster Analysis, Kuramoto Model, Self-organized Feature Map, Oscillatory Network.

Abstract: Despite partial synchronization in the oscillatory networks based on Kuramoto model can be used for cluster

analysis, convergence rate of synchronization processes depends on number of oscillators and number of

links between oscillators. Moreover result of clustering depends on radius of connectivity that should be

chosen in line with input data. We propose double-layer oscillatory network for the two problems. Our net-

work relevant in situation when fast solution is required and when input data should be clustering without

expert estimations. In this paper, we presented results of experiments that confirmed better quality then tra-

ditional algorithms.

1 INTRODUCTION

Recent researches have suggested that synchroniza-

tion among neurons in the brain is used to imple-

ment the cognitive functions, for example, vision,

motion, memory (Haken, 2007). The oscillatory

networks provide biologically plausible and parallel

methods of modeling cognitive functions. The syn-

chronization processes in oscillatory networks have

been applied to various problems such as image

segmentation, cluster analysis, sound and image

recognition (Basar, 1998); (Cumin et al., 2006);

(Benderskaya et al., 2009).

The Kuramoto equation is one of the successful

models of synchronization among phases of oscilla-

tors (Kuramoto, 1984). However, convergence of

synchronization processes depends on number of

oscillators and degree of connectivity between oscil-

lators in networks that are based on Kuramoto mod-

el. For example, clusters may be elongate and placed

close to each other, in this case radius of connectivi-

ty (determines oscillators that should be connected)

should be chosen exactly before starting algorithm

of clustering. Improper radius will cause a false

allocation of clusters. Obviously, that a small radius

is the cause of small number of connections between

the oscillators in the network and as a result it is

cause of low level of convergence rate.

In this paper, we proposed a double-layer oscilla-

tory network SYNC-SOM that ensure faster conver-

gence rate without any estimation such as radius of

connectivity. The input layer is based on self-

organized feature map (SOM) that encodes input

features and the output layer based on oscillatory

network that uses Kuramoto model (Sync) performs

cluster analysis.

2 PRELIMINARIES

2.1 Self-organized Feature Map

Self-organized feature map is special class of artifi-

cial neural networks that are based on unsupervised

competitive learning (Kohonen, 2001). Each neuron

competes for its activation. Self-organization algo-

rithm is divided into three steps: competition, coop-

eration and adaptation.

Competition process finds the best vector w that

represents the weight with the smaller distance to the

input vector x (Haykin, 1999):





arg min .

i xxw

(1)

The neuron-winner determines the spatial location of

the topological neighborhood – cooperation process:



exp .















(2)

305

Novikov A. and Benderskaya E..

SYNC-SOM - Double-layer Oscillatory Network for Cluster Analysis.

DOI: 10.5220/0004906703050309

In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 305-309

ISBN: 978-989-758-018-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Parameter σ is effective width that affects the num-

ber of neurons that will be involved in the adaptation

process, and r

denotes the location of neuron i on

the map grid. Synaptic adaptation is the last step that

allows excited neurons (that are located in topologi-

cal neighborhood) to adjust its weight. In other

words excited neurons move closer to the input

vector:

    



jj j

tttt  ww xw

(3)

2.2 Kuramoto Model

Kuramoto model is able to ensure various type of

synchronization in networks with various structures

(Acebron et al., 2005); (Arenas et al, 2008). Dynam-

ic of the model described by following equation

(Kuramoto, 1984):



sin .

ii ji



 





(4)

Phase of oscillator θ

is basic state variable that dis-

poses in the range from 0 to 2π. Frequency ω

can be

considered as offset parameter. Coupling strength K

affects the rate and the type of synchronization. High

value of coupling strength ensures global synchroni-

zation and low value of coupling strength ensures

local synchronization or desynchronization.

The degree of synchronization between oscilla-

tors can be evaluated by estimate r that helps to

define state of synchronization (Kuramoto, 1984):











(5)

The state of global synchronization occurs when r

→ 1, global de-synchronization occurs when r → 0.

Partial synchronization occurs in case:

rKK

(6)

The degree of partial synchronization depends on

value of critical coupling strength K

that is depends

on the width of the frequency distribution of oscilla-

tor: K

= 2γ.

An important feature of the Kuramoto model is

possibility to provide synchronization processes in

networks with various communication structures.

We performed experimental study using numerical

simulations and found that states of global and par-

tial synchronization can be successfully sets in the

oscillatory networks with communication structures

such as grids, stars, bidirectional list and unidirec-

tional circular list.

2.3 Oscillatory Networks based on

Kuramoto Model

Oscillatory networks are nonlinear dynamic systems

where neuron (unit) is oscillating element that is

called an oscillator. The dynamic of the oscillatory

network is characterized by the type of synchroniza-

tion: global, local (partial) and desynchronization.

Local synchronization can be interpreted as a case of

clustering where each ensemble synchronous oscilla-

tors corresponds to one cluster.

The adapted model for oscillatory network that is

intended for cluster analysis (Miyano et al., 2007);

(Bohm et al., 2010):



sin .

iji













(7)

Each oscillator corresponds to only one input vector

from data set and coordinates of oscillator equals to

coordinates of corresponding object. Parameter N(θ

)

defines number of neighboring oscillators for oscil-

lator i. The set of oscillator neighbors depends on

connectivity radius ϵ that should be chosen in line

with input data.

Figure 1: Illustration of how connections are established

for oscillator in line with radius ϵ.

The connection is established between oscillators

if Euclidian distance (it can be other metric) between

less than connectivity radius ϵ.

We have investigated possibilities of the network

for cluster analysis using the widespread data set

FCPS (Ultsch, 2005). Experiments have shown

problems with elongate or with non-uniform density

clusters that are located closely next to each other,

for example, samples EngyTime, TwoDiamonds and

WingNut. It can be hard to choose right radius con-

nectivity or even impossible.

Moreover convergence rate of synchronization

processes depends on number of oscillators in net-

work based on Kuramoto model. For example, the

oscillatory network with grid structure has quadratic

dependence O(n

) and network with unidirectional

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

306

list structure has cubic dependence O(n

). Therefore

solution of data clustering may have cubic complexi-

ty in worst case.

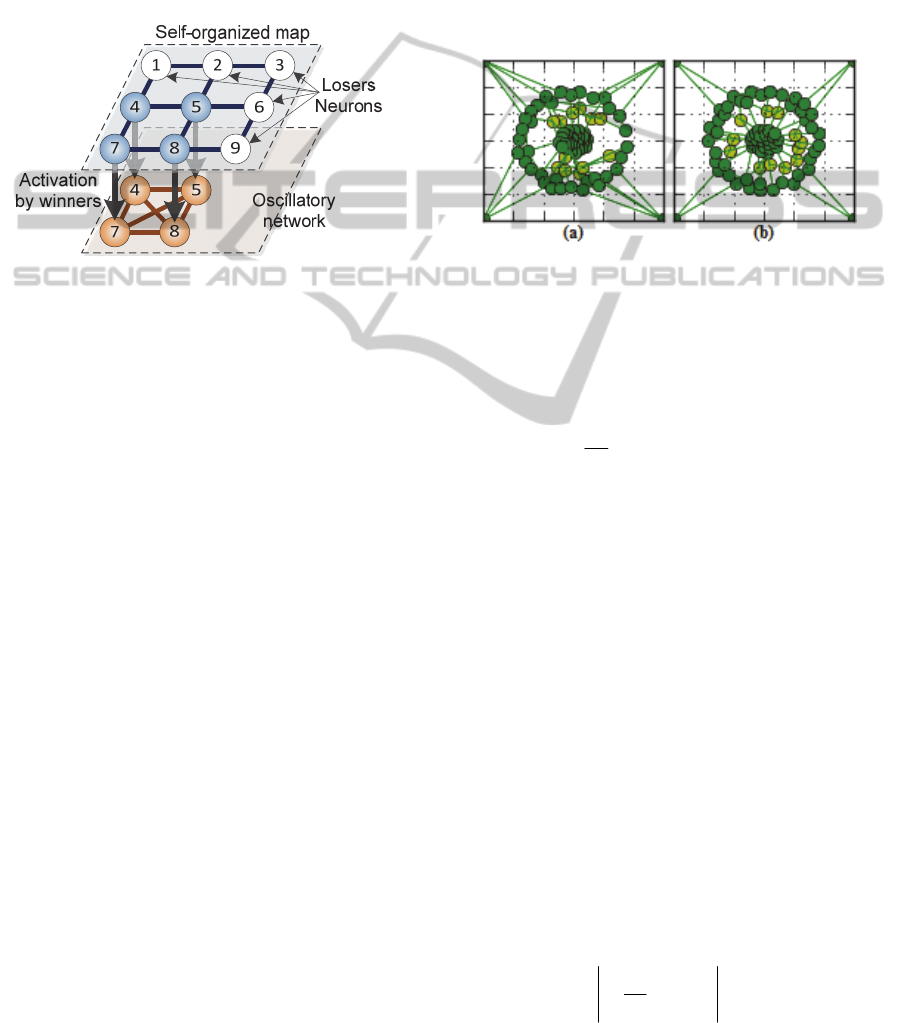
3 THE SYNC-SOM NETWORK

The proposed network SYNC-SOM consists of the

input and the output layers. The architecture of the

network presented on the figure 1.

Figure 2: The architecture of the SYNC-SOM oscillatory

network. The input layer encodes features from input data

set and the output layer performs clustering.

The input layer based on self-organized feature

map that reduces high dimensional input space to a

lower dimensional map space. Final state of input

layer defines number of active oscillators in the

output layer that usually equals to number of neu-

rons-winners. The input layer contains several prin-

ciple differences from conventional self-organized

map that will be described further.

Initial values of weights are initialized by ran-

dom values in the conventional algorithm and it has

a high influence on learning process (self-

organization process). In this case a neuron-winner

is random and spatial location of the topological

neighborhood that is defined each step of learning

becomes random too. And as a result it is the imme-

diate cause of maps with different topologies at the

end of learning process with the same data set.

Moreover, random initialization is cause of the for-

mation of areas in which high and low concentration

of neurons can occurs. Therefore some clusters can-

not be allocated properly by the second layer. It is

especially significant shortcoming for the sample

TwoDiamonds.

We propose to perform initialization of weights

by “uniform grid” in line with input data set. The

“uniform grid” represent rectangular grid that covers

input data in first two dimensions and distance be-

tween the nodes is the same in each of the two di-

mensions of data. Further the “uniform grid” should

be aligned with the center in other dimensions of

data. Thus coordinates of nodes of the “uniform

grid” define initial weights of neurons.

Our approach for the initialization ensures stable

results of learning process and prevents formation of

areas that are crowded by neurons, whereas in other

areas there is a lack of them. Example of difference

of formed featured maps is presented on figure 3.

Also we offer to abandon using of permutations of

objects of input data set during training on each step

as this reduces complexity of learning process, be-

cause complexity of the permutation is O(n!).

Figure 3: Difference of formed feature maps in cases (a)

the random and (b) the “uniform grid” initialization of

weights for the sample “Target”.

The output layer of SYNC-SOM is based on the

oscillatory network whose dynamics described by

the following model:



sin

iji





 





(8)

Number of oscillators N is defined by number of

winner-neurons in the input layer. Each neuron-

winner corresponds to only one oscillator and coor-

dinates of neurons from the input layer corresponds

to coordinates of oscillators in the output layer. The

proposed architecture ensures faster solution than

basic oscillatory neural networks based on Kuramo-

to model because the output layer uses significantly

fewer oscillators due to using neurons-winners of the

input layer instead of objects of an input data.

Connections between oscillators are formed if

Euclidean distance between them is less than aver-

age distance between approximately no more than

ten percent of the total number neurons-winners in

input layer. Additionally, U-matrix P-matrix (Ultsch,

2005), information about active and dead neurons

(losers) from the first layer can be used for forming

more accurate structure of the output layer.

Evaluation of the end of the process clustering r

is described as follows (Novikov et al., 2013):

ijN









(9)

SYNC-SOM-Double-layerOscillatoryNetworkforClusterAnalysis

307

Ending process synchronization (clustering) is indi-

cated when r

→ 1. Oscillators whose phases are

approximately equal to each other belong to the

same cluster with high probability, in other words

each ensemble of synchronous oscillators corre-

sponds to one cluster of data.

4 EXPERIMENTAL RESULTS

To illustrate how SYNC-SOM is used for cluster

analysis, we have performed study using data set

FCPS. Comparison has been performed with algo-

rithms such as K-Means (MacQueen, 1967), ROCK

(Guha et al., 2000), Hierarchical (Anil et al., 1988),

Sync (Bohm et al., 2010) and DBSCAN (Ester et al.,

1996). All experiments have been performed on a

workstation with Intel Core i5-2300 CPU 2.8 GHz

and 4.0 GB RAM.

We can confirm that the oscillatory network

SYNC-SOM is able to ensure accurate results of

clustering for all samples from the FCSP data set.

We have used 100 neurons in the input layer and

coupling strength K in the output was used equal to

1. Several SYNC-SOM results of clustering are

presented on figure 4. It’s important to note that

clusters can be allocated not only by final state of

the output layer. Sometimes global synchronization

can be reached and only one cluster can be allocated

in this case. Analysis of dynamics of the output layer

should be performed by dendogram that shows hier-

archical organization of clusters where uniting time

of clusters is main feature to determine the actual

number of clusters (Wang el al., 2009).

K-Means is not able to allocate clusters properly

from samples Lsun, Target, WingNut and several

others sample where clusters don not have Gaussian

or spherical distribution. Hierarchical algorithm has

problems with clustering Lsun, Target, Chainlink

due to using only minimization of the distance be-

tween objects, i.e. has troubles with elongated clus-

ters that are close to each other. Illustration that

shows shortcomings of K-means and Hierarchical

algorithm is presented on figure 5.

DBSCAN, Sync and ROCK algorithms success-

fully allocate clusters for all samples. DBSCAN

requires finely tuned parameters (number of trusted

neighbors and connectivity radius), especially, it’s

hard to find properly parameters for successful clus-

tering samples TwoDiamonds and WingNut, and

small parameter changes can lead to incorrect re-

sults. But obvious DBSCAN advantage is high per-

formance. Sync and ROCK are parameterized by

connectivity radius too, but they are more robust.

The Sync is robust due to possibility to allocate

clusters by the mentioned before dendogram in case

of global synchronization. And ROCK is robust due

to depth analysis of structures. However, they solve

the problem slowly compared with other considered

algorithms. Table 1 demonstrates comparison of rate

solving between the algorithms.

Figure 4: SYNC-SOM results of clustering. (a) Three

clusters for Lsun. (b) Six clusters for Target. (c) Two

clusters for TwoDiamonds. (d) Two clusters for WingNut.

Figure 5: Illustration of shortcomings. (a) K-means. (b)

Hierarchical.

Table 1: Execution time of various algorithms.

Sample

Algorithm (Execution time)

syncsom sync dbscan rock

Lsun 6.12 26.6 0.37 24.0

Target 12.8 74.3 1.78 174

Two

Diamonds

14.8 299 1.43 194

WingNut 21.1 423 2.30 397

Chainlink 21.7 72.0 2.96 383

Hepta 2.58 0.87 0.12 3.65

Tetra 5.70 127 0.39 24.5

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

308

The SYNC-SOM is much faster than Sync and

ROCK algorithms. Sync can be faster than SYNC-

SOM only for very small input data sets, for exam-

ple, the sample Hepta, because our algorithm spends

some time for encoding features.

5 CONCLUSIONS

In this paper we have proposed novel oscillatory

network SYNC-SOM for cluster analysis that is

based on Kuramoto model and on SOM. We have

investigated problems with convergence rate in the

conventional oscillatory network based on Kuramoto

model and problems with learning processes in

SOM. We have performed comparison with various

algorithms such as K-Means, DBSCAN, ROCK,

Sync and Hierarchical. Our experimental results

have confirmed ability of SYNC-SOM to perform

fast successful clustering.

REFERENCES

Acebron, J. A., Bonilla, L. L., Vicente, C. J. P., Ritort, F.,

and Spigler, R. (2005). The Kuramoto model: A sim-

ple paradigm for synchronization phenomena. Reviews

of modern physics, 77, 137–185.

Anil, K., Dubes, J. C., Dubes, R. C. (1988). Algorithms for

Clustering Data. Prentice Hall, Englewood Cliffs,

New Jersey.

Arenas, A., Diaz-Guilera, A., Kurths, Y. Moreno, Y.

Zhou, C. (2008). Synchronization in complex net-

works. Physics Reports, 469, 93–153.

Basar, E., (1998). Brain function and oscillations. Spring-

er-Varlag, New York.

Benderskaya, E. N., Zhukova, S. V. (2009). Large-

Dimension Image Clustering by Means of Fragmen-

tary Synchronization in Chaotic Systems. Pattern

Recognition and Image Analysis, vol. 10, no. 2, 306-

316.

Bohm, C., Plant, C., Shao, J., Yang, Q. (2010). Clustering

by synchronization. KDD ’10 Proceeding of the 16th

ACM SIGKDD international conference of Knowledge

discovery and data mining, 583-592.

Costa, J. A. F., Hujun, Y. (2010). Gradient-based SOM

Clustering and Visualisation Methods. In Proc. of the

2010 International Joint Conference on Neural Net-

works.

Cumin, D., Unsworth, C. P. (2006). Generalizing the

Kuramoto Model for the Study of Neuronal Synchro-

nisation in the Brain. Report University of Auckland

School of Engineering, 638.

Ester, M., Kriegel, H., Sander, J., Xu, Xiaowei, X. (1996).

A density-based algorithm for discovering clusters in

large spatial databases with noise. Proc. of the 2

Int.

Conf. on Knowledge Discovery and Data Mining, 226-

231.

Guha, S., Rastogi, R., Shim, K. (2000). ROCK: A Robust

Clustering Algorithm for Categorical Attributes. In

Proc. of the 15

Int. Conf. on Data Engineering.

Haken, H., (2007). Brain Dynamics, Springer-Verlag,

Berlin Neidelberg.

Haykin, S. (1999). Neural networks: A comprehensive

foundation. Macmillan College Publishing Company,

New York, 2

edition.

Kohonen, T. (2001). Self-Organizing Maps. 3

edition,

Berlin: Springer.

Kuramoto, Y. (1984). Chemical Oscillations, Waves, and

Turbulence. Berlin: Springer.

MacQueen, J. B. (1967). Some Methods for Classification

and Analysis of Multivariate Observations. Proc. Fifth

Berkley Symp. Math. Statistics and Probability, vol. 1,

281-297.

Miyano, T., Tsutsui, T. (2007). Data Synchronization as a

Method of Data Mining. International Symposium on

Nonlinear Theory and its Applications.

Novikov, A.V., Benderskaya E.N. (2013). The Oscillatory

Neural Networks Based on Kuramoto Model for Clus-

ter Analysis. The 11th International Conference "Pat-

tern Recognition and Image Analysis: New Infor-

mation Technologies" (PRIA-11-2013), vol. 1, 106-

109.

Ultsch, A. (2005). Clustering with SOM: U*C. Proceed-

ings Workshop on Self Organizing Feature Maps. Par-

is, France. 31-37.

Wang, X., Jiao, L Wu. J. (2009). Extracting hierarchical

organization of complex networks by dynamics to-

wards synchronization. Physica A, 388, 2975-2986.

SYNC-SOM-Double-layerOscillatoryNetworkforClusterAnalysis

309