A Pattern based Modelling for Self-organizing Multi-agent Systems with
Event-B
Zeineb Graja
1,2
, Fr
´
ed
´
eric Migeon
2
, Christine Maurel
2
, Marie-Pierre Gleizes
2
,
Linas Laibinis
3
, Amira Regayeg
1
and Ahmed Hadj Kacem
1
1
ReDCAD, Faculty of Economics and Management,University of Sfax, Sfax, Tunisia
2
IRIT, Paul Sabatier University, Toulouse, France
3
˚
Abo Akademi University, Turku, Finland
Keywords:
Self-organizing MAS, Formal Verification, Design Patterns, Refinement, Event-B.
Abstract:
Self-Organizing Multi-Agent Systems (SO-MAS) are defined as a set of autonomous entities called agents
interacting together in order to achieve a given task. Generally, the development process of these systems
is based on the bottom-up approach which focuses on the design of the entities individual behavior. The
main question arising when developing SO-MAS is how to insure that the designed entities, when interacting
together, will give rise to the desired behavior? Our proposition to deal with this question is to use formal
methods. We propose a correct by construction method for systematic design of SO-MAS based on the use
of design patterns and formal stepwise refinements. Our work gives guidelines to assist the designer when
developing the individual behavior of the entities and prove its correctness at the early stages of the design
process. The method is illustrated with the foraging ants’ case study.
1 INTRODUCTION
With the growing complexity of today’s applications,
Self-Organizing Multi-Agent Systems (SO-MAS) are
becoming more and more popular in the software en-
gineering domain. The main characteristic proper-
ties of these systems are decentralized control, robust-
ness and adaptability. Such qualities are very relevant
when designing complex applications since they al-
low the system to overcome from perturbations and
continue its execution autonomously and without any
external control. SO-MAS are defined as a set of au-
tonomous entities called agents, having a local knowl-
edge about their environment and interacting together
in order to achieve a given task. The global behavior
of the overall system emerges from the interactions
between the entities and their interaction with the en-
vironment ((Di Marzo Serugendo et al., 2005)). We
can distinguish two levels in a SO-MAS; the micro
level corresponding to the local behavior of agents
and the macro level referring to the global behavior
of the system.
Generally, the development of SO-MAS is based on
the bottom-up approach which focuses on the design
of the individual behaviour of the entities composing
the system. In order to validate the designed local be-
havior i.e. ensuring that the local behavior of entities
will give rise to the desired system behavior, design-
ers make use of simulation techniques. Our proposi-
tion to deal with SO-MAS validation is to take advan-
tage of formal techniques. We define a correct by con-
struction approach for systematic design of SO-MAS
based on the use of design patterns specified with the
Event-B formal language. The aim is to give guaran-
tees and proofs about the individual behavior correct-
ness at the early stages of the design process. More
precisely, we define three patterns: AGP
0
, GBP
0
and
SOP
0
. The first one gives a sequence of refinement
steps allowing the design of the individual behavior
of the agents and ensuring its correctness. The two
other patterns are devoted to prove the reachability of
the desired global behavior (GBP
0
) and the ability of
the system to self-adapt (SOP
0
). While the AGP
0
can
be expressed by Event-B and its correctness proved
directly by means of the Rodin platform, it was nec-
essary to move to the Linear Temporal Logic (LT L)
in order to specify the desired global properties of the
system. In order to carry on the proofs of the tempo-
ral properties, we are based on the work of Hoang and
Abrial described in (Hoang and Abrial, 2011).
229
Graja Z., Migeon F., Maurel C., Gleizes M., Laibinis L., Regayeg A. and Hadj Kacem A..
A Pattern based Modelling for Self-organizing Multi-agent Systems with Event-B.
DOI: 10.5220/0004906902290236
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 229-236
ISBN: 978-989-758-016-1
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

This paper is organized as follows. Section 2 de-
scribes a background on the Event-B language, design
patterns and LTL. Section 3, presents an overview
of the proposed methodology for the development of
SO-MAS and gives a detailed description of the de-
sign patterns used. Section 4 illustrates our work with
the foraging ants’ example. Section 5 presents a sum-
mary of related works. Section 6 concludes the paper
and draws futur perspectives.
2 BACKGROUND
2.1 The Event-B Formalism
The Event-B formalism was proposed by J.R. Abrial
(Abrial, 2010) as an evolution of the B language. The
concept used to make a formal development is that
of a model which can be a machine or a context.
While a context is the static part of a system, a ma-
chine is its dynamic part and allows describing the
behavior of the designed system. A machine is com-
posed by a collection of variables v and a set of events
ev
i
. The variables are constrained by conditions called
invariants. The execution of the events must preserve
these invariants. An event is described as follows.
ev
i
b=any p where G
evi
(p, v) then A
evi
(p, v,v
0
) end.
An event is defined by a set of parameters p, the
guard which gives the necessary conditions for the
activation of the event G
evi
(p,v) and the action
A
evi
(p,v,v
0
) which describes how variables v are sub-
stituted in terms of their old values and the param-
eters values. The action may consist in several as-
signments which can be either deterministic or non-
deterministic. A deterministic assignment, having the
form x := E(p,v) replaces values of variables x with
the result obtained from the expression E(p,v). A
non-deterministic assignment can be of two forms: 1)
x :∈ E(p, v) which arbitrarily chooses a value from
the set E(p, v) to assign to x and 2) x : |Q(p,v, x
0
)
which arbitrarily chooses to assign to x a value that
satisfies the predicate Q. Q is called a be f ore −
a f ter predicate and expresses a relation between the
previous values v and the new ones v
0
.
Proof Obligations. Proof Obligations (PO) are asso-
ciated to Event-B machines in order to prove that they
satisfy certain properties. As an example, we men-
tion the Preservation Invariant INV and the Feasibil-
ity FIS proof obligations. INV PO is necessary to
prove that invariants hold after the execution of each
event. Proving FIS PO means that when an event
guard holds, every action can be executed.
Refinement. The development of models in Event-
B is based on the principle of refinement. This tech-
nique, allowing a correct by construction design, con-
sists in adding details gradually while preserving the
original properties of the system. The refinement re-
lates two machines, an abstract machine and a con-
crete one. Data refinement consists in replacing the
abstract variables by the concrete ones. The refine-
ment relation is defined by a particular invariant called
gluing invariant. The refinement of an abstract event
is performed by strengthening its guard and reducing
non determinism in its action. The abstract parame-
ters can also be refined. In this case, we need to use
witnesses describing the relation between the abstract
and the concrete parameters. An abstract event can be
refined by more than one event. In this case, we say
that the concrete event is split. Event-B is supported
by the Rodin platform
1
which provides considerable
assistance to developers by automating the generation
and verification of all the necessary POs.
Design Patterns. In (Abrial and Hoang, 2008),
Abrial defines an Event-B design pattern as ”a small
model (with constants, variables, invariants, and
events) devoted to formalize a typical well known sub-
problem”. A design pattern is seen as a template of
a solution for a given problem that can be reused.
Reusability involves not only the model itself, but
also the proofs and the refinement associated with it
(Hoang et al., 2013). The pattern reuse requires es-
sentially two steps which are 1) the matching of the
pattern specification with the problem and 2) the in-
corporation of the refinement of the pattern to create
a refinement of the problem (Hoang et al., 2013).
2.2 Linear Temporal Logic
LTL was proposed for expressing temporal proper-
ties of concurrent systems. It extends propositional
logic based on the Boolean operators: ¬, ∨, ∧, ⇒ by
temporal operators: always (), eventually (♦) and
Until (U). An LTL formula can describe the sys-
tem state evolution through the time. We denote by
φ an LTL formula and by σ a non empty sequence
of states s
0
,s
1
,.... We denote by σ
k
the sequence of
states s
k
, s
k+1
,... and by σ |= φ that φ is true on σ.
The semantic of temporal operators is as follows.
• σ |=  φ iff for all k = 0,1,..., we have σ
k
|= φ
• σ |= ♦ φ iff for some k = 0,1,..., we have σ
k
|= φ
• σ |= φ
1
U φ
2
iff for some k = 0,1,..., we have
σ
k
|= φ
2
and σ
0
|= φ
1
, ..., σ
k−1
|= φ
1
1
http://www.event-b.org/
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
230

2.3 Proving Temporal Properties with
Event-B
In this subsection, we give a summary of the work
of Hoang and Abrial ((Hoang and Abrial, 2011))
related to reasoning about liveness properties with
Event-B. The trace σ of machine M is a sequence of
states s
0
, s
1
, ... where s
0
is the initial state defined
by the initial variables values and for every two
successive states s
i
, s
i+1
, there is an event enabled
when the machine is in state s
i
leading the machine
to the state s
i+1
when executed. We denote by T (M)
the set of all the possible traces of machine M. A
machine satisfies a property φ, denoted by M |= φ, if
all its traces satisfy φ (Hoang and Abrial, 2011). In
the following, we give the three different classes of
liveness properties considered in (Hoang and Abrial,
2011).
- The existence property states that a property P will
always eventually be true ( ♦ P). To prove that a
machine M satisfies an existence property requires to
prove that M is convergent in ¬P, i.e. every event
execution in M decreases the defined variant when M
is on a ¬P state and deadlock-free in ¬P i.e. when
M is in a ¬P state, at least one event of M is enabled.
The necessary assumptions for proving the existence
property are given by the rule LIVE
♦
2
.
M ` ↓ ¬ P
M `  ¬ P LIV E
♦
M `  ♦ P
- The progress property states that a property P2 must
eventually be true if some condition P1 becomes true
( (P1 ⇒ ♦ P2)). Proving that a machine M fulfils
a progress property is insured by the use of the rule
LIVE
progress
.
M ` (P1 ∧ ¬P2 ⇒ P2)
M ` (P3 ⇒ (P3 U P2)) LIV E
progress
 (P1 ⇒ ♦ P2)
The first premise should be declared as an in-
variant in the machine M. The second premise
includes the until temporal operator and states that
P3 is true until P2 holds. This assumption is proved
by the use of the Until rule.
M ` ((P3 ∧ ¬P2) y (P3 ∨ P2))
M ` ♦(¬P3 ∨ P2) Until
M ` (P3 ⇒ (P3 U P2))
The first condition in the Until rule means that
every event in the machine M leads from P3 ∧ ¬P2
to P3 ∨ P2. An event leads from P1 to P2 if
starting from any P1 state, the execution of this event
2
The upper part of the proof rule describes the premises
under which the conclusion mentioned in the lower part is
true. The rule’s name is given at the right.
Figure 1: Patterns based stepwise refinement for formal de-
velopment of SO-MAS.
results in P2 state. The Leads f rom operator (y) is
expressed directly with the first-order logic as shown
below.
P1 y P2 b= P1(v) ∧ G(x,v) ∧ A(x, v,v
0
) ⇒ P2(v
0
)
- The persistence property states that eventually a
property P will be always true (♦P). The proof rule
LIVE
♦
gives the necessary conditions guaranteeing
that a machine M satisfies a persistence property. A
machine M satisfies a persistence property ♦P if
it is divergent in P; i.e. any infinite trace of M ends
with an infinite sequence of states satisfying P and
deadlock-free in ¬P. Proving that a machine M is
divergent in P needs to prove that every execution
of an event in M decreases the defined variant when
M is on a ¬P state and does not increase the variant
when M is on P state.
M ` % P
M `  ¬ P LIV E
♦
M ` ♦  P
3 TOWARDS A FORMAL DESIGN
PROCESS FOR SO-MAS
3.1 Overview of the Design Process
The aim of the proposed method is to construct the
adequate local behavior leading to the desired global
properties by stepwise refinement and the use of de-
sign patterns. We describe the formal design process
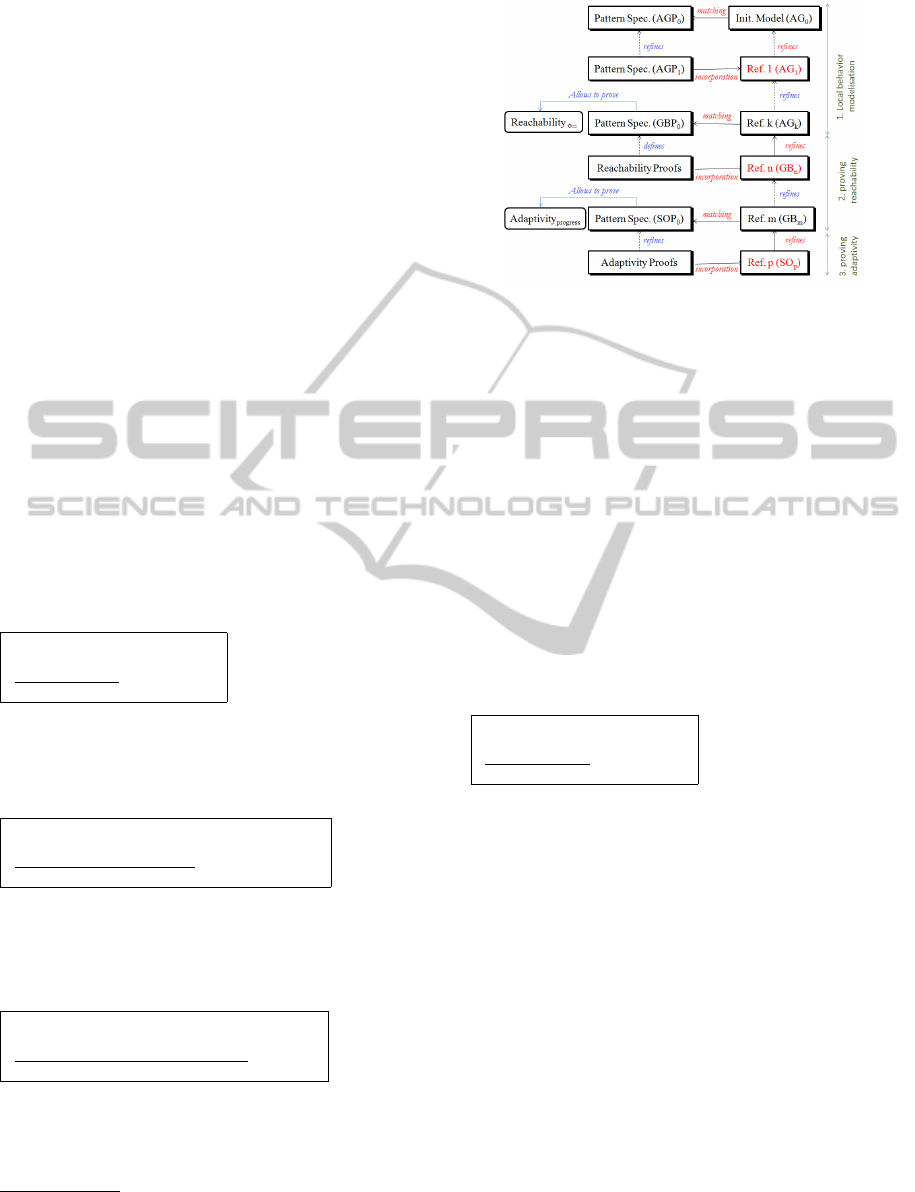
in terms of three phases as depicted in figure 1. In or-
der to guide the designer through the refinement pro-
cess, a design pattern is assigned to each phase giving
the necessary refinements and proof obligations to at-
tain the correct model at the end of each step. The first
phase allows the modeling of the agents’ local behav-
ior based on the model AGP
0
. This phase can be per-
formed for several times if the system is composed
APatternbasedModellingforSelf-organizingMulti-agentSystemswithEvent-B
231

by many types of agents. The next two phases are
devoted to prove convergence and adaptability prop-
erties by using the patterns GBP
0
and SOP
0
respec-
tively. These two patterns can be reused in the case
where convergence can take many aspects and adapt-
ability is needed in many situations.
3.2 Design Patterns for SO-MAS
In this section, we define in details the design patterns
AGP
0
, GBP
0
and SOP
0
. For each pattern, we give an
informal description plus a formal specification with
Event-B. We also mention how it can be refined and
what proof obligations must be discharged.
3.2.1 Agents Pattern:AGP
0
The Agents pattern gives a very abstract modeling of
the designed system as a set of agents executing ac-
cording to the perceive − decide − act cycle. The
pattern AGP
0
is an Event-B machine describing the
system state by means of the set of active agents, the
mode of each active agent (pause or work) and the ac-
tual cycle step for each active agent. The dynamic of
the system is modeled by means of four events. The
events Perceive, Decide and Act model the execution
of any agent according to the perceive − decide − act
cycle. The ActEnv event is triggered when it is the
turn of the environment to be activated. At this level
of abstraction, the only action that this event does is
to reset the active agents in the system at the step of
perception. As an example, we give the Perceive and
the ActEnv events.
EVENT Perceive
ANY
ag
WHERE
grd1 : ag ∈ ActiveAgents
grd2 : agMode(ag) =
work
grd3 : agStep(ag) =
perceive
THEN
act1 : agStep(ag) :=
decide
END
EVENT ActEnv
WHERE
grd1 :
∀ag·ag ∈ ActiveAgents
⇒agMode(ag) = pause
THEN
act1 :
ActiveAgents,agMode, agStep : |
ActiveAgents
0
∈ P(Agents)∧
ActiveAgents
0
6= ∅∧
(∀ag·ag ∈ ActiveAgents
0
⇒
agMode
0
(ag) = work∧
agStep
0
(ag) = perceive)
END
The AGP
0
pattern will be subject to a three steps re-
finement sequence to obtain a more concrete agents
behavior. In the first step, the Act event is split
into the different actions that an agent can perform.
In the second refinement step, agents’ actuators are
introduced. The agent’s actuators should be dis-
abled when the agent move to the state pause. This
property is ensured by adding the gluing invariant:
∀ag. ag ∈ ActiveAgents ∧ agMode(ag) = pause ⇒
actuAction i(ag) = disabled
In addition, Decide events are split in turn. When an
agent takes a decision, it activates the suitable actua-
tor in order to perform the desired action. To link the
agent action with the made decision, we use a witness.
The events modeling the action need also to be refined
according to the refinement of the event Act Action i
from AGP
0
pattern.
EVENT Dec Action i
REFINES Decide
ANY
ag
decideAct
WHERE
grd1 : ag ∈
ActiveAgents
...
grd4 : decideAct=
Action i
THEN
act1 : agStep(ag) :=
act
act2 : actuAction i(ag)
:= activate
END
EVENT Act Action i
REFINES Act Action i
ANY
ag
WHERE
...
grd2:actuAction i(ag)
=activate
WITNESSES
decideAct :decideAct=
Action i
⇔actuAction i(ag)=activate
THEN
act1 : agMode(ag) := pause
act2 : actuAction i(ag)
:= disabled
END
At this refinement step, we should ensure that
once an agent made a decision, it should execute an
action and avoid to be deadlocked in the action step.
This property is specified by the following theorem.
G
Act Action i
(ag, p,v) denotes the guard of an action
event for the agent ag.
∀ag.ag ∈ ActiveAgents ∧ agStep(ag) = act ⇒
(
W
i
(∃p.G
Act Action i
(ag, p,v)))
In the last refinement step, the agents’ sensors
are introduced and the event Perceive is refined.
For each agent, it is necessary that its sensors
are active when it is in the perceive step. This
constraint is captured by the gluing invariant:
∀ag. ag ∈ ActiveAgents ∧ agStep(ag) = perceive ⇔
sensor i(ag) = activate.
Moreover, the action in the event ActEnv is refined
by activating the sensors of each active agent. At
this refinement phase, we should ensure that the
updated perceptions, should allow the agent to make
a decision and thus to avoid to be deadlocked in the
perception step. This property is specified by the
following theorem. G
Dec Action i
(ag, p,v) denotes the
guard of a decision event for the agent ag.
∀ag.ag ∈ ActiveAgents ∧ agStep = decide ⇒
(
W
i
(∃p.G
Dec Action i
(ag, p,v)))
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
232

3.2.2 Global Behavior Pattern:GBP
0
The Global Behavior pattern allows to reason about
the behavior that emerges from the interactions
between agents. It is used to prove convergence of
the system, which means reachability of the desired
global behavior. Convergence of the system can be
captured formally by means of the Reach temporal
property:
Reach b= ♦  taskAchieved = T RUE
taskAchieved describes the state of the system when
it succeed to achieve its task. The modeling of this
property with Event-B can be done according to the
pattern GBP
0
.
GBP
0
VARIABLES
taskAchieved
SysStates
INVARIANTS
SysStates ⊂ SY S STAT ES
taskAchieved ∈ BOOL
VARIANTS
V
EVENT NotYetSuccess
STATUS convergent
ANY ag WHERE
grd1 : taskAchieved
= FALSE
grd2 : V /∈ ∅
grd3 : ag ∈ Agents
THEN
act1 : SysStates :∈ V
0
< V
END
EVENT ObserveSuccess
WHERE
grd1 : taskAchieved = T RU E
THEN SKIP
END
Variable SysStates denotes a subset a the system
state space. Variable taskAchieved, when is TRUE,
indicates that the global task is achieved and allows
to activate ObserveSuccess. This event plays the
role of an external observer (Hoang et al., 2009)
and does not change the system state. The event
NotYetSuccess is activated when the task is not
yet achieved, but must contribute to the fulfillment
of the global task by decreasing at each execution
the variant V . According to the rule LIVE
♦
, to
prove the Reach property, we need to prove the
convergence of event NotYetSuccess. Moreover,
we should prove that the event ObservSuccess does
not increase the variant and that the machine is
deadlock free for all the states where the task is
still not fulfilled. The first statement is guaranteed
since the action of the event ObservSuccess is
SKIP. The second statement is ensured by proving
the following theorem stating that from an inter-
mediate state, the machine can evolve either to
another intermediate state or to the success state.
taskAchieved = FALSE ⇒ ((∃ag,V.ag ∈ ActiveAgents∧
V /∈ ∅) ∨ taskAchieved = T RUE)
The incorporation of this pattern in the design pro-
cess allows to refine AG
k
(Figure 1) with GB
n
. It
is performed by two actions: 1) introducing event
ObserveSuccess and 2)refining each Act event
(an event describing an agent action) with the
NotYetSuccess event. At this level, we should prove
convergence of all the Act events and the deadlock
freeness of GB
n
in a non desirable state. Since
Event-B allows to use only one variant per machine,
GB
n
could be refined in many steps. In each step, the
convergence of one event (or a group of events which
decrease the same variant) is proved. The events
which are not considered by the proof at a given
step, must be anticipated, this means that proving
their convergence is postponed for further refinement
steps. Choosing the suitable variant to prove conver-
gence is not always trivial with SO-MAS. In fact, the
evolution of the agents cannot always be described as
a progression towards fulfillment of their goals. An
agent can change its goal according to the actions of
the other agents. In this work, we don’t address this
problem of proving convergence. But this is still an
ongoing work.
3.2.3 Self-organization Pattern:SOP
0
The Self-Organization pattern allows to reason
about the ability of the system to self-adapt in
order to overcome perturbations in its environment.
A rigorous analysis of self-organization can be
captured by the use of the Adaptivity temporal
formula stating that if a perturbation occurs, the
system will eventually be able to carry on its exe-
cution thanks to its self-organization mechanisms.
Adaptivity b=
(perturb = T RUE ⇒ ♦SuccessSO = T RU E)
The pattern SOP
0
(given below) allows to reason
about this property by applying LIVE
progress
rule and
proving the following two theorems.
Theorem1.
(perturb = T RUE ∧SuccessSO = FALSE
⇒ (∃ag. ag ∈ ActiveAgents ∧V /∈ ∅))
Theorem2.
(∃ag. ag ∈ ActiveAgents ∧V /∈ ∅ ⇒
((∃ag. ag ∈ ActiveAgents ∧V /∈ ∅)
U SuccessSO=TRUE))
According to Until rule, the demonstration of Theo-
rem2 needs to prove the following two theorems.
Theorem2.1.
∃ag. ag ∈ ActiveAgents ∧V /∈ ∅ ∧ SuccessSO = FALSE
⇒ ((∃ag. ag ∈ ActiveAgents ∧V /∈ ∅)
∨SuccessSO = T RUE)
Theorem2.2.
APatternbasedModellingforSelf-organizingMulti-agentSystemswithEvent-B
233

♦((∀ag.ag ∈ ActiveAgents ∧V ∈ ∅)
∨SuccessSO = T RUE)
By applying the rule LIVE
♦
, the proof of The-
orem2.2 necessitates 1) to prove the convergence
of the event ApplySO and 2) to prove deadlock-
freeness in a state satisfying the property ∃ag. ag ∈
ActiveAgents ∧V /∈ ∅ ∧ SuccessSO = FALSE.
The incorporation of this pattern in the design
process allows to refine GB
m
(Figure 1) with SO
p
.
It is performed by three actions: 1) introducing the
event PerturbOccurs performed when a perturba-
tion takes place in the environment, 2) adding the
ObserveSO Success event describing the success
of a self organization operation and 3) refining the
agent actions by the event ApplySO which models
the self-organizing mechanism. Theorem1 and
Theorem2 should be proved for every action refining
the event ApplySO.
SOP
0
VARIABLES
SuccessSO
SysStates
pertturb
INVARIANTS
SysStates ⊂ STAT ES
SuccessSO ∈ BOOL
perturb ∈ BOOL
VARIANTS
V (perturb)
EVENT ObserveSO Success
WHERE
grd1 : SuccessSO = T RUE
THEN SKIP
END
EVENT ApplySO
STATUS convergent
ANY ag WHERE
grd1 : V /∈ ∅
grd2 : ag ∈ ActiveAgents
grd3 : perturb = T RUE
THEN
act1 : SysStates : |
V
0
(perturb) < V (perturb)
END
EVENT PerturbOccurs
REFINES ActEnv
THEN
act1 : perturb := T RU E
END
4 APPLICATION ON THE
FORAGING ANTS
The case study is a formalization of the behavior of
a foraging ants’ colony. The considered system is
composed of several ants exploring the environment
and looking for food. Each ant begins by exploring
the environment and is mainly attracted by food or
pheromone. When discovering food on a location, the
ant collects a part of it and goes back to the nest by
dropping pheromone.
The properties we are trying to prove are summarized
as follows.
- The correctness of the model of the agents’ behav-
ior i.e. Corr
1
: Each ant behaves according to the
perceive − decide − act cycle, Corr
2
: Deadlock free-
ness of the ants in any step of its cycle, Corr
3
: The
ants must avoid obstacles.
- Reach
1
: The ants are able to bring all the food to
the nest. This is the main property of the system: the
reachability property.
- SO
1
: When a source of food is detected, the ants are
able to focus on its exploitation. This property eval-
uates the ability of the ants to self-organize in order
to brought entirely the detected source of food to the
nest.
- SO
2
: When a detected source of food is completely
exploited, the ants can carry on the environment ex-
ploration and detect new food.
In order to guarantee the correctness of our model we
apply the pattern AGP
0
. The Reach
1
property is mod-
eled by applying GBP
0
. Self-organization properties
are modeled by applying twice the pattern SOP
0
. In
the remainder of this section, we illustrate the use
of the AGP
0
pattern. For the three other properties
(Reach
1
, SO
1
and SO
2
), we give a formulation of each
of them in the temporal logic. Their proofs are an on-
going work.
The environment in which the ant interact is formal-
ized as a set of connected locations (Locations) with
a particular one called Nest modeling the nest of the
colony. Guided by the refinement steps indicated in
AGP
0
, we obtain a machine modeling the local be-
havior of ants. Each ant has a current location in the
grid (currentLoc) and can decide about its next lo-
cation (nextLoc). The ant has information about the
environment elements which are inside its perception
field, i.e. food ( f ood), pheromone (pheromone) and
obstacles (obstacles). The definitions of these char-
acteristics in Event-B are given as follows.
inv1 : currentLoc ∈ Ants → P(Locations)
inv2 : nextLoc ∈ Ants →P(Locations)
inv3 : f ood ∈ Ants → P(Locations)
inv4 : pheromone ∈ Ants →P(Locations)
The invariant inv1, for example, is a total function
which defines the current location for each ant. Ants
is the set of the active Ants. The ants behavior is de-
picted by the following events:
- Perceive: enables to each ant to update its percep-
tions according to its current location.
- Dec Move Rand: the ant decide to go randomly be-
cause it does not perceive anything, Dec Move Food:
decide to follow sensed food, Dec Move Phero: de-
cide to follow sensed pheromone, Dec Drop Back:
decide to go back to the nest and drop pheromone
along the return path, Dec Back: decide to go back
to the nest without dropping pheromone along the re-
turn path, Dec Harvest Food: decide to take food,
Dec Drop Food: decide to drop the food at the nest.
- Act Move Rand,Act Move Food, Act Move Phero,
Act Drop Back and Act Back: activated when an ant
moves from one location to another.
- Act Harvest Food: the ant takes some food and
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
234

Ac Drop Food: the ant drop the food on the Nest.
As an example, we give the description of the event
Act Move Food.
EVENT Act Move Food REFINES Act Move Food
ANY
ant
WHERE
grd1 : ant ∈ Ants ∧agMode(ant) = work ∧ agStep(ant) = act
grd2 : paw(ant) = activate
grd3 : actMove(ant) = Follow Food
THEN
act1 : currLoc(ant) := nextLoc(ant)
act2 : agMode(ant) := wait
END
The reachability property is defined as follows.
♦((QuantityFood(Nest) = TotalFood(InitDistFood)∧
∀ loc.loc ∈ Locations\{Nest} ⇒ QuantityFood(loc) = 0)).
The QuantityO f Food relation specifies for each lo-
cation the quantity of food in it, TotalFood calculates
the sum of quantities of food in the environment and
InitDistFood is the initial distribution of food.
The SO
1
property is defined by the following tempo-
ral formula.
(∀ loc.loc ∈ Locations\{Nest}∧
InitDistFood(loc) 6= 0 ∧ Detected(loc) ⇒
♦((QuantityFood(loc) = 0)).
The SO
2
property is defined by the following tempo-
ral formula.
(∀ ant, loc. ant ∈ Ants ∧loc ∈ Locations\{Nest}∧
EntirelyExploited(loc1) ⇒
♦(∃loc2. loc2 6= loc1 ∧ QuantityFood(loc2) 6= 0 ∧ Detected(loc2)).
5 RELATED WORK
Developpement Methods. In (Orfanus et al., 2011),
a design process for the construction of emergent self-
organizing behavior in large-scale distributed embed-
ded systems is proposed. This process relies on
two models: the model of microscopic layer and the
model of macroscopic layer and three steps: simula-
tion, validation and update. The first model should
describe the local activities of the entities composing
the system as well as the local information trigger-
ing these activities. The second one is described by
a set of macroscopic variables. The simulation step
allows adjusting the micro model in order to match
it with the macro one. A top-down property driven
design for swarm robotic, composed by four phases,
was proposed in (Brambilla et al., 2012). The aim of
the first phase is to give a clear and complete formal
specification of the desired properties of the system.
The second phase consists in defining a macroscopic
model of the system and checking whether the desired
properties are satisfied. The phase three is devoted
to the implementation of a simulation of the swarm
system. This phase represents a transition from the
macroscopic model to the microscopic implementa-
tion and is guided by the ingenuity and the expertise
of the designer (Brambilla et al., 2012). In the final
phase, the system is deployed on real robots. The au-
thors choose to specify the swarm model by the Deter-
ministic Time Markov Chains (DTMC) and its prop-
erties by the Probabilistic Computation Tree Logic*
(PCTL*). Moreover, they use the technique of model
checking and particularly the PRISM model checker
for verification.
The Adelfe methodology was proposed for the de-
velopment of self-organizing systems based on the
AMAS (Adaptive MAS) theory ((Bernon et al.,
2005)). The AMAS theory depends on the ability of
the agents to cooperate and thus, the design of the lo-
cal behavior of the entities relies on identifying and
resolving the non cooperative situations an agent may
encounter. In order to guarantee that all non coop-
erative situations are taken into account, the process
of Adelfe is enriched by a simulation step in (Bernon
et al., 2006).
Formal Modelisation of Self-organizing Systems.
In (Gardelli et al., 2006), Gardelli uses stochastic Pi-
Calculus for modeling SO-MAS for intrusion detec-
tion. This formalization was used to perform simu-
lations using the SPIM tool to assess the impact of
the number of agents and frequency of inspections on
the system behavior. In (Casadei and Viroli, 2009),
a hybrid approach has been proposed. This approach
uses stochastic simulations to model the system de-
scribed as Markov chains and the technique of proba-
bilistic model checking for verification. The approach
was tested for the problem of collective sorting us-
ing the PRISM tool. Konur and colleagues ((Konur
et al., 2012)) use also the PRISM tool and proba-
bilistic model checking to verify the behavior of robot
swarm, particularly foraging robots. The authors ver-
ify properties expressed by PCT L logic for several
scenarios. These properties provide information,in
particular, on the probability that the swarm acquires
a certain amount of energy for a certain number of
agents and in a certain amount of time. Simulations
were also used to show the correlation between the
density of foraging robots in the arena and the amount
of energy gained.
An Event-B modeling for fault tolerant MAS was pro-
posed in (Pereverzeva et al., 2012). The authors pro-
pose a refinement strategy that starts by specifying
APatternbasedModellingforSelf-organizingMulti-agentSystemswithEvent-B
235

the main purpose of the system, defines the necessary
agents to accomplish it, then introduces the various
failures of agents and ends by introducing the commu-
nication model and error recovery mechanisms. The
refinement process ensures a set of properties, mainly
1) reachability of the main purpose of the system, 2)
the integrity between agents’ local information and
global information and 3) efficiency of cooperative
activities for error recovery. The aim of the works
presented above is to ensure that the designed indi-
vidual behavior will give rise to the desired global
properties. Some of them make use of simulation,
while others employ formal techniques. The major-
ity of these works utilize a bottom-up approach (ex-
cept (Brambilla et al., 2012) and (Pereverzeva et al.,
2012)) which is ideally suited to self-organizing sys-
tems. The use of Event-B in (Pereverzeva et al., 2012)
is extremely important because of the use of the re-
finement principle that permits a progressive, guided
and correct construction of the desired system, which
is not allowed in the other works. In our proposition,
we combine a bottom-up approach with the use of re-
finement and design patterns in order to give more
guidance to the designer when designing the individ-
ual behavior (AGP
0
pattern) and when doing proofs
(GBP
0
and SOP
0
patterns).
6 CONCLUSIONS
We have presented in this paper a formal approach for
the design of SO-MAS based on design patterns, re-
finement and Event-B. Three patterns were proposed;
AGP
0
gives refinement steps for modeling the local
behavior of the agents and guarantees deadlock free-
ness of any agent, GBP
0
allowing to prove that the
modeled local behavior will converge towards the de-
sired global behavior and finally SOP
0
letting the eval-
uation of the ability of self-organizing mechanisms to
encounter the environment perturbations.
The main challenges for future work can be summa-
rized in the three following points:
- Proving the convergence of the events when apply-
ing the patterns GBP
0
and SOP
0
which is not trivial
task because of the non determinism in SO-MAS. One
possible solution for this is to prove the convergence
under fairness assumption like in (M
´
ery and Popple-
ton, 2013).
- Automation of the refinement process and the gen-
eration of machines according to the design patterns.
- Formal reasoning about the improvement of the sys-
tem performance. A probabilistic approach coupled
with Event-B can be useful in this case.
REFERENCES
Abrial, J.-R. (2010). Modeling in Event-B - System and
Software Engineering. Cambridge University Press.
Abrial, J.-R. and Hoang, T. S. (2008). Using design patterns
in formal methods: An event-b approach. In ICTAC,
pages 1–2.
Bernon, C., Camps, V., Gleizes, M.-P., and Picard, G.
(2005). Engineering Adaptive Multi-Agent Systems:
The ADELFE Methodology . In Henderson-Sellers,
B. and Giorgini, P., editors, Agent-Oriented Method-
ologies , volume ISBN1-59140-581-5, pages 172–
202. Idea Group Pub, NY, USA.
Bernon, C., Gleizes, M. P., and Picard, G. (2006). Enhanc-
ing self-organising emergent systems design with sim-
ulation. In ESAW, volume 4457 of Lecture Notes in
Computer Science, pages 284–299. Springer.
Brambilla, M., Pinciroli, C., Birattari, M., and Dorigo, M.
(2012). Property-driven design for swarm robotics.
In Conitzer, Winikoff, P. and van der Hoek, editors,
AAMAS 2012, pages 139–146.
Casadei, M. and Viroli, M. (2009). Using probabilistic
model checking and simulation for designing self-
organizing systems. In Proceedings of the 2009 ACM
symposium on Applied Computing, SAC ’09, pages
2103–2104, New York, NY, USA. ACM.
Di Marzo Serugendo, G., Gleizes, M.-P., and Karageorgos,
A. (2005). Self-organization in multi-agent systems.
In Knowl. Eng. Rev., volume 20, pages 165–189, New
York, NY, USA. Cambridge University Press.
Gardelli, L., Viroli, M., and Omicini, A. (2006). Exploring
the dynamics of self-organising systems with stochas-
tic π-calculus: Detecting abnormal behaviour in mas.
In (AT2AI5).
Hoang, T. S. and Abrial, J.-R. (2011). Reasoning about
liveness properties in event-b. In ICFEM, pages 456–
471.
Hoang, T. S., F
¨
urst, A., and Abrial, J.-R. (2013). Event-b
patterns and their tool support. Software and System
Modeling, 12(2):229–244.
Hoang, T. S., Kuruma, H., Basin, D. A., and Abrial, J.-
R. (2009). Developing topology discovery in event-b.
Sci. Comput. Program., 74(11-12):879–899.
Konur, S., Dixon, C., and Fisher, M. (2012). Analysing
robot swarm behaviour via probabilistic model check-
ing. Robot. Auton. Syst., 60(2):199–213.
M
´
ery, D. and Poppleton, M. (2013). Formal Modelling and
Verification of Population Protocols. In Johnsen, E. B.
and Petre, L., editors, iFM - 10th International Con-
ference on integrated Formal Methods - 2013, LNCS,
Turku, Finlande. Springer.
Orfanus, D., Janacik, P., Eliassen, F., and Orten, P. (2011).
High-level construction of emergent self-organizing
behavior in massively distributed embedded systems.
In NaBIC, pages 335–341.
Pereverzeva, I., Troubitsyna, E., and Laibinis, L. (2012).
Development of fault tolerant mas with cooperative
error recovery by refinement in event-b. CoRR,
abs/1210.7035.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
236