A Multi-demand Adaptive Bargaining based on Fuzzy Logic

Jieyu Zhan

, Xudong Luo

, Wenjun Ma

and Youzhi Zhang

Institute of Logic and Cognition, Sun Yat-sen University, Guangzhou, China

School of Electronics, Electrical Engineering and Computer Science, Queen’s University Belfast, Belfast, U.K.

Keywords:

Game Theory, Fuzzy Logic, Bargaining Game, Preference, Agent.

Abstract:

Nowadays, decisions in estate investment are made by a group of investors with diﬀerent demands and then

how to ﬁnd an agreement among them become an essential issue. Thus, this paper introduces a fuzzy logic

based bargaining model to solve such problems. Moreover, we also do lots of simulation experiments to reveal

how bargainers’ risk attitude, patience and regret degree inﬂuence the outcome of a game, and benchmark our

model with the previous one. From these experiments, we can conclude that our model can reﬂect the human

intuitions well, has a higher success rate, and bargains more eﬃciently than the previous one.

1 INTRODUCTION

Nowadays, many business decisions are not made by

just one person but a group of people. They often

need to negotiate before making an ultimate deci-

sion. For example, in a problem of real estate in-

vestment some investors demand to build big houses,

while some demand to build economically aﬀordable

houses; some insist on using environmental but ex-

pensive material, while some support low-cost one;

and so on. There are so many inconsistencies among

diﬀerent investors. So, to make a decision accepted

by all, they have to bargain with each other.

In such a problem, it is hard to elicit numerical

utilities and do quantitative analyses (Zhang, 2010).

Thus, some researchers tried to express bargainers’

preferences in an ordinal scale (Shubik, 2006; Zhang

and Zhang, 2008). However, the information relevant

to the bargainers’ risk attitudes, a very important fac-

tor in bargaining (Garc´ıa-Gallego et al., 2012), is lost

(Zhang, 2010).

To deal with this issue, some researchers build

new models. For example, Zhang (2010) introduced

a new ordinal bargaining model, in which the prefer-

ence ordering of a bargainer is deﬁned on the player’s

demands and the risk attitudes of a bargainer can

be represented through the ranking of conﬂicting de-

mands. However, the models of this kind still have

some drawbacks. For example, they cannot explicitly

represent players’ attitudes towards risk; and ignore

that bargainers’ preferences can be changed because

of diﬀerent risk attitudes.

Thus, further Zhan et al. (2013) introduced an-

other new ordinal bargaining model, in which each

bargainer has two preference orderings over his de-

mands: one for reﬂecting the bargainer’s own taste

without considering any information about the bar-

gaining, while the other for reﬂecting not only his own

taste but also his thinking about which demand should

be insisted on or given up earlier. Thus, his risk atti-

tude can be tasted out by comparing the two prefer-

ences. Moreover, in their model, a bargainer’s prefer-

ence could be changed during a bargaining according

to his psychological factors about risk, patience and

regret. A fuzzy logic system is used to calculate the

change of the preference dynamically.

However, Zhan et al. (2013) did not do suﬃcient

empirical analyses upon their model. Moreover, their

fuzzy rules are not very intuitive. So, this paper re-

analyses the psychological experiments of setting the

rules in (Zhan et al., 2013) and simpliﬁes these fuzzy

rules. According to these new rules, we do lots of

experiments to reveal some insights into the model.

In addition, we illustrate our new model by solving a

bargaining problem in the real estate investment.

The rest of the paper is organised as follows. Sec-

tion 2 recaps the bargaining model and its solution

concept. Section 3 presents the improved fuzzy rea-

soning systems. Sections 4 and 5 empirically analyse

the inﬂuence of input parameters in the fuzzy system

and benchmark our solution method with a previous

one. Section 6 illustrates the model by solving the

problem in the investment in real estate. Section 7 dis-

cusses the related work. Finally, Section 8 concludes

577

Zhan J., Luo X., Ma W. and Zhang Y..

A Multi-demand Adaptive Bargaining based on Fuzzy Logic.

DOI: 10.5220/0004907005770585

In Proceedings of the 6th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2014), pages 577-585

ISBN: 978-989-758-015-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

the paper with future work.

2 MODEL DEFINITION

This section recaps the bargaining model of Zhan

et al. (2013).

Deﬁnition 1. A bargaining game is a tuple of

pN, tX

, <

i,o

, <

p0q

i,d

iPN

, A, FLSq, where

• N is the set of all the bargainers in this game;

• X

is the demand set of bargainer i in a propo-

sitional language denoted as L, consisting of a

ﬁnite set of propositional variables and standard

propositional connectives t ,_, ^, Ñu;

• <

i,o

is bargainer i’s original demand preference

ordering, which is a total pre-order on X

(i.e.,

satisfying totality, reﬂexivity and transitivity);

• <

p0q

i,d

is bargainer i’s initial dynamic demand pref-

erence ordering, i.e., a total pre-order on X

(i.e.,

satisfying totality, reﬂexivity and transitivity);

• A is bargainers’ action function deﬁned as:

Apx

,ζ, λq“

’

move down x

two levels

if (ζ ě 0.7) and

(Dx

, x

<CDS

, x

pλq

i,d

, x

move down x

one level

if (0.7 ą ζ ě 0.3 and

D x

< CDS

, x

pλq

i,d

) or

(ζ ě 0.7 and

!D x

<CDS

, x

pλq

i,d

do nothing

otherwise.

(1)

where ζ is the change degree, x

P CDS

(i.e., the

conﬂicting demand set of bargainer i in X

), and n

means the λ-th round of the bargaining game;

• FLS is a fuzzy logic system for calculating the

preference change degree.

The bargainers’ demands are expressed by logical

statements, and every bargainer’s original preference

ordering and initial dynamic preference ordering are

over his demands rather than the agreements of a bar-

gaining game. Because all bargainers’ demands may

be logically inconsistent in a set, the purpose of a bar-

gaining game is to ﬁnd an agreement consisting logi-

cally consistent statements.

In the bargaining model, the dynamic preference

can be changed during a bargaining. Thus, a param-

eter, called change degree (i.e., ζ), is used to capture

the degree to which a bargainer wants to change his

preference. It is calculated by the fuzzy logic system

FLS, which inputs are bargainers’ risk attitude, pa-

tience descent degree and regret degree. Accordingly,

by action function A

, bargainer i will take a proper

action to change his preference. That is, after the λ-

th round, dynamic demand preference structure pX

pλq

i,d

q of bargainer i will be updated to a new one, de-

noted as pX

pλ`1q

, <

pλ`1q

i,d

q, by a certain action chosen

by action function (1), where its input (i.e., change

degree ζ) is determined by the fuzzy logic system.

Let tX

p1,λq

, ¨¨¨ , X

pλq,λq

u be the partition of X

induced by equivalence relation „, which is deﬁned

by preference ordering <

pλq

i,d

, and L

pλq denotes the

height of the hierarchy of bargainer i in the λ-th

round (specially, L

is short for L

p0q). We regard

every partition as diﬀerent levels from high to low,

that is, X

p1,λq

is the demands in the highest level in

pλq

and X

pλq,λq

is the demands in the lowest level

in X

pλq

. There are two steps in every round: (i)

concession, i.e., every bargainer gives up the least

preferred demands (i.e., the demands in the lowest

level in the current round) if their remaining demands

are inconsistent; and (ii) changing the demand pref-

erence after concession. So, according to step (i),

pλ`1q

“ X

pλq

pλq,λq

, and after concession, ac-

cording to step (ii), tX

p1,λq

, ¨¨¨ , X

pλq,λq

u will be up-

dated to tX

p1,λ`1q

, ¨¨¨ , X

pλ`1q,λ`1q

u through action

function A. Formally, we have:

Deﬁnition 2. For bargaining game G “ pN, tX

, <

i,o

, <

p0q

i,d

iPN

, A, FLSq, its dynamically simultaneous

concession solution (DSCS) is:

S pGq “

pνq

, ¨ ¨¨ , X

pνq

q if @i P N, X

pνq

, H,

ν ă mintL

| i P Nu,

pH,. .. ,Hq otherwise,

(2)

where ν is the minimal rounds of concessions of the

game, i.e., ν “ mintk | Y

i“1

pkq

is consistentu (X

pkq

is the set of demands of bargainer i after k rounds of

the bargaining). And the agreement of game G is:

ApGq “

iPN

pGq, (3)

where s

pGq is the i-th element of SpGq.

3 FUZZY LOGIC SYSTEM

This section will present our fuzzy logic system for

calculating the preference change degree.

The fuzzy rules we reset are listed in Table 1. Rule

1 means that if a bargainer does not lose too many

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

578

Table 1: Fuzzy rules.

If regret degree is Low then change degree is Low.

If regret degree is Medium then change degree is Medium.

If regret degree is High then change degree is High.

If patience descent degree is Low then change degree is Low.

If patience descent degree is Medium then change degree is Medium.

If patience descent degree is High then change degree is High.

If initial risk degree is Low then change degree is High.

If initial risk degree is Medium then change degree is Medium.

If initial risk degree is High then change degree is Low.

consistent demands, which makes him regret just a

little, then his desire to change his preference is low.

Other rules can be understood similarly.

In each round of bargaining, when calculating the

change degree, the input parameters of the fuzzy rules

are:

(i) Regret degree (ϑ). Formally, it is calculated by:

pλq

q “

pλq

, (4)

where

is the number of consistent demands of

bargainer i in X

and

pλq

is the number of remain-

ing consistent demands of bargainer i after the λ-th

round of bargaining.

(ii) Patience descent degree (ρ). Formally, it is

given by:

pλq “

, (5)

where λ is the number of completed rounds of bar-

gaining and L

is the height of the initial dynamic pref-

erence hierarchy of bargainer i in the ﬁrst round.

(iii) Initial risk degree. It is deﬁned as follows:

Deﬁnition 3. Let h

pxq and H

pxq be the levels of de-

mand x in the original demand preference hierarchy

and the initial dynamic demand preference hierarchy,

respectively. Speciﬁcally, h

pxq “ 1 means bargainer

i prefers x the most in the original preference and

pxq “ L

means bargainer i prefers x the least in the

original preference, where L

“ maxth

pxq | x P X

Similar things go for H

pxq. Then the initial risk de-

gree of bargainer i is given by:

“

’

PCDS

q´H

PCDS

q´

p1`N

PCDS

q ´ H

qq ą 0,

PCDS

q´H

PCDS

q´N

´1qN

PCDS

q ´ H

qq ă 0,

otherwise.

(6)

where CDS

, N

and L

are bargainer i’s conﬂicting

demand set, conﬂicting demands’ number and initial

dynamic preference level number, respectively.

The meanings of linguistic terms of the fuzzy vari-

ables in Table 1 are as follows. The low regret degree

means that a bargainer just regrets a little for the de-

mands given up in the previous round. The medium

regret degree means that a bargainer cares about the

demands given up and regrets having insisted on the

preference in the previous round. And the high re-

gret degree means that a bargainer regrets very much

for insisting on the preference in the previous round

and more likely changes it because it causes a lot of

consistent demands lost. The linguistic terms of other

two parameters can be understood similarly.

These linguistic terms of the fuzzy variables are

modelled by the following fuzzy member function:

µpxq “

’

0 if x ď a,

x´a

b´a

if a ď x ď b,

1 if b ď x ď c,

d´x

d´c

if c ď x ď d,

0 if x ě d.

(7)

For convenience, we represent formula (7) as µpxq “

pa, b,c,dq. Thus, the linguistic terms of regret degrees

can be expressed as µ

low

pϑq “ p´0.2, 0, 0.2, 0.4),

medium

pϑq “ p0.2, 0.4, 0.6, 0.8q, and µ

high

pϑq “ p0.6,

0.8, 1, 1.2q. Similarly, we can have µ

low

pρq “ p´0.2,

0, 0.2, 0.4q, µ

medium

pρq “ p0.2, 0.4, 0.6, 0.8q, and

high

pρq “ p0.6, 0.8, 1, 1.2q; µ

low

pγq “ p´1.4, ´1,

´0.6, ´0.2q, µ

medium

pγq “ p´0.6, ´0.2, 0.2, 0.6q, and

high

pγq “ p0.2, 0.6, 1, 1.4q; and µ

low

pζq “ p´0.2,

0, 0.2, 0.4q, µ

medium

pζq “ p0.2, 0.4, 0.6, 0.8q, and

high

pζq “ p0.6, 0.8, 1, 1.2q.

We use the standard Mamdani method (Mamdani

and Assilian, 1975) to do fuzzy reasoning as follows:

Deﬁnition 4. Let A

be a Boolean combination of

fuzzy sets A

i,1

, ¨¨¨ , A

i,m

, where A

i, j

is a fuzzy set de-

ﬁned on U

i, j

pi “ 1, ¨¨ ¨ , n; j “ 1, ¨¨¨ , mq, and B

fuzzy set on U

pi “ 1, ¨¨¨ , nq. Then when the inputs

are µ

i,1

q,¨¨¨ , µ

i,m

q, the output of such fuzzy

rule A

Ñ B

is fuzzy set B

deﬁned by:

q“mintf pµ

i,1

q,¨¨¨ , µ

i,m

qq,µ

qu,

(8)

where f is obtained through replacing A

i, j

in A

i, j

q and replacing “and”, “or”, “not” in A

“min”, “max”, “1 ´ µ”, respectively. And the out-

put of all rules A

Ñ B

, ¨¨¨ , A

Ñ B

, is fuzzy set M,

which is deﬁned by:

q “ maxtµ

q,¨¨¨ , µ

qu. (9)

The result what we get is still a fuzzy set. To de-

fuzzify the fuzzy set, we need the following centroid

method (Mamdani and Assilian, 1975):

AMulti-demandAdaptiveBargainingbasedonFuzzyLogic

579

Deﬁnition 5. The centroid point u

cen

of fuzzy set M

given by formula (9) is:

cen

“

qdu

. (10)

Actually, u

cen

in above is the centroid of the area

that is covered by the curve of membership function

and the horizontal ordinate.

4 EXPERIMENTAL ANALYSIS

This section will analyse how bargainer’s risk degree,

patience descent degree and regret degree in the fuzzy

logic based model aﬀects the outcome of a bargaining

game. We will use the measure of the average level

number of remaining demandsin bargainers’outcome

in initial dynamic preference. A smaller average level

number means a higher average level (i.e., a bargainer

gains more what he prefers) and a large average level

number means a lower average level (i.e., a bargainer

gains less what he really wants). In all experiments,

we run 1000 times bargaining under the setting that

every bargainer’s action function is formula (1) and

the fuzzy rules are those in Table 1.

Now we do two experiments to investigate the ef-

fect of attitude towards risk in two dimensions: (i) the

eﬀect upon the average rounds to achieve agreements

and (ii) the average preference levels of remaining de-

mands in certain bargainer’s outcome. We randomly

generate 10 demands in diﬀerent preference levels for

two bargainers and arbitrarily label N (changing from

0 to 10) of them as their conﬂicting ones.

In the ﬁrst experiment, the bargaining is carried

out in the fuzzy logic based model with both bar-

gainers’ risk degrees are ﬁxed in the three cases of

pγ

, γ

q “ p1, 1q, pγ

, γ

q “ p1, ´1q, and pγ

, γ

q “

p´1, ´1q to model: (i) one risk seeker encounters an-

other risk seeker, (ii) one risk seeker encounters one

risk averser, and (iii) one risk averser encounters an-

other risk averser, respectively.

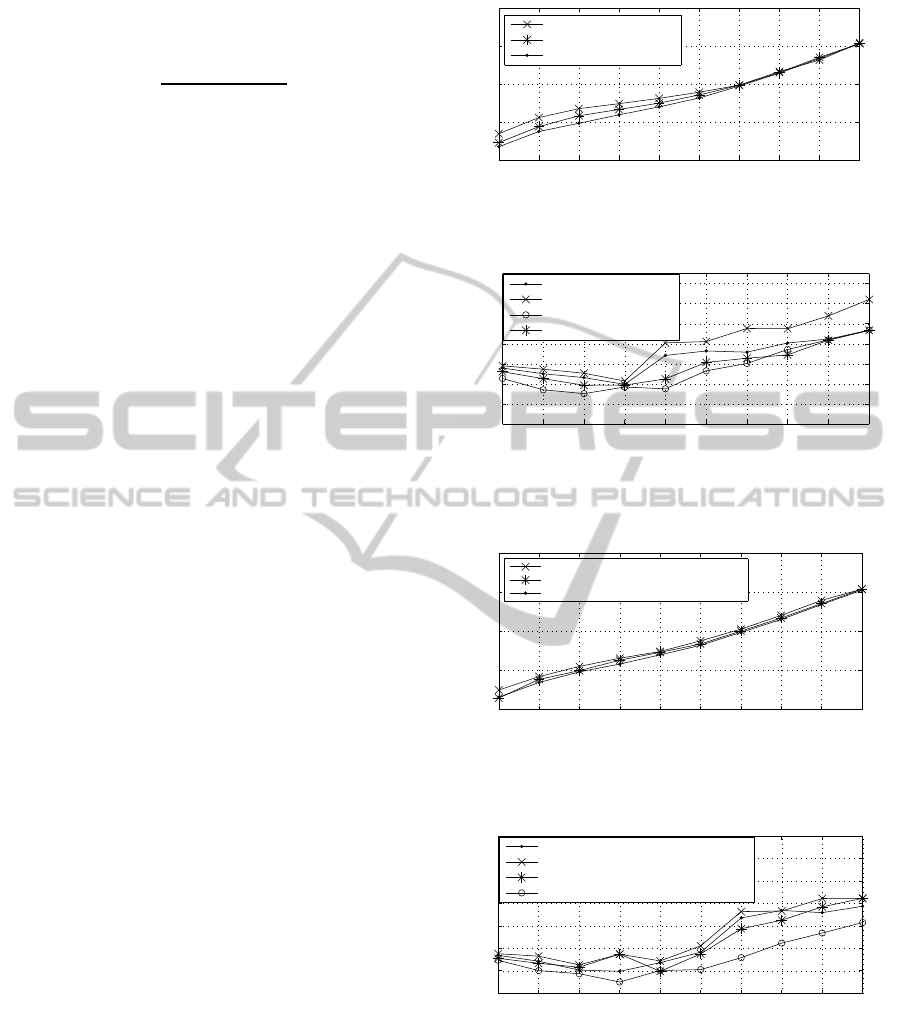
From Figure 1, we can see that the average rounds

to reach agreements is the lowest when one risk

averser encountersanother risk averser in a bargaining

game; and the one is the highest when one risk seeker

encounters another risk seeker. Moreover, comparing

the “´ˆ ´” type of line with the “´ ˚ ´” type of one

and the “´ ˚ ´” type of line with the “´ ¨ ´” type of

one, we can see that if a bargainer chooses to be a

risk seeker, no matter his opponent is a risk seeker or

a risk averser, the bargaining will cost more time and

the bargainer will get fewer demands than when he

chooses to be risk averse.

1 2 3 4 5 6 7 8 9 10

The number of conﬂic ting de mands

Aver age rounds

risk seeker vs risk seeker

risk seeker vs risk averser

risk averser vs risk averser

Figure 1: Average rounds of reaching agreements with the

number of conﬂicting demands about eﬀect of risk degree.

1 2 3 4 5 6 7 8 9 10

4.2

4.4

4.6

4.8

5.2

5.4

The number of conﬂic ting de mands

Aver age levels

risk seeker vs risk seeker

risk seeker vs risk averser

risk averser vs risk seeker

risk averser vs risk averser

Figure 2: The average preference levels of remaining de-

mands in the ﬁrst bargainer’s outcome with the number of

conﬂicting demands for diﬀerent risk attitudes.

1 2 3 4 5 6 7 8 9 10

The number of conﬂicting de mands

Aver age rounds

patient bargainer vs patient bargainer

patient bargainer vs impatient bargainer

impatient bargainer vs impatient bargainer

Figure 3: Average rounds of reaching agreements with the

number of conﬂicting demands about eﬀect of patience de-

scent degree.

1 2 3 4 5 6 7 8 9 10

4.2

4.4

4.6

4.8

5.2

5.4

The number of conﬂicting de mands

Aver age levels

patient bargainer vs patient bargainer

patient bargainer vs impatient bargainer

impatient bargainer vs impatient bargainer

impatient bargainer vs patient bargainer

Figure 4: Average preference levels of remaining demands

in the ﬁrst bargainer’s outcome with the number of conﬂict-

ing demands about eﬀect of patience descent degree.

In the second experiment, we also model the cases

similar to the ﬁrst experiment, but the average prefer-

ence levels of remaining demands in each bargainer’s

outcome are diﬀerent. So, we carry out four cases as

showed in Figure 2, and just draw the ﬁrst bargainer’s

situation. From Figure 2, comparing the “´ ¨ ´” type

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

580

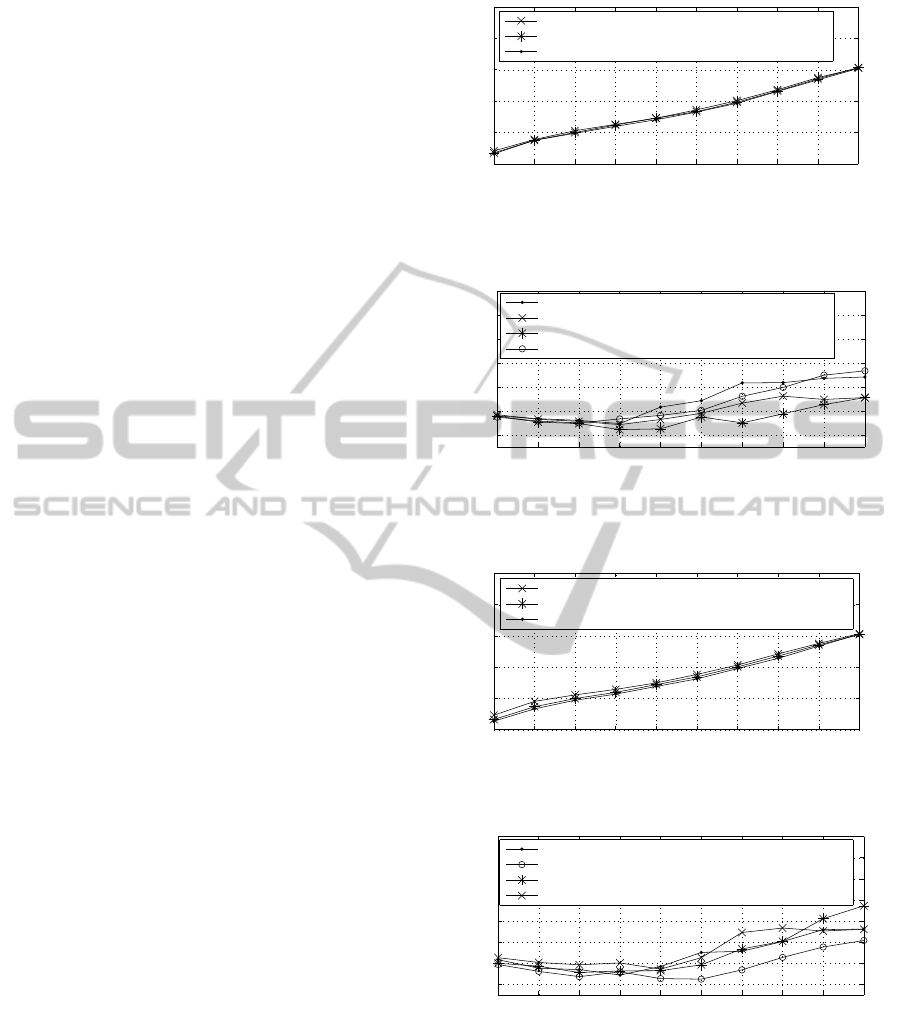
of line with the “´o´” type of one and the “´ ˆ ´”

type of line with the “´ ˚ ´” type of one, we can see

that if a bargainer is risk seeking, no matter his oppo-

nent is risk seeking or averse, his average preference

levels of remaining demands is higher than that when

choosing to be risk averse. That is, a risk seeker can

gain more demands that he prefers.

Accordingly, we can conclude a risk seeking bar-

gainer can gain fewer but more favorite demands than

a risk averse one in the fuzzy logic based model. This

often happens in real life. For example, in stock mar-

kets, a high income often comes with a high risk.

Now we turn to analyse the inﬂuence of patience

descent degree and regret degree by doing other two

groups of experiments. Each contains two experi-

ments similar to those ones in the previous subsection.

Figures 3 and 4 show the inﬂuence of the pa-

tience descent degree, while Figures 5 and 6 show

the eﬀect of regret degree. Similarly to the anal-

yses in the last subsection, from the four ﬁgures,

we can conclude that a patient bargainer can gain

more favourite demands than an impatient one, and a

diﬃcult-regretting one gains more favourite demands

than an easy-regretting one. However, as showed in

Figures 3 and 5, both parameters cannot alone inﬂu-

ence the average rounds of reaching agreements obvi-

ously, but both are positive correlated with the change

degree. So, we do another group of experiments to see

how the two inﬂuence the bargaining together. And

the data is shown in Figures 7 and 8. Comparing Fig-

ures 3, 5 and 7, we can see that the two can together

inﬂuence the outcome of bargaining more obviously

than single one does.

5 BENCHMARK WITH SCS

This section empirically analyses how well the fuzzy

logic based model and its solution concept (i.e.,

DSCS) works against the one of Zhang (2010) (i.e.,

SCS). We will also carry out two groups of experi-

ments to analyse how the outcome qualities change

with the numbers of conﬂicting demands and bargain-

ers, respectively. In addition to success rate, average

rounds, and average level in outcome, we will intro-

duce four more indexes to evaluate an outcome of a

bargaining game: the number of demands in agree-

ment, the number of consistent demands in agree-

ment, and the highest and the lowest levels of de-

mands in agreement. In both experiments, we run

1000 times bargaining under the setting that every

bargainer’s action function is formula (1) and the

fuzzy rules are those in Table 1.

In the ﬁrst experiment, 10 demands are randomly

1 2 3 4 5 6 7 8 9 10

The number of conﬂic ting de mands

Aver age rounds

difficult−regretting bargainer vs difficult−regretting bargainer

difficult−regretting bargainer vs easy−regretting bargainer

easy−regretting bargainer vs easy−regretting bargainer

Figure 5: Average rounds of reaching agreements with the

number of conﬂicting demands about eﬀect of regret de-

gree.

1 2 3 4 5 6 7 8 9 10

3.4

3.8

4.2

4.6

5.4

5.6

The number of conﬂic ting de mands

Aver age levels

difficult−regretting bargainer vs difficult−regretting bargainer

difficult−regretting bargainer vs easy−regretting bargainer

easy−regretting bargainer vs easy−regretting bargainer

easy−regreting bargainer vs difficult−regretting bargainer

Figure 6: Average preference levels of the demands in bar-

gainer 1’s outcome with the number of conﬂicting demands

about eﬀect of regret degree.

1 2 3 4 5 6 7 8 9 10

The number of conﬂic ting de mands

Aver age rounds

difficult−regretting and patient vs difficult−regretting and patient

difficult−regretting and patient vs easy−regretting and impatient

easy−regretting and impatient vs easy−regretting and impatient

Figure 7: Average rounds of reaching agreements with the

number of conﬂicting demands.

1 2 3 4 5 6 7 8 9 10

3.9

4.1

4.3

4.5

4.7

4.9

5.1

5.3

5.4

The number of conﬂic ting de mands

Aver age levels

difficult−regretting and patient vs difficult−regretting and patient

difficult−regretting and patient vs easy−regretting and impatient

easy−regretting and impatient vs easy−regretting and impatient

easy−regretting and impatient vs difficult−regretting and patient

Figure 8: Average preference levels of the demands in bar-

gainer 1’s outcome with the number of conﬂicting demands.

put in diﬀerent preference levels for two bargainers

and arbitrarily label N P r0, 10s of them as their con-

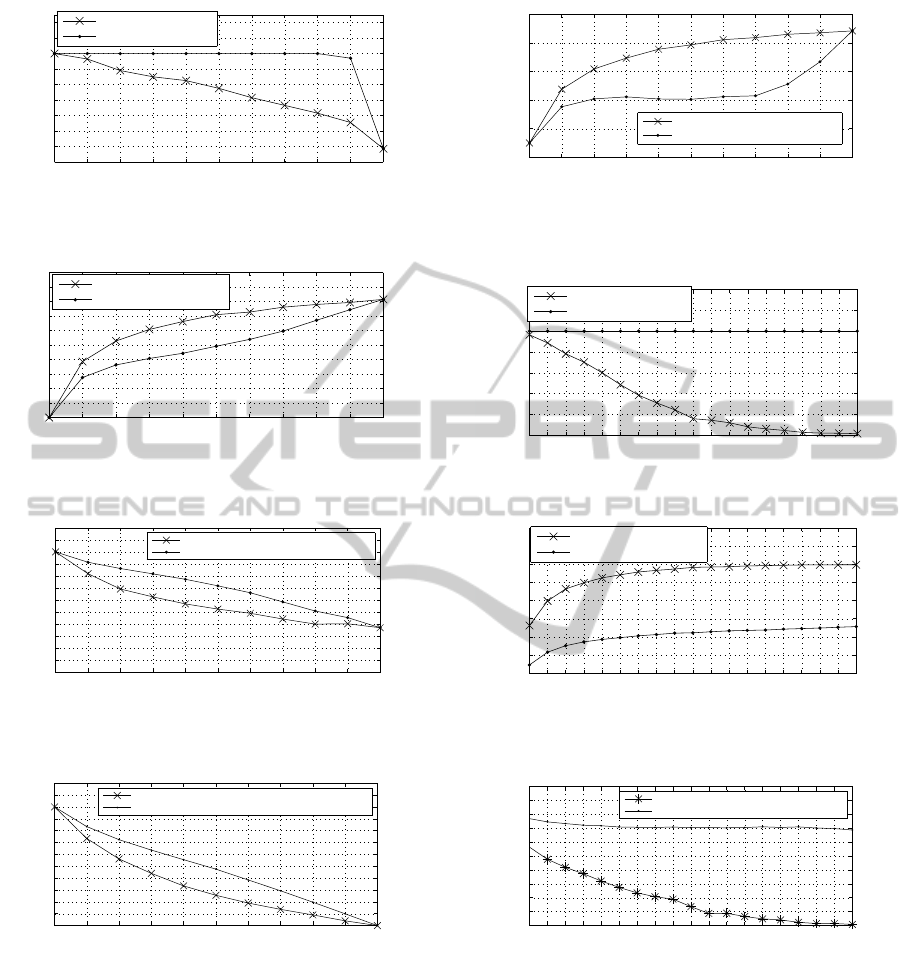
ﬂicting demands. Figure 9 shows that the success rate

of DSCS is higher than that of SCS, especially when

the conﬂicting demands are increasing, such as when

the number of conﬂicting demands is 8, the success

rate of our model is about 10% higher. Figure 10

AMulti-demandAdaptiveBargainingbasedonFuzzyLogic

581

0 1 2 3 4 5 6 7 8 9 10

100

102

104

The number of conﬂic ting demands

Success r ate( %)

success rate by SCS

success rate by DSCS

Figure 9: Success rate with the number of conﬂicting de-

mands.

0 1 2 3 4 5 6 7 8 9 10

The number of conﬂicting demands

Aver age rounds

average rounds by SCS

average rounds by DSCS

Figure 10: Average rounds of reaching agreements with the

number of conﬂicting demands.

0 1 2 3 4 5 6 7 8 9 10

The number of conﬂic ting demands

T he numb e r of de mands

in agree me nt

number of demandss in agreement by SCS

number of demands in agreement by DSCS

Figure 11: The number of demands in agreement with the

number of conﬂicting demands.

0 1 2 3 4 5 6 7 8 9 10

The number of conﬂ ic ting de m ands

T he numb e r of consist e nt

de mands in agre e ment

number of consistent demands in agreement by SCS

number of consistent demands in agreement by DSCS

Figure 12: The number of consistent demands in agreement

with the number of conﬂicting demands.

shows that in DSCS the average rounds of reaching

agreements are about two rounds less than than of

SCS. Figures 11 and 12 show that in DSCS both the

number of demands in agreement and the number of

consistent demands in agreement are larger. Figures

13, 19 and 20 show that when the number of con-

ﬂicting demands increase, the average/the highest/the

lowest preference level in a bargainer’s outcome in

DSCS will be lower than that of SCS.

In the second experiment, we randomly generate

0 1 2 3 4 5 6 7 8 9 10

The number of conﬂ ic ting de m ands

Ave rage le ve ls

average levels in outcome by SCS

average levels in outcome by DSCS

Figure 13: Average preference levels of the demands in the

ﬁrst bargainer’s outcome with the number of conﬂicting de-

mands.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

100

120

140

The numbe r of bargainers

Suc cess r ate( %)

success rate by SCS

success rate by DSCS

Figure 14: Success rate with the number of bargainers.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

The numbe r of bargainers

Aver age rounds

average rounds by SCS

average rounds by DSCS

Figure 15: Average rounds of reaching agreements with the

number of bargainers.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

The number of bargaine rs

The numb e r of de mands

in agr e e me nt

number of demands in agreement by SCS

number of demands in agreement by DSCS

Figure 16: The number of demands in agreement with the

number of bargainers.

10 demands in diﬀerent preference levels for M bar-

gainers (inbetween 2 and 20) and arbitrarily select 4

of them as the conﬂicting demands of all the bargain-

ers. The bargaining will proceed in both models. Fig-

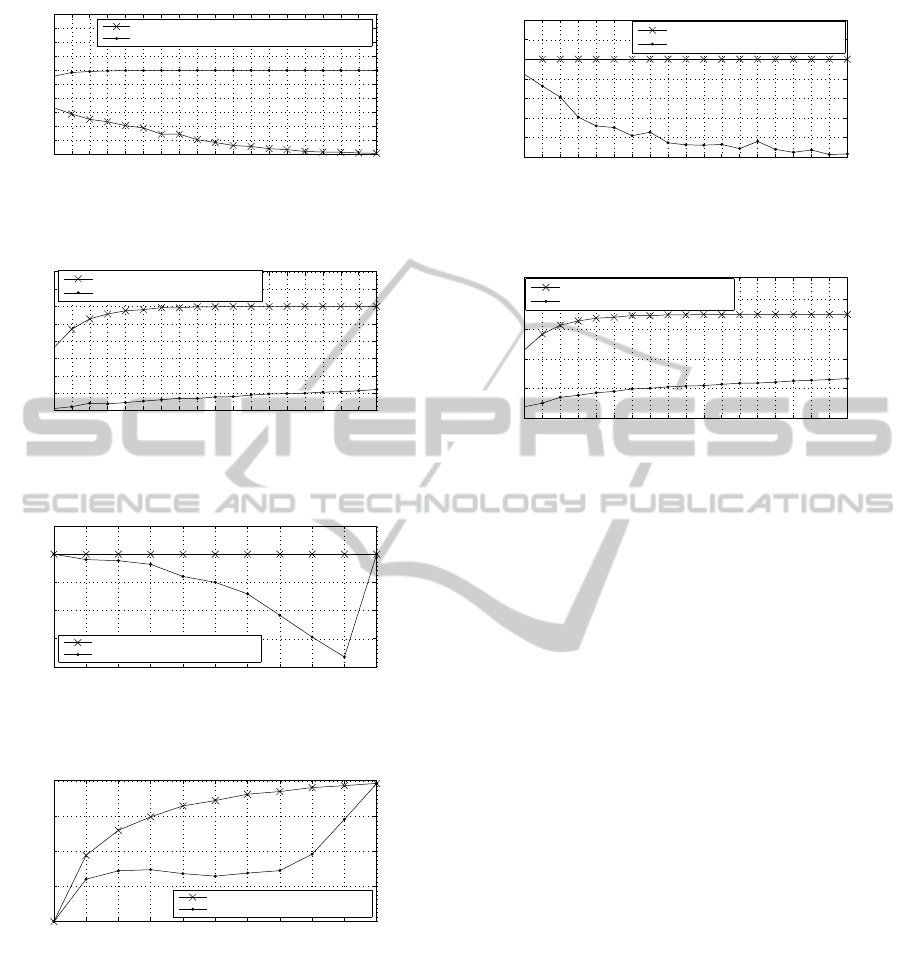
ure 14 shows that DSCS can keep a high success rate

of bargaining even when the number of bargainers

increases, while the success rate will decrease obvi-

ously with SCS. Figure 15 shows that DSCS can also

keep lower rounds of reaching agreements than SCS.

Moreover, Figures 16 and 17 show that more con-

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

582

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

The number of bargaine rs

The numb e r of cons ist e nt

demands in agre e me nt

number of consistent demands in agreement by SCS

number of consistent demands in agreement by DSCS

Figure 17: The number of consistent demands in agreement

with the number of bargainers.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

0.5

1.5

2.5

3.5

The number of bargaine rs

Ave rage le ve ls

average levels in outcome by SCS

average levels in outcome by DSCS

Figure 18: Average preference levels of the demands in the

ﬁrst bargainer’s outcome with the number of bargainers.

0 1 2 3 4 5 6 7 8 9 10

0.9

1.1

1.2

1.3

1.4

The number of conﬂ c ting de mands

The highest le ve l

the highest level in outcome by SCS

the highest level in outcome by DSCS

Figure 19: The highest level of the demands in the ﬁrst bar-

gainer’s outcome with the number of conﬂicting demands.

0 1 2 3 4 5 6 7 8 9 10

The number of conﬂ ic ting de m ands

The lowest le vel

the lowest level in outcome by SCS

the lowest level in outcome by DSCS

Figure 20: The lowest level of remaining demands in the

ﬁrst bargainer’s outcome with the number of conﬂicting de-

mands.

sistent demands can be saved in the ﬁnal agreement

even when the bargainers increase in DSCS. Figures.

18, 21 and 22 show that when the number of bargain-

ers increase, the average/the highest/the lowest pref-

erence level in a bargainer’s outcome in DSCS will be

lower than that of SCS.

Although the average levels of demands are a little

lower than SCS, even when the number of conﬂicting

demands or bargainers increases, DSCS can still re-

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

0.8

0.9

1.1

1.2

1.3

1.4

The number of bargaine rs

The highest le ve l

the highest level in outcome by SCS

the highest level in outcome by DSCS

Figure 21: The highest level of the demands in the ﬁrst bar-

gainer’s outcome with the number of bargainers.

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

The number of bargaine rs

The lowest le vel

the lowest level in outcome by SCS

the lowest level in outcome by DSCS

Figure 22: The lowest level of the demands in the ﬁrst bar-

gainer’s outcome with the number of bargainers.

ﬂect bargainers’ cognitive factors of risk, regret, pa-

tience, keep a high success rate and a high eﬃciency,

and get more consistent demands in an agreement.

6 AN INVESTMENT PROBLEM

This section illustrates our model by solving the bar-

gaining problem of the real estate investment be-

tween two investors. Investor 1 wants building large-

scale apartments (LA), using environmental but ex-

pensive material (EEM), expanding the green area

(GA), building artiﬁcial lake (AL), ﬁtment outsourc-

ing (FO), building a big club house (CH), opening

communal facilities to the public (OP), property man-

agement outsourcing (PMO). Investor 2 wants EEM,

GA, FO and OP; but opposes LA, AL, CH and PMO.

Thus, their demand sets are:

“tEEM, GA, LA, FO, AL, CH, PMO, OPu,

“t PMO, LA,EEM, CH,GA, AL,FO,OPu.

Table 2 shows two investors’s original preferences

over their own demands, which just reﬂect their own

favorites rather than the other side’s situation. How-

ever, when going to the bargaining, they will worry

about their conﬂicting demands and thus adjust the

preferences to form initial dynamic ones, hoping to

reach an agreement more easily meanwhile keep their

demands as many as possible. In this example, In-

vestor 1 demands LA but Investor 2 demands LA,

which is a contradiction. Similarly, we can get their

AMulti-demandAdaptiveBargainingbasedonFuzzyLogic

583

Table 2: Original and dynamic preferences

Rank

Investor 1 Investor 2

original dynamic original dynamic

1 EEM EEM PMO PMO

2 GA LA LA EEM

3 LA AL EEM LA

4 FO GA GH GA

5 AL CH GA CH

6 CH FO AL FO

7 PMO PMO FO OP

8 OP OP OP AL

Table 3: Dynamic bargaining proceeding.

Rank Investor 1 Investor 2

1 EEM PMO

2 LA EEM

3 AL LA

Round 1

4 GA GA

5 CH CH

6 FO FO

7 PMO OP

1 EEM EEM

2 GA PMO

3 LA GA

Round 2

4 AL LA

5 FO FO

6 CH CH

1 EEM EEM

2 GA GA

3 FO PMO

Round 3

4 LA FO

5 AL LA

1 EEM EEM

2 GA GA

3 FO FO

Round 4

4 LA PMO

Rank Investor 1 Investor 2

1 EEM EEM

2 GA PMO

3 LA GA

Round 1

4 AL LA

5 FO FO

6 CH CH

7 PMO OP

1 EEM EEM

2 GA GA

3 FO PMO

Round 2

4 LA FO

5 AL LA

6 CH CH

1 EEM EEM

2 GA GA

3 FO FO

Round 3

4 LA PMO

5 AL LA

1 EEM EEM

2 GA GA

3 FO FO

Round 4

4 LA PMO

conﬂicting demand sets: CDS

“ tLA,Al,CH,PMOu

and CDS

“ t LA, AL, CH, PMOu.

From Table 2, by formula (6), we can obtain two

investors’ risk degrees γ

“ 0.364 and γ

“ ´0.267.

Investor 1 is risk-seeking because he moves up his

conﬂicting demands LA, AL, CH and PMO from the

original preference to the initial dynamic one. Rather,

Investor 2 is risk-averse because he downgrades the

conﬂicting demand PMO, LA, CH and LA.

Now we show how our model solves it. During

the bargaining, the changes of preference and param-

eters are shown in Tables 3 and 4, respectively. There

are two steps in the ﬁrst round of bargaining. Firstly,

as shown in Table2, there are some contradictions in

two investors’ demands, so both give up the demands

in the lowest level in their dynamic preferences, that

is OP of investor 1 and AL of investor 2. Then, the

model will be updated into a new one shown in the

left table in the ﬁrst row (denoted as Round 1). Sec-

ondly, by the parameters’ calculation functions (4),

Table 4: Parameters.

Parameters Round 1 Round 2 Round 3 Round 4

pϑ

, ϑ

q (0.25,0) (0.25,0.25) (0.25,0.25) (0.25,0.25)

pρ

, ρ

q (0.125,0.125) (0.25,0.25) (0.375,0.375) (0.5,0.5)

pγ

, γ

q (0.364,-0.267) (0.364,-0.267) (0.364,-0.267) (0.364,-0.267)

pζ

, ζ

q (0.31,0.46) (0.34,0.46) (0.37,0.47) (0.38,0.47)

(5) and (6), we can obtain ϑ

“ 0.25, ρ

“ 0.125,

“ 0.364, ϑ

“ 0, ρ

“ 0.125, and γ

“ ´0. 267,

respectively. Thus, by fuzzy rules in Table 1, based

on Mamdani method (see Deﬁnition 4), we can ob-

tain ζ

“ 0.322 and ζ

“ 0.376 in this round. Then,

by their action function (formula (1)), their initial

dynamic preferences are updated into new ones as

shown in the right table in the ﬁrst row (denoted as

Round 1

). According to the second choice of action

function (formula (1)), LA, AL, CH, PMO of investor 1

and LA, AL, CH of investor 2 are declined. Sim-

ilarly, we can understand the rest of rounds similarly.

The game ends after the 4th round because two in-

vestors have nothing in contradictory.

From Table 3, we can see that by the dy-

namically simultaneous concession method (see

Deﬁnition 2), the outcome of the game is:

pGq “ tEEM, GA, FO, LAu and S

pGq “

tEEM, GA, FO, PMOu. So, their agreement is:

pGq Y S

pGq “ tEEM, GA, FO, LA, PMOu.

7 RELATED WORK

Like Zhang (2010), Bao and Li (2012) also build an

axiomatic bargaining model, in which the preference

over outcomes is ordinal. However, unlike the model

of Zhan et al. (2013), their model does not reﬂect the

bargainers’ risk attitudes and patience, which are very

important factors for bargaining in real life. More-

over, they did not conduct any simulation experiment

to analyse their model, but we do in this paper.

In (Kolomvatsos et al., 2012), a fuzzy logic based

model is also introduced for a buyer to decide to ac-

cept or reject a seller’s oﬀer according to the proposed

price, the belief about the seller’s deadline, the de-

mand relevancies, and so on. They also do a lot of

simulation experiments to show their model’s capa-

bility, but did not show how the risk attitudes change

the bargainers’ preferences like what we did.

In the bilateral negotiation model of Zuo and Sun

(2009), fuzzy logic is used for oﬀering evaluation.

Moreover, they distinguish three attitudes of bargain-

ers in concession: greedy, anxious and calm. They

also test how diﬀerent concession strategies inﬂuence

agreements. However, they did not compare their so-

lution with the others like what we do in this paper.

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

584

8 CONCLUSIONS

This paper improves the fuzzy logic based bargain-

ing model of Zhan et al. (2013). Moreover, through

empirical analysis we ﬁgure out how human psycho-

logical characteristics about risk, patience and regret

inﬂuence the outcome of a bargaining; and show how

the fuzzy logic based model outperforms the model of

Zhang (2010) in terms of success rate and agreement

reaching eﬃciency. In addition, we use our model to

solve a bargaining problem of estate investment prob-

lem. Many could be done in the future. For exam-

ple, it is interesting to integrate more human psycho-

logical characteristics into our model to solve certain

problems, and carry out more theoretic and empirical

analyses on the extended model.

ACKNOWLEDGEMENTS

This paper is supported by MOE Project of Key Re-

search Institute of Humanities and Social Sciences at

Universities (No. 13JJD720017) China, Bairen Plan

(No. 1309089) and Major Projec Raising Programt

of Sun Yat-sen University, National Natural Science

Foundation of China (No. 61173019), Major Projects

of the Ministry of Education (No. 10JZD0006) China,

and National Social Science Fund of Major Projects

(13&ZD186) China.

REFERENCES

Bao, V. N. Q. and Li, M. (2012). From axiomatic to strategic

models of bargaining with logical beliefs and goals. In

Proceedings of the 11th International Conference on

Autonomous Agents and Multiagent Systems - Volume

1, pages 525–532.

Garc´ıa-Gallego, A., Georgantz´ıs, N., and Jaramillo-

Guti´errez, A. (2012). Gender diﬀerences in ultimatum

games: Despite rather than due to risk attitudes. Jour-

nal of Economic Behavior & Organization, 83(1):42–

49.

Kolomvatsos, K., Anagnostopoulos, C., and Hadjiefthymi-

ades, S. (2012). A fuzzy logic system for bargaining

in information markets. ACM Transactions on Intelli-

gent Systems and Technology, 3(2):32.

Mamdani, E. H. and Assilian, S. (1975). An experiment in

linguistic synthesis with a fuzzy logic controller. In-

ternational Journal of Man-Machine Studies, 7(1):1–

13.

Shubik, M. (2006). Game theory in the social sciences:

Concepts and solutions. MIT Press, Cambridge.

Zhan, J., Luo, X., Sim, K. M., Feng, C., and Zhang, Y.

(2013). A fuzzy logic based model of a bargaining

game. In Knowledge Science, Engineering and Man-

agement, volume 8041 of Lecture Notes in Computer

Science, pages 387–403. Springer.

Zhang, D. (2010). A logic-based axiomatic model of

bargaining. Artiﬁcial Intelligence, 174(16-17):1307–

1322.

Zhang, D. and Zhang, Y. (2008). An ordinal bargaining so-

lution with ﬁxed-point property. Journal of Artiﬁcial

Intelligence Research, 33(1):433–464.

Zuo, B. and Sun, Y. (2009). Fuzzy logic to support bilateral

agent negotiation in e-commerce. In 2009 Interna-

tional Conference on Artiﬁcial Intelligence and Com-

putational Intelligence, volume 4, pages 179–183.

AMulti-demandAdaptiveBargainingbasedonFuzzyLogic

585