
Massive Data Flows
Self-organization of Energy, Material, and Information Flows
Takashi Ikegami
1
and Mizuki Oka
2
1
The University of Tokyo, Tokyo, Japan
2
University of Tsukuba, Tsukuba, Japan
Keywords:
Massive Data Flows, Self-organization, Artificial Life, Complex Systems, Web.
Abstract:
As opposed to “Big Data” as a buzz word, we attempt to find a new pattern or structure generated by self-
organization in the flow of the massive data. We call this approach Massive Data Flows (MDF). Rather than
making use of “Big Data”, we are interested in the new phenomena and theory that allows us to deal with
the data without losing the autonomy, complexity, dynamics and structure that the data itself has. MDF is a
generic term used to identify a new kind of system dynamics: self-organization in complex open environments.
Composed of many interacting heterogeneous elements, MDF systems exhibit self-referential, self-modifying,
and self-sustaining dynamics, that can enable door-opening innovation. While the web may be the best exam-
ple of an MDF system, the concept is generic to natural/artificial systems such as brains, cells, markets and
ecosystems. In this paper, we exemplify five systems; the default mode network and the excitability of the
web, the autonomous sensor network, chemical oil droplets, and court and cave computation with a many-core
system as potential MDF systems.
1 INTRODUCTION
Analyses of “Big Data” from the web and sensory
data have recently become the focus of attention.
However, the development of data mining techniques
is still in progress for the analysis of large data sets,
so conventional techniques are being applied. It is
yet difficult to effectively deal with complex data with
possibly a very large degree of freedom using conven-
tional approaches that execute the analysis in a top-
down manner. Thus, a new kind of bottom-up mining
method, which can be referred to as data driven, is
necessary to deal with the “Big Data.”
As opposed to “Big Data” as a buzz word, we at-
tempt to find a new pattern or structure generated by
self-organization in the flow of the massive data
1
. We
call this approach Massive Data Flows (MDF). MDF
is a generic term used to identify a new kind of sys-
tem dynamics: self-organization in complex open en-
vironments. Composed of many interacting heteroge-
neous elements, MDF systems exhibit self-referential,
1
As part of this effort, we have organized workshops
called Massive Data Flows at Japanese artificial intelli-
gence conferences since 2011 as well as at an international
workshop of the European Conference on Artificial Life in
2013.
self-modifying, and self-sustaining dynamics, that
can enable door-opening innovation. While the web
may be the best example of an MDF system, the con-
cept is generic to natural/artificial systems such as
brains, cells, markets and ecosystems.
Unlike systems studied in isolation or at equi-
librium, MDF systems are open and driven systems
existing within a rich context, constantly changing,
growing, evolving, and thereby autonomously chang-
ing the way in which they interact with the environ-
ment around them. The patterns that they exhibit are
neither imposed from outside, nor arising internally,
but are a consequence of the interface between the
endogenous and exogenous data flows. If “Big Data”
systems exhibit volume, velocity and variety, MDF
systems exhibit vitality.
A series of methods for data analyses and vi-
sualization are being developed, such as a self-
organization map, ant colony optimization, particle
swarm optimization and evolutionary computation.
However, these methods are not created to target large
data, and we need to establish a bottom-up method to
target these data. One of such methods that has re-
cently attracted attention and uses multilayered neu-
ral networks is called deep learning (Hinton et al.,
2006). For example, researchers at Google experi-
237
Ikegami T. and Oka M..
Massive Data Flows - Self-organization of Energy, Material, and Information Flows.
DOI: 10.5220/0004907102370242
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 237-242
ISBN: 978-989-758-016-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Examples of self-organization. (Left) Progogine’s hexagonal lattice; (Middle) Karman vortex street;
(Right) Belousov-Zhabotinsky chemical reaction. Image of B´enard Cell is taken from http://www.dichotomistic.com/
hierarchies
fractals.html. The image of the Karman vortex street is taken from http://en.wikipedia.org/wiki/
Karman
vortex street. The screenshot of the Belousov-Zhabotinsky chemical reaction has been generated by a simulator
at http:// dencity.jp/simulator/bz.html.
mented with the images of YouTube, using an artifi-
cial neural network of 16,000 nodes, and found that
there are specific neurons that react to videos of a
cat and specific ones that respond only to a person’s
body (Le et al., 2012). The deep-learning method
takes the approach of extracting the structure that the
system self-organizes when a large amount of data are
involved and shares some conceptual interests with
the MDF approach.
Another example can be found in a project called
SpeecHome by Deb Roy (Vosoughi et al., 2012). Deb
Roy and his colleagues put up video cameras and au-
dio sensors around his house and recorded the growth
of his own child for over three years. On the ba-
sis of this life-log data, Deb Roy captured the entire
process of language acquisition of the child. There
have been previous studies based on anecdotal theory
about children’s developmental processes, but none
involved a longitudinal study with systematic record-
ing of a child in daily life. In addition, the same data
can be different when the point of reference changes
or has a different context, which was clearly shown
by the SpeecHome project. This kind of study sug-
gests that enormous datasets, including non-typical
and those used anecdotally, are needed for unraveling
complex phenomena.
The emphasis of this paper is that we should create
new methods and language in order to synthesize and
describe the self-organizing aspect of massive data
flows. Here, we extend the meaning of data to include
material, energetics and information flows in order to
capture the kind of complexity that we are exploring.
2 SELF-ORGANIZATION AND
MDF
From the long-term studies on non-linear and non-
equilibrium systems, there are ample examples of
self-organization in various systems ranging from
simple physical systems to complex biological ones.
For example, the B´enard Cell is observed in hori-
zontally layered fluid heated from below; this is also
known as Progogine’s hexagonal lattice (Prigogine,
1980). The Karman vortex street is a successive for-
mation of vortices behind a cylinder in fluid flow from
the front. The Belousov Zhabotinsky chemical reac-
tion on a petri dish shows spatial and temporal oscil-
latory patterns (see Figure 1).
For all these examples, patterns emerge by in-
creasing energy or material flows from outside. Be-
yond a certain critical flow value, the patterns are self-
organized. This can be illustrated with the bifurcating
process from a (thermal) equilibrium state to dynamic
non-steady states with different periodicities and even
chaotic phases. It has also been said that the stripes on
fish and shells are biological examples of these self-
organized patterns (Kondo and Miura, 2010; Mein-
hardt, 2003).
A typical research area that deals with self-
organization is artificial life as a part of complex sys-
tem sciences. The aim of the study of artificial life is
to construct life-like phenomena based on programs
or non-organic components. What we call life-like
phenomena are those that have autonomy, evolvabil-
ity, enaction, and adaptability, which we synthesize
by using autonomous robots or algorithmic chemistry.
Recent studies have also explored these ideas as living
technology in real life (Ikegami, 2013).
What will happen if we further increase the energy
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
238

or material flows beyond the critical values? When
a system is exposed to something beyond the crit-
ical value, and further to excessive flows, patterns
will decay and the system may no longer be able
to sustain itself, i.e., a cylinder in the flow will be
destroyed by the pressure; but it may also generate
second order self-organization, i.e., a higher order
self-organization to cope with the excess input flows.
Examples of second-order self-organization could be
the evolution of new species, technological innova-
tions (Bedau, 2012), and new web services, most of
which are strongly related to biological adaptive sys-
tems. It is not the pattern self-organized on the surface
of the bodies but the system itself that will adapt to
the excess flows. In other words, a self-organization
mechanism is not only attributed to the system’s in-
herent dynamics but also to the excess flows from out-
side.
In the following sections, we will see such second-
order self-organization in examples from our recent
studies.
2.1 Web Default Mode Network
The web is a candidate for life-like phenomena in
which services that run on the web must deal with
massive data flows where the underlying structure and
the overlying information flow changes constantly.
Such spatially and temporally extended web space
can be used as a metaphor for living states and/or con-
scious states. Indeed, the web picks up the uncon-
scious state of collective human behaviors (e.g., rec-
ommendations of products or advertisements based
on the user’s collective behaviors are a classic exam-
ple). Analyzing the web data could open up a new
direction of science.
Social networking services (e.g., Twitter, Face-
book, Google Plus) are now major sources of the web
dynamics, together with web search services (e.g.,
Google, Yahoo, and Bing). These two types of Web
services mutually influence each other but generate
different dynamics. We distinguish two modes of web
dynamics: the reactive mode and the default mode.
It is assumed that Twitter messages (called “tweets”)
and Google search queries react to significant so-
cial movements and events, but they also demonstrate
signs of becoming self-activated, thereby forming a
baseline web activity. We define the former as the
reactive mode and the latter as the default mode of
the web. We investigated these reactive and default
modes of the web’s dynamics using transfer entropy
(TE) (Oka and Ikegami, 2013).
We collected tweets (in Japanese) over a two-
year period by applying morphological analysis to ex-
Figure 2: The role of each keyword. (Top) The ratio of key-
words becoming sources and sinks, shown as a function of
keyword frequency over time. Red shows the source ratio
and blue shows the sink ratio, as a function of keyword fre-
quency over time. The frequent keywords tend to become
source nodes, and infrequent keywords tend to become sink
nodes. (Bottom) Strong mediators are defined as having
ample incoming and outgoing transfer entropy (TE) flow,
and weak mediators are defined as those with both weak
incoming and outgoing TE flow.
tract the 1,000 most frequently used Japanese nouns
in the tweets and used these as keywords. Analysis
of the time series with information transfer measure-
ment shows that the more-frequent keywords become
the upper stream of information flow (in the sense of
transfer entropy), and the less-frequent keywords be-
come the down stream (see Figure 2). The informa-
tion is therefore transferred from the more to less fre-
quent keywords for the minimum time mesh around 1
hour. However, interestingly, the tendency are some-
times reversed for the time mesh of a few minutes.
We interpret this as different causal relationships can
be organized in different time scales, corresponding
to the time scales of local tweeting (less frequent key-
words) and the global atmosphere of Twitter (more
frequent keywords).
Analogous to the default mode network (DMN) in
the brain, we name this information transfer pattern in
Twitter as the web DMN since without a significant
event from the outside, the Twitter system can main-
tain and organize its flow pattern. The web DMN also
transfers information to the less frequent keywords,
which often have a bursting behavior reacting to the
external inputs, so that the upper stream of the trans-
fer information flow of the longer time scale can serve
as a default mode. We argue that DMN is an example
of self-organization of the MDF since internal and ex-
ternal information transfer across the web is the cause
of this DMN. The web network topology is constantly
changing, and the constituent elements are very het-
erogeneous, which is an aspect of second-order self-
organization.
MassiveDataFlows-Self-organizationofEnergy,Material,andInformationFlows
239
12/06/30 12/07/28 12/08/25 12/09/22 12/10/20 12/11/17 12/12/15 13/01/12 13/02/09 13/03/09
12/06/30 12/07/28 12/08/25 12/09/22 12/10/20 12/11/17 12/12/15 13/01/12 13/02/09 13/03/09
Date
12/06/30 12/07/28 12/08/25 12/09/22 12/10/20 12/11/17 12/12/15 13/01/12 13/02/09 13/03/09
Date
12/06/30 12/07/28 12/08/25 12/09/22 12/10/20 12/11/17 12/12/15 13/01/12 13/02/09 13/03/09
Frequency FrequencyFrequency Frequency
Date
Date
Type 1: constant - “joy”
Type 2: periodic (small time scale) - “Monday”
Type 2’: periodic (large time scale) - “flu”
Type 3: intermittent - “earthquke”
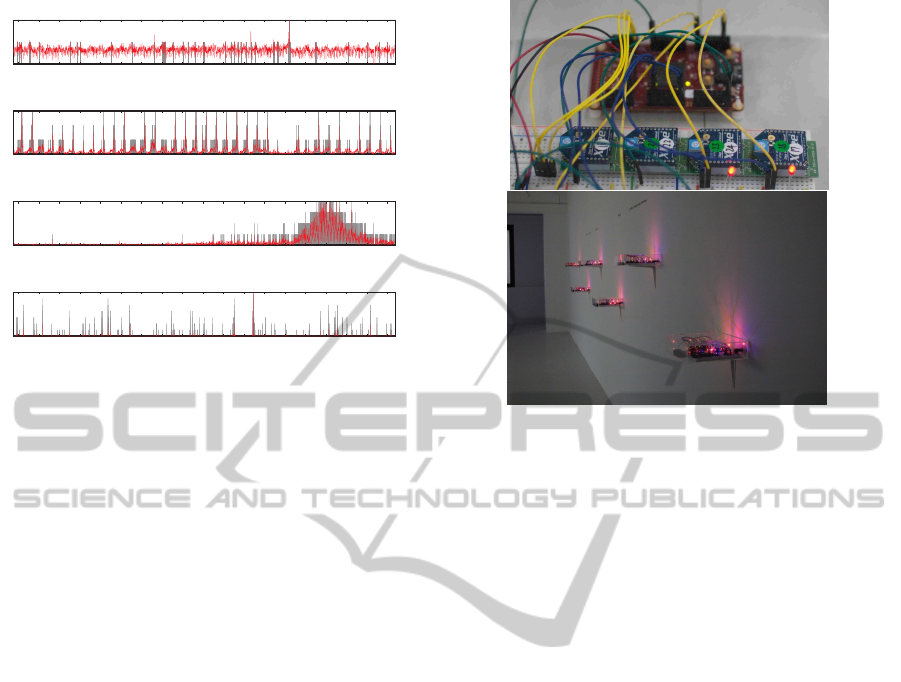
Figure 3: Examples of time series (red lines) and detected
bursts (gray bars; the height indicates the burst level) with
different dynamics: type 1) the noisy type (joy); type 2) the
periodic type with a small time scale (Monday); type 2’) the
periodic type with a large time scale (flu); and type 3) the
intermittent type (earthquake).
2.2 Self-organization of Bursting
Behaviors on Social Media
Twitter can be taken as an extended sensor of people’s
collective interests. The output pattern of the sen-
sor for each fact/event appears in the time series that
contains the keywords in their tweets. An increase
in the popularity of events, which are reflected in the
time series as a burst, cause an increase in frequency
(see Figure 3). We studied bursting behavior in rela-
tion to the structure of fluctuation to reveal the origin
of bursts. More specifically, we studied the tempo-
ral relationship between a preceding baseline fluctu-
ation and the successive burst response, using noun
frequency from Twitter data as described above.
As a result, we found a specific fluctuation thresh-
old beyond which a strong burst occurs (Oka et al.,
2014). The bursts below this threshold are caused by
interactions among the social network, and the thresh-
old is self-organized as a result of such interactions.
Above this threshold, the response size becomes un-
predictable, and a wide range of burst sizes appear.
The threshold is different for a time series of each
noun. Including a power-law behavior of burst sizes,
there are a variety of fluctuation dynamics that self-
organize this threshold for each noun. This excitable
property of Twitter can also be taken as a sign of self-
organization driven by the MDF because the variety
of information flow behind the web and real-world
events mutually affect each other to determine its na-
ture as an excitable media.
Figure 4: (Top) Implemented sensor unit and (Bottom) in-
stallation of the autonomous sensor network (ASN) system
as a sound installation in a gallery in Tokyo.
2.3 Autonomous Sensor Networks
We previously proposed and studied an autonomous
sensor network (ASN) as a new challenge for study-
ing self-organization in a long-term and open-ended
environment (Maruyama et al., 2013). We proposed
an ASN that is spatially distributed in the real world
(see Figure 4.) One node has two sensors, light and
humidity, that sense the corresponding environmen-
tal information with an adaptive sensing periodicity
(or cycle). The sensor information obtained by each
node, which is controlled by two XBees and two Ar-
duinos, is sent to other nodes via wireless connec-
tions. The uniqueness of the sensor network is that
we employ artificial chemistry to control the sampling
rate of each sensor autonomously (i.e., sensors are not
simply reacting to environmental changes but some-
times resisting them).
In each sensor unit, we let the sensory inputs cause
the reaction, and the reaction speed determines the
sampling rates of each sensor. A minimal nonlinear-
ity introduced by the artificial chemistry can foster
some unexpected spontaneous temporal oscillations
in the sampling rates, which we call the resonating
state as opposed to the resting state of the network.
The resonating state can vary drastically depending
on the light intensity and the coupling with the hu-
midity sensor. The resting state is similar to the de-
fault mode of the network, which organizes the base-
line activity of the network. We studied an eight-
node autonomous sensor network to see the dynamic
changes of network states in a week in a half-open
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
240

space. A most interesting behavior of ASN is the
spontaneous transition between a resting state and the
resonating state. We argue that ASN provides a prin-
ciple to make a second-order self-organization driven
by the MDF. Again, the condition for MDF-driven
self-organization is a reaction between internal dy-
namics and huge input flows from outside. In the
case of ASN, light intensity and humidity flow cou-
pled with the sensor network with adaptive sampling
rate dynamicsdetermine the self-organization. We are
still investigating its complex long-term behavior in
open space.
Figure 5: A photo image of self-moving oil droplets emerg-
ing autonomously. The convection flow inside the droplet
is observed and the product of reaction (mostly oleic acid
molecules) being secreted from the tail.
2.4 Self-moving Oil Droplets
Another example of MDF can be found in self-
moving oil droplets (Hanczyc et al., 2007; Hanczyc
and Ikegami, 2010). We experimented and discov-
ered the emergence of self-moving oil droplets about
several hundred micrometers in size by pouring oleic
anhydrous acid into a high pH aqueous solution (see
Figure 5). An oil droplet is covered with oleic acid
as a reaction between the oil and water, it senses the
chemical gradient by generating an internal pH gradi-
ent; it avoids low pH regions (< 10), preferring high
pH (> 11) regions.
Its movement comes from the chemical reaction
on the surface of the droplet, inside convection flows
and the droplet shape. Such a self-moving droplet can
be viewed as the origin of a soft-bodied robot. We say
this is the MDF example, since it is self-sustaining
self-organizing system copying with the environmen-
tal flows. If this droplet could sense and adapt to more
diverse environmental patterns and flows, it would
show more complex functionalities. This also pro-
vides a new design principle for MDF for producing
a self-organizing robot.
Figure 6: Overview of the cave and court computation
scheme on a many-core machine.
2.5 Concurrent Computation
Architecture on a Many-core
Machine
The web is made accessible through search engines,
such as Google, that construct the architecture so that
the system can handle huge amounts of data by opti-
mizing the throughput of the system. In particular,
this can maintain the consistency of the data when
running on many machines with many processors. We
are interested in understanding how concurrently pro-
cessing computational threads can compete indepen-
dently but cooperatively to resolve the inconsistency
produced by the concurrent process.
To examine this question, we investigated a many-
core machine that performs concurrent operations and
found that non-cooperativecomputational threads can
successfully organize a whole computational task.
More specifically, we proposed a concurrent architec-
ture, which enables effective concurrent computation
on a many-core machine by separating two phases;
court and cave (Oka et al., 2013). A unique point of
the court and cave computation is that it performs op-
erations simultaneously on shared resources without
excluding access for each thread (see Figure 6). We
conducted data management experiments by varying
the different number of cores on a multi-core machine
and investigated the characteristic dynamics for when
the highest performance is observed. We discovered
that the temporal dynamics of the number of opera-
tions changes from a noisy to bursty pattern at an op-
timal point.
The cave and court computational architecture is
another type of MDF self-organization since it is self-
modifying system coupling with a large data set. The
input data stream is distributed among many threads
in the cave phase but those threads are interacting in
the court phase in order to resolve inconsistency and
MassiveDataFlows-Self-organizationofEnergy,Material,andInformationFlows
241

re-organizing the CPU resource distributions. Syn-
chronization and desynchronization of the temporal
dynamics of each thread lead to the emergenceof self-
organization in this concurrent computation schema.
3 CONCLUSIONS
The concept of MDF provides a new methodology for
understanding data flows, including material, energy
and information flows. Analogous to the Darwinian
evolution and the organization of an ecological sys-
tem, MDF patterns grow, and this growth determines
the organization of system’s own state autonomously,
i.e. organization of data by the data for the data.
The self-organization we see here is related to
what we call open-ended evolution, i.e., formation of
innovative properties due to evolutionary dynamics.
In the field of artificial life, finding the prerequisite
conditions for having open-ended evolution has been
an obsession. For example, the emergence of popu-
lations of patents issued in the U.S. has been studied
by Bedau et al. (Bedau, 2012) to show which patent
leads the subsequent evolution of patents; they exam-
ined the complexity of the evolution of patents and
compared this to biological evolution.
MDF is the generic term that explains the co-
evolution of excess flows and the adaptive system
in which self-organizational patterns successively oc-
cur. The default mode network and the excitability
of the web, the autonomous sensor network, chemi-
cal oil droplets, and court and cave computation with
a many-core system are examples of potential MDF
systems.
ACKNOWLEDGEMENTS
We would like to express our sincere gratitude to
our collaborators, Dr. Yasuhiro Hashimoto, Profes-
sor Kazuhiko Kato and Norihiro Maruyama for the
studies mentioned in this paper. We would also
like to express the deepest appreciation to Profes-
sor Seth Bullock for stimulating and insightful com-
ments and discussions. This work was supported
by the Japan Society for the Promotion of Science
Grant-in-Aid for Young Scientists (B) (#25730184),
Grant-in-Aid for Scientific Research on Innovative
Areas (#24120704), and Grand-in-Aid for Scientific
Research (B) (#24300080).
REFERENCES
Bedau, M. A. (2012). Minimal memetics and the evolution
of patented technology. Foundations of Science, pages
1–17.
Hanczyc, M. M. and Ikegami, T. (2010). Chemical basis for
minimal cognition. Artificial Life, 16(3):233–243.
Hanczyc, M. M., Toyota, T., Ikegami, T., Packard, N., and
Sugawara, T. (2007). Chemistry at the oil-water inter-
face: Self-propelled oil droplets. J. Am. Chem. Soc.,
129(30):9386–9391.
Hinton, G. E., Osindero, S., and Teh, Y.-W. (2006). A fast
learning algorithm for deep belief nets. Neural Com-
putation, 18(7):15271554.
Ikegami, T. (2013). A design for living technology: Ex-
periments with the mind time machine. Artificial Life,
19(3-4):387–400.
Kondo, S. and Miura, T. (2010). Reaction-diffusion model
as a framework for understanding biological pattern
formation. Science, 329(5999):1616–1620.
Le, Q., Ranzato, M., Monga, R., Devin, M., Corrado, G.,
Chen, K., Dean, J., and Ng, A. (2012). Building high-
level features using large scale unsupervised learning.
In Proc. of the 29th International Conference in Ma-
chine Learning, pages 81–88.
Maruyama, N., Oka, M., and Ikegami, T. (2013). Creat-
ing space-time affordances via an autonomous sensor
network. In Proc. of the 2013 IEEE Symposium on
Artificial Life, pages 67–73.
Meinhardt, H. (2003). The Algorithmic Beauty of Sea
Shells. Springer.
Oka, M., Hashimoto, Y., and Ikegami, T. (2014). Self-
organization on social media: endo-exo bursts and
baseline fluctuations. In submitted, pages –.
Oka, M. and Ikegami, T. (2013). Exploring default mode
and information flow on the web. PLoS ONE,
8(4):e60398.
Oka, M., Ikegami, T., Woodward, A., Zhu, Y., and Kato,
K. (2013). Cooperation, congestion and chaos in con-
current computation. In Proc. of the 12th European
Conference on Artificial Life, pages 498–504.
Prigogine, I. (1980). From Being to Becoming: Time and
Complexity in the Physical Sciences. W.H.Freeman
and Co Ltd.
Vosoughi, S., Goodwin, M. S., Washabaugh, B., and Roy,
D. (2012). A portable audio/video recorder for longi-
tudinal study of child development. In Proc. of the
14th ACM International Conference on Multimodal
Interaction, pages 193–200.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
242
