
Approximation Methods for Determining Optimal Allocations in
Response Adaptive Clinical Trials
Vishal Ahuja
1
, John R. Birge
2
and Christopher Ryan
2
1
The University of Chicago, Center on Aging at NORC, 1155 E 60th Street, Chicago, IL 60637, U.S.A.
2
The University of Chicago Booth School of Business, 5807 S Woodlawn Ave., Chicago, IL 60637, U.S.A.
Keywords:
Adaptive Clinical Trials, Markov Decision Process, Grid Approximation, Approximate Dynamic Program-
ming.
Abstract:
Clinical trials have traditionally followed a fixed design, in which patient allocation to treatments is fixed
throughout the trial and specified in the protocol. The primary goal of this static design is to learn about
the efficacy of treatments. Response-adaptive designs, where assignment to treatments evolves as patient
outcomes are observed, are gaining in popularity due to potential for improvements in cost and efficiency over
traditional designs. Such designs can be modeled as a Bayesian adaptive Markov decision process (BAMDP).
Given the forward-looking nature of the underlying algorithms which solve BAMDP, the problem size grows
as the trial becomes larger or more complex, often exponentially, making it computationally challenging to
find an optimal solution. In this study, we propose grid-based approximation to reduce the computational
burden. The proposed methods also open the possibility of implementing adaptive designs to large clinical
trials. Further, we use numerical examples to demonstrate the effectiveness of our approach, including the
effects of changing the number of observations and the grid resolution.
1 INTRODUCTION
The costs of bringing a new drug to market have been
estimated to be as high as $5 billion (Forbes, 2013).
Clinical trials have been cited as a key factor in rais-
ing these costs; the total cost of a clinical trial can
reach $300–$600 million (English et al., 2010), po-
tentially an order of magnitude higher when includ-
ing the value of remaining patent life. Consequently,
drug manufacturers face pressure to produce conclu-
sive results faster and reduce the number of subjects.
Traditional clinical trials follow a non-adaptive
or fixed randomized designs, where patients are ran-
domly assigned to treatments and are used widely. Al-
though such designs provide a clean way of separat-
ing treatments and are well-understood by most prac-
titioners, they are becoming increasingly costly and
often end up producing inconclusive results. Con-
sequently, regulatory bodies, such as the U.S. Food
and Drug Administration, have recently encouraged
the use of adaptive designs (FDA, 2010).
Response-adaptive designs for clinical trials, typ-
ically Bayesian in nature, are gaining in popularity.
Such designs employ learn-and-confirm concepts, ac-
cumulating data on patient responses to make proce-
dural modifications while the trial is still underway,
increasing the likelihood of selecting the right treat-
ment for the right patient population earlier in a drug
development program. As a result, adaptive designs
can potentially reduce costs and shorten overall de-
velopment timelines significantly.
Bayesian adaptive designs are rooted in the multi-
armed bandit problem that requires balancing reward
maximization based on the knowledge already ac-
quired with attempting new actions to further increase
knowledge, commonly referred to as the exploitation
vs. exploration tradeoff. Berry was one of the pio-
neers, who used this formulation in the clinical trials
context (e.g. (Berry, 1978)).
Sequential allocation designs are the most com-
mon form of response-adaptive designs (e.g. (Berry
and Fristedt, 1985)), where patients are treated one at
a time (in a sequence), and each patient’s responses
is available before making an allocation decision for
the next patient. (Ahuja and Birge, 2014) extends this
model to incorporate simultaneous allocation of mul-
tiple patients and show that this results in an improved
objective function value (e.g., expected patient suc-
cesses) compared to naive implementation of sequen-
tial designs, thus substantially widening the potential
460
Ahuja V., R. Birge J. and Ryan C..
Approximation Methods for Determining Optimal Allocations in Response Adaptive Clinical Trials.
DOI: 10.5220/0004909504600465
In Proceedings of the 3rd International Conference on Operations Research and Enterprise Systems (ICORES-2014), pages 460-465
ISBN: 978-989-758-017-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

for applicability of such designs.
A major barrier to implementing adaptive designs
in practice is computational. Bandit problems in clin-
ical trials context are typically modeled as MDP’s,
where the solution is obtained by solving a finite-
horizon dynamic program (Ahuja and Birge, 2014).
However, the problem size increases exponentially as
the number of time periods, patients, or treatment-
outcome combinations increase, commonly referred
to as the curse of dimensionality (Powell, 2007). As a
result, a direct application of dynamic programming
becomes computationally prohibitive and finding an
optimal policy to this high-dimensional problem be-
comes challenging (Bertsimas and Mersereau, 2007).
Approximation techniques address this problem
and allow users to find a solution by reducing the
problem size and the associated computational bur-
den. When the underlying problem is modeled as an
MDP, the possible approximation techniques are gen-
erally collectively referred to as approximate dynamic
programming (ADP). There currently exist several
techniques to approximate the value function or state
space or both. Although some techniques are more
popular than others, ADP still remains more of an art
than a science.
In this study, we use a grid to approximate the
state space. We numerically evaluate the optimality
loss or the loss in objective value with respect to fully
enumerated solution, as a result of this approximation.
Our proposed approach has implications for clinicians
and policymakers interested in finding an efficient yet
easily implementable design for large clinical trials,
where currently existing adaptive designs either can-
not be implemented or do not perform or scale well.
The rest of the paper is organized as follows. §2
provides an overview of the literature. §3 presents the
model and the proposed approximation method. We
present numerical results in §4. We conclude in §5.
2 LITERATURE
Several methods and techniques have been proposed
in the literature for approximate solutions to large dy-
namic programs (see (Powell, 2007) for a discussion).
Lagrangian decomposition-based ADP approach is
one such method to approximate the value function
(e.g. (Adelman and Mersereau, 2008)). The approach
has been used to find approximate solution in interac-
tive marketing (Bertsimas and Mersereau, 2007, e.g.)
and retail assortment (Caro and Gallien, 2007, e.g.).
Another method is to use polynomials, for example
least squares approximation using Chebyshev poly-
nomials (Judd, 1998). (Ahuja and Birge, 2014) is the
only study that has used approximation in the con-
text of adaptive designs for clinical trials; they use
a truncated-horizon or limited-lookahead approxima-
tion method.
Grid-based methods are commonly used to ap-
proximate the state space. These techniques sample
a finite number of points, called the grid, from the en-
tire state space, compute the value of the points in the
grid and approximate the values of the non-grid points
via some form of interpolation (Sandikci, 2010).
There exists a rich literature on the grid-based
approximation including notable studies within the
operations management literature (Monahan, 1982;
Lovejoy, 1991; Aviv and Pazgal, 2005), as well in the
computer science literature (Hauskrecht, 1997; Zhou
and Hansen, 2001). (Sandikci et al., 2013) is an ex-
ample of a recent study that uses a grid-based approx-
imation approach in a healthcare setting to approxi-
mate the position of the patient on the waiting list.
There are several approaches for grid-based ap-
proximation that depend on the grid construction
choices, for example, uniform vs. non-uniform grid,
fixed vs. variable resolution grid, etc. In general, all
the corner points of the probability simplex are in-
cluded in the grid since that eliminates the need to ex-
trapolate (see (Sandikci, 2010) for a brief overview).
In this paper, we use a fixed-resolution uniform grid
since that allows for an efficient interpolation.
While grid-based approximation methods have
been studied and implemented before, our contribu-
tion lies in the efficient use of such methods in the
clinical trials context, specifically to the response-
adaptive designs for clinical trials, thus widely broad-
ening the practical applicability of such designs. In
a later study, we provide bounds on optimality gap
while noting that the solution obtained by approxima-
tion is a lower bound on the optimal solution obtained
from a fully enumerated problem.
3 MODEL
We follow the Bayes-adaptive Markov decision pro-
cess (BAMDP) model developed in (Ahuja and Birge,
2014). The state in the BAMDP model is a vec-
tor with dimension equal to the number of treatment-
outcome combinations, also called health conditions.
The state thus captures the information observed so
far (history) and is used to derive the distributions that
describe the uncertainty in the transition probabilities.
We first re-define the state in terms of fraction
of patient observations within each health condition.
Each state dimension then represents the fraction of
patient observations observed so far in a given health
ApproximationMethodsforDeterminingOptimalAllocationsinResponseAdaptiveClinicalTrials
461

condition, where the fractions sum up to one.
The key idea behind the approximation approach
is to cap the problem size by discretizing the fractions
that form the component of each state, thus limiting
the state space irrespective of the number of patients
and time periods. Such a setup allows us to choose,
ahead of time, a constant number of health states that
are evaluated explicitly at each time period, thereby
keeping the problem tractable and reducing the com-
putational burden, often substantially. However, this
leads to some optimality loss with respect to the solu-
tion obtained from a fully enumerated problem. Cal-
culating theoretical bounds on the optimality loss is a
subject of future work. The rest of the parameters and
modeling assumptions remain the same as in (Ahuja
and Birge, 2014).
3.1 General Model Specification
Let T be the trial length, n be the number of patients
allocated per period in the trial, and N = nT be the to-
tal number of patients (observations) in the trial. Let J
and O be the set of treatments and outcomes, respec-
tively. The corresponding set of health conditions, I,
is then the Cartesian product (J × O).
The information state is a vector h
t
∈ H ⊆
Z
|J|×|O|
, defined as h
t
= (h
1,1
t
,...,h
|J|,|O|
t
), where h
j,o
t
∈
Z
+
represents the the cumulative number of ob-
served patients to date in health condition ( j,o) at
time t ∈ {0,1,..,T }, for all j ∈ J, o ∈ O, such that
∑
j∈J,o∈O
h
j,o
t
= nt.
The controls,u
t
∈ U ⊆ ℜ
|J|
+
are defined as u
t
=
(u
1
t
,..., u
|J|
t
), where u
j
t
∈ [0, 1] is the probability of
assigning a patient to treatment j ∈ J at time t ∈
{0,..., T − 1} such that
∑
j∈J
u
j
t
= 1. The set of deci-
sions, d
t
, is random and obtained from the controls,
are defined as d
t
= (d
1
t
,..., d
|J|
t
). Here d
j
t
∈ Z
+
is
the number of patients assigned to treatment j ∈ J
such that
∑
j∈J
d
j
t
= n, Pr(d
t
|n,u
t
) ∼ Mu(d
t
;n; u
t
)
1
, and
Ed
j
t
= nu
j
t
. Patients begin arriving at t = 1, and deci-
sions for patients arriving at t are made at t − 1, and
no decision is made at t = T .
Finally, the probabilities are defined as p
j
t
=
(p
j,1
t
,.., p
j,|O|
t
), where, p
j,o
t
represents the probability
of observing outcome o ∈ O at time t + 1 given treat-
ment j ∈ J at time t. We assume a generalized multi-
nomial likelihood on the transition to state h
t+1
from
state h
t
, given p
t
, and use a Dirichlet conjugate prior
1
Mu denotes multinomial distribution.
on p
t
with hyperparameters α
t
= (α
1,1
t
,..., α
|J|,|O|
t
) for
t ∈ {0, ...,T }. If we denote the initial priors by α
0
=
(α
1,1
0
,..., α
|J|,|O|
0
) and assume that the outcomes of pa-
tients in different health conditions are not informa-
tive of each other, then each α
j,o
t
can be updated in-
dependently as follows: α
j,o
t
= α
j,o
0
+ h
j,o
t
, where h
j,o
t
captures all the (random) realizations from the past
for that treatment-outcome combination.
Given the decision d
t−1
, the (random) outcomes
are observed in the next period, captured in the vector
k
t
∈ K ⊆ Z
|J|×|O|
, that we define as the physical state,
k
j
t
= (k
j,1
t
,.., k
j,|O|
t
). Here, k
j,o
t
∈ Z
+
represents the
number of observed patients in health condition ( j, o)
at a given time t ∈ {1, ...,T }, where the treatment j ∈
J is given at time period t − 1 and the outcome o ∈ O
is observed in time t, such that
∑
j∈J,o∈O
k
j,o
t
= n. The
above definitions directly imply the following: for t =
1, h
t
= k
t
and for t = 2,...,T , h
t
= h
t−1
+ k
t
.
The entries of the transition matrix at time t ∈
{0,..., T − 1}, P
t
(h
t+1
|h
t
,d
t
,α
0
), representing the
probability of transitioning to state h
t+1
, given h
t
, d
t
,
and α
0
, is then defined as follows:
P
t
(h
t+1
|h
t
,d
t
,α
0
) =
∏
j∈J
Pr(k
j,·
t+1
|h
j,.
t
,d
j
t
,α
j,.
0
)
=
∏
j∈J
Z
1
0
Pr(k
j,·
t+1
|d
j
t
,p
j,.
t
)g(p
j,·
t
|h
j,.
t
,α
j,.
0
)d p
j,.
t
,
(1)
if d
j
t
∈ Z and k
j,o
t+1
≤ d
j
t
for all j ∈ J, o ∈
O, and 0 otherwise. Here, Pr(k
j
t+1
|d
j
t
,p
j
t
) =
Pr(k
j,1
t+1
,..., k
j,|O|
t+1
;d
j
t
; p
j,1
t
,.., p
j,|O|
t
) is the multinomial
likelihood or the marginal joint distribution of observ-
ing k
j,1
t+1
,..., k
j,|O|
t+1
outcomes from d
j
t
patients given
that the probability of observing these outcomes
is p
j,1
t
,.., p
j,|O|
t
, respectively, and g(p
j
t
|h
j
t
,α
j
0
) =
g(p
j
t
|α
j
t
) = g(p
j,1
t
,.., p
j,|O|
t
;α
j,1
t
,..., α
j,|O|
t
) is the pdf
for the Dirichlet distribution.
Finally, the reward, R
t
, is defined for each objec-
tive function as follows: (a) Patient Health: R
T
=
0 and R
t
= r
T
k
t+1
∀t ∈ {0,..,T − 1}, where r ⊆
ℜ
|J|×|O|
, and (b) Learning: R
T
= max
j∈J
Pr{p
j
T
( ˜o|h
T
) >
max
j
0
∈J\{ j}
{p
j
0
T
( ˜o|h
T
)}} and R
t
= 0 ∀t ∈ {0,..,T − 1},
where ˜o ∈ O is the desired outcome.
The entire formulation is a dynamic program, in
which the objective is to maximize the expected value
function (V
t
) that captures expected total reward and
solves the Bellman equation as follows:
V
t
(α
t
,β
t
) = max
u
t
{R
t
+ E
k
t+1
[V
t+1
(α
t+1
,β
t+1
)]}. (2)
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
462

3.2 Grid-based Approximation of the
State Space
We approximate the state space using a uniform grid,
where each grid point, that we call grid state, repre-
sents a health state
˜
h
t
∈
˜
H ⊆ ℜ
|J|×|O|
, defined as
˜
h
t
= (
˜
h
1,1
t
,...,
˜
h
|J|,|O|
t
),
where
˜
h
t
has the same dimensionality as h
t
and
˜
H is
the approximate state space.
The number of grid points at each time is a func-
tion of the grid resolution, q
s
, where a higher resolu-
tion implies a finer grid and a larger state space. In
this paper, we use a fixed-resolution grid, implying
that the number of states at each time period are the
same but note that it is easy to incorporate variable-
resolution grid, one that varies with time. Each grid
state can then be described in terms of q
s
as follows:
˜
h
j,o
t
=
x
q
s
,
where x ∈ {0,1,2,...,q
s
}. q
s
provides a lever for ad-
justing the granularity of the fraction that we can use
to modify how refined (big) or coarser (small) the
state space is. In other words, q
s
allows us to tradeoff
between a close approximation (and hence a higher
objective value) and the computational burden im-
posed as a result.
A direct consequence of using grid-based approx-
imation is grid state transitions may not belong to the
grid state space and requires approximation. To il-
lustrate, suppose the state to which
˜
h
t
transitions to
at time t + 1 is denoted by h
t+1
= (h
1,1
t+1
,..., h
|J|,|O|
t+1
),
where h
j,o
t+1
=
nt
˜
h
j,o
t
+ k
j,o
t+1
n(t + 1)
. If h
t+1
∈
˜
H , then there
is no need to approximate the state (and consequently
V
t+1
) as we have an exact match. However, if h
t+1
/∈
˜
H we interpolate the value function, as defined in
§3.3. The optimal solution is still obtained by solv-
ing the Bellman equation in (2).
3.3 Value Function Interpolation
We estimate the value function of this transition state,
h
t
, by combining values at neighboring states (called
vertices of the simplex) to obtain an approximation.
For an n-dimensional state, this implies taking linear
combinations of the values at grid points of the sim-
plex that surround the state whose value needs to be
approximated. This leads to to a linear system with
n+1 equations. We formulate this interpolation prob-
lem as a linear program (LP), where the objective is
to maximize the sum of rewards, as shown below.
max λ
t
T
V
t
,
s.t. h
t
=
|H |
∑
k=1
λ
k
t
˜
h
k
t
,
|H |
∑
k=1
λ
k
t
= 1,
λ ≥ 0.
Here, h
t
represents the state whose value function
needs to be approximated using grid states at time
t,
˜
h
k
t
represents the k
th
state amongst the set of grid
states, V
t
represents the associated set of (known)
value function of the grid states, and λ
t
are the co-
efficients that the LP solves for. The constraints and
the relationship 0 ≤
˜
h
j,o
t
≤ 1 ensures that all corner
points of the simplex are included amongst the grid
states. A consequence of this approximation is the
potential loss in optimality, which we discuss further
in the numerical results (see §4).
The model works as follows. First consider the
terminal period, T , where no decision needs to be
made. For the second to last time period, since the
transitions happen into the terminal stage, there is no
more ambiguity. The value function is simply a dot
product of the state and the corresponding reward vec-
tor representing the value of being in that state. How-
ever, for a given state in any other time period,
˜
h
t
,
t ∈ {1,.., T − 2}, the state to which it transitions to
may not belong to the grid state space, in which case
it needs to be approximated as defined above.
4 NUMERICAL RESULTS
In this section, we perform numerical analyses un-
der various scenarios to demonstrate how the pol-
icy derived from the grid-based approximation ap-
proach, π
AO
, compares with the optimal policy. Our
choice of optimal policy for the case of multiple pa-
tients is the Jointly Adaptive policy of (Ahuja and
Birge, 2014), that we denote as π
JO
. Unless oth-
erwise stated, we make the following assumptions.
We consider two treatments, henceforth referred to
as treatments A and B, and two mutually exclusive
outcomes, namely success (s) and failure ( f ) as de-
fined earlier. This implies the following: J = {A,B},
O = {s, f }, and I = {As,A f ,Bs,B f }. It follows then
that
˜
h
t
= (
˜
h
As
t
,
˜
h
A f
t
,
˜
h
Bs
t
,
˜
h
B f
t
) for all t ∈ {1,..,T }. Con-
sequently, the assumed distribution that is used to de-
rive transition probabilities reduces to a beta-binomial
model with a beta prior distribution and a binomial
likelihood resulting in a beta posterior distribution.
We define additional terms as follows: α
j,s
t
= α
j
t
,
ApproximationMethodsforDeterminingOptimalAllocationsinResponseAdaptiveClinicalTrials
463
α
j, f
t
= β
j
t
, α
t
= (α
A
t
,α
B
t
), β
t
= (β
A
t
,β
B
t
) p
j,s
t
= p
j
t
and
p
j, f
t
= 1 − p
j
t
.
The prior distribution on the probability of success
with treatment j at time t is then given as g(p
j
t
) ∼
Beta(α
j
t
,β
j
t
) and Ep
j
t
=
α
j
t
α
j
t
+ β
j
t
. Given that the like-
lihood of observing k
j
t+1
successes out of d
j
t
is Bi-
nomial, i.e. Pr(k
j
t+1
|d
j
t
, p
j
t
) ∼ Bin(k
j
t+1
;d
j
t
; p
j
t
), the
posterior distribution of p
j
t+1
is given as g(p
j
t+1
) ∼
Beta(α
j
t
+ k
j
t+1
,β
j
t
+ d
j
t
− k
j
t+1
). The joint posterior
probability distribution is then the product of individ-
ual probabilities. In the absence of any knowledge
of treatment efficacy, a commonly assumed starting
prior is non-informative, i.e., (α
j
0
,β
j
0
) = (1,1) for all
j ∈ J, equivalent to a uniform[0,1] distribution. Fi-
nally, the rewards are defined for each objective func-
tion. For health, following existing literature (e.g.,
(Berry, 1978)), r = (1, 0,1, 0), implying a reward of
1 for success and 0 for failure.
For numerical illustration, we only consider the
patient health objective and further let S
t
denote the
value function (V
t
) for this objective.
4.1 Calculating Performance of
approximately Optimal Policy
The comparison is between S
π
JO
and S
π
AO
, where cal-
culation of S
π
JO
has been defined in (Ahuja and Birge,
2014). However, a meaningful comparison requires
the application of approximately optimal policy to the
problem instance where no approximation is done that
we call a fully enumerated problem and whose state
space we denote as
b
H . In other words, we first calcu-
late π
AO
by solving the Bellman equation (using grid-
based approximation), given in (2) and then apply it
to the fully enumerated problem.
Given that in general, the approximate state space
is smaller than the fully enumerated space, applica-
tion of π
AO
to
b
H requires finding the grid-state in
˜
H ,
say
˜
h
t
that is “closest” to the fully-enumerated state
in
b
H , say
b
h
t
and then applying π
AO
(
˜
h
t
) to
b
h
t
. To find
the grid-state that is closest to the fully-enumerated
state, we use nearest-neighbor interpolation, one that
minimizes L
1
norm.
2
We compare the two policies under multiple sce-
narios that vary in the number of patient observations
(N) and starting priors, measured as parameters of
beta distribution, (α
j
0
,β
j
0
), j ∈ {A,B}. We used 91
unique combinations of starting priors, same as used
in (Ahuja and Birge, 2014).
2
L
2
or the Euclidean norm yeilds similar results.
Table 1 lists the expected proportion of successes
for all 91 combinations of starting priors under both
policies (
S
π
JO
N
,
S
π
AO
N
) when q
s
= 12 under various sce-
narios. For comparison purposes, we also list the
expected proportion of successes under the fixed de-
sign (π
EA
) as well as the following heuristics - Greedy
(π
Gr
), GGreedy (π
GG
), UCB1 (π
UC
), and BK (π
BK
),
where the policies have been defined in (Ahuja and
Birge, 2014). Comparison with the fixed design other
heuristics provides a measure of the performance
of approximation algorithm, where we note that the
heuristics may not be feasible for large problem sizes.
We note from the table that π
AO
improves patient suc-
cesses compared to fixed designs in most of the cases,
although some heuristics such as π
Gr
provide a supe-
rior performance.
The following quantity provides a measure of
loss in optimality (using expected proportion of suc-
cesses) as a result of using the approximation ap-
proach: δ
AO
:=
S
π
JO
− S
π
AO
S
π
JO
. Figure 1 shows how δ
AO
varies with the number of time periods (alternately, N)
and the grid resolution (q
s
) when the initial priors are
assumed to follow a uniform[0,1] distribution.
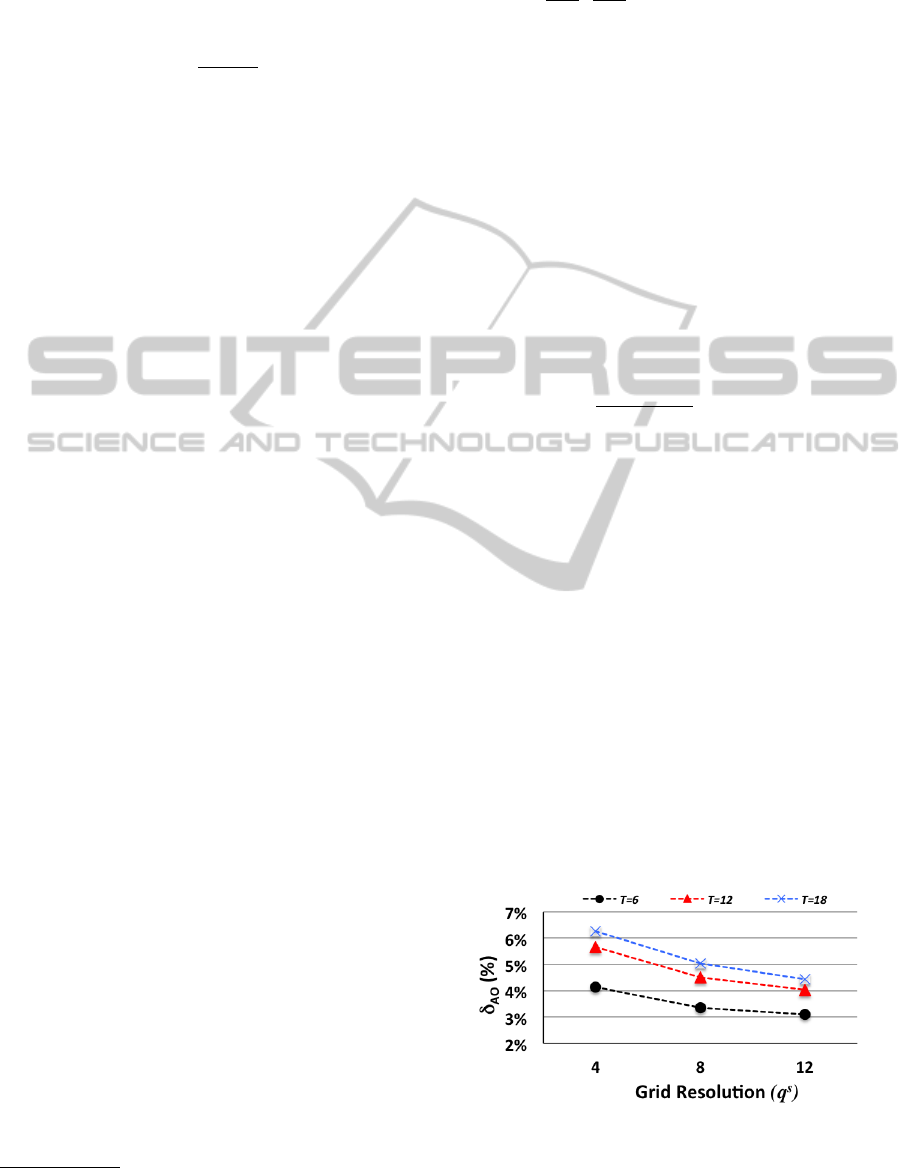
Observations from the figure, include, first, δ
AO
is
increasing in N but decreasing in q
s
, both of which
make sense and are expected. The increase of δ
AO
in
N is expected because a bigger problem size (a func-
tion of N) increases optimality loss. The decrease of
δ
AO
in q
s
also makes sense because a higher q
s
creates
a finer grid with more grid states that can be used for
approximating the true state, thus minimizing oppor-
tunities for optimality loss. We note that δ
AO
can be
substantial but given that we are comparing the two
policies for small problem sizes, where calculating
exact optimal solution is feasible, this may not be as
surprising. It is worth reiterating that this comparison
is only possible for states for which it is computation-
ally feasible to solve the fully enumerated problem.
Figure 1: δ
AO
as a function of q
s
and T; n = 4 and
(α
A
0
,β
A
0
) = (α
B
0
,β
B
0
) = (1, 1).
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
464
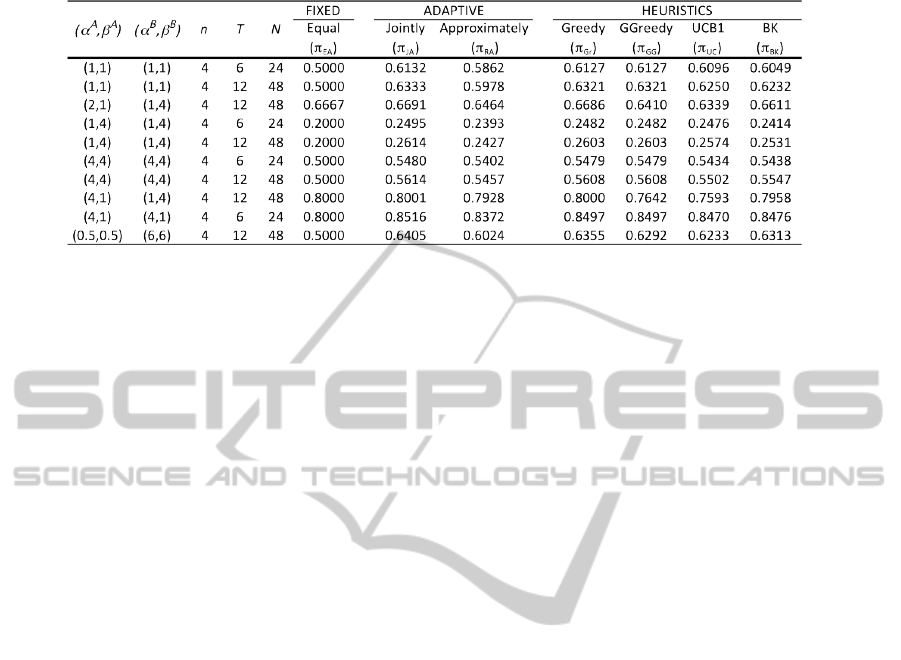
Table 1: Expected proportion of successes for a variety of problem scenarios when q
s
= 12.
5 FUTURE WORK
In the near-term, we aim complete this work grid-
based approximation methods. While the numerical
results provide a sense of the optimality loss with re-
spect to optimal solution, work is underway to estab-
lish theoretical bounds on optimality loss. Further,
we plan to perform numerical analyses to demonstrate
the magnitude of computational burden that can be
reduced by implementing our proposed method. We
also plan to compare our approach with other approx-
imation approaches that have been proposed in the lit-
erature. While this study is focused on clinical trials,
the methods and solution proposed here are relevant
in other contexts such as simultaneous learning about
multiple marketing messages where the set of possi-
ble actions may be very large.
REFERENCES
Adelman, D. and Mersereau, A. J. (2008). Relaxations of
weakly coupled stochastic dynamic programs. Opera-
tions Research, 56(3):712727.
Ahuja, V. and Birge, J. (2014). Fully adaptive designs
for clinical trials: Simultaneous learning from mul-
tiple patients. Working paper available at SSRN:
http://ssrn.com/abstract=2126906.
Aviv, Y. and Pazgal, A. (2005). A partially observed markov
decision process for dynamic pricing. Management
Science, 51(9):14001416.
Berry, D. (1978). Modified two-armed bandit strategies for
certain clinical trials. Journal of the American Statis-
tical Association, 73(362):pp. 339345.
Berry, D. and Fristedt, B. (1985). Bandit problems: se-
quential allocation of experiments. Chapman and Hall
London.
Bertsimas, D. and Mersereau, A. (2007). A learning ap-
proach for interactive marketing to a customer seg-
ment. Operations Research, 55(6):11201135.
Caro, F. and Gallien, J. (2007). Dynamic assortment with
demand learning for seasonal consumer goods. Man-
agement Science, 53(2):276.
English, R., Lebovitz, Y., Griffin, R., et al. (2010). Trans-
forming Clinical Research in the United States: Chal-
lenges and Opportunities: Workshop Summary. Na-
tional Academies Press.
FDA (2010). Adaptive design clinical trials for drugs and
biologics. Guidance for Industry.
Forbes (2013). The cost of creating a new drug now 5 bil-
lion, pushing big pharma to change.
Hauskrecht, M. (1997). Incremental methods for computing
bounds in partially observable markov decision pro-
cesses. In Proceedings of The National Conference on
Artificial Intelligence, pages 734739. Citeseer.
Judd, K. (1998). Numerical Methods in Economics. The
MIT press.
Lovejoy, W. (1991). Computationally feasible bounds for
partially observed markov decision processes. Opera-
tions research, 39(1):162175.
Monahan, G. (1982). State of the arta survey of partially ob-
servable markov decision processes: Theory, models,
and algorithms. Management Science, 28(1):116.
Powell, W. (2007). Approximate Dynamic Program-
ming: Solving the curses of dimensionality. Wiley-
Interscience.
Sandikci, B. (2010). Reduction of a pomdp to an mdp. Wi-
ley Encyclopedia of Operations Research and Man-
agement Science.
Sandikci, B., Maillart, L. M., Schaefer, A. J., and Roberts,
M. S. (2013). Alleviating the patients price of privacy
through a partially observable waiting list. Manage-
ment Science.
Zhou, R. and Hansen, E. (2001). An improved grid-based
approximation algorithm for pomdps. In International
Joint Conference on Artificial Intelligence, volume 17,
pages 707716. Citeseer
ApproximationMethodsforDeterminingOptimalAllocationsinResponseAdaptiveClinicalTrials
465
