Thermal Storage in a Heat Pump Heated Living Room Floor for

Urban District Power Balancing

Effects on Thermal Comfort, Energy Loss and Costs for Residents

R. P. van Leeuwen

1,2

, J. B. de Wit

, J. Fink

2,3

and G. J. M. Smit

Sustainable Energy Group, Saxion University of Applied Sciences, P.O. Box 70.000, 7500 KB Enschede, The Netherlands

Department of Computer Science, Mathematics and Electrical Engineering, University of Twente,

P.O. Box 217, 7500 AE Enschede, The Netherlands

Supported by STW, Project iCare (11854)

Keywords: Thermal Activated Building Systems (TABS), Thermal Storage, Demand Side Management, Power

Balancing, Peak Shaving, Smart Grid, Optimal Control, Renewable Energy System, Thermal Network

Model, Thermal Comfort, Floor Heating System.

Abstract: For the Dutch smart grid demonstration project Meppelenergie, the effects of controlled thermal energy

storage within the floor heating structure of a living room by a heat pump are investigated. Storage

possibilities are constrained by room operative and floor temperatures. Simulations indicate limitations for

floor heating storage due to absorption of solar energy within the house. To balance power for district

renewable energy supply, substantial energy can be stored into the floor without violating comfort limits.

Heat loss to the outside due to floor heating storage is small in case of low energy houses and can be

financially compensated. This may result in a proposition for residents which is equivalent to heating

without thermal storage for power balancing purposes.

1 INTRODUCTION

For the smart grid demonstration project

Meppelenergie, funded by the Dutch program

Switch2Smartgrids, we develop smart grid control

for the energy system of the new Meppel district

Nieuwveense landen (AgentschapNL, N.D.).

The Meppel energy concept consists of a biogas

CHP (Combined Heat and Power engine), heat

pumps and underground thermal storage. The CHP

is the main electric and thermal heat generator. The

heat is used for a district heating system, supplying

part of the houses in the district with domestic hot

water and space heating. The electricity is used to

drive heat pumps placed at houses with no

connection to the district heating. The heat pumps

supply these houses with domestic hot water and

space heating. The heat source for the heat pumps is

an underground aquifer which consists of a warm

and cold well. During the heating season, the warm

well provides heat for the heat pumps, during the

cooling season, the cold well provides cooling

energy for the houses.

Using heat pumps together with underground

aquifers is increasingly applied in the Netherlands

for commercial buildings, e.g. hospitals, office parks

and malls (Rijkswaterstaat, 2013). Within housing

projects, underground aquifers are mainly used for

apartment buildings. Houses often use closed

systems such as underground heat exchangers (CBS,

2011) and as an example (Witte et al., 2006).

For the Meppel district heating, there are large

water stores to store thermal energy from the CHP,

which is beneficial for the heat grid control. The

houses with a heat pump have a domestic hot water

storage but not for space heating. However, some

storage capacity can be provided by thermal storage

within the inert concrete floor heating system, which

we will name Floor Heating Thermal Energy

Storage (FHTES) throughout the paper. The

application and economics of such a storage system

within smart grid electricity control is investigated in

(Toersche et al., 2012) and (Nykamp et al., 2012)

which demonstrates that investments for

strengthening the electricity grid can be avoided by

applying FHTES for demand side control. However,

FHTES has immediate effects on thermal comfort of

van Leeuwen R., de Wit J., Fink J. and Smit G..

Thermal Storage in a Heat Pump Heated Living Room Floor for Urban District Power Balancing - Effects on Thermal Comfort, Energy Loss and Costs

for Residents.

DOI: 10.5220/0004916300430050

In Proceedings of the 3rd International Conference on Smart Grids and Green IT Systems (SMARTGREENS-2014), pages 43-50

ISBN: 978-989-758-025-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

residents and also on energy loss of the building and

therefore costs for the residents, which are not

investigated yet. The problem statement for this

paper is therefore: what are the effects on thermal

comfort if energy is stored in the floor heating

system, what is the energy loss and what are the

related financial consequences?

Contribution of this paper is to develop

mathematical relations and to demonstrate the

relation between FHTES, thermal comfort, energy

loss and energy costs. These insights and relations

are to be used for developing algorithms to control

district heating and heat pumps.

Outline of this paper: Chapter 2 describes related

works on Thermal Activated Building Systems

(TABS), control and performance. Chapter 3 gives

theoretical backgrounds on modelling and thermal

comfort. Chapter 4 describes a case study, followed

by results and discussion in chapter 5. Conclusions

are drawn in chapter 6. The appendix contains a list

of abbreviations and the applied thermal network

model.

2 RELATED WORK

In this section we discuss related work on TABS and

power balancing by FHTES.

FHTES is investigated for different applications.

One of the applications is cooling offices by thermal

activation of floors during night hours (Fellin and

Sommer, 2003), (Lehmann et al., 2007), (Pavlov and

Olesen, 2011), (Rijksen et al., 2010) and (Saelens et

al., 2011). Another application is lowering peak

heating power for residential buildings (Airaksinen

and Vuolle, 2013). More close to our application is a

study on measured performance of heating and

cooling systems using TABS in apartments (Alvi

and Qureshi).

Besides effects on thermal comfort, FHTES also

influences energy loss of the building and therefore

energy costs paid by the residents. In (Scheepens,

2013) the ecocost approach was applied to

investigate a novel house heating/cooling system

with individual room temperature control for the

Meppel project. In (Tahersima et al., 2011) the

contribution of a control strategy for power

balancing and FHTES is investigated. Thermal

tolerance is introduced as a measure for effects on

thermal comfort due to FHTES. In (Verhelst et al.,

2012) optimal heat pump control in case of floor

heating in relation with varying electricity prices is

investigated. Thermal discomfort is introduced as a

measure for effects on thermal comfort. Instead of

using thermal tolerance or thermal discomfort, we

propose in this paper to develop measures from

governing standards on thermal comfort, as outlined

in section 3.2.

Most of the mathematical work within the cited

papers is applicable for general use. However,

effects on thermal comfort, energy loss and energy

costs are not investigated yet in a way corresponding

with thermal comfort standards. Therefore we

investigate how thermal comfort is influenced by

FHTES and from this we deduce constraints and

guidelines for control algorithms.

3 MODELLING APPROACH

In this section we define a simulation model and

constraints from theory on thermal comfort.

3.1 Thermal Network Model

The thermal network approach is a convenient way

to demonstrate the relation between FHTES, energy

demand and effects on thermal comfort. Another

reason to adopt this approach is to use the model

equations for model predictive control within the

TRIANA smart grid control method (Molderink,

2011), which is a part of future work. Accuracy of

thermal networks is demonstrated in (Liu et al.,

2011) and (Bacher and Madsen, 2011).

The applied thermal network for the living room

of typical Dutch low energy house as defined by

(AgentschapNL, 2013) and model equations are

shown in the appendix. The concrete floor, the zone

including internal separation walls, inner and outer

parts of envelope walls and ceiling are modelled as

temperature nodes with a thermal capacitance. Solar

gains are defined at the outer wall node and the zone

node by window transmittance. Heat loss due to

ventilation and infiltration is defined at the zone

node, as well as appliances and people gains.

Heating input is defined at the floor node.

Weather data from Hoogeveen (close to Meppel)

of ambient temperature and global transmittance, i.e.

total solar radiation on the horizontal plane is used

as input data within the model. Solar radiation on

building planes is calculated using correlations by

(Erbs, 1982) and equations by (Duffie, 1980).

Transmitted radiation through the windows is for

25% absorbed by the floor and 75% by the zone

structure. The house orientation is ideal for passive

solar gains and there are no obstacles which could

cast shadows on the house surfaces. In practise, this

may not always be the case, especially not in mid-

SMARTGREENS2014-3rdInternationalConferenceonSmartGridsandGreenITSystems

winter when the sun is quite low above the horizon.

The simulation model includes Proportional

Integral (PI) control of the heating/cooling input to

the floor with the error between the zone

temperature and its set point as controlled variable.

3.2 Theory on Thermal Comfort

The thermal network model of the living room is

defined in such a way that it is possible to calculate

the operative temperature of the zone. The operative

temperature is defined in (ISO, 2005) and

(ASHRAE, 2010) and is the most important comfort

parameter to evaluate the influence of radiation from

surfaces and air convection on experienced human

thermal comfort. For relatively low air velocities

applicable for home situations, the operative

temperature of a zone is calculated from (ASHRAE,

2010):

radair





(1)

In which T

air

is the zone air temperature and T

rad

the mean radiation temperature of all surfaces

surrounding a person. It is impractical to calculate

rad

for each person as this also depends on the place

where the person is situated in a room. Hence an

average for a zone is proposed based on (ASHRAE,

2009).







rad

TAAT

(2)

The living room zone is surrounded by 6 surface

areas A

with surface temperature T

. Guidelines for

the operative temperatures are defined in ISO 7730

and are related to the outdoor temperature in case

adaptivity to outdoor conditions is taken into

account:

• If T

outdoor

< 10°C then 20°C < T

< 24°C

• If T

outdoor

> 15°C then 22°C < T

< 26°C

A heated or cooled floor has an effect on the mean

radiant temperature and on the operative

temperature. But according to ISO 7730, a warm or

cold floor also directly influences the thermal

comfort of people. Limits can be calculated from the

percentage dissatisfied equation given in ISO 7730

which yields: 19,2°C < T

< 28°C.

According to ISO 7730, another constraint is on

dynamic changes of the operative temperature.

Periodic peak-to-bottom variations should be limited

to 1°C which is combined with a maximum rate of

change of less than 2°C/hour.

Limits on radiant asymmetry pointed out in ISO

7730 are quite large and therefore not relevant for

floor heating systems.

For home applications, it is worth to note the

following:

1. ISO standard 7730 is developed and validated

mainly for people working in offices and

schools. People may evaluate thermal comfort

different in a home situation, while people are

more at rest while being at home. Besides that

older aged people tend for higher operative

temperatures than younger people. This causes

differences in energy demand between

households, which is important to take into

account for the energy system configuration.

2. The minimum allowable floor temperature may

not be reached during the heating season, as the

floor heating will have to compromise heat loss

of the house. So the minimum floor temperature

is the floor temperature which is necessary to

maintain a comfortable operative temperature of

the zone.

3. The minimum allowable floor temperature limits

cooling capacity of the floor cooling system

during the summer season.

4 CASE DESCRIPTION

In this section we describe relevant details for the

living room model and define scenarios for the case

study.

Model parameters, i.e. specific mass of the

concrete floor, ceiling and walls are derived from

Dutch building details (Bouwformatie, 2013),

(BUVA, 2013) and (VIEGA, 2009), which are

currently applied for low energy houses in the

Netherlands. The floor is a hollow channel concrete

type. On top of the floor, the floor heating tubes are

laid on a grid mat filled up with a concrete casting.

Specific density of the total floor is typically 514

kg/m

. The ceiling has the same structure as the

floor. The envelope wall consists of a concrete inner

wall, insulation material, air gap and brick outer

wall.

To calculate electricity demand for the heat

pump, a constant COP of 4,5 is assumed at all times.

Weather data of February 2012 from station

Hoogeveen is used. Simulation results are shown for

the 2

week which runs from hour 168 to 336, i.e.

midnight of the 1

until the 7

day.

The following control scenarios are investigated:

1. Control 1: Constant temperature set point of

20°C.

ThermalStorageinaHeatPumpHeatedLivingRoomFloorforUrbanDistrictPowerBalancing-EffectsonThermal

Comfort,EnergyLossandCostsforResidents

2. Control 2: Varying temperature set point: 19,5°C

at night, 20,5°C at day. Control 2 is scheduled in

such a way that operative temperatures are

within thermal comfort limits during daytime

hours and total energy demand is comparable to

control 1.

3. Control 3: Same as scenario 2 but with additional

short term storage for district power balancing.

Besides these control scenarios, the following

energy price schemes are investigated:

1. Conventional: conventional power grid with

lower night time energy rates.

2. Alternative: district power grid based on

renewable PV-generation. Lower rates apply

during hours with sunshine and higher rates

during hours without sunshine.

5 DISCUSSION OF RESULTS

Simulated heating input for control 1 is shown in

Figure 1 together with the global transmission, G

t,h

and the operative temperature of the living room.

The influence of solar absorption by the interior of

the living room can be observed as hours of less or

even no required heating input. Besides this positive

effect, this however reduces the possibilities for

FHTES by the heat pump, as is deduced from the

operative temperature. As explained in section 3.2,

operative temperature variation should be less than

1°C, so the allowable range for this case is 20-21°C.

On the 1st day, 21,3°C is reached due to solar

absorption. As this is just outside the allowable

range and energy can be saved by using the absorbed

solar energy, possibilities to store energy by the heat

pump are limited. It is also observed that as solar

energy decreases the remainder of the week, longer

periods of heating energy are required and operative

temperatures are more stable, enabling more

possibilities for FHTES by a heat pump.

To study heat loss, control 3 is introduced, which

is basically the same as control 2 but with small

additional two hour storage periods taking place at

the indicated circles in Figure 3. As is observed from

Figure 2, the heating input of control 3 is shifted in

time compared to control 2. A simple way to

accomplish this in a smart grid is that the central

controller asks the home controller to temporarily

raise the temperature set point. The total stored

energy in the floor during each shift is 1600 Wh.

Observe from Figure 2 that the total energy demand

for the whole week is almost not influenced by these

storage periods. The additional energy loss is

calculated at 479 Wh, i.e. 6% of the total charged

energy (8.000 Wh). This is rather small because of

(a) good insulation of the house and (b) stored heat

is consumed by the interior and results in a period of

less heating input, observe the larger drop in the

heating input of control 3 after each storage period,

compared to control 2.

The effects of the storage periods on the

operative temperature are shown in Figure 3

(compare control 3 with 2). The last four peaks

almost reach to 21°C, which is just within the

allowable range. The operative temperature seems to

increase quite fast, but still less than 0,5°C/h, well

below the requirements set out in section 3.2.

The short term storage period which was just

calculated is significant for district power balancing.

For the living room, the average heating requirement

during the investigated week is calculated at 475 W.

Figure 1: Floor heating input and operative temperature for control 1.

SMARTGREENS2014-3rdInternationalConferenceonSmartGridsandGreenITSystems

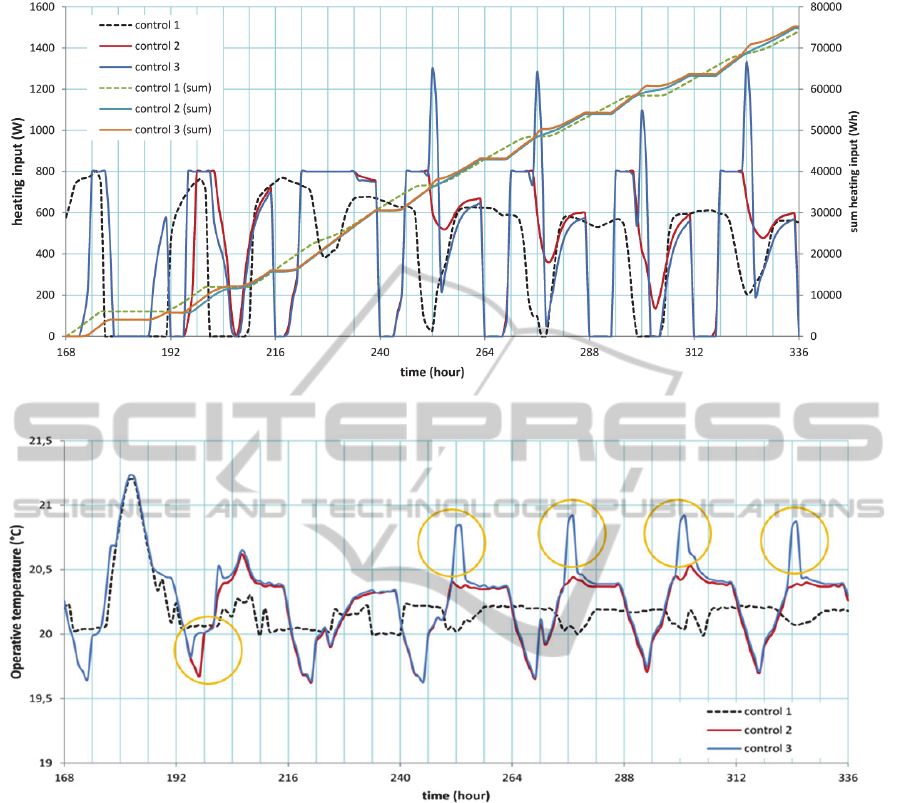
Figure 2: Heating input and sum of heating input to floor heating system.

Figure 3: Operative temperatures.

With the heat pump COP assumed at 4,5 the

CHP has to deliver on average 106 W electric

energy to the living room. The short term storage

period just investigated involved 800 W, i.e. 178 W

electric energy. This is 168% of the average electric

energy demand. Hence we conclude that floor

heating systems can be used very well for short term

periods of storage for district power balancing.

To study energy costs for the residents, the

simulated energy input for the three control methods

is translated into total required electric energy which

is multiplied by energy price rates. A high rate of

€0,30/kWh and low rate of €0,20/kWh including

taxes and network costs are defined, i.e. close to

actual Dutch consumer electricity rates.

Energy costs for the investigated week are

referred to the reference case on the first line (i.e.

100%) in Table 1. As observed from Table 1 costs

are higher for control 2 than for control 1 in case of

a conventional power grid (compare both grey

marked lines), because energy demand for control 2

is shifted towards daytime hours.

In case of PV-generation, control 1 has higher

costs and control 2 has lower costs, as is observed

from the 2

and 4

line of Table 1.

Control 3 (5

line, Table 1) has the same basic

temperature control as control 2 (lower night time

temperature) but with some additional heat storage

periods during day hours, typical for district power

balancing in case of PV-generation. If on average

the heat storage is offered for €0,21/kWh then the

costs are comparable to the reference.

As a general rule for the storage rate, the

standard rate for the applicable hour should be

ThermalStorageinaHeatPumpHeatedLivingRoomFloorforUrbanDistrictPowerBalancing-EffectsonThermal

Comfort,EnergyLossandCostsforResidents

reduced with the percentage energy loss (i.e. 6% in

this case) caused by storage to offer a cost neutral

proposition for the residents.

Table 1: Results energy cost comparison.

control peak rate hours

energy costs (%)

1 07.00-23.00 100

18.00-24.00

0.00-09.00

112

2 07.00-23.00 119

18.00-24.00

0.00-09.00

100

18.00-24.00

0.00-09.00

100

6 CONCLUSIONS

By simulation the amount of Floor Heating Thermal

Energy Storage (FHTES) by a renewable energy

supply system, energy loss and cost strategies

associated with FHTES is investigated. Resulting

values are case specific, but the observed effects on

energy demand and operative temperatures due to

FHTES are valid for any building equipped with

floor heating.

Our simulations show that the amount of energy

that can be stored in a floor heating system depends

on the house and floor heating structure, degree of

insulation, weather and temperature settings by the

residents.

From theory on thermal comfort, we find the

following constraints for FHTES:

• allowable room operative temperature range: 20

to 24°C.

• periodic operative temperature variation: less

than 1°C peak to bottom.

• operative temperature rate of change: less than

2°C/hour.

• allowable floor surface temperature range: 19 to

28°C.

In our simulations we compare three types of

temperature control. A constant day/night

temperature set point (control 1) shows that heating

demand mostly occurs at night hours. A lower set

point during night hours (control 2) shifts heating

demand towards day hours. For district power

balancing, control 2 has the advantage that the heat

pump can be used more flexible during the night for

generating domestic hot water. If additional to

control 2, short storage periods during daytime hours

are introduced (control 3), we find that operative

temperatures remain within allowable comfort

limits. We conclude from this that a house with a

floor heating system provides substantial storage

capacity which can be used to maintain power

balance within a district energy supply system.

Energy loss due to FHTES appears to be small,

at least for low energy houses. However, a fair

energy cost policy should take this loss into account,

e.g. by offering a discount energy storage rate to

residents. In this way FHTES can facilitate district

power balancing while maintaining acceptable levels

of thermal comfort and energy costs for residents.

Our future work will be dedicated to further

research on district power balancing and algorithms

for smart grid control in which we apply knowledge

presented in this paper.

REFERENCES

Agentschapnl. N. D., Meppel heats new housing

development with biogas. Available:

http://www.agentschapnl.nl/sites/default/files/Meppel

heats new housing development with biogas.pdf,

retrieved: 18-10-2013.

Agentschapnl. 2013. Referentiewoningen nieuwbouw

2013. Available: http://www.agentschapnl.nl/sites/

default/files/2013/09/Referentiewoningen.pdf, retrie-

ved: 18-10-2013.

Airaksinen, M. & Vuolle, M. 2013. Heating Energy and

Peak-Power Demand in a Standard and Low Energy

Building. Energies, 6, 235-250.

Alvi, A. & Qureshi, 2011, H. F. Evaluation of Building

Integrated Heating System in Terms of Thermal

Comfort & Energy Efficiency, Mälardalen University,

Sweden.

ASHRAE 2009. ASHRAE Handbook-Fundamentals,

Atlanta, American Society of Heating, Refrigerating

and Air-Conditioning Engineers (ASHRAE).

ASHRAE 2010. ASHRAE standard 55-2010 Thermal

environmental conditions for human occupancy.

Atlanta, USA: American Society of Heating,

Refrigerating and Air-Conditioning Engineers

(ASHRAE).

Bacher, P. & Madsen, H. 2011. Identifying suitable

models for the heat dynamics of buildings. Energy and

Buildings, 43, 1511-1522.

Bouwformatie 2013. Available: http://bouwdetails.

bouwformatie.nl., retrieved: 18-10-2013.

BUVA 2013. BUVA bouwdetails [Online]. Available:

buva.archidat.nl., retrieved: 18-10-2013.

CBS 2011, Hernieuwbare energie in Nederland 2011.

Heerlen: CBS.

Duffie, J. A., Beckman, W. A. 1980. Solar engineering of

thermal processes, New York, Wiley.

Erbs, D. G., Klein, S. A., Duffie, J. A. 1982. Estimation of

the diffuse radiation fraction for hourly, daily and

monthly-average global radiation. Solar Energy, 28,

293-302.

Fellin, F. & Sommer, K. 2003. Study of a low energy

office building with thermal slabs and ground coupled

SMARTGREENS2014-3rdInternationalConferenceonSmartGridsandGreenITSystems

heat pump. Dipartimento di Fisica Tecnica, Università

di Padova (Italia).

ISO 2005. NEN-EN-ISO 7730 Ergonomics of the thermal

environment - Analytical determination and

interpretation of thermal comfort using calculation of

the PMV and PPD indices and local thermal comfort

criteria (ISO 7730:2005,IDT). Delft: NEN.

Lehmann, B., Dorer, V. & Koschenz, M. 2007.

Application range of thermally activated building

systems tabs. Energy and Buildings, 39, 593-598.

Liu, K., Tian, Z., Zhang, C., Ding, Y. & Wang, W. 2011.

Establishment and validation of modified star-type

RC-network model for concrete core cooling slab.

Energy and Buildings, 43, 2378-2384.

Molderink, A. 2011. On the tree step methodology for

smart grids. University of Twente.

Nykamp, S., Molderink, A., Bakker, V., Toersche, H.,

Hurink, J. & Smit, G. 2012. Integration of heat pumps

in distribution grids: Economic motivation for grid

control. 3rd IEEE PES International Conference and

Exhibition on Innovative Smart Grid Technologies

(ISGT Europe), IEEE, 1-8.

Pavlov, G. K. & Olesen, B. W. 2011. Building thermal

energy storage-concepts and applications, Technical

University of Denmark.

Rijksen, D. O., Wisse, C. J. & Van Schijndel, A. W. M.

2010. Reducing peak requirements for cooling by

using thermally activated building systems. Energy

and Buildings, 42, 298-304.

Rijkswaterstaat. 2013. WKO tool. Available:

www.wkotool.nl, retrieved: 21-10-2013.

Saelens, D., Parys, W. & Baetens, R. 2011. Energy and

comfort performance of thermally activated building

systems including resident behavior. Building and

Environment, 46, 835-848.

Scheepens, A. E., Flipsen S.F.J., Vogiatzakis, P., Brezet,

J.C. 2013. An Ecocost-Value Ratio (EVR) approach to

the design of a Product-Service System for

environmentally sustainable residential heating energy

use. Energy and Environment Knowledge Week -

E2KW2013. Toledo, Spain.

Tahersima, F., Stoustrup, J., Meybodi, S. A. &

Rasmussen, H. 2011. Contribution of domestic heating

systems to smart grid control. 50th IEEE Conference

on Decision and Control and European Control

Conference (CDC-ECC), IEEE, 3677-3681.

Toersche, H., Bakker, V., Molderink, A., Nykamp, S.,

Hurink, J. & Smit, G. Controlling the heating mode of

heat pumps with the TRIANA three step methodology.

2012 IEEE PES Innovative Smart Grid Technologies

(ISGT), IEEE, 1-7.

Verhelst, C., Logist, F., Van Impe, J. & Helsen, L. 2012.

Study of the optimal control problem formulation for

modulating air-to-water heat pumps connected to a

residential floor heating system. Energy and

Buildings, 45

, 43-53.

VIEGA 2009. Technische handleiding Fonterra vloer- en

wandverwarming, Available: http://www.viega.nl/cps/

rde/xbcr/nl-nl/Technische_handleiding_Fonterra_

vloer_en_wandverwarming.pdf, retrieved: 18-10-

2013.

Witte, H., Van Gelder, A., Klep, P. & Groenholland, B.

2006. A very large distributed ground source heat

pump project for domestic heating:

Schoenmakershoek, Etten-Leur (the Netherlands).

Proceedings Ecostock, the Tenth International

Conference on Thermal Energy Storage. New Jersey,

2006.

APPENDIX

This appendix contains the applied thermal network

model and state equations for the temperature nodes.

The used symbols and subscripts are listed in Table

Table 2: Symbols and subscripts.

Nomenclature

T Temperature

R thermal resistance

E electric energy

q thermal energy

HP heat pump

Subscripts

z zone

f floor

c ceiling

z2 zone on first floor above living room

cs creeping space

wi interior wall of envelope wall

wo exterior wall of envelope wall

rad radiation

cv convection

a ambient or outdoor

Thermal network model equations

(3)

)

zgain,

zwi

win

C 

















fgain,

fcs

fzf

C 













wo-wi

wiwo

zwi

wizwi









cz2

czc













wogain,

rad-wo

wosky

cv-wo

woa

wo-wi

wowiwo

C 













ThermalStorageinaHeatPumpHeatedLivingRoomFloorforUrbanDistrictPowerBalancing-EffectsonThermal

Comfort,EnergyLossandCostsforResidents

Figure 4: Thermal network model of low energy house living room.

SMARTGREENS2014-3rdInternationalConferenceonSmartGridsandGreenITSystems