Restoration of Archaeological Artifacts by a Genetic Algorithm

with Image Features

Koji Kashihara

Institute of Techonology and Science, The University of Tokushima, 2-1 Minamijyousanjima, Tokushima, Japan

Keywords: Genetic Algorithm, Hill-climbing Algorithm, Three-Dimensional Rebuilding, Image Features.

Abstract: Archaeological artifacts have been discovered all over the world. The restoration work of archaeological

artifacts broken into pieces contains positioning problems. Therefore, an intelligent computer-assisted

system was proposed to rebuild archaeological discoveries from fragments. A real coded genetic algorithm

(GA) and a hill-climbing algorithm was evaluated to reconstruct a 3D object. The fitness function value for

the GA was computed from image features of the object. The ORB (Oriented FAST and Rotated BRIEF)

technique was used for solving the positional problem by the GA. The proposed method based on the GA

with the image features was able to efficiently regulate the 3D surfaces. In further researches, the proposed

method for 3D rebuilding could be applied to various practical applications.

1 INTRODUCTION

Archaeological artifacts have been discovered all

over the world. Because the discovered artifacts are

usually broken into some pieces, it takes a lot of

hours to rebuild them from fragments (Haliř, 1999).

Furthermore, the archaeological rebuilding is

interrupted when pieces are missing or damaged.

Archaeologists or experts must evaluate numerous

possible combinations under such situations, based

on their knowledge and experience.

Efficient methods for the virtual 3D visualization

(Scopigno, 2011) have been reported to make digital

archives, which could assist the restoration work.

Previous computer systems mainly focus on the

reconstruction of 3D objects with symmetric

patterns, comparing the broken surface boundary

curves (Sağiroğlu and Erçil, 2006). Such restoration

work needs computing complicated patterns and

geometric images by using well-defined

mathematical models. However, the 3D rebuilding

cannot be completed when the precise mathematical

models do not exist.

Intelligent computer systems may be able to

address this issue. An easier method for piecing

together archaeological objects without using a

mathematical model for surface curve fitting has not

been established. Here, genetic algorithms (GAs) are

one optimization method of positional regulation

including the evaluation of countless combinations

(Ray and Mahajan, 2002).

Instead of the complicated mathematical model,

the image features of 3D objects may be effective

for the GA process. SIFT - Scale Invariant Feature

Transform (Lowe, 1999) and SURF - Speeded-Up

Robust Features (Bay et al., 2008) are well known as

basic techniques for image feature detection. More

recently, the ORB - Oriented FAST and Rotated

BRIEF (Rublee et al., 2011) technique also shows

accurate performance, compared with the traditional

methods; it is based on the FAST keypoint detector

and the BRIEF descriptor. In addition, after a global

solution was computed from the GA, hill-climbing

methods to find a localized solution may be able to

fine-tune the 3D positions.

The purpose of this study was to investigate

effective methods for 3D reconstruction of artifacts

from fragments, so that the archaeologists can

shorten their working time. The proposed method

based on GA with a hill-climbing algorithm was

evaluated by using image features of a 3D object

without mathematical surface or border models. The

ORB technique was used for solving the positional

problem by the GA because it would be an efficient

method to search for similar image patterns.

691

Kashihara K..

Restoration of Archaeological Artifacts by a Genetic Algorithm with Image Features.

DOI: 10.5220/0004920106910695

In Proceedings of the 6th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2014), pages 691-695

ISBN: 978-989-758-015-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 PROPOSED METHODS

The computer system was proposed to estimate the

correct positioning of archaeological fragments

(Open GL; Open CV ver. 2.4; Microsoft Visual C++

2012). For this system, GA computation can find a

global solution from numerous combinations of 3D

fragments. Fine-tuning is then performed by the hill-

climbing method. The 3D reconstruction is based on

the silhouettes of an object from some camera angles

in order to determine a correct match among

fragments. After the GA process, one of nine

operations in a target 3D fragment (rotations and

parallel movements in each axis) is selected during

the hill-climbing method.

2.1 Real Coded Genetic Algorithm

The real coded GA approach was applied to predict

the spatial positions of some pieces of a 3D object:

angles and coordinate x, y, and z axes. The 3D object

is formed by the polygonal meshes of fragments.

The GA process consists of the following operations.

(a) The initial population of individuals is randomly

generated within a set range. Each individual is

shown by real numbers; its score is calculated

from a fitness function. The fitness function

value is calculated by comparing the current

image results at some viewpoints with the correct

patterns. The best fitness value is maintained to

define the next generation.

(b) A selection operation chooses the individuals for

the generation of offspring, and tournament

selection is used for the choice of individuals.

to generate an offspring. A blend crossover

(BLX-α) operator (Eshelman and Schaffer, 1993)

was selected for this study.

(d) A mutation operator randomly changes some

individuals, altering the variables of a selected

individual to facilitate the diversity in the

population. The mutation can avoid falling into a

local solution.

The above GA operators are repeated to update

the population and create the next generations,

modifying the fitness of the population. The GA

process stopped after creating some generations.

2.2 Hill-climbing Method

The hill-climbing method was performed to fine

tune the positioning after the search spaces have

been reduced by the initial GA operation. This

method is a traditional optimization technique to

maximize a fitness function value. The proposed

system is composed of the following steps.

(a) Set the initial points of fragments in a search

space. These values are determined by the final

results of the GA process.

(b) Compute the fitness function values for all

neighbours based on the current state, changing

each parameter of the angles and positions of the

target fragment.

indicating the largest fitness value and move to

the state.

(d) Repeat the steps (b) and (c) until all the

neighbours become no change or lower quality in

the fitness values. Change the target fragment to

the next one.

2.3 Fitness Function

The similarity of image features of a 3D object from

six viewpoints was evaluated to determine the

correct positions of fragments. This similarity was

the fitness function in the GA and hill-climbing

methods, meaning the accuracy of 3D rebuilding. A

normalized correlation coefficient (i.e., the similarity

between an original image A and an evaluated image

B) is denoted as:















BBAA

)()(

(1)

and B

are the brightness in each pixel and N is the

total number of pixels. 

and 



show the mean value

of the brightness in each image. The correlation

coefficient of Eq. (1) approaches 1 when the

similarity increases.

The fitness function is the summation of

similarities computed from six camera angles.

Additionally, the image feature points were

calculated by the ORB technique. If image feature

points of two images are the same, the slope value

between the feature points will result in zero (Fig.

1A). Therefore, this slope value was added to the

fitness function for the GA.

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

692

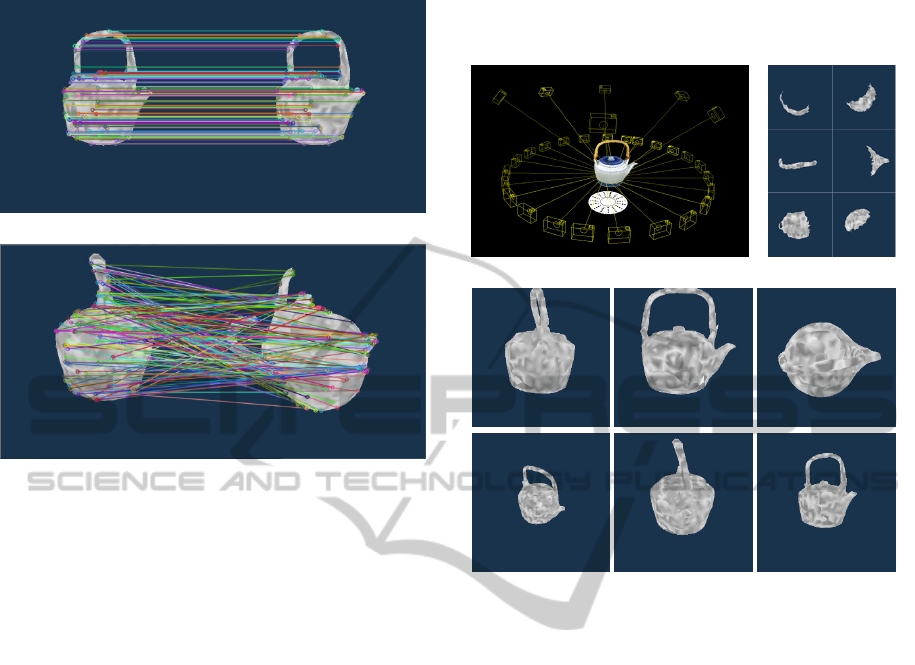
A. Matched case

B. Not matched case

Figure 1: Examples of image features acquired from the

ORB technique. The lines between the two objects

indicate the corresponding relationship between the

extracted feature points.

3 SIMULATION STUDY

The proposed method was assessed by using a 3D

model with asymmetric shapes digitized from an

actual object. The 3D reconstruction was performed

by the following steps: (1) Create correct patterns

using various camera angles; (2) Carry out GA

computation for a localized solution. The fitness

value of the GA was calculated from the image

features obtained from the ORB technique; (3)

Regulate 3D positions by the hill-climbing method.

3.1 Evaluation Method

3.1.1 3D Remodeling

To make a digitized 3D object with fragments,

photographs were taken from thirty camera locations

around the object with a calibration mat (Fig. 2A),

every 15 degrees at low angles (24 points) and every

60 degrees at high angles (6 points). After the

masking process was applied for the backgrounds of

acquired images, the 3D object with 6,000 triangle

polygons was created by fixing the position and

spatial relationship on the calibration mats of all the

images (STRATA FOTO 3D CX2). The 3D model

was output in the VRML 2.0 format to estimate the

optimal fitting and was divided into 7 fragments

(Metasequoia ver. 2.4).

A. Camera angles and fragments

B. Silhouettes of a 3D object

Figure 2: A. Thirty camera angles with a calibration mat to

construct a 3D object (left). Examples of 3D fragments

formed by polygonal meshes with triangles (right). B.

Correct images from various camera angles.

3.1.2 Parameter Setting

The real coded GA parameters were prepared as

follows. The initial population of 30 chromosomes

was randomly generated. The probabilities of

crossover and mutation were set at 0.50 (BLX-α =

0.40) and 0.01, respectively. The number of

iterations in the GA computation was 100

generations.

For the hill-climbing search, step sizes of a

fragment were three degrees in rotation angles and

0.002 in parallel movements to each axis of a 3D

coordinate. The initial values were based on the

result of the GA process. The searching space was

limited within the voxel size of an actual object in

parallel movement to each axis with free rotations.

The maximum number of iterations was set at 200.

As the first fitness function value, the correlation

coefficient between the correct and evaluated images

(24-bit grayscale; 400 × 400 pixels) was calculated

from Eq. (1). The correct images were acquired from

the six viewpoints for a 3D object (Fig. 2B). In

addition, the image features extracted from the ORB

RestorationofArchaeologicalArtifactsbyaGeneticAlgorithmwithImageFeatures

693

technique were output as bitmap images; the image

feature similarities were then computed as the fitness

value for the GA.

3.2 Results

Figure 3 shows the change of fitness values for the

GA process. The fitness function values gradually

increased and the maximum value (r = 3.15) of all

generations was obtained during the later iterations.

The ORB technique to extract the descriptor as an

image feature was also applied to the correct image

patterns to compute the fitness function value.

Figure 3: Simulation results of the GA process. A blue

line: average fitness values; dotted lines: standard

deviations in each generation; a red line: the maximum

fitness values.

Figure 4: Final simulation results of the GA and hill-

climbing methods (six camera angles).

The optimal regulation of fragments was roughly

completed by the GA. The fine-tuning was then

performed by using the hill-climbing method, which

allowed borders of curved surfaces to be smoothly

connected (Fig. 4). This result suggests the positive

effect of this method began with the initial values

determined by the GA process.

4 DISCUSSION

Previous researches for the rebuilding of

archaeological artifacts needed well-defined

mathematical or rule-based models for the surface

curve fitting of broken parts (Haliř, 1999). On the

other hand, the proposed method based on the

silhouettes of a 3D object can be used for nonlinear

and non-continuous surface curves without

mathematical models. In addition, the ORB

technique was able to fine-tune 3D positions because

it can be robust for searching similar images with

various rotations and scales.

Although an evaluation with texture mapping

was not applied to this research, the distribution of

curvatures and drawing patterns of surfaces with

colours may be efficient for 3D rebuilding

(Sağiroğlu and Erçil, 2006). It is also crucial to

prepare a 3D database for a supervised image with

correct or similar patterns because it determines the

accuracy of reconstruction.

As a user interface for the design drawing of a

3D object, the results of reconstruction could be

interactively modified to fine-tune the final

positioning of pieces. Actually, there exist optimal

visual angles with some perspectives to recognize

3D shapes as quickly as possible (Kashihara and

Nakahara, 2011; Kashihara, 2011). Therefore, this

result could be applicable to the user interface and

drawing design for the manual adjustment of a

reconstructed 3D object. The manually adjusted

values could be also used as the initial values for the

proposed algorithms to acquire the higher accuracy

of 3D rebuilding.

5 CONCLUSIONS

The intelligent computer system for reconstructing

archaeological artifacts with broken surfaces was

designed to assist archaeologists and to reduce

unnecessary manual operation. The GA with the

hill-climbing algorithm was optimal for determining

the best positions of fragments in a 3D object.

Furthermore, the ORB technique which can extract

the image features of an object was suitable for the

fitness function of the GA. In future studies, the

proposed method should be applied to practical

applications, improving the searching time and user

interface. In addition to the virtual repairing of

archaeological finds, the proposed system could be

available for restoration work on personal

possessions such as mementos.

1.5

2.5

3.5

0 20406080100

Fitness function values [-]

Generations [-]

average

maximum

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

694

ACKNOWLEDGEMENTS

This study was funded by a Grant-in-Aid for the

Okawa Foundation for Information and

Telecommunications.

REFERENCES

Bay, H., Ess, A., Tuytelaars, T., Gool, L. V., 2008.

Speeded-Up Robust Features (SURF). Computer

Vision and Image Understanding, vol. 110, pp. 346–

359.

Eshelman, L. J., Schaffer, J. D., 1993. Real-coded genetic

algorithms and interval-schemata. Foundations of

Genetic Algorithms, vol. 2, pp. 187–202.

Haliř, R., 1999. An automatic estimation of the axis of

rotation of fragments of archaeological pottery: A

multi-step model-based approach. Proc. of the 7th

International Conference in Central Europe on

Computer Graphics, Visualization and Interactive

Digital Media (WSCG’99).

Kashihara, K., Nakahara, Y., 2011. Evaluation of task

performance during mentally imagining three-

dimensional shapes from plane figures. Perceptual

and Motor Skills, vol. 113, pp. 188–200.

Kashihara, K., 2011. Optimal view angles in three-

dimensional objects constructed from plane figures as

mental images. International Journal of Human-

Computer Interactions, vol. 27, pp. 606–619.

Lowe, D. G., 1999. Object recognition from local scale-

invariant features. Proc. of the International

Conference on Computer Vision 2, pp. 1150–1157.

Ray, P. K., Mahajan, A., 2002. A genetic algorithm-based

approach to calculate the optimal configuration of

ultrasonic sensors in a 3Dposition estimation system.

Robotics and Autonomous Systems, vol. 41, pp. 165–

177.

Rublee, E., Rabaud, V., Konolige, K., Bradski, G. R.,

2011. Orb: An efficient alternative to sift or surf. In

ICCV.

Sağiroğlu, M. S., Erçil, A. A., 2006. Texture based

matching approach for automated assembly of

puzzles. Proc. of the 18th International Conference

on Pattern Recognition (ICPR 2006), vol. 3, pp.

1036–1041.

Scopigno, R., 2011. 3D Models for Cultural Heritage:

Beyond Plain Visualization. Computer, vol. 44, pp.

48–55.

RestorationofArchaeologicalArtifactsbyaGeneticAlgorithmwithImageFeatures

695