
Robot Cognition using Bayesian Symmetry Networks
Anshul Joshi
1
, Thomas C. Henderson
1
and Wenyi Wang
2
1
School of Computing, University of Utah, Salt Lake City, UT, U.S.A.
2
Department of Mathematics, University of Utah, Salt Lake City, UT, U.S.A.
Keywords:
Concept Representation, Wreath Product, Perceptual Organization, Bayesian Network.
Abstract:
(Leyton, 2001) proposes a generative theory of shape, and general cognition, based on group actions on sets
as defined by wreath products. This representation relates object symmetries to motor actions which produce
those symmetries. Our position expressed here is that this approach provides a strong basis for robot cognition
when:
1. sensory data and motor data are tightly coupled during analysis,
2. specific instances and general concepts are structured this way, and
3. uncertainty is characterized using a Bayesian framework.
Our major contributions are (1) algorithms for symmetry detection and to realize wreath product analysis, and
(2) a Bayesian characterization of the uncertainty in wreath product concept formation.
1 INTRODUCTION
Our goal is to develop cognitive capabilities for au-
tonomous robot agents. (Vernon et al., 2007) state
that cognition ”can be viewed as a process by which
the system achieves robust, adaptive, anticipatory, au-
tonomous behavior, entailing embodied perception
and action.” For us, this includes the ability to:
1. analyze sensorimotor data in order to determine a
rational course of action,
2. represent and recognize important concepts de-
scribing the world (including its own self),
3. recognize similarities between concepts,
4. extend concepts to new domains, and
5. determine likelihoods of assertions about the
world.
1.1 Related Work
Bayesian networks have been used previously for in-
ference in cognitive frameworks. Closely related is
the work of (Binford, 1987) who proposed a Bayesian
network approach for object recognition based on
generalized cylinders, but our method differs in that
we use the more general wreath product representa-
tion (which can handle generalized cylinders) and in-
clude actuation in the description; furthermore, we
derive the Bayesian network directly from the hi-
erarchical structure of the wreath product; also see
(Zhang and Ji, 2011). Others have addressed issues
such as spatial awareness and a conceptual model for
place classification; e.g., (Vasudevan and Siegwart,
2008). However, in their approach the robot is as-
sumed to have high-level object extraction capability
(SIFT-based), is taught exemplars, and then searches
for instances of those in the environment. They use
a ”bag-of-words” approach, and no explicit geomet-
ric information in used. In contrast to that, we pro-
pose a group-theoretic approach to conceptualization
and classification (here - of surfaces based on their
3D geometry). Our methods perform structure anal-
ysis (i.e., detection and organization of symmetries)
and could feed information into a system like Vasude-
van’s.
(Gold and Scassellati, 2007) have proposed a way
for a robot to perceive ”self and ”other” through mo-
tion analysis, however their method is limited to the
robot differentiating between itself and other animate
objects based on probabilistic inference.
(Buisson, 2001) has proposed a Piagetian ap-
proach which resembles our in that it is based on the
following ideas (direct quote):
• Idea 1. An interaction is a rhythmic succession
of actions, each step being assorted with a set of
sensory anticipations.
696
Joshi A., C. Henderson T. and Wang W..
Robot Cognition using Bayesian Symmetry Networks.
DOI: 10.5220/0004920606960702
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 696-702
ISBN: 978-989-758-015-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

• Idea 2. Each and every interaction of the agent
with its environment is recorded. This recording
does not necessarily amount to a large volume of
data, since only the sensorial and motor elements
actively implicated in the interaction are stored.
• Idea 3. All past stored interactions try perma-
nently to get synchronized spatially and tempo-
rally with the current situation, in order to influ-
ence the ongoing interaction. In a word, the cur-
rent interaction is guided by previous ones, and
will itself serve later as a guide for others.
We also assume that action is essential to the devel-
opment of concepts about the world, and that these
concepts are used to guide current action.
Finally, (Tenenbaum and Griffiths, 2001) and
(Jia et al., 2013) have looked at generalization and
similarity in terms of Bayesian inference; the latter
has applied this to visual concept learning. However,
Tenenbaum proposes generalization as the more basic
cognitive function, wheras we hold that similarity
is more primitive being based on innate symmetry
theories (in terms of similarity of sensor and actuator
signals). These theories constitute the learner’s
knowledge about consequence regions. Gener-
alization is achieved by manipulating the wreath
product representation (e.g., by replacing one group
by another), and the learner acquires knowledge by
finding wreath product structure in the sensorimotor
data produced in interacting with the environment.
We believe that such an active methodology is more
robust and helps explain a number of findings, e.g.,
mirror neurons.
1.2 Wreath Product Representation
We have previously argued that an effective basis for
robot cognition requires some form of innate knowl-
edge; see (Henderson et al., 2009). In fact, most
current robot implementations rely mostly on innate
knowledge programmed in by the system builder
(e.g., sensor data analysis algorithms, object recogni-
tion, kinematics and dynamics, planning, navigation,
etc.), although some aspects of the robot’s knowl-
edge may be learned from experience. This ap-
proach to establishing robot cognitive faculties does
not scale well, and as a more effective and efficient
paradigm, we have proposed that a collection of sym-
metry theories form the basic innate knowledge of
an autonomous agent (Grupen and Henderson, 1988;
Henderson et al., 2011; Henderson et al., 2012a; Hen-
derson et al., 2012b). These are defined as formal,
logic-based systems, and then the robot proceeds to
use this knowledge by analyzing sensorimotor data to
Figure 1: Models for Theories are Discovered: (1) A theory
is defined; (2) Sets and Operators are Hypothesized from
Sensorimotor Data; (3) Axioms are Validated for Hypothe-
ses; (4) Theory is Exploited.
discover models for the theories. For example, the
axioms which define a group require a set of elements
and an operator that acts on the set such that the clo-
sure, identity, inverse and associativity properties are
satisfied. Figure 1 shows how this works.
Namely, sets and operators are found in the sen-
sorimotor data and checked to see if they satisfy the
axioms. If so, then the robot may use the theory to
test new assertions (i.e., theorems) that follow from
the axioms and have direct meaning for the model,
but which may never have been experienced by the
robot.
We propose that in addition to a logical frame-
work to allow assertions about the world, robot cog-
nition requires a representational mechanism for sen-
sorimotor experience. The wreath product provides
this; for a more detailed account of wreath products,
see (Chang, 2004; Foote et al., 2000; Leyton, 2001).
The wreath product is a group formed as a splitting
extension of its normal subgroup (the direct prod-
uct of some group) and a permutation group. As an
example, consider the wreath product representation
of the outline of a square shape: {e} o Z
2
o ℜ o Z
4
,
where {e} represents a point, Z
2
is the mod 2 group
meaning select the point or not, ℜ is the continu-
ous (one-parameter Lie) translation group, Z
4
is the
cyclic group of order 4, and o is the wreath product.
[Note that: ℜ o Z
4
= ℜ × ℜ ×ℜ × ℜ o Z
4
where o is
the semi-direct product.] Leyton (Leyton, 2001) de-
scribes this representation in great detail and explains
the meaning of the expression as follows:
1. {e}: represents a point. (More precisely, the ac-
tion of the group consisting of just the identity act-
ing on a set consisting of a point.)
2. {e}o Z
2
: represents the selection of a point or not;
i.e., to get a line segment from a line, just select
the points on the line segment by assigning the 1
element to them.
RobotCognitionusingBayesianSymmetryNetworks
697
3. {e} o Z
2
o ℜ: represents a line segment; i.e., one
side of the square.
4. {e} o Z
2
o ℜ o Z
4
: represents the fact that each side
of the square is a rotated version of the base seg-
ment; i.e., the four elements of Z
4
represent rota-
tions of 0, 90, 180 and 270 degrees.
Each new group to the right side of the wreath sym-
bol defines a control action on the group to the left,
and thus provides a description of how to generate
the shape. E.g., to draw a square, start at the speci-
fied point (details of the x,y values of the point, etc.
are left to annotations in the representation), translate
some length along a straight line, then rotate 90 de-
grees and draw the next side, and repeat this two more
times. Figure 2 shows how control flows from the
rotation group, Z
4
, down to copies of the translation
group, ℜ.
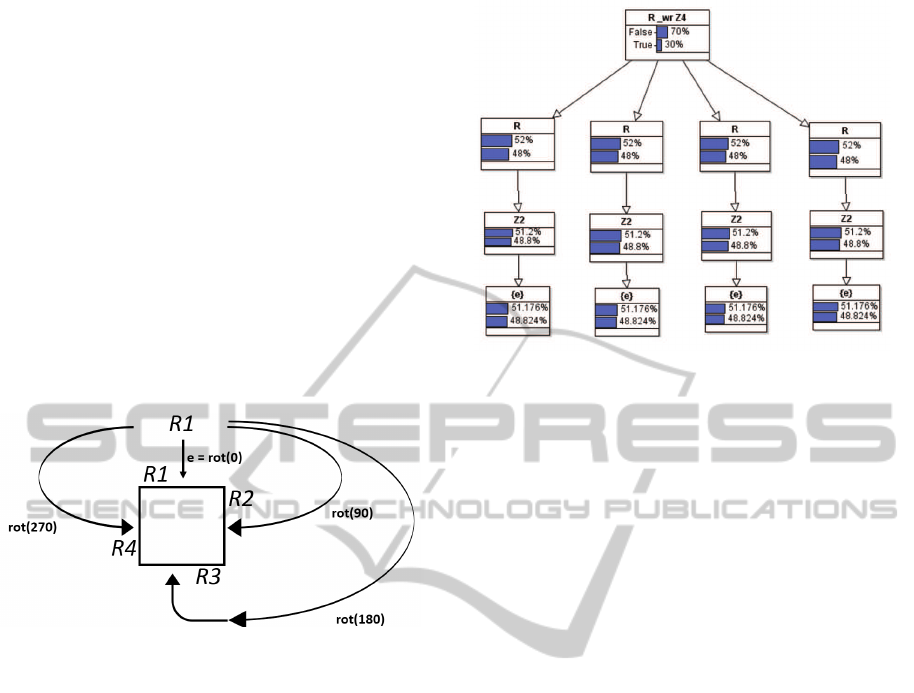
Figure 2: Control Flow in a Wreath Product gives an Ex-
plicit Definition in Terms of Actuation of how to Generate
the Shape; e, the group identity (rotate by 0 degrees) acts on
the first copy, ℜ
1
to obtain the top of the square; r
90
acts on
ℜ
1
by rotating it 90 degrees about the center of the square to
obtain the right side, ℜ
2
; r
180
acts on ℜ
1
by rotating it 180
degrees to obtain ℜ
3
, and finally, r
270
acts on ℜ
1
rotating it
270 degrees to obtain ℜ
4
.
Thus, taken together, innate theories allow the dis-
covery of the basic algebraic entities (i.e., groups) of
the wreath products, and wreath products allow the
description of concepts of interest (here restricted to
shape and structure). In the following sections, we ex-
pand on the exploitation of sensorimotor data (actua-
tion is crucial) in operationally defining wreath prod-
ucts.
Finally, we propose a probabilistic framework
for characterizing the uncertainty in wreath products.
The wreath product maps directly onto a Bayesian
network (BN) as follows:
1. The rightmost group of the wreath product forms
the root node of the BN. Its children are the direct
product group copies to the left of the semi-direct
product operator.
2. Recursively find the children of each interior node
by treating it as the rightmost group of the remain-
ing wreath product.
Figure 3: Bayesian Network for the Wreath Product of a
Square Created by Rotation.
For example, consider the square expressed as {e} o
Z
2
o ℜ o Z
4
. Figure 3 shows the corresponding BN.
[Note that the continuous translation group ℜ calls
for an uncountable number of cross product groups
(one for each real), but we do not implement this
explicitly.] The following sections describe how the
conditional probability tables can be determined from
frequencies encountered in the world (e.g., the likeli-
hood of squares versus other shapes), and experience
with the sensors and actuators (e.g., the likelihood of
the detection of the edge of a square given that the
square is present in the scene).
2 ROBOT CONCEPT
FORMATION
We now describe an architecture to allow object rep-
resentations to be constructed from groups discovered
in sensorimotor data, and combined to form wreath
products. Figure 4 gives a high-level view of the in-
teraction of innate knowledge and sensorimotor data
to produce derived knowledge. A lower level archi-
tecture is given in Figure 5 involving long-term mem-
ory, short-term memory, behavior selection and sen-
sorimotor data. Cognition can be driven by the data
(bottom-up) or by a template presented in the behav-
ior selection unit (top-down). In the former case, sym-
metries are detected in the data which gives rise to
the assertion of groups. Then the structure of these
groups is determined to form wreath products.
Suppose that data from a single object (a square)
is to be analyzed. Figure 6 shows a number of group
elements that can be discovered by symmetry detec-
tors applied to image data of a square; this includes
translation, reflection and rotation symmetries; we
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
698

Figure 4: High-Level Cognitive Process.
Figure 5: Lower Level Layout of Cognitive Process.
Figure 6: Symmetry Detection in Image of a Square.
have described symmetry detectors for 1D, 2D and
3D data elsewhere (Henderson et al., 2011; Hender-
son et al., 2012a; Henderson et al., 2012b). The sym-
metry groups would allow the synthesis of ℜ oD
4
(this
is the same as ℜ × ℜ × ℜ × ℜ o D
4
) as a representa-
tion of the data. On the other hand if the drawing of
the square were observed, and it was done by starting
with the top most edge and drawing clockwise around
the square, then ℜ o Z
4
would be generated. If first the
top edge were drawn, then the bottom edge, then the
right, then the left, this would give rise to: Z
2
o Z
2
Actuation used to observe the data can also be used
to determine the appropriate wreath product; e.g., if
motors move the camera so that the center of the im-
age follows the contour of the square, then this gives
rise to a symmetry in the angles followed (one angle
ranges from 0 to 2π, while the other follows a periodic
trajectory. [Also, note that all these wreath products
could have a pre-fixed {e} o Z
2
which represents se-
lecting the points on the line segment.]
Next consider the 3D cube. Just like the square,
there are several wreath product representations, each
corresponding to a distinct generative process. Actual
3D data (e.g., from a Kinect), will most likely come
from viewing one face of the cube or three faces.;
Figure 7 shows an example Kinect image for these
two situations in the case of a cube-shaped footstool.
For the 3-face view, each visible face has a corre-
sponding hidden parallel face which can be viewed
as either generated from the visible face by reflec-
tion or rotation. The Z
2
group represents either of
these (in the specific encoding, we choose reflection).
Figure 8(a)(Top) shows the cube viewed along a di-
agonal axis through two corners of the cube, and the
Z
3
rotational symmetry can be seen; i.e., a rotation of
120 degrees about the axis (K in Figure 8(a)(Bottom))
sends each pair of parallel faces into another pair. The
wreath product for this is then ℜ
2
o Z
2
o Z
3
while the
tree structure shown in Figure 8(b) gives the control
action tree.
Figure 7: (a) One Face View RGB (b) One Face View Depth
Map (c) Three Face View RGB (d) Three Face View Depth
Map.
Figure 8: (a) View of Cube along Diagonal Axis with Z
3
Symmetries (b) the Control Action Tree for ℜ
2
o Z
2
o Z
3
.
RobotCognitionusingBayesianSymmetryNetworks
699

3 BAYESIAN SYMMETRY
NETWORKS
We have already described how the wreath product
provides a nested description of an object which maps
in a natural way onto a causal graph structure for a
Bayesian network. As a working example, we con-
tinue with the cube as described in Figure 8(b) for
which the corresponding Bayesian network
1
is shown
in Figure 9. The graph structure is defined by the
wreath product, and the conditional probability tables
are determined by considering the context (indoors),
the sensor data noise, and the algorithm error. The
top-most node Z
3
has been assigned a prior of 5%
true based on occurence statistics of the environment.
The Z
2
nodes have a probability of 30% if there is
no known Z
3
symmetry, otherwise 80%, and the ℜ
2
flat face nodes have conditional probability of 70% if
no Z
2
symmetry is known, otherwise 95%. The fig-
ure shows the likelihoods of each symmetry assertion
with no evidence. Figure 10 shows the changes in
probabilities for the network when it is known that 3
faces exist, and that there is a Z
3
symmetry for them.
Note that the likelihoods for the unseen parallel faces
rise to 91% in this case. This type of information may
not be readily available to a robot without this cogni-
tive structure.
Figure 9: Bayesian Network for Cube.
This works reasonably well in practice; Figure 11
shows Kinect data for a cube shape viewed along a
diagonal and surface normals. To determine if the Z
3
symmetry exists, we determine the average normal for
each face, then check the symmetry of the three nor-
mals rotated through 2π radians about their mean vec-
tor. Figure 12(a) shows the similarity measure (best
match of three original normals with rotated versions
of themselves, while (b) shows the trajectories of the
three normal endpoints under the rotation.
1
This network was constructed using the AgenaRisk
software which accompanies (Fenton and Neil, 2013).
Figure 10: Bayesian Network for Cube with Observations
Asserted.
Figure 11: Kinect Cube Data, and Surface Normals.
0 100 200 300 400
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
Angle of Rotation about Mean Vector
Similarity of 3 Normal Directions
−0.5
0
0.5
1
−1
−0.5
0
0.5
1
−0.6
−0.4
−0.2
0
0.2
0.4
0.6
0.8
1
X Axis
Y Axis
Z Axis
Figure 12: (a) Similarity of 3 Surface Normals under Ro-
tation about their Mean Vector; (b) Trajectories of Normal
Endpoints under Rotation.
4 CONCLUSIONS AND FUTURE
WORK
Our position is that wreath product representations of
objects provide a very powerful object concept mech-
anism, especially when combined with deep connec-
tions to sensorimotor data, tied to specific object de-
scriptions, and embedded in a probabilistic inference
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
700
framework. Current issues include:
• General Concept Representation. Arbitrary ob-
jects can be represented by use of tensor spline
groups, as well as shape modification processes
as described by Leyton. Implementation will re-
quire careful attention. In addition, Leyton argued
that wreath products could represent any concept;
therefore, extensions need to be found for struc-
tural, material properties, social, and other types
of relations.
• Combining Sensor and Actuation Data. A de-
tailed characterization of how sensorimotor data is
embedded in the wreath product representation is
required. There are limitations in what the actua-
tors can achieve compared to what the sensors can
perceive, depending on the robot used and its De-
grees of Freedom (DoF). In the cube example, we
mentioned that a robot with a head having 360
◦
3-DoF can actuate the concepts as motions. Sim-
ilarly, a robot with a dextrous hand will be able to
manipulate the object and be able to map the ac-
tuations to the concepts: e.g., in 2D the robot can
draw the square, given the generative concept of
a square, while in 3D it can trace its fingers along
the smooth faces of a cube and infer the object
type based on the Bayesian network for a cube.
On the contrary, a two-wheeled robot with only a
range sensor and no movable head or hands can
only move on the ground, and will thus have lim-
itations in relating actuations directly to concepts
(especially 3D shape concepts).
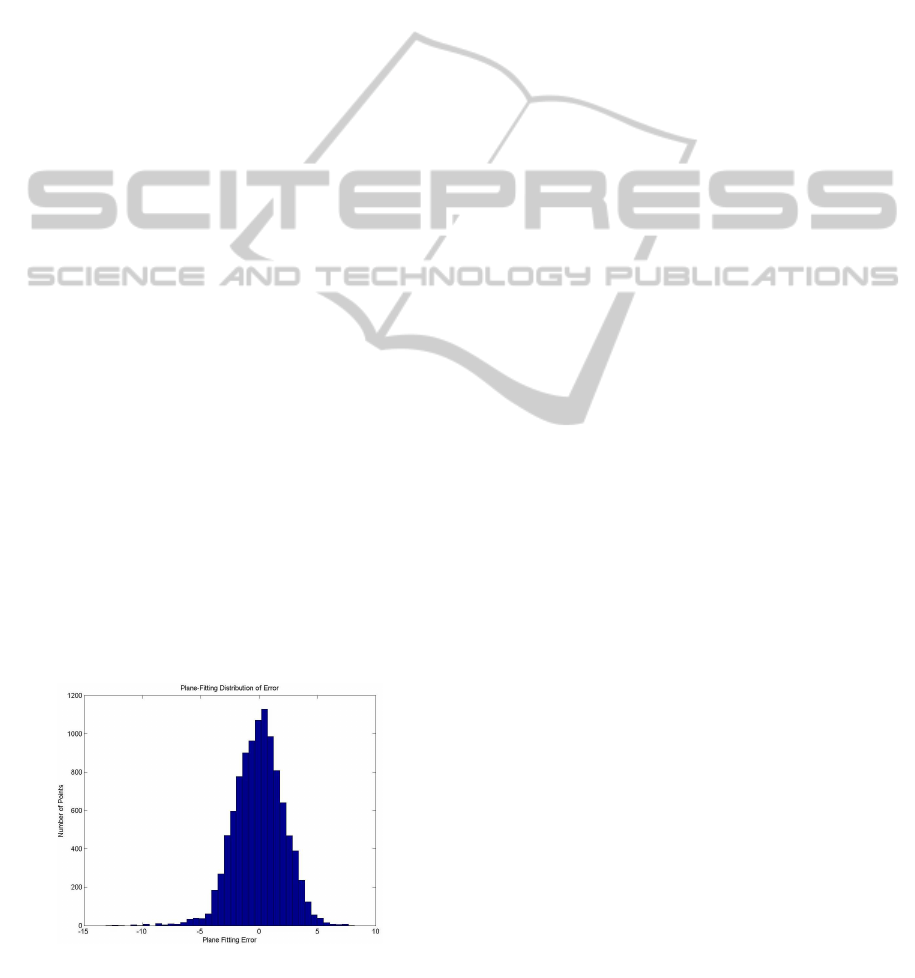
• Prior and Conditional Probabilities: must be
determined for the networks. This requires a rig-
orous learning process for the statistics of the en-
vironment and the sensors. For example, we are
studying the error in fitting planes to Kinect data,
and first results indicate that the noise appears
Gaussian (see Figure 13).
Figure 13: Error Distribution in Plane-Fitting for Kinect
Data.
• Prime Factorization. In the shapes we address, a
Bayesian network can be created in multiple ways
for the same shape; e.g., two square representa-
tions are ℜ o Z
4
and ℜ o Z
2
× Z
2
o Z
2
. The equiv-
alence of resulting shape must be made known
to the agent (even thought the generative mech-
anisms are different); we are exploring whether
subgroups of the largest group generating the
shape allow this to be identified.
• Object Coherence and Segmentation. Object
segmentation is a major challenge, and object
classification processing will be more efficient if
related points are segmented early on. We are
looking at the use of local symmetries (e.g., color,
texture, material properties, etc.) to achieve this.
Moreover, object coherence can be found from
motion of the object; namely, there will be a sym-
metry in the motion parameters for all parts of
a rigid object which can be learned from experi-
ence.
REFERENCES
Binford, T., Levitt, T. and Mann, W. (1987). Bayesian Infer-
ence in Model-Based Machine Vision. In Uncertainty
in Artificial Intelligence 3 Annual Conference on Un-
certainty in Artificial Intelligence (UAI-87), pages 73–
95, Amsterdam, NL. Elsevier Science.
Buisson, J.-C. (2001). A Computer Model of Interactivism
and Piagetian Assimilation Applied to Visual Percep-
tion. In Proc. in the 31th. annual symposium of the
Jean Piaget Society, Berkeley, CA.
Chang, W. (2004). Image Processing with Wreath Prod-
ucts. Master’s thesis, Harvey Mudd College, Clare-
mont, CA.
Fenton, N. and Neil, M. (2013). Risk Assessment and De-
cision Analysis with Bayesian Networks. CRC Press,
Boca Raton, FL.
Foote, R., Mirchandani, G., Rockmore, D., Healy, D., and
Olson, T. (2000). A Wreath Product Group Approach
to Signal and Image Processing: Part I – Multiresolu-
tion Analysis IEEE-T Signal Processing, 48(1):102–
132.
Gold, K. and Scassellati, B. (2007). A Bayesian Robot that
Distinguishes ”self” from ”other”. In Proceedings of
Twenty-ninth Annual Meeting of the Cognitive Science
S ociety, pages 384–392, NJ. Lawrence Erbaum.
Grupen, R. and Henderson, T. (1988). Apparent Sym-
metries in Range Data. Pattern Recognition Letters,
7:107–111.
Henderson, T., Fan, Y., Alford, A., Grant, E., and Cohen, E.
(2009). Innate Theories as a Basis for Autonomous
Mental Development. Technical Report UUCS-09-
004, The University of Utah.
Henderson, T., Joshi, A., and Grant, E. (2012a). From Sen-
sorimotor Data to Concepts: The Role of Symmetry.
RobotCognitionusingBayesianSymmetryNetworks
701

Technical Report UUCS-12-012, University of Utah,
School of Computing, Salt Lake City, UT.
Henderson, T., Peng, H., Sikorski, C., Deshpande, N., and
Grant, E. (2011). Symmetry: A Basis for Sensorimo-
tor Reconstruction. Technical Report UUCS-11-011,
University of Utah, School of Computing, Salt Lake
City, UT.
Henderson, T. C., Cohen, E., Grant, E., Draelos, M., and
Deshpande, N. (2012b). Symmetry as a Basis for Per-
ceptual Fusion. In Proceedings of the IEEE Confer-
ence on Multisensor Fusion and Integration for Intel-
ligent Systems, Hamburg, Germany.
Jia, Y., Abbott, J., Austerweil, J., Griffiths, T., and Darrell,
T. (2013). Visual Concept Learning: Combining Ma-
chine Vision and Bayesian Generalization on concept
Hierarchies. In Neural Information Processing Sys-
tems 2013, Lake Tahoe, NV.
Leyton, M. (2001). A Generative Theory of Shape.
Springer, Berlin.
Tenenbaum, J. and Griffiths, T. (2001). Generalization,
Similarity and Bayesian Inference. Behavioral and
Brain Sciences, 24:629–640.
Vasudevan, S. and Siegwart, R. (2008). Bayesian Space
Conceptualization and Place Classification for Se-
mantic Maps in Mobile Robots. Robotics and Au-
tonomous Systems, 56:522–537.
Vernon, D., Metta, G., and Sandini, G. (2007). A Survey
of Artificial Cognitive Systems: Implications for the
Autonomous Development of Mental Capabilities in
Computational Agents. IEEE Transactions on Evolu-
tionary Computation, 11(2):151–180.
Zhang, L. and Ji, Q. (2011). A Bayesian Network Model for
Automatic and Interactive Image Segmentation. IEEE
Transactions on Image Processing, 30(9):2582–2593.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
702
