Hierarchical HMM-based Failure Isolation for Cognitive Robots

Dogan Altan and Sanem Sariel-Talay

Artiﬁcial Intelligence and Robotics Laboratory,

Department of Computer Engineering, Istanbul Technical University, Istanbul, Turkey

Keywords:

Probabilistic Failure Isolation, Cognitive Robots, Hierarchical Hidden Markov Models, Model-based Diagno-

sis, Uncertain Reasoning.

Abstract:

Robots execute their planned actions in the physical world to accomplish their goals. However, since the real

world is partially observable and dynamic, failures may occur during the execution of their actions. These

failures should be detected immediately, and the underlying reasons of these failures should be isolated to

ensure robustness. In this paper, we propose a probabilistic and temporal model-based failure isolation method

that maintains Hierarchical Hidden Markov Models (HHMMs) in order to represent and reason about different

failure types. The underlying reason of a failure can be isolated efﬁciently by multi-hypothesis tracking.

1 INTRODUCTION

A monitoring system is pivotal in order to achieve

goals robustly in the face of uncertainties. During the

execution of plans, robots may face several types of

failures (Karapinar et al., 2012). A monitoring pro-

cedure should take place which can be in both plan

and action level to detect these failures. Although de-

tecting failures is one of the central problems for ro-

bust execution (Pettersson, 2005; Usug et al., 2012;

Karapinar et al., 2013), the robot should also identify

the reason of the failures to efﬁciently recover from

them. Isolation of a failure requires an inference pro-

cess to ﬁnd the underlying reason behind the failure.

In this research, our focus is on a probabilistic fail-

ure isolation method. We address action execution

failures that may arise due to hardware/sensor limita-

tions, limited knowledge on some environmental fea-

tures (Bouguerra et al., 2008) or external events.

Monitoring and reasoning about failures requires

interpreting data from one or more sensors (e.g., vi-

sion, force, touch or pressure). Therefore, in order to

detect a failure, the robot needs to interpret the scene

and apply certain reasoning tools to come up with cor-

rect conclusions. A similar procedure should be ap-

plied in order to isolate a failure. To achieve accurate

isolation, the robot needs to maintain a priori informa-

tion on the models of failures that are likely to occur

in the environment.

In some cases, the reason of the failure may not be

directly related to the action in execution. The reason

of the failure may be an undesired effect of a previ-

ous action that is executed by the robot or an exter-

nal event. For example, in the blocks world domain,

when the base block structure is not properly formed,

the execution of a stack action on the existing tower

may fail, and the whole structure may be completely

destroyed. In order to isolate these types of failures,

a temporal reasoning model is needed. Furthermore,

there may be more than one cause of a failure. To

deal with such cases, a probabilistic temporal model

is required to identify the possible failure cases.

We propose a Hierarchical Hidden Markov Model

(HHMM)-based isolation method to determine the

cause of a failure. Our method includes parallel HH-

MMs representing different failure types that are be-

ing modelled. The HHMM model provides temporal

analysis of states and propagates temporal failure in-

formation over time after a deviation occurs. Multiple

hypotheses are tracked at the same time to identify the

underlying cause in a probabilistic manner. Our main

contribution in this paper is modelling each failure

type as a distinct HHMM considering action-failure

relations and using these models in parallel. This rep-

resentation makes it possible to isolate several types

of failures including persistent ones on a speciﬁc ob-

ject or event. The rest of the paper is organized as

follows. First, literature review on fault isolation is

presented. Then, our proposed method is explained

as a proof of concept. Finally, the paper is concluded.

299

Altan D. and Sariel-Talay S..

Hierarchical HMM-based Failure Isolation for Cognitive Robots.

DOI: 10.5220/0004921502990304

In Proceedings of the 6th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2014), pages 299-304

ISBN: 978-989-758-016-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK

Failure detection and isolation (diagnosis) is an in-

tensively investigated issue for robot systems due to

the need for safe plan execution (Pettersson, 2005;

Fritz, 2005). A common approach to detect failures is

using an observer-based approach (Nan et al., 2008;

Steinbauer and Wotawa, 2009). In this approach, pre-

deﬁned models and inconsistencies between the ex-

pected and observed outcomes are checked to detect

failures. Uncertainties may lead a robot to faulty sit-

uations. This is handled with semantic knowledge-

based execution monitoring where the robot estimates

a probability distribution according to its expectations

(Bouguerra et al., 2007).

Model-based failure diagnosis has been investi-

gated by many researchers previously (Frank et al.,

2000). Structural abstraction is used for model-based

diagnosis in an earlier work (Chittaro and Ranon,

2004). In some model-based fault detection and iso-

lation systems, HMMs are used to monitor processes

(Hovland and McCarragher, 1998) or to diagnose fail-

ures in different domains (Kwon and Kim, 1999; Ying

et al., 2000; Ocak and Loparo, 2001; Ge et al., 2004;

Lee et al., 2004; Li et al., 2005). However, none

of these models uses hierarchical models. Dynamic

Bayesian Networks and Particle Filters are also used

for failure diagnosis (Flores-Quintanilla et al., 2005;

Verma et al., 2004). In another work (Verma et al.,

2002a), Partially Observable Markov Decision Pro-

cesses (POMDPs) and Particle Filters are used in or-

der to model and track failures in autonomous sys-

tems. In another work, a hierarchical representation

is used for failure diagnosis (Verma et al., 2002b);

however, it can not handle multiple faults. Hierarchi-

cal HMMs are also used in prognostics for estimating

remaining useful time (RUL) in machinery processes

(Camci and Chinnam, 2010).

Logic programming with situation calculus is also

studied in order to explain the unexpected devia-

tions in task execution depending on inconsisten-

cies among the hypotheses using their costs (Gspandl

et al., 2012).

Our HHMM-based failure isolation method dif-

fers from earlier work because of its ability in recog-

nizing failures hierarchically in parallel and its usage

of relations between actions and failure types. Our

system can determine that a failure may be caused by

multiple fault sources, and it may provide several ex-

planations for the cause of a failure if there is no clear

indication of the failure. Moreover, persistent failures

on a speciﬁc object or event can be isolated.

3 PROBABILISTIC FAILURE

ISOLATION FOR ROBOTS

In the symbolic level, a robot maintains the models

of its operators corresponding to the actions that it

can execute in the real-world such as pick-up, stack,

move and put-down. Each action is represented by a

set of facts to be satisﬁed before executing it, namely

preconditions, and its effects that occur in the world

after the action is executed by the robot.

In order to reach a desired goal, the robot should

come up with a symbolic plan. After executing the

consecutive actions in this plan, the robot is expected

to reach its desired goal state. However, due to unex-

pected deviations, failures may prevent the robot from

reaching its goal. When a failure is detected, the robot

should reason about the main cause of the failure for

robust execution. In order to safely end up with its

goal state, the robot should apply a failure isolation

procedure to analyse the faulty situation and ﬁnd the

reason of this failure. The main focus of our research

is a failure isolation method to determine the reasons

behind a failure after it is detected.

3.1 A Motivating Scenario

Assume that a robot is responsible for transporting

objects to their desired positions in an object manip-

ulation scenario. Initially, all objects are in their ini-

tial positions. The robot is capable of executing some

actions, namely move-to-loc, pick-up, put-down and

move-to-obj. move-to-loc is executedin order to move

the robot from one location to another, whereas move-

to-obj moves the robot to a desired object location.

Action pick-up is executed on an object by the robot’s

gripper to grasp the object. Similarly, put-down is ex-

ecuted for releasing an object from the gripper on the

ground. Considering these actions, the robot comes

up with the following symbolic plan in order to move

an object from its initial location to its desired loca-

tion: [move-to-obj(object), pick-up(object), move-to-

loc(destination), put-down(object)]. After the execu-

tion of the constructed plan, the goal is achieved.

Several types of failures may be faced by the robot

during the execution of its actions in the given plan.

For example, the robot may fail in executing pick-up

action on the object because of wrong grasp position

or its size. Another failure may occur if the robot’s

vision system fails while recognizing the object. Yet

in another scenario, the object may be manipulated by

other agents without any a priori information. In such

cases, the isolation model should give relevant expla-

nations for the causes of these unexpected situations.

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

300

3.2 Hierarchical HMM-based Failure

Isolation

Hidden Markov Models (HMMs) (Baum and Petrie,

1966) are probabilistic temporal structures to model

Markov processes. Since failures that occur during

the execution of a plan generally propagate over time,

the problem of identifying failures should be analysed

from a temporal dimension. Furthermore, uncertain-

ties in sensing and non-determinism of actions make

HMM-based models suitable for the failure isolation

problem.

An HMM consists of ﬁve components, namely

states, observations, transition probabilities, observa-

tion probabilities and the initial state distribution.

• There are N hidden states in an HMM. Each hid-

den state is denoted with s

∈ S where S is the set

of hidden states.

• Transition model, A = a

, deﬁnes the probability

of transferring from state s

to state s

where s

, s

∈ S.

• Observations, denoted by the y

, represent the sen-

sory information gathered at time t.

• Observation model, denoted by B = b

(y), deﬁnes

the probability of gathering the observation y at

state s

• Initial state probability distribution is represented

with π = π

An HHMM is a derived structure of an HMM in

which each state in the model is itself an HMM (Fine

et al., 1998). Once a node at time step t is activated

in the HHMM, a new HMM is created under the cor-

responding node for that time step. Transitions inside

that newly created HMM in the lower level are called

horizontal transitions. Whenever the newly generated

HMM comes to an end, a vertical transition occurs,

and the process of updating HHMMs goes on from

the node in the corresponding upper level in the cor-

responding model. Note that a horizontal transition

does not take place in the upper level before the newly

created HMM reaches its ﬁnal state.

In our approach, we employ two-level HHMMs

running in parallel. The type of a failure that may oc-

cur during the execution of an action, is modelled as a

distinct HHMM. HHMMs are used to represent fail-

ure models instead of classical HMMs because a hier-

archy between the plan and actions is needed in order

to isolate persistent failures. For instance, the robot’s

vision system may fail to recognize a speciﬁc object

in the environment continually. Each model running

parallel is denoted by M

∈ M where i is the index

of the corresponding failure type. Each state in M

is deﬁned as M

[ws

] where ws

is the representation

of the world state at discrete time step j of the plan.

Each M

[ws

] in the models has a latent value that is

either success or failure. The problem is to ﬁnd mod-

els that include latent variables labelled with failure

and have probabilities over a given threshold. These

models are treated as possible reasons of a failure.

Table 1: Action-Failure relations used in the model.

Action FailureType

move-to-obj(object)

Vision(object), ExternalEvent

Localization(Robot)

move-to-loc(destination) Localization(Robot)

pick-up(object)

ExternalEvent, Gripper(Robot)

Vision(object), Localization(Robot)

put-down(object) Gripper(Robot)

Causes of action execution failures that are ad-

dressed in this paper are: vision failures for all

objects, localization failures, hardware limitations

(actuator/effector) and external events. Vision(X)

is a failure model for a speciﬁc object(X) repre-

senting a faulty situation in the vision algorithm

to recognize a speciﬁc object. HardwareLimita-

tion(actuator/effector) model indicates situations that

are beyond the physical capabilities of the robot. Ex-

ternalEvent model stands for exogenous events that

change the world outside the control of the robot. Lo-

calization failure model represents the faulty situa-

tions where the robot cannot correctly localize itself.

Depending on the action that is being executed at a

given world state and its parameters, the related fail-

ure models are activated and treated as active mod-

els where unrelated models are considered as passive

models. The relations that deﬁne which action is re-

lated to which failure type are given in Table 1 for a

speciﬁc object.

Table 2: Predicates and the related sensory data.

Predicate Source

object RGB-D Camera

clear RGB-D Camera

onground RGB-D Camera

segment RGB-D Camera

handempty Pressure sensor

holding Pressure sensor

The world state of the robot is maintained by using

sensory and motor information. Table 2 lists the ob-

servable predicates of the world state that we consider

and the related sensors providing the relevant data.

object predicate is for representing the veriﬁed exis-

tence of an object. clear is for stating that the object

has nothing on it. onground stands for the situation

that an object is on the ground. segment corresponds

to a point cloud clustered by the segmentation algo-

rithm but not detected by the vision algorithm. These

HierarchicalHMM-basedFailureIsolationforCognitiveRobots

301

predicates are observed with the on-board RGB-D

camera using a template-based vision algorithm in our

system (Ersen et al., 2013). handempty states that the

robot’s gripper is available to hold an object whereas

holding is for stating that an object is grasped by the

robot. Observation probabilities are deﬁned regarding

to the statistical analysis on the outputs of the sensors

and the related predicate computations. A scene inter-

pretation (Ozturk et al., 2014) module maintains these

predicates in the robot’s knowledge base, and updates

them according to new observations. It should also

be noted that transition and observation probabilities

for different failure types are different from each other

due to the difference in models.

Algorithm 1: FailureIsolation(P,M).

Input: P, Plan; M, Failure models

Output: list, the list of the candidate causes of a failure

while P 6=

0 and status == success do

action = POP(P)

while (status = execute(action)) == inExecution do

updateLowerLevelModels(M, action)

end while

applyVerticalTransition(M, ws

)

updateHigherLevelModels(M, action)

end while

for all M

labelUpperLevelLatents(M

)

end for

list = isolateModels(M)

return list

Our failure isolation method is applied by running

Algorithm 1. It accepts a plan and failure models as

parameters. Plan P includes a sequence of actions to

be executed by the robot. Failure models, represented

with M, include parallel HHMM-based failure mod-

els. After the execution of the given algorithm, a list,

initially empty, that contains possible candidates of a

failure is returned. Actions in the given plan is exe-

cuted consecutively. An action can be in one of the

following states: inExecution, success and failure. in-

Execution corresponds to the state in which the robot

executes that action. success stands for the state that

the robot reached the expected outcomes of the corre-

sponding action. failure corresponds to the situations

where the expected outcomes of an action are not met.

During the execution of each action, all HHMM-

structured models’ lower levels related to the cor-

responding failure types are considered as active

models, and updated by the updateLowerLevelMod-

els(M,action). Predeﬁned relations between actions

(with their parameters) and failure types are used to

determine whether the executed action is related to the

failure type. If an action is related to a failure type, the

corresponding failure type’s HHMM is treated as an

active model, and it is activated for that time step.

Algorithm 2: updateHigherLevelModels(M, action).

Input: M, Failure models; action, Current action

Output: M

, Updated models

for all M

if isRelated(M

, action) then

addNewState(M

)

else

extendPreviousState(M

)

end if

end for

Observations are gathered from the sensors of the

robot (e.g., pressure sensor, RGB-D sensor, etc.), and

these observations are mapped into a probability dis-

tribution which depends on the sensors’ statistical

analysis. Depending on the observations gathered at

the current state, the new state’s properties are cal-

culated considering the previous state because of the

Markov property with the following formulas where

is the Viterbi value which is calculated for each

time step t, and δ

is the state index that maximizes

the given statement.

) = max

t−1

(k) ∗ a(k, s

)) ∗ b

)

) = argmax

t−1

(k) ∗ a(k, s

))

After the execution of the corresponding

action, a vertical transition occurs with the

applyVerticalTransition(M,S

) function by using

the minimum observation probability in the related

model’s lower layer for that action’s time interval.

updateHigherLevelModels(M,action) updates all

HHMMs’ upper levels considering the action-failure

relations. This procedure is implemented in Algo-

rithm 2. This algorithm updates all related models

according to the action in execution and its current

outcomes. In order to infer action-failure relations,

the predeﬁned relations (Table 1) and the parameters

of the executed action are used. In an active model

case, a new state is generated and the v

) and δ

)

values are updated according to the given formulas.

Otherwise, if a failure model is not related to the

action in execution, it is treated as a passive model,

and the last state of the corresponding HHMM’s time

interval is extended without generating a new state.

This procedure goes on until the robot reaches

the goal state or a failure is detected. We as-

sume that failure detection is done by applying

an observer-based approach. In case of a fail-

ure, labelUpperLevelLatents(M

) procedure assigns

the hidden valuesof each state in the upper level of the

model by using the Viterbi algorithm (Viterbi, 1967).

Viterbi algorithm is invoked to label latent variables

with a value that is either success or failure in each

HHMM. It simply starts from the end node of an

HMM and labels the latent variables for each node

considering the calculated v and δ values during the

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

302

Plan

action

...

Failure Model (i)

...

Failure Model (i)

...

Figure 1: An illustration of an HHMM failure model corresponding to the actions of a given plan.

execution of the plan. At the end of the Algorithm

1, a list that contains the possible causes of the fail-

ure with a probability exceeding a given threshold is

returned with the Algorithm 3.

Algorithm 3: isolateModels(M).

Input: M, Failure models

Output: list, the list of the candidate causes of a failure

list =

for all M

for all ws

if M

.getHiddenState(ws

) == failure and

.getProbability(ws

) ≥ threshold then

list.add(M

)

break

end if

end for

return list

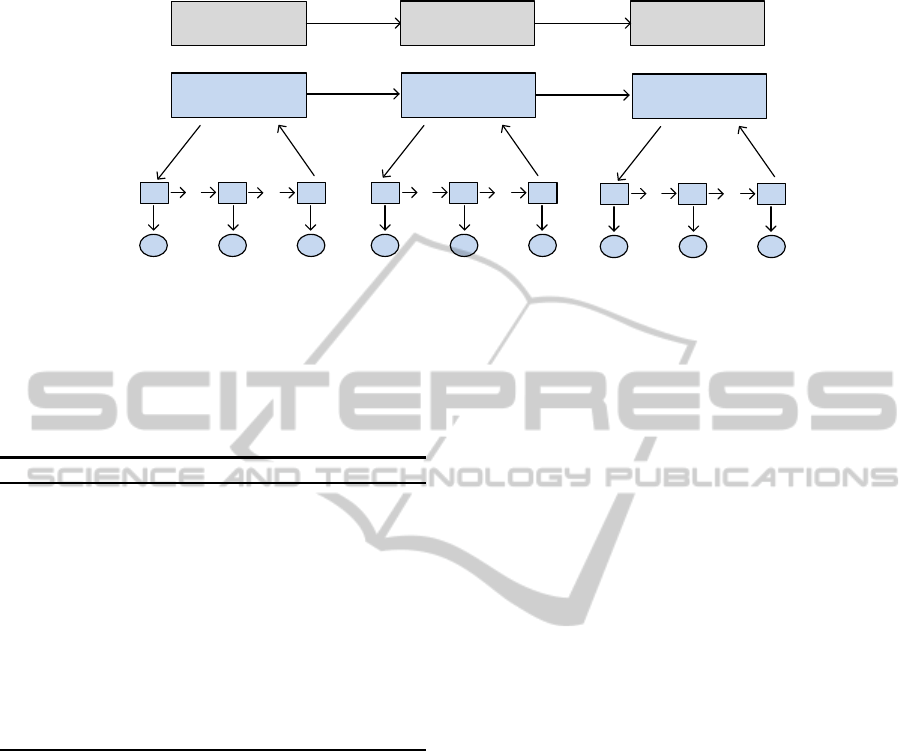
Figure 1 is given in order to give the general

overview of using parallel HHMMs for failure isola-

tion. Upper level in the ﬁgure represents the sym-

bolic plan given to the robot. Under this plan, a

failure model (M

) represented as an HHMM. In this

HHMM, each top node has its own HMM. During the

execution of action

, the ﬁrst top node of the model’s

lower level HMM is updated with the sensory infor-

mation (y

). After mapping each observation in each

discrete time step into a probability distribution by us-

ing conditional probability tables (CPTs), properties

of the newly generated node of the HMM are com-

puted. This procedure is repeated similarly for the

other related failure models considering the action-

failure relations. In case of a failure, Viterbi algorithm

is invoked, and the candidate models explaining the

faulty situation are determined.

4 CONCLUSIONS

In this paper, we present a temporal model for fail-

ure isolation that maintains HHMMs. HHMMs are

used for modelling the possible failure types. Us-

ing the temporal ﬁltering property of the HMMs, fail-

ures that occur because of a previously executed ac-

tion can efﬁciently be isolated. Using the relations

between the actions and the failure types, only corre-

sponding models are updated. This reduces the com-

putational cost of the method. Moreover, HHMMs

ensure isolation of multiple faults and propose expla-

nations for possible faulty situations. Our future work

includes evaluation of the proposed method in several

real robot scenarios.

ACKNOWLEDGEMENTS

This research is funded by a grant from the Scien-

tiﬁc and Technological Research Council of Turkey

(TUBITAK), Grant No. 111E-286. TUBITAK’s sup-

port is gratefully acknowledged. Authors would also

like to thank Mustafa Ersen, Melis Kapotoglu, Ca-

gatay Koc, Melodi Deniz Ozturk and Mehmet Biberci

for their helpful comments on this research.

REFERENCES

Baum, L. E. and Petrie, T. (1966). Statistical inference for

probabilistic functions of ﬁnite state markov chains.

The Annals of Mathematical Statistics, 37(6):pp.

1554–1563.

Bouguerra, A., Karlsson, L., and Safﬁotti, A. (2007). Han-

dling uncertainty in semantic-knowledge based exe-

cution monitoring. In Intelligent Robots and Systems,

2007. IROS 2007. IEEE/RSJ International Conference

on, pages 437–443.

HierarchicalHMM-basedFailureIsolationforCognitiveRobots

303

Bouguerra, A., Karlsson, L., and Safﬁotti, A. (2008). Mon-

itoring the execution of robot plans using seman-

tic knowledge. Robotics and Autonomous Systems,

56(11):942–954.

Camci, F. and Chinnam, R. (2010). Health-state estima-

tion and prognostics in machining processes. Automa-

tion Science and Engineering, IEEE Transactions on,

7(3):581–597.

Chittaro, L. and Ranon, R. (2004). Hierarchical model-

based diagnosis based on structural abstraction. Ar-

tiﬁcial Intelligence, 155(12):147 – 182.

Ersen, M., Sariel-Talay, S., and Yalcin, H. (2013). Extract-

ing spatial relations among objects for failure detec-

tion. In Proceedings of the KI 2013 Workshop on Vi-

sual and Spatial Cognition.

Fine, S., Singer, Y., and Tishby, N. (1998). The hierarchi-

cal hidden markov model: Analysis and applications.

Machine Learning, 32(1):41–62.

Flores-Quintanilla, J., Morales-Menendez, R., Ramirez-

Mendoza, R., Garza-Castanon, L., and Cantu-Ortiz, F.

(2005). Towards a new fault diagnosis system for elec-

tric machines based on dynamic probabilistic models.

In American Control Conference, 2005. Proceedings

of the 2005.

Frank, P. M., Ding, S. X., and Marcu, T. (2000). Model-

based fault diagnosis in technical processes. Trans-

actions of the Institute of Measurement and Control,

22(1):57–101.

Fritz, C. (2005). Execution monitoring – a survey. Technical

report, University of Toronto.

Ge, M., Du, R., and Xu, Y. (2004). Hidden markov model

based fault diagnosis for stamping processes. Me-

chanical Systems and Signal Processing, 18(2):391 –

408.

Gspandl, S., Podesser, S., Reip, M., Steinbauer, G., and

Wolfram, M. (2012). A dependable perception-

decision-execution cycle for autonomous robots. In

Robotics and Automation (ICRA), 2012 IEEE Inter-

national Conference on, pages 2992–2998.

Hovland, G. and McCarragher, B. J. (1998). Hidden markov

models as a process monitor in robotic assembly. I. J.

Robotic Res., 17(2):153–168.

Karapinar, S., Altan, D., and Sariel-Talay, S. (2012). A

robust planning framework for cognitive robots. In

Proceedings of the AAAI-12 Workshop on Cognitive

Robotics (CogRob).

Karapinar, S., Sariel-Talay, S., Yildiz, P., and Ersen, M.

(2013). Learning guided planning for robust task ex-

ecution in cognitive robotics. In The AAAI-13 Work-

shop on Intelligent Robotic Systems, Bellevue, USA.

Kwon, K.-C. and Kim, J.-H. (1999). Accident identiﬁ-

cation in nuclear power plants using hidden markov

models. Engineering Applications of Artiﬁcial Intelli-

gence, 12(4):491 – 501.

Lee, J. M., Kim, S.-J., Hwang, Y., and Song, C.-S. (2004).

Diagnosis of mechanical fault signals using continu-

ous hidden markov model. Journal of Sound and Vi-

bration, 276(35):1065 – 1080.

Li, Z., Wu, Z., He, Y., and Fulei, C. (2005). Hidden markov

model-based fault diagnostics method in speed-up and

speed-down process for rotating machinery. Mechan-

ical Systems and Signal Processing, 19(2):329 – 339.

Nan, C., Khan, F., and Iqbal, M. T. (2008). Real-time fault

diagnosis using knowledge-based expert system. Pro-

cess Safety and Environmental Protection, 86(1):55 –

71.

Ocak, H. and Loparo, K. (2001). A new bearing fault de-

tection and diagnosis scheme based on hidden markov

modeling of vibration signals. In Acoustics, Speech,

and Signal Processing, 2001. Proceedings. (ICASSP

’01). 2001 IEEE International Conference on, vol-

ume 5, pages 3141–3144 vol.5.

Ozturk, M. D., Ersen, M., Kapotoglu, M., Koc, C., Sariel-

Talay, S., and Yalcin, H. (2014). Scene interpre-

tation for self-aware cognitive robots. In AAAI-14

Spring Symposium on Qualitative Representations for

Robots.

Pettersson, O. (2005). Execution monitoring in robotics: A

survey. Robotics and Autonomous Systems, 53:73–88.

Steinbauer, G. and Wotawa, F. (2009). Robust plan ex-

ecution using model-based reasoning. Advanced

Robotics, 23(10):1315–1326.

Usug, U. C., Altan, D., and Sariel-Talay, S. (2012). Robots

that create alternative plans against failures. In 10th

IFAC Symposium on Robot Control.

Verma, V., Fernandez, J., Simmons, R., and Chatila, R.

(2002a). Probabilistic models for monitoring and fault

diagnosis. In The Second IARP and IEEE/RAS Joint

Workshop on Technical Challenges for Dependable

Robots in Human Environments.

Verma, V., Gordon, G., Simmons, R., and Thrun, S.

(2004). Real-time fault diagnosis [robot fault diagno-

sis]. Robotics Automation Magazine, IEEE, 11(2):56–

66.

Verma, V., Simmons, R., and Fernndez, J. (2002b). Proba-

bilistic models for monitoring and fault diagnosis. In

The Second IARP and IEEE/RAS Joint Workshop on

Technical Challanges for Dependable Robots in Hu-

man, pages 43–67.

Viterbi, A. (1967). Error bounds for convolutional

codes and an asymptotically optimum decoding al-

gorithm. Information Theory, IEEE Transactions on,

13(2):260–269.

Ying, J., Kirubarajan, T., Pattipati, K., and Patterson-Hine,

A. (2000). A hidden markov model-based algorithm

for fault diagnosis with partial and imperfect tests.

Systems, Man, and Cybernetics, Part C: Applications

and Reviews, IEEE Transactions on, 30(4):463–473.

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

304