
GPU Solver with Chi-square Kernels for SVM Classification of Big
Sparse Problems
Krzysztof Sopyla and Pawel Drozda
Department of Mathematics and Computer Science, University of Warmia and Mazury, Olsztyn, Poland
Keywords:
SVM Classification, GPU Computing, Sparse Data Formats, SVM Kernels.
Abstract:
This paper presents the ongoing research on the GPU SVM solutions for classification of big sparse datasets.
In particular, after the success of implementation of RBF kernel for sparse matrix formats in previous work
we decided to evaluate Chi
2
and Exponential Chi
2
kernels. Moreover, the details of GPU solver are pointed.
Experimental session summarizes results of GPU SVM classification for different sparse data formats and
different SVM kernels and demonstrates that solution for Exponential Chi
2
achieves significant accelerations
in GPU SVM processing, while the results for Chi
2
kernel are very far from satisfactory.
1 INTRODUCTION
The Support Vector Machine (Cortes and Vapnik,
1995; Vapnik, 1995; Boser et al., 1992; Chapelle
et al., 1999) algorithm (SVM) is considered to be
a robust and effective machine learning method for
many classification tasks in a variety of scientific
fields, for example Information Retrieval (Joachims,
1998), Content Based Image Retrieval (Lazebnik
et al., 2006; Gorecki et al., 2012) , Bioinformatics
(Acir and Guzelis, 2004) and many other.
Its popularity is proven by a great number of im-
plementations, which differ greatly in many aspects,
starting from the way in which underling optimiza-
tion problem is solved (Platt, 1998; Fan et al., 2005;
Joachims et al., 2009; Bottou, 2010), through special-
ized formulations with a particular kind of kernels,
like the linear one and ending on platforms, program-
ming languages and computing devices.
In recent years, many researchers began using the
cheap computing power of the Graphical Processor
Units (GPU) for time-consuming calculations. Dis-
tribution of computing tasks allows for a significant
acceleration of the whole process, but it requires a
skillful use of appropriate data structures as well as
the organization of computing in the parallel manner.
The main issue discussed in this paper is adapta-
tion of General Purpose GPU computing (GPGPU)
for solving SVM binary classification problems. Es-
pecially, we focus on the problems with a large num-
ber of features which can not be solved with the uti-
lization of standard GPU SVM solutions due to huge
memory occupation.
We extend our previous researches on SVM accel-
eration, in which the possibility of introducing sparse
matrix formats: CSR (Sopyla et al., 2012) and Sliced
Ellpack in SVM process was investigated. In partic-
ular, in previous works we have proven that the us-
age of sparse matrix formats significantly accelerates
kernel matrix computation for RBF kernel and makes
processing of large sparse datasets possible.
Whereas, in this paper we try to replace the com-
putationally expensive RBF kernel with Chi
2
and Ex-
ponential Chi
2
kernels and examine whether is is pos-
sible to obtain the acceleration of the SVM training
at the similar level as for RBF kernel. Moreover, the
detailed description of GPU solver is provided, which
improves the work (Sopyla et al., 2012) where slower
CPU solver was used.
Obtained results indicates that Exponential Chi
2
works well in GPU SVM processing with sparse ma-
trix formats achieving accelerations up to 24 times,
while for Chi
2
the results are far from satisfactory.
All presented algorithms are included in a free and
open source KMLib library, which is available for
download from https://github.com/ksirg/KMLib.
The paper is organized as follows. The next
section describes the SVM algorithm with available
CPU and GPU solvers. The implementations of GPU
solver and two SVM kernels are presented in section
3. In section 4 we presents experiments, which in-
dicates the achieved accelerations. The last section
concludes the paper.
331
Sopyla K. and Drozda P..
GPU Solver with Chi-square Kernels for SVM Classification of Big Sparse Problems.
DOI: 10.5220/0004922603310336
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 331-336
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 SUPPORT VECTOR MACHINES
The SVM algorithm is one of the most frequently
used binary classifier whose main task is to solve the
quadratic optimization task. As a result, the SVM re-
turns a hyperplane which separates the input dataset
into two distinct classes. It can be done by solving
one of the SVM formulations from which we chose
the dual form (1):
min
α
1
2
α
T
Qα− e
T
α, (1)
y
T
α = 0,
∀
i=1···l
0 ≤ α
i
≤ C,
where (x
i
, y
i
) is a given set of instance-label pairs,
i = 1, . . . , l; x
i
∈ R
n
;y
i
∈ {−1, +1}, α is a vector of
Lagrange multipliers, e = [1, ..., 1] is the ones vector
and Q is an l by l positive semidefinite matrix, defined
as Q
ij
= y
i
y
j
K(x
i
, x
j
) with K(x
i
, x
j
) = φ(x
i
)
T
φ(x
j
) as
the kernel function.
The kernel function can take many different
forms. A linear approach is the one which is the most
frequently used and is thoroughly investigated in the
literature. In cases where the linear kernel is not suffi-
cient for solving the considered classification problem
the ”Kernel Trick” is often introduced. It involves re-
placing a linear function by one of the non-linear solu-
tions. In that group RBF, Polynomial and Chi
2
are the
most important for the SVM classification purposes.
The decision for the new object is made on the ba-
sis of the support vector and the chosen kernel func-
tion and is represented by the following formula (2):
F(x
new
) = sign
l
∑
i=1
y
i
α
i
K(x
i
, x
new
) + b
!
. (2)
2.1 CPU SVM Solvers
As the SVM classification became hard and time con-
suming there arose a need for SVM optimizing meth-
ods. The most significant researches in this field
without any parallel processing includes the SMO
(Sequential Minimal Optimization) algorithm (Platt,
1998), where author reduces greatly the number of
updated variables, paper (Keerthi et al., 2001) with
the maximal violating pair approach in the variable
selection procedure and (Fan et al., 2005), where the
second order information for the working set selection
was applied. The algorithm proposed by Fan is avail-
able in the state of the art library LibSVM (Chang and
Lin, 2011). A different but important solution was
proposed by Joachims in SVM
light
(Joachims, 1999).
Next direction in SVM acceleration was based on
CPU parallel processing, where the synchronization
between CPU cores is one of the most challenging
tasks. In this group CascadeSVM (Graf et al., 2005)
is one of the successful implementation, where au-
thors used cascade of SVM in the form of invertedtree
and reported 4-5 times speed up for 16 CPU cores.
Keerthi et al. (Cao et al., 2006) used parallel ver-
sion of SMO with gradient based heuristics of choos-
ing optimization variables and reached linear accel-
eration for 8-16 processors. Next work (Zanni et al.,
2006) adopts SVM
light
(Joachims, 1999), where au-
thors achieve the speed up, which varies from 5 up to
12 times for 16 processors. Special attention should
be given to PSVM (Chang et al., 2007), since authors
use computing cluster consisting of 500 machines.
They achieved 71 times speed up for 150 units, while
for 500 units the acceleration reached 169 times. It
has been also shown that the problem of scalability
for a large number of CPU nodes is still unsolved. Fi-
nally, the paper (Zhao and Magoules, 2011) applies
Map Reduce in MRPsvm algorithm with reported ac-
celerations varied from 2.1 to 5.2 times for 4 cores.
2.2 GPU SVM Solvers
The next step in SVM acceleration is associated with
applying modern hardware architectures (GPU) into
the classification process. Catanzaro et al. (Catan-
zaro et al., 2008) are considered the first who ap-
plied GPU processing for Support Vector algorithms.
In particular, the authors proposed the adaptation of
the SMO algorithm for parallel processing on the
GPU. A similar approach can be observed in (Car-
penter, 2009), where Carpenter proposed the solution
for SVM training, and additionally provided the sup-
port for single and double precision calculations. An-
other approach developed by (Herrero-Lopez et al.,
2010) focused on the multi-class classification prob-
lem, in which the main attention was given to the op-
timization of thread management. All the solutions
described above were implemented with the use of
Nvidia CUDA technology, involved only one graph-
ical unit each and reached the speed up by 12 to 37
times (depending on the test dataset).
The main disadvantage of the aforementioned im-
plementations results from the encoding of the dataset
as the dense matrix, where each row contains dense
feature vector. This greatly reduces the applicability
of this solution to feature rich problems. On the other
hand, such representation simplifies many operations
performed during classification such as computation
of the kernel matrix column, which is equivalent to
dense matrix (all dataset vectors) dense vector multi-
plication. For this reason (Catanzaro et al., 2008) use
level 2 BLAS operation implemented in CUBLAS,
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
332

whereas (Carpenter, 2009) exploits the efficient
Volkov et al. (Volkov and Demmel, 2008) matrix im-
plementation.
The paper (Lin and Chien, 2010) was the first
work which tackles the problem of learning SVM for
big sparse datasets. The authors used the Ellpack-
R(V´azquez et al., 2009) sparse matrix format, so
that large datasets can be processed by Support Vec-
tor Machine algorithms. The second successful im-
plementation of the sparse matrix format for SVM
method is described in (Sopyla et al., 2012). Authors
used the CSR matrix format and (Bell and Garl, 2008)
CSR Vector matrix multiplication in order to achieve
good compress capabilities and noticeable accelera-
tion. The Ellpack-R format is well structured which
facilitates SVM implementation but does not reduce
the size of dataset greatly. It results in problems of
processing the vast amount of data. Second solution
with CSR format provides accurate data compression,
which makes computing of large datasets possible.
Moreover, after the introduction of NVidia Keppler
architecture the solutions with CSR format achieve
similar performance as for Ellpack-R format.
There should be also mentioned the work
GTSVM (Cotter et al., 2011) in which authors applied
a special clustering procedure in order to group vec-
tors which similar sparse patterns, which eventually
speed up the CUDA computations. As a solver they
use the approach similar to Joachims(Joachims, 1999)
SVM
light
. Experiments conducted by authors of this
paper shows that GTSVM solution significantly ac-
celerates the SVM training process for data sets where
number of features is moderate (200 - 1000).
The major drawback of this solution is that it
can not handle large datasets(in terms of objects and
features), nevertheless in authors opinion is one of
the fastest SVM GPU implementation for medium
datasets.
In this paper we provide extension of (Sopyla
et al., 2012) by GPU solver as well as Chi
2
and Ex-
ponential Chi
2
kernel implementations for GPU, de-
tailed in next section.
3 GPU IMPLEMENTATIONS
This section presents our contribution to the field of
GPU SVM, where we investigate the usefulness of
sparse matrix formats for accelerating large feature
rich classification process. In particular, we provide
GPU solver as well as implementations of two ker-
nels for GPU processing. All the created solutions are
gathered in KMLib open source library which can be
downloaded from https://github.com/ksirg/KMLib.
3.1 GPU Solver
Following the work of (Catanzaro et al., 2008), (Car-
penter, 2009) and (Lin and Chien, 2010) as a SVM
solver we choose the SMO with a further modifica-
tion by (Fan et al., 2005).
In presented solution the goal of CPU host is
only to provide preliminary settings, call appropri-
ate CUDA functions and synchronize intermediate
stages. Whereas all main and the most time consum-
ing tasks are delegated to GPU computing. Moreover,
all kernel computations are also performed on the
GPU. Such approach results in no need of constantly
copying memory blocks between the CPU and GPU
which could considerably slow down the algorithm.
Finally, we provide a separation of kernel and solver
codes by defining them in separate classes which sig-
nificantly relaxes our implementation for the kernel or
solver changes.
The initial step of the main loop executed on GPU
involves searching the index i by each running block
with the use of the modified parallel reduction method
(Harris, 2008), which is performed with ’max’ opera-
tor to reduce the target function gradient. As a result
the 128 dimensional vector is generated, since the ex-
periments reported the best efficiency for 128 running
blocks. Next, the resulting vector is transferred to the
CPU host where the final reduction is made and the
final i and gradient value are obtained. Further step
involves the computation of i-th kernel matrix column
which is delegated to the kernel function and executed
on GPU. With the use of i-th vector, the j-th kernel
matrix column is calculated, which is performed in
the similar way as for i-th value. Finally, two La-
grange multipliers are updated on CPU host and the
new value of gradient is computed on GPU.
It should be noted, that in our solution accessing to
the dense vector is done through the texture cache. It
can be also achieved with the use of the shared mem-
ory, which is significantly faster than texture, but it is
also strongly limited. For instance for GeForce 460
card there is 48KB, thus maximum dimension of the
vector stored in floats(4B) can be 12288. Due to this
restriction the texture cache is more appropriate for
feature rich problems.
Our implementation of GPU solver is quite simi-
lar to cuSVM solution. The main differences lie in the
way of the code organization. For the cuSVM there is
no clear separation of solver and kernel code, which
causes great difficulty when trying to change the ker-
nel function. In our approach, a separate class is cre-
ated for each element, so changing the kernel func-
tion or type of solver involves the swapping of classes
only.
GPUSolverwithChi-squareKernelsforSVMClassificationofBigSparseProblems
333

3.2 Chi-square and Exponential
Chi-square Kernels
This subsection presents two additional kernels for
SVM classification. In particular, the details of
Chi
2
and Exponential Chi
2
kernel implementation are
shown and the way in which they are combined with
sparse data formats is provided. The main goal of us-
ing these kernels is to verify whether it is possible to
obtain significant acceleration of GPU SVM training
for other kernels than RBF.
The Chi
2
kernel for SVM classification is defined
for x, y ∈ R
D
+
and is given by formula (3):
K(x, y) =
D
∑
i=1
2x
i
y
i
x
i
+ y
i
. (3)
while Exponential Chi
2
is presented in equation (4):
K(x, y) = exp(−γ χ
2
(x, y)),
having χ
2
(x, y) =
1
2
D
∑
i=1
(x
i
− y
i
)
2
x
i
+ y
i
.
(4)
where x, y ∈ R
D
+
.
The choice of these kernels derives from the fact
that both kernel functions are easy to implementas the
scalar product and are very popular in CBIR domain.
The Chi Square kernel formula is in the form of scalar
product, while for Exponential Chi Square it can be
converted to (5):
K(x, y) = exp
−γ
1
2
D
∑
i=1
x
i
+
D
∑
i=1
y
i
− 4
D
∑
i=1
x
i
y
i
x
i
+ y
i
!!
.
(5)
It greatly limits the number of ’if’ instructions,
which are the very high computationally expensive
operations in CUDA programming. In particular, for
multiplication of sparse and dense vector the scalar
product needs only the operation for non-zero ele-
ments of sparse vectors.
A next essential factor, apart from choosing appro-
priate kernel, is the organization of sparse data format
processing on GPU in such a way as to use parallel
processing in the most efficient way. In particular,
the way in which the considered formats are handling
nonzero values greatly affects the final performance.
Regarding the Ellpack-R format, which is the most
regular and CUDA friendly, only one thread is as-
signed to computation of one kernel value, firstly the
column index of nonzero value based on thread and
block number is determined and then, i− th nonzero
value is read and added to the accumulator. However,
this simplicity is associated with the increased mem-
ory occupation. The Sliced EllR-T implementation
use T threads (in our case T=4) for one matrix row, all
the nonzero values are grouped into blocks each size
of 4. It provides coalesced reads and forces utilization
of shared memory for reduction T partial results.
4 EXPERIMENTS
The main goal of the experiments was to verify if the
usage of Chi
2
and Exponential Chi
2
kernels on GPU
devices for SVM algorithm allows for achieving sig-
nificant acceleration with respect to LibSVM algo-
rithm launched on 8 CPU cores with use OpenMP
technology. For this purpose, we used the machine:
Intel Core i7-2600 3.4GHz with 4 physical cores ex-
tended to 8 with the ’Intel Hyper Treading’ Technol-
ogy and GPU GeForce 690. For the tests the most
frequently used machine learning datasets were cho-
sen, downloaded from LibSVM web page (see the
first column of Tables 1 and 2). The SVM stop-
ping criterion is equal to 0.001 and the parameters for
kernels were set to the values: C = 4 for Chi
2
and
C = 4, γ = 0.5 for Exponential Chi
2
.
The results of the experiments are summarized in
the Tables 1 and 2. Table 1 includes training times of
GPU solver with Chi
2
kernel, where the Ellpack and
Sliced EllR-T sparse matrix formats are utilized. The
experiment summarized in Table 2 was conducted in
the same manner, but the kernel was changed to the
Exponential Chi
2
. In both cases, the results were
compared with training times of LibSVM algorithm.
Firstly, it is worth noting, that the processing of
the 20 Newsgroup, Real-Sim and Rcv1.binary rev.
datasets in Ellpack format is impossible. It derives
from the fact that these datasets do not fit into the Ell-
pack format into the GPU memory. Secondly, the re-
sults for Chi
2
kernel are very far from the expected.
In the most cases GPU Chi
2
solution obtains much
worse performance than standard LibSVM algorithm,
where Chi
2
solution is from 1.2 up to 11 times slower.
This is due to the fact that LibSVM uses caching and
needs much less power for the calculation of ’i’ and
’j’ kernel column for the Chi
2
kernel for small and
medium-sized datasets. For the Chi
2
kernel, from a
certain moment of the SVM process, indexes i and j
change very slightly, which allows retrieving recently
selected vectors from the cache. In our solution there
is no cache, which causes the necessity of i and j vec-
tors computation in every iteration of algorithm. Only
for Dominionstats.scale and web-spam Chi
2
solution
overperforms LibSVM, since these datasets are much
larger than others.
For the Exponential Chi
2
the obtained results are
significantly better. For all datasets the training is
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
334
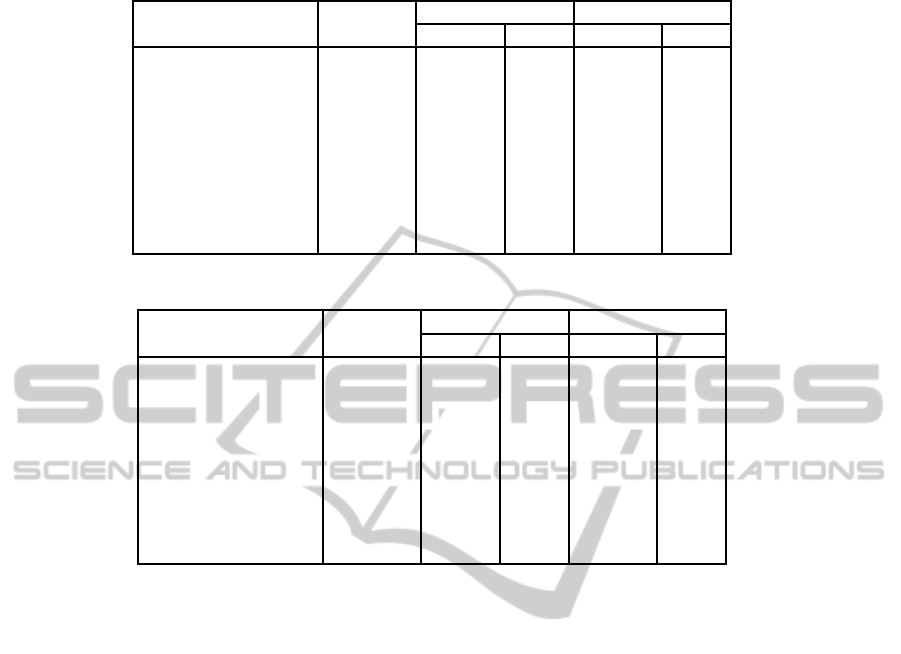
Table 1: SVM training times for Chi
2
kernel (C = 4).
Dataset LibSVM
Ellpack Sliced EllR-T
T[s] x T[s] x
Web (w8a) 13.3 147.7 0.09x 126.6 0.10x
Adult (a9a) 30.8 92.2 0.33x 97.4 0.31x
20 Newsgroup 338.9 - - 404.0 0.83x
Real-Sim 218.7 - - 355.3 0.61x
Rcv1.binary rev. 37287.4 - - 43521.9 0.85x
Mnist* 7211.4 12763.7 0.56x 10979.6 0.65x
Dominionstats.scale 120423.1 43600.3 2.76x 41103.0 2.92x
Tweet.full 2352.8 1909.7 1.23x 1963.0 1.20x
web-spam 3409.1 596.9 5.71x 611.3 5.57x
Table 2: SVM training times for ExpChi
2
kernel (C = 4, γ = 0.5).
Dataset LibSVM
Ellpack Sliced EllR-T
T[s] x T[s] x
Web (w8a) 150.2 40.8 3.7x 35.0 4.3x
Adult (a9a) 79.8 24.1 3.3x 26.9 3.0x
20 Newsgroup 755.3 - - 498.7 1.5x
Real-Sim 1461.7 - - 452.5 3.2x
Rcv1.binary rev. 163799.1 - - 15882.1 10.3x
Mnist* 7486.6 571.8 13.1x 495.7 15.1x
Dominionstats.scale 98582.2 4377.0 22.5x 4120.2 23.9x
Tweet.full 6562.6 491.1 13.4x 511.8 12.8x
web-spam 3116.7 384.6 8.1x 396.6 7.9x
much faster and the acceleration varies from 1.5x for
20 Newsgroup to 23.9x for Dominionstats.scale.
5 CONCLUSIONS
This paper presents the ongoing research which aim is
to combine different SVM kernels with sparse matrix
formats in GPU SVM processing. The successful so-
lutions were presented in (Sopyla et al., 2012) where
in the first work CSR format was combined with RBF
kernel and in the second paper Ellpack and Sliced
EllR-T formats were introduced for RBF and com-
pared with popular sparse GPU solutions. This paper
showed the detailed description of GPU solver as well
as the possibility of the usage of Chi
2
and Exponential
Chi
2
kernels with Ellpack and Sliced EllR-T sparse
matrix formats. Chi
2
kernel proved to be completely
unsuitable for the proposed approach while the results
for the second kernel seem to be very promising. To
complete our contribution we plan to implement sim-
ilar solutions for CSR format and to collate all imple-
mented GPU solutions with the state of the art GPU
algorithms.
ACKNOWLEDGEMENTS
The research has been supported by grant N N516
480940 from The National Science Center of the Re-
public of Poland and by grant 1309-802 from Min-
istry of Science and Higher Education of the Republic
of Poland.
REFERENCES
Acir, N. and Guzelis, C. (2004). An application of support
vector machine in bioinformatics: automated recogni-
tion of epileptiform patterns in eeg using svm clas-
sifier designed by a perturbation method. In Pro-
ceedings of the Third international conference on
Advances in Information Systems, ADVIS’04, pages
462–471, Berlin, Heidelberg. Springer-Verlag.
Bell, N. and Garl, M. (2008). Efficient sparse matrix-vector
multiplication on cuda. Technical report, NVidia.
Boser, B. E., Guyon, I. M., and Vapnik, V. N. (1992). A
training algorithm for optimal margin classifiers. In
Proceedings of the fifth annual workshop on Compu-
tational learning theory, COLT ’92, pages 144–152,
New York, NY, USA. ACM.
Bottou, L. (2010). Large-scale machine learning with
stochastic gradient descent. In Proceedings of the 19th
GPUSolverwithChi-squareKernelsforSVMClassificationofBigSparseProblems
335

International Conference on Computational Statistics
COMPSTAT 2010, pages 177–187. Springer.
Cao, L. J., Keerthi, S. S., Ong, C. J., Zhang, J. Q., Periy-
athamby, U., Fu, X. J., and Lee, H. P. (2006). Paral-
lel sequential minimal optimization for the training of
support vector machines. IEEE Transactions on Neu-
ral Networks, 17(4):1039–1049.
Carpenter, A. (2009). Cusvm: A cuda implementation of
support vector classification and regression. Technical
report.
Catanzaro, B., Sundaram, N., and Keutzer, K. (2008). Fast
support vector machine training and classification on
graphics processors. In Proceedings of the 25th inter-
national conference on Machine learning, ICML ’08,
pages 104–111, New York, NY, USA. ACM.
Chang, C.-C. and Lin, C.-J. (2011). Libsvm: A library for
support vector machines. ACM Transactions on Intel-
ligent Systems and Technology, 2:27:1–27:27.
Chang, E. Y., Zhu, K., Wang, H., Bai, H., Li, J., Qiu, Z., and
Cui, H. (2007). Psvm: Parallelizing support vector
machines on distributed computers. In NIPS.
Chapelle, O., Haffner, P., and Vapnik, V. N. (1999). Support
vector machines for histogram-based image classifica-
tion. Neural Networks, IEEE Transactions on, pages
1055–1064.
Cortes, C. and Vapnik, V. (1995). Support-vector networks.
Mach. Learn., 20(3):273–297.
Cotter, A., Srebro, N., and Keshet, J. (2011). A gpu-tailored
approach for training kernelized svms. In Proceed-
ings of the 17th ACM SIGKDD conference, KDD ’11,
pages 805–813.
Fan, R.-E., Chen, P.-H., and Lin, C.-J. (2005). Working
set selection using the second order information for
training svm. JOURNAL OF MACHINE LEARNING
RESEARCH, 6:1889–1918.
Gorecki, P., Artiemjew, P., Drozda, P., and Sopyla, K.
(2012). Categorization of similar objects using bag
of visual words and support vector machines. In Fil-
ipe, J. and Fred, A. L. N., editors, ICAART (1), pages
231–236. SciTePress.
Graf, H. P., Cosatto, E., Bottou, L., Durdanovic, I., and Vap-
nik, V. (2005). Parallel support vector machines: The
cascade svm. In In Advances in Neural Information
Processing Systems, pages 521–528. MIT Press.
Harris, M. (2008). Optimizing Parallel Reduction in
CUDA. Technical report, nVidia.
Herrero-Lopez, S., Williams, J. R., and Sanchez, A. (2010).
Parallel multiclass classification using svms on gpus.
In Proceedings of the 3rd Workshop on General-
Purpose Computation on Graphics Processing Units,
GPGPU ’10, pages 2–11, New York, NY, USA. ACM.
Joachims, T. (1998). Text categorization with support vec-
tor machines: learning with many relevant features. In
N´edellec, C. and Rouveirol, C., editors, Proceedings
of ECML-98, 10th European Conference on Machine
Learning, number 1398, pages 137–142. Springer
Verlag, Heidelberg, DE.
Joachims, T. (1999). Advances in kernel methods. chap-
ter Making large-scale support vector machine learn-
ing practical, pages 169–184. MIT Press, Cambridge,
MA, USA.
Joachims, T., Finley, T., and Yu, C. J. (2009). Cutting-plane
training of structural svms. Mach. Learn., 77(1):27–
59.
Keerthi, S., Shevade, S., Bhattacharyya, C., and Murthy,
K. (2001). Improvements to platt’s smo algorithm
for svm classifier design. Neural Computation,
13(3):637–649.
Lazebnik, S., Schmid, C., and Ponce, J. (2006). Beyond
bags of features: Spatial pyramid matching for rec-
ognizing natural scene categories. In Proceedings
of the 2006 IEEE Computer Society Conference on
Computer Vision and Pattern Recognition - Volume 2,
CVPR ’06, pages 2169–2178, Washington, DC, USA.
IEEE Computer Society.
Lin, T.-K. and Chien, S.-Y. (2010). Support vector ma-
chines on gpu with sparse matrix format. Machine
Learning and Applications, Fourth International Con-
ference on, 0:313–318.
Platt, J. (1998). Fast training of support vector machines
using sequential minimal optimization. In Advances
in Kernel Methods - Support Vector Learning. MIT
Press.
Sopyla, K., Drozda, P., and Gorecki, P. (2012). Svm with
cuda accelerated kernels for big sparse problems. In
Proceedings of the ICAISC, volume 7267 of Lecture
Notes in Computer Science, pages 439–447. Springer.
Vapnik, V. N. (1995). The nature of statistical learning the-
ory. Springer-Verlag New York, Inc., New York, NY,
USA.
V´azquez, F., Garz´on, E. M., Martinez, J. A., and Fern´andez,
J. J. (2009). The sparse matrix vector product on gpus.
Technical report, University of Almeria.
Volkov, V. and Demmel, J. W. (2008). Benchmarking gpus
to tune dense linear algebra. In Proceedings of the
2008 ACM/IEEE conference on Supercomputing, SC
’08, pages 31:1–31:11, Piscataway, NJ, USA. IEEE
Press.
Zanni, L., Serafini, T., and Zanghirati, G. (2006). Parallel
software for training large scale support vector ma-
chines on multiprocessor systems. J. Mach. Learn.
Res., 7:1467–1492.
Zhao, H. X. and Magoules, F. (2011). Parallel support vec-
tor machines on multi-core and multiprocessor sys-
tems. In Proceedings of the 11th International Confer-
ence on Artificial Intelligence and Applications (AIA
2011).
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
336
