
Iterative Robust Registration Approach based on Feature Descriptors
Correspondence
Application to 3D Faces Description
Wieme Gadacha and Faouzi Ghorbel
Cristal lab.Grift research group, National School of Computer Science, La Mannouba, Tunisia
Keywords:
3D Rigid Registration, Hausdorff Distance in Shape Space, 3D Parametrisation, Matching, Face Description,
Shannon Theorem.
Abstract:
In this paper, we intend to introduce a fast surface registration process which is independent from the original
parameterization of the surface and invariant under 3D rigid transformations. It is based on a feature descrip-
tors correspondence. Such feature descriptors are extracted from the superposition of two surfacic curves:
geodesic levels and radial ones from local neighborhoods defined around reference points already picked on
the surface. A study of the optimal number of those curves thanks to a generalized version of Shannon the-
orem is developed. Thus, the obtained discretized parametrisation (ordered descriptors) is the basis of the
matching phase that becomes obvious and more robust comparing to the classic ICP algorithm. Experimen-
tations are conducted on facial surfaces from the Bosphorus database to test the registration of both rigid and
non-rigid shapes (neutral faces vs. faces with expressions). The Hausdorff distance in shape space is used as
an evaluation metric to test the robustness to tessellation. The discriminative power in face description is also
estimated.
1 INTRODUCTION
Global registration is a fundamental issue in shape ac-
quisition and shape modeling. The principle is as fol-
lows: given two shapes, the model and the data, the
goal is to find the optimal rigid transformation that
readjusts or registers the data to the model. Many re-
search works focused on this topic while it is applied
in several fields, essentially two key ones: the com-
bination of partial models of a same object in order
to obtain a numerical complete model and 3D shapes
recognition.
Several approaches have been proposed to solve the
problem of registration of two tridimensional shapes
(a cloud of points, triangulated surfaces, implicit or
parametric surfaces)(Fallavollita, 2009).
The most popular algorithm is the Iterative Closest
Point (ICP). Its principle consists on iteratively alter-
nating two steps: a matching step and a transforma-
tion estimation one.
Indeed, the matching phase necessitates finding
for each point p on a first surface, the ” best ” match-
ing point q on the second one. The second step is
an optimization of the rigid transformation that aligns
temporarily the data to the model. This process is it-
erated until a convergence criterion is reached.
The main limitation of ICP is that a local con-
vergence could not necessarily guaranty an optimal
global convergence. To overcome this limitation, the
registration process can be improved by the use of ge-
ometric descriptors. In fact, a local geometric descrip-
tor is a quantity defined for each point and based on
the shape of a local neighborhood around that point.
The idea is to suggest that the points whose de-
scriptors correspond, could potentially correspond.
Thus, the choice of those points is based on the com-
putation of a given geometric descriptor.
In fact, the description of 3D shapes remains an
open issue and many works have been proposed. The
three-dimensional surface description methods can be
classified into four major categories: the transform
based approaches, the 2D views, the graph ones and
those based on statistical features.
For the transform based approaches, after the con-
version of the surface onto 3D voxels or a spheri-
cal grid, specific transformations are applied. The
most known ones are 3D Fourier, the 3D Radon,
the rotation-invariant spherical harmonics (Dutagaci
et al., 2005).
In the two dimensional view based methods, a
337
Gadacha W. and Ghorbel F..
Iterative Robust Registration Approach based on Feature Descriptors Correspondence - Application to 3D Faces Description.
DOI: 10.5220/0004922903370342
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 337-342
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

collection of 2D projections from canonical view-
points is realized. Then, planar image descriptors are
computed as Zernike moments and Fourier descrip-
tors(Daoudi and Ghorbel, 1998).
The graph based approaches have the potential to
code geometrical and topological shape properties in
an intuitive manner. The usually used descriptors are
Reeb graphs and the skeletal ones (Tung and Schmitt,
2005).
We especially focus on the fourth class of methods
that are based on the extraction of numerical attributes
(local or global) of the 3D objects. We cite in particu-
lar, the works for the determination of high curvature,
the 3D moments, and the canonical 3D Hough trans-
form descriptor (Hallinan et al., 1999).
Authors in (Scovanner et al., 2007) have proposed
to generalize the SIFT algorithm, well known for 2D
images, to the 3D field.
Many works have introduced geometric descrip-
tors extracted from curves defined on 3D surfaces.
Several representations of curves were proposed in
the literature:
(Maalej et al., 2011) define levels of curves with
reference to a function distance taken to be the Eu-
clidean distance or the geodesic one.
(Samir et al., 2006) and (Mpiperis et al., 2007) de-
fined local coordinates by the exponential map around
a point belonging to the surface. This coordinate sys-
tem is obtained by wrapping a neighborhood of that
point by the polar coordinates of the tangent plane at
it.
Indeed, the registration algorithm accuracy
doesn’t only depend on the choice of points used but
remains also tributary to the number of those points.
The key idea is that only an optimal number of se-
lected points would ensure the effectiveness of the
registration process.
Contributions
In this paper, we present an iterative registration ap-
proach based on features correspondence using geo-
metric descriptors. The main contributions of the pro-
posed approach are as follows:
- The shape descriptor introduced is constructed to en-
sure invariance to small variations in shape and is rel-
atively isotropic towards the 3D motion group.
- The proposed process ensures more robustness in
the correspondence phase thanks to the identification
of particular feature points obviously correspondent.
- The number of points involved in the registration
process is fixed as result of an optimization sampling
technique.
- The proposed approach shows effective discrimina-
tion in face description.
Thus, this paper will be structured as follows: We
present in the second section the descriptor construc-
tion steps. In particular, its mathematic formulation
and its optimal resolution are explained. We show
in the next section the registration algorithm phases.
Then, the used similarity metric to compare shapes
(the Hausdorff distance in the shape space) is clarified
in section 4. In section 5, the experimentations results
are showed, particularly the robustness to sampling
and the applicability to face description are tested. In
the last section, a conclusion and some perspectives
of the work are envisaged.
2 CONSTRUCTION OF THE
DESCRIPTOR
This section is devoted to explain the extraction pro-
cedure of the local surface representation in order to
obtain the geometric descriptors.
2.1 Determination of Descriptor Points
Relatively to a given Reference Point
Let S be a differential manifold of dimension two and
r a reference point taken on the surface.
We denote a function U
r
: S → R to be a surface
distance function from r to any point p on the surface.
In fact, U
r
(p) is the length of the shortest geodesic
path joining r to p (Yin et al., 2006).
We define the level set of the geodesic curves
around r as the n level sets of the function U
r
(p) as
following:
ξ
λ
j
r
= {p ∈ S,U
r
(p) = λ
j
} ⊂ S (1)
such that λ
j
∈ [0, ∞)and1 ≤ j ≤ n
Now, we note the geodesic path C(t) as the solu-
tion of the system (Γ ) where ∇ is the gradient. This
curve is called radial line respectively to the angular
direction θ (Yin et al., 2006).
(Γ)
dC(t)
dt
= −∇U
r
(C)
C(0) = r
dC(t)
dt
|
t=0
= θ
(2)
Consequently, the set of these curves emanating from
the reference point r, respectively to an angular direc-
tion θ
1≤k≤m
are denoted by ξ
θ
k
r
. It is important to no-
tice that the reference angular direction (θ =0) could
be chosen arbitrary.
The superposition of both level sets of curves ξ
θ
k
r
and ξ
λ
j
r
constitutes a curvilinear local coordinate sys-
tem.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
338

Then, the intersections of the sets of radial lines
ξ
θ
k
r
and the geodesic level curves ξ
λ
j
r
define a set of
points relatively to a given reference point r that are
given by:
N
r
= {p
j,k
∈ ξ
λ
j
r
\
ξ
θ
k
r
1 ≤ j ≤ n, 1 ≤ k ≤ m} (3)
2.2 Determination of Descriptor Points
Relatively to Several Reference
Points
Let’s consider now several reference points
{r
i,1≤i≤n
r
} ∈ S and let denote by ξ
θ
r
i
and ξ
λ
r
i
their respective set of geodesic level curves and radial
lines with reference to each reference point r
i
.
The resulting set of local coordinates respectively
to each reference point r
i
is defined as follows:
N = {N
r
i
;1 ≤ i ≤ n
r
} (4)
– To be useful in registration process, a descriptor
should be invariant towards rigid transformations and
reflects the local geometry of the surface. Thus, the
obtained set of points is relatively isotropic towards
the 3D motion group. They are also parametric (and
thus ordered) because each point is indexed by the
level of geodesic curve and radial line it belongs to;
relatively to each reference point.
Moreover, the volume of points participating in
the registration process is of a paramount importance.
In fact: More the number of points involved in the reg-
istration process is bigger; more the consuming time
is greater. Thus, the issue is to guaranty that a mini-
mum number of points picked from the surface is suf-
ficient to ensure an optimal registration result.
The determination of that minimal number of points
is defined as follows.
2.3 Optimal Descriptor Points Number
The variation of both the number of geodesic curves
and the number of radial ones makes several resolu-
tions of the discretized representation.
The key idea now is to find the optimal number
of those curves that ensures a good description of the
given surface sufficiently precise.
So, we intend to propose a criterion that allows
fixing the optimal number of curves composing the
parametric system. That criterion consists in apply-
ing a generalized version of the Shanoon theorem to
the surface representation already developed (Daoudi
and Ghorbel, 1998). The principle is as follows:
Given a surface S that is a differential manifold of
dimension two and r
i
a reference point taken on S.
There exists necessarily a map (V
ri
, ϕ) where V
ri
is a
neighborhood of r
i
and ϕ is a α-diffeomorphism be-
tween a disk D of R
2
and V
ri
.
ϕ(u, v) = (x(u, v), y(u, v), z(u, v))
t
(5)
With (x, y, z) the three-dimensional components of
the extracted parametric points.
(u, v) the two-dimensional parametrization 0 ≤ u ≤ 1
and 0 ≤ v ≤ 1.
t means the transpose.
We denote by F
ϕ
the two-dimensional Fourier
Transform of each coordinate given by:
F
ϕ
(ϑ
u
, ϑ
v
) = (F
x
, F
y
, F
z
)(ϑ
u
, ϑ
v
) (6)
Where
F
x
(ϑ
u
, ϑ
v
) =
Z Z
D
x(u, v)e
−2iΠ(uϑ
u
+vϑ
v
)
dudv (7)
The spectrum of the map is obtained by calculating
the standard Fourier transform of ϕ:
kF
ϕ
(ϑ
u
, ϑ
v
)k =
q
(F
x
(ϑ
u
, ϑ
v
))
2
+ (F
y
(ϑ
u
, ϑ
v
))
2
+ (F
z
(ϑ
u
, ϑ
v
))
2
(8)
We propose to apply the Shannon theorem to the
local parametrisation ϕ in order to fix the frequencies
ϑ
0
u
and ϑ
0
v
so that:
supp{F
ϕ
(ϑ
u
, ϑ
v
) ⊆ [−ϑ
0
u
, ϑ
0
u
] × [−ϑ
0
v
, ϑ
0
v
]} (9)
Where supp(g) is the support of the function g. So,
with this way and thanks to Shanoon theorem, we fix
the optimal number of geodesic level curves and ra-
dial lines and therefore the optimal number of points
extracted from the intersection of those curves.
–So, with this way and thanks to an optimiza-
tion sampling process based on the Shannon theorem,
we fix the optimal number of geodesic level curves
and radial lines and therefore the optimal number of
points extracted from the intersection of curves. Only
this optimal number of points will participate in the
registration process. The feature points extraction
procedure is summarized in figure 1.
3 REGISTRATION ALGORITHM
Here, we will illustrate the matching algorithm proce-
dure.
3.1 Generation of Homologous Points
Pairs
Only the parametric points extracted respectively
from the model shape and the data shape, are involved
IterativeRobustRegistrationApproachbasedonFeatureDescriptorsCorrespondence-Applicationto3DFaces
Description
339
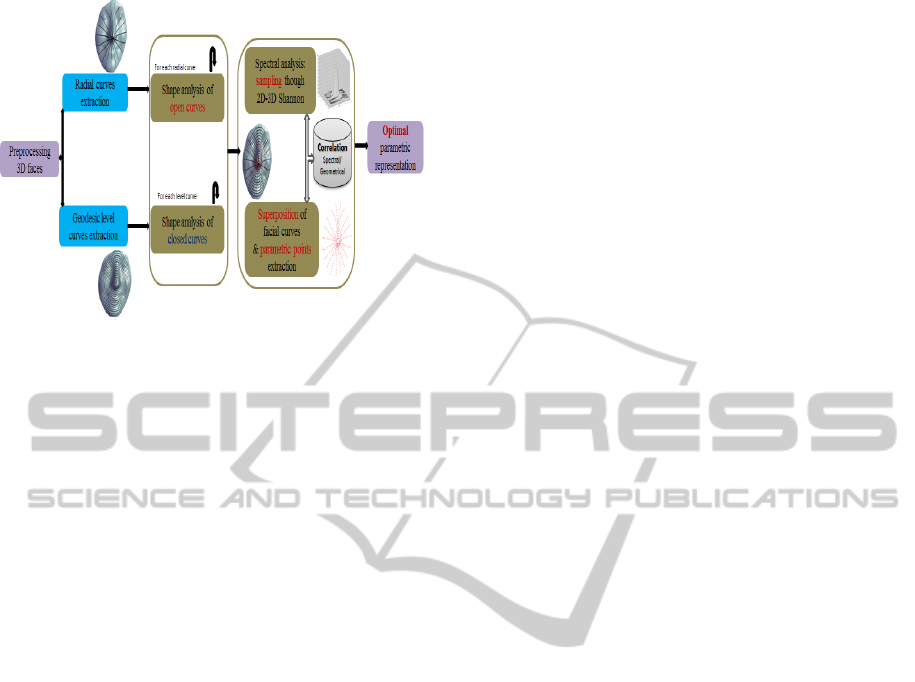
Figure 1: Optimal parametric points extraction.
in the registration procedure and thus in the matching
phase. Those selected feature points are chosen such
a way to make the correspondence phase easier and
robust. In fact, each point is indexed by the geodesic
curve and the radial line owned to. Thus, a pair of
corresponding points is those belonging to the same
level of radial line and geodesic curve respectively to
the test and the reference surface.
3.2 Iterative Transformation Estimation
We notice that an initialization step is realized by the
computation of the inertia matrix in order to globally
readjust the two surfaces (this makes the surfaces in
frontal position).
Then, the correspondence pairs of points are used
to estimate temporarily the rigid transformation (rota-
tion and translation) existing between the two shapes.
The rotation is estimated thanks to the SVD technique
and the translation is estimated between gravity points
positions.
Such process is iterated until a convergence crite-
rion is reached.
–That fine registration of two 3D shapes is based
on several iterative local registrations around the
given reference points.
This technique allows the registration of two ob-
jects with non-rigid transformations thanks to several
rigid local registration processes around small neigh-
borhoods.
4 SIMILARITY METRIC
It is important to define the used similarity metric to
compare between different shapes. The well known
Hausdorff shape distance introduced by Ghorbel
in (Ghorbel, 1998) is chosen. Following the same
process, we denote by G the group representing all
possible normalized parametrisations of surfaces
which can be the real plane R
2
or the unit sphere S
2
.
We consider the space of all surface pieces as the set
of all 3D objects assumed diffeomorphic to G which
can be assimilated to a subspace of L
2
R
3
(G) formed by
all square integrated maps from G to R
3
. The direct
product of the Euler rotations group SO(3) by the
group G , acts on such space in the following sense:
SO(3) × G × L
2
R
3
(G) → L
2
R
3
(G) (10)
{A, (u
0
, v
0
), S(u, v)} → AS(u + u
0
, v+v
0
)
The 3D Hausdorff distance ∆ can be written for
every S
1
and S
2
belonging to L
2
R
3
(G) and g
1
and g
2
to
SO(3) as follows:
∆(S
1
, S
2
) = max(ρ(S
1
, S
2
), ρ(S
2
, S
1
)) (11)
Where:
ρ(S
1
, S
2
) = sup
g
1
∈SO(3)
in f
g
2
∈SO(3)
k g
1
S
1
− g
2
S
2
k
L
2
(12)
k S k
L
2
denotes the norm of the functional banach
space L
2
R
3
(G).
Due to the fact that the euclidean rotations preserve
this norm, it is easy to show that this distance is re-
duced to the following quantity:
∆(S
1
, S
2
) = inf
h∈SO(3)
k S
1
− hS
2
k
L
2
(13)
After that, we consider a normalized version of ∆ so
that the variations of this normalized distance are con-
fined to the interval [0,1].
5 EXPERIMENTAL RESULTS
This section presents experiments used to investigate
the following questions:
- How robust is the descriptor with respect to point
sampling?
- How well does the algorithm discriminate the human
faces?
5.1 Robustness to Sampling
In this section, we aim to test the robustness of the
descriptor by evaluating how efficient those features
points extracted from discrete points sampling con-
verges to those picked from the surface.
Because the number of points (as proved in sec-
tion 2.3) is so important in the registration algorithm
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
340
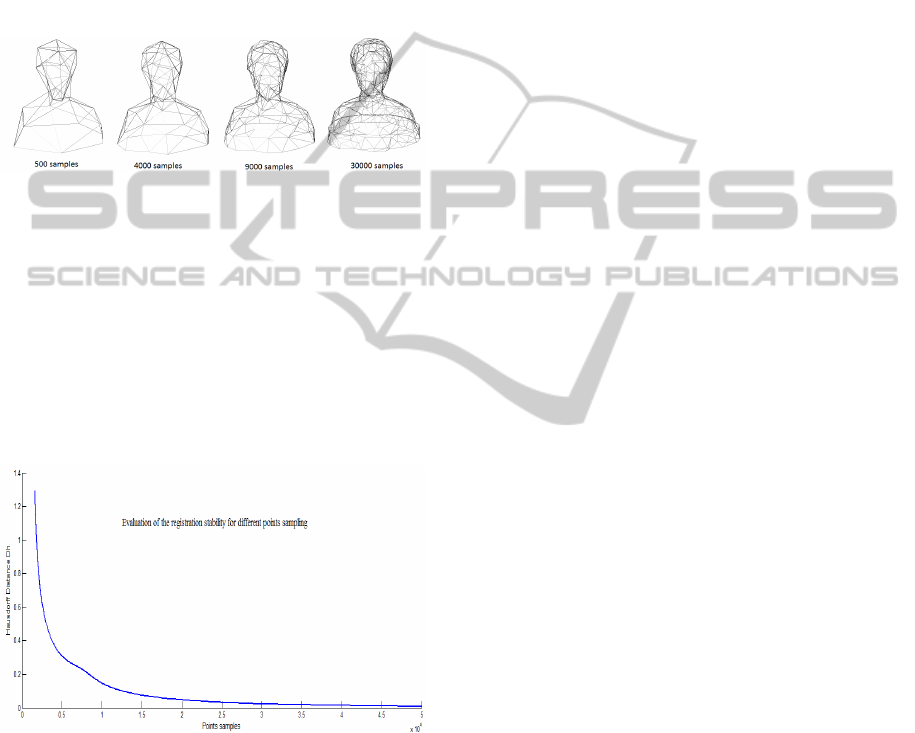
and also to evaluate our proposal to fix the optimal
number of descriptor points thanks to the Shannon
theorem. The experimental protocol is as follows:
For a given model S, we generate a set of points
S
N
consisting of N randomly placed samples on the
surface S (the same process as described in (Osada
et al., 2001)). We compute then the Hausdorff dis-
tance in the Shape space (as described in section 4)
between the features points of S and those of S
N
. Fig-
ure 2 visualizes the distance values for Laurana model
for different resolutions of sampling points.
Figure 2: Several samples of Laurana model.
Figure 3 shows the results of the experiments for
the Hausdorff distance where the values of N vary
from 100 to 10
4
. We notice that even when using the
set of samples that is not bigger, the descriptor ob-
tained from the points set approximates well the one
computed on the surface. The robustness of the de-
scriptor to point sampling indicates that it can be used
even when the initial input of the model is a sampling
set of points from the surface (for example for data
obtained by scanning).
Figure 3: Robustness to sampling.
5.2 Application to 3D Face Description
The experimentations were conducted on facial sur-
faces from the Bosphorus database (Savran et al.,
2008). We have used a collection of faces belonging
to two classes. A first class contains faces of the same
person with different expressions (fear, sadness, hap-
piness, surprise and disgust) in addition to the neutral
expression. And, the second class represents faces of
different persons.
Indeed, the construction of the parametric repre-
sentation supposes that the surface is a two dimen-
sional differential manifold. Although, in numeri-
cal three-dimensional imaging field, the most com-
mon surface representation is the 3D triangular mesh.
Moreover, the reference points are chosen as land-
marks taken on the facial surface. An MPEG4 specifi-
cation of 83 facial feature points that reflect key posi-
tions on human faces has been presented in (Yin et al.,
2006).
So, we have calculated the parametric representa-
tion respectively to reference points taken to be the
two inner and outer corners of the eyes, the tip nose
and the two centers of the cheek (calculated as the
middle of the geodesic path between the tip nose and
the outer corner of the eye). Then, the whole registra-
tion process was computed using a subset of models
respectively from the gallery and the test dataset; the
same process as in (Gadacha and Ghorbel, 2013).
–Complexity and Computation time
The complexity of the matching phase is of O(n) order
where n is the number of points involved in the pro-
cess. The complexity of the same step in the classic
well-known Iterative Closest Point algorithm (ICP) is
of O(N
2
) order where N is the number of points on the
surface (N >>n). Thanks to the calculation accuracy,
the algorithm is less costly in time consuming.
In order to evaluate the accuracy and effectiveness
of the proposed approach, the Hausdorff distance in
shape space is used as an evaluation metric. The pair-
wise normalized distances between ten faces is com-
puted (figure 4): only are involved the parametric
features points. The first class belongs to the same
person while the others correspond to different indi-
viduals. In this display, the distances have been scaled
to values between 0 and 1.
As expected, the matrix shows that the distances
between the faces of the same person are smaller than
the ones respectively to different individuals. This
proves that our parametric representation has a good
discriminative power allowing applications of facial
recognition.
6 CONCLUSIONS
In this work, we have focused on 3D rigid registra-
tion issue. We have presented a global registration ap-
proach that aligns two three-dimensional shapes. The
proposed registration approach is based on many it-
erative registration processes operated on local neigh-
borhood around given interest points already taken on
the surface. The approach has proved its efficiency
in comparison to the most popular algorithm (the ICP
IterativeRobustRegistrationApproachbasedonFeatureDescriptorsCorrespondence-Applicationto3DFaces
Description
341

Figure 4: Matrix of pairwise normalized shape distance be-
tween facial surfaces. The first class of faces belongs to the
same person while the others correspond to different indi-
viduals.
one) thanks to the robustness of the matching phase.
Indeed, the features points extracted present several
desirable properties such as parametrizations over a
canonical domain, stability and invariance to scale
and 3D motion group. They are also ordered. This
makes the correspondence step useless for registra-
tion application. Moreover, the neighborhood reso-
lution (number of geodesic level curves and radial
lines around a given interest point) affects the accu-
racy and quality of the matching results. Therefore, a
study on the optimal resolution of the curves has been
fixed thanks to a generalized version of the Shannon
theorem. Thus, the relationship between the size of
the features and the performance registration has been
studied. Because the features points properties are ro-
bust towards tessellation, an application in 3D imag-
ing field especially 3d face description has been cho-
sen. A good discriminative power in face description
has been noticed over experimentation on 3D facial
database. This works suggests a number of questions
to be addressed in future research such that adopting
database with several class of objects to be applied in
other fields (medical imaging, indexing, etc).
REFERENCES
Daoudi, M. and Ghorbel, F. (1998). Shape distances for
contour tracking and motion estimation. In Pattern
Recognition.
Dutagaci, H., Sankur, B., and Yemez, Y. (2005). Transform-
based methods for indexing and retrieval of 3d objects.
In Fifth international conference 3D digital imaging
and modeling.
Fallavollita, P. (2009). 3d/2d registration of mapping
catheter images for rhythmia interventional assis-
tance. In International Journal of Computer Sciences
Issues,4.
Gadacha, W. and Ghorbel, F. (2013). A stable and accu-
rate multi-reference representation for surfaces of r
3
:
Application to 3d faces description. In 10 IEEE Inter-
national Conference on Automatic face and Gesture
Recognition.
Ghorbel, F. (1998). Towards a unitary formulation for in-
variant image description: application to image cod-
ing. In Annales des telecommunications, 53 (5-6).
Hallinan, P., Gordon, G., Yuille, A., Giblin, P., and Mun-
ford, D. (1999). Two and three dimensional patterns
of face. In A.K.Peters.
Maalej, A., BenAmor, B., Daoudi, M., Srivastava, A., and
Berretti, S. (2011). Shape analysis of local facial
patches for 3d facial expression recognition. In Pat-
tern Recognition 44 (8).
Mpiperis, I., Malassiotis, S., and Strintzis, M. (2007). 3d
face recognition with the geodesic polar representa-
tion. In IEEE Trans. on Information Forensics and
Security 3 (2).
Osada, R., Funkhouser, T., Chazelle, B., and Dobkin, D.
(2001). Matching 3d models with shape distributions.
In Shape Matching International. IEEE Computer So-
ciety Press.
Samir, C., Srivastava, A., and Daoudi, M. (2006). Three-
dimensional face recognition using shapes of facial
curves. In IEEE Trans. on Pattern Analysis and Ma-
chine Intelligence, vol. 28.
Savran, A., Alyz, N., Dibeklioglu, H., eliktutan, O., Gk-
berk, B., Sankur, B., and Akarun, L. (2008). Bospho-
rus database for 3d face analysis. In The First COST
2101 Workshop on Biometrics and Identity Manage-
ment.
Scovanner, P., Ali, S., and Shah, M. (2007). A 3-
dimensional sift descriptor and its application to ac-
tion recognition. In 15th international conference on
multimedia.
Tung, T. and Schmitt, F. (2005). The augmented multireso-
lution reeb graph approach for content-based retrieval
of 3d shapes. In Int J Shape Model 11(1).
Yin, L., Wei, X., Sun, Y., Wang, J., and Rosato, M. (2006).
A 3d facial expression database for facial behavior re-
search. In 7th IEEE International Conference on Au-
tomatic face and gesture recognition.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
342
